2. 中国海洋大学 工程学院,山东 青岛 266000
2. Ocean University of China, College of Engineering, Qingdao 266000, China
为满足经济的快速发展和面向海洋主权管控能力提升的重大需求,船舶的大型化、专业化成为趋势,我国港口工程建设也不断走向深海和远海,导致船舶在码头停泊或系泊作业时面临更加严峻的水流条件。因此,有必要对复杂水流条件下的系泊船水动力特性进行研究。
Zhang等[1]试验测量了不同方向水流作用下,模型船所受顺流和与水流垂直方向的作用力,并与经验公式进行了对比。张怀新等[2]基于N-S方程,研究了船体的横摇阻尼问题,数值模拟了船体二维横剖面在横摇时的粘性流场,发现横摇阻尼中的压力成分大于剪切应力成分。邹志利等[3]讨论了不同水位和不同风浪流夹角对系缆力和碰撞力的影响。Xiang等[4]通过求解系泊方程研究了波浪、水流、风等外荷载对系泊缆绳张力的影响,并利用试验结果对计算结果进行了验证。Varyami等[5]考虑船舶航行所产生的波浪和水流对系泊船的影响,并与已有的试验与理论结果进行了对比。胡毅等[6]应用多体水动力学软件AQWA,研究了在风、浪、流联合载荷作用下大型LNG船码头系泊时的运动响应,得到了LNG船码头系泊时的运动响应和系缆绳所受拉力。嵇春艳等[7]利用水动力软件AQWA研究了不同浪向角对码头系泊船舶运动响应幅值算子和一阶波激力的影响,并对系泊系统进行了优化。李焱等[8]开展了不同流速和流向角条件下系泊船的物理模型试验,得到典型工况下船舶系泊安全的水流强度限制值。
现有研究工作主要考虑了特定系缆时几种常见流态下船舶的系缆力和运动响应,然而,深水码头面临的水流环境更加复杂,船舶的最佳系缆方式取决于水流对船舶的作用力。在复杂水流环境下,常规系缆方式可能无法保证船舶的泊稳安全。因此,对复杂流环境下系泊船水动力特性进行研究就显得十分重要。在定常流作用下(不考虑波浪),系泊船的最终姿态会保持稳定,因此可以用固定船近似替代系泊船。这种方法不仅简化了模型,还可以更好地探讨复杂水流下船舶水动力的变化规律。
本文利用双精度的STAR-CCM+求解器,采用VOF方法捕捉自由液面,应用SIMPLE算法对压力和速度耦合,通过求解RANS方程和Realizable k-ε湍流模型,并结合重叠网格方法,对不同流速(傅汝德数)、不同流向角度以及流向沿水深变化条件下KCS船模绕流场进行瞬态数值模拟,探讨复杂水流条件下系泊船纵向力、横向力、首摇力矩的变化规律,对复杂流态下系泊船进行基础的研究。
1 数值模拟方法 1.1 研究对象及工况选取3 600 TEU集装箱船KCS(KRISO container ship)模型为研究对象。与该船有关的水动力试验结果可参考Tokyo 2015[9]等会议资料。表1给出了KCS船的主尺度要素,模型的缩比尺为31.5994。
|
|
表 1 KCS船主尺度要素 Tab.1 Main parameters of KCS ship |

|
图 1 KCS船模型图 Fig. 1 KCS ship model diagram |
具体工况设置如表2所示,水流流速的变化范围为Fr=0.036~0.237,水流流向角度β的变化范围为与船舶纵轴顺时针夹角0° ~ 90°的范围。复杂流态条件为水流流向沿船舶吃水深度从0°方向转变到90°方向以及从90°方向转变到0°方向。
|
|
表 2 工况设置 Tab.2 Case setting |
探讨复杂水流条件下系泊船纵向受力、横向受力以及首摇力矩的变化规律,各物理量的无量纲表达式如下:
| $ {C_x} = \frac{{{F_x}}}{{0.5\rho {U^2}A}} {\text,}$ | (1) |
| $ {C_y} = \frac{{{F_y}}}{{0.5\rho {U^2}A}}{\text,} $ | (2) |
| $ {C_N} = \frac{N}{{0.5\rho {U^2}A{L_{pp}}}}{\text。} $ | (3) |
式中:
图2为计算域示意图。根据ITTC关于船舶CFD应用的指南[10],计算域尺寸设置为:入口距船首1.5 Lpp,出口距船尾2.5 Lpp,左右边界距船中心线2.5 Lpp,顶部据自由面1.5 Lpp,底部距自由面2.5 Lpp。边界条件设置如下:右侧、后侧及上下侧为速度进口边界,左侧和前侧为压力出口边界,船模表面为无滑移壁面。

|
图 2 计算域及边界条件 Fig. 2 Computational domain and boundary conditions |
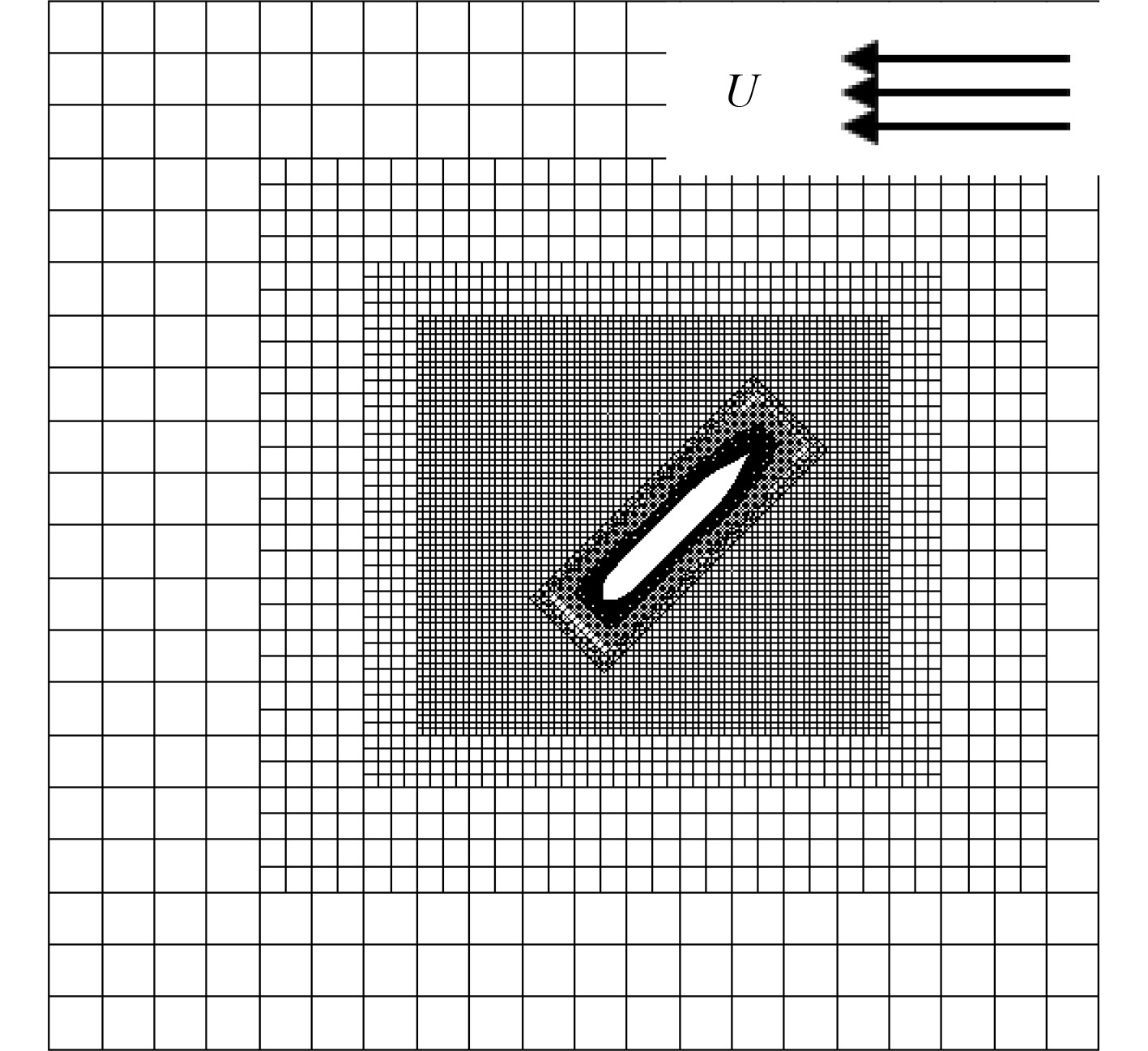
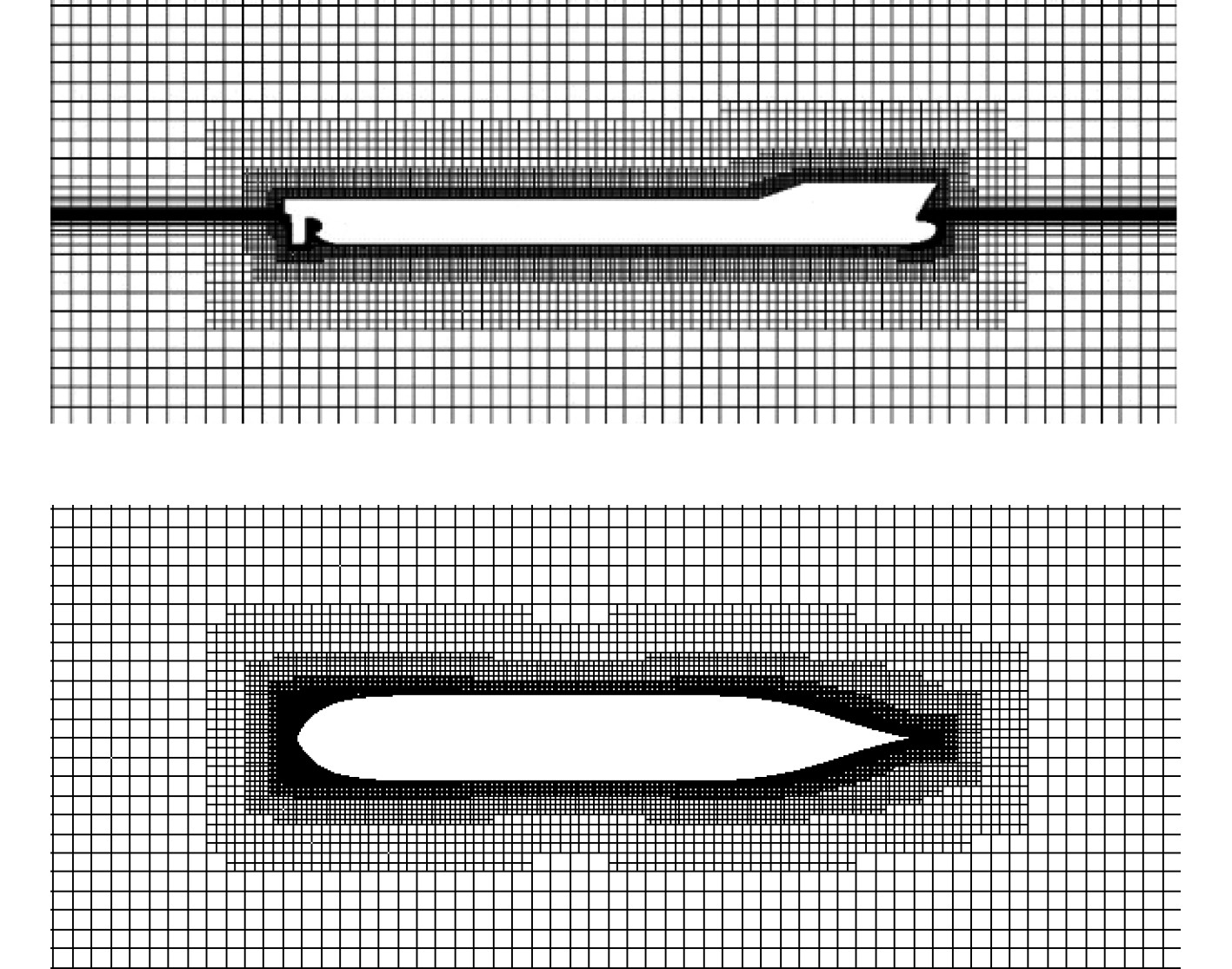
应用切割体网格技术对计算域进行离散。切割体网格技术同时包含了非结构网格和结构网格的优点,便于对自由面进行各向异性加密。利用重叠网格方法改变船舶姿态来实现流向的变化。重叠网格用于对一个计算区域进行任意重叠的几个不同网格的离散,适用于处理多个或移动的物体问题以及优化研究,能在改变船体姿态后不必对网格重新设置,如图3所示。为保证计算的准确性,对自由液面和近壁处的网格进行了加密(见图4)。船体表面的平均Y+值约为60,满足壁面函数对近壁面第一层网格高度的要求。
|
图 3 z = 0 m,β = 45°时网格示意图 Fig. 3 Mesh when z = 0 m,β = 45° |
|
图 4 船体周围及自由面网格加密示意图 Fig. 4 Mesh refinement around hull and free surface |
对于雷诺平均后的不可压缩粘性流问题,采用的连续性方程和动量方程如下:
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \left( {\rho {u_i}} \right)}}{{\partial {x_i}}} = 0{\text,}\quad {i = 1,2,3} {\text,}$ | (4) |
| $\begin{split} \rho \frac{{\partial {u_i}}}{{\partial t}} + \rho {u_j}\frac{{\partial {u_i}}}{{\partial {x_j}}} =& - \frac{{\partial p}}{{\partial {x_j}}} + \frac{\partial }{{\partial {x_j}}}\left( {\mu \frac{{\partial {u_i}}}{{\partial {x_j}}} - \rho \overline {u_i'u_j'} } \right){\text,}\\ & {i,j = 1,2,3} {\text。} \end{split}$ | (5) |
式中:
以工况为Fr = 0.237,β = 90°下的系泊船为例,设计3套不同精细程度的网格。相邻密度网格间的基础尺寸比为
|
|
表 3 网格无关性分析结果 Tab.3 Mesh independence analysis results |
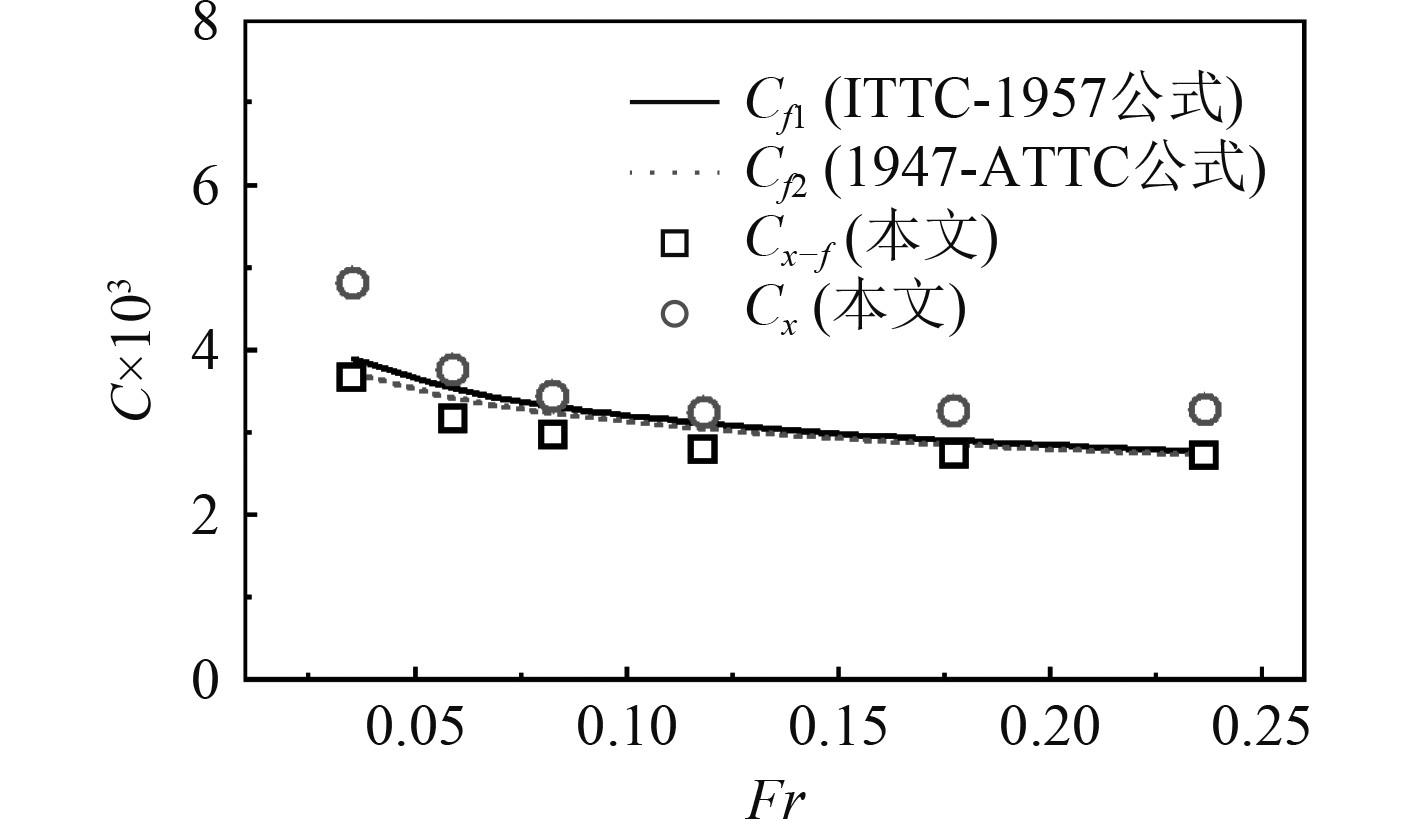
将流向角度β= 0°、不同傅汝德数Fr条件下船舶所受纵向力系数及其摩擦分量系数与平板摩擦阻力经验公式对比分析,平板摩擦阻力经验公式采用ITTC-1957公式[11]和1947-ATTC公式[12]。
| $ \quad {C_{f1}} = \frac{{0.075}}{{{{(\lg {Re} - 2)}^2}}}{\text,}\quad {\text{ITTC}} - 1957{\text,} $ | (6) |
| $ \frac{{0.242}}{{\sqrt {{C_{f2}}} }} = \lg ({Re} - {C_{f2}}){\text,}\quad 1947 - {\text{ATTC}}{\text。} $ | (7) |
其中:
由图5可知,船舶纵向力系数Cx及其摩擦分量系数Cx-f与传统经验公式的计算结果Cf1,Cf2随着Fr变化的趋势基本一致。不同傅汝德数Fr下Cx都要大于Cf1,Cf2,因为Cx中还包含了船舶纵向力压差分量。整体来看,数值结果与经验公式能够较好的吻合(最大误差不超过10%),本文所采用的数值模型能够较好地对系泊船的粘性流场进行预报。
|
图 5 船舶纵向受力系数及其摩擦分量系数与经验公式对比 Fig. 5 Comparison of ship longitudinal force coefficient and friction component coefficient with empirical formula |
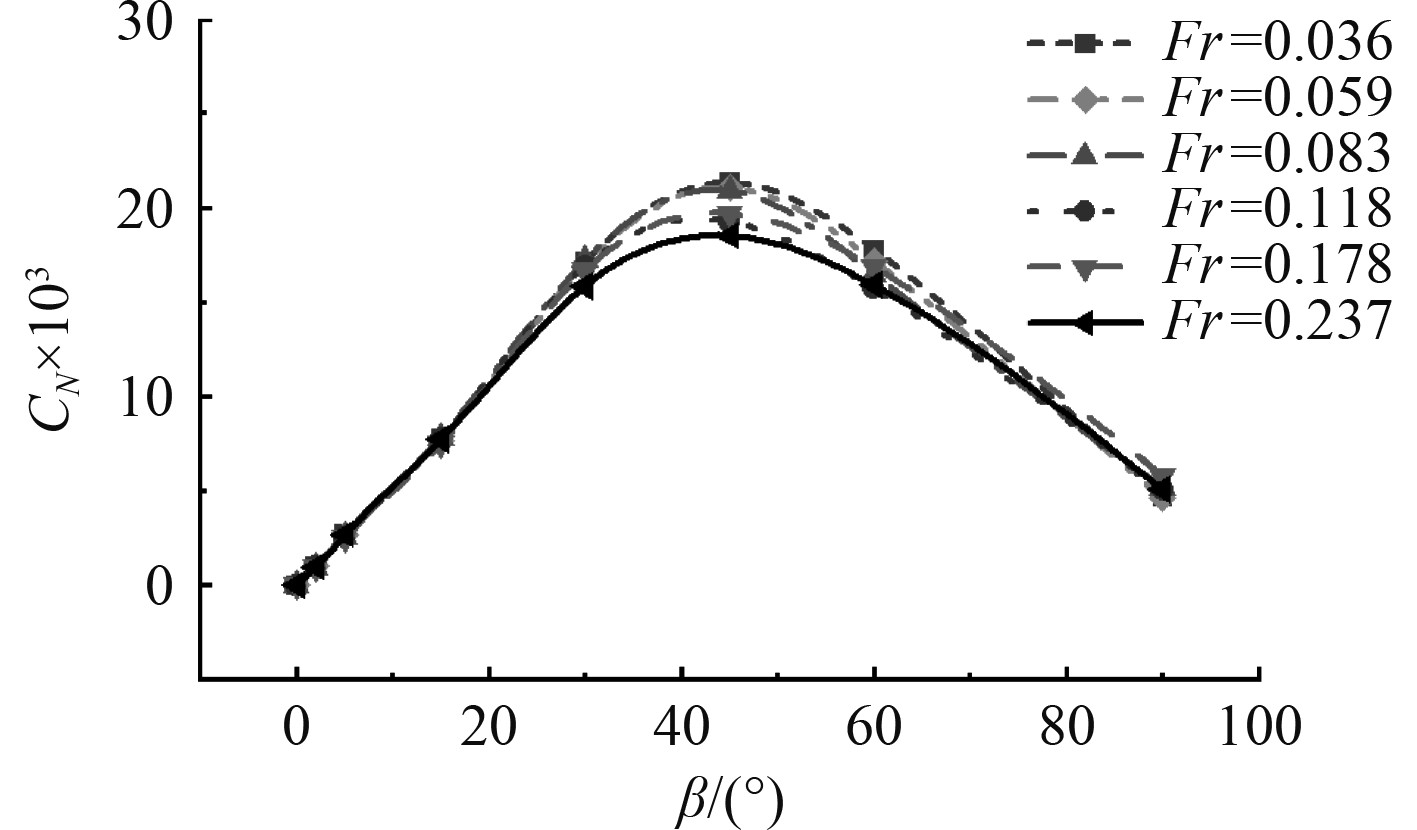
图6给出了不同傅汝德数Fr下船舶首摇力矩系数CN随流向角度β变化的曲线。总体来看,系泊船所受首摇力矩系数CN呈现为关于β = 45°对称的趋势,在β = 0° ~ 45°范围内,CN随着β的增大逐渐增大,在β= 45°时达到最大值;在β= 45° ~ 90°的范围内,CN随着β的增大而逐渐减小;在流向角度β = 90°时,船体受力点在船体中心位置,使得CN较小。
|
图 6 不同傅汝德数下船舶首摇力矩系数随流向角度的变化 Fig. 6 Variation of ship yaw moment coefficient with flow direction angle under different Froude numbers |
图7给出了不同傅汝德数Fr下船舶横向受力系数Cy随流向角度β变化的曲线。随着β的增加,Cy逐渐增大,在β = 90°时达到最大值。其中,由船体两侧水流压差引起的横向力压差分量为主导部分,而因流体粘性引起的横向力摩擦分量较小,其影响可以忽略。
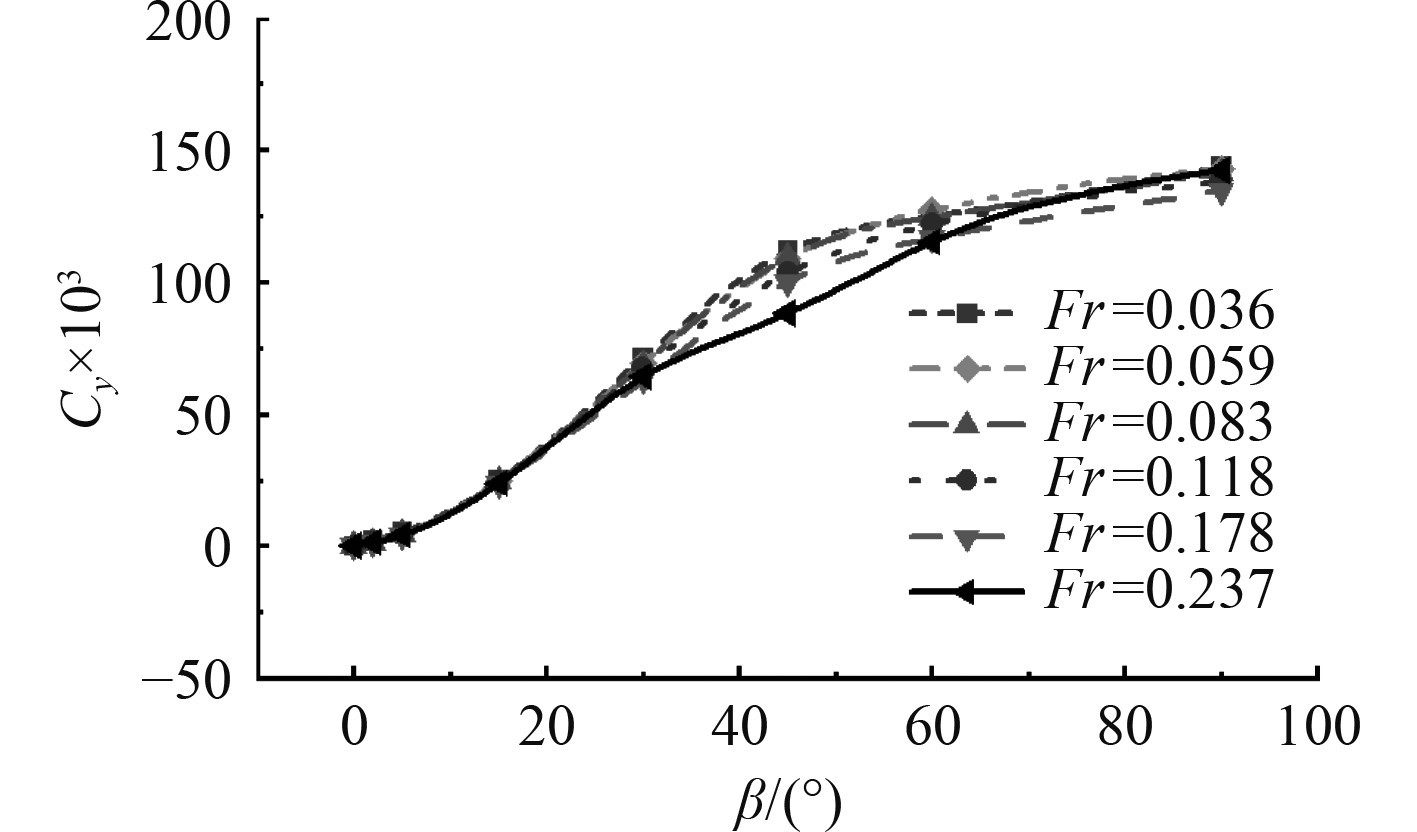
|
图 7 不同傅汝德数下船舶横向力系数随流向角度变化 Fig. 7 Variation of ship lateral force coefficient with flow direction angle under different Froude numbers |
图8给出了不同傅汝德数Fr下船舶纵向力系数Cx随流向角度β变化的曲线。图中船舶纵向力系数Cx变化较为复杂,整体随着Fr增加而下降,但在Fr较大时,Cx在β = 45°时会有一个极大值,此时船体周围水流分离现象明显,使得船体沿流向两侧水流压差变化较大,流速越大效果越明显,这也是导致纵向力趋势变化复杂的原因。
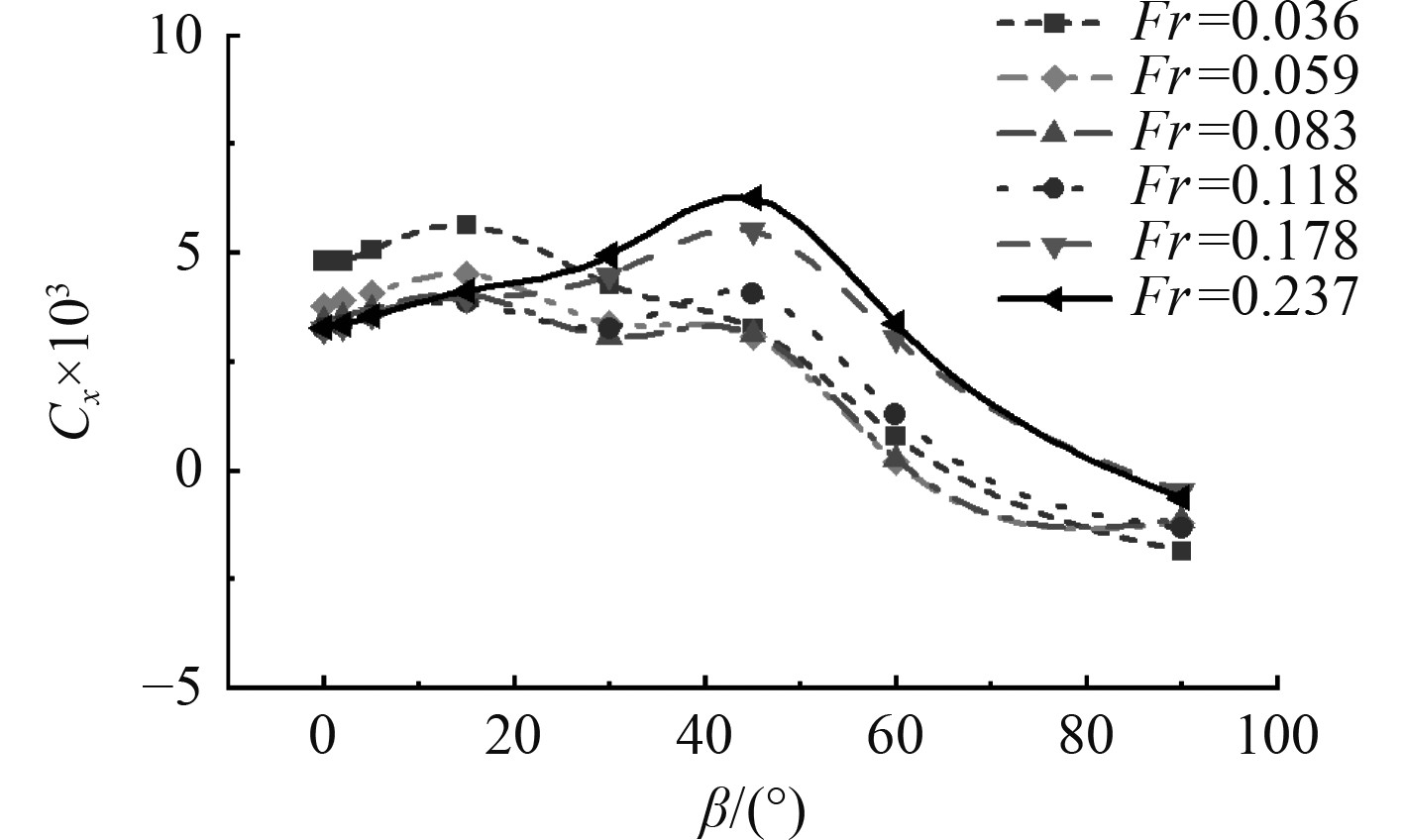
|
图 8 不同傅汝德数下船舶纵向力系数随流向角度变化 Fig. 8 Variation of ship longitudinal force coefficient with flow direction angle under different Froude numbers |
图9给出了不同流向角度β下船舶首摇力矩系数CN随傅汝德数Fr变化的曲线。β相同时,CN随Fr的增大变化不大,整体呈现水平的趋势,在β = 45°时最大。当β = 30°和β = 60°时,船体姿态相似,CN在数值上相差不大,2条曲线也几乎重合。图10中不同流向角度β下船舶横向力系数Cx随傅汝德数Fr变化的趋势基本相同。随着Fr的逐渐增加,Cx基本处于稳定的范围内,不同β之间的差异体现在Cx值的大小上面。β逐渐增大,横向力逐渐转变为船舶主要受力,在β = 30°之后现象就十分明显。
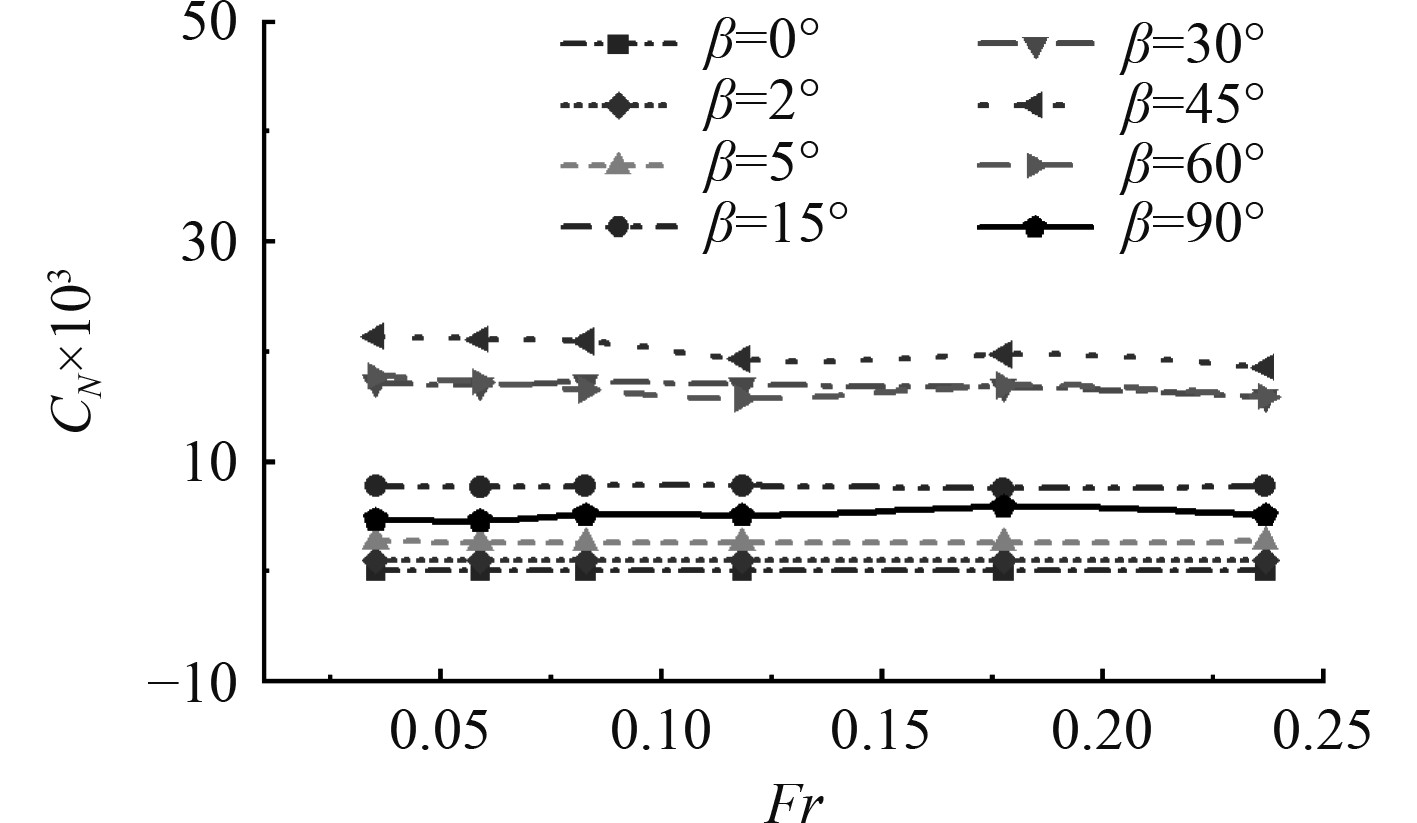
|
图 9 不同流向角度下船舶首摇力矩系数随傅汝德数的变化 Fig. 9 Variation of ship yaw moment coefficient with Froude number under different flow direction angles |
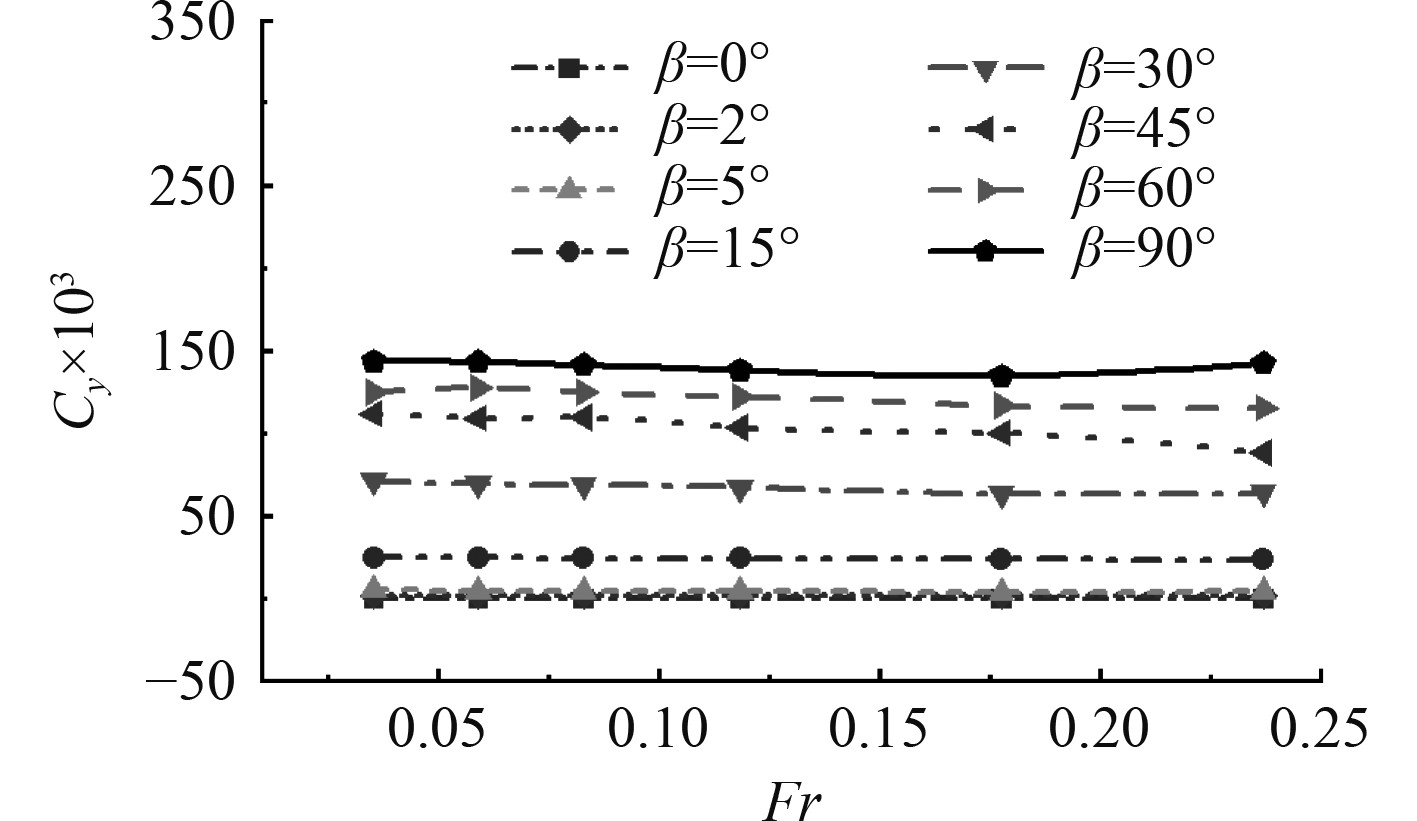
|
图 10 不同流向角度下船舶横向力系数随傅汝德数的变化 Fig. 10 Variation of ship lateral force coefficient with Froude number under different flow direction angles |
图11给出了不同流向角度β下船体纵向力系数Cy随傅汝德数Fr变化的曲线。在β较小时,Cy随Fr的增加呈现缓慢下降然后逐渐平缓的趋势;在β较大时,Cy随Fr的增加先减小然后逐渐增大。原因在于随着β的变化,船体逐渐受侧向来流的作用。小角度时纵向力主要以粘性力为主,大角度时船体周围流体分离现象愈发明显,压差力变化剧烈,使得纵向力以压差力为主,流速越大,纵向力也随之增大。
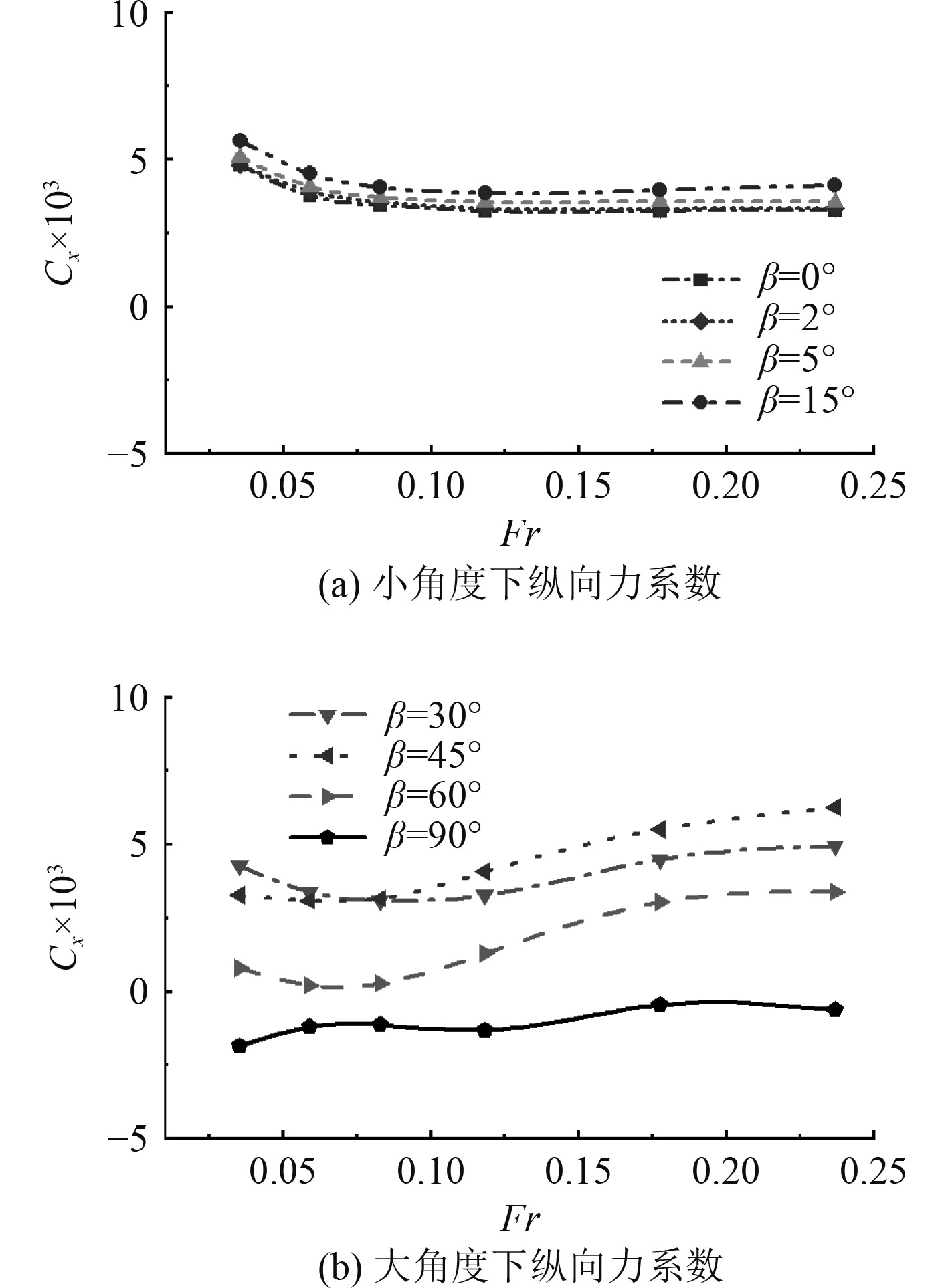
|
图 11 不同流向角度下船舶纵向力系数随傅汝德数的变化 Fig. 11 Variation of ship longitudinal force coefficient with Froude number under different flow direction angles |
图12给出了复杂流态下(流向角度β沿吃水由0°变化为90°以及由90°变化为0°)的船舶水动力系数的变化曲线。分别选取β = 15°,β = 30°,β = 40°,β = 60°和β = 90°工况下的水动力系数进行对比分析
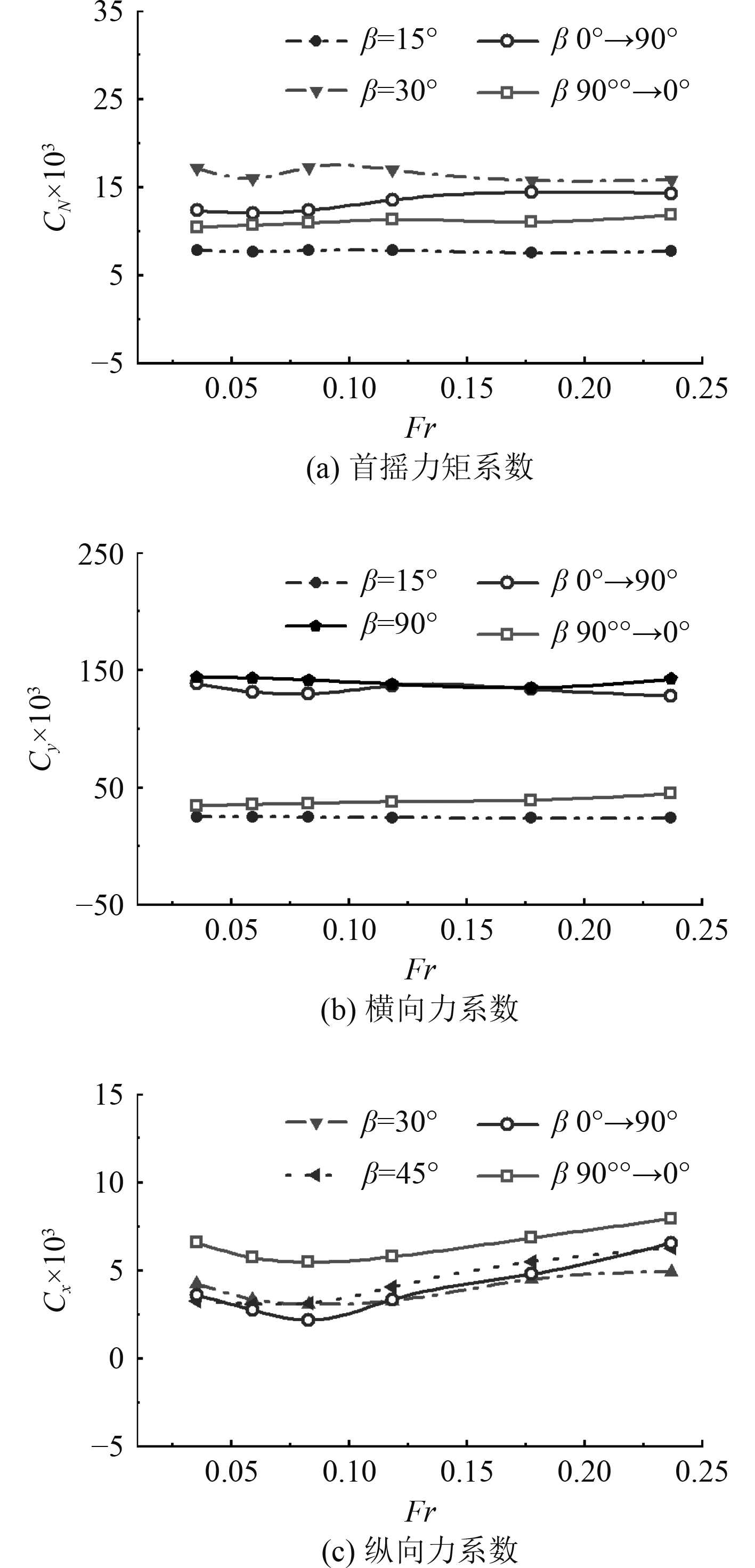
|
图 12 复杂流态下船舶水动力系数变化 Fig. 12 Variation of ship hydrodynamic coefficient under complex flow |
从整体上来看,2种复杂流态下船舶水动力系数随Fr的变化趋势与其他流向角度变化趋势基本一致。
二者在船舶首摇力矩系数CN以及纵向力系数Cx在数值上相差不大(见图12(a));横向力系数Cx着在β沿吃水由0°变化为90°工况下要比β沿吃水由90°变化为0°工况下大得多(见图12(b)),说明前者工况下来流对船舶侧面的作用更大;纵向力系数Cy在Fr范围内2种复杂流态工况下都呈现先下降后上升的趋势(见图12(c)),Fr较大时船体周围流动分离现象明显,纵向力的压差分量增大,使得纵向力系数上升。
另外,图12(b)和图12(c)显示,β从0°变化为90°工况下,船舶横向力系数Cy与β = 90°时以及船舶横向力系数Cx与β = 45°时变化曲线十分接近,而β从90°变化为0°工况下,船舶船舶横向力系数Cy与β = 15°时较为接近。上述现象说明,在本文所设定的复杂流态工况下,船舶水动力系数随傅汝德数变化的情况会与某一流向角度工况类似,船舶受到相似的水流作用力。
4 结 语本文应用计算流体力学理论,通过CFD软件STAR-CCM+建立了复杂流态下系泊船的粘性流场,对不同流速(傅汝德数)、不同流向角度以及流速和流向沿水深变化条件下KCS船舶绕流场进行了瞬态数值模拟,得到了复杂水流条件下系泊船纵向力、横向力、首摇力矩的变化规律,主要结论如下:
1)对于水流不同流向角度工况,系泊船所受首摇力矩系数在β = 45°时达到最大值,横向力系数随着流向角度的增大而逐渐增大,纵向力系数的变化规律较为复杂。
2)对于水流不同流速工况,系泊船的水动力特性系数变化不明显,首摇力矩系数和横向力系数随着流速的增大变化趋势较为平缓;纵向力系数在较小流向角度时随流速增加先减小后逐渐平缓,在流向角度较大时,纵向力系数随着流速的增加先减小后增大。
3)对于复杂流态,水流流向沿船舶吃水由0°变化到90°时,水流对船体侧面作用较为明显,船体横向受力系数远大于纵向受力系数,在实际工程中应当注意;水流流向沿船舶吃水由0°变化到90°时,水流对船体侧面作用较弱,体现在船舶横向力系数远小于前者工况。
4)对于本文所设定的复杂流态工况,船舶水动力系数会与某一流向角度工况相似。因此在类似的实际工程中,可以参照相似的流向角度进行参考和设计。
| [1] |
ZHANG F, ZHAO J, ZHANG X q. Test study on current force on mooring ships[J]. China Ocean Engineering, 1993(2): 225-242. |
| [2] |
张怀新, 刘应中, 缪国平. 船体各种剖面的横摇阻尼与旋涡的形状[J]. 水动力学研究与进展, 2001(3): 382-389. ZHANG Huai-xin, LIU Ying-zhong, MIU Guo-ping. Vortex patterns and roll damping at various cross sections of ship[J]. Journal of Hydrodynamics, 2001(3): 382-389. |
| [3] |
邹志利, 张日向, 张宁川, 等. 风浪流作用下系泊船系缆力和碰撞力的数值模拟[J]. 中国海洋平台, 2002, 17(2): 22-27. ZOU Zhi-li, ZHANG Ri-xiang, ZHANG Ning-chuan, et al. The numerical simulation of mooring force & impact force of ship moored to offshore platform[J]. China Offshore Platform, 2002, 17(2): 22-27. DOI:10.3969/j.issn.1001-4500.2002.02.005 |
| [4] |
XIANG Y, TAN J H. Analysis of mooring lines forces of a berthed ship [J]. Journal of Ship Mechanics, 2002.
|
| [5] |
VARYANI K S. Force on the mooring lines of a ship due to the hydrodynamic interaction effects of a passing ship[J]. International Shipbuilding Progress, 2004, 51. |
| [6] |
胡毅, 胡紫剑, 刘元丹, 等. 基于AQWA的大型LNG船码头系泊分析[J]. 舰船科学技术, 2012, 34(2): 70-73+110. HU Yi, HU Zi-jian, LIU Yuan-dan, et al. Analysis of the large LNG ships moored against a quay based on AQWA[J]. Ship Science and Technology, 2012, 34(2): 70-73+110. |
| [7] |
嵇春艳, 郭建廷, 崔杰, 等. 船舶码头系泊的耦合动力响应分析[J]. 舰船科学技术, 2016, 38(19): 46-51. JI Chun-yan, GUO Jian-ting, CUI Jie, et al. Analysis of coupling dynamic response of ship mooring at the dock[J]. Ship Science and Technology, 2016, 38(19): 46-51. |
| [8] |
李焱, 陈汉宝, 高峰, 等. 复杂水流作用下船舶系泊条件试验分析[J]. 港口科技, 2019(2): 24-28. LI Yan, CHEN Han-bao, GAO Feng, et al. Experimental analysis of ship mooring conditions under complex flow[J]. Science and Technology of Ports, 2019(2): 24-28. |
| [9] |
Proceedings, Tokyo 2015 Workshop on CFD in Ship Hydrodynamics[C]. Tokyo, 2015.
|
| [10] |
ITTC. ITTC-Recommended Procedures and Guidelines: Practical Guidelines for Ship CFD Application [S]. 2011.
|
| [11] |
ITTC, 1957. Report of resistance committee. In: Presented at the Proceedings of 8 th ITTC[C]. Madrid, 1957.
|
| [12] |
SCHOENHERR, K. E. , Resistance of flat surfaces moving through a fluid [J]. Transactions-The Society of Naval Architects and Marine Engineers. 1932, 40: 279–313.
|
 2022, Vol. 44
2022, Vol. 44
