电磁轨道炮以电能作为发射能源,推进弹丸加速的电磁力与输入发射装置电流的平方成正比。为了向发射装置提供足够的电能,实现大电流汇流,紧凑型炮尾馈电装置的设计是电磁轨道炮关键技术中的一项。馈电装置的功能是实现电源输出同轴电缆与发射装置输入同轴电缆间的连接,即连接轨道与脉冲电源,为轨道提供可靠强大的脉冲电流,承受高速弹丸发射时对导轨产生的反作用力,同时为弹药自动装填和反后坐装置提供安装接口[1-3]。本文针对T型炮尾馈电方式进行了磁场分析和耦合仿真计算。进行磁场计算的目的是:计算电流密度分布,了解涡流损耗;计算铜板与同轴电缆内芯的受力状况,校验紧固措施的有效性。
1 炮尾馈电方式分析目前美国的电磁轨道炮技术走在世界的最前端,可谓是代表了电磁轨道炮研究的最高技术水平。美国电磁轨道炮的研究正由实验阶段向工程阶段转变,其炮尾馈电装置的发展循序渐进,不断优化。炮尾馈电方式也是随着研制阶段的不同而变化,通过调研搜集国内外电磁轨道炮炮尾馈电装置的现状和发展趋势,典型的炮尾馈电方式[4-6]如表1所示。
|
|
表 1 炮尾馈电方式比较 Tab.1 Comparison of gun tail feeding mode |
本文试验装置炮尾馈电方式选择T型结构对其研究并进行仿真。炮尾馈电简易T型结构的组成及安装方式如图1所示。
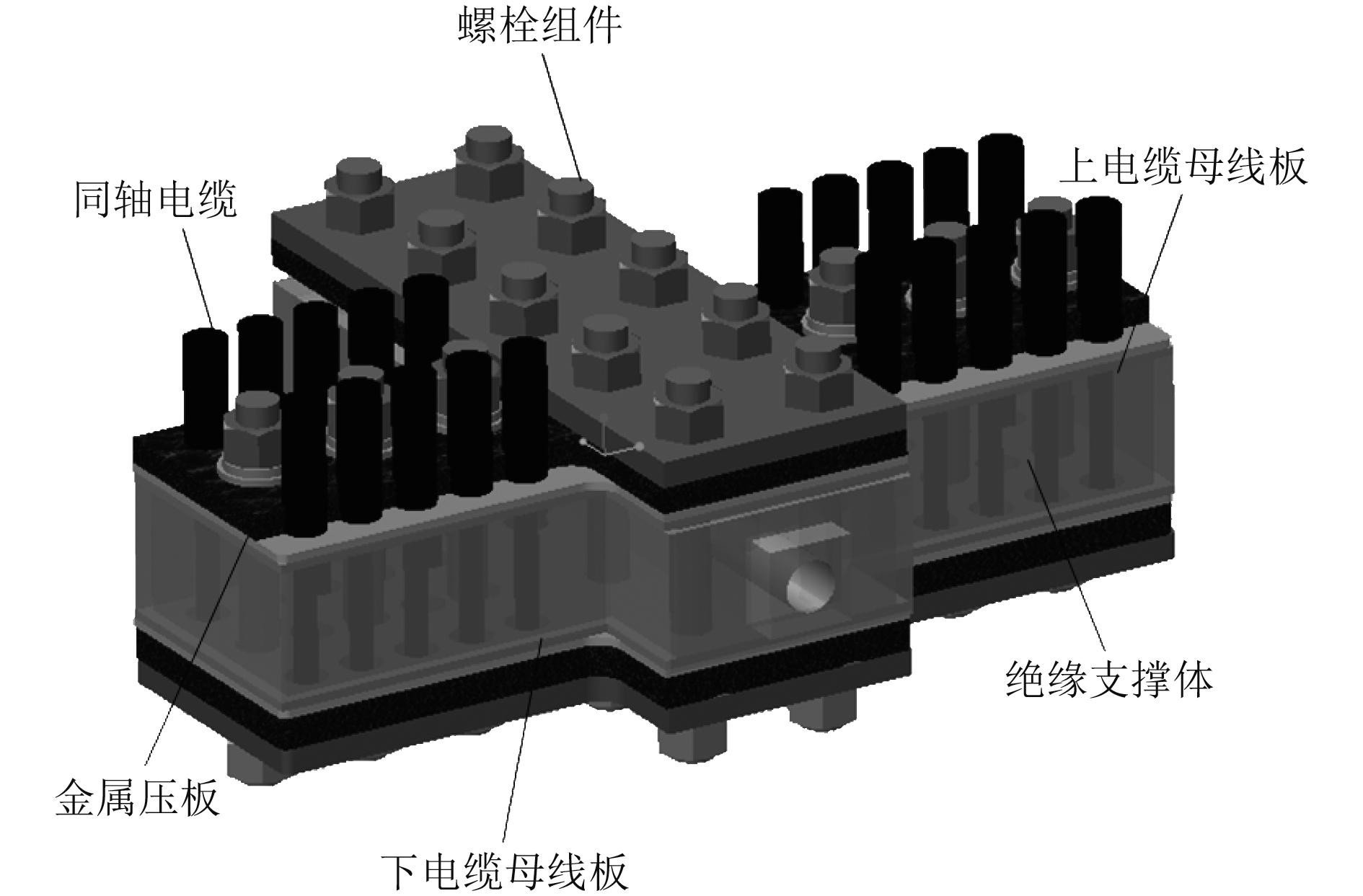
|
图 1 炮尾馈电装置简易模型 Fig. 1 A simple model of gun tail feeder |
炮尾馈电装置采用20根同轴电缆连接,实现电源输出同轴电缆与发射装置输入同轴电缆间的连接。上、下2个母线铜板直接压接在上、下轨道上,中间由绝缘材料支撑,保证两母线铜板之间的固定间距,上、下2个金属压板与两母线板间垫有一层绝缘材料,通过螺栓连接将上、下母线铜板压紧,并承受母线铜板上传递的压力,防止上、下母线铜板受力变形破坏。同轴电缆外芯由电缆压紧装置固定在上母线铜板上,同轴电缆内芯和内绝缘层穿过上母线板及绝缘支撑材料,通过电缆压紧装置固定在下母线铜板上,实现向轨道馈电功能。
2 电磁场及应力场计算理论 2.1 Maxwell方程描述从理论框架上看,Maxwell方程组加上洛仑兹力计算公式构成了静止或运动媒质中电动力学的基础,概括了电机、变压器及其他电磁装置的工作原理,同时也概括了电磁波的发射、传播和接收的原理[7-10]。
Maxwell方程组的微分形式可表示为:
| $ \nabla \times \vec H = \vec J + \frac{{\partial \vec D}}{{\partial t}} ,$ | (1) |
| $ \nabla \times \vec E = - \frac{{\partial \vec B}}{{\partial t}} ,$ | (2) |
| $ \nabla \cdot \vec{B} = 0 ,$ | (3) |
| $ \nabla \cdot \vec D = \rho 。$ | (4) |
式中:
将式(1)求散度结合式(3),根据偏导和散度运算可以互换,得到电流连续性方程:
| $ \nabla \cdot \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {J} = - \frac{{\partial \rho }}{{\partial t}},$ | (5) |
将3个独立的式(1)、式(2)、式(5)结合洛仑兹力方程
由Maxwell方程可以得到变量
| $ \left\{ \begin{gathered} {\boldsymbol{B}} = \nabla \times {\boldsymbol{A}},\hfill \\ {\boldsymbol{E}} = - \nabla \varphi - \frac{{\partial {\boldsymbol{A}}}}{{\partial t}}。\hfill \\ \end{gathered} \right. $ | (6) |
由于空气中只求解磁场,因此可以只定义矢量磁位
| $ \boldsymbol{B}=\nabla \times \boldsymbol{A},$ | (7) |
对于矢量
| $ \nabla \cdot {\boldsymbol{A}} = 0,$ | (8) |
在暂态问题求解中,一般采用的解法是引入时间积分电动势,引入时间积分电动势后,利用时域有限元求解方程时最终形成的线性方程组的系数矩阵具有对称性,对称的系数矩阵对于求解方程组兼具稳定性和快速性的优势。对于三维问题,时间积分电动势定义如下:
| $ VOLT(t,x,y,z) = \int_{ - \infty }^t {\phi (\tau ,x,y,z){\rm{d}}\tau }。$ | (9) |
以字母
导体运动的电枢区域中的方程为:
| $ \left\{ \begin{gathered} \nabla \times \frac{1}{{{\mu _1}}}\nabla \times {\boldsymbol{A}} - \nabla \frac{1}{{{\mu _1}}}(\nabla \cdot {\boldsymbol{A}}) +\hfill \\ \qquad {\sigma _1}\left( {\nabla \frac{{\partial V}}{{\partial t}} + \frac{{\partial {\boldsymbol{A}}}}{{\partial t}} - {\mathbf{v}} \times \nabla \times {\boldsymbol{A}}} \right) = 0 ,\hfill \\ \nabla \cdot {\sigma _1}\left( { - \nabla \frac{{\partial V}}{{\partial t}} - \frac{{\partial {\boldsymbol{A}}}}{{\partial t}} + {\mathbf{v}} \times \nabla \times {\boldsymbol{A}}} \right) = 0。\hfill \\ \end{gathered} \right. $ | (10) |
导体轨道中的方程为:
| $ \left\{ \begin{gathered} \nabla \times \frac{1}{{{\mu _2}}}\nabla \times {\boldsymbol{A}} - \nabla \frac{1}{{{\mu _2}}}(\nabla \cdot {\boldsymbol{A}}) + {\sigma _2}\left( {\nabla \frac{{\partial V}}{{\partial t}} + \frac{{\partial {\boldsymbol{A}}}}{{\partial t}}} \right) = 0 ,\hfill \\ \nabla \cdot {\sigma _2}\left( { - \nabla \frac{{\partial V}}{{\partial t}} - \frac{{\partial {\boldsymbol{A}}}}{{\partial t}}} \right) = 0。\hfill \\ \end{gathered} \right. $ | (11) |
空气中的方程为:
| $ \nabla \times \frac{1}{{{\mu _3}}}\nabla \times {\boldsymbol{A}} - \nabla \frac{1}{{{\mu _3}}}(\nabla \cdot {\boldsymbol{A}})\; = 0,$ | (12) |
交界面条件为:
| $ \left\{ \begin{gathered} {{\boldsymbol{A}}_{1t}} - {{\boldsymbol{A}}_{2t}} = 0 ,\hfill \\ \frac{1}{{{\mu _1}}}{(\nabla \times {{\boldsymbol{A}}_1})_t} - \frac{1}{{{\mu _2}}}{(\nabla \times {{\boldsymbol{A}}_2})_t} = 0 ,\hfill \\ {\sigma _2}{\left( - \nabla \frac{{\partial {V_2}}}{{\partial t}} - \frac{{\partial {{\boldsymbol{A}}_2}}}{{\partial t}}\right)_n} -\hfill \\ \qquad{\sigma _1}{\left( - \nabla \frac{{\partial {V_1}}}{{\partial t}} - \frac{{\partial {{\boldsymbol{A}}_1}}}{{\partial t}} + {\mathbf{\upsilon }} \times \nabla \times {{\mathbf{A}}_1}\right)_n} = 0 ,\hfill \\ \end{gathered} \right. \in {\varGamma _{1,2}}。$ | (13) |
式中:下标
由经典力学理论可知,物体的动力学通用有限元方程为[11]:
| $ {\boldsymbol{M}}x''+ {\boldsymbol{C}}x'+ {\boldsymbol{K}} x= F(t)。$ | (14) |
式中:
线性静力学分析有两方面的含义:首先就是材料为线性,应力应变关系为线性,变形是可恢复的;另外结构发生的是小位移、小变形、小转动,结构刚度不因变形而变化。静力就是结构受到静态载荷的作用,惯性和阻尼可以忽略,并且一般结构中与时间t相关的量都将被忽略,于是静力学分析方程为:
| $ {\boldsymbol{K}}x = F。$ | (15) |
Ansys软件能实现前后处理、分析求解及多场耦合分析一体化,能实现前后处理、分析求解及多场耦合分析统一数据库。利用Ansys软件可以进行结构静力分析(包括线性分析及非线性分析)、结构动力学分析(瞬态动力学分析谐响应分析和随机振动响应分析)等。
在有限元分析中,多物理场的耦合方式分为2种:一种是使用一种单元,此单元包括所要计算的所有自由度,称为直接耦合。实际应用时,尤其是在特殊领域,一种单元的自由度难以包括所要计算的所有相关量,造成了此方法应用的局限性;另一种方式称为间接耦合,即将一个单元的计算结果作为另一个单元的载荷进行加载计算,此方式有时会造成程序运行的不稳定,例如单元损坏等。
本文采用单向间接耦合的方式进行电磁-应力结构耦合仿真。
3 T型馈电装置电磁场有限元仿真模型 3.1 基于Ansoft Maxwell涡流场的电流密度仿真若要对整个装置的电磁作用效果进行全面的分析,首先应该明确电流密度的大致分布状态,后续局部分析对电流密度的集中部位进行重点研究,忽略电流密度极小部位对局部分析的影响,以简化模型[8]。图2为母线铜板的电流密度分布,电流密度在铜板拐角处比较集中,一个是母线铜板拐角处,另一个是母线铜板与轨道连接拐角处。

|
图 2 母线铜板电流密度分布图 Fig. 2 Current density distribution diagram of bus copper plate |
如若导电圆柱体的周围没有其他通电导体对其造成影响或者对其造成的影响叠加作用为零,那么当导电圆柱体通以瞬态电流,则只表现为普通的电流趋肤效应,即内空外实。反之,则表现为某侧电流密度过高。如图3所示,针对左侧同轴电缆内芯电流的分布进行了仿真,从图中看出穿过母线铜板的同轴电缆内芯的电流分布很好诠释这个现象。靠近母线铜板与轨道连接拐角处的同轴电缆内芯电流分布极不均匀,距其最远的同轴电缆内芯则只表现出了普通的电流趋肤效应。

|
图 3 左侧同轴电缆内芯电流分布云图 Fig. 3 Left coaxial cable core current distribution cloud diagram |
电磁场-应力场耦合方法为逐步加载42个时间步上的电磁场计算结果,分别对各个时间点进行静力学求解。铜材料的弹性模量为106×109 Pa,铜泊松比均为0.3。
同轴电缆内芯的应力分布如图4所示。可以看出,靠近轨道侧的前排第1根电缆内芯应力值最大,原因是其受力最大,且电磁力分布不均匀,当内芯两端均与母线铜板连接时,其最大应力值出现在与母线铜板连接处,值为65.9 MPa。
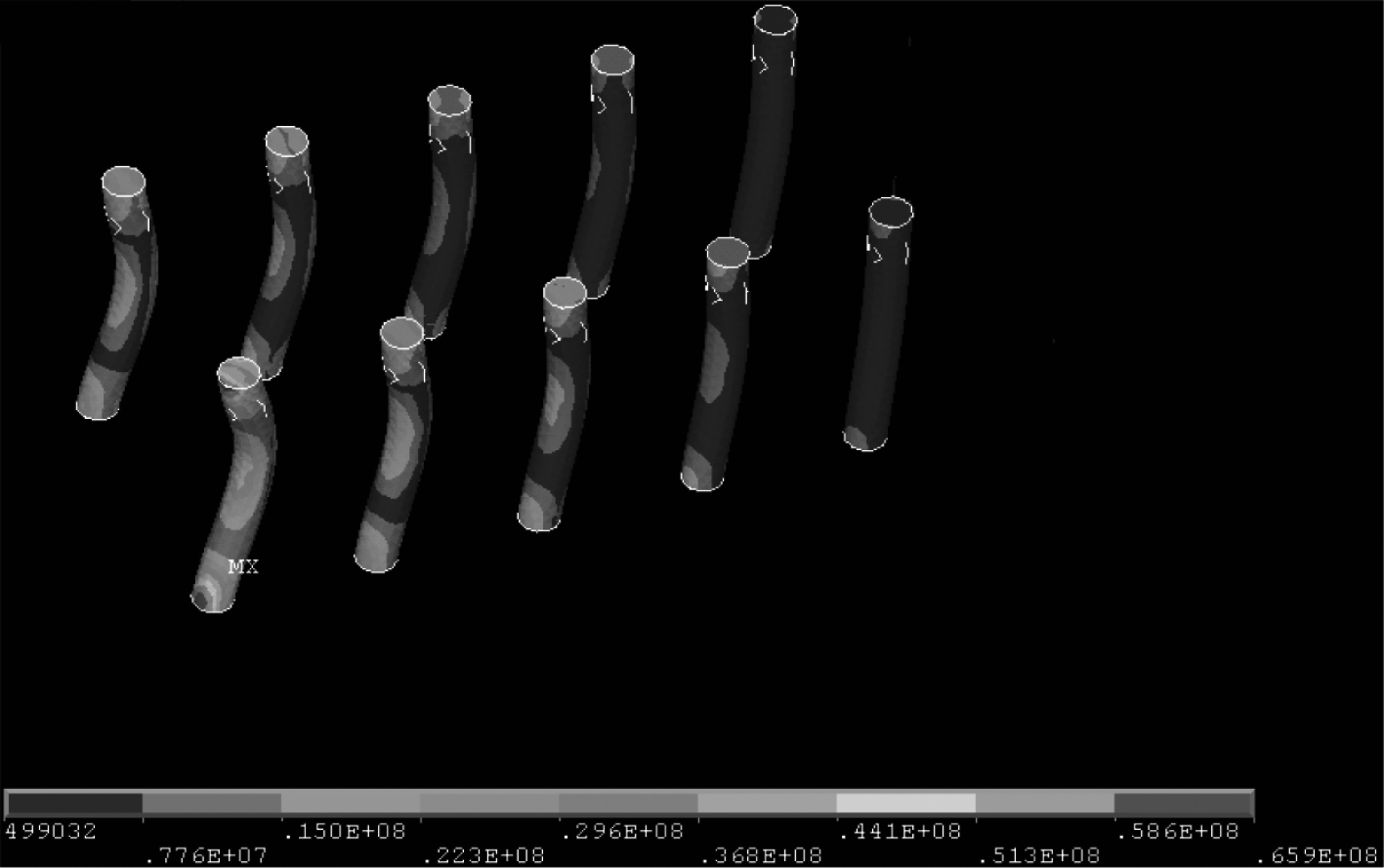
|
图 4 同轴电缆内芯应力分布云图 Fig. 4 Stress distribution cloud diagram of coaxial cable inner core |
图5给出了母线铜板的应力分布图。除了最大应力内芯与其连接处的应力最大,母线铜板的拐角处应力也比较集中,其大小约为10~20 MPa。

|
图 5 母线铜板应力分布云图 Fig. 5 Stress distribution cloud diagram of bus copper plate |
由于同轴电缆内芯两端连接母线铜板,是不允许有断裂的,故在计算过程中,将电缆内芯的两端均设置为各向零变形量,来计算其他部位的变形量。
从图6可以看出,将电缆内芯两端固定时,靠近轨道的前排电缆中间部位的型变量最大,最大值约为0.1 mm。
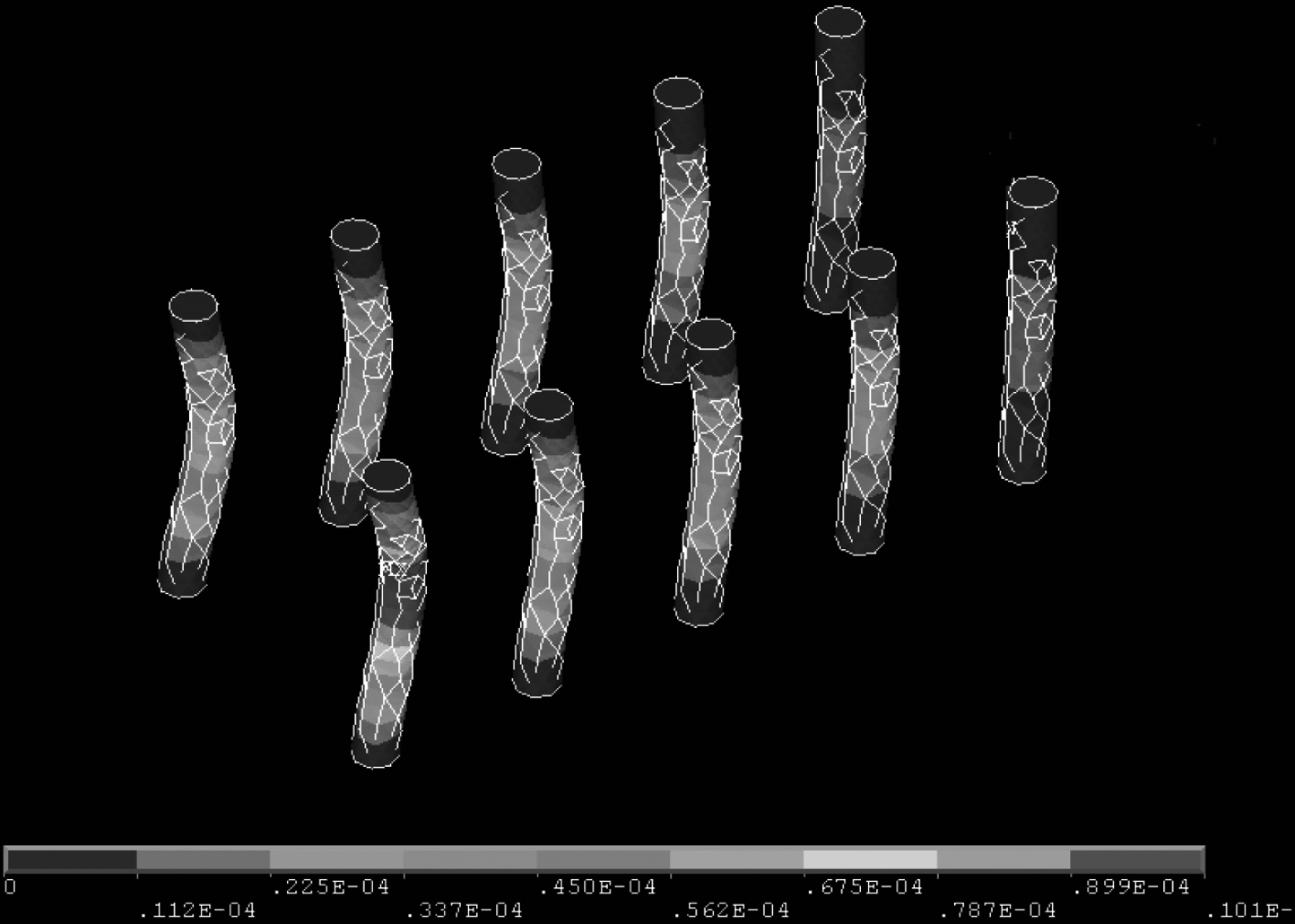
|
图 6 同轴电缆内芯应变图 Fig. 6 Strain diagram of coaxial cable inner core |
从图7可以看出,母线铜板上的最大形变发生在与最大形变电内芯的连接处,并且在母线铜板拐角处及其与轨道连接处形变量也比较大,不过最大值只有3.8 μm左右。
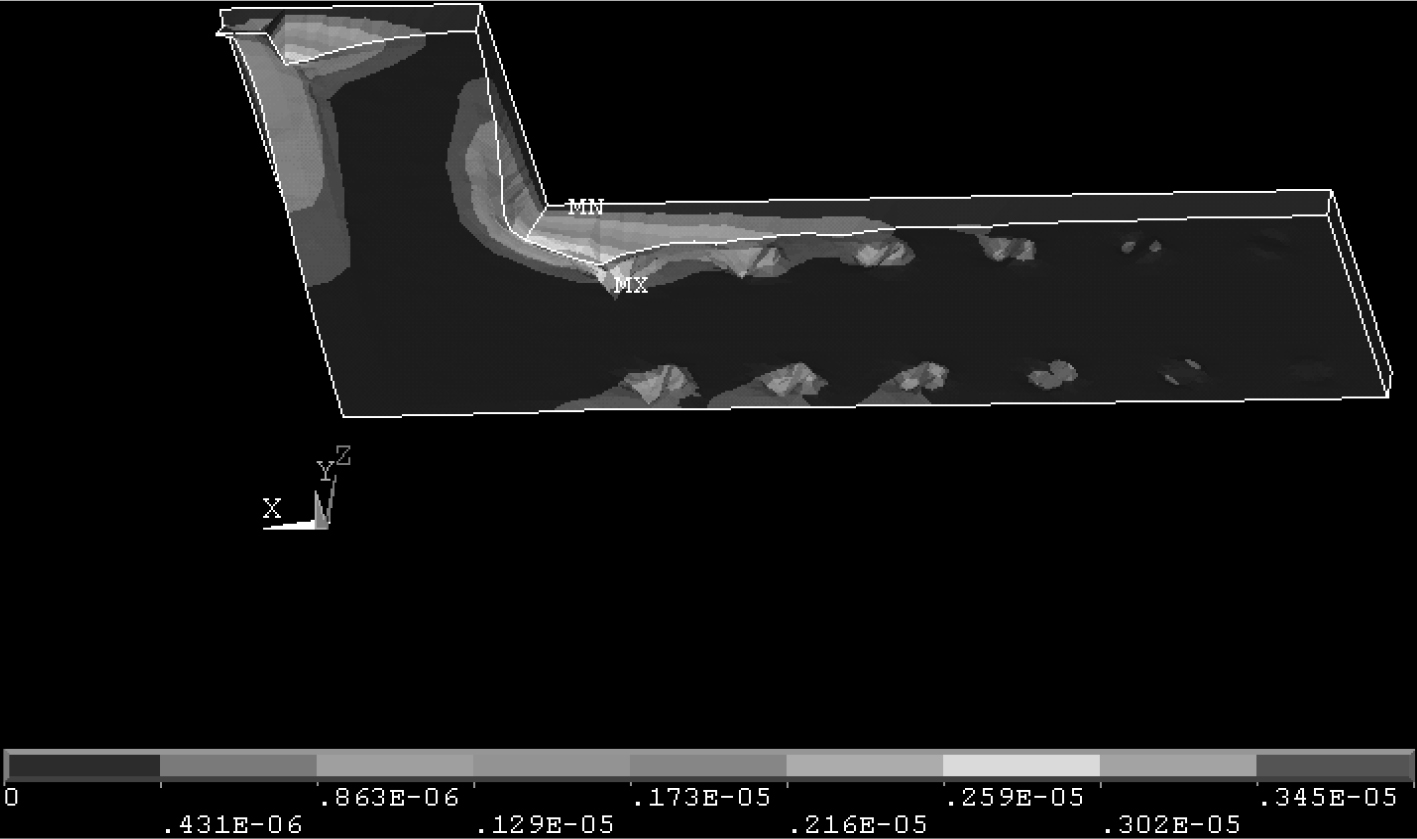
|
图 7 母线铜板应变图 Fig. 7 Strain diagram of bus copper plate |
本文围绕T型馈电方式进行了分析,并利用电磁场有限元软件对母线铜板和同轴电缆进行了电流密度分布和电磁-应力场耦合仿真分析。结果仿真分析表明,在电流密度集中部位出现了应力集中的现象,应力集中(应变较大)部位有:前排靠近轨道侧的同轴电缆内芯、母线铜板拐角处以及母线铜板与轨道连接处,就仿真结果看来,均不影响各结构部件的正常工作。本文针对T型馈电结构进行仿真分析和计算,为后续工作中更多馈电装置的设计和研究提供依据。
| [1] |
马歇尔, 王莹. 电磁轨道炮的科学与技术[M]. 北京: 兵器工业出版社, 2006.
|
| [2] |
王莹, 肖峰. 电炮原理[M]. 第1版. 北京: 国防工业出版社, 1995.
|
| [3] |
TOWER M, HAIGHT C. Development of a high-energy distributed energy source electromagnetic railgun with improved energy conversion efficiency[J]. IEEE Transactions on Magnetics, 1984, 20(2): 298-301. DOI:10.1109/TMAG.1984.1063093 |
| [4] |
TZENG J T. Structural mechanics for electromagnetic railguns[J]. IEEE Transactions on Magnetics, 2005, 41(1 II): 246–250.
|
| [5] |
袁建生, 李军, 等. 不同截面形状轨道的电磁炮电流分布特性分析[C]. 2011中国电工技术学会学术年会论文集. 北京: 2011: 253.
|
| [6] |
刘恋. 电磁轨道炮系统的建模与仿真研究[D]. 武汉: 华中科技大学, 2014.
|
| [7] |
乔志明, 雷彬, 吕庆敖, 等. 电磁轨道炮关键技术与发展趋势分析[J]. 火炮发射与控制学报, 2016, 37(2): 91-95. |
| [8] |
赵泽洋. 电磁轨道炮建模与仿真分析[D]. 长沙: 国防科学技术大学, 2013.
|
| [9] |
HILMAR P, FRANCIS J, VOLKER W. Technical aspects of railguns[J]. IEEE Transactions on Magnetics, 1995, 31(1): 348-353. DOI:10.1109/20.364663 |
| [10] |
Bhag Singh Guru, 周克定. 电磁场与电磁波[M]. 北京: 机械工业出版社, 2006: (40-50).
|
| [11] |
赵博, 张洪亮, 等. Ansoft 12在工程电磁中的应用[M]. 北京: 中国水利水电出版社, 2010.
|
 2021, Vol. 43
2021, Vol. 43
