TR组件是舰载雷达的关键部件,具有放大发射和接收信号、改变信号幅值相位等功能。雷达天线面阵由多个TR组件组成,TR组件研制过程中除满足低噪声、高效率和大功率等基本要求外,应考虑小型化和轻量化设计。
抗冲击决定了舰载设备的生命力,TR组件结构需具备良好的刚强度以提高其抗冲击性能。同时因轻量化设计降低了其刚强度,增大了抗冲击设计难度。安装隔振系统的雷达天线面阵在外界载荷作用下,隔振系统产生位移来达到减振效果,但天线定位识别精度受到干扰。因此,雷达天线面阵不适合采用隔振缓冲设计,相对于含隔振系统的机柜,其冲击环境更为恶劣。为满足TR组件轻量化、抗冲击的设计要求,需采用可靠的计算方法对TR组件进行冲击计算。
徐俊东等[1]对舰载雷达阵面DDAM设计冲击谱进行理论推导,计算得到各阶模态质量,并将其代入GJB1060.1-91规定的甲板部位冲击加速度和速度计算公式,将各阶模态求解得到的应力用NRL求和方法合成总冲击应力,分析阵面框架上结构强度薄弱环节,并给出结构优化改进意见。XIE Zui-wei等[2]给出DDAM的算法原理和冲击计算流程,对舰用燃气轮机进行DDAM抗冲击结构强度校核,对支架等重要部位的应力和变形进行分析,以确定其危险区域,对比研究金属橡胶隔振器的隔振缓冲性能,提出舰用燃气轮机安装基础处缓冲设计方法。计晨等[3]使用时域模拟法对舰用齿轮箱进行冲击计算,以组合三角波作为载荷输入,将不同的冲击加速度峰值和脉宽时间组合成54种输入工况,探讨齿轮箱的冲击极限载荷。由于技术保护原因,TR组件抗冲击设计过程中缺乏可靠的冲击计算数据作为理论支撑。因此,对舰载雷达的核心部件TR组件开展轻量化抗冲击分析具有较高的研究价值。
本文分别采用DDAM和时域模拟法2种冲击计算方法对舰载雷达TR组件进行抗冲击分析,首先对TR组件分析模型进行描述,建立有限元模型并给出边界约束条件;然后依据国军标GJB1060.1-91和德军标BV0430-85规定的冲击载荷计算公式,输入相应的DDAM和时域模拟法设计冲击载荷,在有限元软件中进行冲击计算并对冲击响应进行后处理。最后对比分析2种冲击计算方法,针对TR组件结构强度薄弱环节提出设计改进建议。
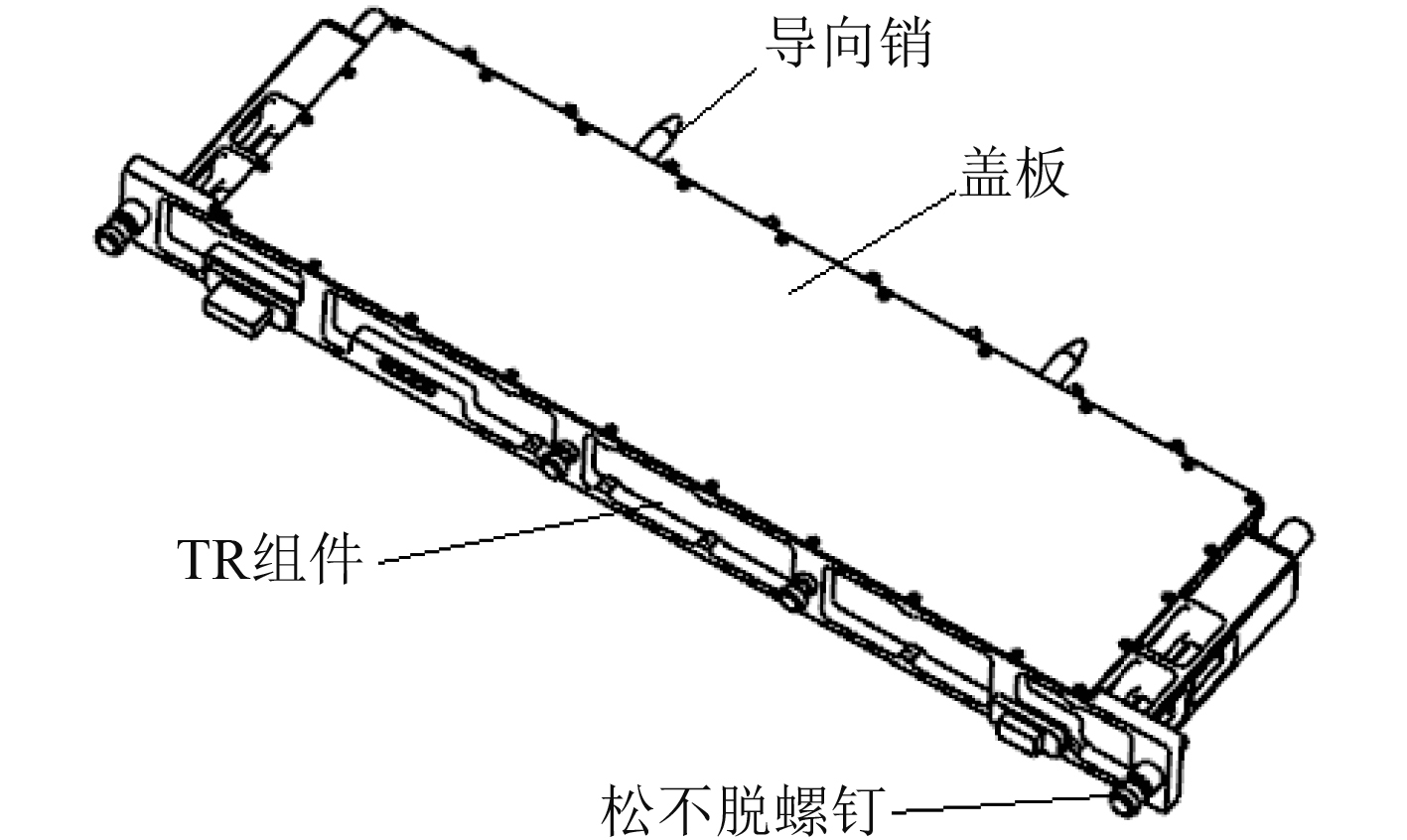
1 分析模型描述图1为TR组件模型,TR组件上设计盖板并在内部安装印制板模块,通过前面板2个松不脱螺钉和后侧2个导向销将其安装在雷达天线面阵框架上。为满足轻量化设计要求,组件侧面设计减重槽,印制板模块安装面设计减重孔。
|
图 1 TR组件结构几何模型 Fig. 1 Geometric model of TR module structure |
对TR组件进行冲击计算前需对模型进行前处理,对盒体上圆孔、圆角、倒角、凸台等小的特征进行简化处理,以提高盒体网格单元划分质量,从而提高计算结果的可靠性。组件内盖板、印制板模块等采用质量点等效代替。
图2为TR组件有限元模型,采用四面体单元对其进行网格划分,有限元单元数量为36151,节点数量为70653。

|
图 2 TR组件有限元模型 Fig. 2 Finite element model of TR module |
DDAM(Dynamic Design Analysis Method)计算方法由美国海军实验室提出,美国海军结合大量实船水下非接触爆炸试验采集的设备冲击响应数据,归纳得到舰载设备冲击设计谱。DDAM基于模态叠加法,将分析模型从单个多自由度系统转化成多个单自由度系统,依据对TR组件分析模型模态计算得到的各阶模态频率、模态质量和模态参与因子,推导出相应的冲击输入响应谱,合成每一阶的模态应力和位移以计算组件的冲击最大响应量[4-5]。对TR组件DDAM计算方法进行理论分析。
| $ {\boldsymbol{M}}\ddot x + {\boldsymbol{K}}x = - {\boldsymbol{M}}n\ddot y(t)。$ | (1) |
式中:M和K分别为TR组件的质量矩阵和刚度矩阵;x为位移矢量;n为冲击方向矢量;
模态参与因子受到TR组件结构特性影响,模态参与因子Pk的表达式为:
| $ {P_k} = \frac{{{\alpha _k}^{\rm{T}}Mn}}{{{\alpha _k}^{\rm{T}}M{\alpha _k}}},$ | (2) |
式中:αk为第k阶模态矢量。
第k阶模态质量mk的表达式为:
| $ {m_k} = \sum\limits_n {\left( {{m_n}{\phi _{kn}}{P_k}} \right)}。$ | (3) |
TR组件总质量为各阶模态质量之和,第k阶模态质量即冲击作用下第k阶模态被激励的质量。
由TR组件每一阶模态质量、振型、模态参与因子和冲击设计谱推导出该阶冲击应力、应变和位移响应,采用NRL求和方法合成所有阶冲击响应量,即可获得总冲击响应数据[8]。
TR组件DDAM设计冲击谱与其模态质量有关,由于冲击响应量受到雷达天线阵面和固定基础处相互作用影响,设计冲击谱数值与舰船种类、分析对象安装区域等因素有关,雷达天线阵面安装在舰船甲板部位,TR组件采用弹性设计,表1为GJB 1060.1-91规定的DDAM设计冲击谱。
|
|
表 1 DDAM设计冲击谱 Tab.1 Shock design spectrum of DDAM |
| $ {A_s} = 98.1 \times \frac{{19.05 + {{m}}{}_k}}{{2.72 + {{m}}{}_k}} ,$ | (4) |
| $ {V_s} = 1.52 \times \frac{{5.44 + {{m}}{}_k}}{{2.72 + {{m}}{}_k}} 。$ | (5) |
DDAM计算方法规定每个方向参与分析的模态质量之和与总质量的比例大于80%,并提取模态质量占比大于1%的模态参与计算,以提高TR组件冲击求解精度和可靠性。设计冲击加速度取A和Vωk两者的较小值, ωk为第k阶模态质量mk的圆频率[9]。
对TR组件前20阶进行模态计算,固定约束其前面板2个松不脱螺钉安装孔和后侧2个导向销。图3为TR组件前6阶模态振型。一阶模态频率为314.76 Hz,远高于雷达天线面阵所处的桅杆区最高振动激励频率50 Hz,表明TR组件结构刚性良好。

|
图 3 TR组件前6阶模态振型 Fig. 3 The first six-orders mode shapes of TR module |
表2~表4分别为TR组件在垂向、横向、纵向冲击方向上的设计冲击谱。垂向为TR组件盖板的法线方向,纵向为TR组件前面板的法线方向,前20阶垂向、横向、纵向模态质量总占比分别为 95.92%,96.02%,97.19%,都高于DDAM规定的最低值80%。即提取的模态阶数满足DDAM计算要求。
|
|
表 2 垂向冲击设计谱 Tab.2 Shock design spectrum in vertical direction |
|
|
表 3 横向冲击设计谱 Tab.3 Shock design spectrum in transversal direction |
|
|
表 4 纵向冲击设计谱 Tab.4 Shock design spectrum in longitudinal direction |
在有限元软件分别输入TR组件垂向、横向、纵向的冲击设计谱,进行相应的冲击计算。
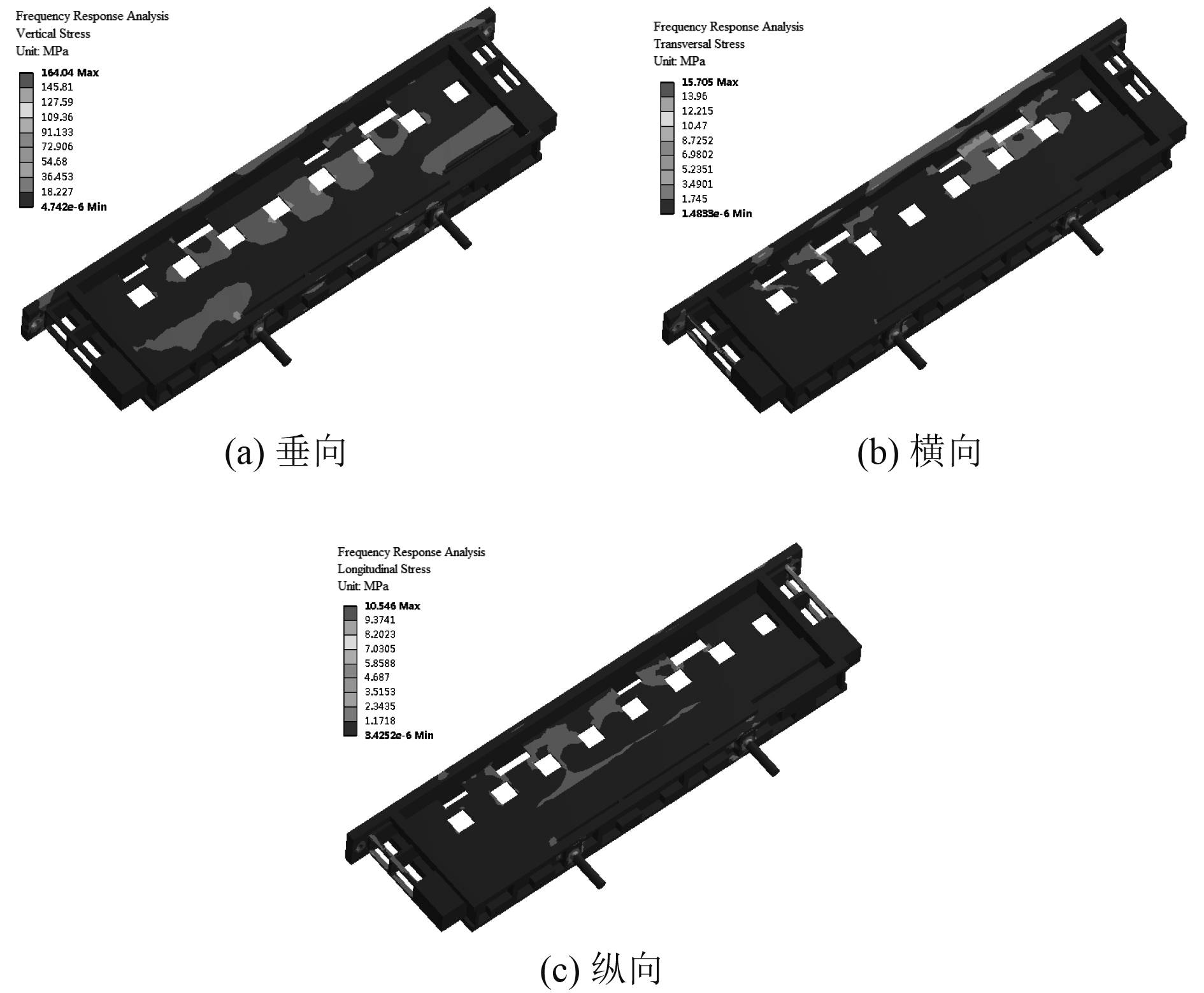
图4为TR组件垂向、横向、纵向DDAM计算应力云图。3个冲击方向上最大应力分别为164.04 MPa,15.71 MPa,10.55 MPa,垂向和横向冲击最大应力均位于右侧导向销根部,纵向冲击最大应力位于左侧导向销根部,3个冲击方向上盒体上最大应力依次为97.65 MPa,5.86 MPa,5.5 MPa,应力主要分布于前面板松不脱螺钉安装孔、后侧导向销、盒体上减重槽和两侧加强筋等区域。由于垂向冲击设计谱明显高于横向和纵向,因此TR组件垂向冲击应力最大,纵向冲击应力最小。导向销材料圆钢17-4PH的屈服强度为725 MPa,盒体材料铝合金6063的屈服强度为214 MPa,3个冲击方向TR组件导向销和盒体上最大冲击应力均小于相应材料屈服强度,TR组件未发生塑性变形,即TR组件结构设计满足DDAM冲击计算强度要求。
|
图 4 DDAM计算应力云图 Fig. 4 Stress nephogram computed by DDAM |
DDAM基于模态计算,通过对各阶模态冲击响应进行NRL合成得到总的冲击响应,NRL合成法中最大应力值为绝对值,未考虑设备非线性结构特性、阻尼效应和各阶模态响应相位差对计算结果的影响。因此,DDAM计算量小,对计算机硬件要求较低,且计算结果具有可靠性,但计算应力值偏保守,不利于TR组件等舰载设备的轻量化抗冲击设计。早期受到计算机硬件的限制,具有线性或者弱非线性的舰载设备适合采用DDAM进行冲击计算。近些年来,计算机硬件性能有了明显的提升,有限元软件冲击算法趋于成熟完善,研究人员逐渐采用求解精度更高但计算量大的时域模拟法代替DDAM对舰载设备进行瞬态动力学计算,时域模拟法可对线性或者非线性的复杂模型进行求解,冲击输入载荷为实测冲击时域曲线或者标准冲击时域曲线,实测冲击时域曲线更为真实,但其冲击波形复杂,每次试验舰载设备处采集的冲击谱都不一致,具有随机性。标准冲击时域曲线参考德国军标BV0430-85规定的冲击谱,将冲击试验数据归纳得到的三折线冲击频域响应谱转化成等效的标准冲击时域曲线,标准时域曲线参数较为简单,且接近实测冲击谱,适合作为时域模拟法的输入载荷。
冲击载荷作用下的TR组件时域冲击响应方程为:
| $ {\boldsymbol{M}}\mathop z\limits^{..} (t + \Delta t) + {\boldsymbol{C}}\mathop z\limits^. (t + \Delta t) + {\boldsymbol{K}}(t)z(t) = R(t + \Delta t) - F(t)。$ | (6) |
式中:C为TR组件的阻尼矩阵,z(t)为t时刻的节点位移矢量,R(t+Δt)为t+Δt时刻的外界激励矢量,F(t)为t时刻TR组件内应力产生的等效节点矢量。
在有限元软件进行时域模拟法计算时,首先将式(6)在单个时间步长进行离散,该方程以对时间的差分形式来表达且可按线性方程求解,下一个时间步长求解的初始条件是上一个时间步长求解得到的冲击响应数据,每个时间步长的运动方程均作为线性方程来计算,对单个时间步长计算得到的瞬态应力和变形进行修正。时域模拟法的计算原理是将非线性动力学方程转化成一系列线性方程来求解,在不同时间步长内进行迭代计算,即可推导出随时间变化的应力和变形曲线[10]。
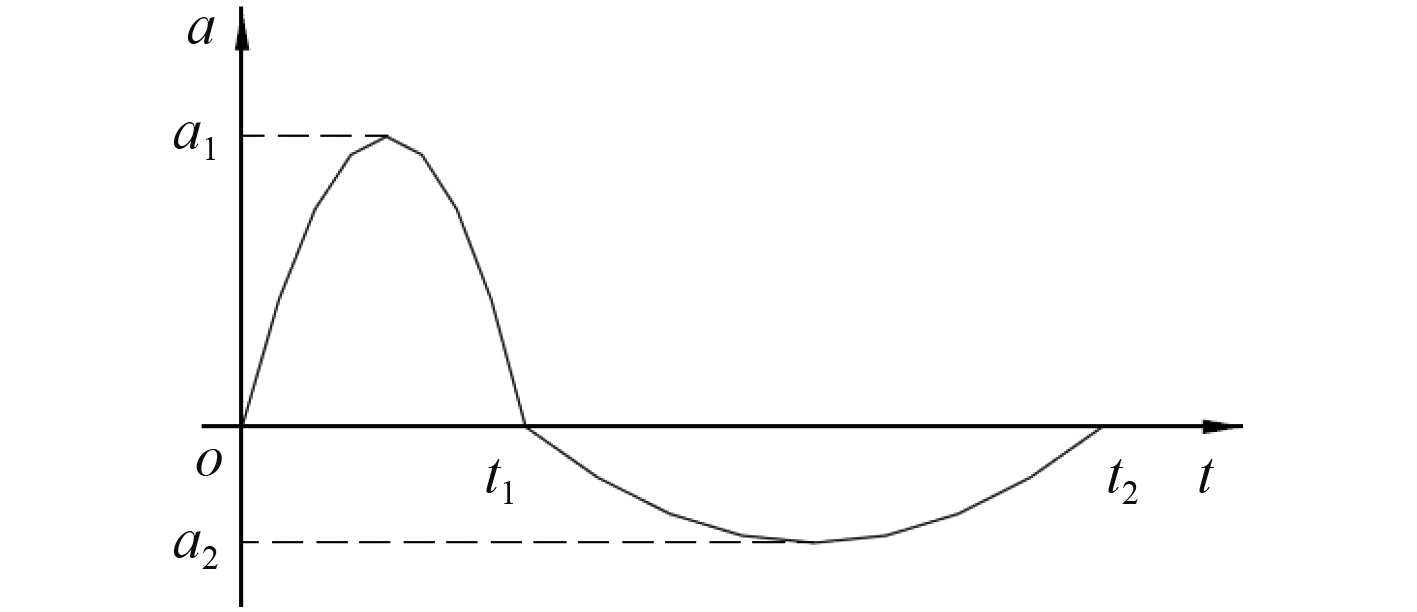
时域模拟法的标准时域冲击输入曲线参数包括冲击波形类型、冲击加速度峰值和脉冲时间等,组合半正弦波为常用的标准时域冲击输入曲线[11]。图5所示的组合半正弦波由2个半正弦波组成,正半波面积v1和负半波面积v2均为三折线冲击响应谱中等速度谱V0的2/3,正半波的冲击加速度峰值a1为等加速度谱A0的1/2,对该冲击加速度时域曲线进行2次积分可得到等位移谱D0。正半波结束时刻t1=πv1/2a1,负半波结束时刻t2=2D0/v1,负半波冲击加速度峰值a2=πv1/2(t2-t1)。
|
图 5 组合半正弦波时历曲线 Fig. 5 Two-time history of half-sine wave |
将垂向、横向、纵向三折线冲击谱的等加速度谱A0、等速度谱V0、等位移谱D0分别代入上式,可得到表5所示的组合半正弦波曲线参数,
|
|
表 5 组合半正弦波曲线参数 Tab.5 Combination of half-sine wave parameters |
TR组件时域模拟法计算中的分析模型前处理和边界约束条件和DDAM相同,在有限元软件中输入组合半正弦波时间历程曲线载荷后对其进行瞬态动力学计算。
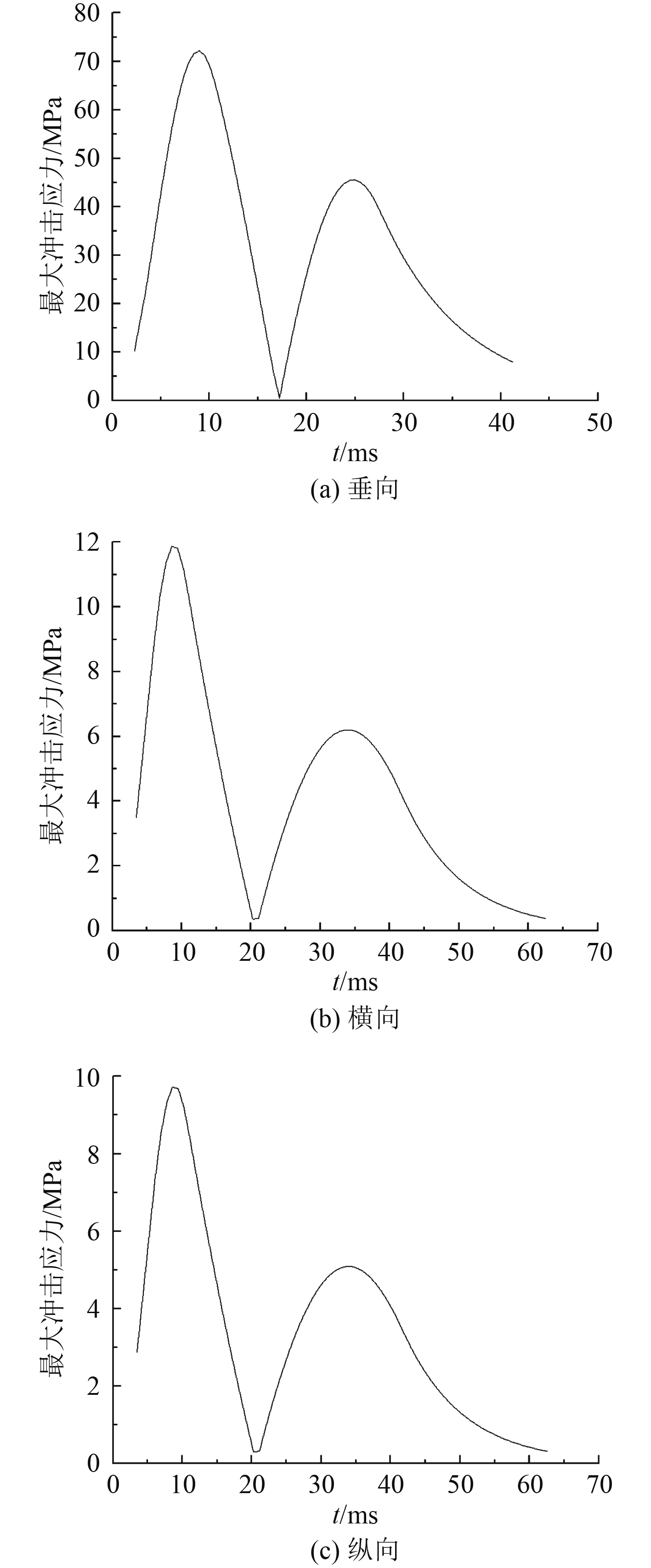
时域模拟法计算时间是DDAM的3倍,图6为TR组件不同冲击方向上最大应力时间历程曲线,正负半正弦波载荷先后作用在TR组件上,3个冲击方向上最大应力时间历程曲线变化趋势相同,均出现2个峰值。由于负波加速度峰值小于正波,负波冲击作用时间上的最大应力小于正波。组合半正弦波冲击结束后TR组件内部应力随着时间增大逐渐衰减至零,最大应力时间历程曲线总的持续时间大于组合半正弦波脉冲时间。最大应力峰值分别为72.13 MPa,11.87 MPa,9.73 MPa,对应的时刻依次为8.96 ms,8.58 ms,8.58 ms,横向和纵向冲击输入时域曲线相同,最大应力峰值出现的时刻相同,横向最大应力大于纵向,表明TR组件纵向抗冲击强度好于横向。
|
图 6 不同冲击方向上最大应力时历曲线 Fig. 6 Time history of maximum stress in different shock directions |
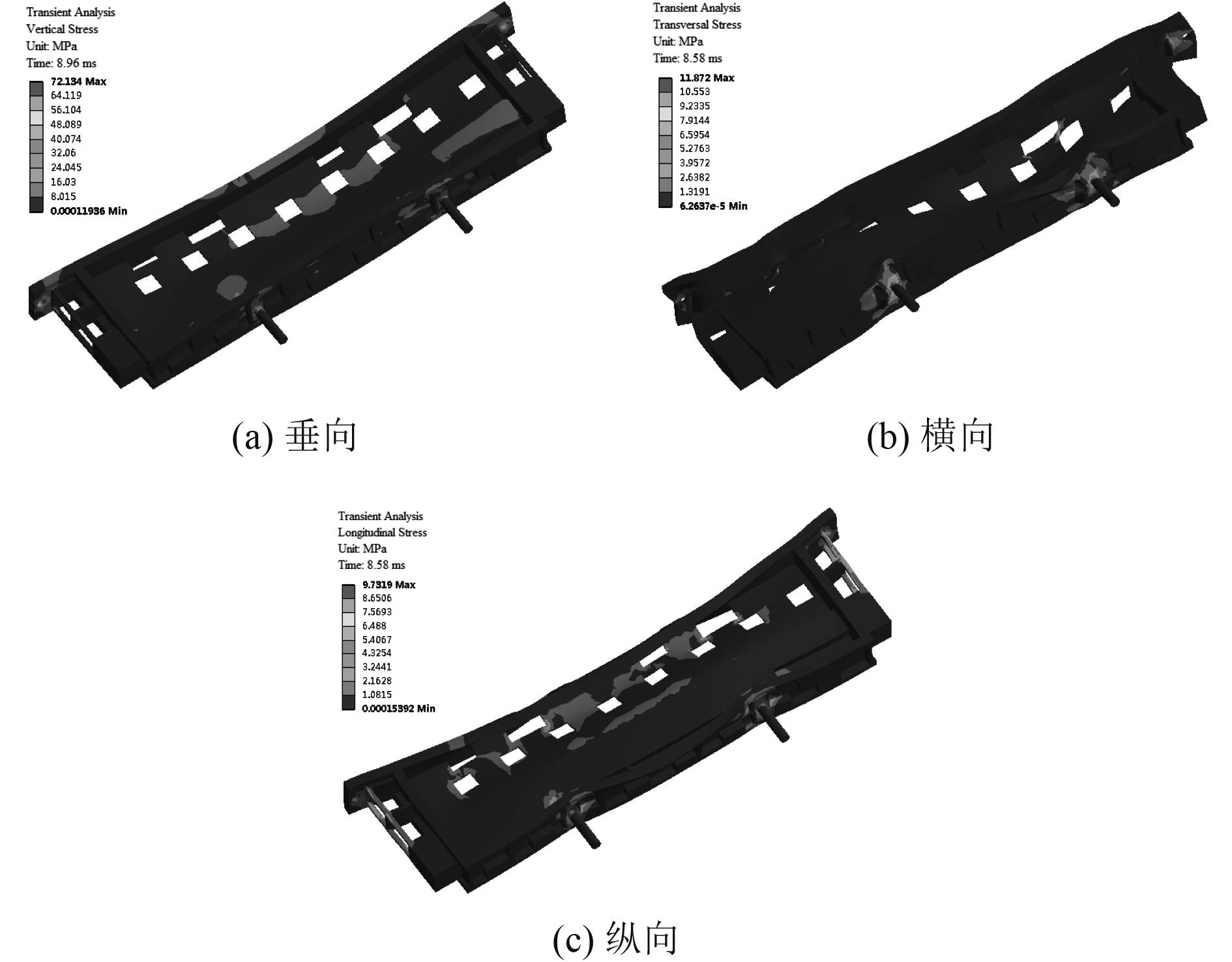
图7为时域模拟法计算应力云图,应力分布区域和DDAM相同,3个冲击方向上最大应力均小于DDAM,时域模拟法和DDAM计算最大应力均位于导向销根部。可知,TR组件结构满足时域模拟法冲击计算强度要求。
|
图 7 时域模拟法计算瞬时应力云图 Fig. 7 Stress nephogram computed by time domain simulation method |
为提高TR组件抗冲击结构强度,满足其重量要求的前提下,可增大TR组件两侧加强筋厚度、盒体壁厚和导向销直径,在导向销根部设计圆弧过渡。
4 冲击计算方法比较对TR组件这种具有线性结构特性的舰载设备进行冲击计算时,DDAM和时域模拟法均可采用。2种计算方法得到的应力分布区域和危险区域基本一致,但因DDAM对各阶模态冲击响应进行NRL合成时最大应力值为绝对值,导致其计算应力值偏保守,满足DDAM抗冲击结构强度要求的舰载设备仍有较大的余量进行减重设计。不同于基于频域分析的DDAM忽略了随时间变化的结构刚度对计算结果的影响,且仅能对线性或者弱非线性的舰载设备进行计算,时域模拟法求解过程中考虑了阻尼和非线性等因素,不仅能对TR组件这种线性舰载设备进行计算,还能对含隔振系统具有较强非线性的舰载设备进行计算,通过后处理可得到随时间变化的最大应力时间历程曲线,计算精度高于DDAM,计算应力值小于DDAM。但由于时域模拟法计算中需设置时间步长并反复进行数值迭代求解,计算量明显高于DDAM。对于安装在桅杆区重量限制严格的舰载设备,在计算机硬件资源配置高的前提下,建议使用计算精度高且结果完善合理的时域模拟法代替DDAM进行舰载设备抗冲击轻量化设计。
5 结 语由舰载雷达TR组件DDAM和时域模拟法冲击计算结果可知,TR组件一阶模态频率314.76 Hz,远高于其所处的桅杆区最高振动激励频率50 Hz,表明TR组件结构刚性良好。垂向、横向、纵向3个冲击方向上DDAM计算最大应力分别为164.04 MPa,15.71 MPa,10.55 MPa,时域模拟法计算最大应力分别为72.13 MPa,11.87 MPa,9.73 MPa,对应的时刻依次为8.96 ms,8.58 ms,8.58 ms。2种计算方法都能对TR组件这种具有线性结构特性的舰载设备进行冲击分析,3个冲击方向上最大应力均位于TR组件后侧导向销上,垂向应力最大,应力主要集中区域和结构强度薄弱环节相同,最大应力均小于相应材料的屈服强度,即TR组件满足DDAM和时域模拟法抗冲击强度要求。和DDAM相比,时域模拟法计算时间增大2倍,但计算应力值偏小且更接近于实测值,可分析不同时刻应力分布情况,安装在舰船桅杆区重量控制严格的舰载设备进行抗冲击轻量化设计时,建议采用求解精度高的时域模拟法替代DDAM进行计算分析,
| [1] |
徐俊东, 周世新. 基于DDAM的舰载雷达阵面抗冲击分析[J]. 电子机械工程, 2012, 28(5): 18-21. XU Jun-dong, ZHOU Shi-xin. Shock-resistant capability analysis of a shipborne array antenna based on DDAM[J]. Electro-Mechanical Engineering, 2012, 28(5): 18-21. DOI:10.3969/j.issn.1008-5300.2012.05.005 |
| [2] |
XIE Zui-wei, HE Shao-hua, WU Xin-yue. Anti-shock optimization of a certain gas turbine foundation by DDAM[J]. Advanced Materials Research, 2010, 129-131: 376-380. DOI:10.4028/www.scientific.net/AMR.129-131.376 |
| [3] |
计晨, 汪玉, 杨莉, 等. 水下爆炸载荷作用下舰用齿轮箱强度极限数值仿真研究[J]. 北京理工大学学报, 2011, 31(1): 8-11. JI Chen, WANG Yu, YANG Li, et al. Numerical simulation study on intensity threshold of marine gearbox subjected to underwater explosion load[J]. Transactions of Beijing Institute of technology, 2011, 31(1): 8-11. |
| [4] |
李晓明, 陈凤. 舰船浮筏隔振装置DDAM抗冲击计算[J]. 噪声与振动控制, 2012(6): 34-39. LI Xiao-ming, CHEN Feng. Shock Response computation of vibration-isolating system of marine floating raft using DDAM[J]. Noise and Vibration Control, 2012(6): 34-39. |
| [5] |
浦军, 石邦凯. 基于DDAM的某舰用升降装置抗冲击分析[J]. 舰船科学技术, 2017, 39(8): 128-132. PU Jun, SHI Bang-kai. Shock resistance analysis on certain ship lift based on DDAM[J]. Ship Science and Technology, 2017, 39(8): 128-132. DOI:10.3404/j.issn.1672-7649.2017.08.027 |
| [6] |
JIANG X, ZHANG Z O, SHEN W W. Researches on the anti-shock capability of a ship-borne cabinet based on DDAM, IET[C]//Asia International Symposium on Mechatronics, 2016.
|
| [7] |
赵应龙, 何琳, 吕志强. 应用DDAM进行船舶浮筏隔振装置抗冲击计算[J]. 工程力学, 2007, 24(4): 159-167. ZHAO Ying-long, HE Lin, LV Zhi-qiang. The application on DDAM on the computation on shock response of marine floating raft vibration-isolating system[J]. Engineering Mechanics, 2007, 24(4): 159-167. DOI:10.3969/j.issn.1000-4750.2007.04.028 |
| [8] |
郭君, 孙占忠, 黄式璋, 等. 舰艇气瓶基座结构抗冲击性能评估方法[J]. 中国舰船研究, 2018, 13(3): 90-96. GUO Jun, SUN Zhan-zhong, HUANG Shi-zhang, et al. Shock resistance evaluation method of ship air bottle-base connection structure[J]. Chinese Journal of Ship Research, 2018, 13(3): 90-96. |
| [9] |
程方训, 孙海军, 刘磊. 海上浮动核电站压力容器DDAM抗冲击计算[J]. 舰船科学技术, 2019, 41(3): 108-111. CHEN Fang-xun, SUN Hai-jun, LIU Lei. Shock response computation of floating nuclear power plant pressure vessel using DDAM[J]. Ship Science and Technology, 2019, 41(3): 108-111. |
| [10] |
韩江桂, 吴新跃, 贺少华. 船舶推进轴系冲击响应计算方法[J]. 舰船科学技术, 2012, 34(1): 45-49. HAN Jiang-gui, WU Xin-yue, HE Shao-hua. Research on shock response method of ship propulsive shafting[J]. Ship Science and Technology, 2012, 34(1): 45-49. DOI:10.3404/j.issn.1672-7649.2012.01.011 |
| [11] |
刘海超, 闫明, 冯麟涵. 带限位隔振系统的冲击响应分析[J]. 振动与冲击, 2019, 38(21): 172-177. LIU Hai-chao, YAN Ming, FENG Lin-han. Shock response of a vibration isolation system with displacement restrictors[J]. Journal of Vibration and Shock, 2019, 38(21): 172-177. |
 2021, Vol. 43
2021, Vol. 43
