2. 广州市顺海造船有限公司,广东 广州 511440
2. Guangzhou Shunhai Shipyards Ltd., Guangzhou 511440, China
水下航行器系统的航行预报是水下航行器系统设计和研究的一项重要工作内容,采用计算流体力学方法对水下航行器系统的航行特性进行数值分析,是开展这一工作的其中一种手段。对于水下航行器系统航行性能研究的数值分析方法一般分为两大类:体积力法和整体建模法。体积力法建模简单,但是不能直观的获取导管螺旋桨的水动力性能细节。整体建模法可以对真实流场细节进行计算模拟,其结果能直接获取螺旋桨作用区域的复杂流场信息,为水下航行器系统的研发提供设计依据,因而使用更为广泛[1]。
近年来国内外学者针对水下航行器系统航行预报进行了许多研究。杨琴等[2]采用数值模拟方法系统地研究了全附体潜艇+螺旋桨的三维黏性流场和水动力性能,通过改变螺旋桨转速得到潜艇在既定航速下的自航点。吴召华等[3]利用体积力模型计算了船体航行性能相关参数,验证了体积力法预报船体航行性能的准确性。Phillips[4]通过使用CFX/BEMT迭代的方法对KVLCC2在位于航行点时不同舵角下的斜航运动进行数值模拟,计算得到的力和力矩与实验结果符合。傅慧萍[5]使用体积力模型对KCS船进行自由液面的航行预报研究。
已有的研究通常是基于运动的相对性来对水下航行器系统进行航行预报,这种方法要么忽略了水下航行器系统在实际运动中水下航行器主体运动产生的伴流场影响;要么没有考虑推进系统在受到水下航行器主体影响时的推进性能变化。从提高水下航行器系统水动力数值预报结果与真实状态符合程度角度考虑,有必要采用更加完善和有效的计算方法来分析水下航行器系统的水动力特性。本文采用重叠网格和滑移网格相结合的混合网格技术,对某水下航行器系统整体航行进行直接模拟,研究水下航行器系统的航行预报和流场特性变化规律。
1 数值模拟基础 1.1 控制方程设定所研究的流体为不可压缩流体,则只考虑流场的连续性方程和动量方程,不计入能量方程,本文所研究问题的控制方程为[6]:
连续性方程
| $ \frac{{\partial {u_i}}}{{\partial {x_i}}} = 0, $ | (1) |
动量方程
| $ \rho \left(\frac{{\partial {u_i}}}{{\partial t}} + \frac{{\partial ({u_i}{u_j})}}{{\partial t}}\right) = \rho \frac{\partial }{{\partial {x_j}}}\left[\mu \left(\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}\right) - {u_i'u_j'}\right] + \rho {g_i} - \frac{{\partial p}}{{\partial {x_i}}}\text{。} $ | (2) |
其中:
本文使用
| $ \frac{{\partial (\rho k)}}{{\partial t}} + \frac{{\partial (\rho k{u_i})}}{{\partial {x_i}}} + \frac{{\partial (\rho k)}}{{\partial t}} = \frac{\partial }{{\partial {x_j}}}\left[{\varGamma _k}\frac{{\partial k}}{{\partial {x_j}}}\right] + {G_k} - {Y_k} + {S_k}, $ | (3) |
| $ \frac{{\partial (\rho \varepsilon )}}{{\partial t}} + \frac{{\partial (\rho \varepsilon {u_i})}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[{\varGamma _\omega }\frac{{\partial \omega }}{{\partial {x_j}}}\right] + {G_\omega } + {D_\omega } - {Y_\omega } + {S_\omega }, $ | (4) |
其中:
| $ {\varGamma _k} = \mu + \frac{{{\mu _t}}}{{{\sigma _k}}}, $ | (5) |
| $ {\varGamma _\omega } = \mu + \frac{{{\mu _t}}}{{{\sigma _\omega }}}\text{。} $ | (6) |
式中:
通过对不同的计算域采用不同的网格方法,对水下航行器的航行运动特性进行数值分析。重叠网格是由Steger等[8]提出的网格划分方法,相较于传统网格划分,重叠网格将计算域分成为多个互相重叠的小计算域,彼此之间独立生成网格,当不同计算域的重叠网格进行运动的时候,避免了运动中网格的变形和重构,只有处于重叠网格区域的边界点会进行插值计算,无需重新生成网格。对水下航行器系统这种复杂外形几何体的数值模拟使用重叠网格可以保证网格质量和精度,提高计算准确性[9]。
滑移网格[10]则是通过将计算区域划分为小的子区域,子区域各自独立运动,子区域之间的交界面相互滑动。不同于重叠网格,交界面两侧的网格不需要重合,但是为了能够使用交界面技术时对不同子区域的数值计算结果进行交换,交界面两侧的网格尺寸差距不应过大,以减小误差。
本文通过将航行器主体周围与导管内流场之间的流场分别使用重叠网格和滑移网格相结合的混合网格技术对对本课题组自主研发的水下航行器系统模型进行直接模拟,对使用混合网格技术模拟水下航行器系统航行运动条件下水动力特性的技术特点进行观察。
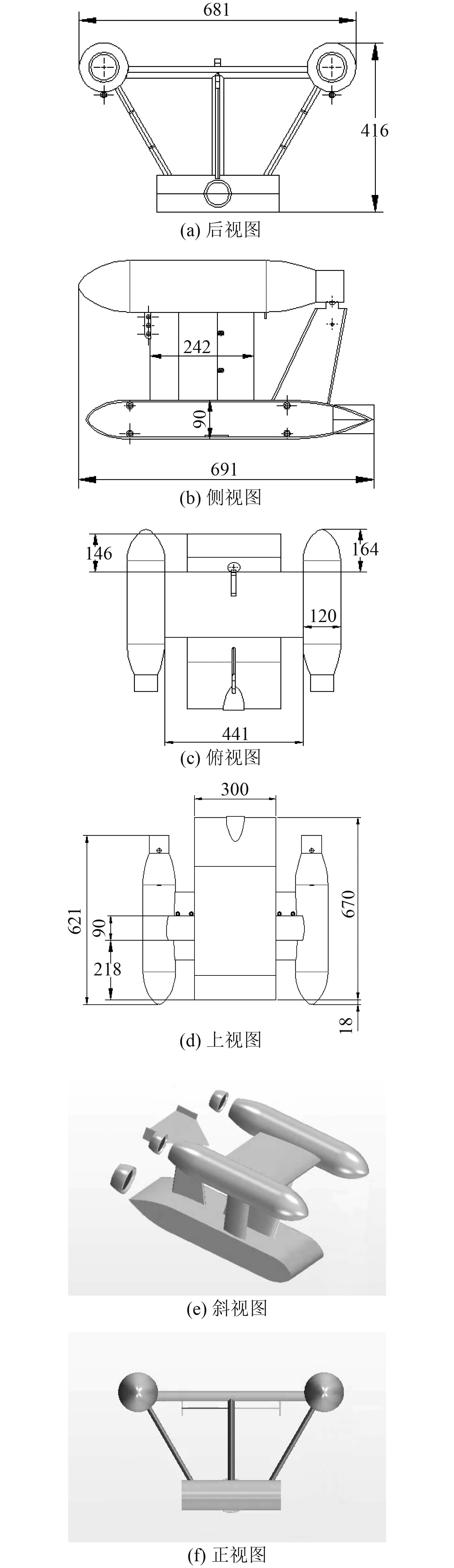
2 计算对象 2.1 水下航行器系统模型本文使用的计算对象为本项目组所研发的一种水下航行器系统,它包括水下航行器主体、作为推进系统的导管螺旋桨以及其余附体,导管螺旋桨设计参数如表1和表2所示。为了进行数值计算,首先通过三维建模软件SolidWorks对水下航行器系统进行几何建模,水下航行器系统结构设计参数与完成后得到的水下航行器系统三维几何模型如图1所示。
|
|
表 1 浮筒后导管螺旋桨设计参数 Tab.1 Design parameters of no.1 ducted propeller |
|
|
表 2 吊舱后导管螺旋桨设计参数 Tab.2 Design parameters of no.2 ducted propeller |
|
图 1 水下航行器系统三维几何模型 Fig. 1 The model of the underwater vehicle system |
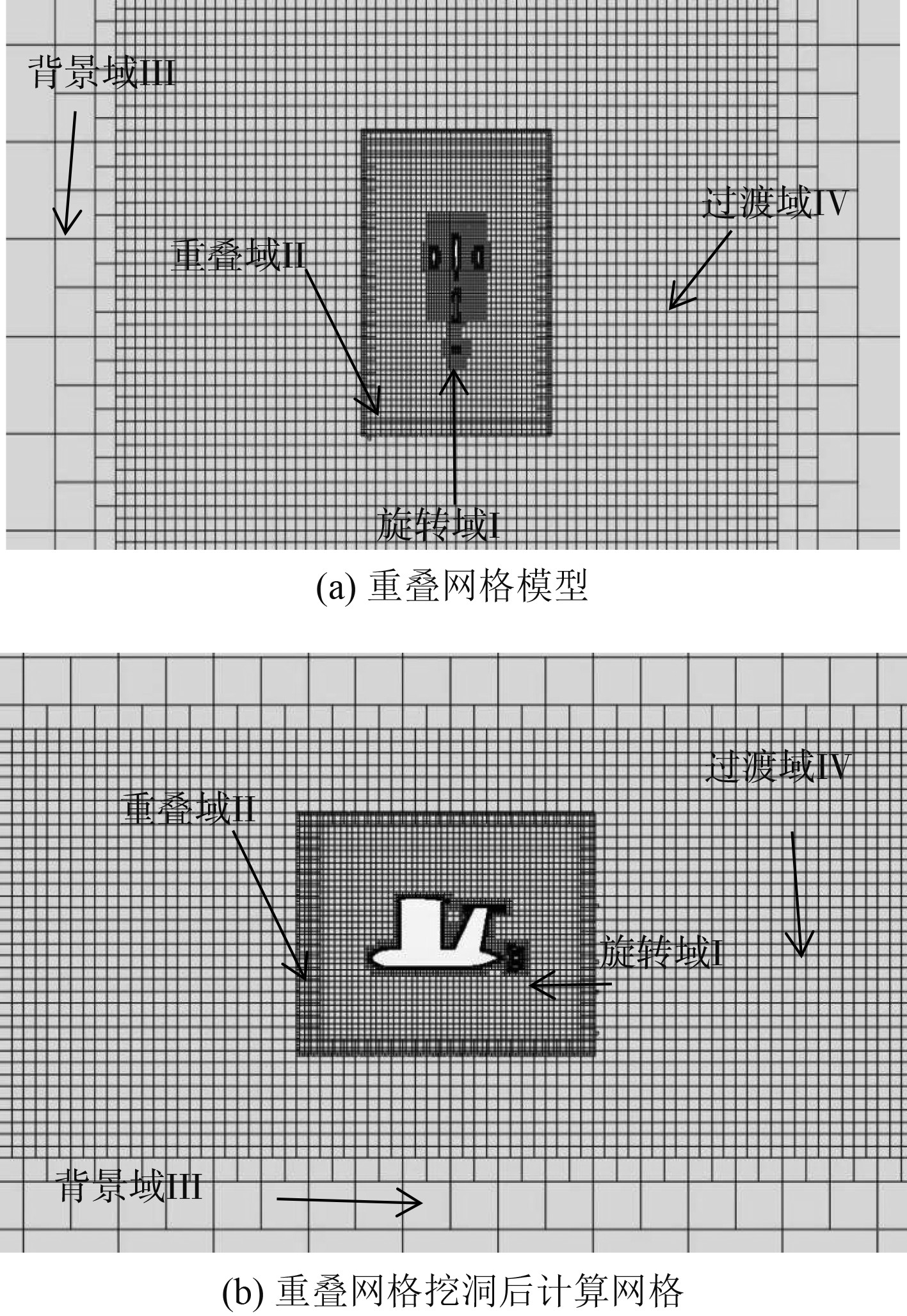
对本文使用的水下航行器系统进行计算域的设置。整个计算域划分为包含螺旋桨的旋转计算域I、包含水下航行器系统的重叠域II和包含整个数值水池的背景域III,为避免重叠域和背景域网格尺寸相差过大,设置一个过渡计算域IV。其中,旋转计算域I是直径为1.2倍螺旋桨直径,长度为3 cm的圆柱体,重叠域II为长为1.6 m,宽为1.3 m,高为1.3 m的长方体,背景域III为一尺度为长为24 m,宽为23 m,高为14 m的长方体,过渡计算域IV为长为12 m,宽为3 m,高为2 m的长方体。通过这样一种方式构成一个整体后的组合计算域的外围边界即为原来矩形背景域III的边界。图2 ~ 图4为水下航行器主体与导管螺旋桨的网格划分、水下航行器系统周围流场网格构建,以及本文所使用的计算域整体划分结果图。

|
图 2 水下航行器表面网格 Fig. 2 The surface mesh of the underwater vehicle system |
|
图 3 水下航行器系统周围流场网格 Fig. 3 The flow field mesh of the underwater vehicle system |
|
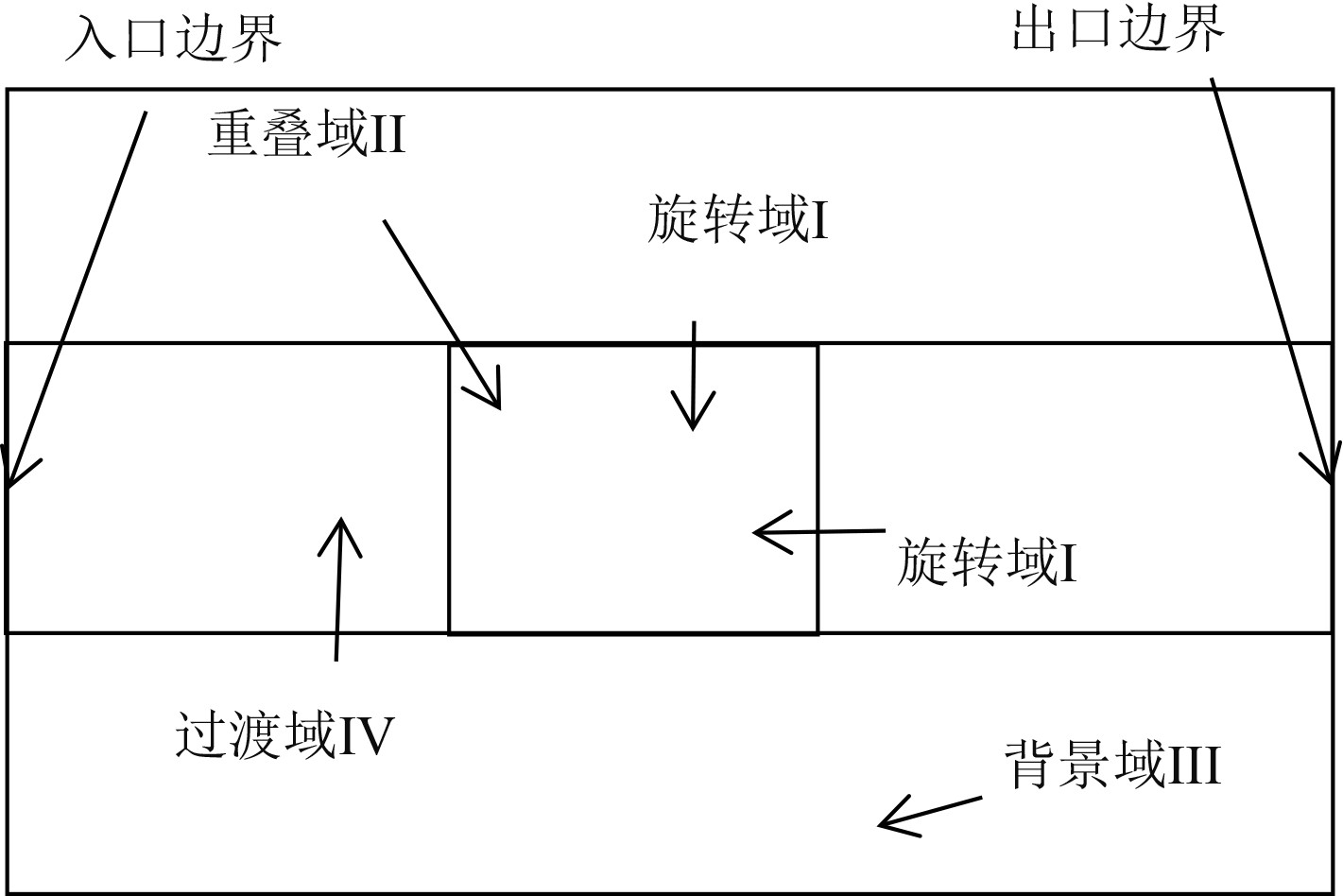
图 4 计算域整体划分 Fig. 4 Computational domain division of system |
如图4所示,立方体的左侧面为入口边界,右侧面为出口边界,其余为对称边界。将入口边界设置为速度入口,出口边界设置为压力出口,其余各面设置为对称面。针对不同的工况,改变不同的物理条件进行初始化设置,表3和表4给出了计算中所使用的计算域边界条件和初始条件。
|
|
表 3 边界条件 Tab.3 The boundary conditions |
|
|
表 4 初始条件 Tab.4 The initial conditions |
利用构建的计算域对图1所示的水下航行器系统在水平面上的航行运动特性进行计算观察,计算中设定水下航行器系统在水平面操纵运动时,其重力与浮力平衡,即系统在垂直方向上所受的合力为零。为了得到不同推力下水下航行器系统的航行速度,使用STAR CCM+中的重叠网格和滑移网格相结合的混合网格技术与DFBI模块,以数值模拟手段分析水下航行器系统在推力作用下,从静止到达到最大航行速度的运动过程,观察在这一过程中航行器主体所受的阻力变化,同时计算各个导管螺旋桨在受到主体影响时所产生的推力和航行状态下的动力学特征。其基本分析流程如下:
1)对放置在浮筒后方和吊舱后方的导管螺旋桨进行模拟计算,取3种螺旋桨转速分别表示螺旋桨高速旋转、中速旋转、低速旋转情况,得到在主体影响下的导管螺旋桨的转速-推力曲线。
2)设置好初始条件和边界条件后,对水下航行器系统进行直接模拟。施加恒定轴向推力
3)将获得的结果绘制推力-速度曲线,通过插值可以得到水下航行器系统在任一轴向推力作用下的航行速度,或达到任一最大航行速度推进系统所需要提供的推力大小。
4)为使水下航行器系统能够在实际航行中以工程所需的航速航行,可以通过推力-速度曲线获得所需航速对应的推力大小,再通过得到的导管螺旋桨转速-推力曲线,进行推力分析得到对应的导管螺旋桨转速,在此基础上进行稳定性计算,即可通过调整不同导管螺旋桨转速产生相应推力,使其满足推力要求的同时也能保持航行稳定。
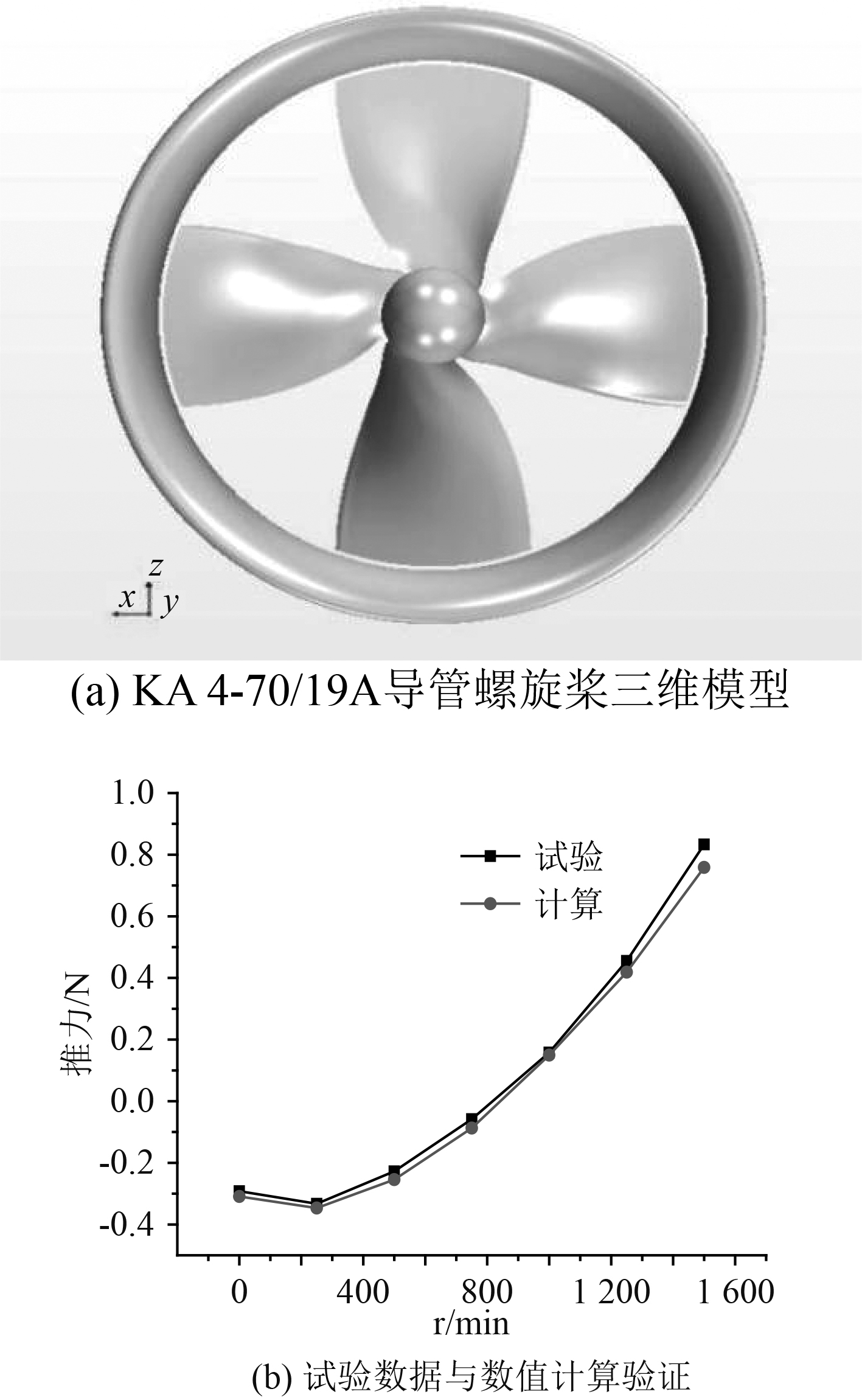
3 计算结果与分析 3.1 数值模型验证为了检验本文所提出数学模型的有效性,选用与水下航信器系统中类似的KA 4-70 /19A 导管螺旋桨,在已有试验数据的基础上[11],以与该类导管螺旋桨敞水试验相同的条件下,采用本文所使用的计算域IV、计算网格与计算方法对导管螺旋桨在轴向流条件下的推力特性进行数值模拟,将数值模拟结果与试验结果进行比较,观察本文采用的计算方法预报导管螺旋桨推力的可靠性。在数值模拟中,导管螺旋桨的计算参数取为与敞水试验条件一致的数值,分析中采用了如图4所示的计算域,来流的方向垂直于进口边界,导管螺旋桨的主要参数以及计算域的参数取值表1~表4。图5给出KA 4-70 /19A导管螺旋桨数值模拟时所产生推力与试验结果的比较,可以看出数值模拟结果与试验结果符合良好。由此可知:
|
图 5 KA 4-70/19A导管螺旋桨数值验证 Fig. 5 Numerical validation of KA 4-70/19A ducted propeller |
在使用重叠网格时,当水下航行器系统运动时,重叠网格会一起运动,由于涉及到网格挖洞和插值计算,重叠域网格和背景域网格的大小尺度比对于计算结果至关重要,当尺度差距过大时,会带来误差[12],甚至无法有效进行数值模拟。本文针对3种不同尺度的背景网格大小,研究背景网格尺度对计算结果的影响。
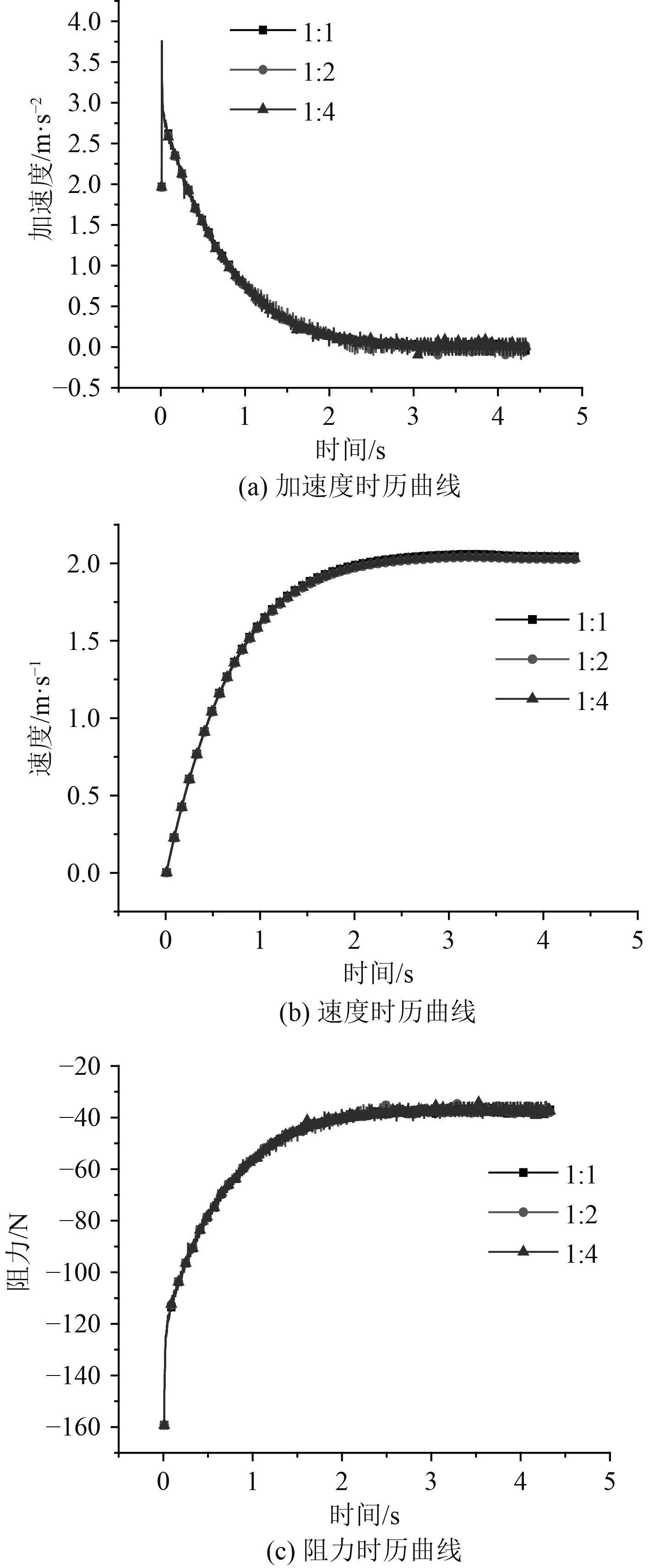
图6给出了不同网格尺度时,水下航行器系统在38 N恒定推力作用下进行航行时的各物理量历时曲线。通过观察可以发现,在相同数量级网格尺寸下,重叠域网格和背景域网格的尺度比对计算结果影响很小。当尺度比不同时,计算产生的结果误差很小,同时不同尺度比都呈现了相同的规律。随着水下航行器系统速度的增加,水下航行器系统受到的阻力也在增加,同时由于推力不变,合力变小,加速度也在减小。这说明当网格尺度都保持相同数量级的时候,增大或减小尺度比对计算结果的影响不大,但过多的网格数需要更大计算资源。为了平衡计算资源和计算结果的精度,本文采用尺度比为1∶2的网格划分方法进行计算。
|
图 6 不同网格尺度比计算结果比较 Fig. 6 The results of different mesh scale ratios |
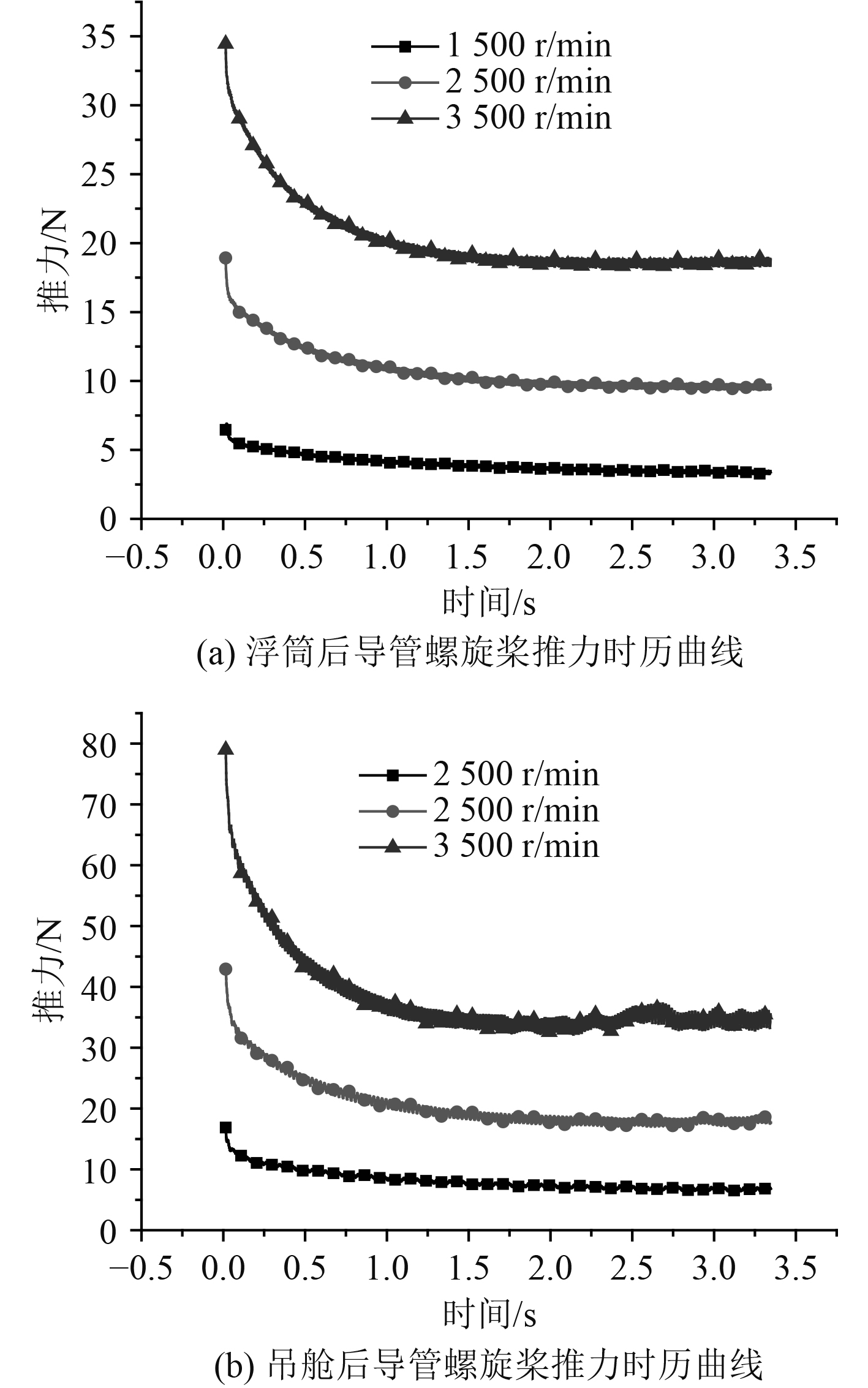
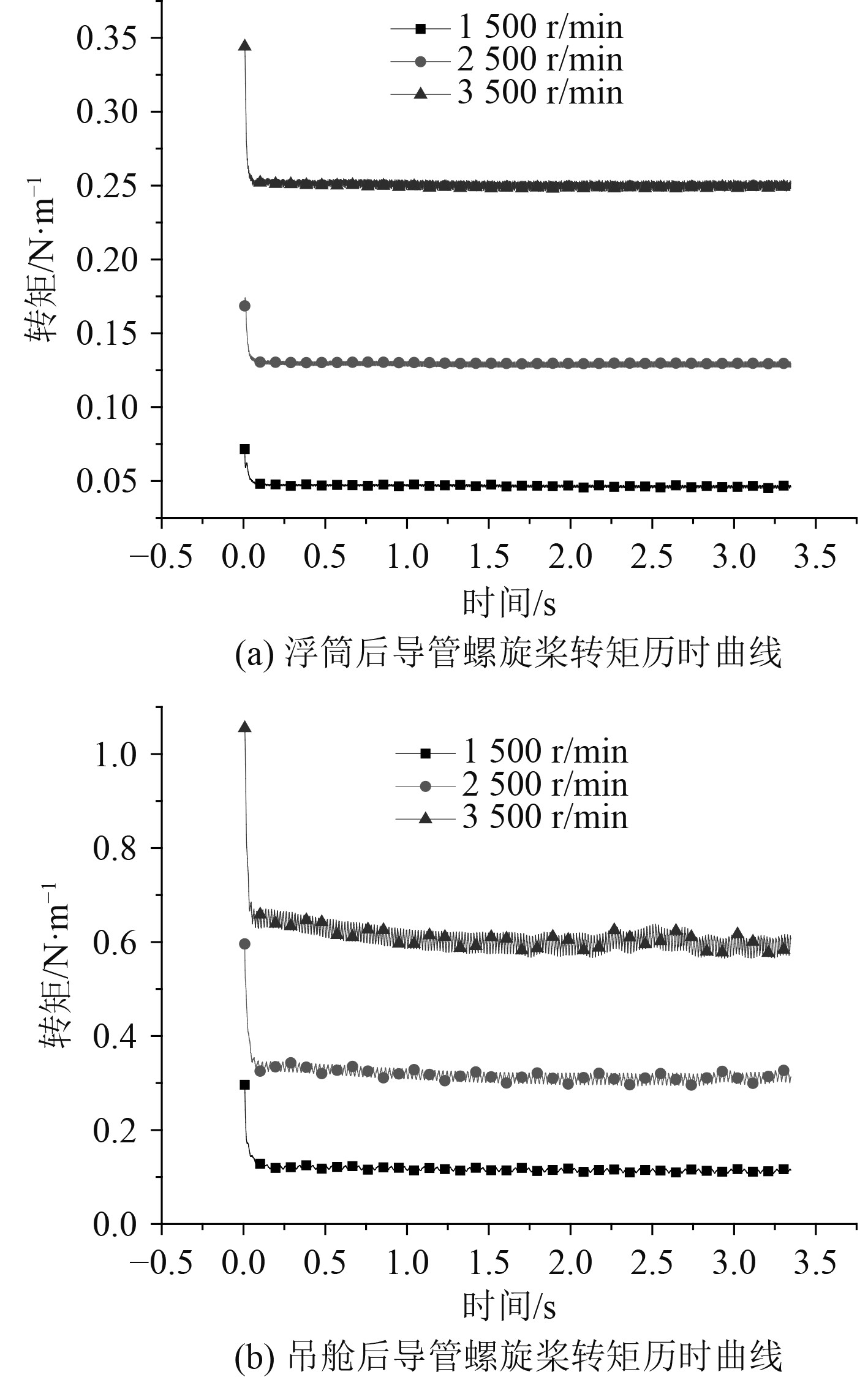
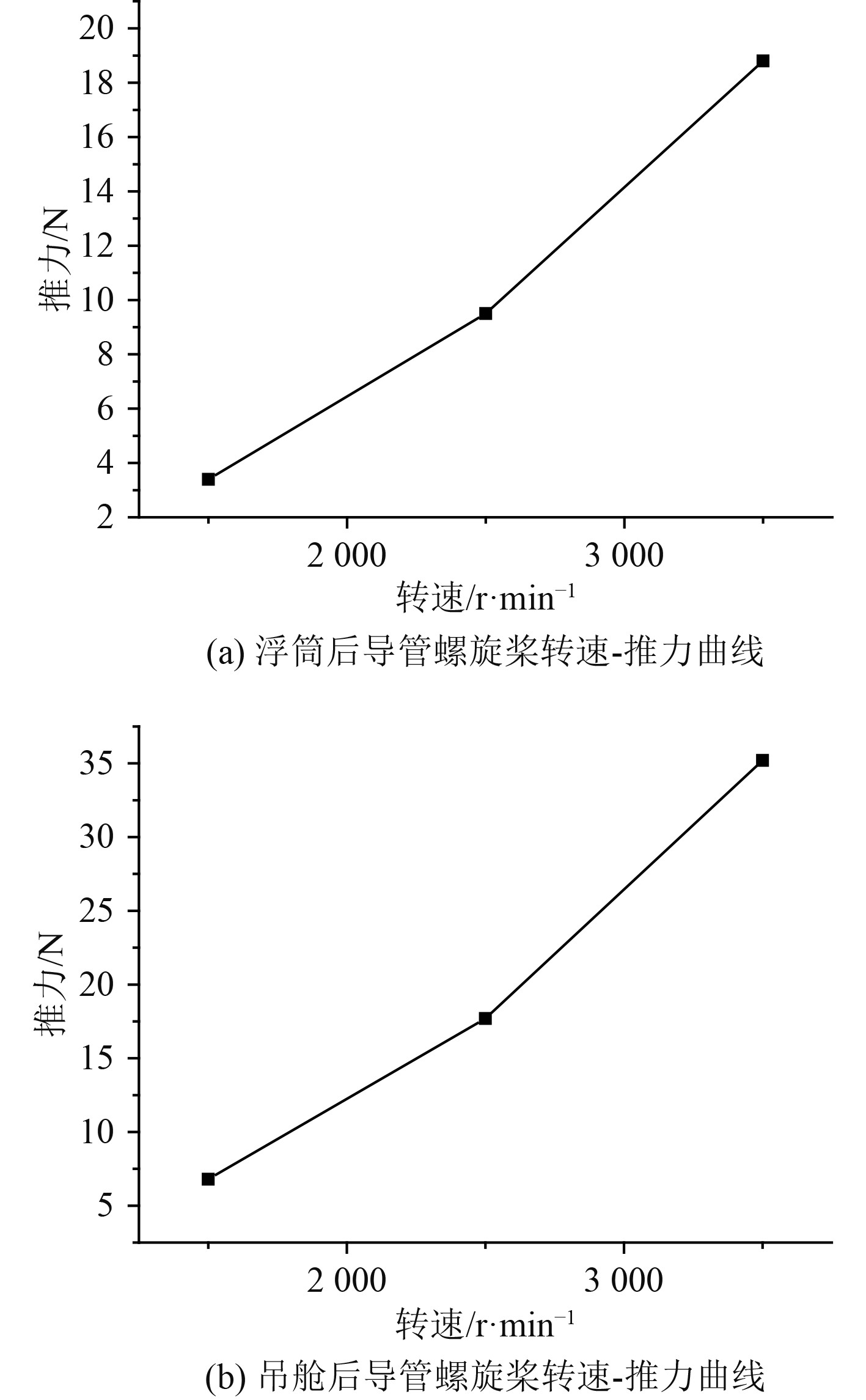
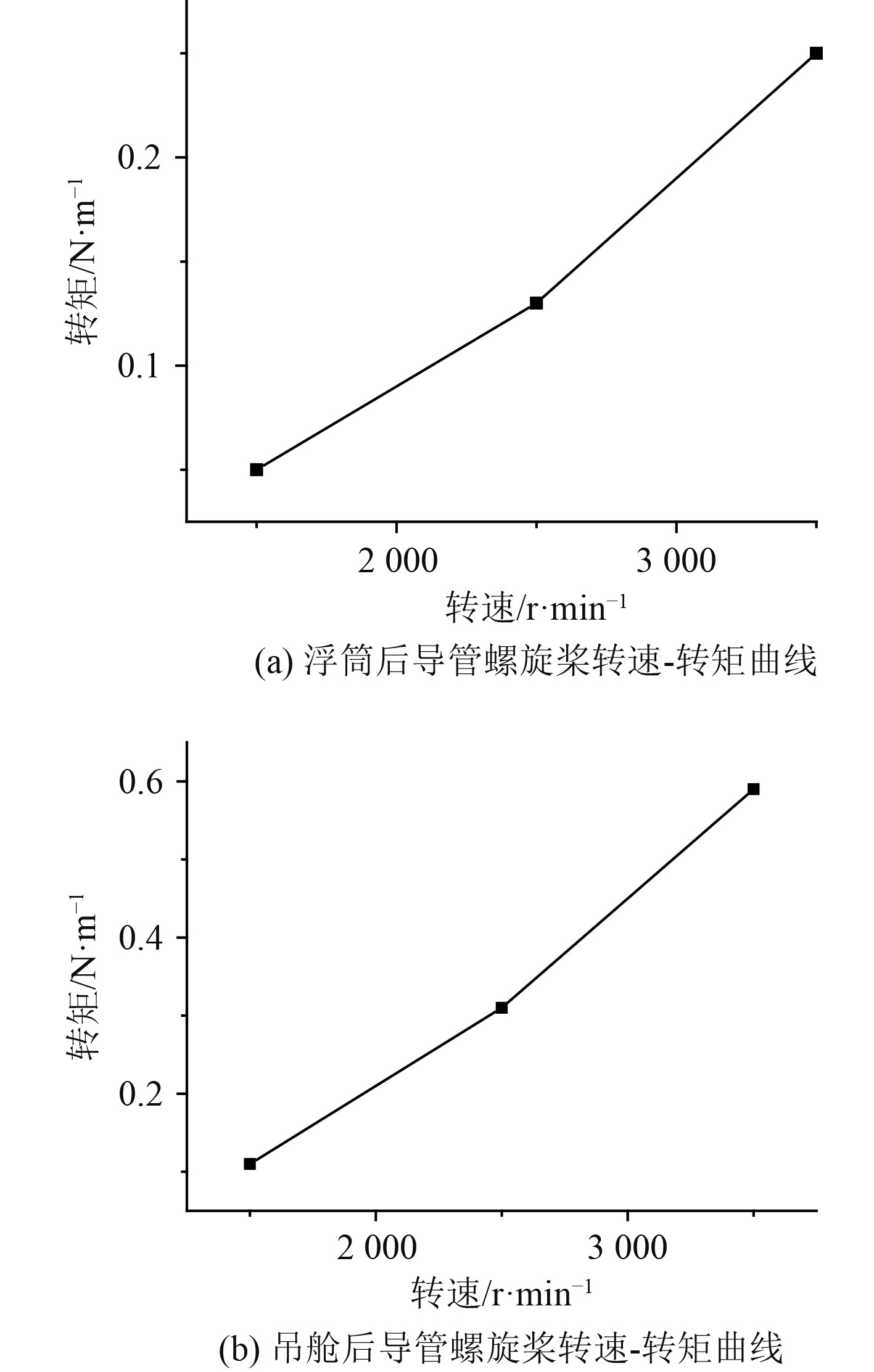
为得到导管螺旋桨在受到水下航行器主体影响下的转速-推力曲线,对静水环境下导管螺旋桨不同转速时的水动力性能进行分析。本文所使用的导管螺旋桨参数见表1和表2,由于导管螺旋桨最大支持转速为4000 r/min,设置1500 r/min,2500 r/min,3500 r/min分别表示低转速、中转速和高转速情况下,导管螺旋桨的工作情况。图7和图8为3种转速下导管螺旋桨受到主体影响的推力历时曲线和转矩历时曲线,从中观察到导管螺旋桨的推力和转矩迭代结果稳定,螺旋桨转速越大,其推力值和转矩值也越大。图9和图10为导管螺旋桨在水下航行器主体影响下的转速-推力曲线和转速-转矩曲线,通过插值的方法可以得到不超过最大转速时任一转速下的推力和转矩结果。
|
图 7 导管螺旋桨推力时历曲线 Fig. 7 Thrust duration curve of ducted propeller |
|
图 8 导管螺旋桨转矩时历曲线 Fig. 8 Torque duration curve of ducted propeller |
|
图 9 导管螺旋桨转速-推力曲线 Fig. 9 Speed of ducted propeller and thrust curve |
|
图 10 导管螺旋桨转速-力矩曲线 Fig. 10 Speed of ducted propeller and torque curve |
使用图4所示的计算域及表3和表4设置的边界条件和初始条件,分别设置3种推力分别对应水下航行器的低速前进、中速前进和高速前进情况,进行水下航行器系统航行模拟,计算工况如表5所示。
|
|
表 5 水下航行器系统计算工况 Tab.5 The calculated conditions |
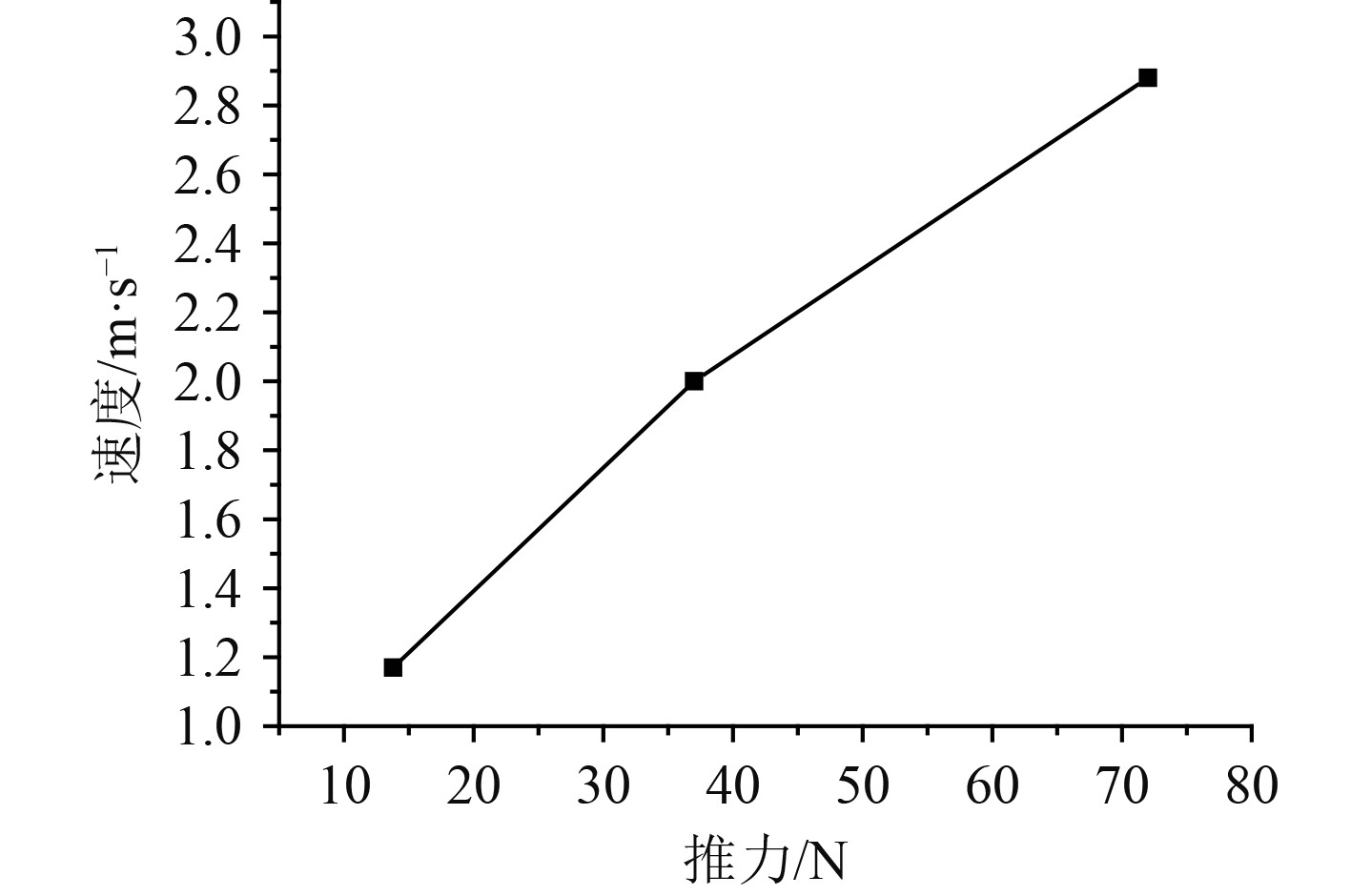
当水下航行器系统轴向合力为0时,说明水下航行器系统加速度为0,当前速度即为水下航行器系统的最大航行速度,当数值计算中水下航行器系统的推力和阻力大小相同、加速度在0附近周期性振荡、速度不再发生变化时,可以认为水下航行器系统已经达到受力平衡状态,取此时的结果作为最大航行速度值。图11为整理得到的推力-速度曲线,根据航行特性分析流程,可以通过图11所示曲线插值得到静水环境中任一推力下水下航行器系统的航行速度。
|
图 11 水下航行器系统推力-速度曲线 Fig. 11 Speed of underwater vehicle system and thrust curve |
图12为水下航行器系统在不同来流速度下时表面所受压力云图和导管螺旋桨不同转速时的流场分布,可以发现不同条件下水下航行器系统在前进时所受表面压力规律相同,迎流面所受压力最大,浮筒和吊舱所受压力较为均匀,而低压区出现在吊舱侧面和斜撑表面等位置。同时观察可以发现水下航行器系统在不同导管螺旋桨转速旋转时周围流场分布规律相似,吊舱首部迎流面、吊舱尾部和导管螺旋桨周围流场更为复杂,尾部螺旋桨后方都会产生回流现象,回流范围与螺旋桨转速成正比,当转速较大时,回流范围更长;周围流场的复杂度与螺旋桨转速呈正比,当转速越大时,周围流场更为复杂

|
图 12 水下航行器系统表面压力云图与流场分布 Fig. 12 Surface pressure nephogram and flow field distribution |
本文使用重叠网格和滑移网格相结合的混合网格技术对某水下航行器系统进行了航行预报的研究,直观清晰地描述了水下航行器系统航行预报的方法,并计算得到了水下航行器系统的推力-速度曲线,对水下航行器主体在航行时的表面压力分布情况以及水下航行器系统周围伴流场进行了分析,得出如下基本结论:
1)使用本文所描述的数值模型能够有效的计算实际运动中的相关物理量,对KA 4-70/19A导管螺旋桨的敞水试验模拟,得到的结果与试验数据较好地拟合,间接验证了使用混合网格技术进行航行预报的可靠性。
2)通过对不同推力作用下水下航行器系统运动进行分析,得到了水下航行器系统的推力-速度曲线,通过对曲线进行插值可以得到不同推力下水下航行器系统的航行速度或达到设计航速时需要的推力大小,完成对水下航行器系统的航行预报。
3)不同的网格尺度比对计算结果有影响,但是当网格尺度在同一数量级的时候,增大或减小尺度比对计算结果的影响较小,考虑到计算资源和计算时间的大小,合理的选择网格尺度比可以达到计算资源与计算精度之间的平衡。
4)对导管螺旋桨在水下航行器主体影响下的推力和力矩特性进行了分析,计算得到了静水环境下导管螺旋桨的推力和转矩数据,绘制了转速-推力曲线和转速-转矩曲线。
| [1] |
沈兴荣, 冯学梅, 蔡荣泉. 大型集装箱船桨舵干扰黏性流场的数值计算研究[J]. 船舶力学, 2009, 13(4): 540-550. DOI:10.3969/j.issn.1007-7294.2009.04.005 |
| [2] |
杨琴, 王国栋, 张志国, 等. 基于CFD的潜艇模型航行仿真分析[J]. 中国舰船研究, 2013, 8(4): 22-27. |
| [3] |
吴召华, 陈作钢, 代燚. 基于体积力法的船体航行性能数值预报[J]. 上海交通大学学报, 2013, 47(60): 943-949. |
| [4] |
PHILLIPS A B, TUMOCK S R, FURLONG M. Evaluation of manocuvring coefficients of a self-propelled ship using a blade element momentum propeller model coupled to a Reynolds averaged Navier Stokes flow solver[J]. Ocean Engineering, 2009, 36(15-16): 1217-1225. DOI:10.1016/j.oceaneng.2009.07.019 |
| [5] |
傅慧萍. 一种基于体积力螺旋桨模型的航行计算方法[J]. 船舶力学, 2015, 19(7): 791-796. DOI:10.3969/j.issn.1007-7294.2015.07.005 |
| [6] |
VERSTEEG M. An introduction to computational fluid dynamics: the finite volume method[M]. Wiley, New York, 1995.
|
| [7] |
MENTER, F. R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications[J]. AIAA Journal, vol. 32, no 8 pp. 1598-1605.
|
| [8] |
STEGER J L, DOUGHERTY F C, BENEK J A. A chimera grid scheme[C]//Mini Symposium on Advances in Grid Generation, 1982.
|
| [9] |
PEACE DG, ATANLEY S, MARTIN F, et al. Development of a large Chimera grid system for space shuttle. AIAA 930533, 1993.
|
| [10] |
沈海龙, 苏玉民. 基于滑移网格技术的船桨相互干扰研究[J]. 哈尔滨工程大学学报, 2010, 31(1): 1-7. DOI:10.3969/j.issn.1006-7043.2010.01.001 |
| [11] |
STEPHEN C. S, DANIEL M. E, et al. Design and characterization of a small-scale azimuthing thruster for a mobile offshore base module[J]. Marine Structures. 2001, 14: 215-229.
|
| [12] |
李鹏, 高振勋, 蒋崇文. 重叠网格方法的研究进展[J]. 力学与实践, 2014, 36(5): 551-565. DOI:10.6052/1000-0879-14-011 |
 2021, Vol. 43
2021, Vol. 43
