圆柱壳是水下航行器的重要组成结构,其振动声辐射特性的研究具有重要的工程意义。Wang[1]研究了有限长圆柱壳的振动特性。内部含有肋骨[2]、铺板[3]、舱壁[4]等结构的圆柱壳也得到了学者的关注。
Pan等[5]采用波动法研究了加筋圆柱壳的自由振动特性,环肋采用平摊法处理,该方法局限于均匀分布的小尺寸环向加筋。庞福振等[6]采用精细传递矩阵法评估水下加筋圆柱壳的辐射声压,应用叠加原理、增量存储以及改进非齐次项求解方法,提出了改进的精细传递矩阵法,并进一步分析了边界条件、流体介质以及圆柱壳厚度对辐射声压的影响。肖邵予[7]基于Hamilton变分原理研究了两端用端板封口的加筋圆柱壳声辐射特性,以及圆柱壳内声场对其声振特性的影响。陈美霞等[8]采用波动法研究了多舱段加筋圆柱壳的振动特性,加筋采用圆环板模型,舱壁采用圆板模型,给出了舱段截断时边界条件的选取原则。Wei等[9]采用波动法研究了非均匀加筋圆柱壳的自由振动特性。
然而,在实际工程中,圆柱壳内部的结构是不规则的,解析方法不再适用。有限元法和边界元法可以用来分析复杂结构的振动声辐射问题,但是随着分析频率增大,网格数量急剧增多,计算效率会降低。
Maxit[10]提出一种子结构法CAA(Circumferential Admittance Approach)来分析水下含轴对称内部结构(环肋、舱壁、端板等)圆柱壳的振动声辐射,圆柱壳在波数域中求解,内部结构利用轴对称有限元法处理。由于轴对称有限元法只能分析轴对称结构,这在一定程度上限制了CAA的应用范围。
本文结合解析法计算效率高和有限元法适用范围广的优点,将水下含内部结构圆柱壳分为水下圆柱壳和内部结构两部分。首先,采用轴对称边界元法[11-12]计算圆柱壳表面声阻抗;其次,结合Flügge壳体理论[13]以及三角函数,建立水下圆柱壳的数理模型;再次,采用有限元法得到内部结构的动力学方程,并对方程进行动力学缩聚,以缩减计算规模。最后,根据圆柱壳与内部结构接触点的位移协调和内力平衡条件,建立整个结构的动力学方程,求解方程得到壳体表面振动速度,再采用边界元法计算壳体辐射声压。
1 数理模型整个模型可分解为圆柱壳和内部结构,由于采用有限元法对内部结构进行动力学建模,内部结构可以是梁、板以及其他复杂结构,为方便陈述,以内部基座为代表进行本文方法的介绍,如图1所示。柱坐标系

|
图 1 含内部结构圆柱壳示意图 Fig. 1 Schematic diagram of the cylindrical shell with internal structures |
基于Flügge壳体理论,水下圆柱壳运动微分方程可写为:
| $ \begin{split}\dfrac{{Eh}}{{1 - {\mu ^2}}}\left[ {\boldsymbol{L}} \right]\left\{ {\begin{array}{*{20}{c}} u \\ v \\ w \end{array}} \right\} =& \left\{ {\begin{array}{*{20}{c}} {{F_x} + \dfrac{1}{{2R}}\dfrac{{\partial {M_r}}}{{\partial \theta }}} \\ {{F_\theta } + \dfrac{1}{R}{M_x} - \dfrac{1}{2}\dfrac{{\partial {M_r}}}{{\partial x}}} \\ {{F_r} - \dfrac{1}{R}\dfrac{{\partial {M_x}}}{{\partial \theta }} + \dfrac{{\partial {M_\theta }}}{{\partial x}}} \end{array}} \right\}\times\\ &\delta (x - {x_0})\delta (\theta - {\theta _0}) - \left\{ {\begin{array}{*{20}{c}} 0 \\ 0 \\ p \end{array}} \right\} \text{。}\end{split}$ | (1) |
式中,
对于两端简支圆柱壳,
| $ \left\{ \begin{gathered} u = \sum\limits_{m = 1}^M {\sum\limits_{n = - N}^N {{U_{mn}}\cos ({k_m}x)\exp (jn\theta )\exp (j\omega t)} }\text{,} \hfill \\ v = \sum\limits_{m = 1}^M {\sum\limits_{n = - N}^N {{V_{mn}}\sin ({k_m}x)\exp (jn\theta )\exp (j\omega t)} }\text{,} \hfill \\ w = \sum\limits_{m = 1}^M {\sum\limits_{n = - N}^N {{W_{mn}}\sin ({k_m}x)\exp (jn\theta )\exp (j\omega t)} }\text{。} \hfill \\ \end{gathered} \right. $ | (2) |
式中:
对一封闭结构,
| $ c(P)p(P) = \int\limits_S \left[ {p(Q)\frac{{\partial G(P,Q)}}{{\partial {n_q}}} + j{\rho _0}\omega \bar v(Q)G(P,Q)} \right]{\text{d}}{S_q}\text{。} $ | (3) |
式中:
| $ c(P) = 1 + \int\limits_S {\frac{\partial }{{\partial {n_q}}}\left[ {\frac{1}{{4\text{π} \bar R(P,Q)}}} \right]{\text{d}}{S_q}}\text{。} $ | (4) |
对于轴对称封闭结构(见图2),式(3)中的物理量可展开为Fourier级数:
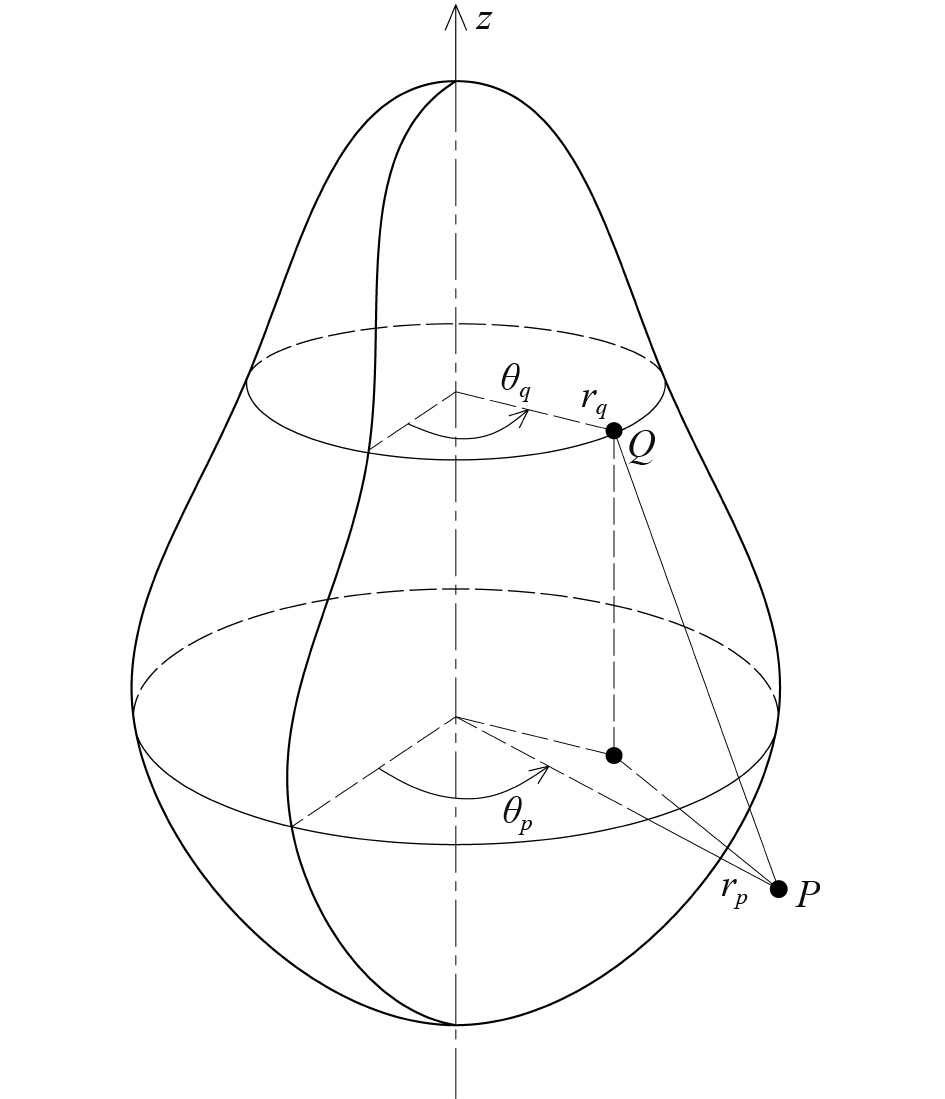
|
图 2 轴对称结构示意图 Fig. 2 Schematic diagram of a axisymmetric structure |
| $ \begin{split} & p(P) = \sum\limits_{n = 0}^\infty {\left[ {p_n^{c * }\cos (n{\theta _p}) + p_n^{s * }\sin (n{\theta _p})} \right]} \text{,} \\ & p(Q) = \sum\limits_{n = 0}^\infty {\left[ {p_n^c\cos (n{\theta _q}) + p_n^s\sin (n{\theta _q})} \right]} \text{,} \\ & \bar v = \sum\limits_{n = 0}^\infty {\left[ {\bar v_n^c\cos (n{\theta _q}) + \bar v_n^s\sin (n{\theta _q})} \right]} \text{,} \end{split} $ | (5) |
式中,
经过数学推导[11-12],式(3)可转化为柱坐标系中的线积分方程:
| $ \begin{split} & c(P)p_n^{c * }(P) = \int_\Gamma {\left[ {p_n^cH_n^\prime + j{\rho _0}\omega \bar v_n^c{H_n}} \right]{r_q}{\text{d}}{\varGamma _q}} \text{,} \\ & c(P)p_n^{s * }(P) = \int_\Gamma {\left[ {p_n^sH_n^\prime + j{\rho _0}\omega \bar v_n^s{H_n}} \right]{r_q}{\text{d}}{\varGamma _q}} \text{。} \end{split} $ | (6) |
其中:
| $ {H_n} = \int_0^{2\text{π} } {\frac{{{e^{ - jk\bar R}}}}{{4\text{π} \bar R}}\cos (n\theta ){\text{d}}\theta }\text{。} $ | (7) |
针对式(6)采用高斯求积公式,将母线
| $ r = \sum\limits_{i = 1}^3 {{r_i}{N_i}(\xi )} ,\;\;z = \sum\limits_{i = 1}^3 {{z_i}{N_i}(\xi )} \text{。}$ | (8) |
式中:
母线
| $\begin{split} {\text{d}}\Gamma =& \sqrt {{{{\text{(d}}r)}^2} + {{({\text{d}}z)}^2}} = \sqrt {{{\left(\frac{{{\text{d}}r}}{{{\text{d}}\xi }}\right)}^2} + {{\left(\frac{{{\text{d}}z}}{{{\text{d}}\xi }}\right)}^2}} {\text{d}}\xi = \\ &\sqrt {{{\left(\sum\limits_{i = 1}^3 {{r_i}\frac{{{\text{d}}{N_i}}}{{{\text{d}}\xi }}} \right)}^2} + {{\left(\sum\limits_{i = 1}^3 {{z_i}\frac{{{\text{d}}{N_i}}}{{{\text{d}}\xi }}} \right)}^2}} {\text{d}}\xi = J{\text{d}}\xi\text{,}\end{split} $ | (9) |
采用节点插值,单元内的声压和法向速度可以表示为:
| $ \begin{split} & p_n^c = \sum\limits_{i = 1}^3 {p_{ni}^c{N_i}(\xi )} ,\;\;\;\bar v_n^c = \sum\limits_{i = 1}^3 {\bar v_{ni}^c{N_i}(\xi )} \text{,} \\ & p_n^s = \sum\limits_{i = 1}^3 {p_{ni}^s{N_i}(\xi )} ,\;\;\;\bar v_n^s = \sum\limits_{i = 1}^3 {\bar v_{ni}^s{N_i}(\xi )} \text{。} \end{split} $ | (10) |
将式(8)~式(10)代入式(6),可将母线
| $ \begin{split} c(P)p_n^{c * }(P) =& \sum\limits_{e = 1}^{{N_e}} \left[ \int_{ - 1}^1 {p_{en}^cH_{en}^\prime {r_{eq}}{J_e}{\text{d}}\xi } + \right.\\ &\left.j{\rho _0}\omega \int_{ - 1}^1 {\bar v_{en}^c{H_{en}}{r_{eq}}{J_e}{\text{d}}\xi } \right]\text{,} \\ c(P)p_n^{s * }(P) = &\sum\limits_{e = 1}^{{N_e}} \left[ \int_{ - 1}^1 {p_{en}^sH_{en}^\prime {r_{eq}}{J_e}{\text{d}}\xi } +\right.\\ &\left.j{\rho _0}\omega \int_{ - 1}^1 {\bar v_{en}^s{H_{en}}{r_{eq}}{J_e}{\text{d}}\xi } \right]\text{,} \end{split} $ | (11) |
式中,
| $ \begin{split} c(P)p_n^{c * }(P) =& \sum\limits_{e = 1}^{{N_e}} \left[ \sum\limits_{g = 1}^{{N_g}} {{\kappa _g}p_{en}^c({\zeta _g})H_{en}^\prime ({\zeta _g}){r_{eq}}({\zeta _g}){J_e}{\text{(}}{\zeta _g}{\text{)}}} + \right.\\ &\left.j{\rho _0}\omega \sum\limits_{g = 1}^{{N_g}} {{\kappa _g}\bar v_{en}^c({\zeta _g}){H_{en}}({\zeta _g}){r_{eq}}({\zeta _g}){J_e}{\text{(}}{\zeta _g}{\text{)}}} \right] \text{,} \\ c(P)p_n^{s * }(P) =& \sum\limits_{e = 1}^{{N_e}} \left[ \sum\limits_{g = 1}^{{N_g}} {{\kappa _g}p_{en}^s({\zeta _g})H_{en}^\prime ({\zeta _g}){r_{eq}}({\zeta _g}){J_e}{\text{(}}{\zeta _g}{\text{)}}} +\right.\\ &\left.j{\rho _0}\omega \sum\limits_{g = 1}^{{N_g}} {{\kappa _g}\bar v_{en}^s({\zeta _g}){H_{en}}({\zeta _g}){r_{eq}}({\zeta _g}){J_e}{\text{(}}{\zeta _g}{\text{)}}} \right] \text{。} \end{split} $ | (12) |
其中:
采用“配点法”,将式(12)中的
| $ \begin{split} &{\boldsymbol{{\rm A}}}_n^c \cdot {\boldsymbol{p}}_n^c = {\boldsymbol{B}}_n^c \cdot {\boldsymbol{\bar v}}_n^c \text{,} \\ &{\boldsymbol{{\rm A}}}_n^s \cdot {\boldsymbol{p}}_n^s = {\boldsymbol{B}}_n^s \cdot {\boldsymbol{\bar v}}_n^s \text{。} \end{split} $ | (13) |
式中,若单元
根据式(2)和式(13),可计算圆柱壳表面的声阻抗,即圆柱壳表面声压与法向速度的关系,可表示为:
| $ \begin{split}p =& C\bar v = j\omega Cw = \\ &j\omega C\sum\limits_{m = 1}^M {\sum\limits_{n = - N}^N {{W_{mn}}\sin ({k_m}x)\exp (jn\theta )\exp (j\omega t)} }\text{,} \end{split}$ | (14) |
将式(2)和式(14)代入式(1),可得
| $ \left[ {{\boldsymbol{K}} + j\omega {\boldsymbol{C}}} \right]{\left\{ {{U_{mn}}\;\;{V_{mn}}\;\;{W_{mn}}} \right\}^{\rm T}} = {\boldsymbol{F}} \text{。}$ | (15) |
求解上式,可得
| $ \begin{split}{{\boldsymbol{U}}_0} = &\sum\limits_{m = 1}^M \sum\limits_{n = - N}^N {\left[ {{{\boldsymbol{R}}_{mn}}} \right]{{\left\{ {\begin{array}{*{20}{c}} {{{\boldsymbol{U}}_{mn}}}&{{{\boldsymbol{V}}_{mn}}}&{{{\boldsymbol{W}}_{mn}}} \end{array}} \right\}}^{\rm T}}} = \\ &\sum\limits_{m = 1}^M {\sum\limits_{n = - N}^N {\left[ {{{\boldsymbol{R}}_{mn}}} \right]{{\left[ {{\boldsymbol{K}} + j\omega {\boldsymbol{C}}} \right]}^{ - 1}}} {\boldsymbol{F}}} =\\ &\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{D}}_1}}&{{{\boldsymbol{D}}_2}} \end{array}} \right]{\left\{ {\begin{array}{*{20}{c}} {{{\boldsymbol{F}}_1}}&{{{\boldsymbol{F}}_2}} \end{array}} \right\}^{\rm T}}\text{。}\end{split} $ | (16) |
其中:
内部结构采用有限元法进行分析,材料损耗因子以复杨氏模量的形式考虑,内部结构的动力学方程可写为:
| $ \left( {\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{{ K}}}_{mm}}}&{{{\boldsymbol{{ K}}}_{ms}}} \\ {{{\boldsymbol{{ K}}}_{sm}}}&{{{\boldsymbol{{ K}}}_{ss}}} \end{array}} \right] - {\omega ^2}\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{{ M}}}_{mm}}}&{{{\boldsymbol{{ M}}}_{ms}}} \\ {{{\boldsymbol{{ M}}}_{sm}}}&{{{\boldsymbol{{ M}}}_{ss}}} \end{array}} \right]} \right)\left\{ {\begin{array}{*{20}{c}} {{{\boldsymbol{U}}_m}} \\ {{{\boldsymbol{U}}_s}} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} {{{\boldsymbol{F}}_m}} \\ {\mathbf{0}} \end{array}} \right\} \text{。}$ | (17) |
式中:
| $ {{\boldsymbol{U}}_s} = - {\left( {{{\boldsymbol{{ K}}}_{ss}} - {\omega ^2}{{\boldsymbol{{\rm M}}}_{ss}}} \right)^{ - 1}}\left( {{{\boldsymbol{{ K}}}_{sm}} - {\omega ^2}{{\boldsymbol{{\rm M}}}_{sm}}} \right){{\boldsymbol{U}}_m}\text{,} $ | (18) |
将式(18)代入式(17)的第1组方程,可得:
| $ \left[ {{{\boldsymbol{Z}}_b}} \right]\left\{ {{{\boldsymbol{U}}_m}} \right\} = \left\{ {{{\boldsymbol{F}}_m}} \right\}\text{。} $ | (19) |
其中:
| $\begin{split} {{\mathbf{Z}}_b} =& \left( {{{\boldsymbol{K}}_{mm}} - {\omega ^2}{{\boldsymbol{M}}_{mm}}} \right) - \left( {{{\boldsymbol{K}}_{ms}} - {\omega ^2}{{\boldsymbol{M}}_{ms}}} \right)\times\\ &{\left( {{{\boldsymbol{K}}_{ss}} - {\omega ^2}{{\boldsymbol{M}}_{ss}}} \right)^{ - 1}}\left( {{{\boldsymbol{K}}_{sm}} - {\omega ^2}{{\boldsymbol{M}}_{sm}}} \right)\text{,}\end{split} $ | (20) |
进一步对主自由度
| $ {{\boldsymbol{U}}_m} = {\left\{ {\begin{array}{*{20}{c}} {{{\boldsymbol{U}}_{b1}}}&{{{\boldsymbol{U}}_{b2}}} \end{array}} \right\}^{\rm T}}\text{,} $ | (21) |
式中,
| $ \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{Z}}_{b11}}}&{{{\boldsymbol{Z}}_{b12}}} \\ {{{\boldsymbol{Z}}_{b21}}}&{{{\boldsymbol{Z}}_{b22}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{{\boldsymbol{U}}_{b1}}} \\ {{{\boldsymbol{U}}_{b2}}} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} {{{\boldsymbol{F}}_{b1}}} \\ {{{\boldsymbol{F}}_{b2}}} \end{array}} \right\} \text{。}$ | (22) |
其中:
在圆柱壳与内部结构的接触节点,位移和耦合载荷应满足:
| $ {{\boldsymbol{U}}_{b2}} = {{\boldsymbol{U}}_0} \text{,}$ | (23) |
| $ {{\boldsymbol{F}}_{b2}} = - {{\boldsymbol{F}}_2}\text{。} $ | (24) |
综合圆柱壳位移响应函数式(16)、内部结构缩聚动力学方程式(22),以及式(23)和式(24),经过简单的数学推导,整个结果的动力学方程可表示为:
| $ \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{Z}}_{b11}}}&{{{\boldsymbol{Z}}_{b12}}{{\boldsymbol{D}}_2}} \\ {{{\boldsymbol{Z}}_{b21}}}&{{{\boldsymbol{Z}}_{b22}}{{\boldsymbol{D}}_2} + {\boldsymbol{I}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{{\boldsymbol{U}}_{b1}}} \\ {{{\boldsymbol{F}}_2}} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} {{{\boldsymbol{F}}_{b1}} - {{\boldsymbol{Z}}_{b12}}{{\boldsymbol{D}}_1}{{\boldsymbol{F}}_1}} \\ { - {{\boldsymbol{Z}}_{b22}}{{\boldsymbol{D}}_1}{{\boldsymbol{F}}_1}} \end{array}} \right\}\text{。} $ | (25) |
求解上式,可以得到圆柱壳与内部结构接触节点的耦合力
以水下含内部基座圆柱壳为例验证本文方法的正确性,圆柱壳长度0.8 m,半径0.2 m,厚度0.003 m;内部基座长度0.6 m(由
将本文方法与数值计算方法结果进行对比,以验证本文方法的正确性。在保证本文方法收敛的前提下,模态截断数M和N的值均取15。数值计算的过程为:在Ansys16.0中建立水下含内部基座圆柱壳的有限元模型(见图3),计算结构在水中振动响应;基于圆柱壳表面振动,在Virtual.Lab13.6中采用直接边界元法计算辐射声压。

|
图 3 水中含内部基座圆柱壳有限元模型示意图 Fig. 3 Schematic diagram of the finite element model of an immersed cylindrical shell with a base |
本文方法与有限元法计算得到的基座面板中心点速度和圆柱壳均方速度(MQV)如图4所示。可以看出,除了部分峰值频率略有偏移,本文方法和有限元法的计算结果吻合良好,验证了本文方法计算水中含内部结构圆柱壳振动响应的正确性。
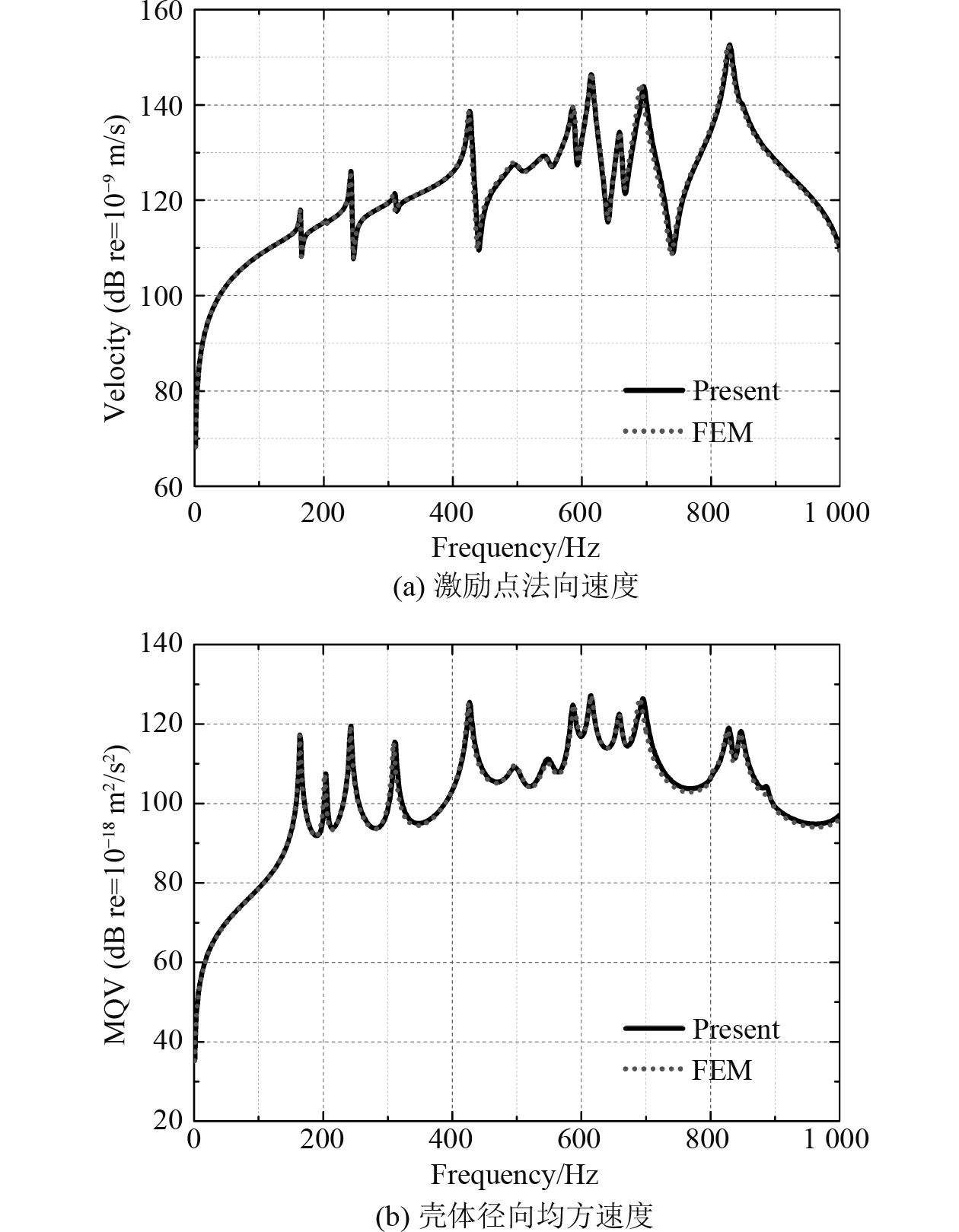
|
图 4 本文方法与FEM计算水中含内部基座圆柱壳振动响应对比 Fig. 4 Comparisons of vibration responses of present method and FEM |
图5给出了2种方法在场点P1和P2的辐射声压对比曲线,本文方法与有限元耦合边界元方法计算结果吻合较好。为进一步对本文方法辐射声压预报结果的进行验证,图6给出了243 Hz和427 Hz的声压指向性曲线,2种方法的计算结果有较高的吻合度,验证了本文方法预报含内部结构圆柱壳辐射声压的正确性。
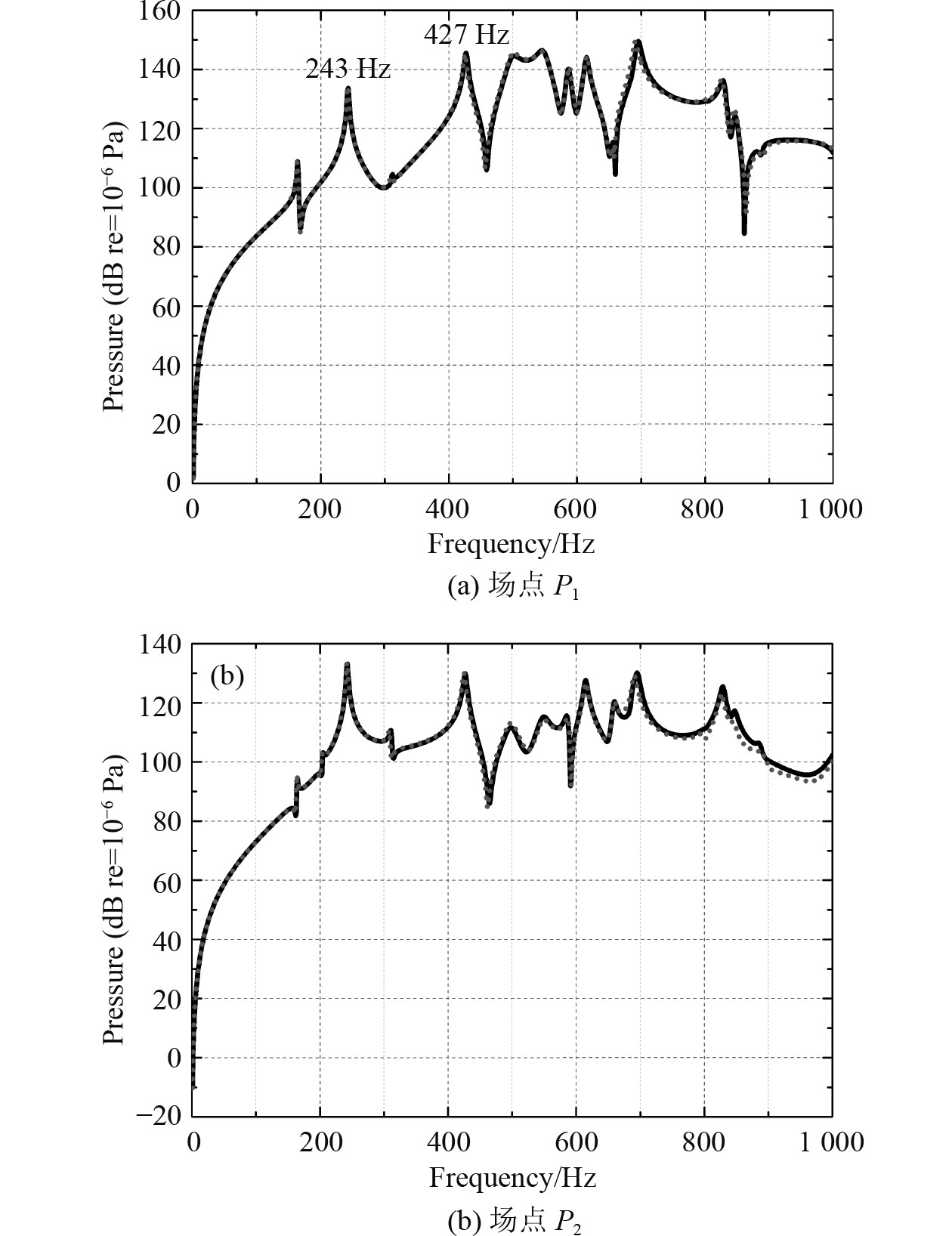
|
图 5 本文方法与FEM/BEM计算水中含内部基座圆柱壳辐射声压对比 Fig. 5 Comparisons of the sound radiation of present method and FEM/BEM |
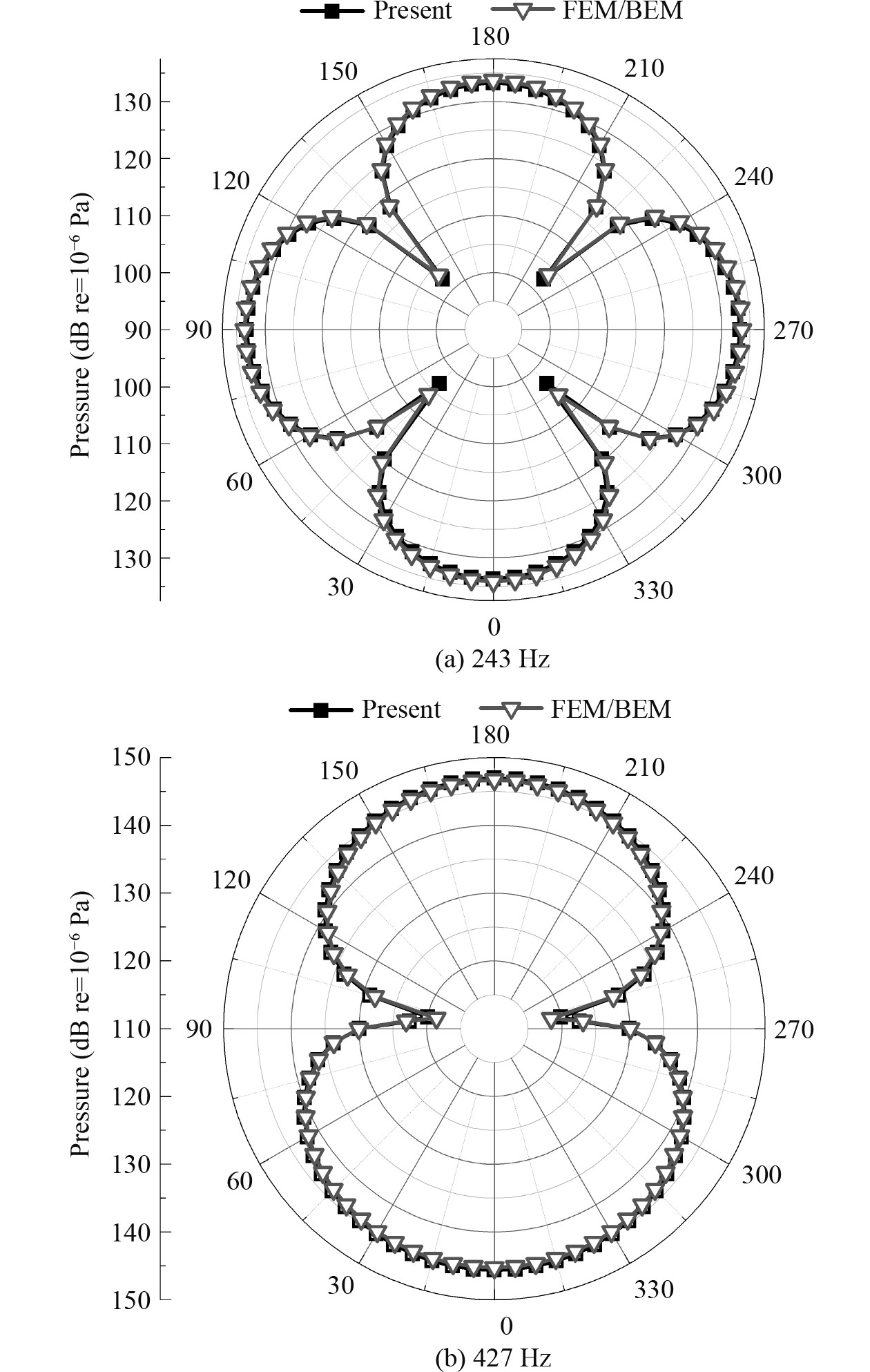
|
图 6 本文方法与FEM/BEM计算水中含内部基座圆柱壳辐射声压指向性对比 Fig. 6 Comparisons of the sound directivity of present method and FEM/BEM |
与有限元耦合边界元法相比,当内部结构变化时,本文方法不需要重新进行声-固耦合计算,只需刷新内部结构的动力学方程,可快速预报结构的辐射声压,这在内部结构变化的多方案对比分析时具有显著优势。
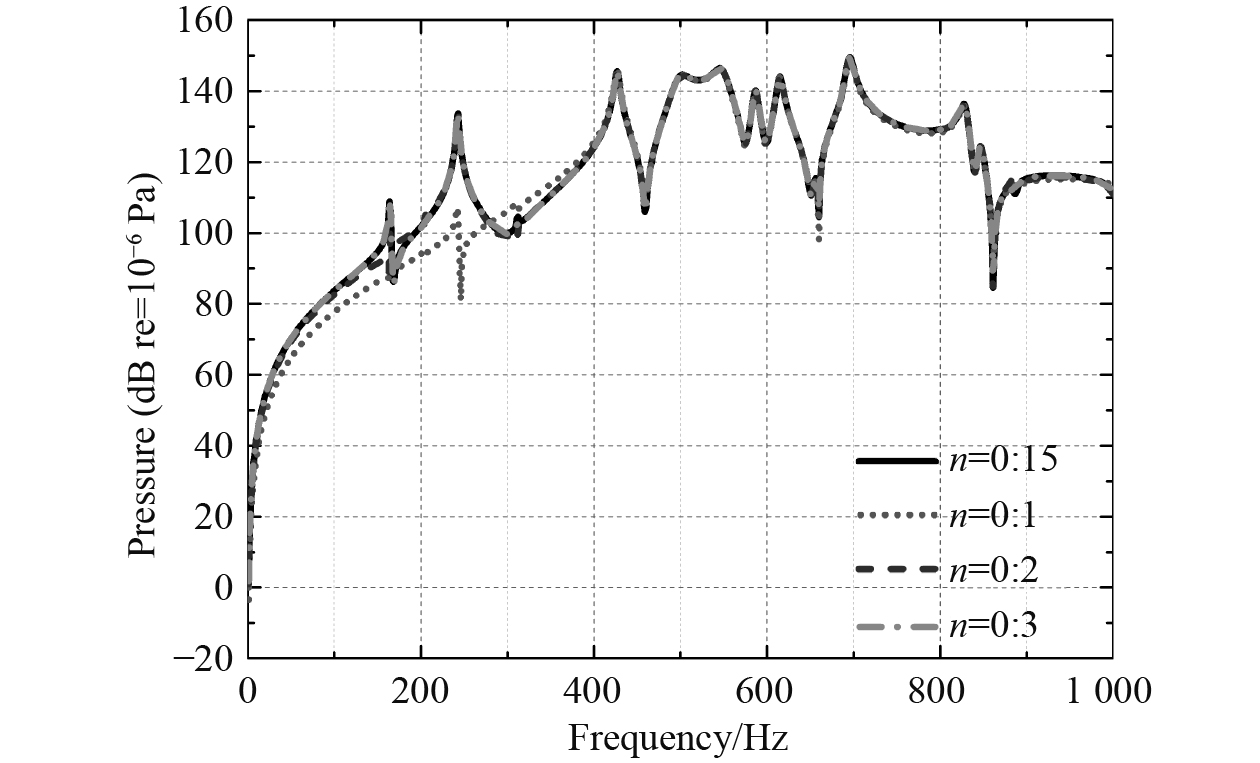
2.2 周向模态对辐射声压贡献量分析图7给出了不同周向模态对应的场点P1辐射声压对比曲线。可以看出,n=0∶3与n=0∶15的辐射声压曲线基本重合。这说明针对本文的研究模型,在1~1 000 Hz的频段内,结构向外场的辐射声压主要由
|
图 7 周向模态辐射声压贡献量 Fig. 7 Contribution of circumferential mode to sound pressure |
本文以含内部结构圆柱壳为研究对象,结合解析法效率高和有限元法适用性广的优点,将整个结构分为水下圆柱壳和内部结构两部分。针对水下圆柱壳,采用轴对称边界元法计算壳体表面声阻抗,再结合Flügge壳体理论,建立水下圆柱壳的数理方程;针对内部结构,采用有限元法进行动力学建模。最后,根据圆柱壳与内部结构在连接点的内力平衡及位移连续条件,建立整个结构的控制方程。该方法可较为准确地预报含内部结构的水下圆柱壳的振动和辐射声压,且当内部结构发生变化时,不需要重新进行声-固耦合计算,只需更新内部结构的动力学方程,即可快速预报结构的声振特性,这在改变内部结构的多方案对比分析时具有显著的计算速度优势。
| [1] |
WANG C, LAI JCS. Prediction of natural frequencies of finite length circular cylindrical shells[J]. Applied Acoustics, 2000, 59(4): 385-400. DOI:10.1016/S0003-682X(99)00039-0 |
| [2] |
PAN Z, LI XB, MA JJ. A study on free vibration of a ring-stiffened thin circular cylindrical shell with arbitrary boundary conditions[J]. Journal of Sound and Vibration, 2008, 341(1–2): 330-342. |
| [3] |
WANG ZH, XING JT, PRICE WG. A study of power flow in a coupled plate-cylindrical shell system[J]. Journal of Sound and Vibration, 2004, 271(3): 863-882. |
| [4] |
CHENG L, NICOLAS J. Free vibration analysis of a cylindrical shell—circular plate system with general coupling and various boundary conditions[J]. Journal of Sound and Vibration, 1992, 155(2): 231-247. DOI:10.1016/0022-460X(92)90509-V |
| [5] |
PAN Z, LI X, MA J. A study on free vibration of a ring-stiffened thin circular cylindrical shell with arbitrary boundary conditions[J]. Journal of Sound and Vibration, 2008, 314(1-2): 330-342. DOI:10.1016/j.jsv.2008.01.008 |
| [6] |
庞福振, 吴闯, 王献忠, 等. 水下加筋圆柱壳声辐射特性分析的改进精细传递矩阵法[J]. 振动与冲击, 2017, 36(22): 131-137. PANG Z, WU C, WANG X, et al. An improved precise transfer matrix method for the analysis of acoustic radiation of ring-stiffened cylindrical shells[J]. Journal of Vibration and Shock, 2017, 36(22): 131-137. |
| [7] |
肖邵予. 两端用圆板封口的环肋柱壳振动声辐射性能分析[D]. 武汉: 华中科技大学, 2004. XIAO S. Vibroacoustic analysis of a finite stiffened-cylindrical shell closed by circular plates[D]. Wuhan: Huazhong University of Science and Technology, 2004. |
| [8] |
陈美霞, 谢坤, 魏建辉. 多舱段圆柱壳振动特性研究[J]. 振动工程学报, 2014, 27(4): 555-564. CHEN M, XIE K, WEI J. Vibration characteristics of multiple cabins of cylindrical shell[J]. Journal of Vibration Engineering, 2014, 27(4): 555-564. DOI:10.3969/j.issn.1004-4523.2014.04.011 |
| [9] |
WEI J, CHEN M, HOU G, et al. Wave based method for free vibration analysis of cylindrical shells with nonuniform stiffener distribution[J]. Journal of Vibration and Acoustics, 2013, 135(6): 061011. DOI:10.1115/1.4024055 |
| [10] |
MAXIT L, GINOUX J M. Prediction of the vibro-acoustic behavior of a submerged shell non periodically stiffened by internal frames[J]. The Journal of the Acoustical Society of America, 2010, 128(1): 137-151. DOI:10.1121/1.3436526 |
| [11] |
SOENARKO B. A boundary element formulation for radiation of acoustic waves from axisymmetric bodies with arbitrary boundary conditions[J]. Journal of the Acoustical Society of America, 1993, 93(2): 631-639. DOI:10.1121/1.405482 |
| [12] |
WANG W, ATALLA N, NICOLAS J. A boundary integral approach for acoustic radiation of axisymmetric bodies with arbitrary boundary conditions valid for all wave numbers[J]. The Journal of the Acoustical Society of America, 1997, 101(3): 1468-1478. DOI:10.1121/1.418174 |
| [13] |
LEISSA A W. Vibration of shells[M]. New York: Acoustical Society of America, 1993.
|
 2021, Vol. 43
2021, Vol. 43

