船舶水下辐射噪声源主要有三类:机械噪声、螺旋桨噪声和水动力噪声[1]。其中,机械噪声是指由船舶航行或作业时各类机械设备运转产生的振动噪声,如主辅机、泵浦、液压机械等;螺旋桨噪声是指螺旋桨旋转时叶片和水相互作用产生的噪声;水动力噪声是指船体与水流相对运动以及船体内管路系统吸、排水时产生的噪声。在常规船舶中由机械振动产生的辐射噪声是船舶水下辐射噪声的主要成分。随着船舶隐身性能需求的提升,机械设备隔振技术和低噪声大侧斜螺旋桨在静音型船舶中得到广泛应用,机械振动和螺旋桨噪声在整个船舶水下辐射噪声中的贡献占比日益下降,而水动力噪声的贡献占比日益上升。
船舶海水系统的进、出口端均与海洋环境直接连通,海水泵的流量一般较大,其运动产生的机械振动不仅沿着安装基座和系统管路经支承吊架传递至船体结构,由船体结构向船外辐射噪声,还会通过管路内的流体通过进、出口端直接向海洋环境辐射噪声,是船舶管路噪声辐射的主要噪声源之一,由于其在整个辐射过程中传递路径复杂,难以进行有效控制。目前,船舶管路系统噪声已成为静音型水面舰船、潜艇声隐身性能新的研究、控制方向。
近年来,在静音型船舶中,随着海水泵采用弹性隔振安装、进口在处应用挠性接头[2]、管路安装时采用弹性支、吊架、橡胶隔振衬垫[3]等,管路系统振动直接通过船体结构的辐射路径得到有效控制,而通过管路内的流体经进、出口端直接向海洋环境的噪声辐射已成为海水系统辐射噪声的主要成分。对于海水系统的进口端,海底门与海底格栅产生的流噪声,是由于流场有较高的雷诺数,湍流导致管道表面产生压力脉动,成为主要噪声源。
董自虎等[4]对通海阀的内部流道结构进行建模,仿真分析了通海阀的内部流场分布,通过对比分析通海阀不同通流道结构下的噪声,得出了影响通海阀噪声性能的主要原因,并给出了改进模型。张冠军等[5]以双层加筋板为研究对象,分别采用传统的结构有限元耦合声学边界元(FEM/BEM)方法和FEM/AML直接声振耦合计算方法计算了双层加筋板单面触水的声辐射,结果显示2种方法计算结果基本吻合,但FEM/AML方法具有建模工作量少、计算资源需求小、计算流程简单的优势。
本文以船舶海底门为对象,采用直接声振耦合计算方法(FEM+AML),针对其不同工作状态下的噪声进行预报分析,并对比不同海底门方案对流噪声辐射的影响,为船舶海水冷却系统海底门的降噪设计指出方向。
1 控制方程对Helmholtz方程进行数值求解是应用有限元法(FEM)求解流噪声的思路[6]。
假定声场V被边界Ω所包围,并满足声振耦合边界(声压边界)、速度边界、阻抗边界:
| $ {\nabla }^{2}{p}\left({x},{y},{z}\right)+{{k}}^{2}\cdot {p}\left({x},{y},{z}\right)=-{{j}}{{\rho }}_{0}{\omega }\cdot {q}\left({x},{y},{z}\right) 。$ | (1) |
式中:
边界条件同时满足以下条件:
1)压力边界条件
| $ {p}=\stackrel-{{p}},$ | (2) |
2)法向阻抗条件
| $ {p}=\overline{{Z}}\cdot {\mathrm{\nu }}_{\mathrm{n}}=\frac{{j}\overline{{Z}}}{{{\rho }}_{0}{\omega }}\frac{\partial {p}}{\partial {n}} ,$ | (3) |
3)法向速度边界条件
| $ \nu_{\mathrm{n}}=\frac{{j}}{{{\rho }}_{0}{\omega }}\frac{\partial {p}}{\partial {n}}={\overline{{\nu }}}_{{n}} 。$ | (4) |
式中:
声场的低频波动特性可以采用有限元法真实的模拟并进行全域计算,其计算结果相对于采用边界元法更加准确。因此有限元法在求解内声场和声辐射方面有较大的优势[7]。
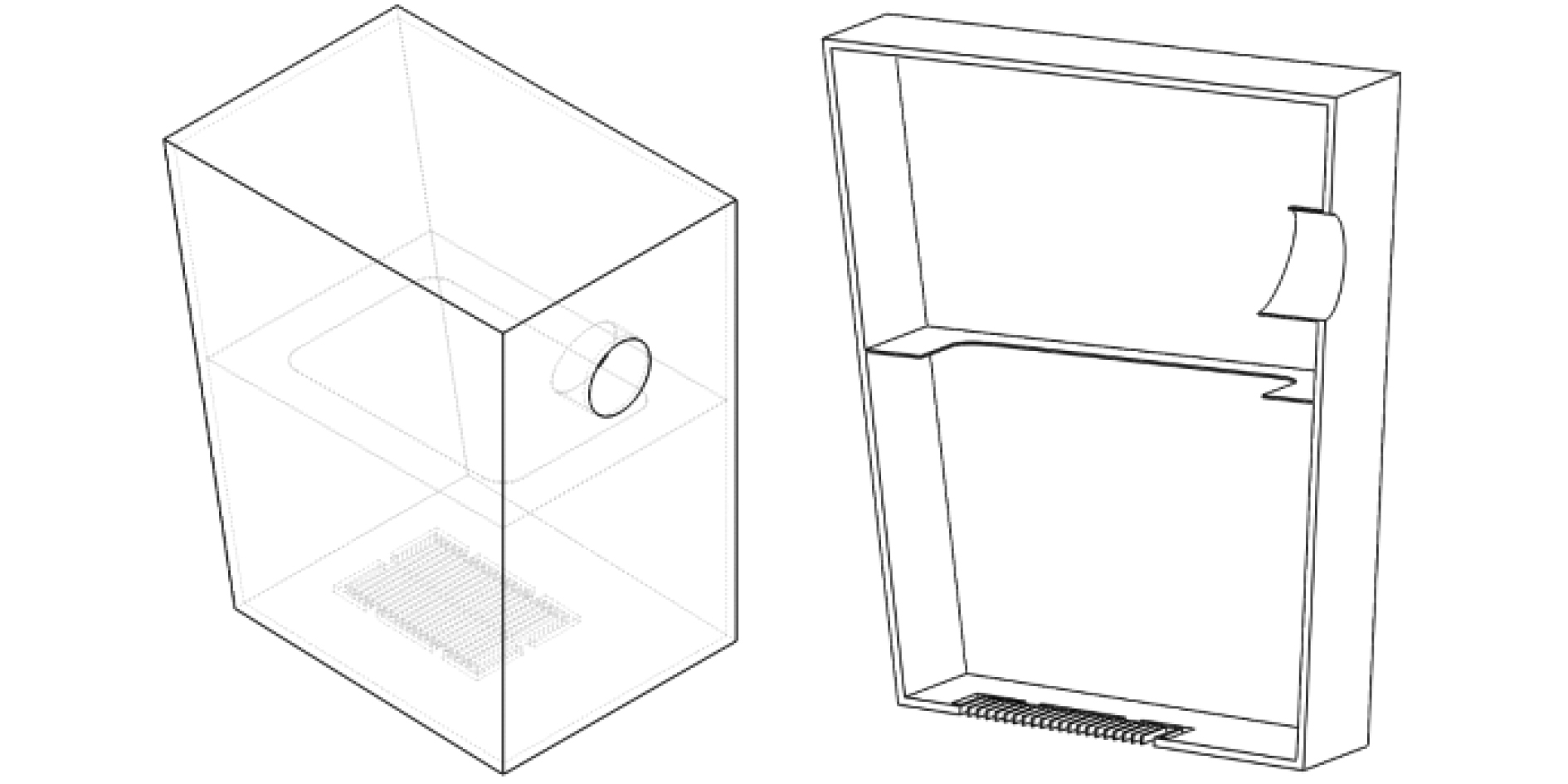
2 计算模型及方法 2.1 计算模型以某船主机舱左舷海底门为研究对象,进行建模。常规设计中为增大海水总管进水截面积,并进一步分离海底门海水中混入的空气,增加分离效果,一般设置一段深入海底门的吸入管路,切面斜向上,如图1所示。
|
图 1 主机舱左舷海底门模型 Fig. 1 Medol sea water chest at main engine room port side |
该船海底门较高,船体结构设计决定了需在中间设加强隔板,每个海底门设有1个海水总管吸入口和1个吸入格栅。
2.2 计算方法通常认为,在低马赫数下,表面分布的偶极子是流场的主要噪声源,为了加快计算速度一般将体积分布的四极子声源忽略,只考虑管路表面分布的偶极子声源[8]。
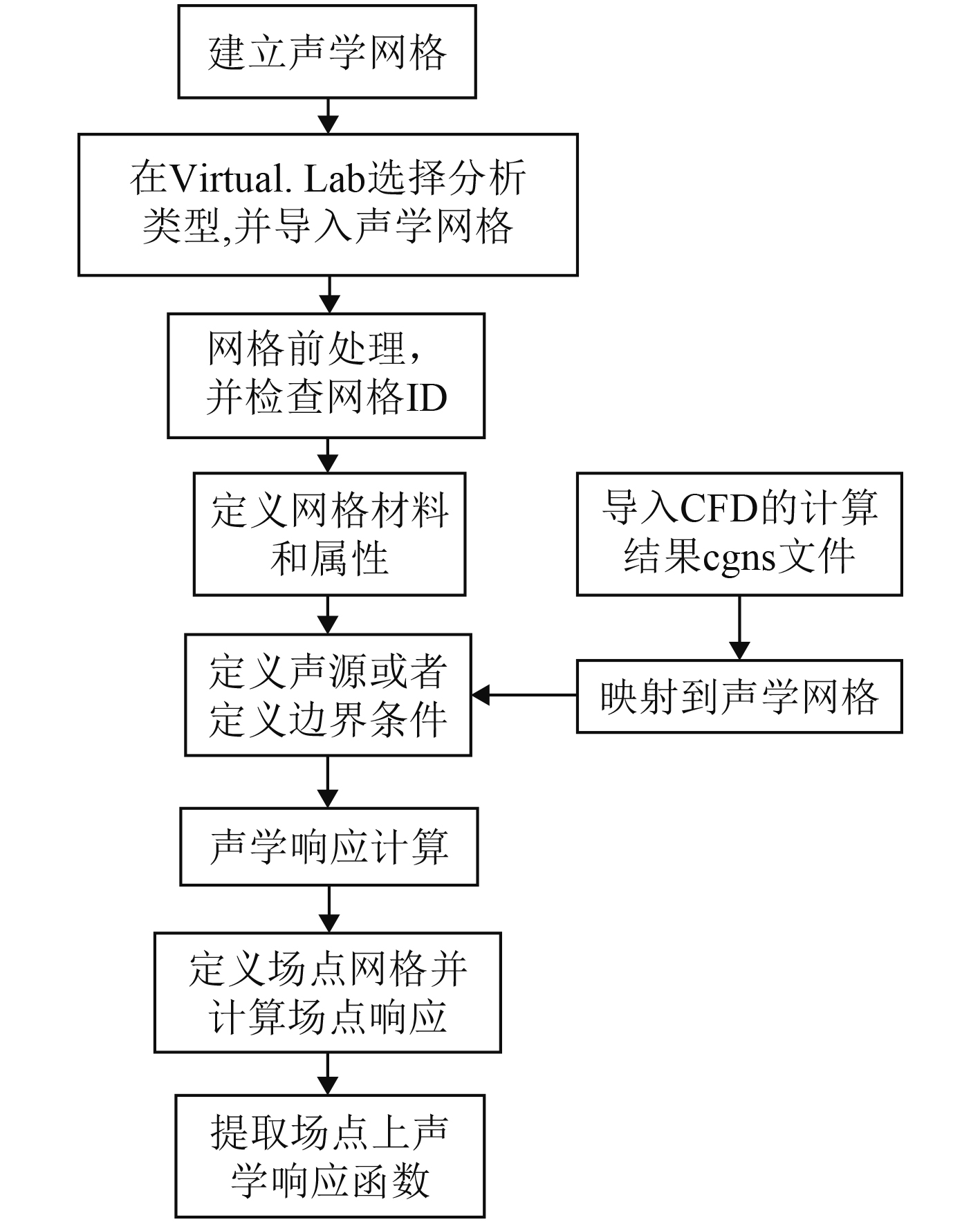
本文先利用Fluent软件对分析模型进行稳态分析,待计算收敛后,再以收敛的稳态流场的基础上进行瞬态计算,同时将流固耦合面的压力脉动数据导出。然后将导出的流固耦合面脉动压力数据处理后作为偶极子声源导入 Virtual. Lab中,采用直接声振耦合计算方法(FEM/AML)法进行声场仿真计算,仿真流程如图2所示。
|
图 2 仿真流程 Fig. 2 Calculation Procedure |
在声学仿真计算中,计算网格的单元尺寸与计算频率之间有对应关系,当声学网格过于稀疏时,将会产生较大的误差,为保证计算精度,一般要求最小波长内至少有6个声单元,也即是最大网格单元的边长要小于分析频率点处波长的1/6。
3 流场计算先在软件Ansys Icemcfd中将图1所示的分析模型进行有限元网格划,网格采用六面体-四面体混合网格,流场求解时采用SST k-Ω湍流模型,并采用基于压力的求解器进行求解,边界条件的设置如表1所示。
|
|
表 1 流场边界条件 Tab.1 The boundary conditions of flow field |
稳态计算收敛之后,在进行瞬态计算时,先取大时间步长再取小时间步长。具体步骤为:在流场脉动压力稳定前先采用大时间步长进行计算,在流场脉动压力稳定后再采用小时间步长进行计算,使流场压力时域计算时,其分析频率和频率分辨率均适宜。海底门稳态压力分布计算结果如图3所示,海底门中心竖直面内湍流动能分布计算结果如图4所示。

|
图 3 海底门稳态压力分布图 Fig. 3 The steady-state pressure distribution of Sea water chest |

|
图 4 海底门中心竖直面内湍流动能分布图 Fig. 4 The urbulence energy distribution of Sea water chest along vertical plane |
计算模型的频率分辨率为5 Hz,分析频率上限为2 500 Hz。
4 声场计算声场计算模型由声学计算网格和场点网格组成,在本次计算模型中,声学计算网格采用四面体单元,根据计算要求,网格尺寸需满足最大单元边长不大于分析频率点处波长1/6的要求,实取网格尺寸为0.02 m。
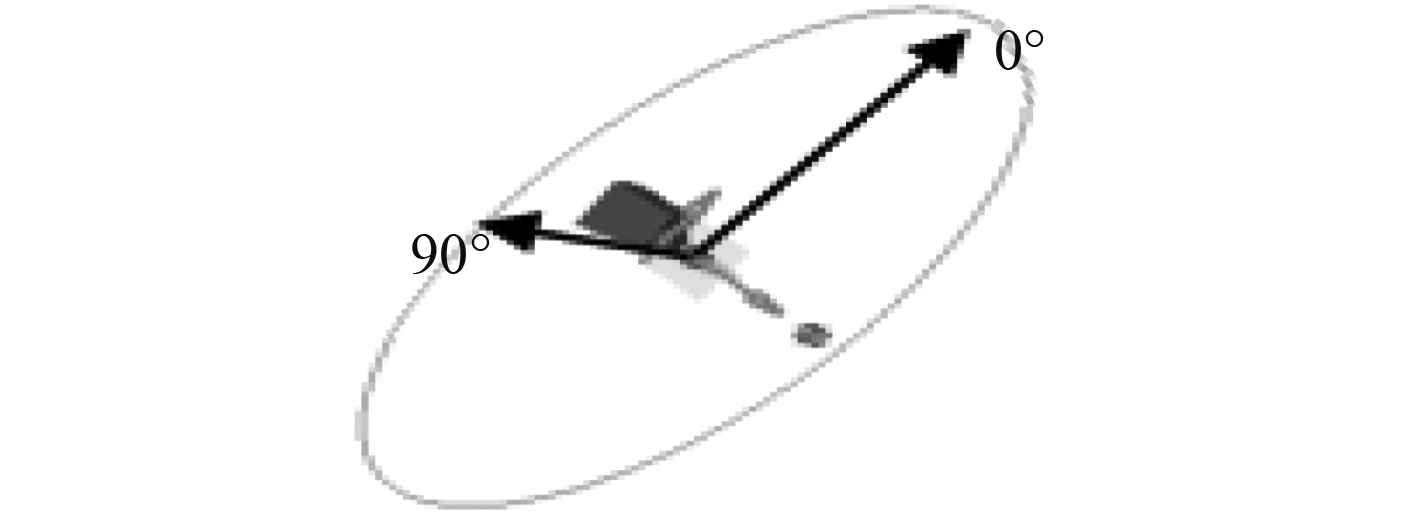
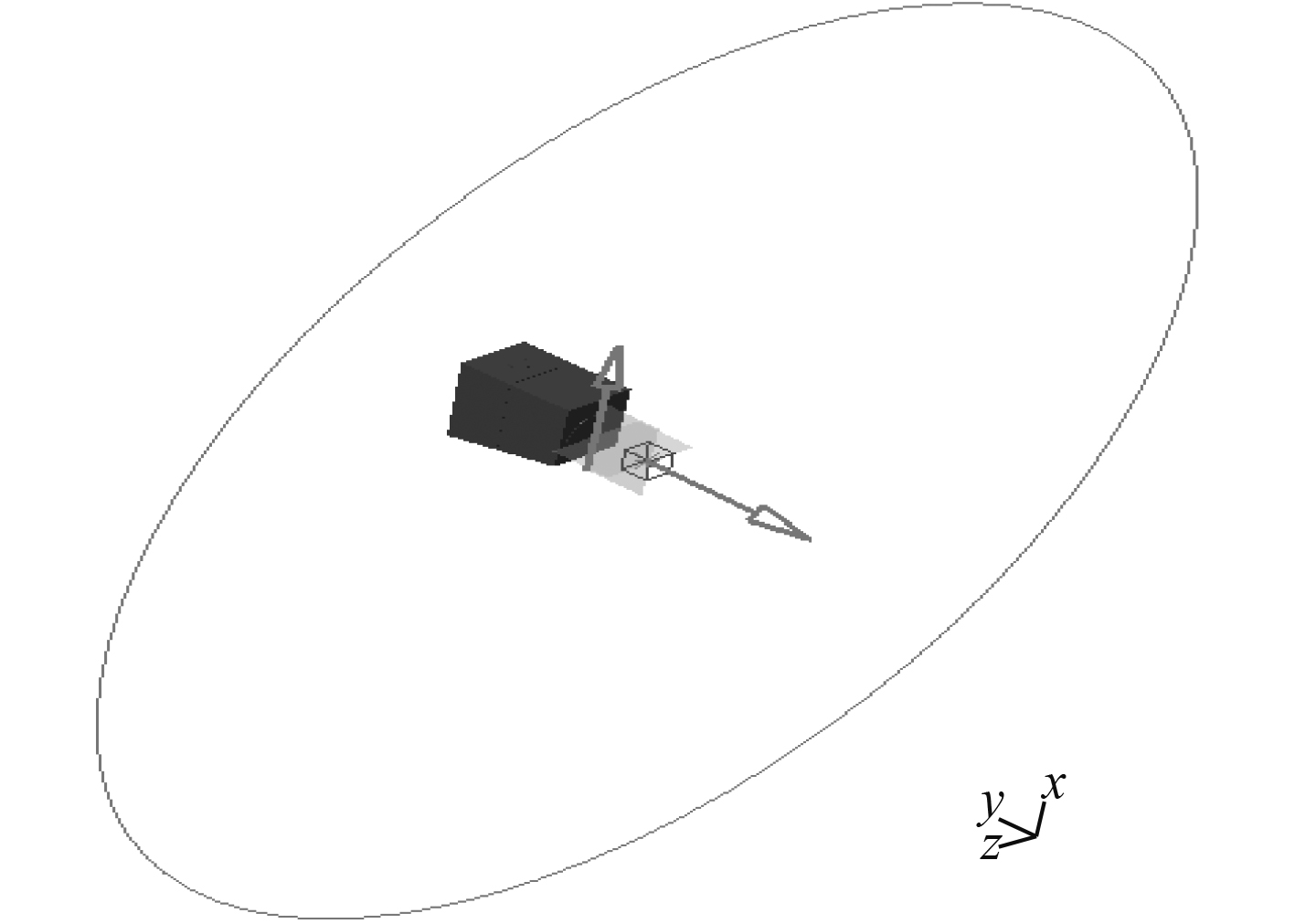
场点网格:在海底门出口格栅正前方1 m设指向性场点,并分别在海底门出口格栅正前方1 m,50 m设声场观测点,如图5所示。所设指向性场点以海底门入口轴线方向为法向,入口平面的对称轴为0°,从左向右顺时针为正向,场点间隔为5°,半径为10 m;还设有以海底门入口轴线轴线为对称轴,互相相交垂直的平面场点,如图6所示。
|
图 5 海底门场点网格 Fig. 5 The field point grid of sea water chest |
|
图 6 海底门场点网格局部放大 Fig. 6 The partial magnification grid of sea water chest |
计算得到海底门入口对应的10 Hz,100 Hz,1 000 Hz和2 500 Hz辐射声压云图,如图7~图10所示。
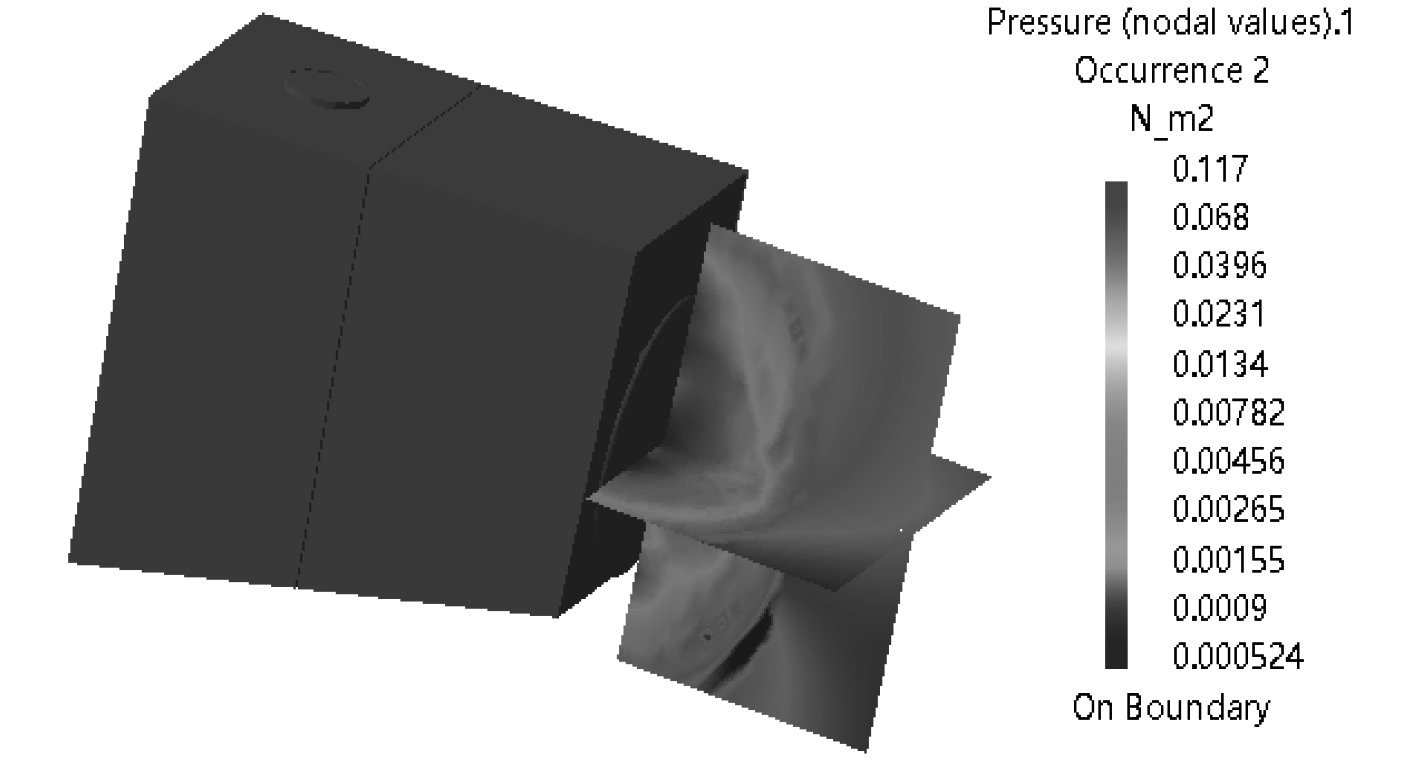
|
图 7 海底门辐射噪声云图(10 Hz) Fig. 7 The acoustic pressure distribution of sea water chest (10 Hz) |
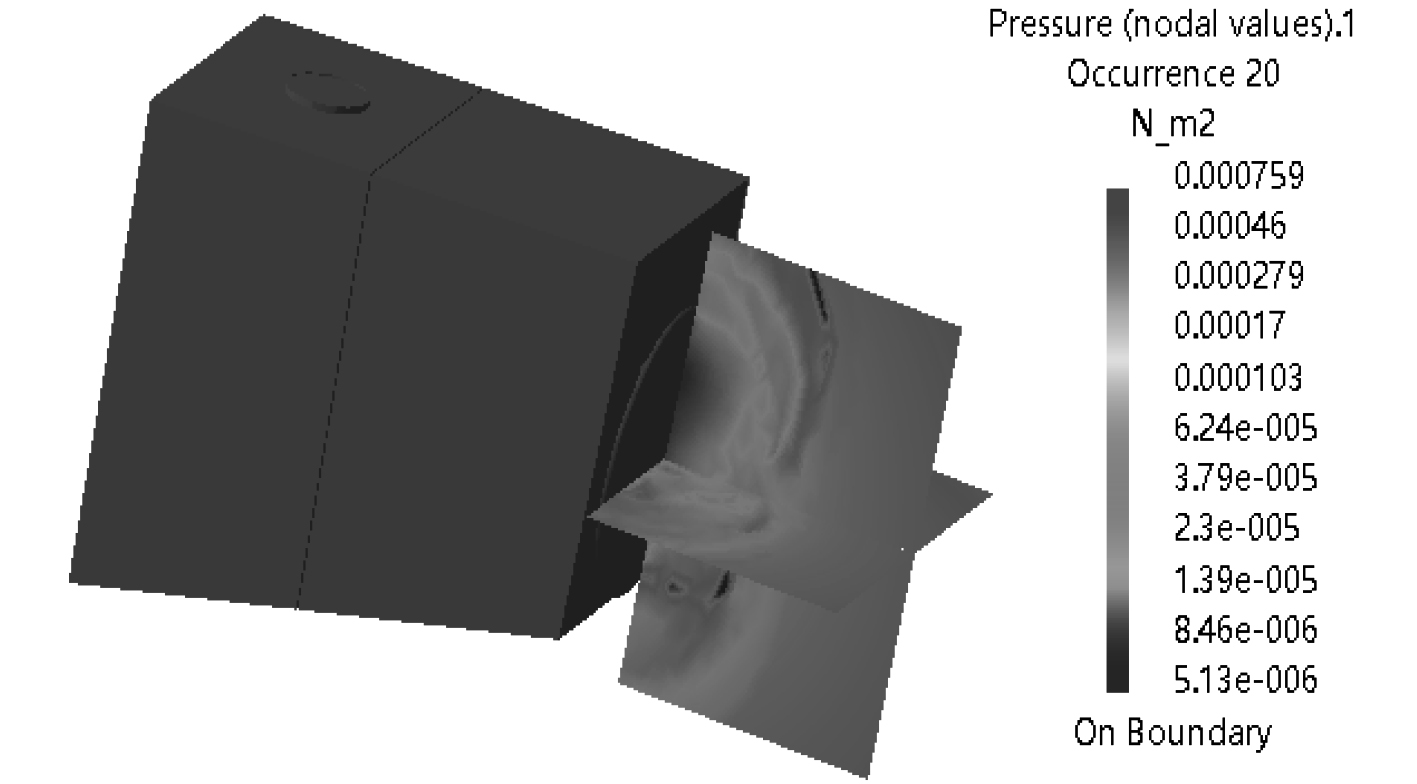
|
图 8 海底门辐射噪声云图(100 Hz) Fig. 8 The acoustic pressure distribution of sea water chest (100 Hz) |
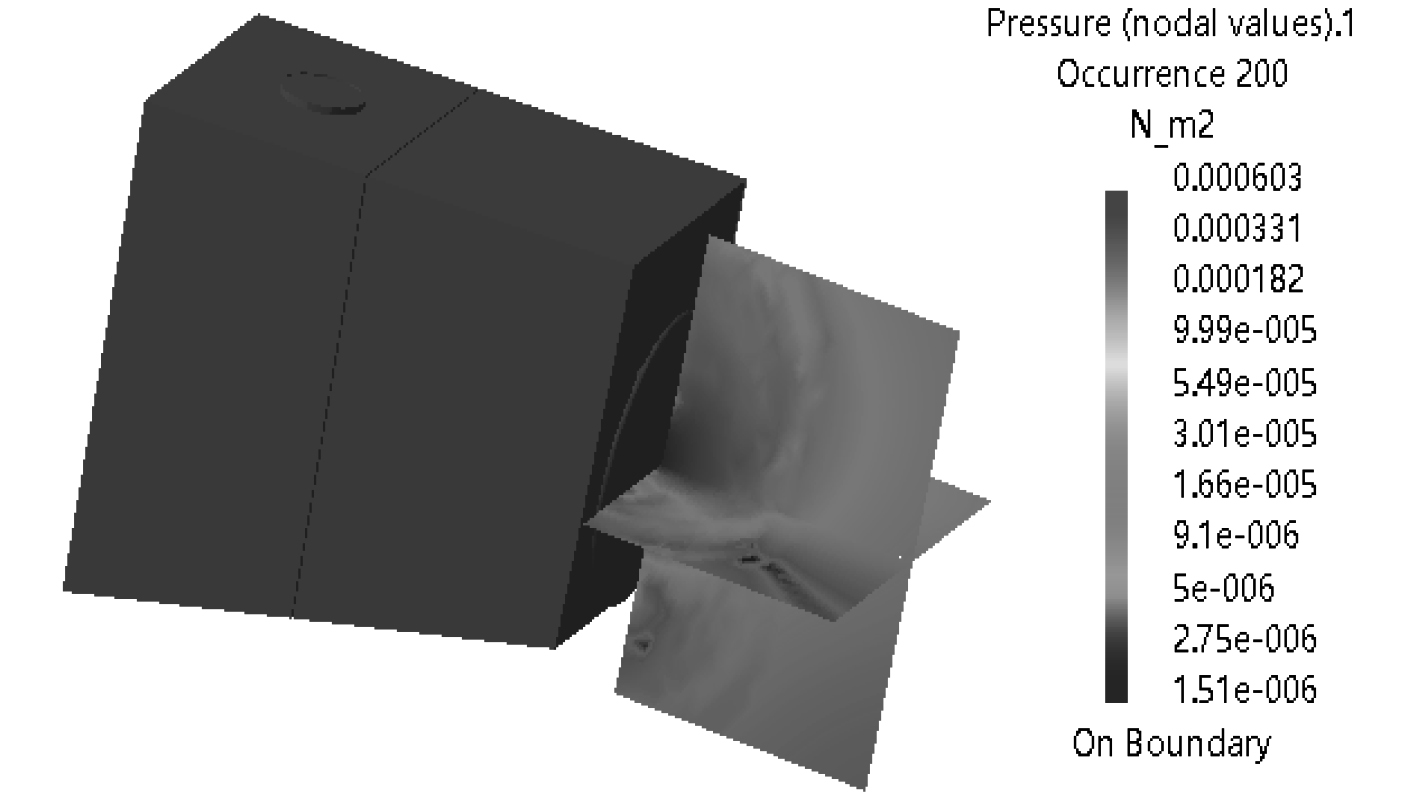
|
图 9 海底门辐射噪声云图(1 000 Hz) Fig. 9 The acoustic pressure distribution of sea water chest (1 000 Hz) |
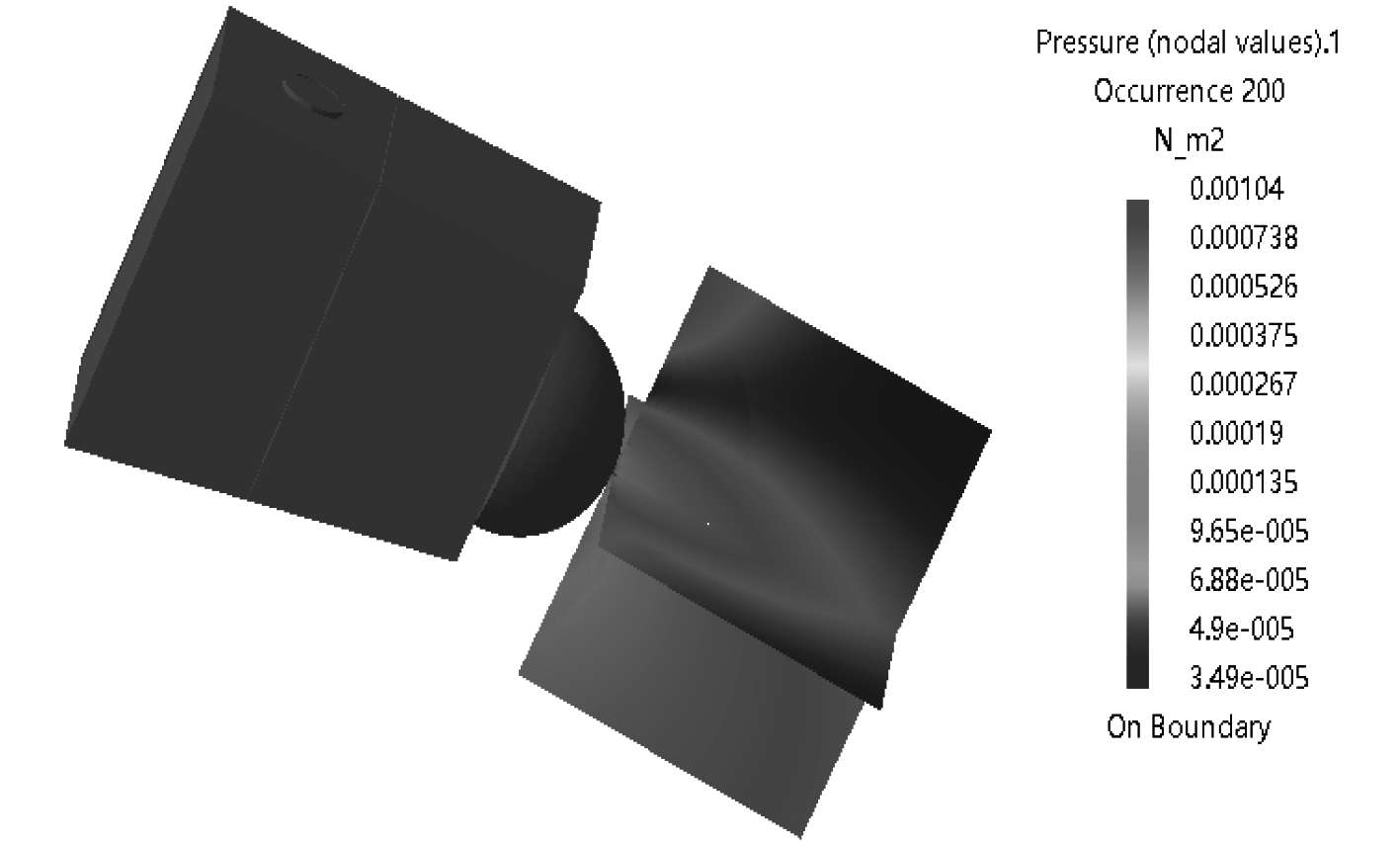
|
图 10 海底门辐射噪声云图(2 500 Hz) Fig. 10 The acoustic pressure distribution of sea water chest (2 500 Hz) |
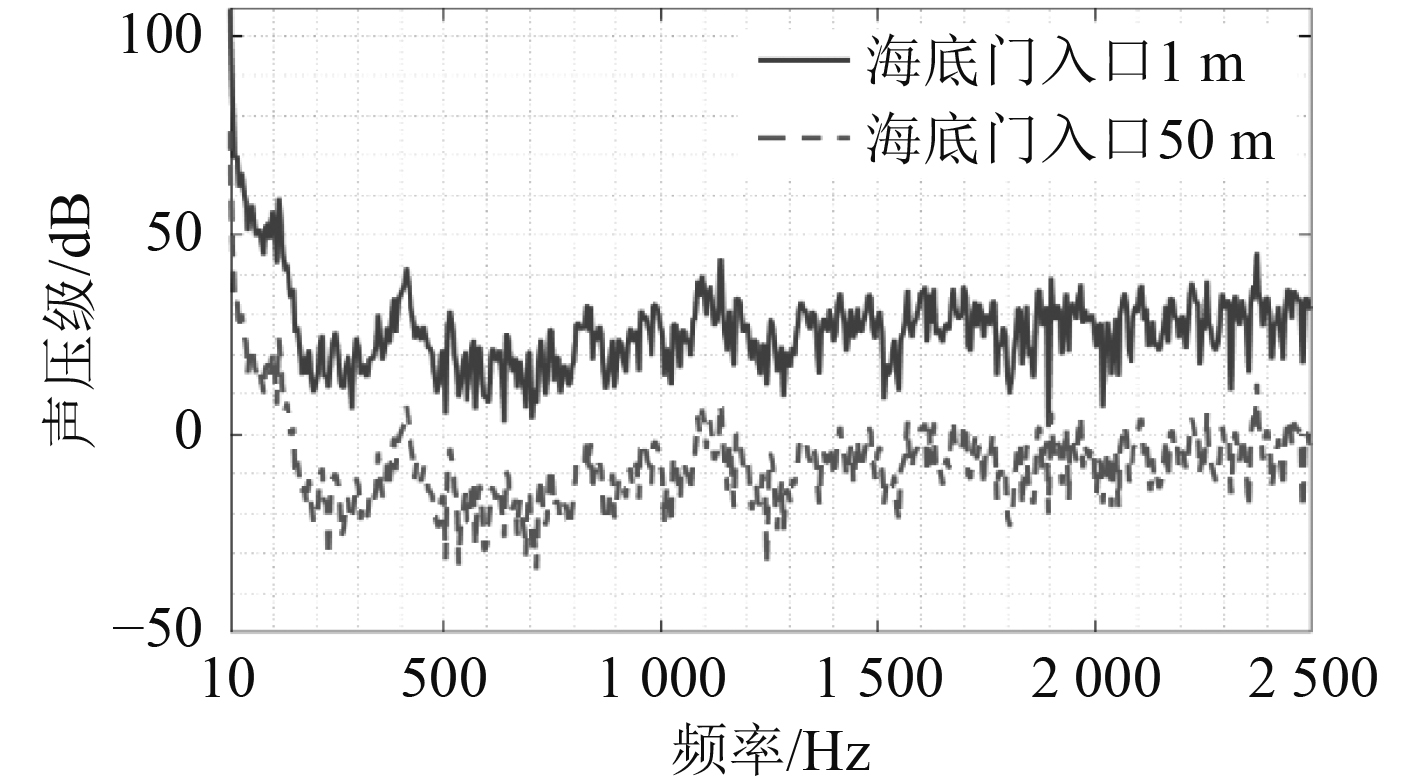
计算得到海底门出口正前方1 m,50 m处的声压级频谱和各分频段及通频段声压级,分别如图11和表2所示。
|
图 11 海底门出口正前方1 m和50 m处的声压级频谱(参考声压10−6 Pa) Fig. 11 Sound pressure spectrum at 1 m and 50 m ahead of sea water chest exit (reference sound pressure 10−6 Pa) |
|
|
表 2 海底门出口1 m,50 m处各分频段及通频段声压级对比(参考声压10−6 Pa) Tab.2 Sound pressure levels of each sub-band and cross-band at 1m and 50m ahead of sea water chest exit for different schemes (reference sound pressure 10−6 Pa) |
从图11可以看出,海底门声辐射能量主要集中在低频段0~50 Hz,近场1 m处最大声压约为106.7 dB,而近声场高频声压在40 dB左右。
5 系统方案低噪声优化为分析海底门内部结构对流场噪声的影响,结合海底门的实际设计情况,提出对比方案2和方案3。
在方案2中,海水总管直接于海底门连接,取消伸入海底门内的吸入管;而方案3则方案2的基础上优化:在上层水箱加设圆弧形导流板,引导海水流向管道入口,试图减轻流体撞击上层空间壁面的可能、减轻涡旋程度。
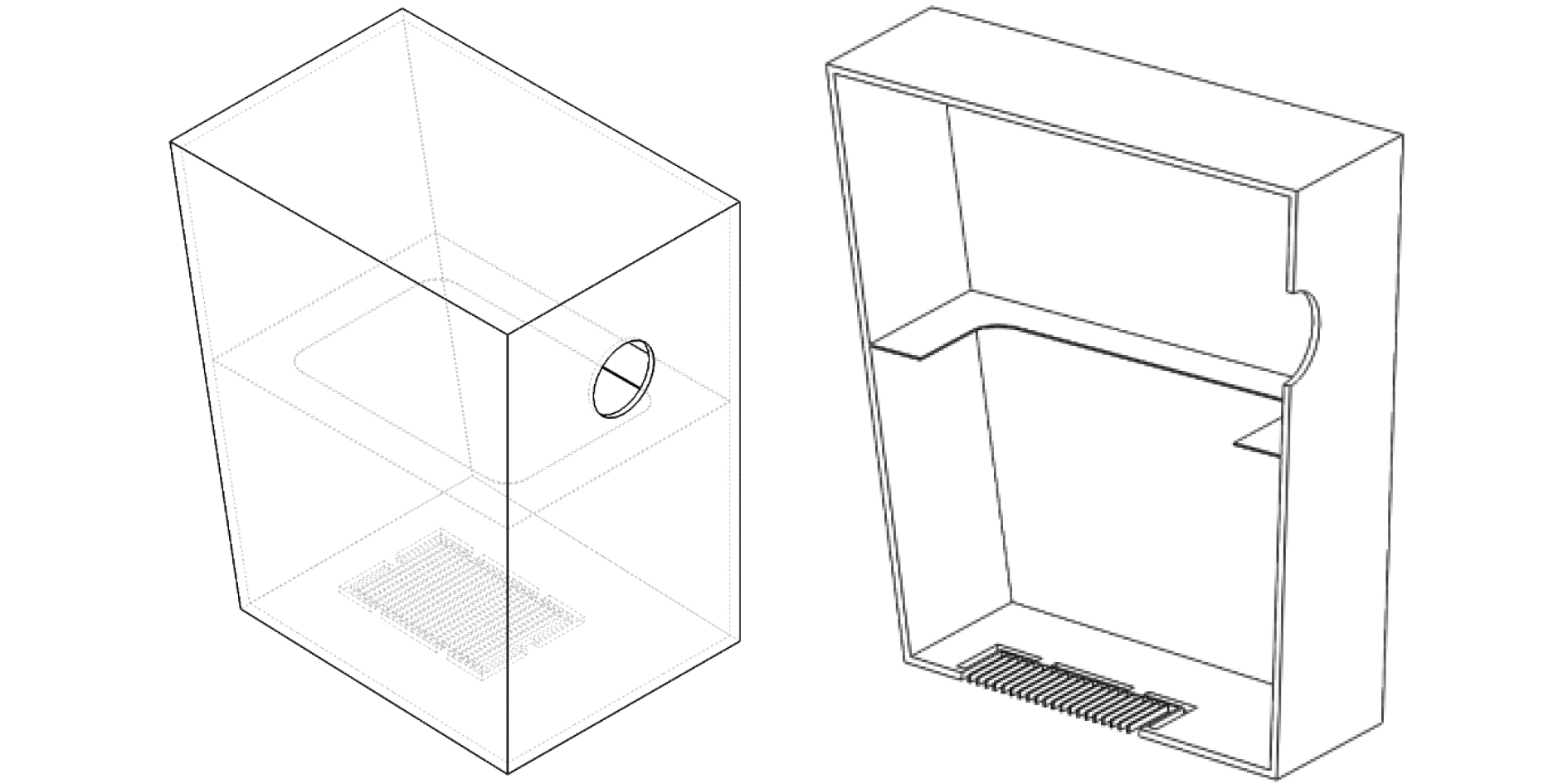
|
图 12 主机舱左舷海底门模型(方案2) Fig. 12 Medol sea water chest at main engine room port side (the second scheme) |
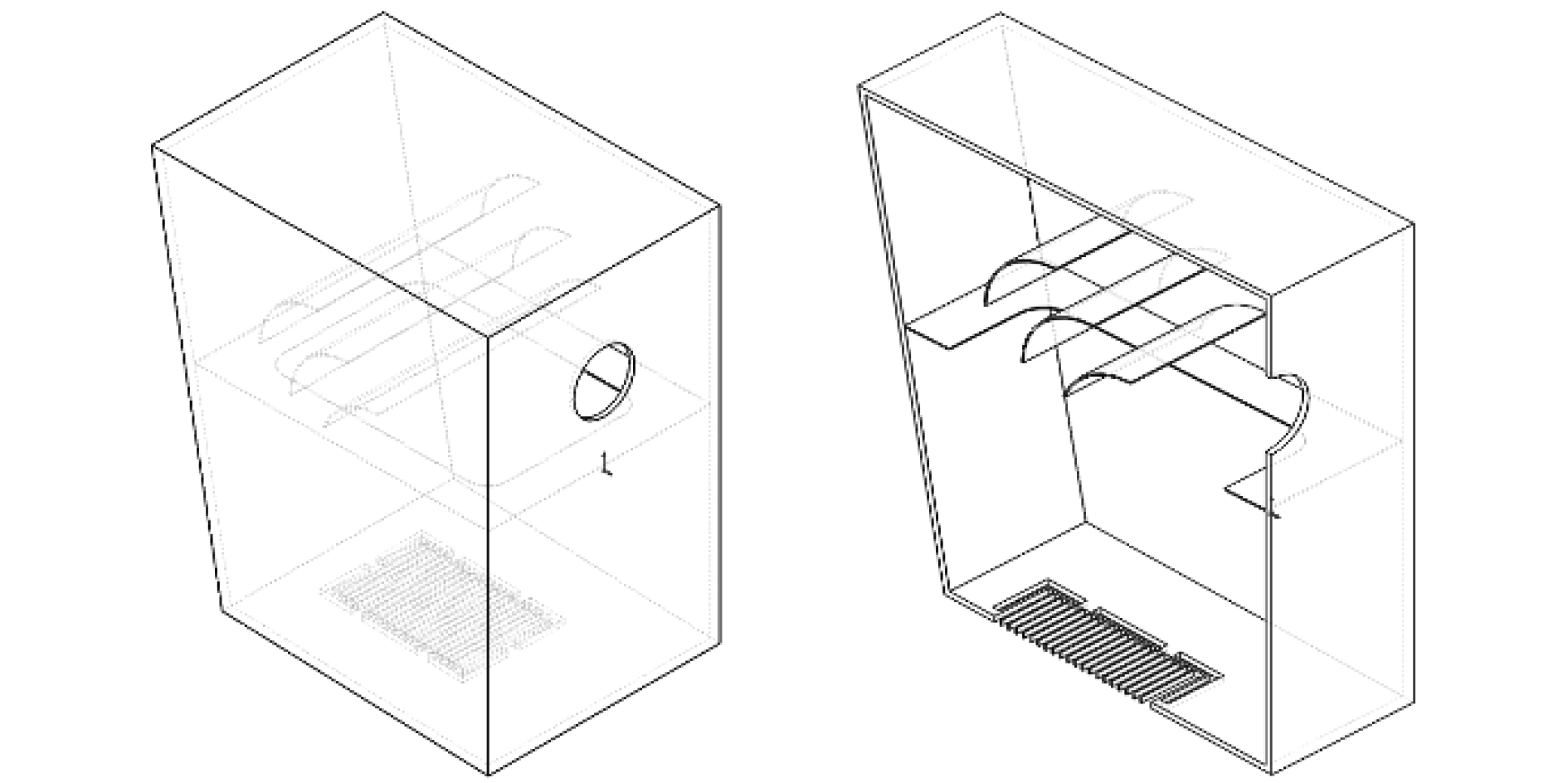
|
图 13 主机舱左舷海底门模型(方案3) Fig. 13 Medol sea water chest at main engine room port side (the third scheme) |
根据仿真计算结果,方案2和方案3的声场情况分别如图14和图15所示。
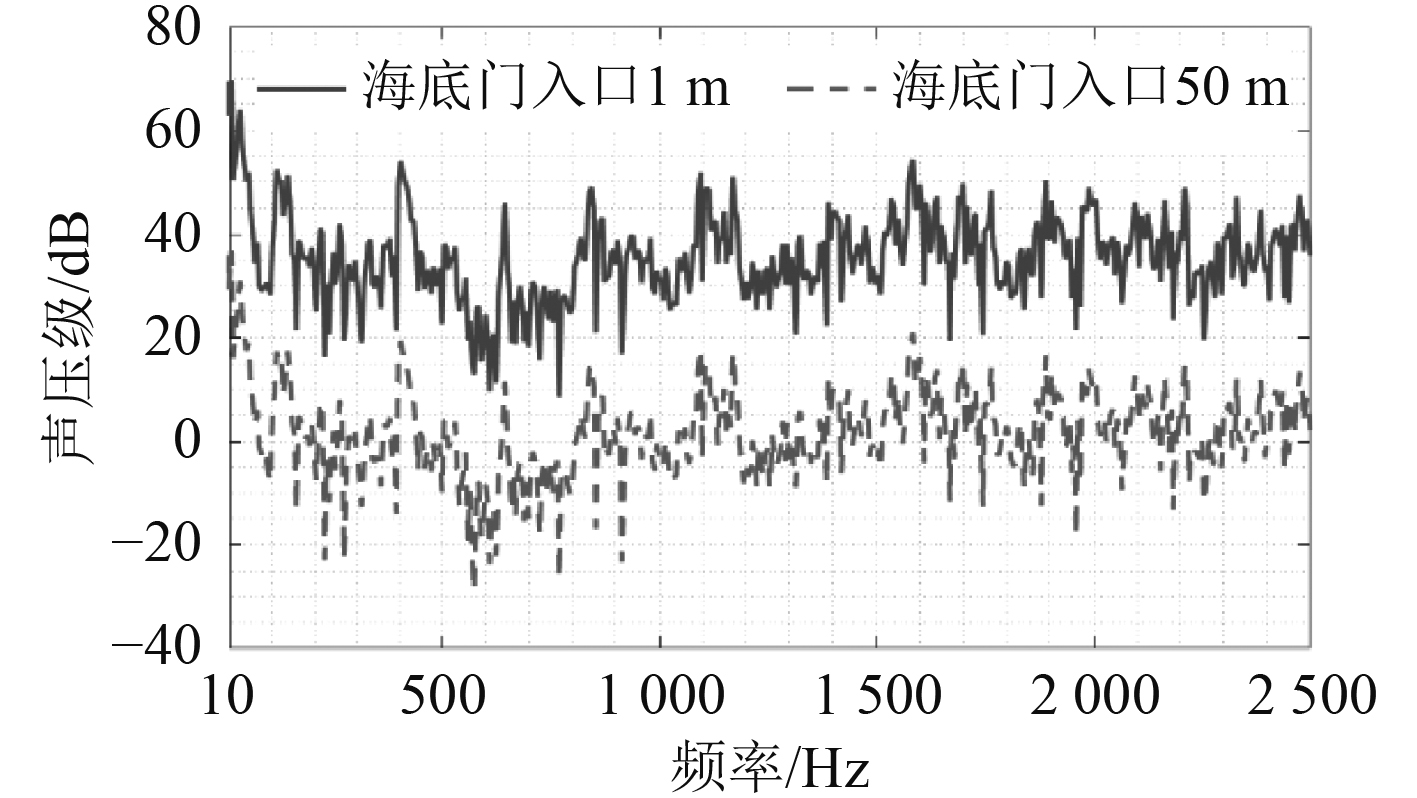
|
图 14 海底门出口1 m,50 m处的声压级频谱(方案2,参考声压10−6 Pa) Fig. 14 Sound pressure spectrum at 1 m and 50 m ahead of sea water chest exit (the second scheme, reference sound pressure 10−6 Pa) |
|
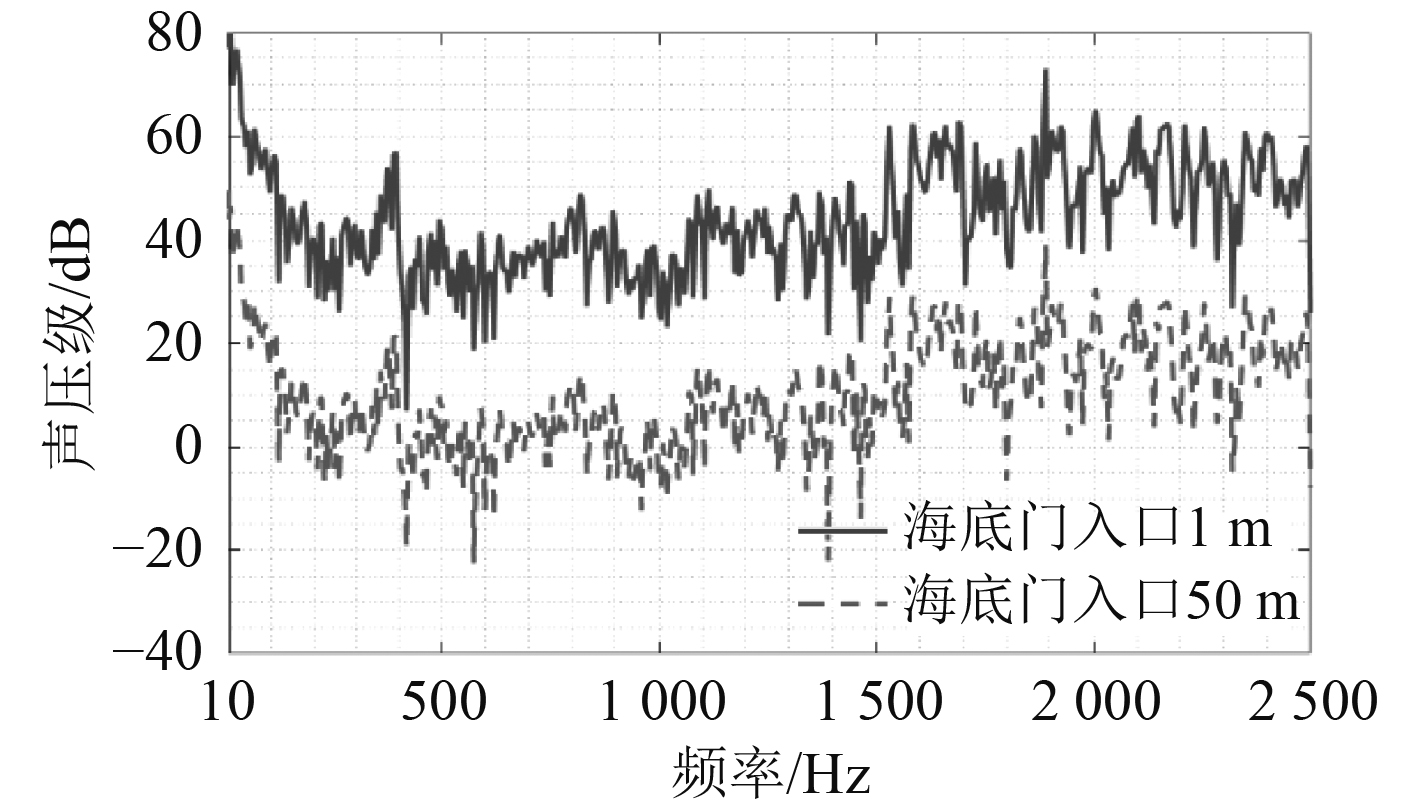
图 15 海底门出口1 m、50 m处的声压级频谱(方案3,参考声压10−6 Pa) Fig. 15 Sound pressure spectrum o at 1 m and 50 m ahead of sea water chest exit (the third scheme , reference sound pressure 10−6 Pa) |
3种方案下,距海底门出口1 m,50 m处的水下辐射噪声在各分频段及通频段的声压级如表3和表4所示。
|
|
表 3 海底门出口1 m处各分频段及通频段声压级(参考声压10−6 Pa) Tab.3 Sound pressure levels of each sub-band and cross-band at 1 m ahead of sea water chest exit for different schemes (reference sound pressure 10−6 Pa) |
|
|
表 4 海底门出口50 m处各分频段及通频段声压级(参考声压10−6 Pa) Tab.4 Sound pressure levels of each sub-band and cross-band at 50 m ahead of sea water chest exit for different schemes (reference sound pressure 10−6 Pa) |
通过对比,可以发现在低频段,方案2的声压级最小;在高频段,方案1的声压级最小。海底门的流噪声辐射以低频为主,所以方案2在通频段的辐射噪声声压级最小。取消伸入海底门内的短管可改善海底门内流场,降低湍流强度,减小流噪声辐射;而在海底门内设置导流板,造成流噪声辐射增加。
6 结 语本文对船舶海底门在设定流量下的流场环境进行了模拟计算,并基于FEM+AML方法开展了海底门出口辐射噪声特性研究,对比不同海水门内部结构对流场和水下辐射噪声的影响,得出以下结论:
1)海底门声辐射能量以低频为主,主要集中在低频段0~50 Hz。
2)伸入海底门内的短管会低湍流强度,增大流噪声辐射;
3)在海底门内设置导流板,会造成流噪声辐射增加。
| [1] |
何祚镛. 水下噪声及其控制技术进展和展望[J]. 应用声学, 2002. 21: 26−34.
|
| [2] |
胡家雄. 关于潜艇橡胶减振接管隔振效果的思考 [C]//船舶水下噪声学术讨论会, 2005.
|
| [3] |
蔡标华, 俞健, 白亚鹤. 舰船系统管路弹性减振设计与试验[J]. 舰船科学技术, 2011. 33: 61−64.
|
| [4] |
董自虎, 李超. 某船用通海阀流道优化仿真分析研究[J]. 舰船电子工程, 2016, 36: 95−100.
|
| [5] |
张冠军, 朱翔, 李天匀, 等. 水中双层加筋板结构的声振耦合特性[C]//中国造船工程学会船舶力学学术委员会第八次全体会议, 2014.
|
| [6] |
张跃, 郑轶, 王振, 等. 基于 LES 和 FEM/AML 方法对潜标结构流噪声预报研究[J]. 海洋技术学报, 2018(12): 22−27.
|
| [7] |
De Langhe, Koen, et al. Advanced simulation techniques for vehicle acoustic panel loading predictions, including FEM AML and Fast Multipole BEM (FMBEM) [C]//Internoise 2011.
|
| [8] |
刘翠伟, 李玉星, 王武昌, 等. 输气管道气体流经阀门气动噪声产生机理分析[J]. 振动与冲击, 2014, 33(2): 152-157. DOI:10.3969/j.issn.1000-3835.2014.02.029 |
 2021, Vol. 43
2021, Vol. 43
