2. 江苏科技大学,江苏 镇江 212100
2. Jiangsu University of Science and Technology, Zhengjiang 212100, China
含周期空腔结构的覆盖层被广泛应用于水下减振降噪领域[1-7],相较于均匀材料制作的覆盖层,含空腔覆盖层利用空腔共振、波形转换等方式,可以极大地提高覆盖层的声学性能。但是这种覆盖层结构对水下低频声波的吸收较低,因此为了提高声学覆盖层对低频声波的吸收,国内外研究人员设计出由声子晶体构成的声学覆盖层。
类比于电磁波在光子晶体中的传播特点,M.S.Kushwahas等[8]首次提出声子晶体概念,将具有弹性波带隙特征的一类复合材料定义为声子晶体,该复合材料中相连的部分称为基体,不相连的部分称为散射体。采用平面波展开法,研究了铝基体中嵌入镍形成的复合结构的弹性波带隙。R.Martinez-Sala等[9]第一次在实验上证明了弹性波带隙的存在。温激鸿等[10]研究了弹性波在板状周期结构中的传播特征,并指出声子晶体带隙范围受散射体和基体的影响。何晓栋等[11]基于有限元法,分析了晶格常数对局域共振结构隔声性能的影响。刘正猷提出局域共振声子晶体的概念,指出在弹性波的作用下,基体中的散射单元发生共振,并抑制了弹性波的传播。利用刘正猷提出的局域共振理论,研究人员设计出低频水声吸声材料[12-13]。
本文利用COMSOL有限元软件,首先对比分析声子晶体带隙范围与吸声系数之间的关系,然后研究声子晶体材料类型、平面波入射角度等对覆盖层吸声性能的影响,进一步分析了声子晶体覆盖层的吸声机理,为提高覆盖层低频吸声提供参考。
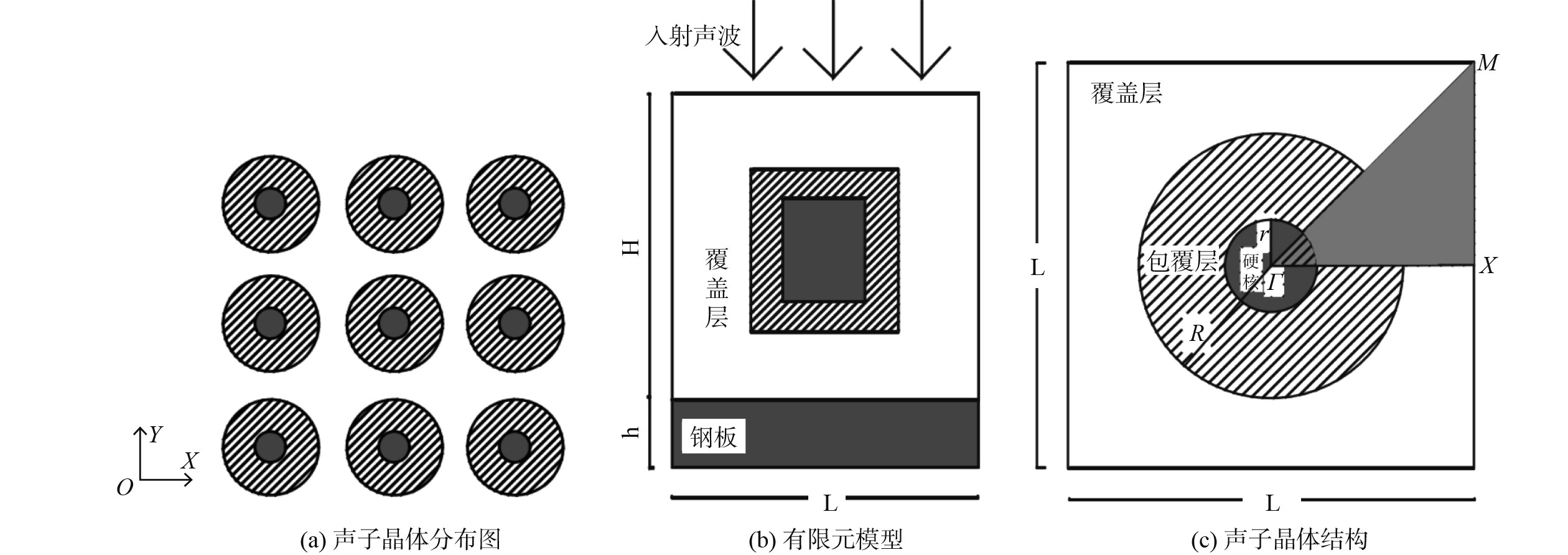
1 模型及理论简介 1.1 计算模型简介假设覆盖层沿xoy平面无限延伸,如图1(a)所示,因此根据Bolch周期定理,只需计算单胞结构即可得到整个覆盖层的声传播特征。基于上述理论,本文所建立的有限元模型如图1(b)所示,计算模型由粘弹性基体和背衬组成,基体内部为周期排列的声子晶体,设覆盖层高度为H,长度为L,底部背衬厚度和h,整个模型浸没在水中。图1(c)为覆盖层横截面图,覆盖层边长为L,内部声子晶体由硬核振子和包覆层组成,振子的半径为r,包覆橡胶层后整个振子的半径为R。
|
图 1 模型图 Fig. 1 Model diagram |
利用覆盖层内部声子晶体周期分布的特点,从单个元胞结构即可计算出整个覆盖层的声传播。计算单元包括水层、粘弹性层,用杨氏模量的衰减因子体现声阻尼,
| $ E = E \times (1{\text{ + }}i\eta ),$ | (1) |
利用有限元法对整个模型进行分析,得到弹性体和流体耦合有限元方程为:
| $ \left( {\begin{array}{*{20}{c}} {\boldsymbol{R}}&{{{\boldsymbol{K}}_T} - {\omega ^2}{{\boldsymbol{M}}_T}} \\ {{{\boldsymbol{K}}_S} - {\omega ^2}{{\boldsymbol{M}}_S} - {C_\phi }}&{ - \rho {\omega ^2}{\boldsymbol{R}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {u} \\ {p} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} F \\ {{C_0}} \end{array}} \right)。$ | (2) |
式中:
周期单元性单元对应边界处的周期性条件的表达式为:
| $ {{\boldsymbol{F}}_{dst}} = {{\boldsymbol{F}}_{src}}{e^{ - i{\boldsymbol{n}}({{\boldsymbol{r}}_{dst}} - {{\boldsymbol{r}}_{src}})}}。$ | (3) |
式中:下标
由位移和声压连续的条件,即可得到整个覆盖层的反射、透射和吸声系数分别为:
| $ R = \sqrt {\sum\limits_{k_{ij}^2 > 0} {{{\left| {{R_{ij}}} \right|}^2}} },$ | (4) |
| $ T = \sqrt {\sum\limits_{k_{ij}^2 > 0} {{{\left| {{T_{ij}}} \right|}^2}} } ,$ | (5) |
| $ \alpha = 1 - {R^2} - {T^2}。$ | (6) |
式中:
能带结构是表征声子晶体覆盖层声学特性的重要参数,能带的形成主要依赖于介质中传播的弹性波,因此对声子晶体覆盖层声学性能的研究,就是分析弹性波在基体中的传播规律。
弹性波的波动方程为:
| $ (\lambda + 2\mu )\nabla (\nabla {{u}}) - \mu \nabla \times \nabla \times {{u}} = \rho \frac{{{\partial ^2}{{u}}}}{{\partial {t^2}}},$ | (7) |
设位移u与时间t之间的关系为:
| $ {{u(r,t)}} = {{u(r)}}{{\rm{e}}^{j\omega t}} 。$ | (8) |
则式(7)可以表示为:
| $ (\lambda + 2\mu )\nabla (\nabla {{u}}) - \mu \nabla \times \nabla \times {{u}} = - \rho {\omega ^2}{{u}} ,$ | (9) |
当弹性波在声子晶体中传播满足Bloch定理时,波动方程的解为:
| $ {{u(r + d)}} = {{u(r)}}{{\text{e}}^{jkd}}。$ | (10) |
式中:d为晶格常数;k为倒格波矢。
由于结构具有周期性,在有限元计算中,若想获得声子晶体的带隙,只需用波矢k扫掠与结构相对应的不可约布里渊区即可。即波矢对图1(c)中的声子晶体模型从
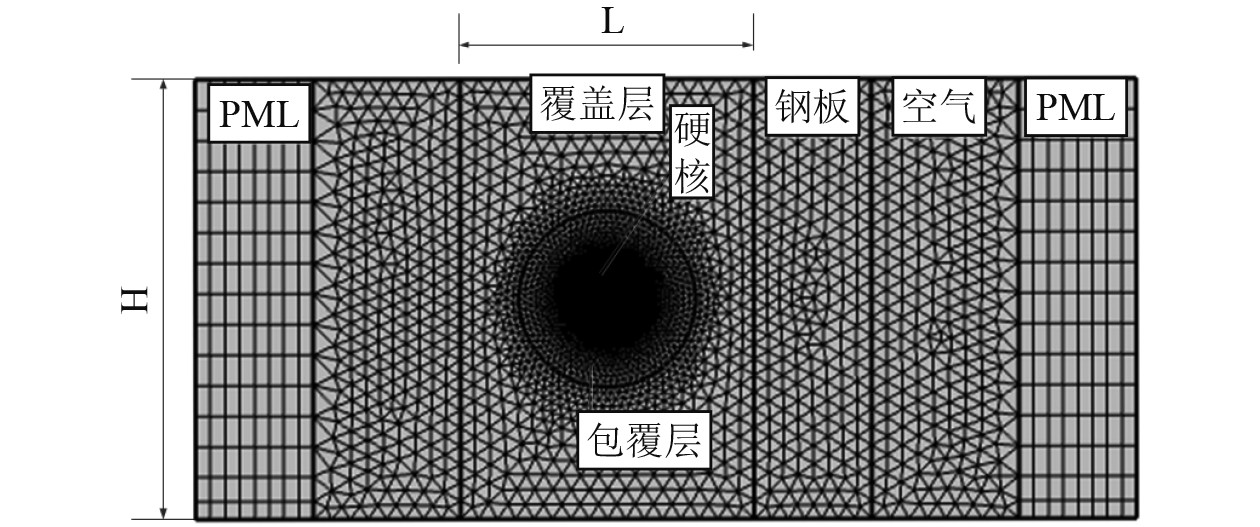
为了验证本文计算方法的准确性,在COMSOL有限元软件中建立如图2所示的有限元模型。
|
图 2 有限元模型 Fig. 2 Finite element model |
将覆盖层置于流体介质中,在覆盖层与流体界面处,应用“声-结构”边界条件模拟不同介质之间的相互作用。由于“声-结构”边界条件的存在,不同物理场之间发生了完全耦合的相互作用,在两端水域设置完美匹配层(PML),同来模拟无限大水域。
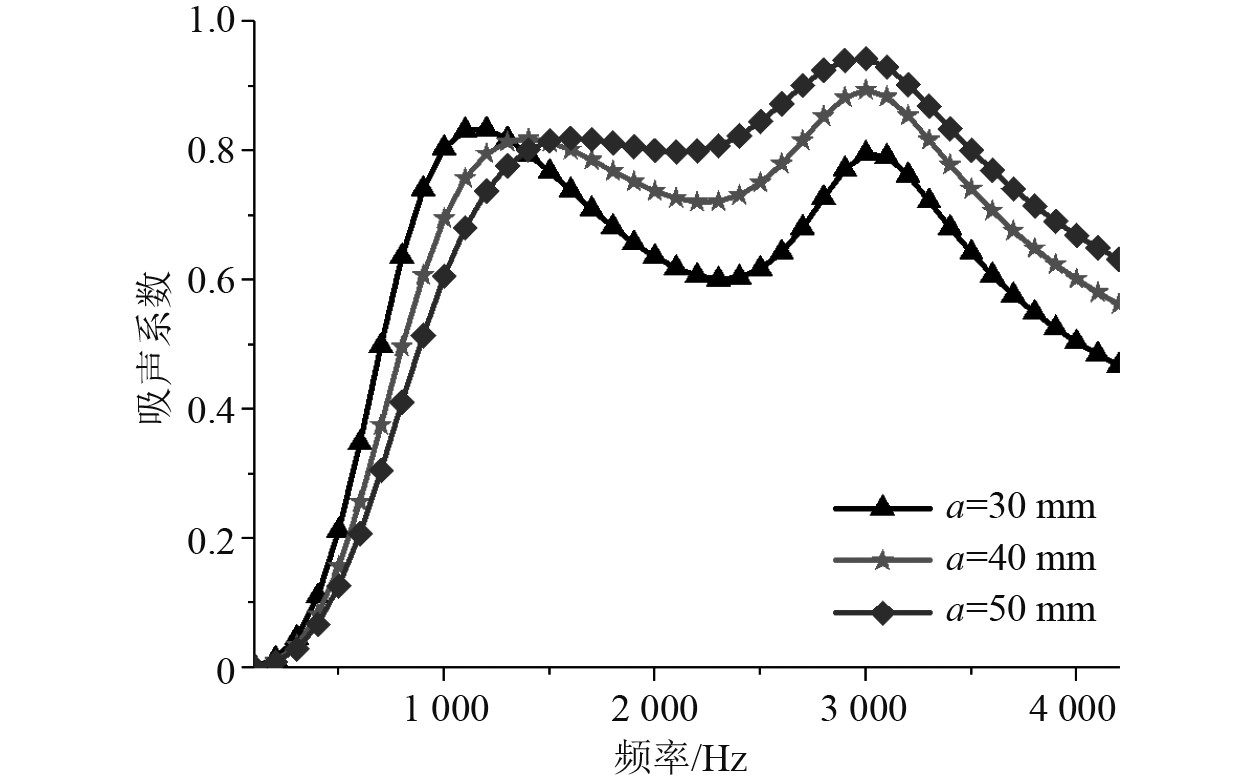
按照文献[14]给出的参数,对比不同尺寸的硬核对覆盖层吸声系数的影响,计算结果如图3所示。
|
图 3 本文计算的吸声曲线 Fig. 3 Sound absorption curve calculated in this paper |
|
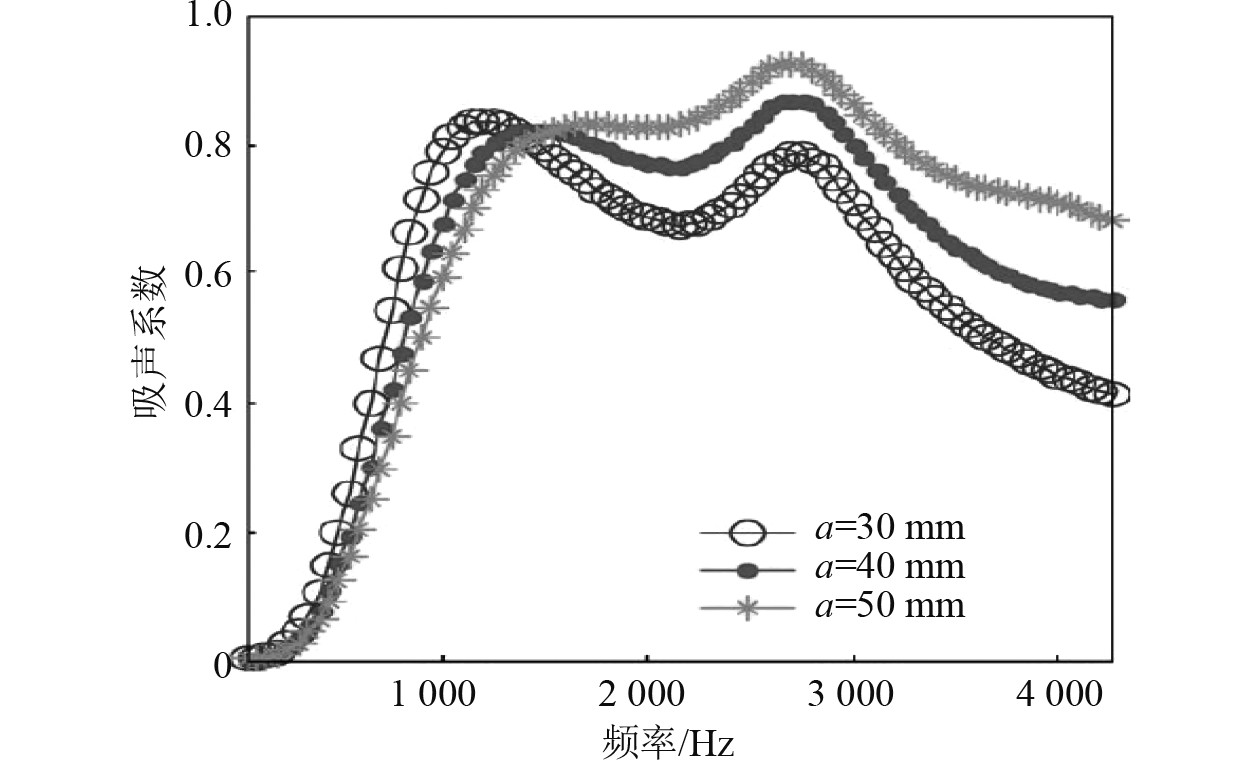
图 4 文献计算中吸声曲线 Fig. 4 Sound absorption curve in literature calculation |
对比两图吸声曲线可知,本文采用的数值计算与文献中计算结果吻合较好,说明本文采用的方法是可行的。
2.2 验证声子晶体带隙理论为验证本文计算声子晶体带隙方法的正确性,按照文献[15]给出的参数,基于COMSOL有限元软件,建立如图5所示的声子晶体模型,并计算能带结构图。

|
图 5 声子晶体有限元模型 Fig. 5 Finite element model of phononic crystal |
扫掠第一布里渊区边界,即可得到如图6所示的能带结构图。
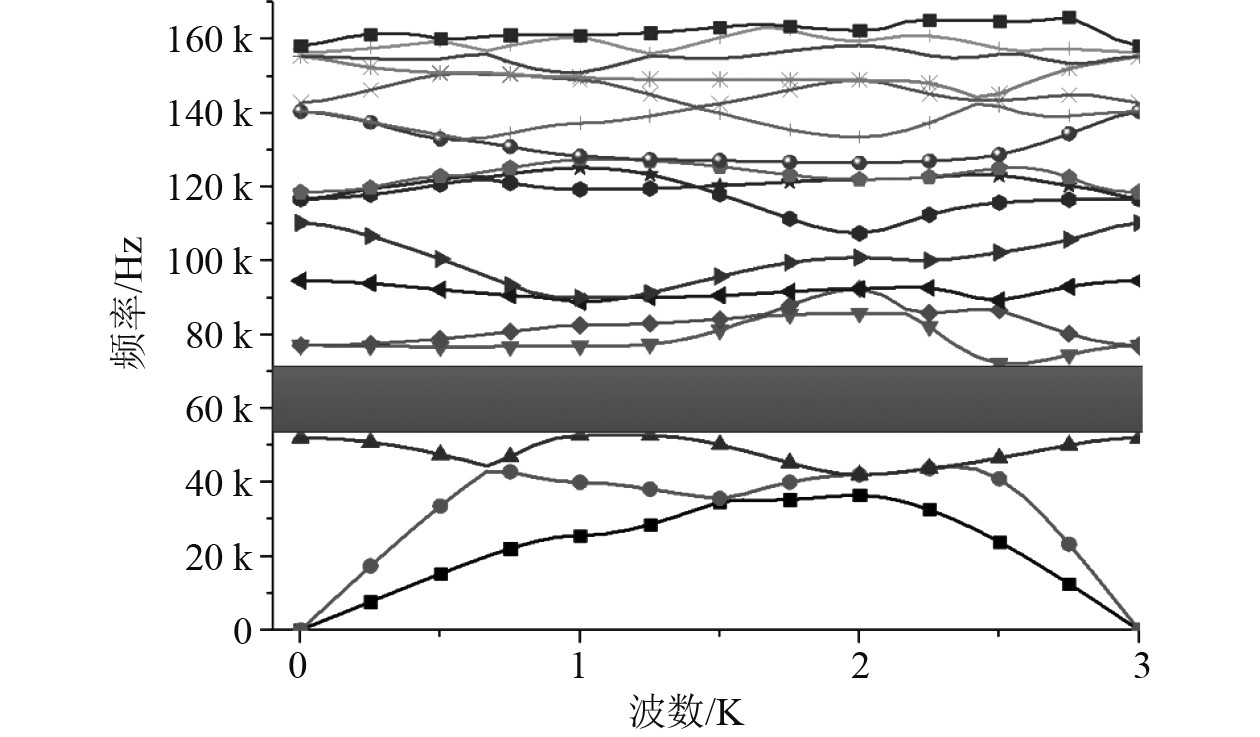
|
图 6 本文能带结构图 Fig. 6 Band structure of this paper |
对比图6和图7的计算结果可知,两图能带结构均存在一个完全带隙,并且两图的带隙频率范围基本一致,说明本文采用的方法是可行的。
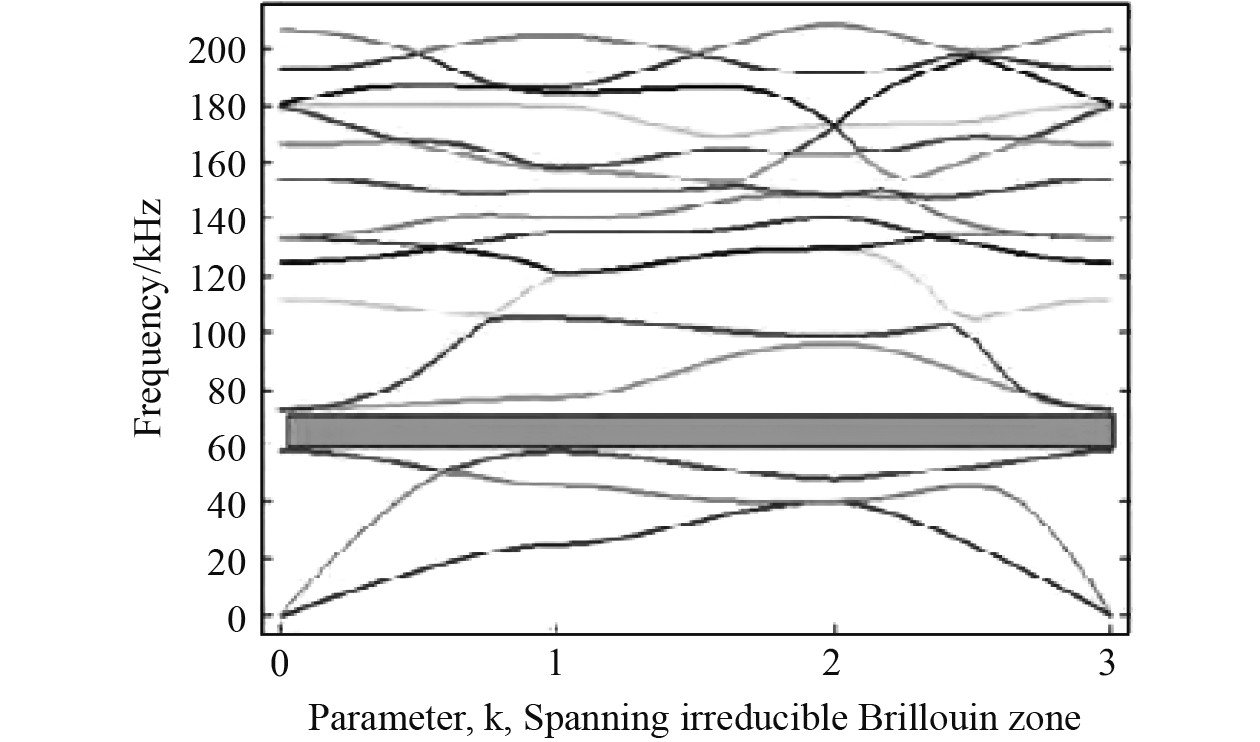
|
图 7 文献能带结构图 Fig. 7 Band structure of literature |
声子晶体覆盖层模型如图8所示。
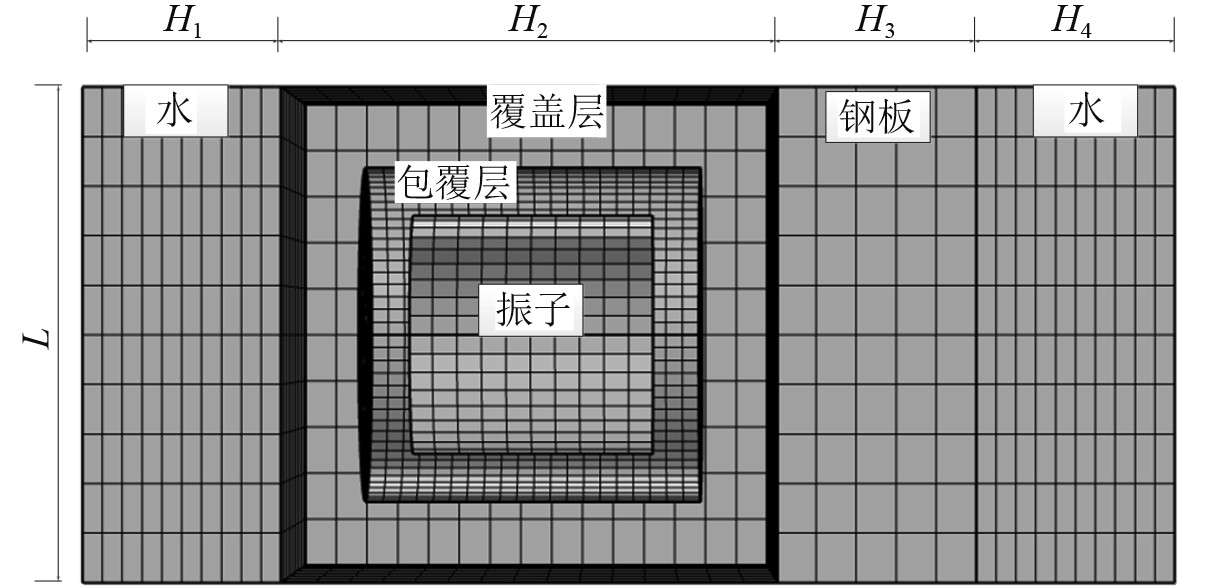
|
图 8 仿真模型 Fig. 8 Simulation model |
覆盖层置于无限大水域之中(通过平面波辐射模拟无限大水域),底部为钢板背衬,覆盖层内部几何中心位置为声子晶体,内部为圆柱形硬核振子,振子外部包覆一层不同于覆盖层材质的软橡胶。
覆盖层材料为:密度
扫掠图8有限元模型中声子晶体的不可约布里渊区,即可得到声子晶体的能带结构,如图9所示。
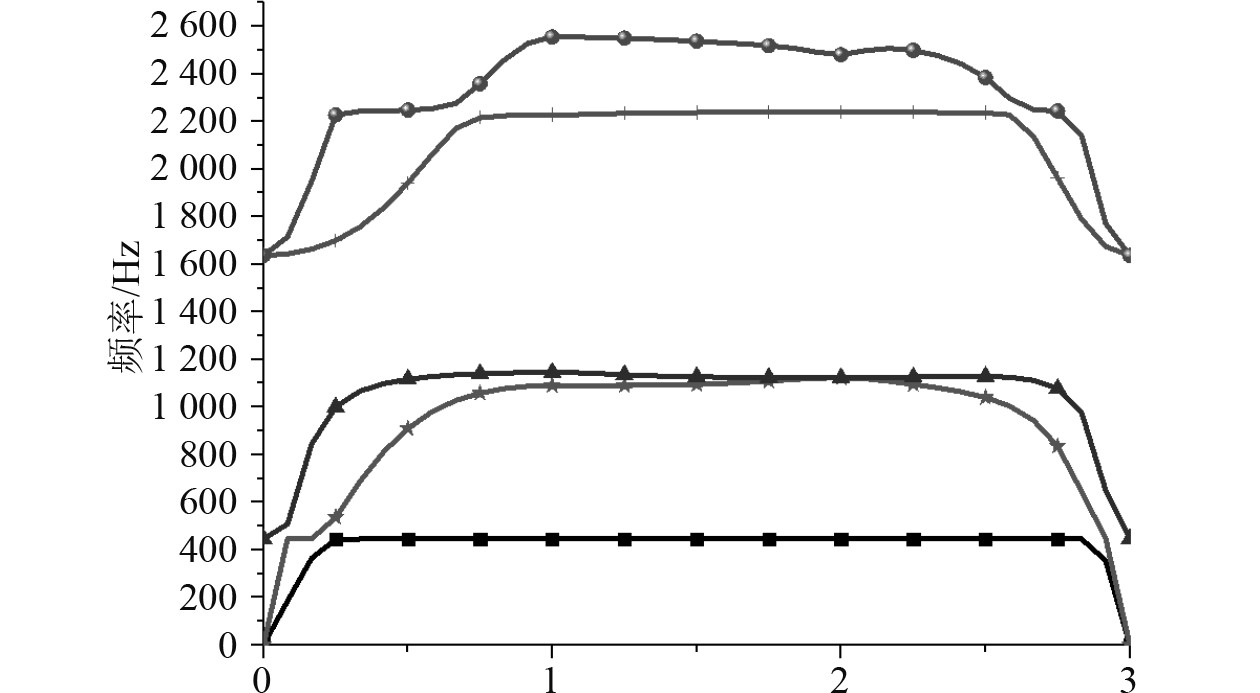
|
图 9 能带结构图 Fig. 9 Band structure diagram |
观察图9可知,在第3、第4能带之间出现一个完全带隙,带隙的起始频率为1.2 kHz,截止频率为2.2 kHz,中心频率为1.7 kHz。分析起始、截止频率处能带图机理。
图10为能带图起始、截止频率处覆盖层模态位移云图。可知,在能带图起始频点处,覆盖层内部声子晶体位移幅值远大于基体的位移,说明在该频点下,声子晶体发生共振现象,带隙的产生依赖于硬核的振动。而在能带图截止频率下,包覆层的位移大于硬核和基体的位移量,说明此时包覆层随声能的耗散是产生带隙的主要原因。

|
图 10 不同频率处模态位移云图 Fig. 10 Modal displacement nephogram at different frequencies |
上述分析表明,影响声子晶体带隙的因素不止一个,它往往是在多种机理作用下共同产生的。将分析带隙频率范围对声子晶体覆盖层吸声性能的影响,图11为图8有限元模型的吸声系数图。
|
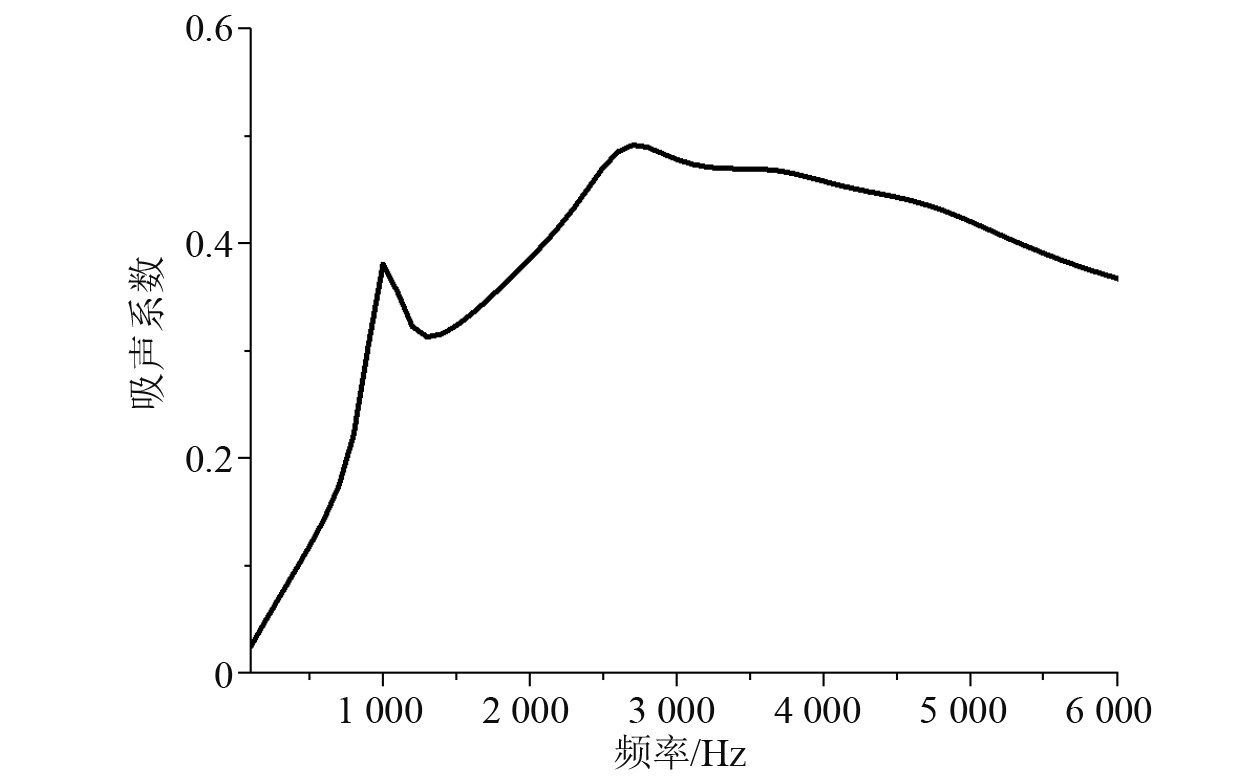
图 11 吸声系数 Fig. 11 Sound absorption coefficient |
观察图11吸声系数曲线可知,覆盖层吸声系数在1.2 kHz和2.7 kHz频点处分别出现吸声峰,分析吸声曲线出现这种变化的原因。图12分别为吸声系数曲线在第1、第2吸声峰频点处,声子晶体覆盖层位移云图。

|
图 12 吸声峰频点处覆盖层位移图 Fig. 12 Displacement diagram of overburden at absorption peak frequency point |
观察图12覆盖层位移移云图可知,在第1吸声峰频点处,覆盖层内部硬核的位移幅值远大于基体和包覆层的位移幅值,说明在该频点下对声能的损耗依赖于硬核的振动。而在第2吸声峰处,覆盖层包覆层和基体的位移较明显,说明在该频点下,入射的声能大部分被包覆层和覆盖层基体消耗,即第2吸声峰依赖于基体和包覆层的振动。
对比图12和图10可知,覆盖层吸声峰值频点处的位移,与声子晶体在带隙起始、截止频率处振动位移云图基本一致,说明对局域共振型覆盖层来说,带隙范围是影响覆盖层吸声性能的重要因素。
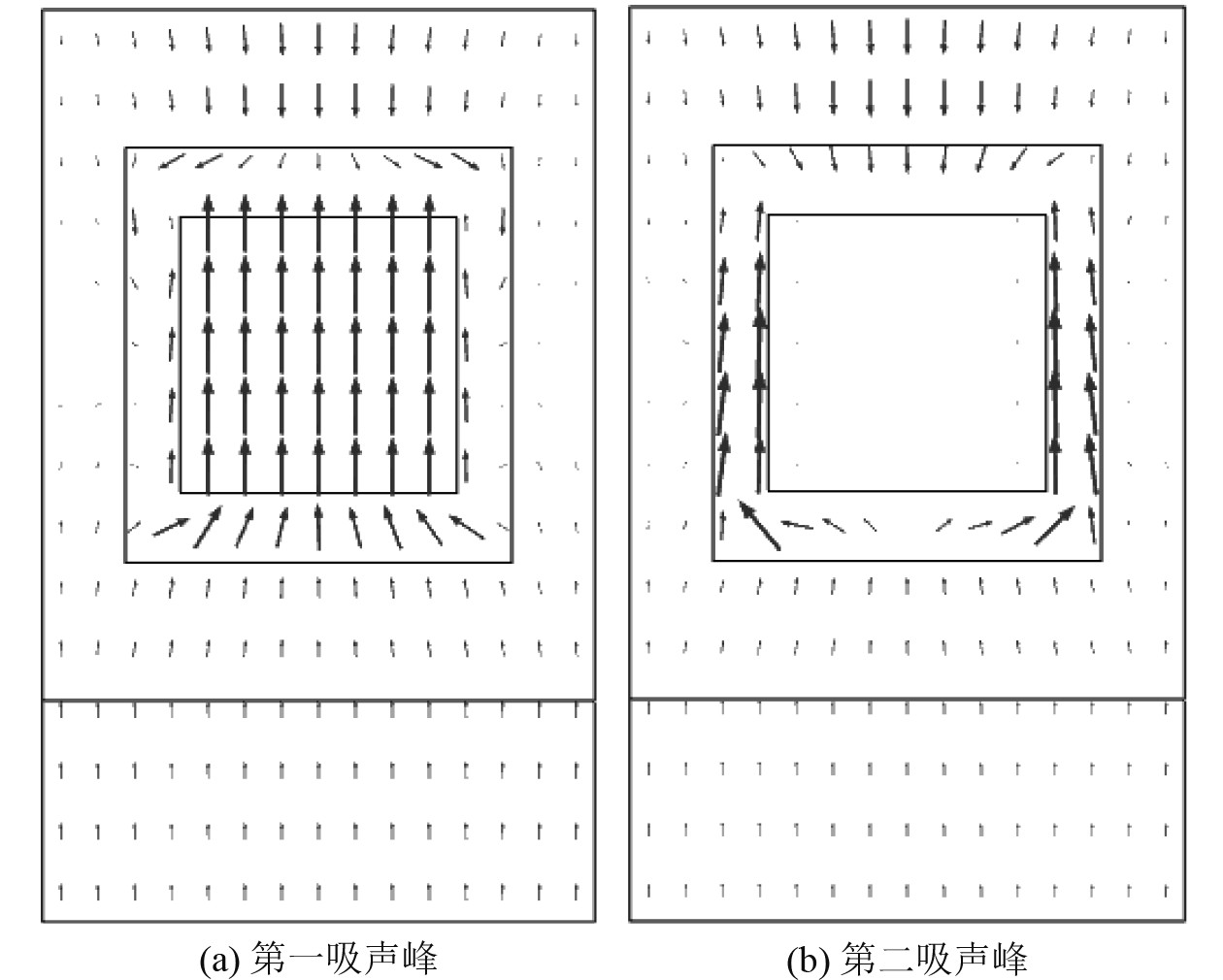
为了进一步分析覆盖层的吸声机理,研究吸声峰频点下覆盖层位移矢量图,如图13所示。
|
图 13 吸声峰频点处位移矢量图 Fig. 13 Displacement vector diagram at absorption peak frequency point |
由图13(a)可知,在第1吸声峰频点处,在硬核的纵向位移和粘弹性包覆层剪切变形共同作用下,实现了对声能的耗散,从而进一步证明了声子晶体的振动是影响覆盖层低频吸声性能的主要因素。观察图13(b)并结合图12(b)可知,在第2吸声峰频点下,入射的声能被截留在包覆层中,通过包覆层的剪切变形,使入射的纵波转换成横波,实现对声能的损耗。
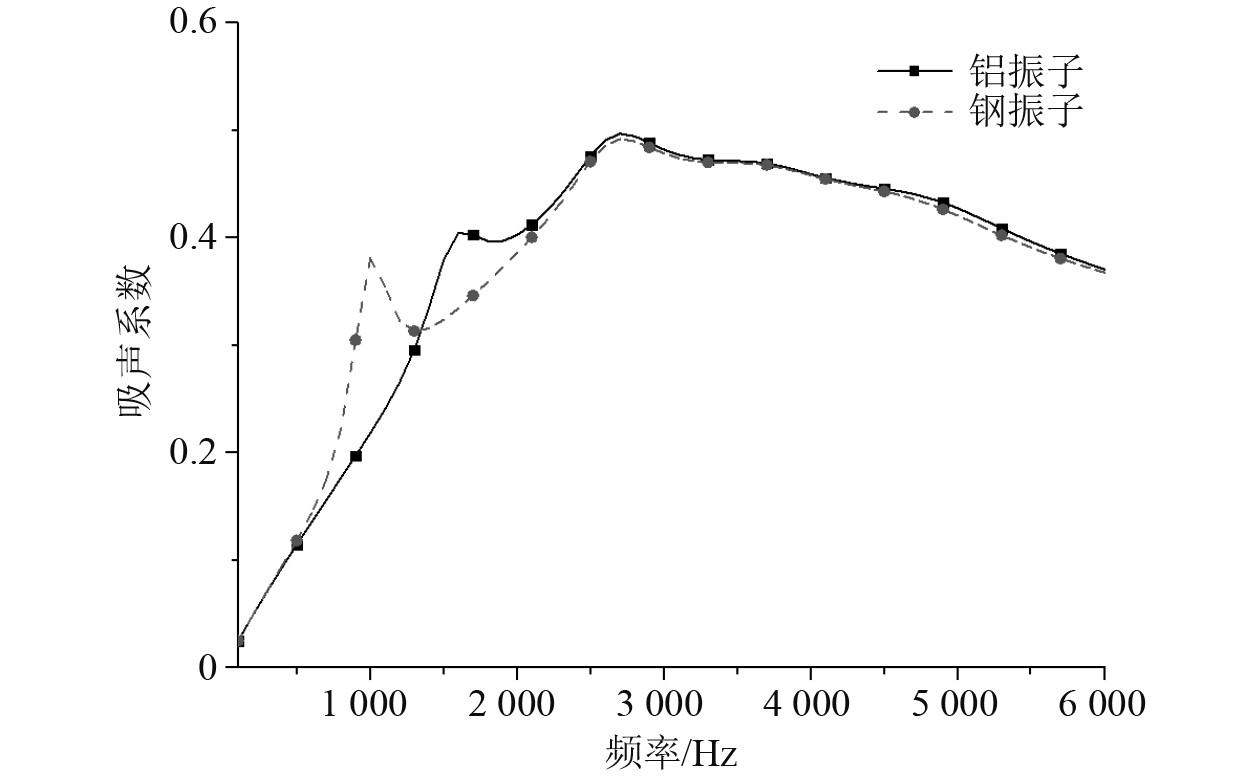
3.2 振子材料对吸声的影响本节讨论硬核振子材料对覆盖层吸声系数的影响,将包覆层中的硬核材料由钢改为铝,2种不同硬核材料的吸声系数对比如图14所示。
|
图 14 不同材料振子的吸声系数 Fig. 14 sound absorption coefficient of different materials |
由图14两种不同工况下吸声系数曲线对比图可知,改变振子的质量仅影响第1吸声峰频率,随着振子质量的减小,第1吸声峰频率增大,即共振频率增大。振子质量的变化并未改变第2吸声峰频率,但是由于振子质量的降低,导致第1吸声峰向高频移动,并在一定程度上提高了第1、第2吸声峰之间的峰谷,所以在2个吸声峰之间的频率范围,铝振子覆盖层的吸声系数优于钢振子覆盖层。
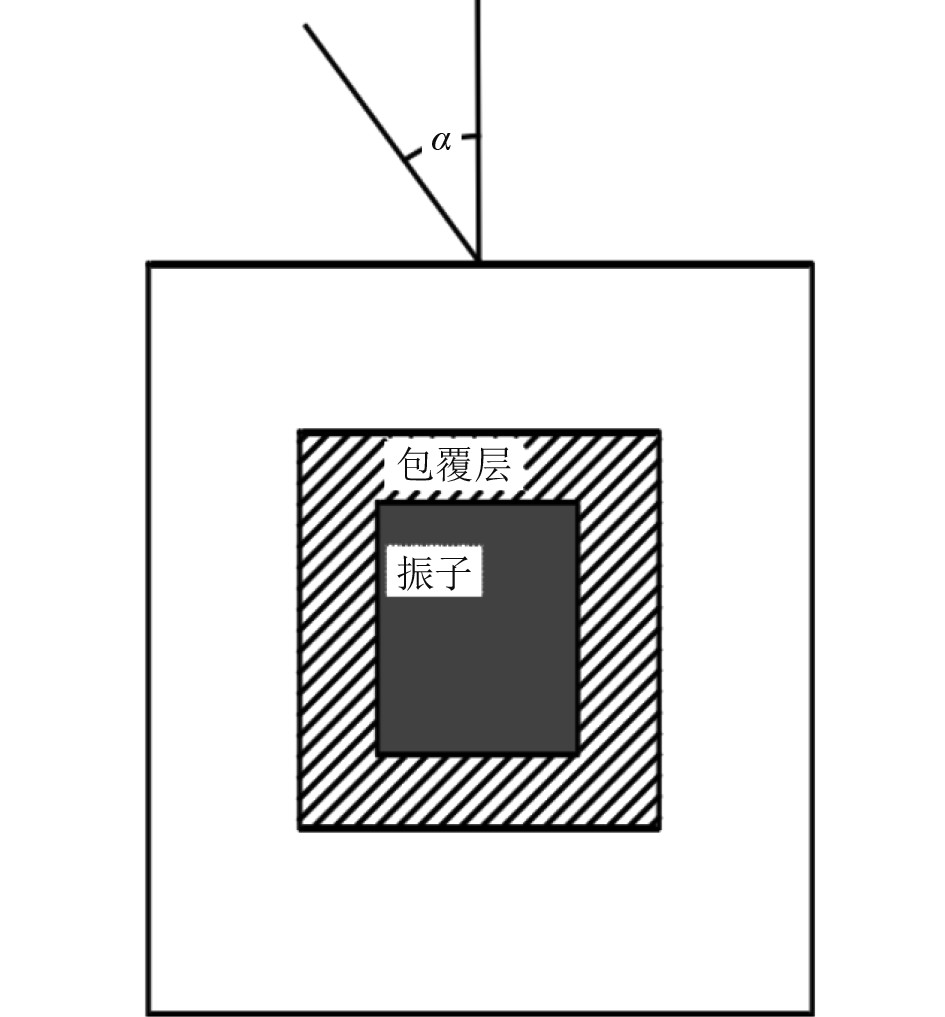
3.3 声波入射角度对吸声的影响分析声波入射角度对覆盖层吸声性能的影响,图15为平面波斜入射示意图,声波从覆盖层顶部以不同的角度入射,设入射角度
|
图 15 斜入射示意图 Fig. 15 oblique incidence diagram |
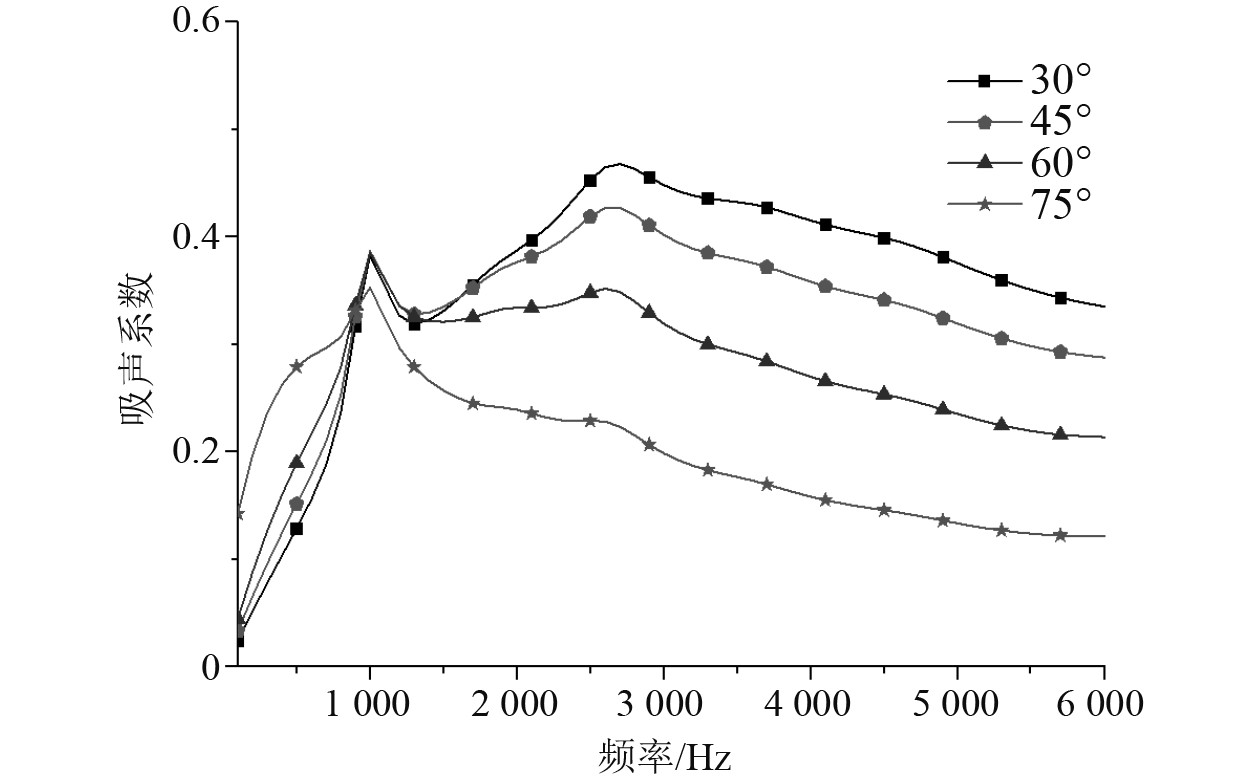
图16为不同入射角度下,声学覆盖层吸声系数对比图。观察图16可知,第1吸声峰频率不受入射角度的影响,这是因为第1吸声峰依赖于振子的共振频率,当声子晶体的质量不变时,改变声波入射角度并不会影响声子晶体的共振频率。第2吸声峰峰值随入射角度的增大而降低,分析可知,覆盖层第2吸声峰依赖于包覆层和基体的振动,而斜入射声波包含轴向和径向2个方向,这2种方向的波矢在包覆层中相互耦合,降低了包覆层对声能的耗散,因此吸声系数随入射角度的增大而降低。
|
图 16 不同入射角度吸声系数对比 Fig. 16 comparison of sound absorption coefficient at different incident angles |
本文针对声子晶体覆盖层声吸收问题,利用有限元法,重点分析了声子晶体带隙、振子材料参数和平面波入射角度等对覆盖层吸声性能的影响,得出以下结论:
1)声子晶体的带隙范围决定覆盖层吸声峰频率,通过改变带隙的起始和截止频率,可以调整覆盖层吸声峰位置,提高覆盖层在低频段的吸声系数;
2)改变振子的质量,不仅能调整第1吸声峰的位置,还会使第1、第2吸声峰之间相互耦合,从而在一定频率范围内实宽带吸声。
3)对于声子晶体覆盖层来说,第1吸声峰主要依赖于硬核的共振,改变声波入射角度,不会影响到吸声峰位置,但是入射角度会影响覆盖层的声吸声性能。
| [1] |
曹君晖, 赵宏刚, 王洋. 一种含周期柱形空腔覆盖层的吸声特性研究[C]. 中国力学学会产学研工作委员会, 2020: 191−194.
|
| [2] |
柯李菊, 刘成洋, 方智. 基于COMSOL的组合空腔结构声学覆盖层的声学性能分析[J]. 中国舰船研究, 2020, 15(5): 167-175+182. |
| [3] |
杨培凯, 陈美霞. 基于分层等效方法的吸声覆盖层声学特性研究[C]. 中国造船工程学会, 2019: 590−595.
|
| [4] |
赵静波, 陈鑫, 姚宏. 含倒圆台空腔覆盖层吸声性能研究[C]//中国声学学会微声学分会: 《声学技术》编辑部, 2019: 64−67.
|
| [5] |
YE Changzheng, LIU Xuewei. Influence of hole shape on sound absorbtion of underwater anechoic layers. Journal of sound and Virbration.
|
| [6] |
冯常慧, 兰清, 葛印超. 一种含有空腔的声学覆盖层隔声性能研究[J]. 声学与电子工程, 2018(3): 13-17. |
| [7] |
杨立军, 张冲, 楼京俊, 刘国强. 静压下多层材料椭球形空腔吸声覆盖层的吸声性能分析[J]. 舰船科学技术, 2017, 39(5): 54-57. |
| [8] |
KUSHWAHA M S, HALEVI P. Acoustic band structure of periodic elastic composites[J]. Physical Review Letter, 1993, 71: 2022-2025. DOI:10.1103/PhysRevLett.71.2022 |
| [9] |
Martinez Sala R, Sancho J. Sound attenuation by sculpture[J]. Nature, 1995, 378: 241
|
| [10] |
温激鸿, 王刚, 郁殿龙. 声子晶体振动带隙及减振特性研究[J]. 中国科学(E辑: 技术科学), 2007(9): 1126-1139. |
| [11] |
何晓栋, 肖勇, 温激鸿. 晶格常数对声学超材料板隔声特性的影响研究[J]. 噪声与振动控制, 2018, 38(S1): 51-55. |
| [12] |
卢少杰, 孟晓宇, 蔡子青. 承压条件下声子晶体吸声性能研究[J]. 合成材料老化与应用, 2013, 42(5): 16-19. DOI:10.3969/j.issn.1671-5381.2013.05.005 |
| [13] |
XIAO Y, WEN J, WEN X. Flexural wave band gaps in locally resonant thin plates with periodically attached spring-mass resonators[J]. Journal of Physics D:Applied Physics, 2012, 45(19): 195401. DOI:10.1088/0022-3727/45/19/195401 |
| [14] |
杨海滨, 李岳, 赵宏刚, 等. 一种含圆柱形谐振散射体的黏弹材料低频吸声机理研究[J]. 物理学报, 2013, 62(15): 223-229. |
| [15] |
陈龙飞, 游世辉, 赵小英. 二维声子晶体薄板隔声特性研究[J]. 材料导报, 2020, 34(S1): 90-93. |
 2021, Vol. 43
2021, Vol. 43
