2. 深海载人装备国家重点实验室,江苏 无锡 214082
2. State Key Laboratory of Deep-sea Manned Vehicles, Wuxi 214082, China
随着海洋开发的不断深入,水下潜器越来越为人们所倚重。目前水下潜器通常采用潜浮系统、均衡系统和推进系统协同完成潜器上浮、下潜和水下机动等运动。这种机动方式由于系统组成复杂,不仅占用水下潜器较多的布置空间,增大水下潜器的主尺度;同时控制操纵系统复杂,完成潜浮任务所需时间较长;更重要的是水下潜器丢失后,难以搜寻。
为解决以上问题,提出扇翼推进水下潜器的新概念。这种新型水下潜器较常规水下潜器的优势在于只用一套扇翼推进系统就能代替潜浮系统、浮力调节系统以及推进系统,完成潜器的下潜、上浮以及水下机动。这主要是由于扇翼推进器可同时产生平衡水下潜器储备浮力和水下阻力的负升力和推力,但推进器种类繁多,能同时提供推力和负升力的推进器也不在少数,比如可倾斜轴导管桨。因此要论证扇翼推进水下潜器概念方案的可行性应先确定扇翼推进器的推进效率是否优于其他推进器。
扇翼推进水下潜器的核心装置是扇翼推进器,这是该潜器的主要动力来源。扇翼推进器的空气动力特性在国内外已得到广泛的研究,Klaus Koegler[1]在帝国理工大学完成了扇翼的风洞试验,并将试验结果与直升机相关指标进行对比,得出的结论是风扇翼的效率比一般的直升机高出35%。S.Askari[2]运用CFD方法探究了来流速度和风扇转速对扇翼飞行器的气动力性能及机翼表面压强分布的影响,结果表明扇翼的升力和推力高度依赖于扇叶转速,升力和推力的大小可以通过增大转速来提高。吴浩东[3]使用CFD手段对风扇翼内部偏心涡的形成过程进行仿真,分析其形成机理。在此基础上,探究了风扇翼设计参数对风扇翼内部偏心涡的影响。刘乐[4]运用CFD方法计算了不同的来流速度、叶片数量、转速、来流迎角和后缘夹角下的扇翼推进器的流场,揭示了扇翼推进器偏心涡、负升力和推力产生的机理,以及上述设计参数对扇翼推进器水动力的影响规律。综上可知,关于扇翼的气动性能国内外学者已经做了大量研究,但关于扇翼的水动力特性研究较少。
关于螺旋桨的敞水性能研究方法已相当成熟,常欣[5]通过CFD方法计算了DTMB4679螺旋桨在斜流中的非定常水动力性能,结果表明相比纯轴向流,在斜流中工作的螺旋桨推力和转距均会增大。张志荣[6]针对DTMB4679在斜流中的性能进行了试验以及数值方法的研究,结果表明非定常方法计算精度相对较高。
本文基于CFD方法,在来流速度一定的条件下,预报分析了扇翼推进器和可倾斜轴导管桨在定深直航工况下,产生相同负升力和推力时的敞水效率,为扇翼推进水下潜器概念方案的可行性论证提供支撑。
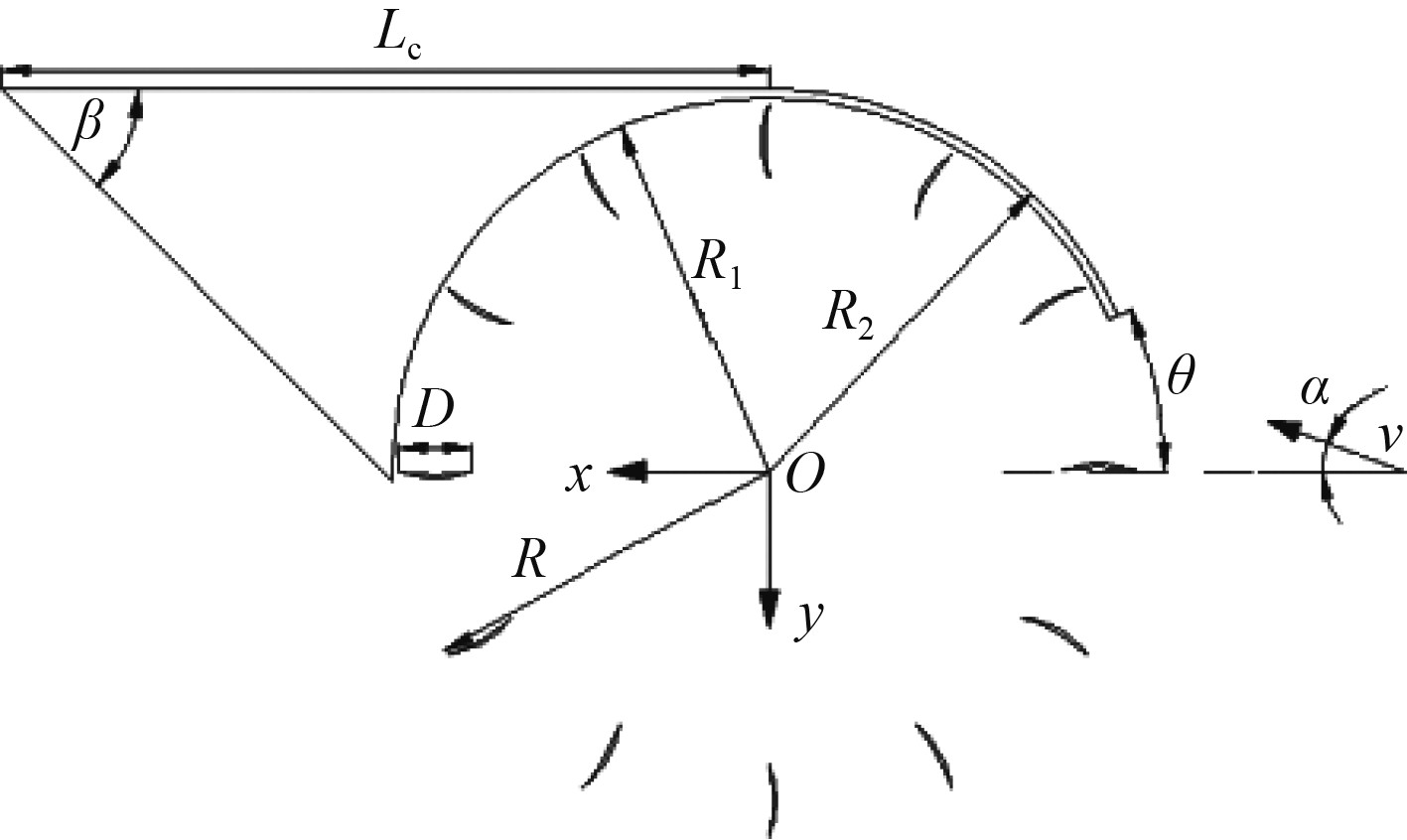
1 数值模拟 1.1 计算模型介绍由于扇翼推进器外形及流场具有典型的二维特性,同时在扇翼推进器设计时,会在扇翼展长方向两端加装挡板,以减小扇翼推进器的三维效应,因此研究扇翼推进器的敞水性能时采用二维模型。扇翼推进器是由旋转的扇叶和固定的机翼组成,坐标系原点固定在扇翼圆弧段的圆心处,指向机翼去流段为X轴正半轴,垂直于X轴背离机翼圆弧段为Y轴正半轴,推力沿X轴负半轴方向,负升力沿Y轴正半轴方向。扇翼推进器的二维外形示意图及主要参数见图1和表1。
|
图 1 扇翼推进器几何示意图 Fig. 1 Geometric diagram of the fanwing propeller |
|
|
表 1 扇翼推进器主要几何参数表 Tab.1 Main geometrical parameters of the fanwing propeller |
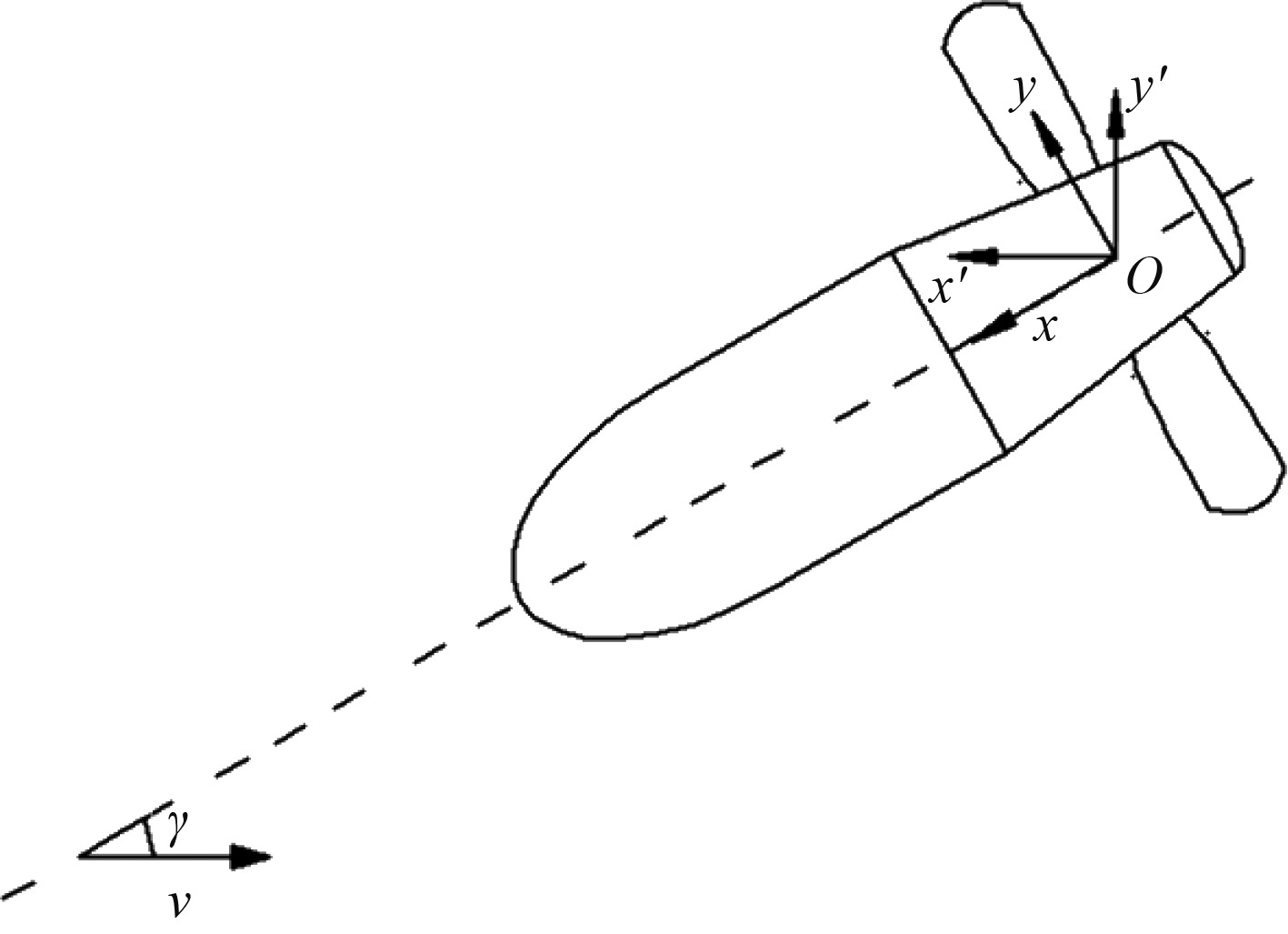
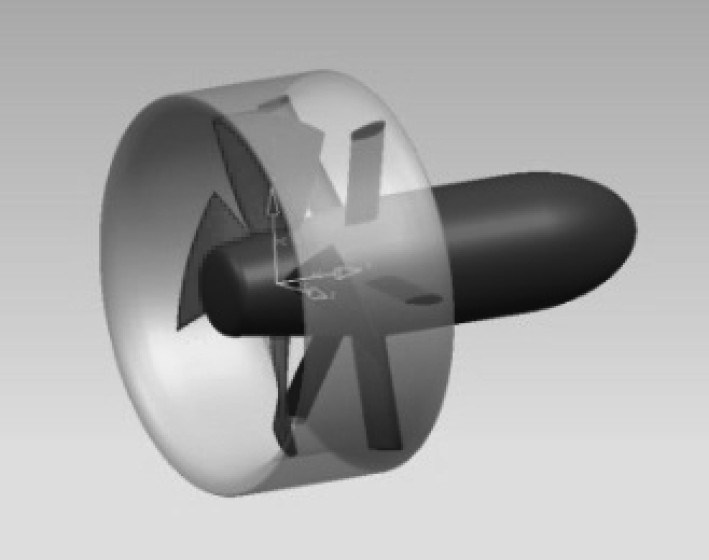
可倾斜轴导管桨的全局坐标系原点O固定在桨毂轴线与叶面参考线的交点处,沿桨毂来流段为X轴正方向,从尾向首看,指向左侧的为Y轴正方向,依据右手准则确定Z轴正方向。可倾斜轴导管桨是通过改变桨轴倾斜角γ来同时提供推力和负升力,其外形和主要参数见图2和图3及表2。
|
图 2 可倾斜轴导管桨几何示意图 Fig. 2 Geometric diagram of the tiltable duct propeller |
|
图 3 可倾斜轴导管桨模型 Fig. 3 Geometrical model of thetiltableduct propeller |
|
|
表 2 可倾斜轴导管桨主要几何参数表 Tab.2 Main geometrical parameters of the tiltable duct propeller |
本文研究采用的CFD软件以RANS方程和时均连续性方程为基本方程,时均连续性方程具体形式如下:
| $ \frac{\partial {u}_{i}}{\partial {x}_{i}}=0 \text{,}$ | (1) |
RANS方程具体形式如下:
| $ \frac{{\partial u}_{i}}{\partial t}+\frac{\partial }{\partial {x}_{j}}\left({u}_{i}{u}_{j}\right)=-\frac{1}{\rho }\frac{\partial p}{\partial {x}_{i}}+{S}_{i}+\frac{1}{\rho }\frac{\partial }{\partial {x}_{j}}\left(\mu \frac{\partial {u}_{i}}{\partial {x}_{j}}-\rho \overline{{u}_{i}{\text{′}}{u}_{j}{\text{′}}}\right) \text{。}$ | (2) |
式中:ρ为流体密度;μ为流体粘度;p为静水压力;Si为质量力;ui,uj为速度分量。
1.3 扇翼推进器计算域设置及网格划分计算域大小设置为11 m×10 m,湍流模型选择Realizable k-ε模型,鉴于扇翼推进器偏心涡形成过程,流场是非定常的,因此本次计算采用非定常求解器求解,采用滑移网格技术来模拟。每个时间步扇叶旋转2°,迭代18次,网格数为180万左右,Y+在30~200之间。计算域边界条件设置如下:1)来流边界、上边界和底部边界的边界条件均设置成速度入口;2)出口边界的边界条件设置成压力出口;3)叶片和机翼的边界条件设置成无滑移、不可穿透壁面;4)运动区域和静止区域的边界条件设置成交界面。
1.4 可倾斜轴导管桨计算域设置及网格划分可倾斜轴导管桨的计算域大小设置为14 m×14 m×14 m,湍流模型选择Realizable k-ε模型,采用非定常求解器求解,每个时间步步进1°,每个时间步迭代10次,网格数为400万左右,Y+在30~180之间。和扇翼推进器流场计算一样,采用滑移网格求解,边界条件与扇翼推进器设置一致。
2 扇翼推进器敞水性能分析 2.1 定深直航工况下扇翼推进器的敞水效率定义定深直航工况下扇翼推进器负升力系数CL、推力系数CT和敞水效率η的计算公式为:
| $ {C}_{L}=\frac{L}{0.5\rho {V}^{2}S} \text{,}$ | (3) |
| $ {C}_{T}=\frac{T}{0.5\rho {V}^{2}S} \text{,}$ | (4) |
| $ \mathrm{\eta }=\frac{TV}{2\text{π} NQ} \text{。}$ | (5) |
式中:L为产生的负升力;T为产生的推力;V为来流速度;N为扇叶转速;Q为扇叶转矩;ρ为水的密度,取值998 kg/m3;S为参考面积,
式中:K为扇翼推进器展长。
由上式可知,在忽略三维效应的前提下,三维扇翼推进器的敞水效率和二维扇翼推进器是一样的。同时在升推比一定时,可以通过调整展长K来等比例的放大或缩小三维扇翼推进器负升力和推力的大小以匹配潜器的储备浮力和水下阻力。
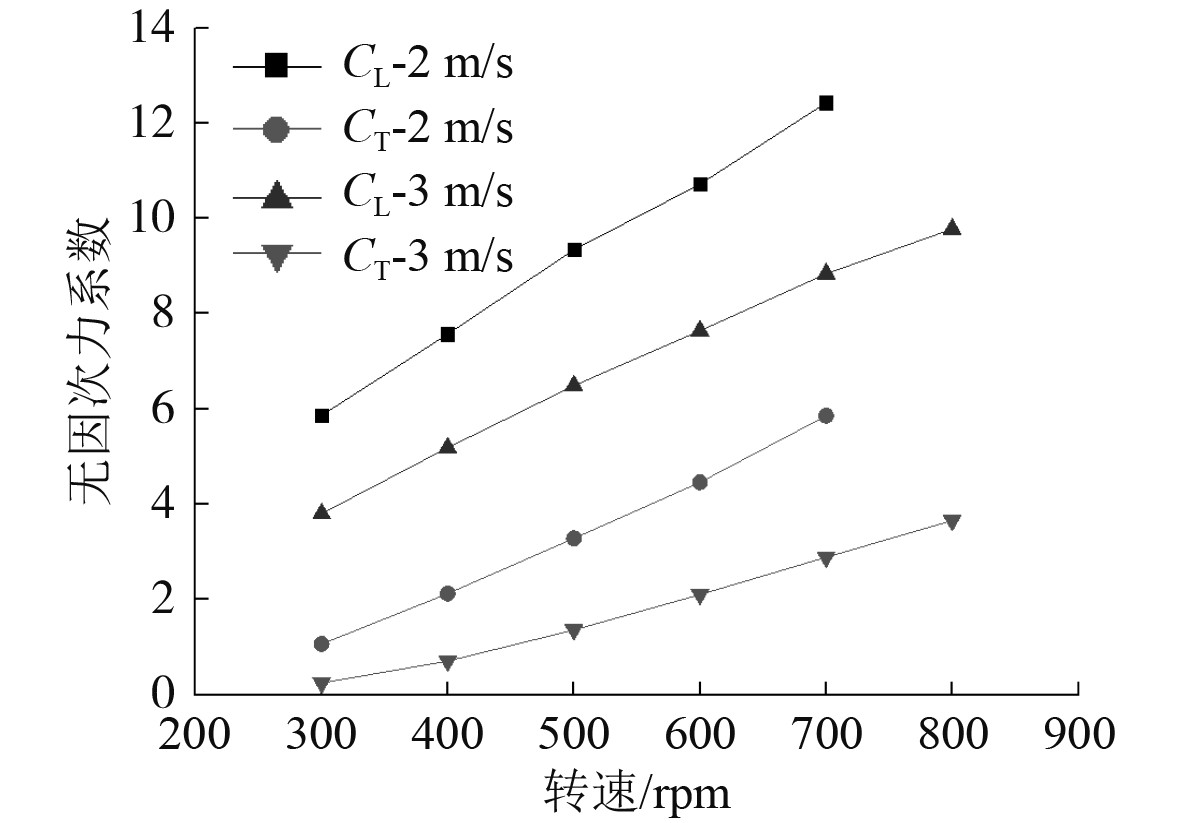
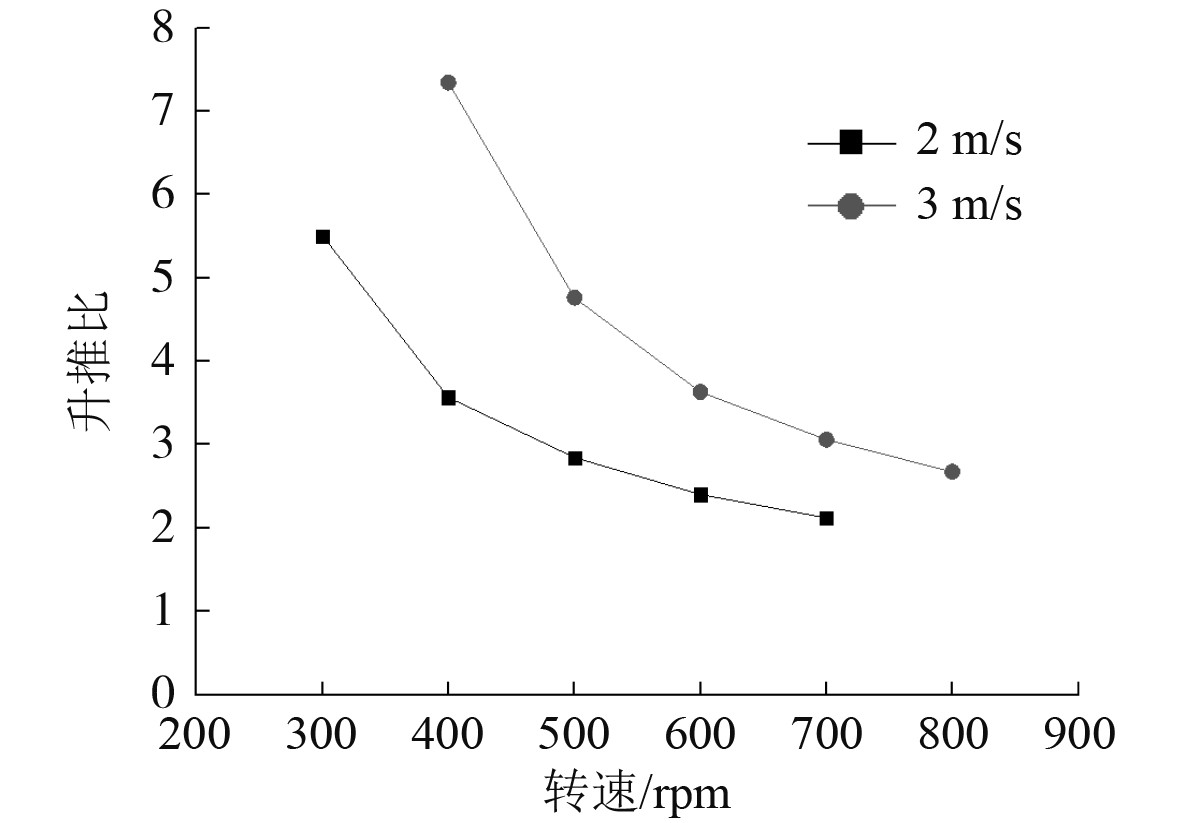
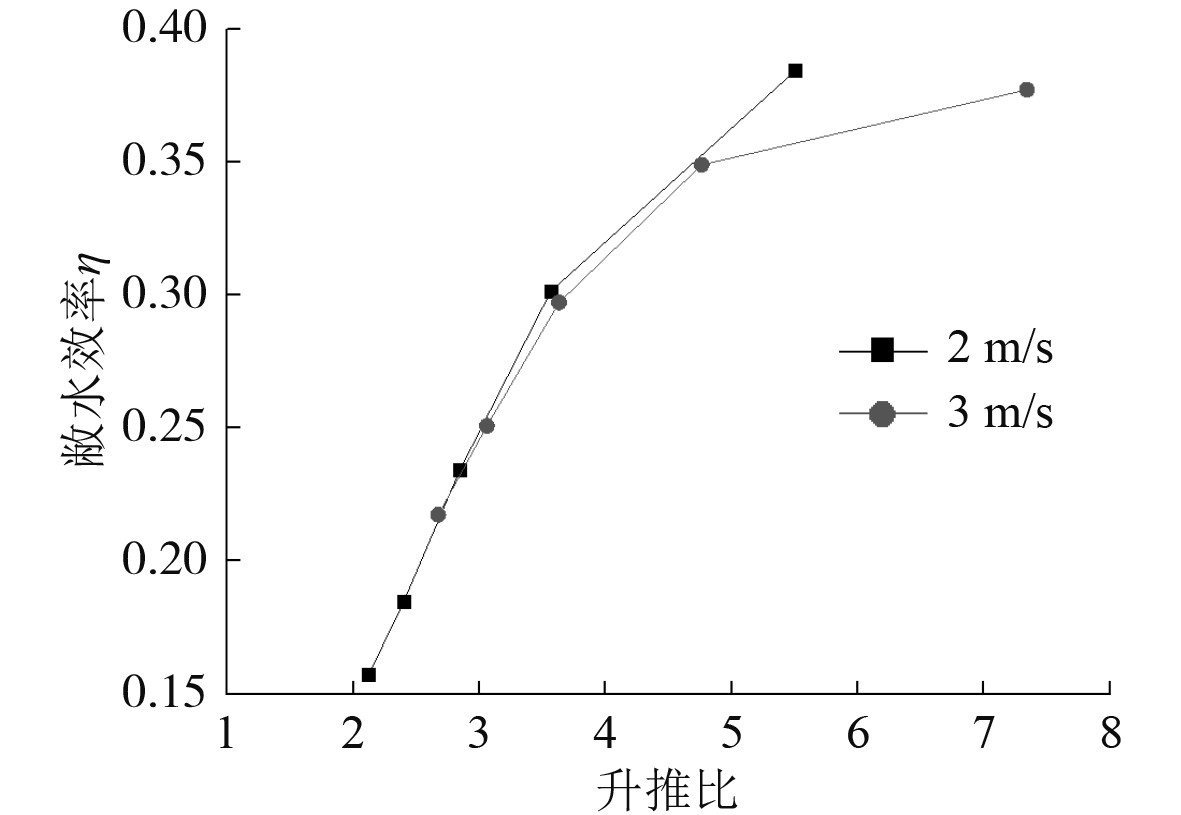
扇翼推进器的计算参数为来流速度2 m/s和3 m/s,来流迎角0°,机翼后缘夹角35°,通过改变扇叶的转速来改变扇翼推进器的升推比,以得到不同升推比下的敞水效率,扇叶的转速分别为300 r/min,400 r/min,500 r/min,600 r/min,700 r/min和800 r/min,则扇翼推进器的负升力系数、推力系数、升推比随转速的变化曲线如图4和图5所示,扇翼推进器的敞水效率随升推比的变化曲线如图6所示。可以看出,在来流速度一定时,扇翼推进器的负升力系数和推力系数随转速的增大而增大;扇翼推进器的转速越高,升推比越低;扇翼推进器的升推比越大,其敞水效率就越高,即扇翼推进器转速越低,其敞水效率越高。同时升推比一定时,不同来流速度下,扇翼推进器敞水效率基本相同。
|
图 4 扇翼推进器力系数随转速变化曲线 Fig. 4 The curve that force coefficient of the fanwing propeller varies to rotate speed |
|
图 5 扇翼推进器升推比随转速变化曲线 Fig. 5 The curve that lift-thrust ratio of the fanwing propeller varies to rotate speed |
|
图 6 扇翼推进器敞水效率随升推比变化曲线 Fig. 6 The curve that open water efficiency of fanwing propeller varies to lift-thrust ratio |
定义定深直航工况下可倾斜轴导管桨负升力系数CL、推力系数CT和敞水效率η的计算公式为:
| $ {C}_{L}=\frac{L}{\rho {n}^{2}{D}^{4}} \text{,}$ | (7) |
| $ {C}_{T}=\frac{T}{\rho {n}^{2}{D}^{4}}\text{,} $ | (8) |
| $ \mathrm{\eta }=\frac{TV}{2\text{π} nQ} \text{。}$ | (9) |
式中:L为产生的负升力;T为产生的推力;n为导管桨转速;D为螺旋桨直径;V为来流速度;Q为螺旋桨转矩;ρ为水的密度,取值998 kg/m3。
可倾斜轴导管桨是通过桨轴轴线和来流方向之间形成夹角来同时提供沿来流方向推力和垂直于来流方向的负升力,实现和扇翼推进器一样的作用。定义来流坐标系
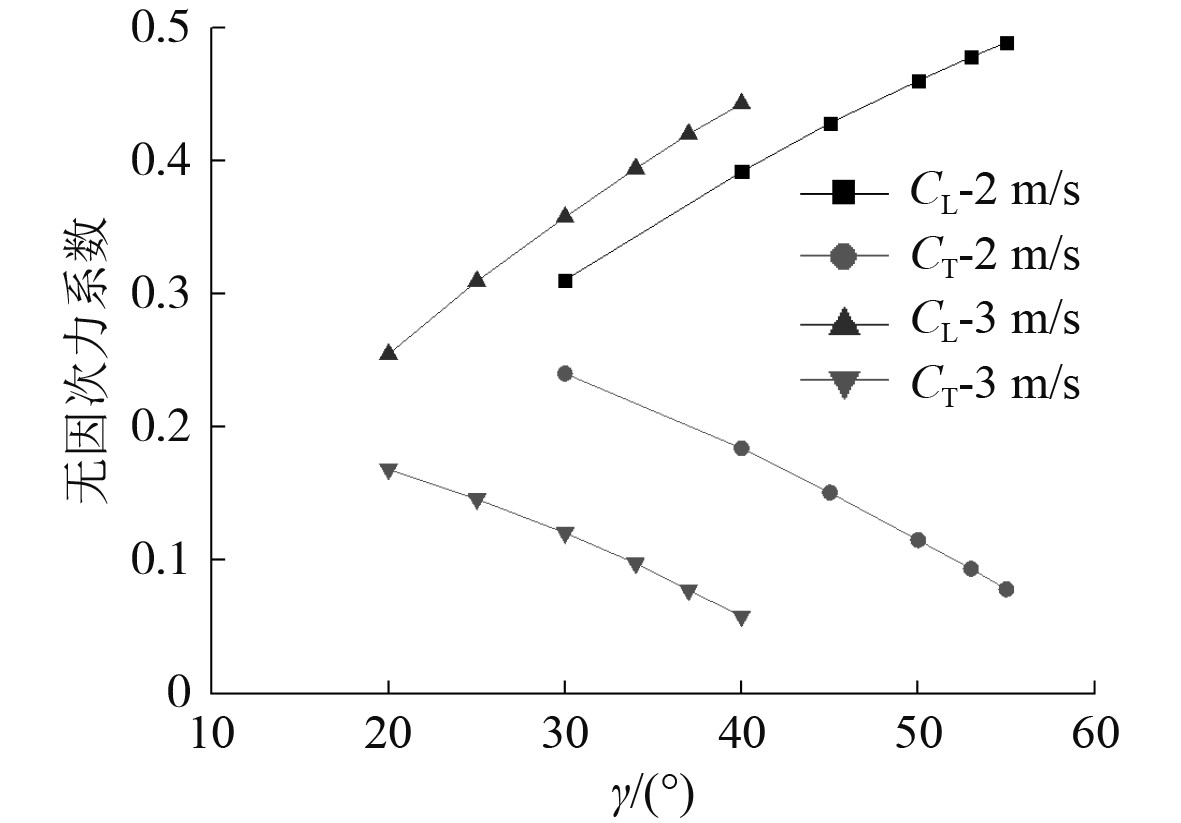
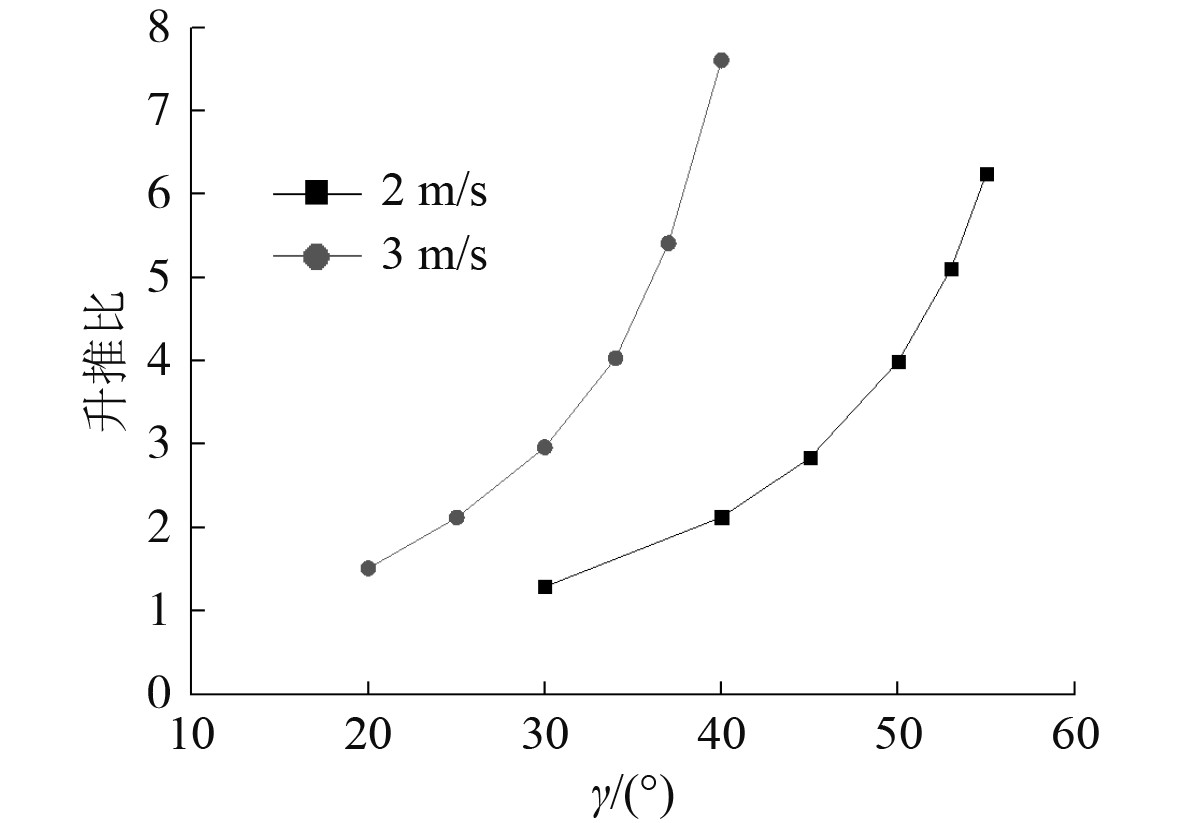
可倾斜轴导管桨的计算参数为来流速度2 m/s和3 m/s,转速为500 r/min,通过改变可倾斜轴导管桨桨轴倾斜角γ来改变导管桨的升推比,以得到不同升推比下的敞水效率,桨轴倾斜角γ分别为20°、25°,30°,34°,37°,40°,45°,50°,53°和55°,则可倾斜轴导管桨的负升力系数、推力系数和升推比随γ的变化曲线如图7和图8所示,可倾斜轴导管桨的敞水效率随升推比的变化曲线如图9所示。由图可知,来流速度一定时,可倾斜轴导管桨的负升力系数随轴倾斜角的增大而增大,但推力系数却随轴倾斜角的增大而减小;同时可倾斜轴导管桨的敞水效率是随升推比的增大而减小,这和扇翼推进器的规律刚好相反;升推比一定时,来流速度越大,可倾斜轴导管桨敞水效率越高。
|
图 7 可倾斜轴导管桨力系数随γ的变化曲线 Fig. 7 The curve that force coefficient of the tiltable duct propeller varies to rotate speed |
|
图 8 可倾斜轴导管桨升推比随γ的变化曲线 Fig. 8 The curve that lift-thrust ratio of the tiltable duct propeller varies to rotate speed |

|
图 9 可倾斜轴导管桨敞水效率随升推比的变化曲线 Fig. 9 The curve that open water efficiency of the tiltable duct propeller varies to lift-thrust ratio |
扇翼推进器和可倾斜轴导管桨的敞水效率对比是指在定深直航工况下,2种推进器在相同的来流速度下,产生同等的负升力和推力时,对比其敞水效率。由于扇翼推进器的负升力和推力可以通过改变其展长来调节,因此只要扇翼推进器的升推比和可倾斜轴导管桨的升推比相等,那么总存在一个确定的展长,使三维扇翼推进器和可倾斜轴导管桨的负升力和推力分别相等。
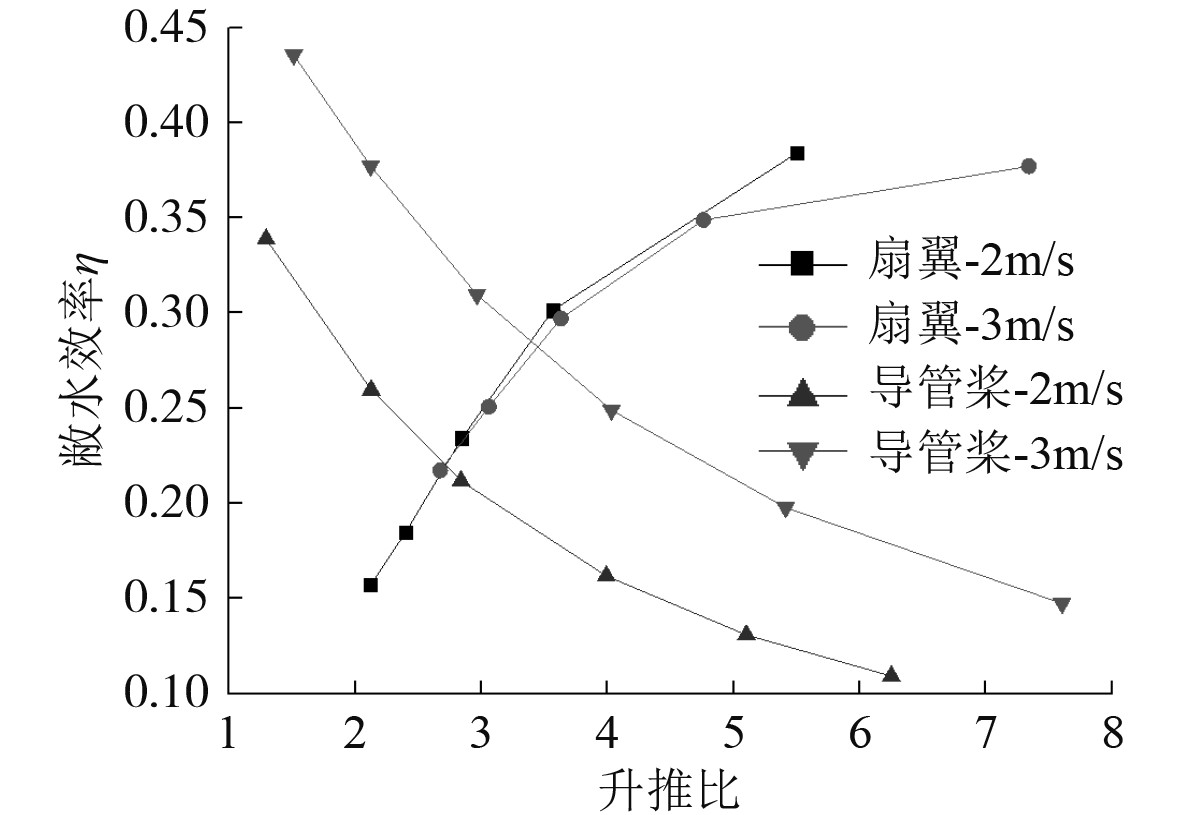
本文对比来流速度为2 m/s和3 m/s时2种推进器的敞水效率,结果见图10。可以看出,由于扇翼推进器与可倾斜轴导管桨的敞水效率随升推比的变化规律相反,因此总存在一个确定的升推比值,使低于该升推比值时,扇翼推进器的敞水效率低于可倾斜轴导管桨;高于该升推比值时,扇翼推进器的敞水效率高于可倾斜轴导管桨,同时随着来流速度的增大,该升推比值也越来越大。这说明扇翼推进器适合应用在升推比较大的水下潜器上,而不适合升推比小的水下潜器。
|
图 10 两种推进器敞水效率对比曲线 Fig. 10 Comparison curve of open water efficiency of the two propellers |
通过对已有的常规潜艇英国2400型以及德国209型1100级的储备浮力与阻力的比值进行粗估,发现2艘潜艇的储备浮力与阻力的比值均大于6。由图10可以看出,在升推比大于6时,扇翼推进器的敞水效率远大于可倾斜轴导管桨,这说明扇翼推进水下潜器概念方案具有一定的可行性。
3 结 语本文通过对比相同来流速度下扇翼推进器和可倾斜轴导管桨在定深直航状态下的敞水效率,说明应用在高升推比的水下潜器上,扇翼推进器的敞水效率高于可倾斜轴导管桨,一定程度上论证了扇翼推进水下潜器概念方案的可行性。后续研究将会从2个角度深化论证扇翼推进水下潜器概念方案的可行性:一是在一个完整的作业周期内,扇翼推进水下潜器与常规潜器相比,能耗是否更小;二是扇翼推进水下潜器的总体设计难度以及航行操纵稳定性是否优良。
| [1] |
KOEGLER K . FanWing: experimental evaluation of a novel lift and propulsion device[R]. Report to FanWing Ltd, 2002.
|
| [2] |
ASKARI S, SHOIAEEFARD M H. Numerical simulation of flow over an airfoil with a cross flow fan as a lift generating member in a new aircraft model[J]. Aircraft Engineering and Aerospace Technology, 2009.
|
| [3] |
吴浩东. 风扇翼内部偏心涡特性研究[D]. 南京: 南京航空航天大学, 2012.
|
| [4] |
刘乐, 邢福, 渠继东. 基于CFD扇翼推进器水动力特性数值分析[J]. 舰船科学技术, 2021, 43(1): 48-52+66. |
| [5] |
常欣, 梁宁, 王超, 等. 斜流中螺旋桨非定常水动力性能的数值分析[J]. 哈尔滨工程大学学报, 2017, 38(7): 1048-1055. |
| [6] |
张志荣, 洪方文. 斜流中螺旋桨性能数值分析方法研究[A]. 中国造船工程学会船舶力学学术委员会. 2007年船舶力学学术会议暨《船舶力学》创刊十周年纪念学术会议论文集[C]// 中国造船工程学会船舶力学学术委员会: 中国船舶科学研究中心《船舶力学》编辑部, 2007: 6.
|
 2021, Vol. 43
2021, Vol. 43
