2. 中国船舶工业系统工程研究院,北京 100094
2. Systems Engineering Research Institute, Beijing 100094, China
国内外仿生降噪研究通常选取鲨鱼和海豚为研究对象。1989年,美国海军海洋系统中心[1]通过试验研究了表面带有条纹薄膜的回转体阻力和噪声特性,试验发现带有条纹薄膜的回转体在阻力和噪声性能方面都有很大的提升。Park[2]通过研究沟槽内速度及切应力的分布,发现沟槽表面可以降低噪声1%左右。同时也有学者以鸮为仿生研究对象,这是由于大多数种类的鸮都可以做到无声飞行。Graham[3]于1934年提出,鸮类之所以可以无声飞行,是因为翅膀边缘的锯齿结构,它可以改变流体的流动状态,控制流体涡的脱落,从而起到降低噪声的作用。NASA艾姆斯研究中心的 Soderman[4]在受到鸮翼前缘锯齿结构的启发后对2种不同尺寸大小的旋翼前缘添加锯齿形结构并进行了降噪试验,发现增加了锯齿形结构最高可以降噪8 dB。国内对仿生减阻降噪的研究最早于1994年在西北工业大学开展,石秀华等[5]通过试验研究了不同形状和尺寸沟槽条纹的降噪效果,经过对比发现降噪量在5 dB左右。包云平等[6]首先从湍流产生的机理入手,通过反向旋转流向涡对的反馈机理讨论了仿生沟槽条纹薄膜减阻降噪的机理。此外吉林大学的学者们也做了很多关于仿生降噪方面的工作。张春华[7]对风扇叶片进行了改形设计,通过在风扇的表面添加沟槽得到了2 dB的降噪效果。陈坤等[8]进一步对风机叶片做了改形设计,对风机叶片的两边均设计了仿生结构,通过2种仿生结构的耦合,降噪量最大可以达到6 dB。石磊[9]在圆柱杆件两侧添加锯齿形结构,并通过风洞试验对锯齿形圆柱进行气动噪声试验,试验发现锯齿结构可以延缓涡的脱落,降低圆柱杆件的压力脉动。锯齿形圆柱杆件在气动噪声方面有很好降低的同时,阻力并没有增加。孙少明设计了仿生轴流风机叶片[10]和仿生蜗舌[11],同样取得了很好的降噪效果,最高的降噪量为5.8 dB。刘海涛[12]基于仿生思想对圆柱杆件进行了改形设计,设计了6种仿生圆柱结构,并对其进行了气动噪声数值研究。结果显示采用环状波纹凹槽杆件结构,其噪声值降低了18.14 dB。通过以上研究可以发现,锯齿形结构可以改变流体的流动状态,延缓涡的脱落从而很好地降低噪声。
本文受仿生思想的启发,对圆柱壳表面进行仿生改进,采用大涡模拟(LES)结合Lighthill声类比方法对仿生圆柱壳的流噪声进行求解,并讨论了仿生圆柱壳流动噪声的特性和机理,可以为减小圆柱周围流阻和降低噪声提供一定的参考。
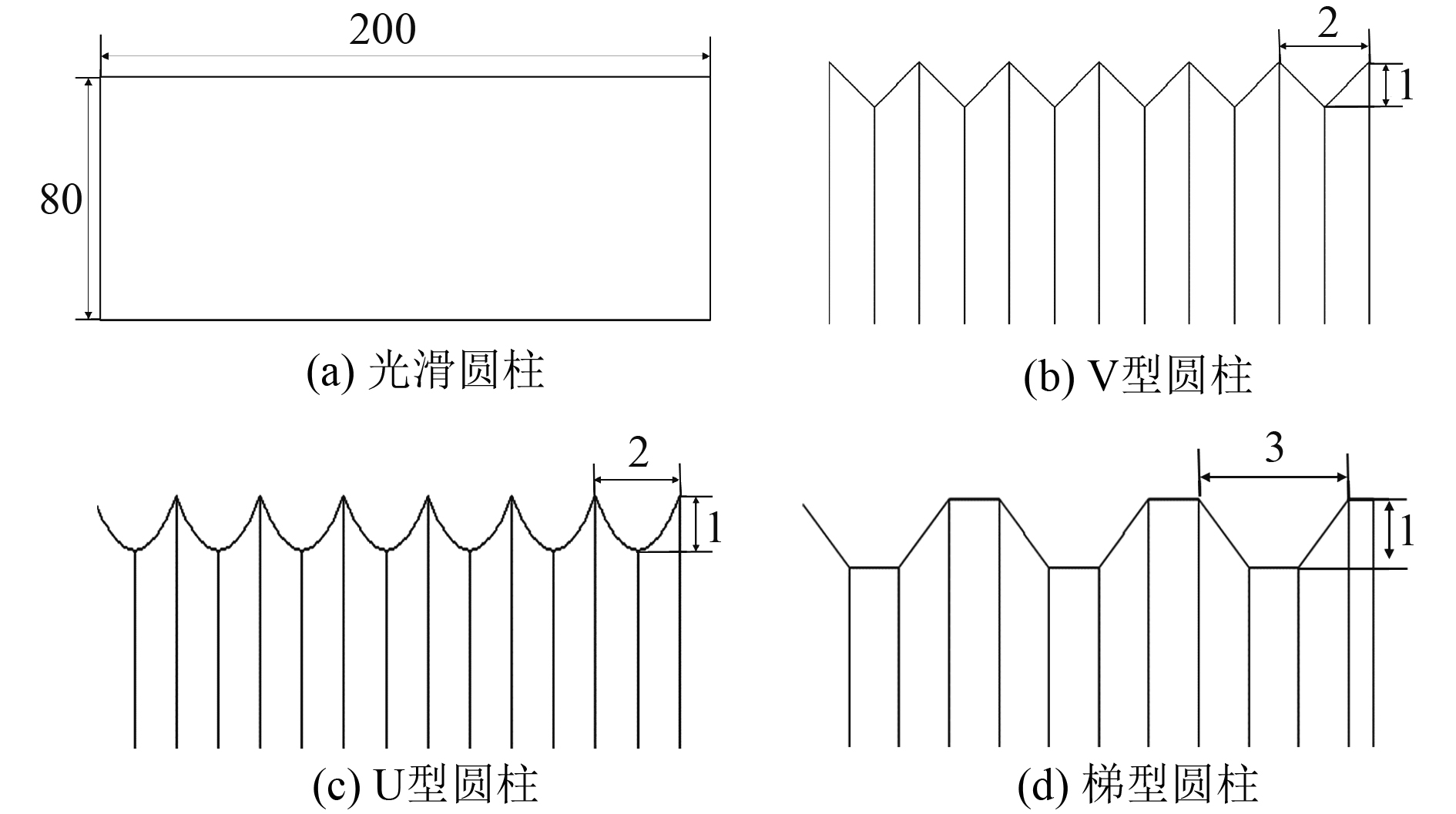
1 仿生圆柱壳绕流计算模型本文设计1种光滑圆柱模型和3种仿生圆柱模型,几何模型如图1所示,圆柱模型长径比均为2.5∶1。
|
图 1 光滑圆柱及仿生圆柱几何模型 Fig. 1 Geometric model of smooth cylinder and bionic cylinder |
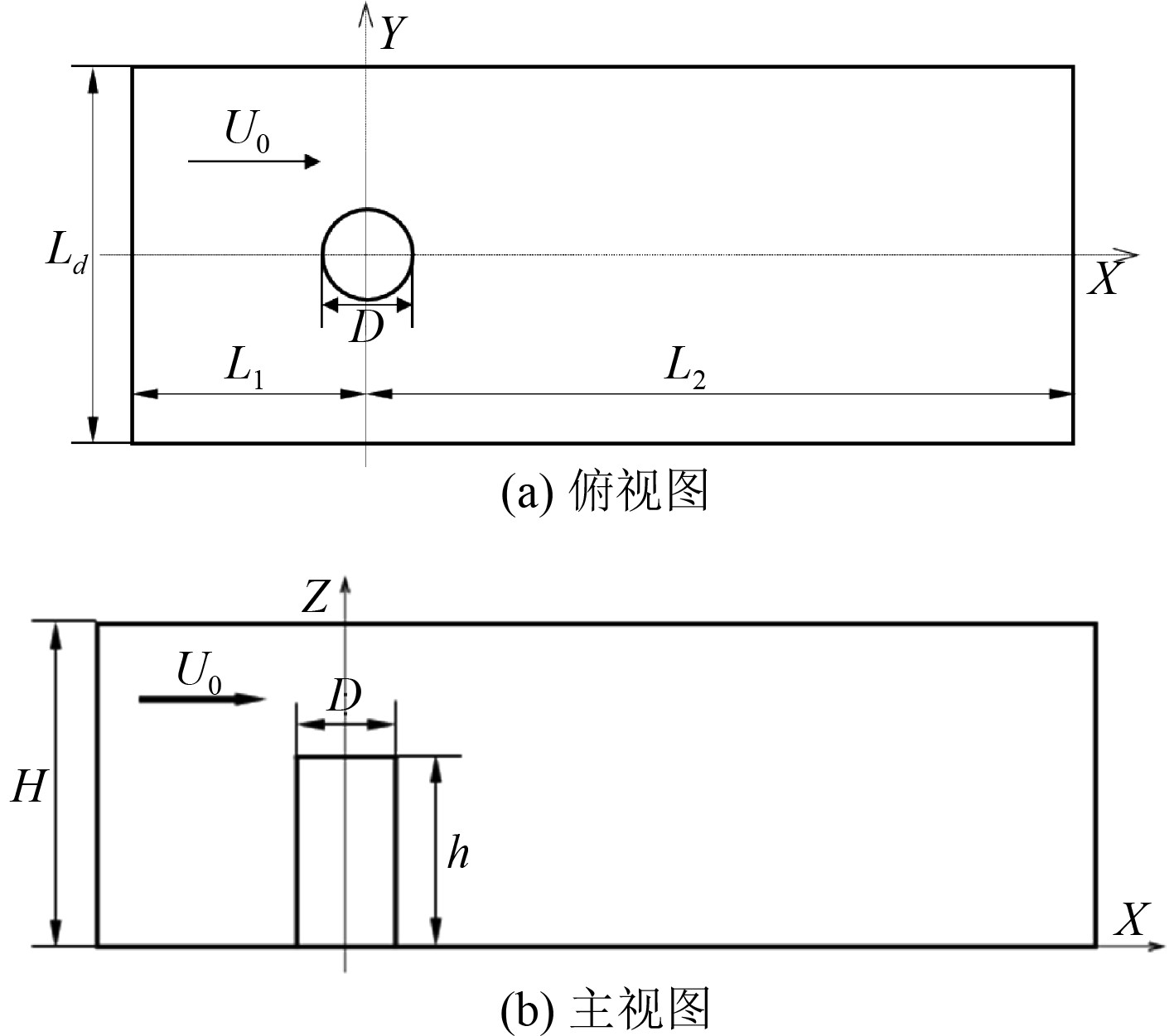
如图2所示,为了保证计算精度同时节约计算资源,需要确定合适的计算区域,结合前期流场试算结果,确定计算区域如下:来流域长度L1 =4D,去流域长度L2 =15D,流域宽度Ld =7D,流域高度H=1.5h。
|
图 2 计算流域几何模型 Fig. 2 Computational drainage basin geometry model |
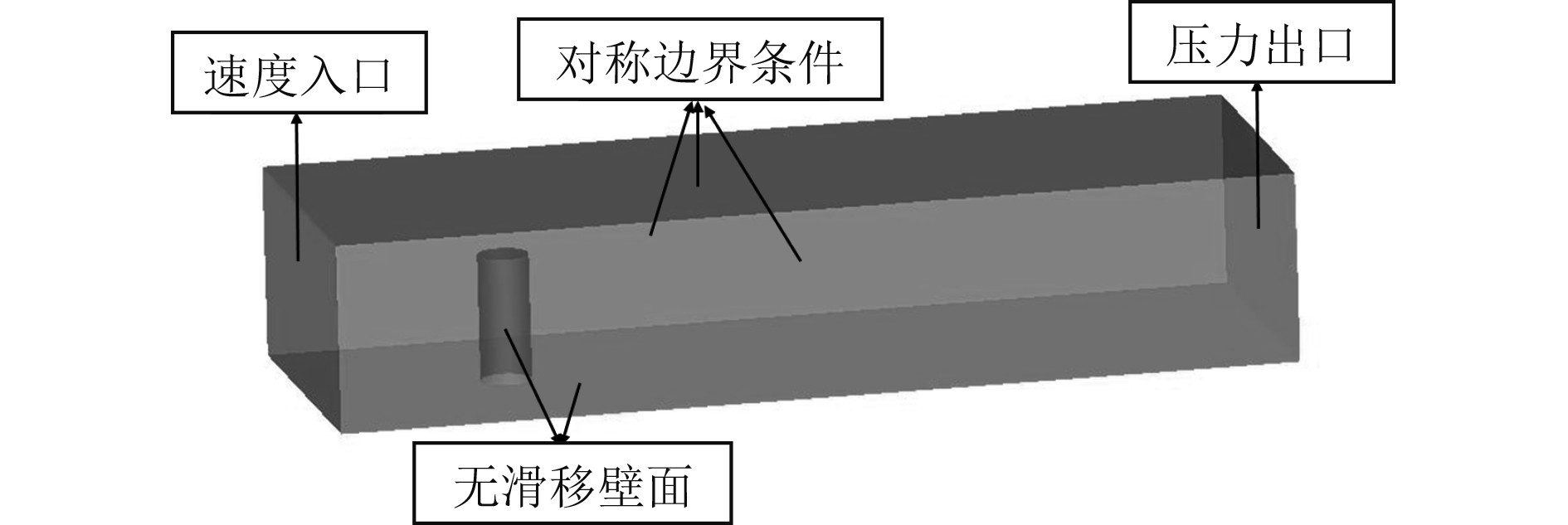
边界条件设置如图3所示,圆柱表面为无滑移壁面边界条件,计算流域的进口设置为速度入口,入口速度为69.19 m/s,流场出口设置为压力出口,相对压力为0 pa,圆柱展向的2个面设置为对称边界条件,外流域的2个侧面设为自由滑移壁面。首先采用k-ω湍流模型对流场进行定常计算,目的是使流场快速收敛,为非定常计算提供一个比较稳定的流场;其次基于定常解采用LES湍流模型对流场进行瞬态计算。时间步长取为2×10−5s,因为是气动噪声,因此把空气作为流体介质,参考压力为一个标准大气压,即101.325 kPa,空气密度设为1.29 kg/m3。
|
图 3 计算流域边界条件 Fig. 3 Calculation of watershed boundary conditions |
由于4种圆柱模型网格划分方式相同,仅以光滑圆柱为例,对网格的划分方式进行详细介绍。如图4所示,计算流域采用结构化网格,对圆柱模型边界层采用O型网格以确保边界层的划分。从局部视图上可以看到网格节点沿圆柱的周向平均分布,在圆柱的边界层上网格尺寸逐渐增加,网格节点沿圆柱展向均匀分布,从圆柱上端到计算流域上表面,网格尺寸逐渐增大。网格的最大尺寸为0.3D,网格节点数为1027万,网格质量在0.8以上。

|
图 4 光滑圆柱计算流域网格示意图 Fig. 4 Schematic diagram of smooth cylindrical calculation watershed grid |
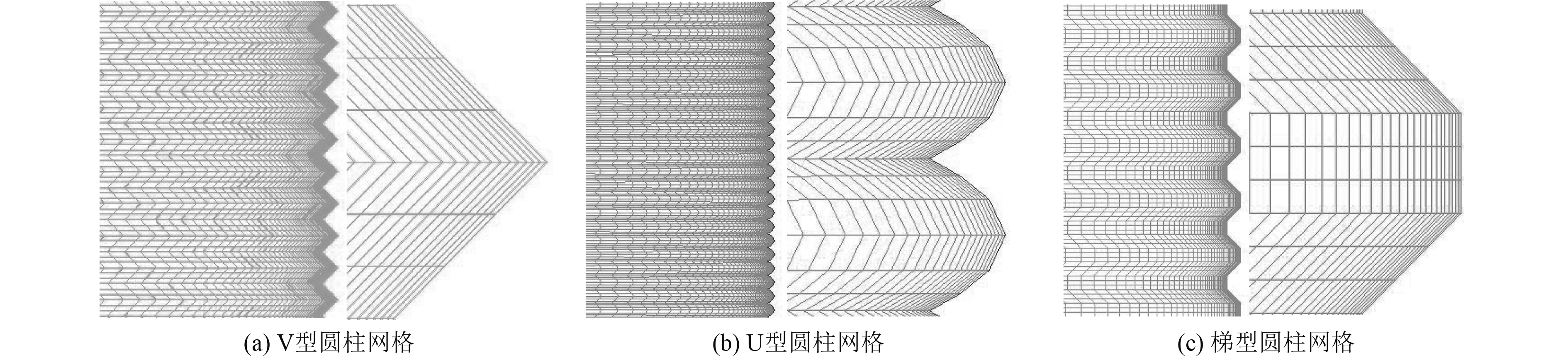
|
图 5 仿生圆柱计算流域网格示意图 Fig. 5 Schematic diagram of watershed grid for calculation of bionic cylinder |
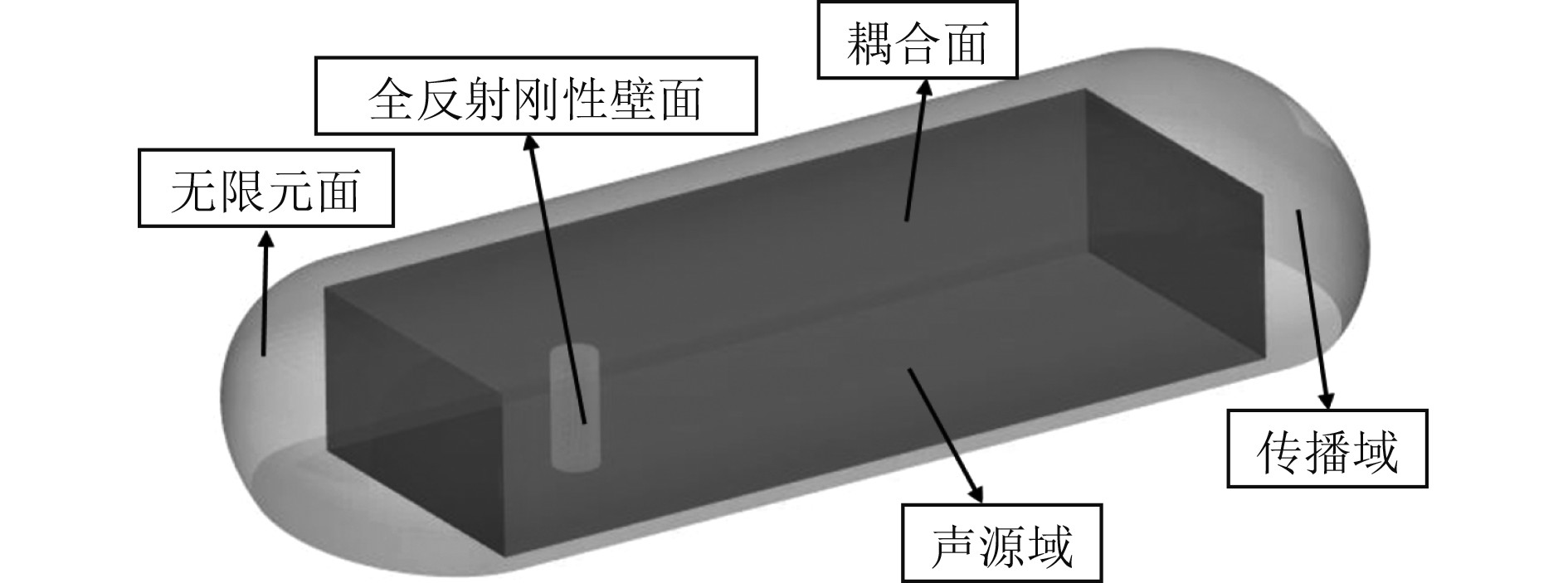
图6给出了本文计算圆柱噪声的声学模型。半椭球上表面设置为无限元边界条件,计算阶数采用20,用于模拟无限远处无反射边界,时间步长Δt = 1×10−3 s,流体计算需要导出1000步的速度时域信息。设圆柱表面为全反射刚性壁面,传播域和声源域重合的面为耦合面。
|
图 6 声学计算模型 Fig. 6 Acoustic calculation model |
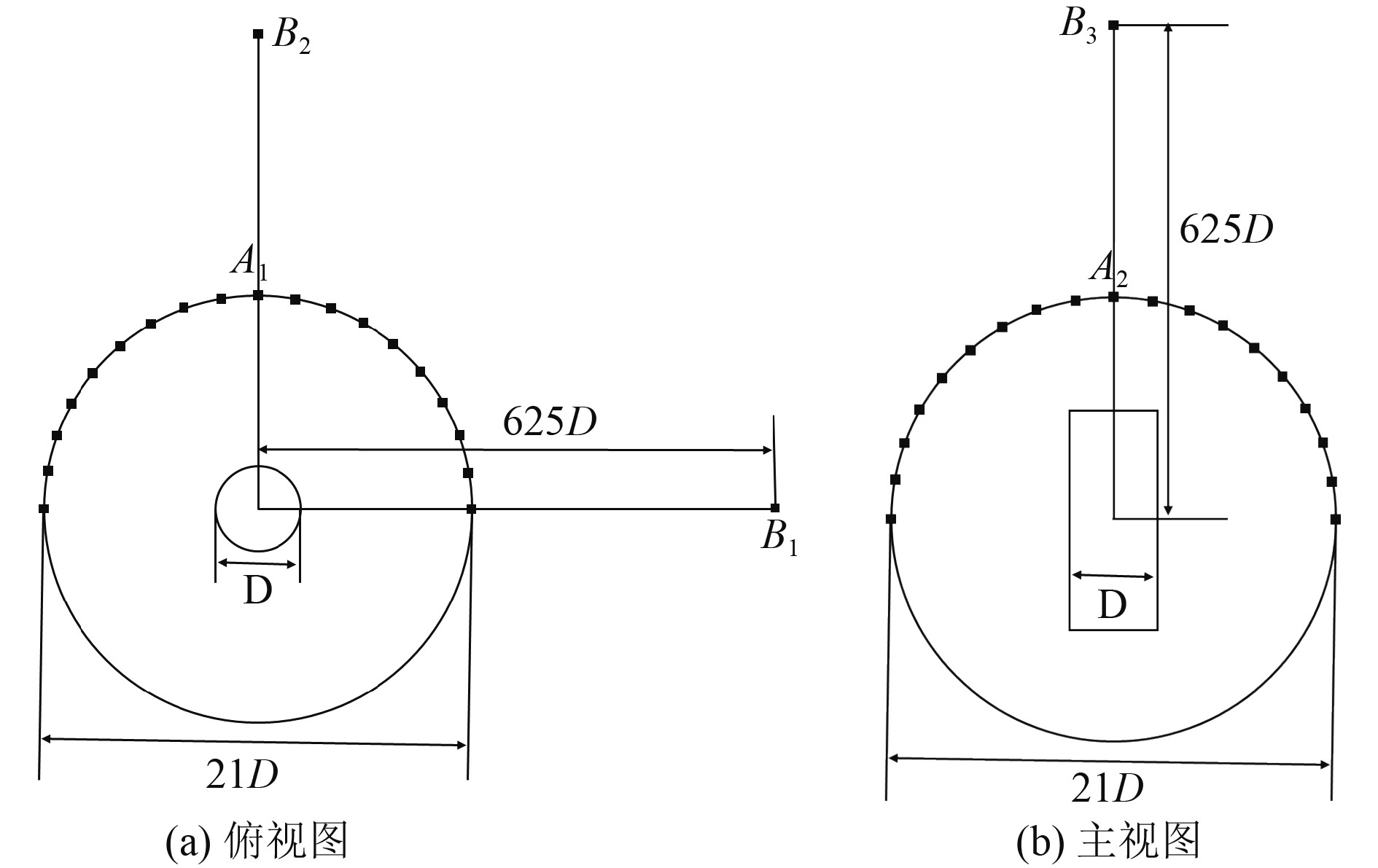
为了更好地了解仿生圆柱模型的声场特性,需要在声学计算域内布置若干监测点。监测点布置分为2组,第1组为沿圆柱布置若干监测点,布置方式为在XY平面内距圆柱中心10.5D距离,0~180°均匀布置19个点,设为A1组,在YZ平面内距圆柱中心10.5D距离,0~180°均匀布置19个点,即每隔10°布置一个监测点,设为A2组。第3组为3个方向上距圆柱底面中心50 m处设置3个监测点,分别为B1(625D,0,0.1)、B2(0,625D,0.1)、B3(0,0,625D)。此时监测点距原点距离远大于计算区域,因此对于B组监测点,声源可以认为是点声源。监测点的布置如图7所示。
|
图 7 声场计算监测点示意图 Fig. 7 Schematic diagram of sound field calculation monitoring points |
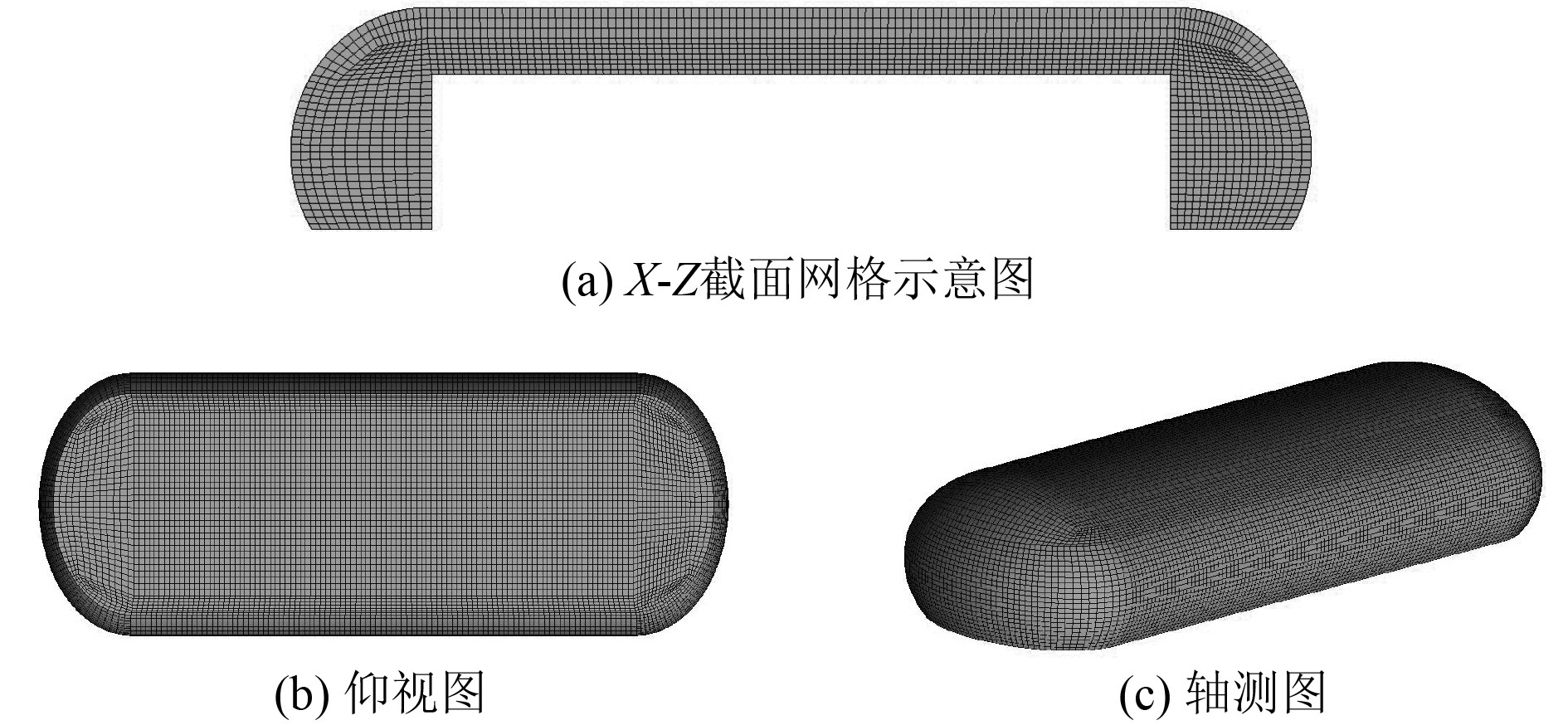
与流场计算所需的网格不同,声学计算网格对网格的质量和数量要求较低,因此声学网格的划分形式与流场网格相同,在尺寸方面较流场网格稍大,网格的尺寸为500 mm。由于流体计算中已给出声源域网格,因此图8只给出了传播域的网格。
|
图 8 传播域网格示意图 Fig. 8 Schematic diagram of propagation domain grid |
基于LES流体计算结果,采用Lighthill声类比方法对3.99 ×104,2.39 ×105以及3.99 ×105三个雷诺数下流体流过有限高圆柱模型时的声学特性进行数值模拟。表1~表3给出了光滑圆柱与仿生圆柱模型在B组监测点处的声压总级,均值为B组3个点的声压总级平均值,降噪量为仿生圆柱与光滑圆柱在监测点出的声压总级之差。可以看出相较于光滑圆柱,V型和U型仿生圆柱均有降噪作用,梯型圆柱在Re=3.99×104时具有增加噪声的作用。V型仿生圆柱在Re=2.39×105时的降噪量最大,为7.32dB,降噪效果最好,其次是U型圆柱,最后为梯型圆柱。
|
|
表 1 B组监测点的声压总级(Re=3.99×104) Tab.1 The total sound pressure level of the monitoring points in group B (Re=3.99×104) |
|
|
表 2 B组监测点的声压总级(Re=2.39×105) Tab.2 The total sound pressure level of the monitoring points in group B (Re=2.39×105) |
|
|
表 3 B组监测点的声压总级(Re=3.99×105) Tab.3 The total sound pressure level of the monitoring points in group B (Re=3.99×105) |
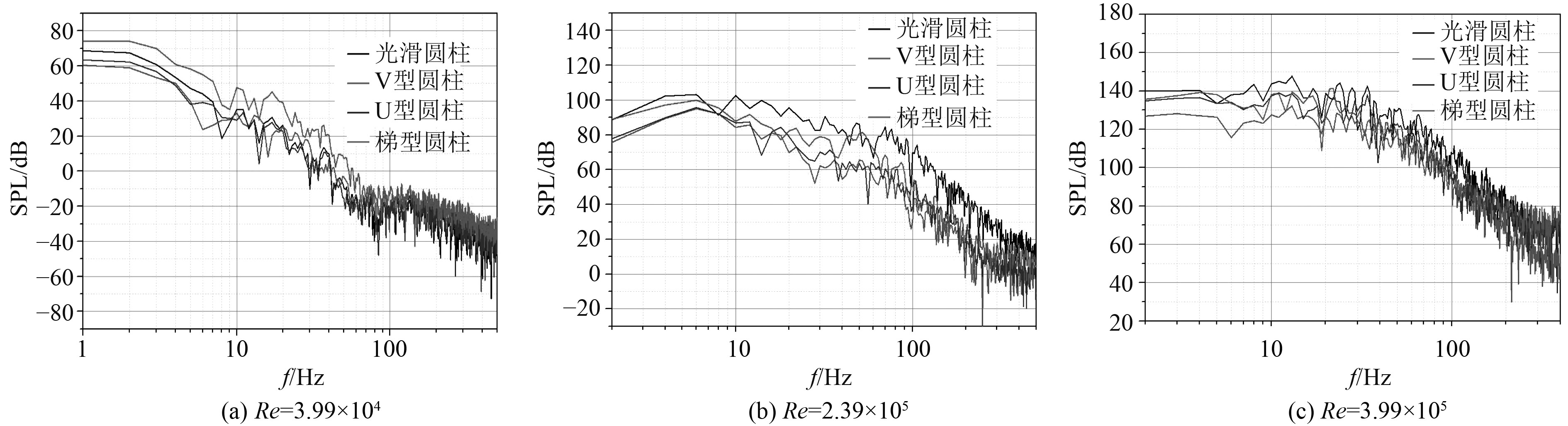
图9分别给出了光滑圆柱与仿生圆柱在Re=3.99×104、Re=2.39×105和Re=3.99×105时监测点B1处的声压级频谱图。随着频率的增加,声压会快速衰减,声压级逐渐降低,圆柱绕流的流噪声主要集中在低频段内,因此降低圆柱绕流低频噪声可以快速降低圆柱绕流产生的流噪声。另外,V型仿生圆柱在Re=2.39×105时的降低噪声最多,降噪量为7.32 dB。为了揭示仿生圆柱的降噪机理,有必要对该情况加以讨论。
|
图 9 光滑圆柱与仿生圆柱在监测点B1处的声压级频谱 Fig. 9 Sound pressure level spectrum of smooth cylinder and bionic cylinder at monitoring point B1 |
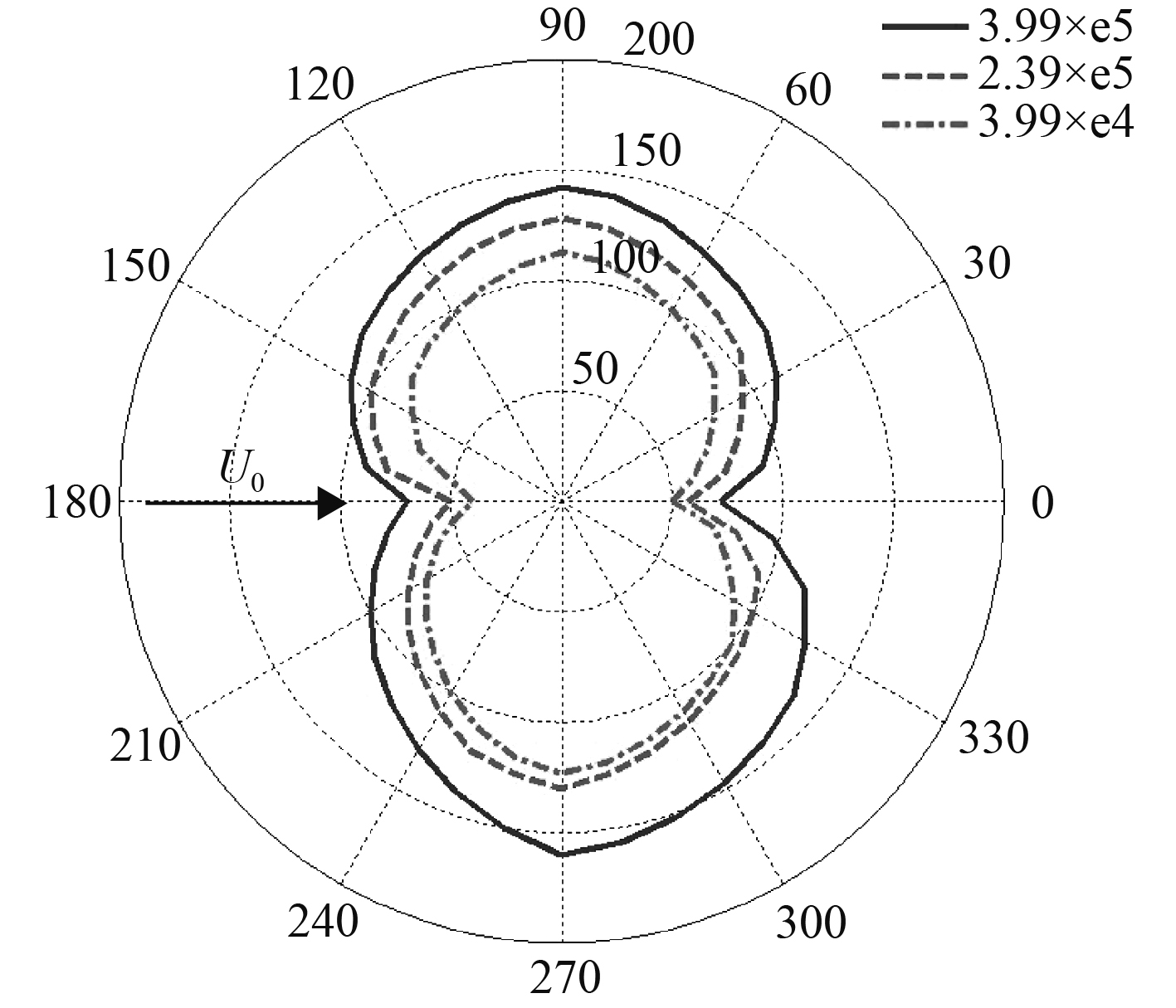
图10给出了V型圆柱在不同雷诺数下的声指向。从图中可以看出V型圆柱的声源特性与偶极子相似,说明圆柱绕流引起的流噪声主要是由于水流过圆柱表面时,在圆柱壁面交替脱落的涡旋引起壁面瞬态压力脉动产生的,因此减小压力脉动的幅值可以有效降低圆柱绕流产生的偶极子噪声。
|
图 10 光滑圆柱在不同雷诺数下的声指向图 Fig. 10 Acoustic patterns of smooth cylinders under different Reynolds numbers |
从图中还可以发现,最大辐射声压级在垂直于流入方向的轴上。因此,垂直于流入方向的轴是偶极轴,与来流方向一致的地方声压很小。说明这部分声压是由四极声源产生的,即涡旋从圆柱体脱落时产生的湍流应力。声压的一部分是由四极声源产生的,也就是说,当涡流从圆柱体上掉落时产生的湍流应力。
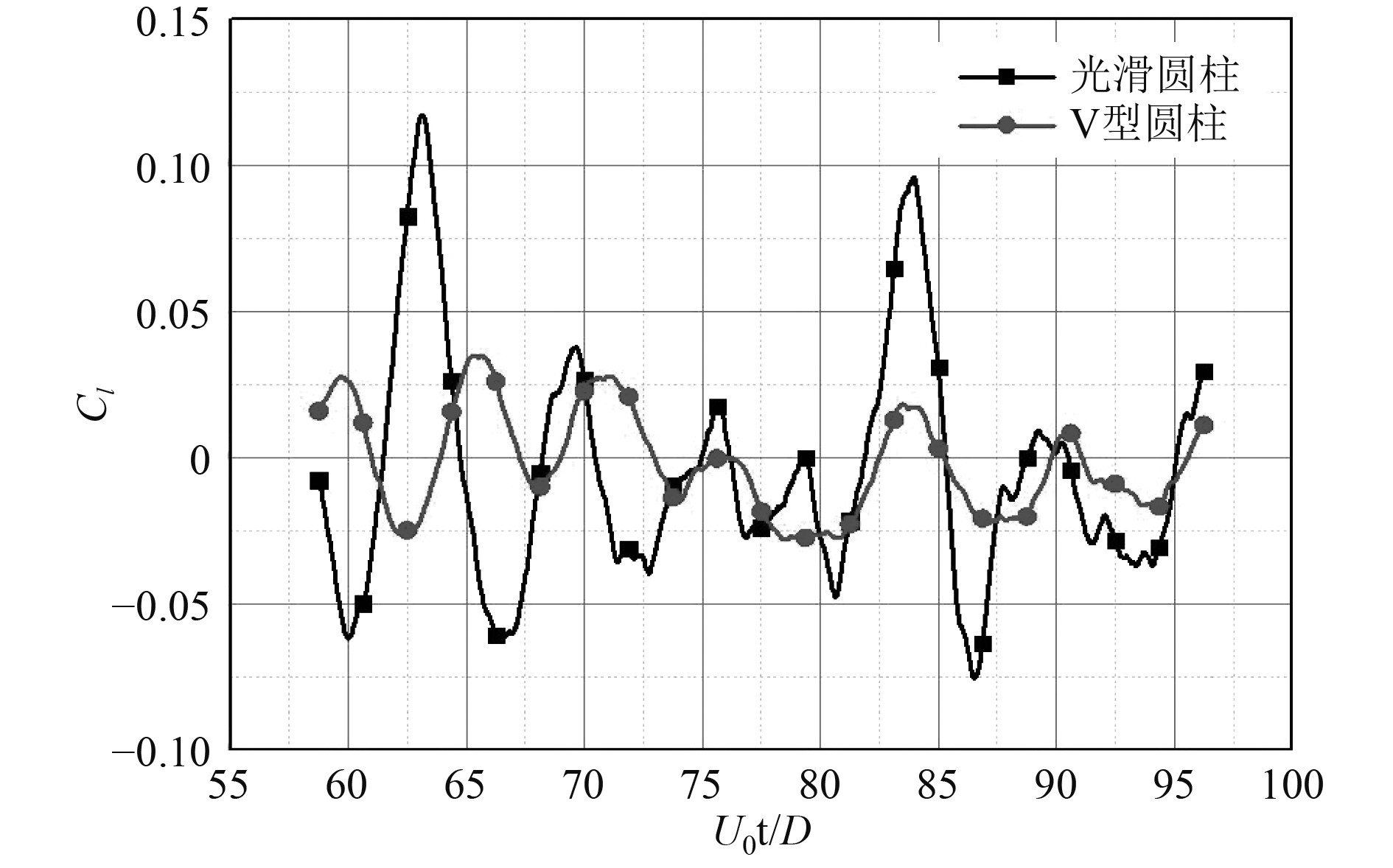
2.2.2 升力系数脉动对比图11给出了光滑圆柱与V型仿生圆柱的升力系数对比。从图中可以看出升力系数均在正负之间呈周期性波动。相比于光滑圆柱升力系数脉动幅值,V型圆柱的明显小一些,因此,圆柱体上的V形槽结构可以减小由圆柱体周围的涡流脱落引起的升力脉动的幅度,从而有效地减少由涡流脱落引起的偶极子噪声。
|
图 11 光滑圆柱与V型仿生圆柱升力系数对比 Fig. 11 Comparison of lift coefficient between smooth cylinder and V-shaped bionic cylinder |
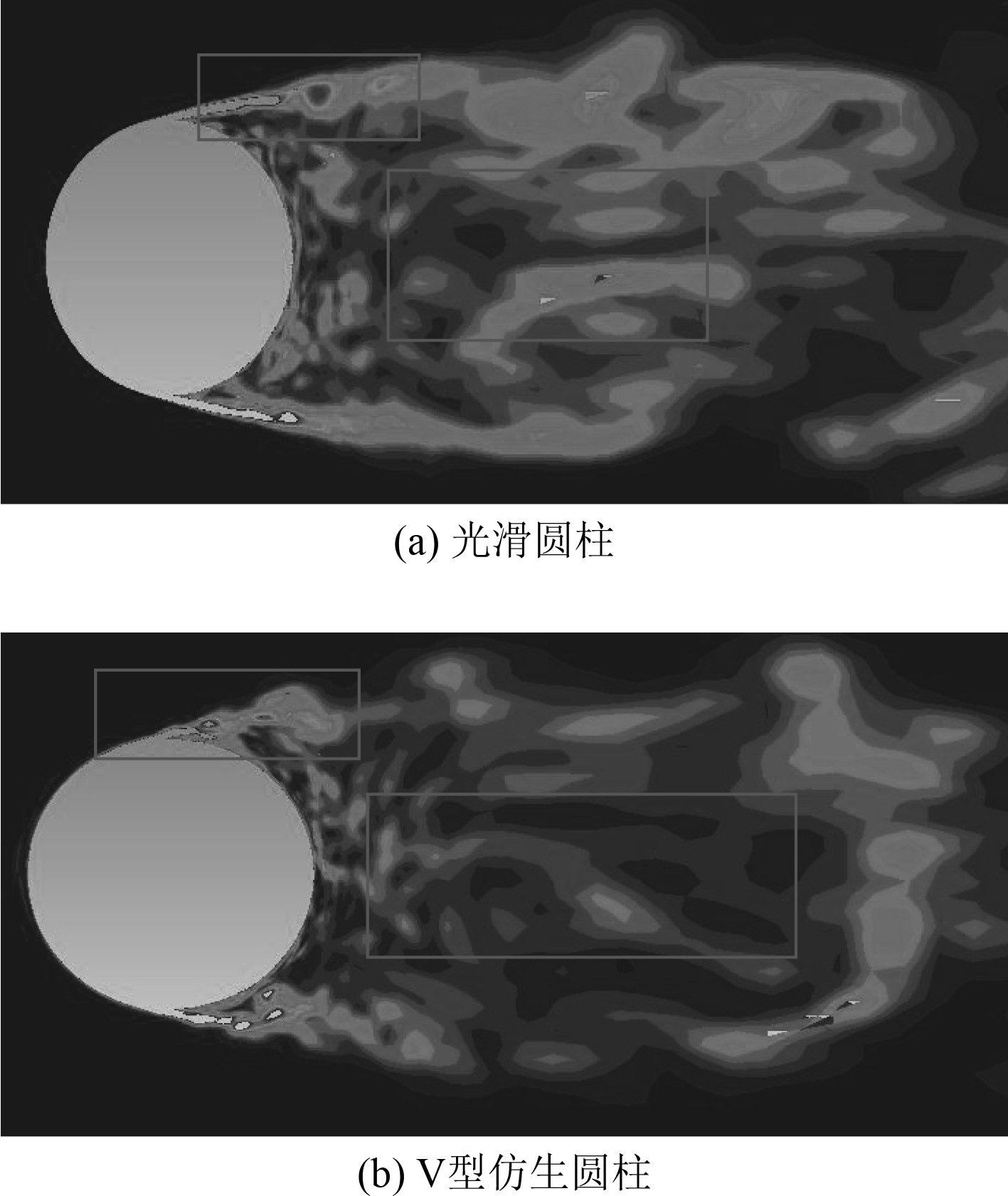
图12为Re=2.39×105光滑圆柱和V型仿生圆柱在U0T/D=75时的尾流涡量图。从图中可以看出当流体流过圆柱时,圆柱绕流边界层分离成2个剪切层,分离剪切层在模型后方交替脱落,形成漩涡。相比于光滑圆柱的尾流,V型仿生圆柱的尾流涡量明显比光滑圆柱的小,说明V型圆柱可以阻碍圆柱两侧的分离剪切层向湍流的转变,使得涡量减小,同时尾流的分离剪切层脱落变缓,使得剪切层的分离变得更加稳定,因此降低了由涡旋脱落引起的流噪声。
|
图 12 光滑圆柱与 V 型仿生圆柱模型尾流涡量图 Fig. 12 Wake vorticity diagram of smooth cylinder and V-shaped bionic cylinder model |
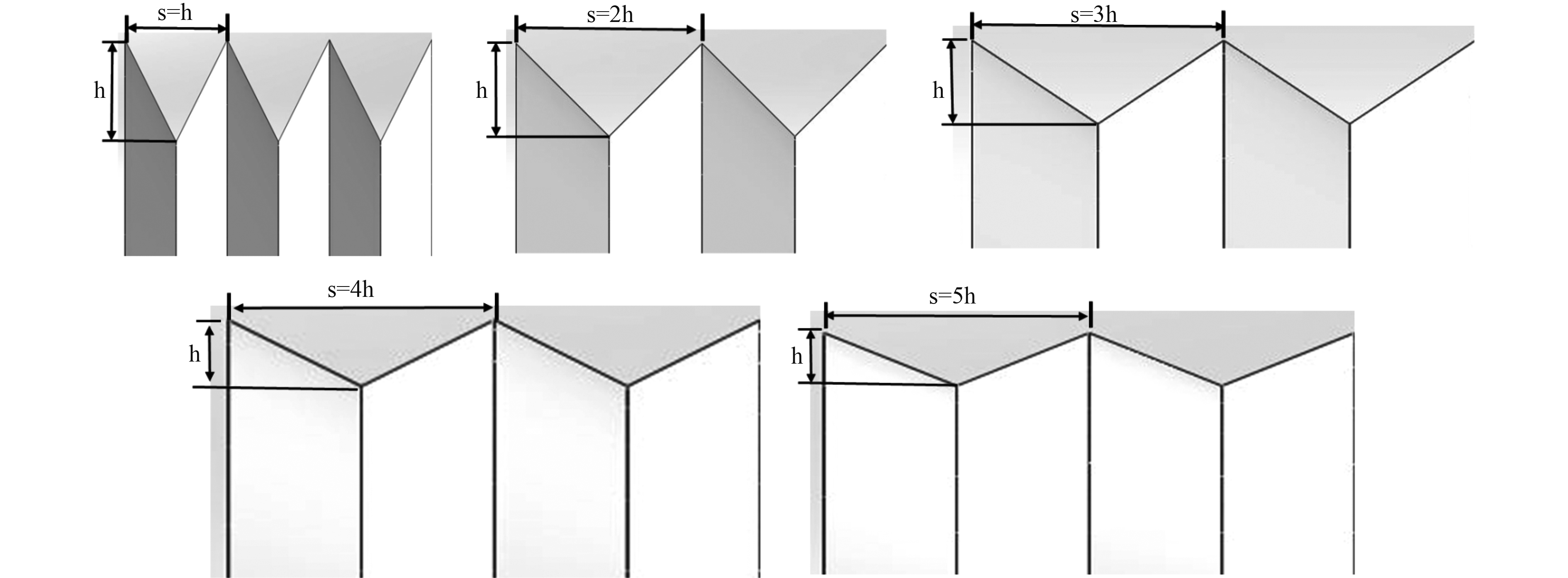
通过以上分析得出,V型圆柱结构可以有效降低圆柱绕流噪声,因此针对不同尺寸的V型结构对流噪声的影响进行研究。设V型结构的高度为h=1 mm,宽度s分别为h,2h,3h,4h,5h,如图13所示。
|
图 13 不同s/h比例的 V 型圆柱 Fig. 13 V-shaped cylinder with different s/h ratio |
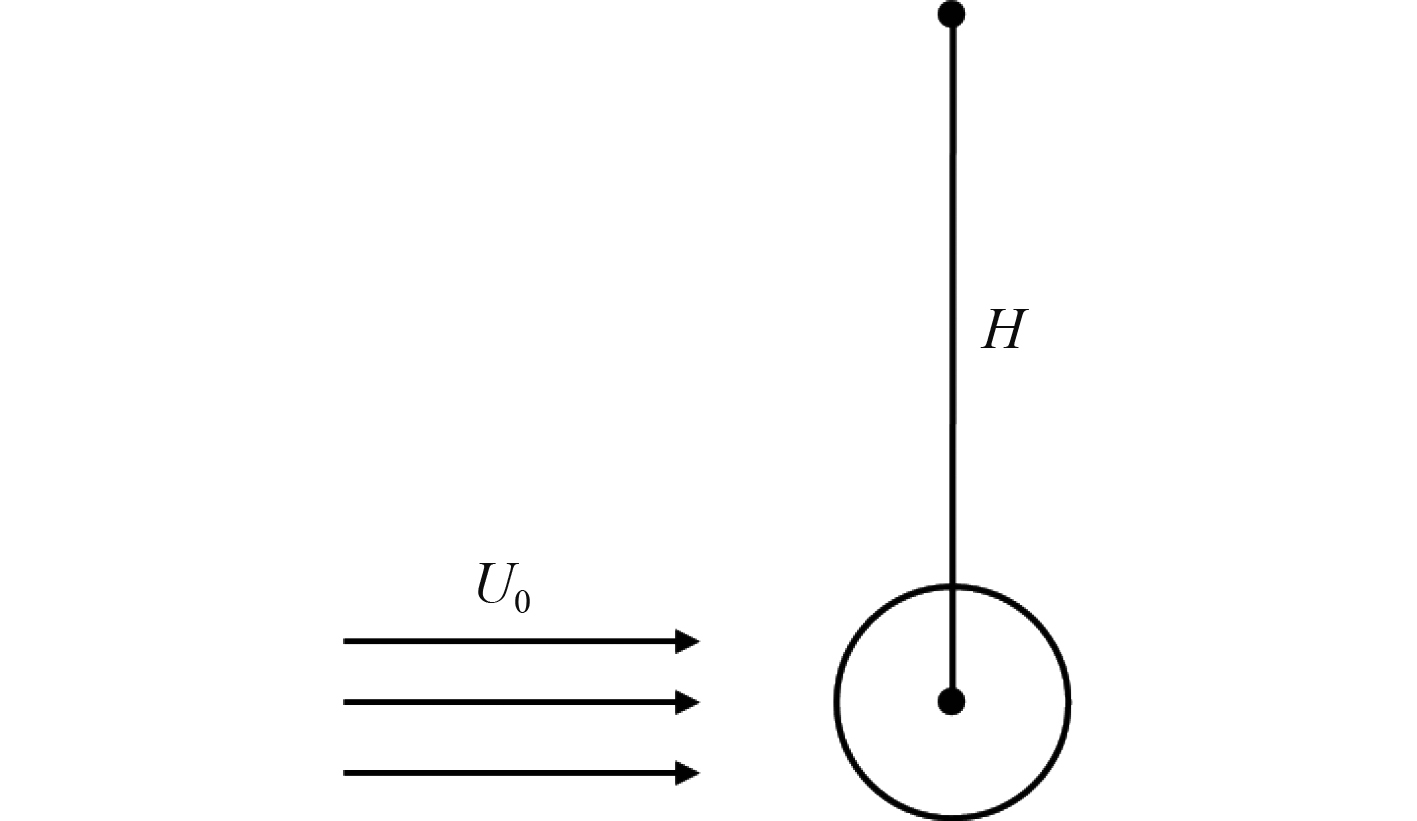
对光滑圆柱和5种不同s/h的V型仿生结构在各监测点处的声压总级进行对比,设置6个监测点,监测点位置为垂直于来流方向上距圆心H处,H分别为10D,50D,75D,100D,125D,150D,6个监测点编号为M1-M6。监测点示意图如图14所示。
|
图 14 监测点示意图 Fig. 14 Schematic diagram of monitoring points |
表4给出了光滑圆柱与不同s/h的V型仿生圆柱在监测点M1-M6处的声压总级。可以看出在相同来流速度下,当s/h=1和2时,V型仿生圆柱具有明显的降噪效果,且当s/h=1时,降噪效果最好,降噪量为12 dB左右。当s/h增加到3时,V型仿生圆柱反而起到了增加噪声的作用,s/h=4和5时,两者圆柱绕流引起的噪声几乎相同,且均起到了增阻作用。
|
|
表 4 光滑圆柱与不同s/h的V型仿生圆柱在各监测点处的声压总级(dB) Tab.4 The total sound pressure level of smooth cylinder and V-shaped bionic cylinder with different s/h at each monitoring point (dB) |
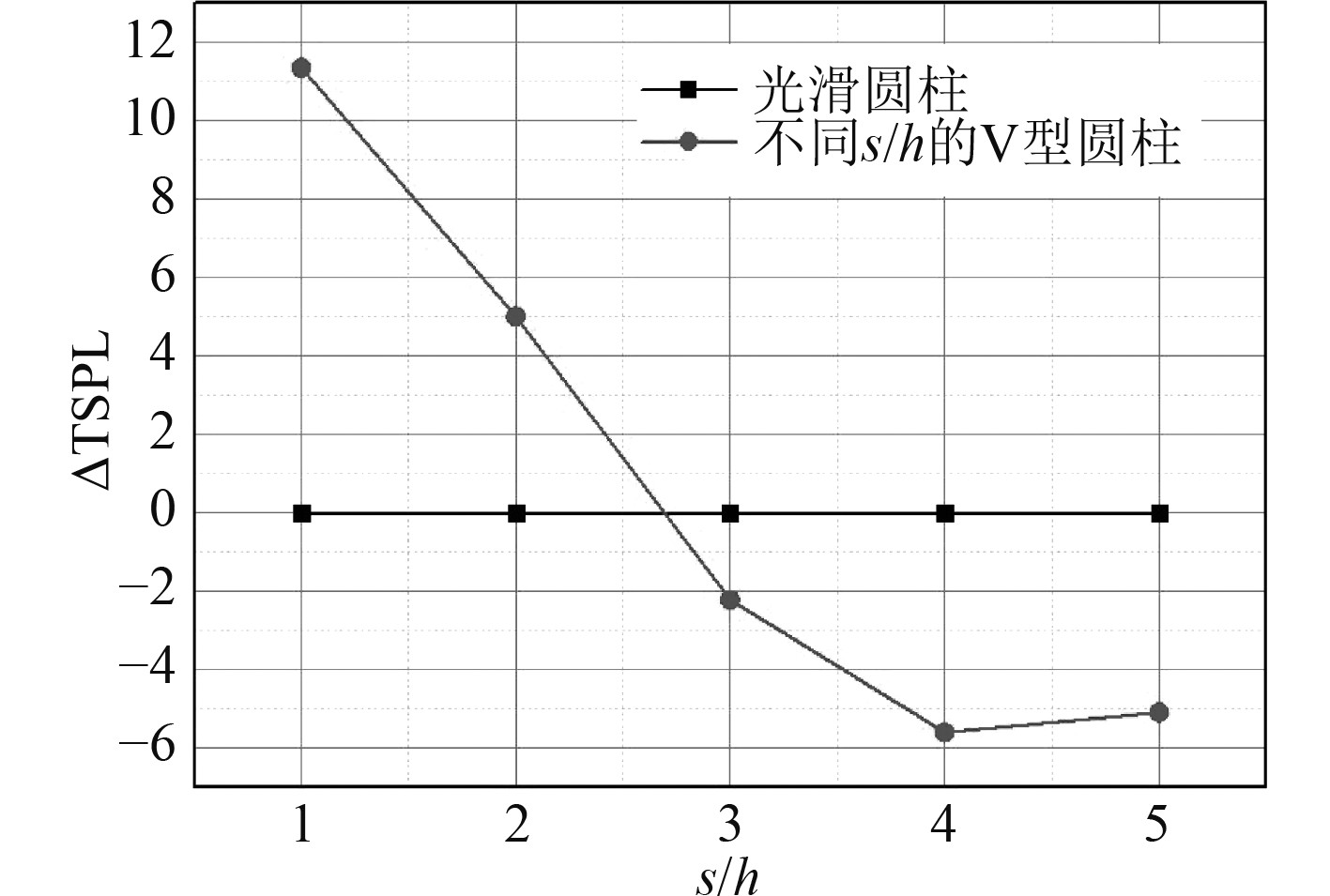
图15给出了不同s/h的V型仿生圆柱在监测点M6处的降噪量,正值表示具有降噪效果,负值表示具有增加噪声的作用。从图中可以看出V型仿生圆柱的降噪作用与s/h有明显的关系,随着s/h的增加,逐渐出现增加噪声的作用,s/h的临界值在2~3之间。
|
图 15 不同s/h的 V 型仿生圆柱在监测点 M6 处的降噪量 Fig. 15 Noise reduction of V-shaped bionic cylinder with different s/h at monitoring point M6 |
仿生V型圆柱具有降噪作用的同时,阻力不能增加,这样才能起到减阻降噪的作用。表5给出了不同s/h的V型仿生圆柱的时均阻力系数和噪声值,减阻率为正表示具有减阻作用,减阻率为负表示具有增阻作用,降噪量亦相同。从表5可以看出,V型仿生圆柱的减阻与降噪随s/h具有一致的变化趋势,当s/h≤2时,V型仿生圆柱具有减阻降噪效果,当s/h≥3时,V型仿生圆柱不在具有减阻降噪作用,反而具有增阻和增加噪声的作用,s/h的临界值在2-3之间。
|
|
表 5 不同s/h的V型仿生圆柱的时均阻力系数和噪声值 Tab.5 Time-averaged drag coefficient and noise value of V-shaped bionic cylinder with different s/h |
从图15可以预测,当s/h=2.5时,V型仿生圆柱在监测点M6处的降噪量在−2.22 dB~5.01 dB之间,即s/h=2和3时V型仿生圆柱的降噪量之间。为了验证图15中不同s/h的V型仿生圆柱的降噪规律的正确性,设计了s/h=2.5的V型仿生圆柱,并对其进行了声学计算,结果如表6所示。
|
|
表 6 s/h=2.5、s/h=2和3时在各监测点处的声压总级对比(dB) Tab.6 Comparison of the total sound pressure level at each monitoring point when s/h=2.5, s/h=2 and 3 (dB) |
从表6可以看出,s/h=2.5时的V型圆柱在监测点处的声压总级在s/h=2和3之间,符合图15给出的不同s/h的V型仿生圆柱的降噪量规律,并且可以看到s/h=2.5的声压总级和光滑圆柱绕流产生的声压总级基本相同,因此就仿生圆柱的降噪而言,s/h的临界值为2.5左右。
综上所述,可以看出V型仿生圆柱的降噪作用与s/h呈近似线性关系,且随着s/h的增加,降噪效果逐渐降低。相较于光滑圆柱,在不增加阻力的前提下,V型仿生圆柱的降噪作用对应的s/h的临界值在2.5左右,当s/h<2.5时,V型仿生圆柱具有降噪作用,当s/h>2.5时,V型仿生圆柱不在具有降噪作用,当s/h增大到4~5之间时,噪声趋于稳定。
3 结 语本文主要是基于流场瞬态计算结果采用Lighthill声类比方法对不同雷诺数下光滑圆柱和3种典型仿生圆柱的声学特性进行讨论,揭示了仿生圆柱的降噪机理,对比了不同尺寸比例的V型仿生圆柱的降噪效果,可以得到以下结论:
1)3种典型仿生圆柱中,V型仿生圆柱的降噪效果最好。圆柱上的V槽形结构可以减缓尾流的脱落,从而降低由尾流脱落引起的压力脉动幅值,进而有效地降低了由尾流周期性脱落引起的偶极子噪声。另外V型圆柱可以阻碍圆柱两侧的分离剪切层向湍流的转变,使得涡量减小,同时尾流的分离剪切层脱落变缓,变得更加稳定,进而降低了由涡旋脱落造成的噪声。
2)V型仿生圆柱的降噪作用与s/h呈近似线性关系,且随着s/h的增加,降噪效果逐渐降低。相较于光滑圆柱,V型仿生圆柱的降噪作用对应的s/h的临界值在2.5左右,当s/h<2.5时,V型仿生圆柱具有降噪作用,当s/h>2.5时,V型仿生圆柱不在具有降噪作用,当s/h增大到4~5之间时,噪声趋于稳定。
| [1] |
CHOI K S. The wall-pressure fluctuations of modified turbulent boundary layer with riblets[M]//Turbulence Management and Relaminarisation. Springer, Berlin, Heidelberg, 1988: 149−160.
|
| [2] |
PARK S R, WALLACE J M. Flow alteration and drag reduction by riblets in a turbulent boundary layer[J]. AIAA journal, 1994, 32(1): 31-38. DOI:10.2514/3.11947 |
| [3] |
GRAHAM, R. R.. The Silent Flight of Owls[J]. Journal of the Royal Aeronautical Society, 1934, 38(286): 837-843. DOI:10.1017/S0368393100109915 |
| [4] |
SODERMAN P T . Leading edge serrations which reduce the noise of low-speed rotors[J]. 1973.
|
| [5] |
石秀华, 宋保维. 条纹薄膜降低水下航行器流噪声的实验研究[J]. 西北工业大学学报, 1997(3): 395-398. |
| [6] |
包云平. 条纹薄膜的减阻降噪研究[D]. 西安: 西北工业大学, 1994.
|
| [7] |
张春华. 基于信鸽体表的减阻降噪功能表面耦合仿生[D]. 吉林: 吉林大学, 2008.
|
| [8] |
陈坤. 仿生耦合风机叶片模型降噪与增效研究[D]. 吉林: 吉林大学, 2009.
|
| [9] |
石磊. 圆柱杆件气动噪声仿生控制研究[D]. 吉林: 吉林大学, 2013.
|
| [10] |
孙少明, 徐成宇, 任露泉. 轴流风机仿生叶片降噪试验研究及机理分析[J]. 吉林大学学报(工学版), 2009, 39(2): 382-387. |
| [11] |
孙少明, 任露泉, 梅涛. 仿生降噪蜗舌试验研究与数值模拟分析[J]. 振动与冲击, 2009, 28(5): 32-34. DOI:10.3969/j.issn.1000-3835.2009.05.008 |
| [12] |
刘海涛, 徐志龙. 基于仿生非光滑结构的高速列车受电弓杆件减阻降噪研究[J]. 噪声与振动控制, 2018, 38(S1): 269-272. |
 2021, Vol. 43
2021, Vol. 43
