随着船舶轻量化需求的提高,越来越多的新型材料得到应用。铝合金材料的密度仅有钢材1/3左右,但其强度较高且具有耐腐蚀性强以及可塑性优良等特点,因此被广泛应用于高速艇、船舶上层建筑和海洋结构物的建造中[1]。然而,铝合金结构在焊接时,温度变化较大,容易产生较大的焊接残余应力,这是工程应用需要克服的难点。
国内外学者开展了一系列铝合金焊接实验和数值模拟研究。Jose[2]开展了铝合金MIG焊实验和数值模拟,验证了数值模拟的精度满足工程需要。Asadi[3]和Lu[4]分别采用顺序耦合法进行了TIG焊与MIG焊的数值模拟和实验测试,发现模拟结果与实验数据吻合较好。张鹏飞[5]对6061-T6铝合金箱型构件的焊接残余应力进行了研究,发现板厚对残余应力峰值影响较低。胡云瑞[6]研究了快速冷却工艺对于6005A铝合金焊接残余应力的影响,指出该工艺能使残余应力显著降低。虽然国内外学者对铝合金焊接性能开展了一定的研究,但是目前我国对于船用铝合金的焊接性能掌握仍不充分,焊接工艺有待完善[7-8]。
为了掌握铝合金加筋板结构的焊接性能,本文基于顺序耦合法开展船用5083铝合金角接焊接头的焊接过程数值模拟,分析其焊接温度场和残余应力分布特性,为铝合金焊接工艺优化提供参考。
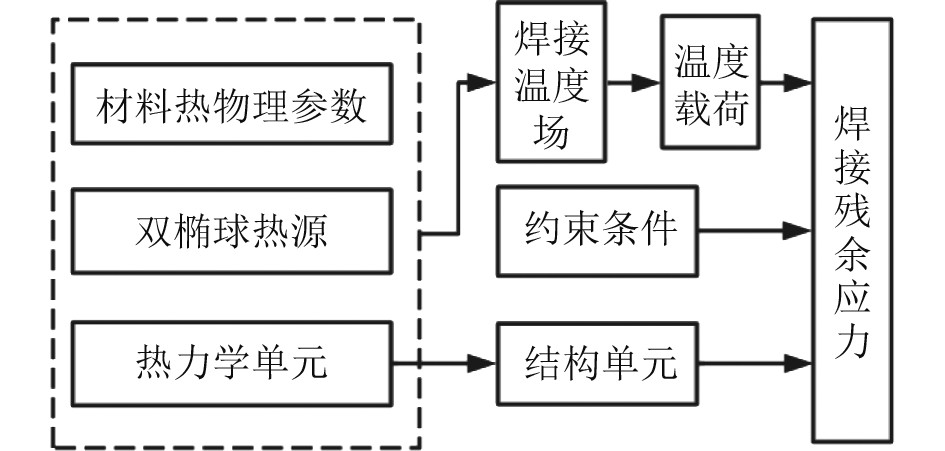
1 焊接数值模拟方法与建模 1.1 数值模拟方法与流程目前,焊接数值模拟方法主要有直接耦合法和顺序耦合法[9]。直接耦合法是指使用一种单元同时考虑结构性能和热学性能,并在数值模拟过程中直接模拟焊接过程中单元的变形场和温度场耦合变化的方法,这种方法能够较为精确地模拟焊件温度场和变形场的耦合变化,但是需要耗费大量的计算资源;顺序耦合法则先考虑单元的热学性能,即模拟热学单元温度场变化,再将热学单元转为结构单元并将温度场时历导入结构单元中来重现焊接过程中力学性能的变化,这种间接耦合的方法在材料的结构性能对热学性能影响小的时候使用是合适的。由于顺序耦合法的计算效率高,且精度满足一般工程需求,所以应用更为普遍。本文使用顺序耦合法对铝合金加筋板角接焊的焊接温度场和力学响应进行仿真,仿真流程如图1所示。
|
图 1 数值模拟流程图 Fig. 1 Numerical simulation process |
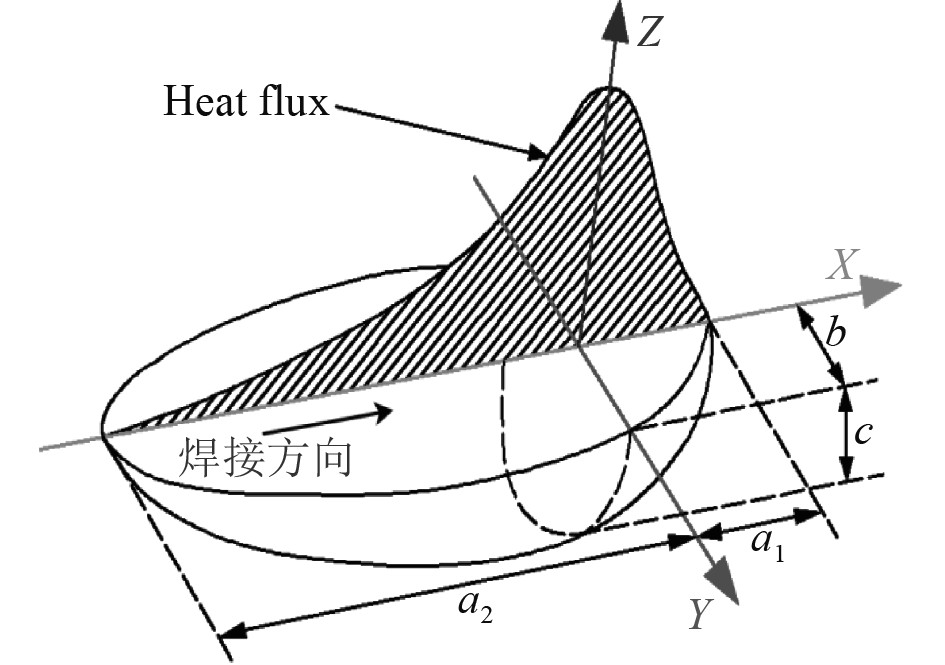
热源模型的有效性直接关系到焊接过程数值模拟精度。双椭球热源模型是目前熔化焊数值模拟应用最广泛的热源模型之一[10],其通过划分前后半弧椭球的方式将热输入量分成非均匀的两部分并施加在焊缝上,如图2所示。
|
图 2 双椭球热源模型 Fig. 2 Double ellipsoidal heat source model |
假设焊接是沿x轴进行且焊枪电弧垂直于焊接平面,则位于焊接电弧前方的第一个半椭球内一点的功率密度分布可描述为:
| $ {q_1}\left( {x,y,x} \right) = \frac{{6\sqrt 3 {f_1}\eta UI}}{{abc_1\text{π} \sqrt {\text{π}} }}\exp \left( { - {{\frac{{3x}}{{c_1^2}}}^2} - {{\frac{{3y}}{{{b^2}}}}^2} - {{\frac{{3z}}{{{a^2}}}}^2}} \right),x \geqslant 0 。$ | (1) |
类似地,对于覆盖弧后部的第二半椭球内的点,功率密度方程描述为:
| $ {q_2}\left( {x,y,x} \right) = \frac{{6\sqrt 3 {f_2}\eta UI}}{{{a}bc_2\text{π} \sqrt {\text{π}} }}\exp \left( { - {{\frac{{3x}}{{c_2^2}}}^2} - {{\frac{{3y}}{{{b^2}}}}^2} - {{\frac{{3z}}{{{a^2}}}}^2}} \right),x < 0。$ | (2) |
式中:
实际焊接过程中,焊接热量的分布是不均匀的,电弧所在位置的金属温度急速升高并熔化形成熔池,而随着电弧移动,熔池后部温度会快速下降,双椭球热源通过改变前后长半轴大小和前后量椭球热量分配系数可以很好的模拟此现象,从而较好地模拟MIG焊的热量分布特点。焊接参数如表1所示,焊接速度为4 mm/s。
|
|
表 1 双椭球热源参数 Tab.1 Parameter of double ellipsoidal heat source |
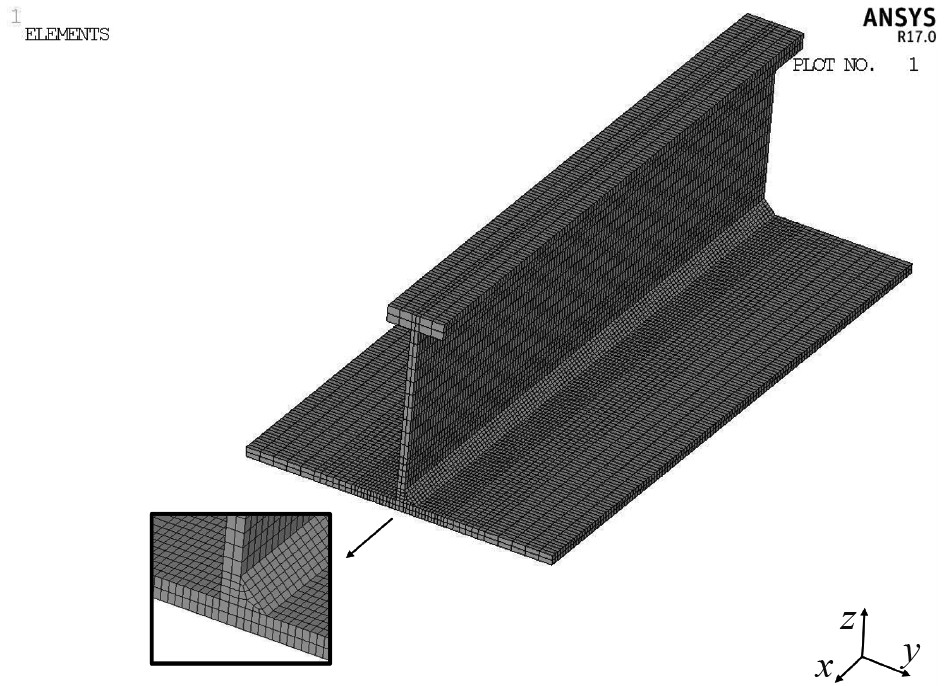
铝合金加筋板的长和宽分别为400 mm×196 mm,厚度6 mm;骨材为T型材,其中腹板高110 mm,厚度5 mm;面板宽36 mm,厚度10 mm,材料为5083铝合金材料,其热物理参数见表2。基于Ansys有限元软件,采用六面体单元SOLID70单元建立加筋板分析模型,如图3所示。
|
|
表 2 5083铝合金的热物理参数 Tab.2 Thermal physical parameters of 5083 aluminum alloy |
|
图 3 铝合金加筋板有限元模型 Fig. 3 Finite element model of stiffened aluminum plate |
由于焊缝及附近区域的温度变化明显,温度梯度和应力梯度较高,为了保证计算精度并提高计算效率,对焊缝及附近网格进行加密处理,焊缝处网格尺寸控制为2×2 mm,远离焊缝部分的网格尺寸则逐渐增大。同时,为了更真实地模拟焊接时焊料填充的过程,在数值分析中引入了生死单元法[11],即在模拟焊接时,先在焊接路径上布置好焊料(单元),并通过将其各项属性(如刚度、质量)乘以极大的折减系数的方法来停用这些单元,当需要这些单元参与模拟时,再将其折减系数去除来达到“生”的效果。
2 焊接温度场数值模拟结果分析图4为不同时刻铝合金加筋板角接焊的温度场。可以发现,各个时刻的温度极值都处于焊接作用中心点,焊接热源在前进的过程中不断向“填充”的焊料提供极大热量,焊料在与四周单元热交换的过程中将能量逐渐向外扩散,在焊接接头的焊缝及周围区域上形成椭圆状的热量扩散轨迹。在焊接过程结束后,热量继续向四周扩散并和外界环境进行热交换,焊接接头的温度也随之迅速降低,最终趋近于环境温度。

|
图 4 角接接头温度场云图 Fig. 4 Nephogram of temperature field of fillet-welded joint |
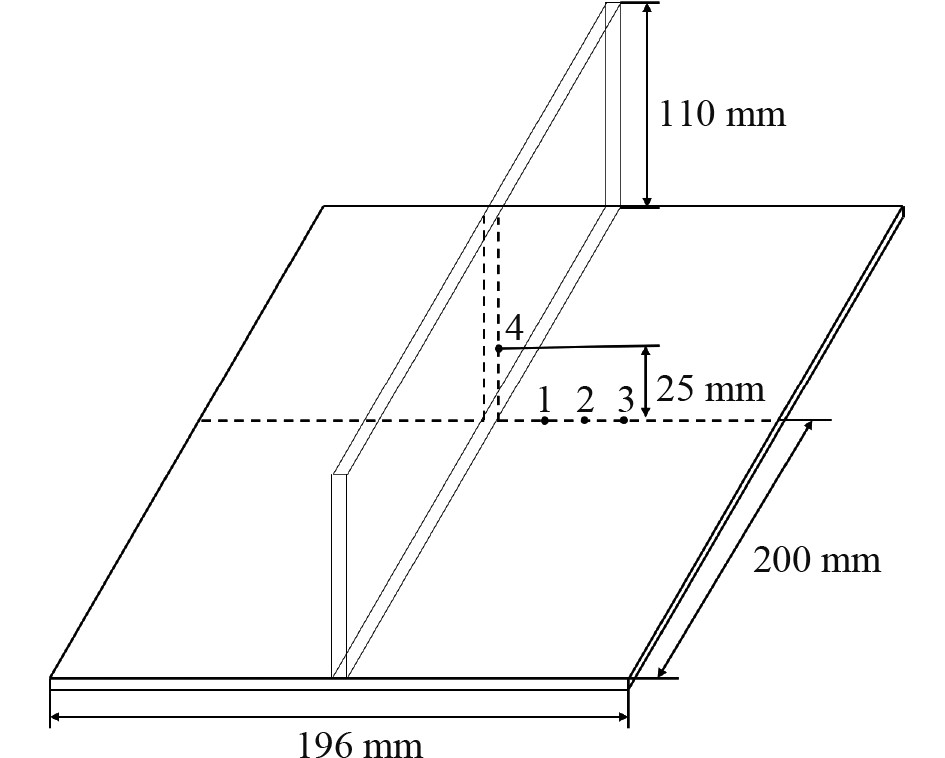
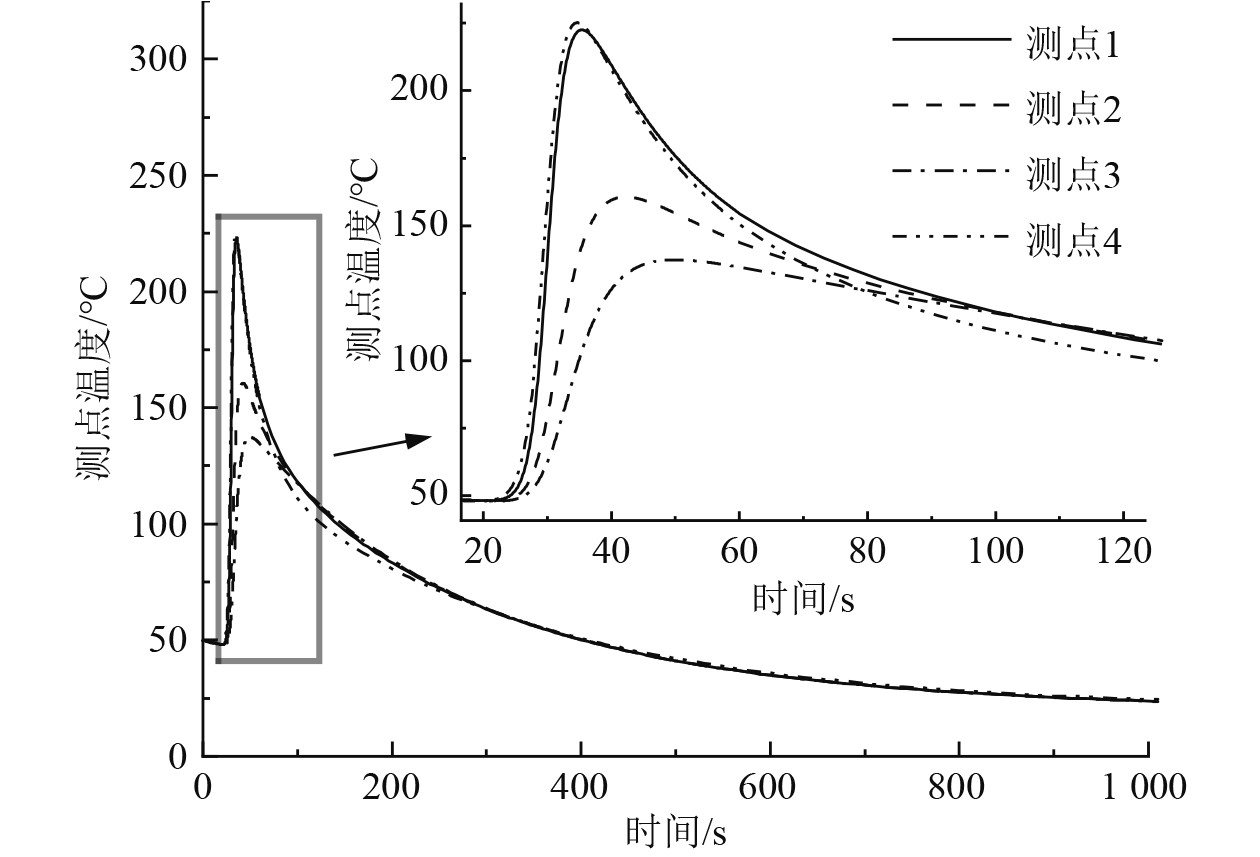
为了分析焊接接头温度变化规律,进一步在角接焊接头面板的一侧选取4处测点(见图5),提取相关测点的温度时历,如图6所示。可以发现,测点温度变化图还原了焊接过程中各测点上的温度时历,即焊接进行至测点时,焊接热源的高热量使得该点温度迅速上升;当热源远离,热单元和外界热交换使得温度又迅速下降。随着单元温度的降低,单元与外界的温度差也不断减小,这导致温度下降的速率不断变小。由于选取的温度测点1和测点4与焊缝的距离相近,因此温度的变化曲线也基本一致。各测点的温度变化趋势相同,但温度的峰值随测点与焊缝中心的距离增大而减小。
|
图 5 焊接接头温度测点 Fig. 5 Temperature measuring points of welding joint |
|
图 6 测点温度时历曲线 Fig. 6 Temperature vs. time curve of measuring points |
焊接应力场模型可由温度场模型转化单元类型获得,不用重新建模划分网格,但是热学单元转化为结构单元后需要施加合适的边界条件。首先,考虑到实际焊接时一般在焊缝两端焊引弧板,限制了试件的横向变形,因此模型相应位置设置y方向位移约束。在此基础上,根据实际焊接工艺采用了两点约束和三点约束两种不同的约束方式。其中,两点约束指对试件焊缝两端部位进行刚固约束;三点约束指对试件其中3个角点进行刚固约束。
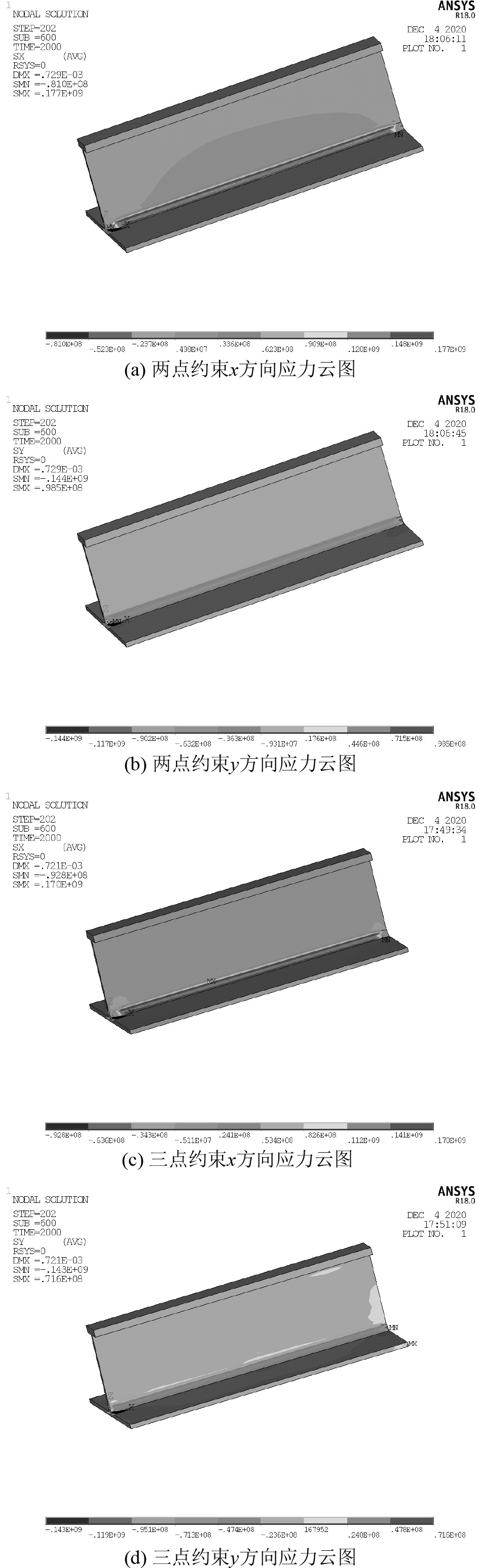
在进行温度场热载荷施加时,需要读取模型相应时间点的节点温度,为保证精确度,使用与温度场计算相同的时间步和生死单元设置。同时参考温度也与温度场模拟相同。焊接力学响应计算完毕后,提取各个约束方式在x,y方向上的残余应力云图进行分析,如图7所示。可以发现,2种约束形式下角接焊接头的横向焊接残余应力峰值均比纵向焊接残余应力峰值小。两点约束下的横向残余应力峰值为144 MPa,小于纵向残余应力最大值177 MPa;三点约束方式的y方向残余应力峰值为143 MPa,小于x方向上的残余应力最大值170 MPa。
|
图 7 角接接头的残余应力分量分布云图 Fig. 7 Nephogram of residual stress component distribution of fillet-welded joint |
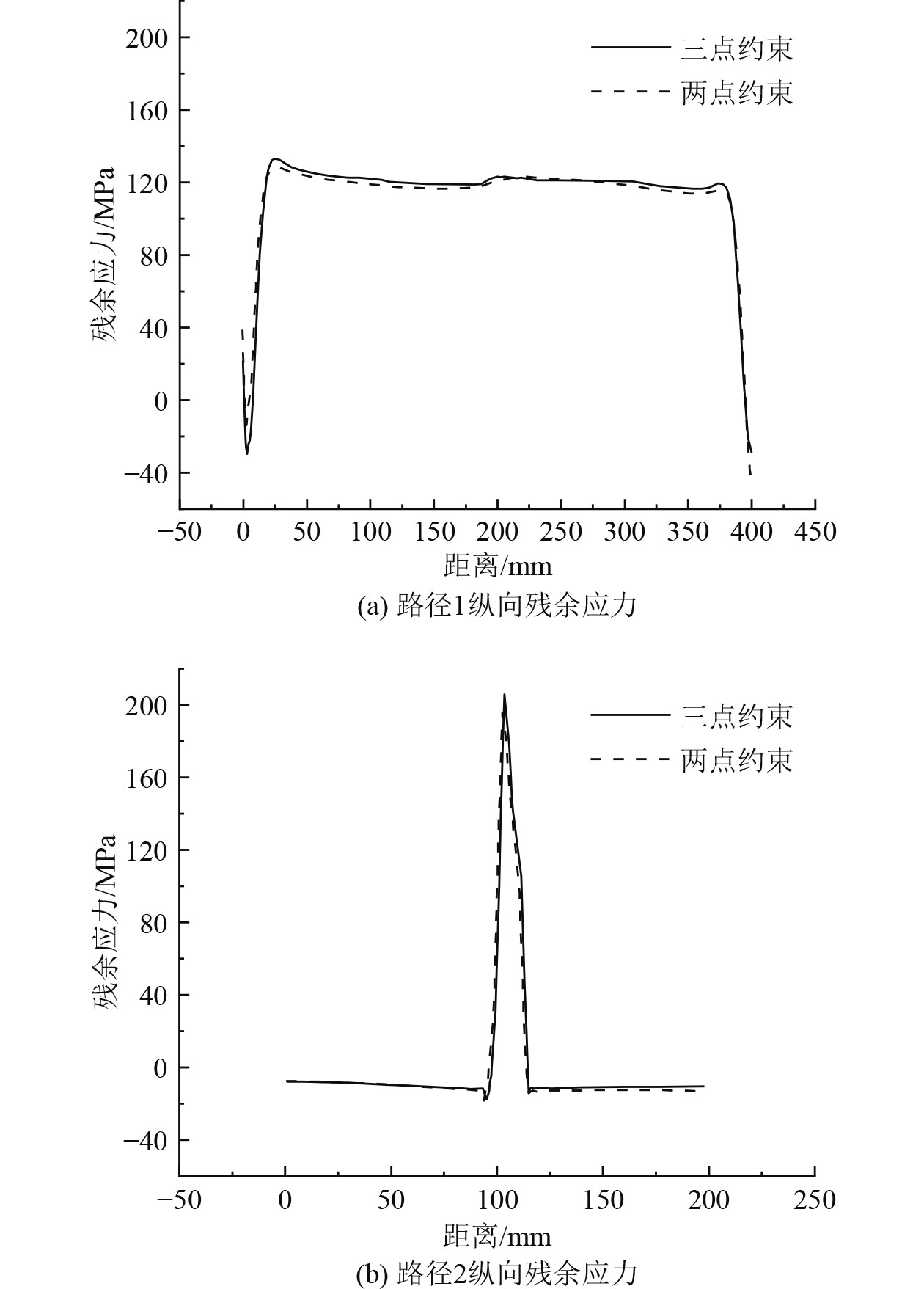
在铝合金焊接后产生的残余应力中,纵向残余应力分量对铝合金结构的抗拉压强度有很大的影响。为了更好地观察纵向残余应力的分布情况,分别取纵向的焊缝中心线作为路径1和垂直焊缝的横向板中线作为路径2来绘制残余应力分布情况,2种焊接接头各路径上的纵向残余应力分布如图8所示。
|
图 8 角接接头沿路径的纵向残余应力曲线 Fig. 8 Longitudinal residual stress curve of the fillet-welded joint along the path |
由图8可知,角接焊纵向残余应力主要集中在角焊缝及附近区域,2种残余应力在焊缝中心位置处达到峰值,分别表现为三点约束204 MPa和两点约束的194 MPa。2种约束形式下板中线处的纵向残余应力峰值变化仍旧不大,各路径上的残余应力曲线也基本一致,这说明两点约束和三点约束并不会显著地改变焊接残余应力的分布趋势。然而,通过路径1的残余应力曲线图可以发现,三点约束还是造成了轻微的残余应力分布不均的现象,这使得板缘两端的残余应力曲线走向并不对称。
4 结 语基于顺序耦合法结合双椭球热源模型和生死单元法,本文开展铝合金加筋板角接焊的数值模拟研究,得到了铝合金MIG焊焊接过程中的温度场和残余应力分布,分析了约束条件对残余应力的影响,主要结论如下:
1)当热源作用焊接区域时,温度迅速升高,随后随时间迅速下降,温度的下降速率随时间不断减小,而焊接接头各部位的温度峰值不仅与热源参数有关,同时也与距焊缝距离有关;
2)角接焊纵向残余应力主要集中在角焊缝及附近区域,在焊缝中心位置处达到峰值,应力水平与材料屈服限接近;
3)不同约束方式下的焊接残余应力分量的峰值差异很小,沿焊缝中心和板中线的残余应力曲线也基本一致,但是在板缘处,三点约束还是使得加筋板的残余应力分布产生不均匀、不对称现象。
| [1] |
HAZARI H R, BALUBAI M, KUMAR D S, et al. Experimental investigation of TIG welding on AA 6082 and AA 8011[J]. Materials Today:Proceedings, 2019, 19(2): 818-822. |
| [2] |
MESEGUER-VALDENEBRO J L, MARTINEZ-CONESA E, PORTOLES A. Numerical-experimental validation of the welding thermal cycle carried out with the MIG welding process on a 6063-T5 aluminium tubular profile[J]. Thermal Science, 2019, 23(6A): 3639-3650. |
| [3] |
ASADI P, ALIMOHAMMADI S, KOHANTORABI O, et al. Numerical investigation on the effect of welding speed and heat input on the residual stress of multi-pass TIG welded stainless steel pipe[J]. Journal of Engineering Manufacture, 2021, 235(6-7): 1007-1021. DOI:10.1177/0954405420981335 |
| [4] |
Lu Y, Zhu S, Zhao Z, et al. Numerical simulation of residual stresses in aluminum alloy welded joints[J]. Journal of Manufacturing Processes, 2020, 50: 380-393. DOI:10.1016/j.jmapro.2019.12.056 |
| [5] |
张鹏飞, 卢嘉玮, 张兆年, 等. 6061-T6铝合金构件焊接残余应力分布[J]. 兰州交通大学学报, 2021, 40(30): 15-19. |
| [6] |
胡云瑞, 李鸣申, 王留芳, 等. 快速冷却对6005A铝合金多道次MIG焊接残余应力的影响[J/OL]. 热加工工艺, 2022(1): 103−106
|
| [7] |
Li C, Ren H, Zhu Z, et al. Numerical investigation on the ultimate strength of aluminium integrally stiffened panels subjected to uniaxial compressive load[J]. Thin-Walled Structures, 2018, 127: 221-234. DOI:10.1016/j.tws.2018.01.003 |
| [8] |
Li C, Ren H, Zhu Z, et al. Influence of model extension and boundary conditions on the buckling behaviour of aluminium integrally stiffened panels under uniaxial compressive loading[J]. Ocean Engineering, 2020, 216: 108066. DOI:10.1016/j.oceaneng.2020.108066 |
| [9] |
Chen Z, Li C, Han X, et al. Sensitivity analysis of the MIG welding process parameters based on response surface method[J]. Journal of Adhesion Science and Technology, 2020, 10: 1-20. |
| [10] |
GOLDAK J, CHAKRAVARTI A, BIBBY M. A new finite element model for welding heat sources[J]. Metallurgical Transactions B, 1984, 15(2): 299-305. DOI:10.1007/BF02667333 |
| [11] |
Chen B Q, HASHEMZADEH M, SOARES C G. Numerical and experimental studies on temperature and distortion patterns in butt-welded plates[J]. The International Journal of Advanced Manufacturing Technology, 2014, 72(5-8): 1121-1131. DOI:10.1007/s00170-014-5740-8 |
 2021, Vol. 43
2021, Vol. 43
