船舶的操纵性和耐波性是评价船舶性能的重要指标。船体在波浪中会产生六自由度摇荡运动,对船舶性能提出了更高的要求。提高船舶的水动力性能,最常见的、最简单的方式是通过增加船舶附体的方式,在不变动原有船体线型的情况下,改善船体周围流场。其中尾压浪板是船体尾部延展出来的结构,常用来降低阻力,改善船体尾部流场。水翼和鳍[1]常用于抑制船体摇荡。但是安装水翼和鳍会增加船体湿表面积,导致了阻力的增加。附体在减阻减摇方面具有较大的应用前景,因此有必要对附体的水动力性能进行研究。
刘英和等[2]运用二维切片理论研究尾压浪板对穿浪双体船纵摇和垂荡的影响,发现尾压浪板布置在距离中心较远的位置,可以抑制船体纵摇,最大可以减弱10%,但对垂荡影响较微弱。蒋一等[3]以断级滑行艇为研究对象,研究不同尾压浪板安装角对其性能的影响。结果表明,低速下,随尾压浪板安装角的增加,滑行艇的水动力性能更优。高速下,对水动力性能提升影响较小。Natio[4]研究了水翼对船体摇荡程度和波浪增阻的影响,研究发现,水翼的添加可以改善摇荡幅值大小、波浪增阻,并且在首安装水翼能够产生较大的推力,水动力性能也较为优越。Ulysses[5]对船首安装的固定式水翼进行理论分析,研究发现,固定水翼可以改善船体的纵摇运动。Eirik等[6]以固定水翼为研究对象,对其运动响应进行数值模拟,研究发现,水翼在特定的波高和周期下,可减少船体阻力50%以上,船舶的垂荡运动幅值和纵摇运动幅值减少40%以上。朱航等[7]等在渔政船添加减摇鳍并进行优化,研究表明,减摇鳍可以抑制横摇运动,横摇最大可以减弱80%。
本文将添加球鼻首的DDG100驱逐舰作为原始船体,添加尾压浪板,利用caeses参数化建模软件,进行全参数化建模,并基于粘性流体理论,进行尾压浪板的结构优化。结果表明,经过优化后的带有尾压浪板的船体,在2.02 m/s和1.77 m/s的速度下,阻力都减少2.5%。同时将优化后带有尾压浪板的船体,在球鼻首上添加三角形侧鳍和船首位置安装水翼,并进行全参建模及优化。结果表明,安装水翼和三角形侧鳍会导致船体总阻力的增加,但是可以通过抑制兴波,减小剩余阻力。最后将安装尾压浪板、鳍与水翼附体后的船体,在规则波条件下,进行数值模拟,发现波浪增阻增大,当λ/L超过0.9时,波浪增阻小于优化后,升沉、纵摇以及耐波性均得到不同程度的改善。
1 原始船型及其水动力性能 1.1 原始船体本文将DDG1000驱逐舰穿浪首改成垂直首,并添加球鼻首,按照1∶70的比例,进行缩尺,将缩尺后的模型作为添加附体的原始船体模型,如图1所示。其主要参数如表1所示。

|
图 1 原始船体模型 Fig. 1 The original hull model |
|
|
表 1 原始船体模型主要参数 Tab.1 Main parameters of the original hull model |
坐标原点位于原始模型尾封板位置处,指向首部为x轴正方向,左舷为y轴正方向。模型坐标系如图2所示。

|
图 2 计算模型及坐标系 Fig. 2 Calculation model and coordinate system |
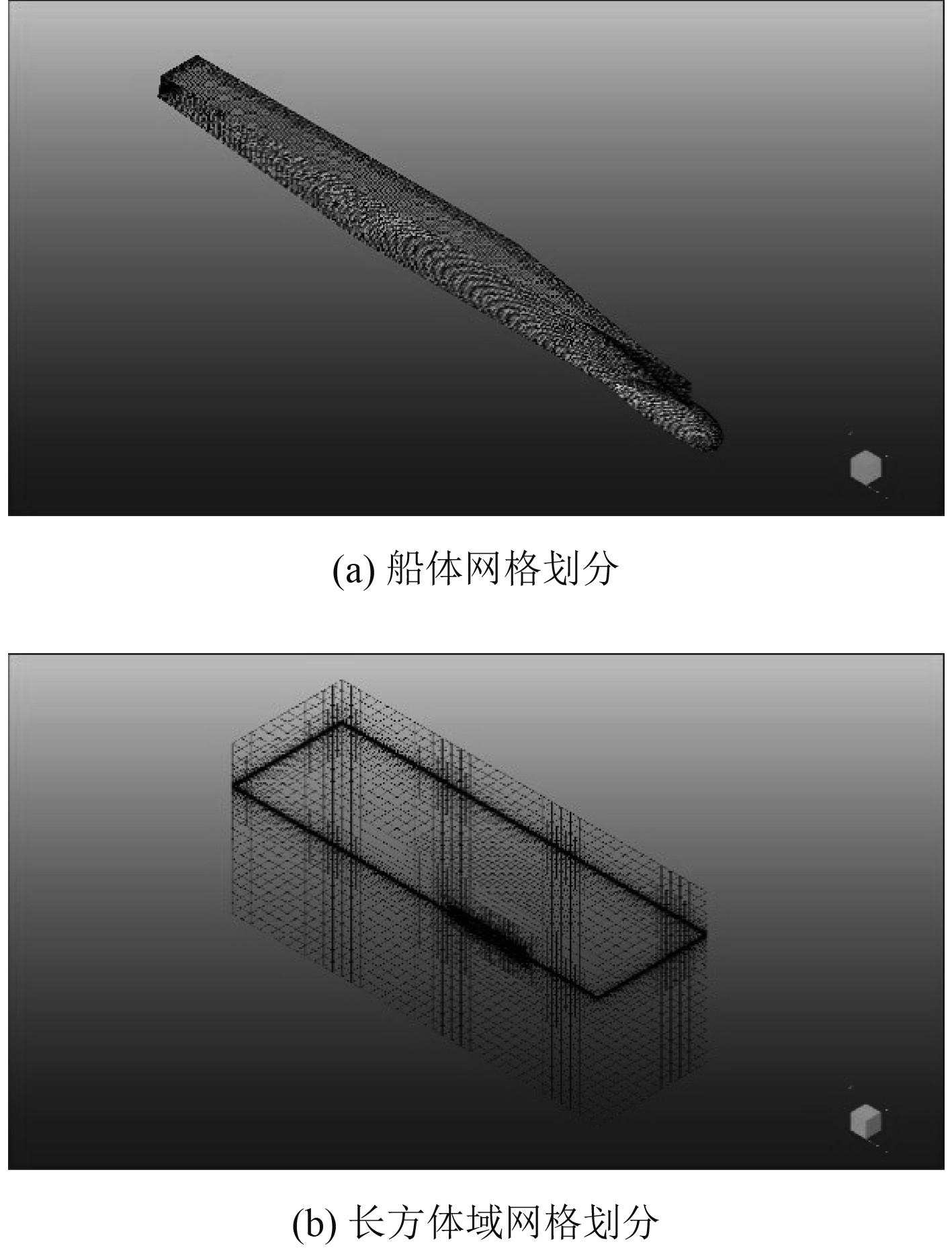
利用CFD计算软件FINE/Marine对初始模型进行数值计算。网格划分时,采用全六面体非结构网格,便于对模型更好描述,并且遵循整体非结构化,局部加密的原则,将无限大海域简化为5L×1.5L×2L(L为船长)长方体域。因为原始船型左右对称,为节约计算机资源和节约划分时间,本文采用半模计算。网格划分如图3所示。
|
图 3 模型网格划分 Fig. 3 model meshing |
基于粘性流体理论,进行约束模式下相关设置。采用非稳态时间布局,单向流(模拟15°海水),对于上下边界选择指定压力,对称设置为mir,剩余壁面设置为速度远场。对于船壁面都选择标准壁面函数。给定来流作为计算的初始条件,时间步长设置为0.01 s,表2给出原始模型在速度为2.02 m/s,1.77 m/s下的各阻力成分及对应数值。
|
|
表 2 阻力组成及数值大小 Tab.2 Resistance composition and numerical value |
全参数化建模是将模型的控制参数定义为变量,变量值的变动,即可产生对应的变种。节约了重新绘制变种模型的时间,提升了模型生成速率。利用caeses软件进行参数化建模流程:
1) 编写Feature功能程序,生成控制点、线以及驱动特征参数;
2) 利用软件内置的曲面生成器,关联驱动变量及驱动特征;
3) 通过软件内置的曲面生成器,通过对UV度及角度容差的调节,生成光顺曲面。
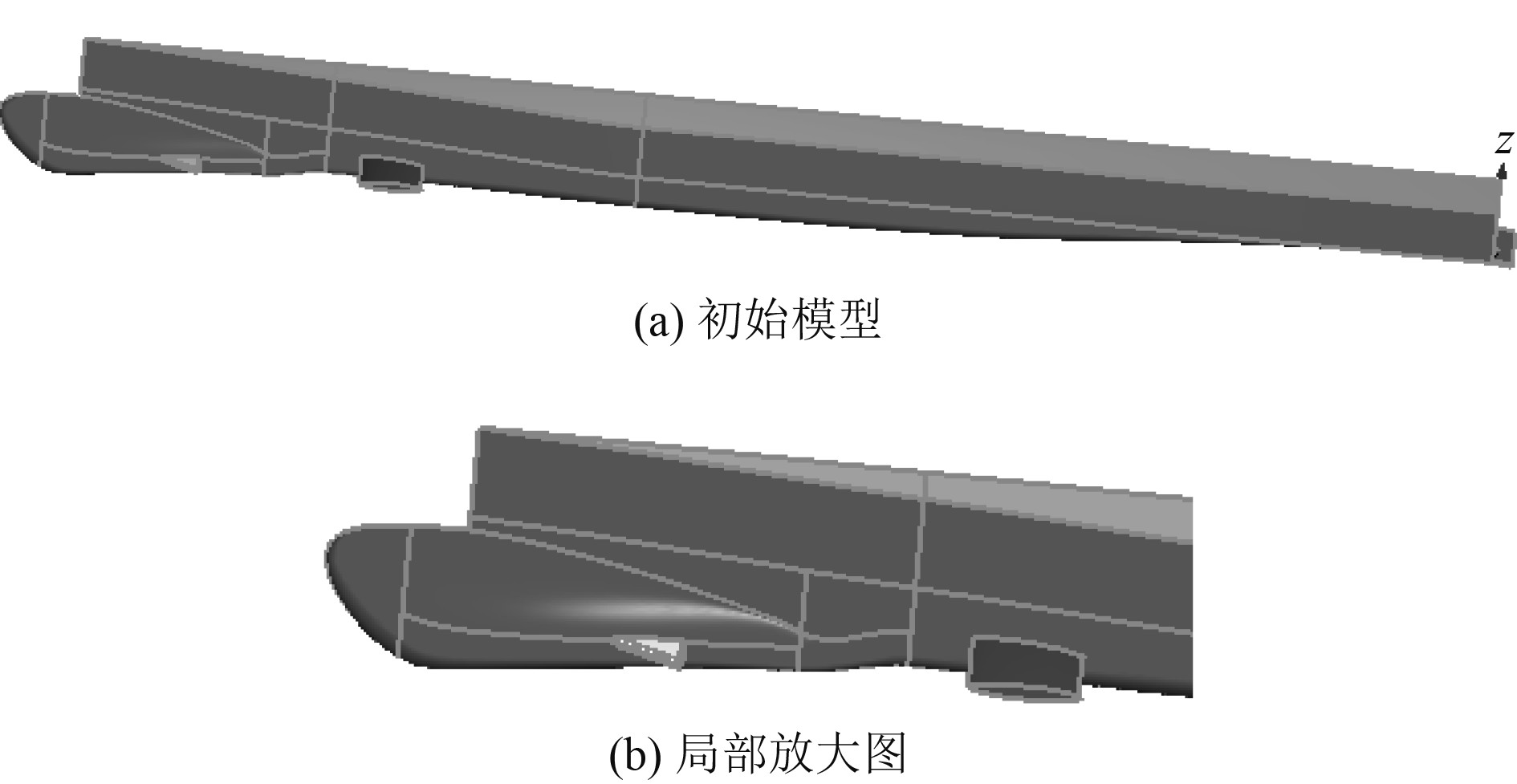
尾压浪板是船舶中减少阻力的常用装置。本文利用caeses建模软件,按照参数化建模流程,建立船体和尾压浪板的全参数化模型,作为优化的初始模型,如图4所示。建模时候,将尾压浪板的高度、厚度、以及安装角度定义为变量,给定初始变量值,并对尾压浪板进行优化,研究尾压浪板对船体阻力的影响。

|
图 4 添加尾压浪板的初始模型 Fig. 4 The initial model of adding the tail pressure wave board |
caeses 软件内置了多种可以调用的单目标和多目标优化算法,其中sobol算法[8]可以实现对整个变量空间的覆盖,批量生成变量的正交组合模型。Tsearch算法[9]在sobol算法的基础上,增加对变量周围搜索寻优的功能。NSGA-II优化算法是一种基于种群选择、杂交、遗传、变异的随机搜索算法[10]。
本文采用组合优化策略,设计2套组合优化方案。方案1:Sobol与NSGA-II组合优化方案,其中Sobol算法样本个数为20,NSGA-II算法种群数50,进化迭代数12,交叉概率0.8,变异概率0.1。方案2:sobol算法和Tsearch算法的组合方案,其中sobol算法样本数为20,Tsearch算法样本数50。2套优化方案都按照优化的三要素逐一设定。
1)设计变量
将尾压浪板的长度、厚度与安装角度3个作为设计变量,并给定变量的变化范围。
2)目标函数
将设计航速2.02 m/s下总阻力最小值作为目标函数,进行单目标优化。
3)约束条件
尾压浪板的排水量不超过总排水量的2%。
2.3 优化结果分析1)组合优化方案对比
对比2套优化方案,其中方案2因小样本取样,使其在优化时间上占有优势。但是方案2最终优化目标结果相近,可能陷入局部最优解中。通过对最终优化结果的对比,方案1的优化结果更为理想。
2)设计变量结果分析
方案1的优化更具优势,所以将方案1优化方案得到的优化模型作为优化后的模型,对该模型进行设计变量分析。
由表3可以看出,对于该初始模型,当尾压浪板长度0.0354 m、厚度0.006 m、安装角度−6.875°时,总阻力最小。
|
|
表 3 尾压浪板优化前后设计变量对比 Tab.3 Comparison of design variables before and after optimization of wake board |
3)船体阻力及自由液面波形对比
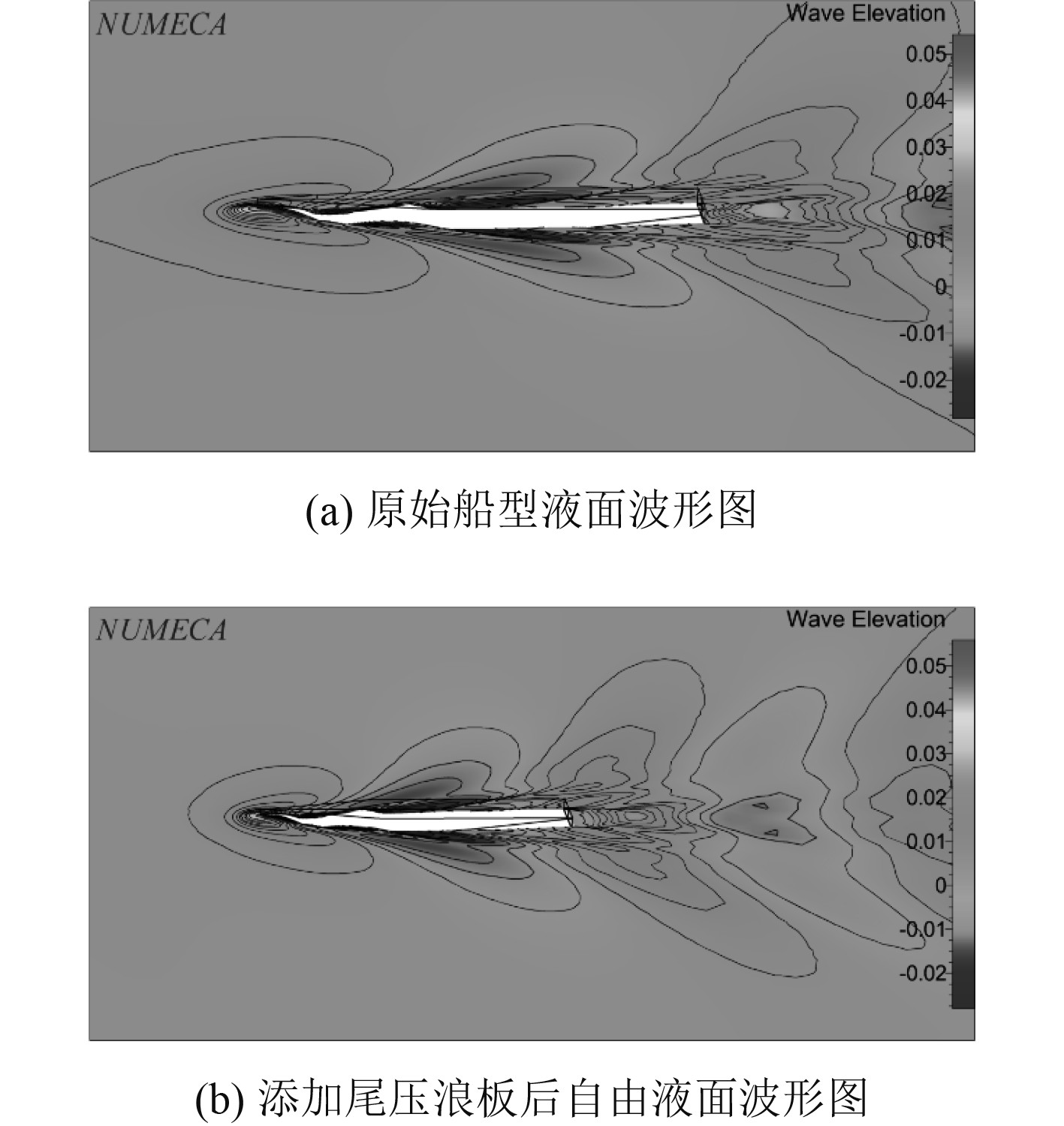
表4给出添加尾压浪板后的船体在2.02 m/s和1.77 m/s 航速下阻力成分变化情况。分析可知,对原始船型添加尾压浪板优化后,在2个速度下,总阻力及阻力组成部分相比初始模型都有下降趋势。在航速2.02 m/s 的工况下,总阻力、摩擦阻力、剩余阻力下降比例分别为2.5%,0.14%和8.1%。在1.77 m/s速度下,分别下降2.5%,0.57%,6.1%。结合图5自由液面的波形图可知,尾压浪板改善船体尾部和船体周围的流场,特别是对船体尾部流场,减缓了流场的分离,使得船尾压力减小,通过减少粘压阻力达到减少剩余阻力的目的,但尾压浪板的安装对摩擦阻力影响较小。
|
|
表 4 添加尾压浪板前后船体阻力对比 Tab.4 Comparison of hull resistance before and after adding stern wave plate |
|
图 5 添加尾压浪板前后自由液面波形图对比 Fig. 5 Comparison of free liquid surface waveform before and after adding tail pressure wave board |
将优化完的添加尾压浪板的船体模型,作为新优化的初始模型,并在caeses中,依照参数化建模的流程,依次对船首部位安装的水翼和在球鼻首上安装的三角形侧鳍进行参数化建模,如图6所示。进行优化研究,探究水翼和三角形侧鳍的添加对船体阻力的影响。
|
图 6 添加水翼和侧鳍的初始模型 Fig. 6 Initial model with hydrofoil and side feed added |
同样采用组合优化的策略,设置2套组合优化方案,并对优化三要素进行逐一设定。
1)优化目标
选择设计航速2.02 m/s下的总阻力最小值,进行单目标优化。
2)约束条件
排水量的变化不超过总排水量的3.5%。
3)设计变量
其中一共包含11个设计变量。
并耦合调用CFD计算软件FINE/Marine,进行数值计算。
3.3 优化结果分析通过对2套优化方案的分析,最终选择方案1的优化结果作为最终的模型,并进行分析。
1) 设计变量结果分析
从表5并结合敏感度分析的结果可知,优化目标与水翼安装角度负相关,与三角形侧鳍安装角度呈正相关。对于该船体水翼和鳍的安装角分别为−9.75°和−3.125°时,船体阻力最小。同时,鳍的安装高度与优化目标呈负相关,所以适当增加鳍的安装高度,有助于减少阻力。
|
|
表 5 水翼和鳍优化前后设计变量对比 Tab.5 Comparison of design variables before and after optimization of hydrofoil and bear |
2) 优化前后阻力对比
在2.02 m/s和1.77 m/s两个航速下阻力成分对比如表6所示。安装尾压浪板、鳍与水翼后的模型,较原始船型和只添加尾压浪板船体,总阻力都有所增加。其中与只添加尾压浪板船体阻力相比,在2.02 m/s航速下,总阻力、剩余阻力、摩擦阻力,分别增加了4.1%,8.4%,2.5%,都呈现增加趋势 。在1.77 m/s的速度下,总阻力和摩擦阻力有增加趋势,增长率分别为4.1%和11.1%,而剩余阻力减少10%。说明鳍与水翼的安装,会引起船体总阻力的增加,在一定航速下,鳍与水翼可以抑制兴波,进而减少剩余阻力。
|
|
表 6 船体阻力对比 Tab.6 Comparison of hull resistance |
在对添加附体结构优化时,优化目标是以设计航速下的静水阻力,并没有考虑波浪状况下船体的水动力性能,因此对优化后添加附体的船体模型进行试验工况下的规则波数值模拟,航速选取1.52m/s,λ/L分别为0.49,0.54,0.60,0.66,0.74,0.93,1.06七个工况。表7给出了安装附体优化前后的对比结果。
|
|
表 7 规则波条件下船体安装附体前后对比 Tab.7 Comparison of the hull before and after the appendage is installed under regular wave conditions |
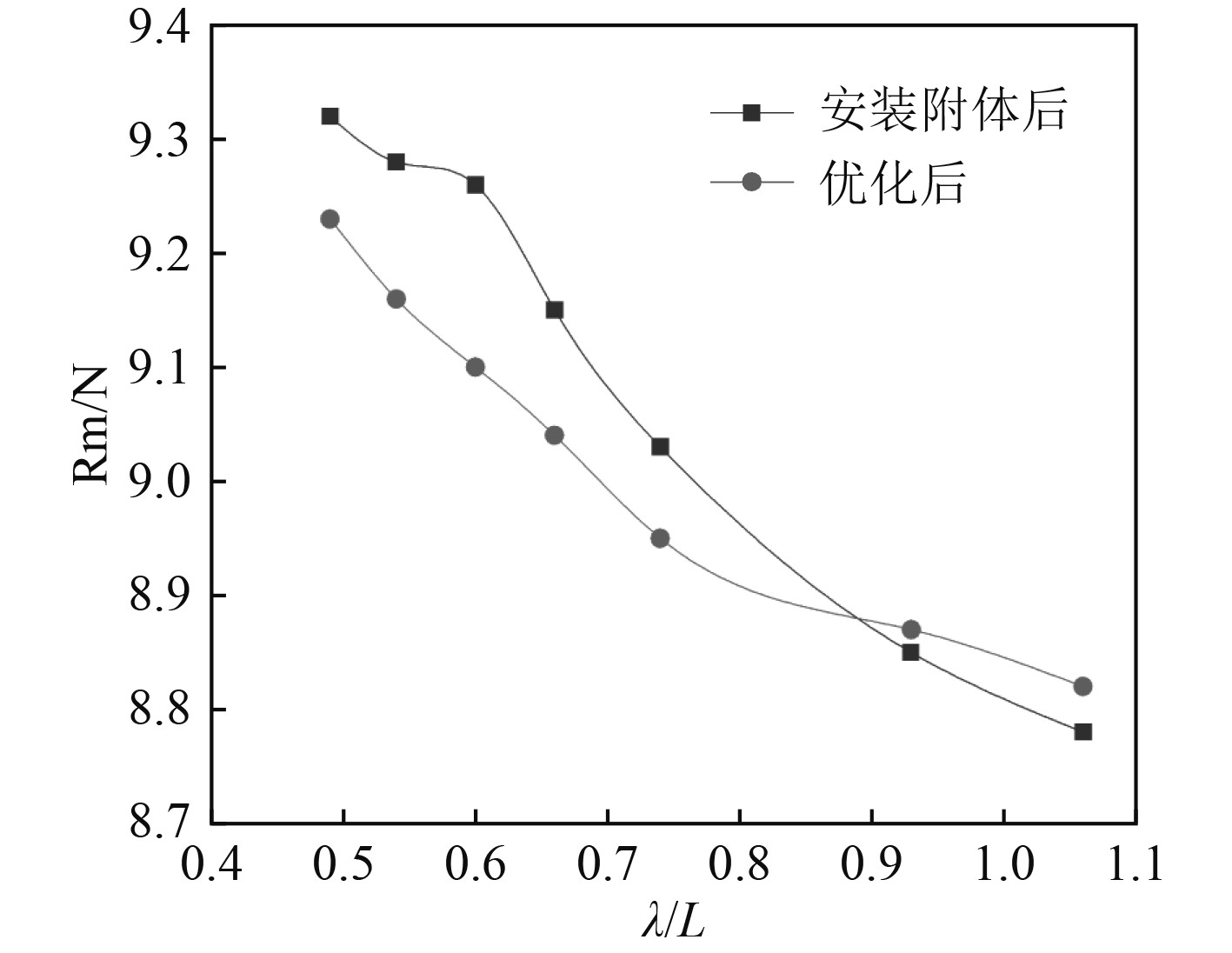
由图7~图11可知,在规则波条件下,安装附体后,波浪增阻增大,当λ/L大于0.9时,波浪增阻小于优化后。安装附体后船体的升沉与纵摇得到改善,船体附体后在规则波条件下耐波性得到改善,所以不需要在规则波下继续优化。
|
图 7 规则波条件下安装附体前后阻力对比 Fig. 7 Comparison of resistance before and after installation of appendages under regular wave conditions |
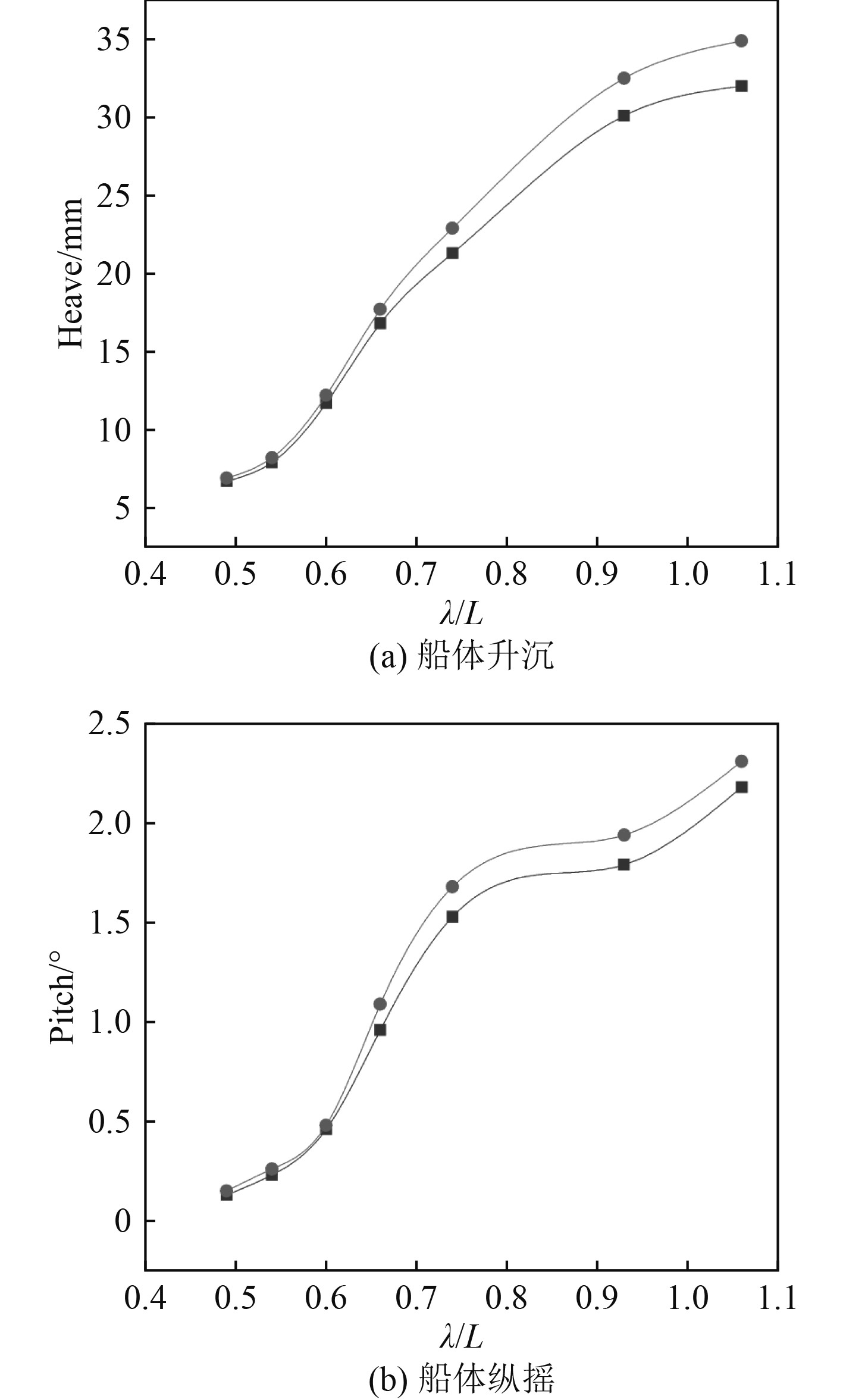
|
图 8 规则波条件下安装附体前后升沉与纵摇对比 Fig. 8 Heave and pitch alignment before and after the attachment is installed under regular wave conditions |

|
图 9 原始船型自由液面波形图 Fig. 9 The waveform of the free surface of the original ship |

|
图 10 添加尾压浪板后自由液面波形图 Fig. 10 Waveform of free liquid surface after adding tail pressure wave plate |

|
图 11 添加尾压浪板、水翼与鳍后自由液面波形图 Fig. 11 waveform of free liquid surface after adding tail pressure wave board, hydrofoil and fin |
通过对原始船型安装尾压浪板并进行优化,可以看出,尾压浪板对降低船体阻力有明显的效果,在速度为2.02 m/s和 1.77 m/s的航速下,总阻力较原始船型减少率相近,均为2.5%。将添加尾压浪板并优化后的模型,在球鼻首上添加了三角形侧鳍和船首位置安装了水翼,结果表明安装完水翼和三角形侧鳍会导致船体总阻力的增加,但鳍与水翼可以通过抑制兴波,减小剩余阻力。在规则波条件下,进行数值模拟,发现安装尾压浪板、鳍与水翼附体后,波浪增阻增大,当λ/L超过0.9时,波浪增阻小于优化后,安装附体后船体,升沉与纵摇以及耐波性均得到不同程度的改善。
| [1] |
李创兰. 基于动网格的船舶及其附体阻力预报研究[D]. 哈尔滨: 哈尔滨工程大学, 2015.
|
| [2] |
刘英和, 王桂云, 王侨, 等. 尾压浪板对穿浪双体船耐波性影响[J]. 中国水运(下半月), 2016, 16(2): 12-13+163. |
| [3] |
蒋一, 孙寒冰, 邹劲, 等. 变角度尾压浪板对断级滑行艇阻力性能的影响[J]. 上海交通大学学报, 2017, 51(3): 320-325. |
| [4] |
NAITO, S, HIGAKI, S, KATO, J, et al. Reduction of added resistance and thrust generation by using a bow wing in waves[J]. Journal of KSNAJ, 2011, 235: 79–89.
|
| [5] |
ULYSSES, A. P. Study of the sea behavior of a marine-class ship equipped with anti-pitching bow fins [R]. DTMB Report 1084, 1958
|
| [6] |
朱航, 游贵标, 孙义平, 等. ZHU Hang, YOU Gui-biao, SUN Yi-ping, ZHANG Chunlong, ZHANG Xian-yu-[J].造船技术, 2015(4):
|
| [7] |
刘强, 张恒, 彭必业, 等. 改进Sobol’方法在船型优化模型中的应用[J]. 船舶工程, 2020, 42(2): 44-48+69. |
| [8] |
LI Shaodong, DU Zhijiang, YU Hongjian, et al. A Robust multi-circle detector based on horizontal and vertical Search analysis fitting with tangent direction[J]. International Journal of Pattern Recognition and Artificial Intelligence, 2019, 33(4).
|
| [9] |
GOLDBERG D E. Genetic algorithms in search optimizaion and machine learning [M]. MA: Addison-Wesley Publishing Company Inc, 1989.
|
 2021, Vol. 43
2021, Vol. 43
