0 引　言

在船舶自动避碰研究的早期阶段，更多的是研究如何规划出一条路线使船舶避免发生碰撞，对于国际海上避碰规则（International Regulations for Preventing Collisions at Sea, COLREGS，以下简称《规则》）的要求基本不考虑，或者考虑很少。例如：用于辅助两船避碰决策LOSCAN算法^[1]；基于改进ARC-Theta*的算法^[2]；用于开阔水域内船舶路径规划的遗传算法^[3]，人工免疫算法^[4]，遗传算法^[5]等。上述算法都只是在寻找最优路径，在路径的规划并没有考虑《规则》要求。近年来，更多的学者在研究船舶自动避碰的同时考虑了《规则》的要求，如速度障碍法^[6]、粒子群算法^[7]、蚁 ${\text{CRI = }}0$ 群优化算法^[8]、多智能体^[9]，以及混合智能系统如拟人智能避碰决策^[10]等，但部分算法未能严格遵守《规则》，如日本东京商船大学实验船“汝路丸”号^[11]上的船舶避碰决策系统，该系统在规划最优避碰航线时，并没有按照《规则》第十六条的要求，采取大幅度的避让措施；部分算法只能处理其他船舶航向和航速不变的情况，没有考虑船舶间可能发生的避碰行动不协调问题^[8,12]。基于偏心膨胀（Eccentric Expansion）的动态避障算法^[13]通过船舶偏心膨胀法来保证船舶安全和《规则》之间的平衡，但会导致部分会遇局面下的避碰行动背离《规则》。此外，对于更复杂的多船自动避碰越来越受到重视，基于深度强化学习(DRL)的多船自动避碰算法^[14]将人类的避碰经验与《规则》通过转换为航行限制多边形或线而结合起来，实现开阔水域多船避碰；基于AIS的海上多船行驶自动避碰系统^[15]依靠船舶行动特征进行避碰控制,但需要可靠的海上无线通信手段作为支撑。

1986年，Khatib^[16]首次提出人工势场法（Artificial Potential Field，APF），并应用于路径规划中。其仿照物理学中的电势场和电势的概念，建立一个虚拟势场，目标点对智能体产生引力势场，障碍物产生斥力势场，2种势场叠加后得到全局势场，智能体沿着全局势场负梯度的方向实现避障和路径规划，最终到达目标点。Ge等^[17-18]在2000年通过重新设计势场函数解决了目标不可达问题，并于2002年提出了能够应用于动态环境的势场函数。目前，成熟的APF方法在机器人、船舶等路径规划和避碰领域应用已经比较广泛。韩君^[19]利用人工势场技术,使船员能够快速对导航的位置信息进行监测,实现船舶自动化智能航行功能。Du^[20]在无人机实时避碰中改进了势场力，势场力的大小可根据周围障碍物的危险程度自动调整。障碍物的危险程度取决于无人机与障碍物之间的相对位置、速度和飞行姿态，保留传统人工势场相对位置的斥力，增加转向力改变无人机的飞行方向，加快了避碰速度。Xu^[21]提出了一种基于碰撞锥分层人工势场的动态避碰算法，为减少避免碰撞的无效行为，根据危险系数的大小，将势场划分为4层，并引入具有风险检测功能的碰撞锥，以相对距离和相对速度为变量建立碰撞风险模型，基于速度力矩、引力和斥力共同作用，改变USV的速度和方向。吕红光^[22-23]提出一种基于改进人工势场法的实时路径规划方法，其规划路径时间短，计算时间几乎不受障碍物数量和目标船随机航向变化的影响，并有解决多船紧急碰撞的潜力。其提出的路径引导的混合人工势场法，考虑了动态和静态障碍，将规划分为离线阶段和在线阶段，消除了静态障碍物所产生的局部极小值，并基于不同条件下的斥力，增加风险判断改进避碰算法，提出一种实时路径规划方法，解决当目标附近有障碍物船舶无法到达的问题。以上方法对于APF计算时间长、局部最小、目标不可达等的问题有了较好的优化，但在《规则》遵守尤其是在避让责任和紧迫局面的判断问题上有所欠缺。

本文重点针对文献[23]进行更进一步的研究工作，将船舶会遇态势判断机制和船舶碰撞危险度引入到势力场的构建中，解决判断避让责任和紧迫局面的问题，采取避让措施的过程中更严格遵守《规则》的要求，解决传统人工势场法在船舶自动避碰应用中无法判断避让责任和紧迫局面的问题。

1 船舶碰撞危险度

船舶碰撞危险度（Collision Risk Index，CRI）是度量船舶发生碰撞概率大小的参数，其取值为[0,1]，当CRI=0时，此时不存在碰撞危险，船舶不会发生碰撞事故；当CRI=1时，说明此时两船不能在安全距离内驶过。当CRI达到以及超过某一阈值时，让路船应采取避碰措施；若让路船没有采取合理的避让措施，使得CRI继续扩大，当达到相应阈值时，让路船和直航船都应该采取避碰措施来避免碰撞。

本文首先分别计算空间碰撞危险度（Space Collision Risk，SCR）和时间碰撞危险度（Time Collision Risk ，TCR），再将SCR和TCR合成，得出最终的船舶碰撞危险度CRI。

空间碰撞危险度反映的是2艘船舶在空间距离上的紧迫程度，根据最近会遇距离( Distance of Close Point of Approaching，DCPA)、船舶安全会遇距离 ${{d}_1}$ 以及船舶安全通过距离 ${{d}_2}$ 的关系来确定。其空间碰撞危险度SCR的隶属函数 $udt$ 如下式：

$ udt = \left\{ \begin{array}{*{20}{c}} 1\text{，}&{\left| {DCPA} \right| \leqslant {d_1}}\text{，} \\ {{{\left[ {\dfrac{{{d_2} - \left| {DCPA} \right|}}{{{d_2} - {d_1}}}} \right]}^{3,03}}}\text{，}&{{d_1} \leqslant \left| {DCPA} \right| \leqslant {d_2}}\text{，} \\ 0\text{，}&{{d_2} \leqslant \left| {DCPA} \right|} \text{。} \end{array} \right. $

(1)

式中： ${{d}_1}$ 为船舶安全会遇距离，根据Goodwin的船舶领域模型计算； ${{{d}}_2}$ 为船舶安全通过距离，在本文中 ${{d}_2}{=}2{{d}_1}$ 。

$ {d_1} = \left\{ \begin{aligned} &{1.1 - \frac{{Tr}}{{{{180}^ {\circ} }}} \times 0.2\text{，}}&{{0^{\circ} } \leqslant Tr \leqslant {{112.5}^ {\circ} }}, \\ &{1.0 - \frac{{Tr}}{{{{180}^{\circ} }}} \times 0.4}\text{，}&{{{112.5}^{\circ} } \leqslant Tr \leqslant {{180}^{\circ} }}, \\ & {1.0 - \frac{{{{360}^{\circ} } - Tr}}{{{{180}^ {\circ} }}} \times 0.4}\text{，}&{{{180}^{\circ} } \leqslant Tr \leqslant {{247.5}^ {\circ} }}, \\ & {1.1 - \frac{{{{360}^{\circ} } - Tr}}{{{{180}^ {\circ} }}} \times 0.4}\text{，}&{{{247.5}^ {\circ} } \leqslant Tr \leqslant {{360}^ {\circ} }} \text{。} \end{aligned} \right. $

(2)

式中： ${T_r}$ 为来船的相对方位。

时间碰撞危险度反映的是2艘船舶在时间上的紧迫程度，根据最近会遇时间( Time of Close Point of Approaching，TCPA)与 ${t_1}$ 和 ${t_2}$ 的关系来确定。当来船与本船距离为12 n mile时（ ${t_2}$ ）TCR为0，当直航船所处位置到其最晚施舵点处的时间（ ${t_1}$ ）为0时，TCR为1。其隶属度函数 $utt$ 如下式：

当 ${\text{TCPA > 0}}$ 时，隶属度函数

$ utt = \left\{ {\begin{array}{*{20}{c}} 1\text{，}&{TCPA \leqslant {t_1}}, \\ {{{\left[ {\dfrac{{{t_2} - TCPA}}{{{t_2} - {t_1}}}} \right]}^{3,03}}}\text{，}&{{t_1} \leqslant TCPA \leqslant {t_2}}, \\ 0\text{，}&{{t_2} \leqslant TCPA}\text{；} \end{array}} \right. $

(3)

当 ${\text{TCPA}} \leqslant {\text{0}}$ 时，隶属度函数

$ utt = \left\{ {\begin{array}{*{20}{c}} 1\text{，}&{|TCPA| \leqslant {t_1}}, \\ {{{\left[ {\dfrac{{{t_2} + TCPA}}{{{t_2} - {t_1}}}} \right]}^{3.03}}}\text{，}&{{t_1} \leqslant |TCPA| \leqslant {t_2}}, \\ 0\text{，}&{{t_2} \leqslant |TCPA|}\text{。} \end{array}} \right. $

(4)

式中： ${t_1} = \dfrac{{\sqrt {DLM{A^2} - DCPA_{DLMA}^2} }}{{Vr}}$ ； ${t_2} = \dfrac{{\sqrt {{{12}^2} - DCP{A^2}} }}{{Vr}}$ 。

${DLMA}$ 为本船的最晚施舵距离， $DCP{A_{DLMA}}$ 为最晚施舵点处的 ${DCPA}$ 值。

CRI的计算模型如下式：

$ CRI=\left\{\begin{array}{*{20}{c}}0\text{，}&{udt}=0\text{或}{utt=0},\\ {\min}(udt,utt)\text{，}&udt\ne 0\text{，}utt\ne 0\text{。}\end{array}\right. $

(5)

2 船舶会遇态势划分

在航海实践中，船舶会遇态势的判断是避碰的重要组成部分，船舶驾驶员需要根据《规则》来分析会遇态势，判断船舶的让路责任，并依据《规则》和船员通常做法来进行相应的避碰行动。

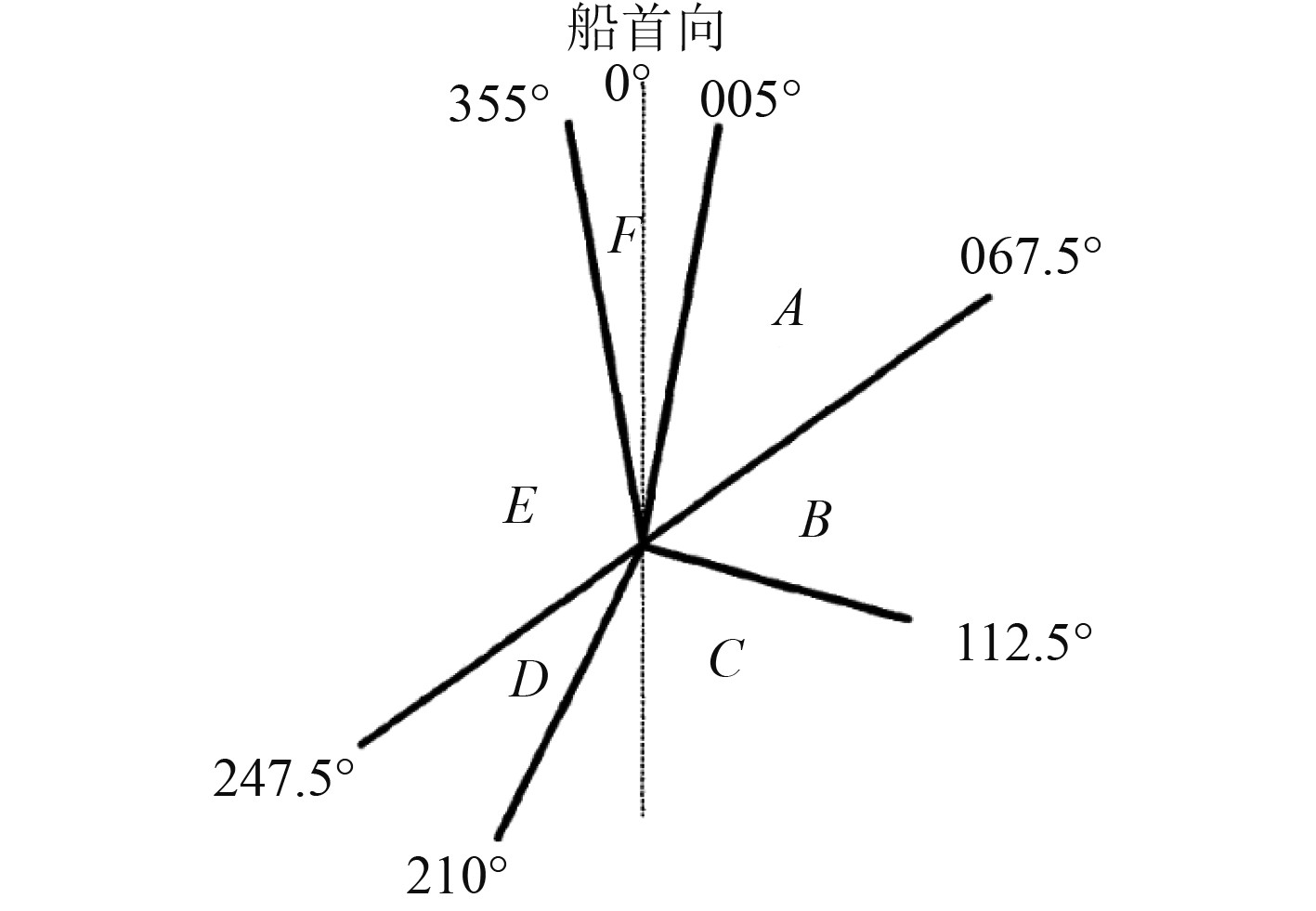
本文将两船的会遇态势划分为6个区域，具体划分如图1所示。

本船应当采取的行动如表1所示。

其中，当本船为直航船，目标船为让路船，并且目标船没有采取合理的避让措施保证两船在安全距离驶过时，按照《规则》规定，本船应采取相应避让措施，避免发成碰撞。

3 人工势场法

将船舶会遇态势的判断及船舶碰撞危险度CRI加入到人工势场中，使其能够清晰地判断会遇态势，划分出避碰责任，并按照《规则》的要求采取避碰行动。

3.1 引力场构建及引力计算

首先构建全局引力势场函数，引力势场 ${U_{att}}(p)$ 定义为我船与目标点之间的相对距离即 $\rho ({p_{os}},{p_{ts}})$ 的函数：

$ {U_{{{att }}}}(p) = \frac{1}{2}{\varepsilon _p}{\rho ^2}\left( {{p_{{\text{os }}}},{p_g}} \right), $

(6)

其中， ${\varepsilon _p}$ 为正比例权重系数。

对 ${U_{att}}(p)$ 求负梯度得到引力 ${F_{att}}(p)$ 的表达式为：

$ {F_{att}}(p){\text{ }} = {\varepsilon _p}\rho \left( {{p_{os}},{p_g}} \right){n_{og}}\text{。} $

(7)

其中， ${n_{og}}$ 为单位矢量，方向是本船位置 ${p_{os}}$ 指向目标点 ${p_g}$ 的位置。

3.2 斥力场分区

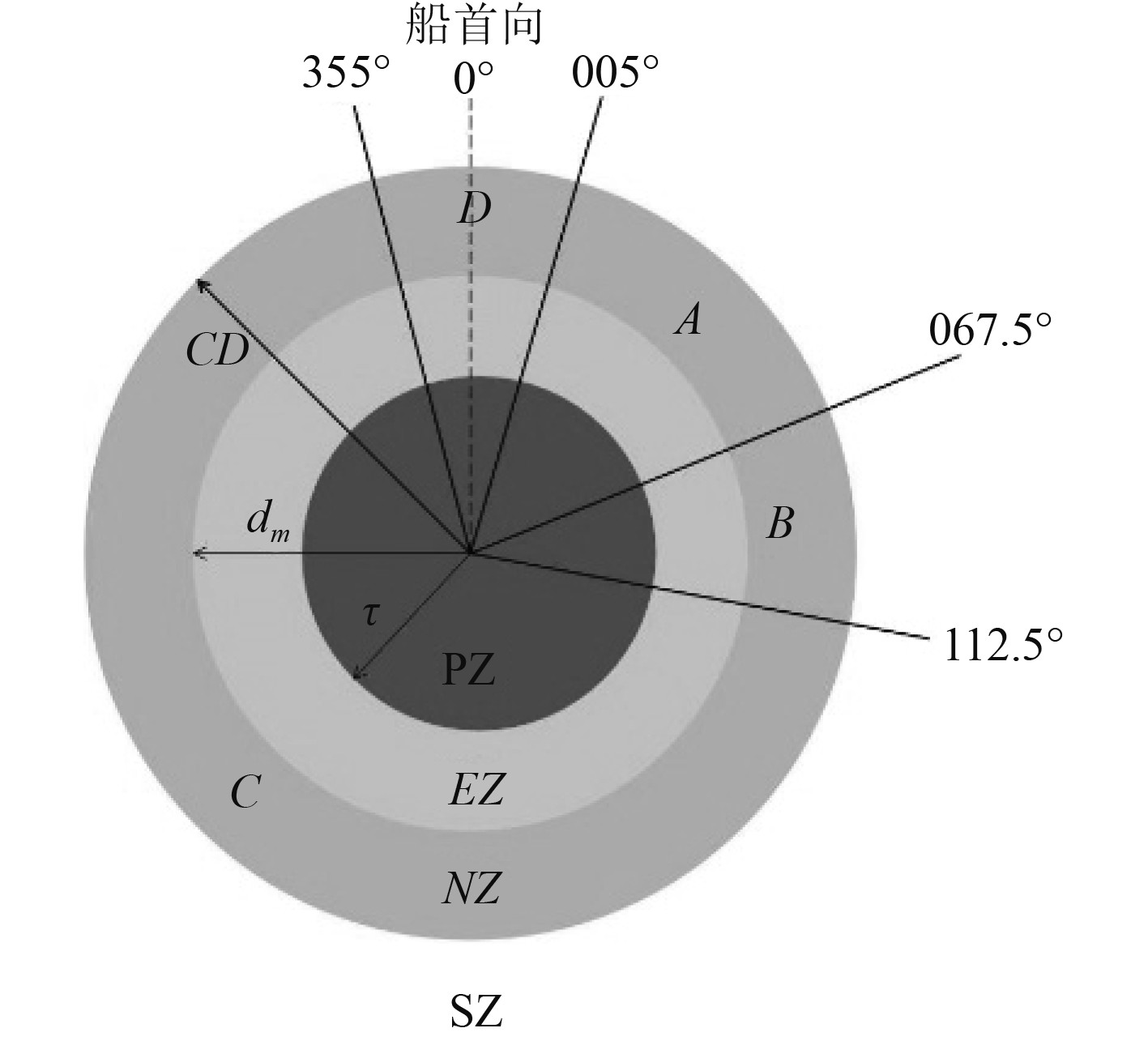
以本船为中心，根据本船到其他船舶或障碍物的距离和船舶碰撞危险度等因素，将斥力场划分为以下4个区域，如图2所示。

安全区：其他船舶或障碍物与本船的距离d大于势场检测距离CD的区域，该区域内没有斥力作用；

协商避碰区：其他船舶或障碍物与本船的距离d>d_m而 $\leqslant {\rm{CD}} $ 的区域，当满足判断条件 $TCPA\geqslant 0，$ $ {\text{C}}_{1}\leqslant {{CRI < {\rm{C}}}}_{2}$ 时，产生斥力场，

在协商避碰区内，若来船在A，B和D区内，本船为让路船或为同等避让责任，本船应采取避碰行动来避免碰撞，若来船在C区内，我船为直航船，应保向保速，并时刻观察来船行动。

紧急避碰区：他船（障碍物）与本船的距离d大于 $\tau $ 小于d_m的区域，在满足 ${CRI} \geqslant {{\text{C}}_2}$ 时，我船应采取紧急避碰行动，该行动可以暂时违背《规则》。

禁止区：以本船为中心，以 $\tau $ 为半径的圆形区域，该区域禁止任何他船或障碍物进入， $\tau $ 可根据船舶尺度进行相应调整。

SZ:安全区， $d > CD$

图中，d为我船与其他船舶或障碍物距离，d_m为我船到其他船舶的安全距离，CD为碰撞危险检测距离。

3.3 斥力场构建

在文献[23]的基础上，对其斥力势场模型进行改进，改进模型如下：

当满足 $ {v_{ts}} \ne 0,{d_m} < d \leqslant CD,TCPA \geqslant 0 $ , ${{C}_1} \leqslant CRI < $ $ {{C}_2}$ , $ 0 \leqslant {T_r} \leqslant {67.5^ \circ } $ 或 $ {355^ \circ } \leqslant {T_r} < {360^ \circ } $ 时，来船在A区和D区，本船为让路船或同等避让责任，此时斥力势场为：

$ {U}_{rep}（p,v)={\eta }_{d}{R}_{ts}({e}^{{\theta }_{m}-\theta }-1)\left(\frac{1}{d-{d}_{m}}-\frac{1}{{\rho }_{0}}\right){d}_{g}^{2}, $

(8)

当满足 $ {v_{ts}} \ne 0,{d_m} < d \leqslant CD,TCPA \geqslant 0 $ , ${{C}_1} \leqslant CRI < $ $ {{C}_2}$ , $ {67.5^ \circ } < {T_r} \leqslant {112.5^ \circ } $ , $ {v_t}/{v_0} > 0.95 $ 时，来船在B区，本船为让路船，按照《规则》和船员通常做法应右转避让，此时斥力势场为：

$ {U}_{rep}（p,v)={\eta }_{d}{R}_{ts}({e}^{{\theta }_{m}-\theta }-1)\left(\frac{1}{d-{d}_{m}}-\frac{1}{{\rho }_{0}}\right){d}_{g}^{2}, $

(9)

当满足 $ {v_{ts}} \ne 0,{d_m} < d \leqslant CD,TCPA \geqslant 0 $ , ${{C}_1} \leqslant CRI < $ $ {{C}_2}$ , $ {67.5^ \circ } < {T_r} \leqslant {112.5^ \circ } $ , $ {v_t}/{v_0} \leqslant 0.95 $ 时，来船在B区，本船为让路船，按照《规则》和船员通常做法应右转避让，此时斥力势场为：

$ {U}_{rep}（p,v)=-{\eta }_{d}{R}_{ts}({e}^{{\theta }_{m}-\theta }-1)\left(\frac{1}{d-{d}_{m}}-\frac{1}{{\rho }_{0}}\right){d}_{g}^{2}, $

(10)

当满足 $ {v_{ts}}{\text{ = }}0,{d_m} < d \leqslant CD,\theta < {\theta _m} $ 时，本船需避让障碍物，此时斥力势场为：

$ {U}_{rep}（p,v)=\frac{1}{2}{\eta }_{s}{R}_{ts}{\left(\frac{1}{d-\tau }-\frac{1}{{\rho }_{0}}\right)}^{2}{d}_{g}^{2}, $

(11)

当满足 $ \tau < d \leqslant {d_m},CRI \geqslant {{\text{C}}_2} $ 时，本船需进行紧急避让，此时斥力势场为：

$ {U}_{rep}（p,v)={\eta }_{e}{R}_{ts}\left[{\left(\frac{1}{d-\tau }-\frac{1}{{\rho }_{0}}\right)}^{2}+{(\Vert {v}_{ot}\Vert \mathrm{cos}\theta )}^{2}\right]{d}_{g}^{2}\text{。} $

(12)

当 $d > CD$ 或来船在C区且 ${CRI} < {{\text{C}}_2}$ 时，不做定义即斥力为0。

式中： ${{C}_1}$ 和 ${{C}_2}$ 分别为进行协商避碰和紧急避碰的CRI阈值； ${\eta _d}$ 为在协商避碰区内针对其他动态船舶的斥力场系数； ${\eta _{\text{s}}}$ 为在协商避碰区内针对障碍物的斥力场系数； ${\eta _e}$ 为在紧急避碰区内的斥力场系数； ${R_{ts}}$ 为本船膨化圆半径； ${\theta _m}$ 为最大相对位置线夹角； $\theta $ 为本船和他船相对位置线 ${p_{ot}}$ （ ${p_{ot}} = {p_{ts}} - {p_{os}}$ ）与相对速度线 ${v_{ot}}$ （ ${v_{ot}} = {v_{os}} - {v_{ts}}$ ）之间的夹角。

3.4 斥力计算

根据不同的分区，得到斥力表达式如下式：

$\begin{split}&Frep(p,v)=\\&\left\{\begin{array}{*{20}{l}}{F}_{rdA}={F}_{rd1}+{F}_{rd2}+{F}_{rd3}, {v}_{ts}\ne 0,\\{d}_{m} < d\leqslant CD,TCPA\geqslant 0，\text{ }{C}_{1}\leqslant CRI < {C}_{2},\\ 0\leqslant {T}_{r}\leqslant {67.5}^{\circ }或{355}^{\circ }\leqslant {T}_{r} < {360}^{\circ },\\ {F}_{rd{B}_{1}}={F}_{rd1}+{F}_{rd2}+{F}_{rd3}, {v}_{ts}\ne 0,\\{d}_{m} < d\leqslant CD,TCPA\geqslant 0，{C}_{1}\leqslant CRI < {C}_{2},\\ {67.5}^{\circ } < {T}_{r}\leqslant {112.5}^{\circ },{v}_{t}/{v}_{0} > 0.95,\\ {F}_{rd{B}_{2}}=-({F}_{rd1}+{F}_{rd2}+{F}_{rd3}), {v}_{ts}\ne 0,\\{d}_{m} < d\leqslant CD,TCPA\geqslant 0，{C}_{1}\leqslant CRI < {C}_{2}, \\{67.5}^{\circ } < {T}_{r}\leqslant {112.5}^{\circ },{v}_{t}/{v}_{0}\leqslant 0.95,\\ {F}_{rs}={F}_{rs1}+{F}_{rs3}, {v}_{ts}=0,{d}_{m} < d\leqslant CD,\theta < {\theta }_{m},\\ {F}_{re}={F}_{re1}+{F}_{re2}+{F}_{re3}, \tau < d\leqslant {d}_{m},CRI\geqslant {C}_{2},\\ \text{未定义}, d > CD或CRI < {C}_{1}\text{及其他情况}\text{。}\end{array}\right.\end{split}$

(13)

具体推导过程和斥力计算方程可参考文献[23]。

3.5 合力计算

本船所受到的斥力为各个障碍船和障碍物对本船所产生的斥力之和为：

$ {F_{rep}} = \sum\limits_{s = 1}^n {{F_{re{p_s}}}} \text{。}$

式中： ${F_{re{p_s}}}$ 为第s个障碍物或者其他船对本船产生的斥力；n为障碍物和其他船舶的总数量。

在本文所建立的势场中，本船所受到的合力为：

$ {F_{total}} = {F_{att}} + {F_{rep}}\text{。} $

(14)

本船会在该合力的作用下采取相应的避碰行动，并向目标点移动，最终到达目标点。

4 仿真实验与分析

在航海实践中，船舶在对遇、交叉相遇和追越局面中有较大的碰撞危险，也是出现最多的局面，因此对本船和他船的对遇、交叉相遇和追越局面进行仿真，并对这3种局面下的避碰仿真进行分析。

在仿真实验中全局参数为： ${\varepsilon _p} = 3\;000\text{，}{\eta _d} = 2\;000$ ， ${\eta _s} = 300\;000\text{，} {\eta _e} = 2\;000\text{，}\tau =0.3{\text{ n mile}}\text{，}{d_m}= 1.5{\text{ n mile}} $ ， ${\ \rho _0}{\text{ = }} 5{\text{ n mile}}\text{，} \max {\text{turn = }}{5^ \circ }{\text{time step = 15 s}}$ 。

$\begin{split} &{\varepsilon _p} = 3\;000\text{，}{\eta _d} = 2\;000\text{，}{\eta _s} = 300\;000\text{，}\\ &{\eta _e} = 2\;000\text{，}\tau {\text{ = }}0.3{\text{ n mile}}\text{，}{d_m} = 1.5{\text{ n mile}}\text{，}\\ &{\rho _0}{\text{ = }}5{\text{ n mile}}\text{，}\\ &\max {\text{turn = }}{5^ \circ }{\text{time step = 15 s}}\text{。}\end{split} $

3种局面仿真实验的初始输入如表2所示，包含他船与本船初始位置，初始速度，其中本船速度（10,10）代表，本船在坐标x轴正方向和y轴正方向速度分量都为10 kn，以及本船的避让行动和避让时与他船距离。

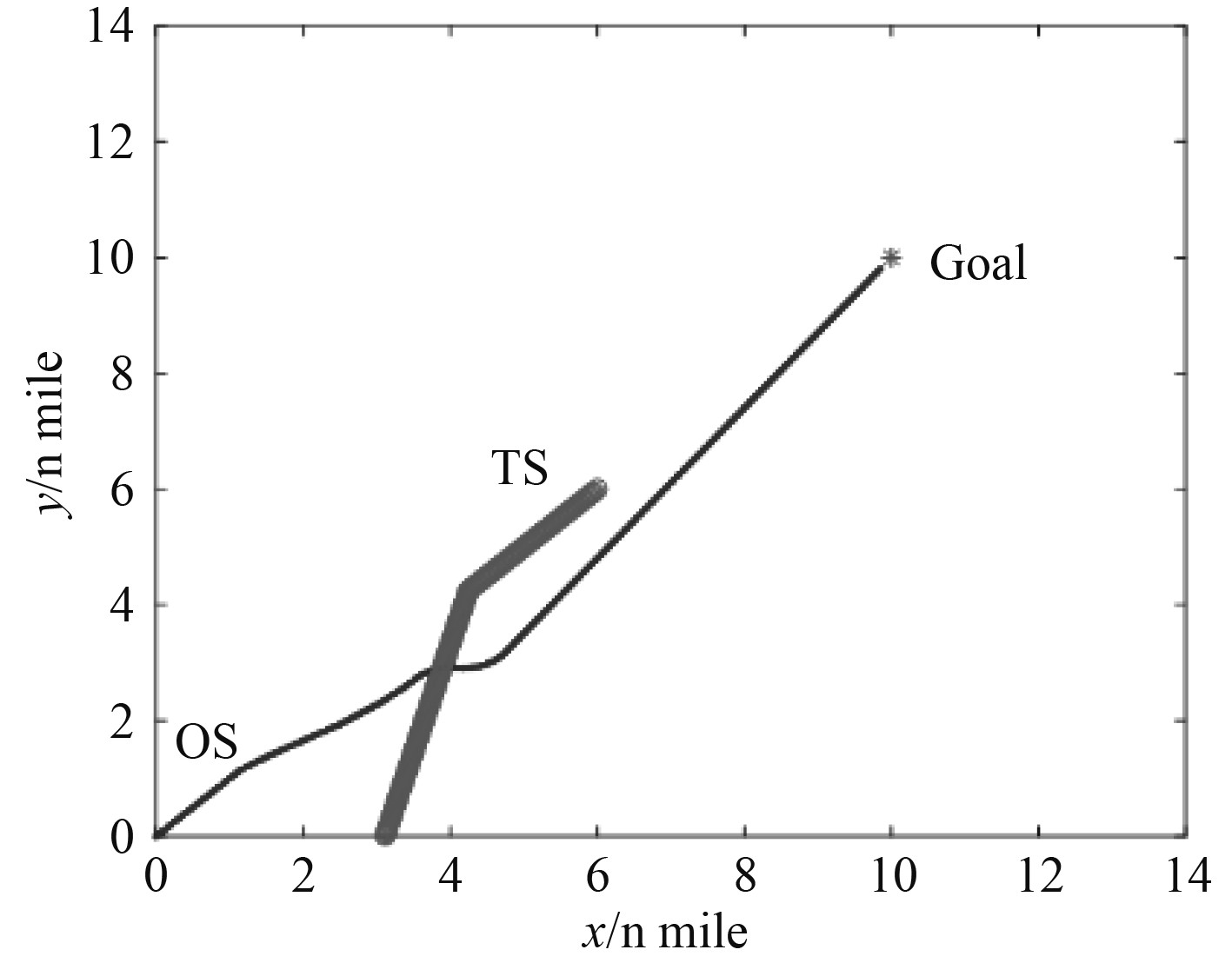
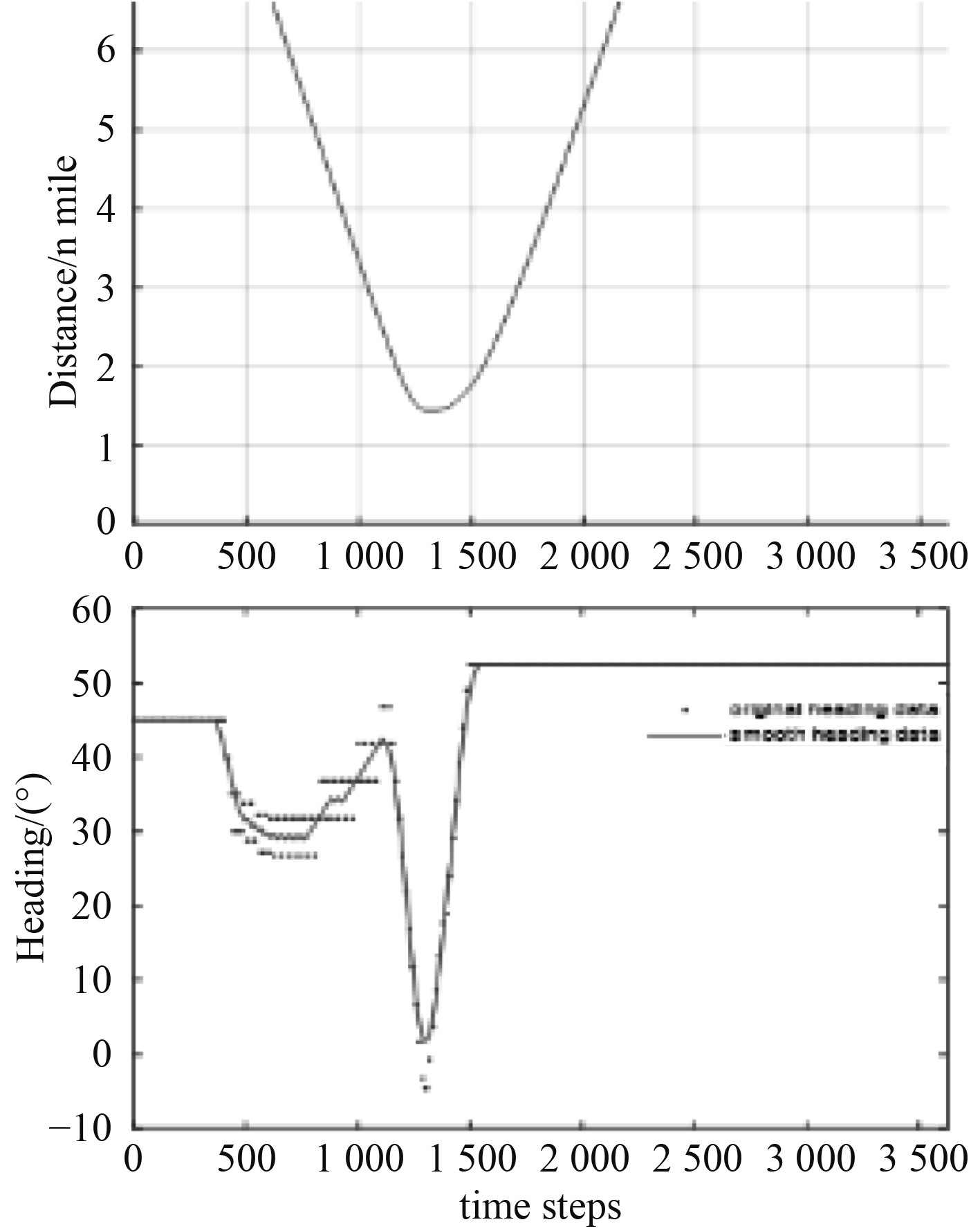
图3中，他船与本船相对方位为0°，位于图1船舶会遇态势划分中的F区，两船构成对遇局面，为同等避让责任，根据《规则》第十四条，两船应各向右转向。在第20步长时，本船采取右转15°的避让措施，准备从他船左舷驶过。但他船并未采取避让措施，并在第70步长时，突然左转30°向本船驶来，算法实时为本船规划右转20°的避让措施，最终本船在距他船1.4 n mile以上距离通过，最终到达目标点。

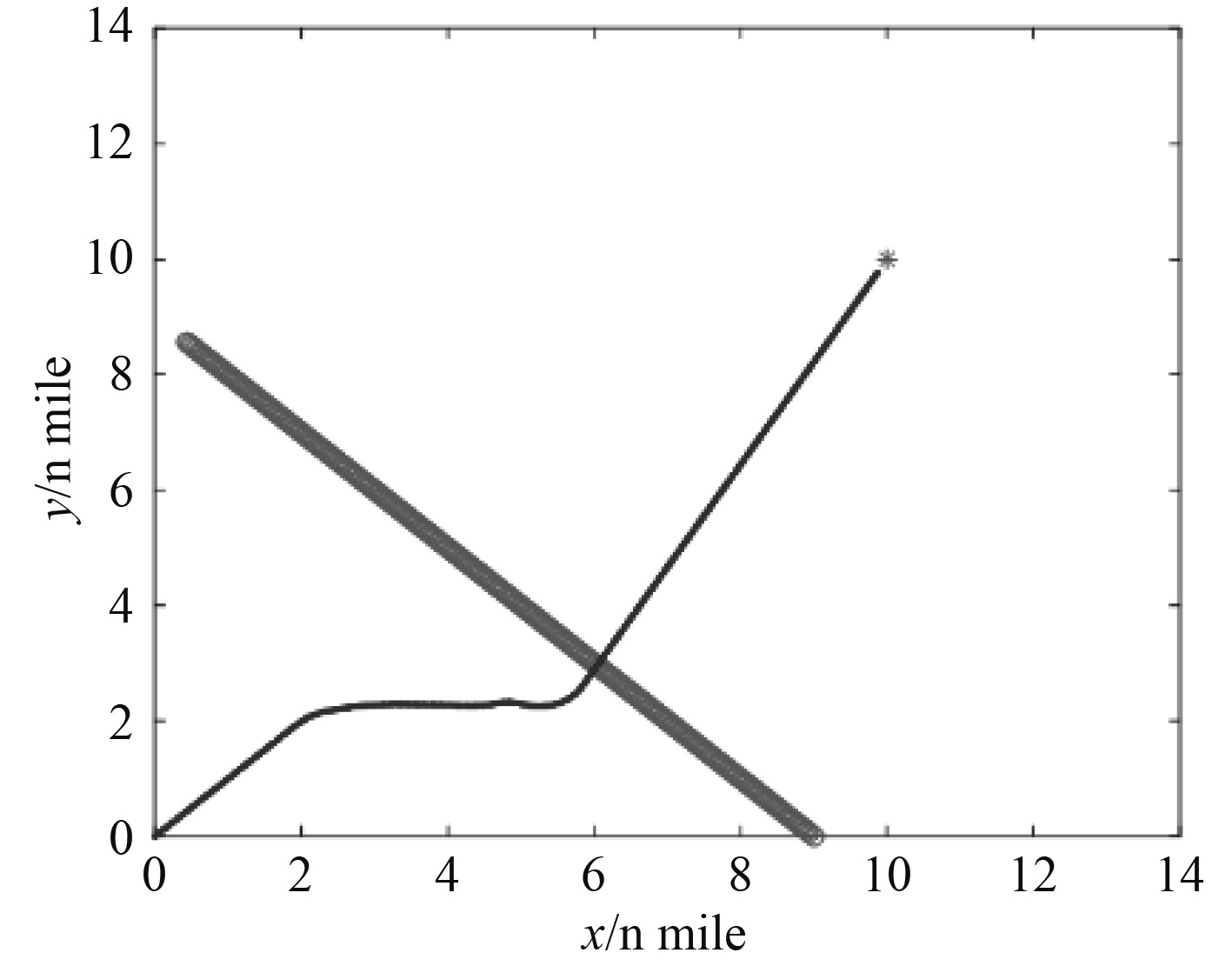
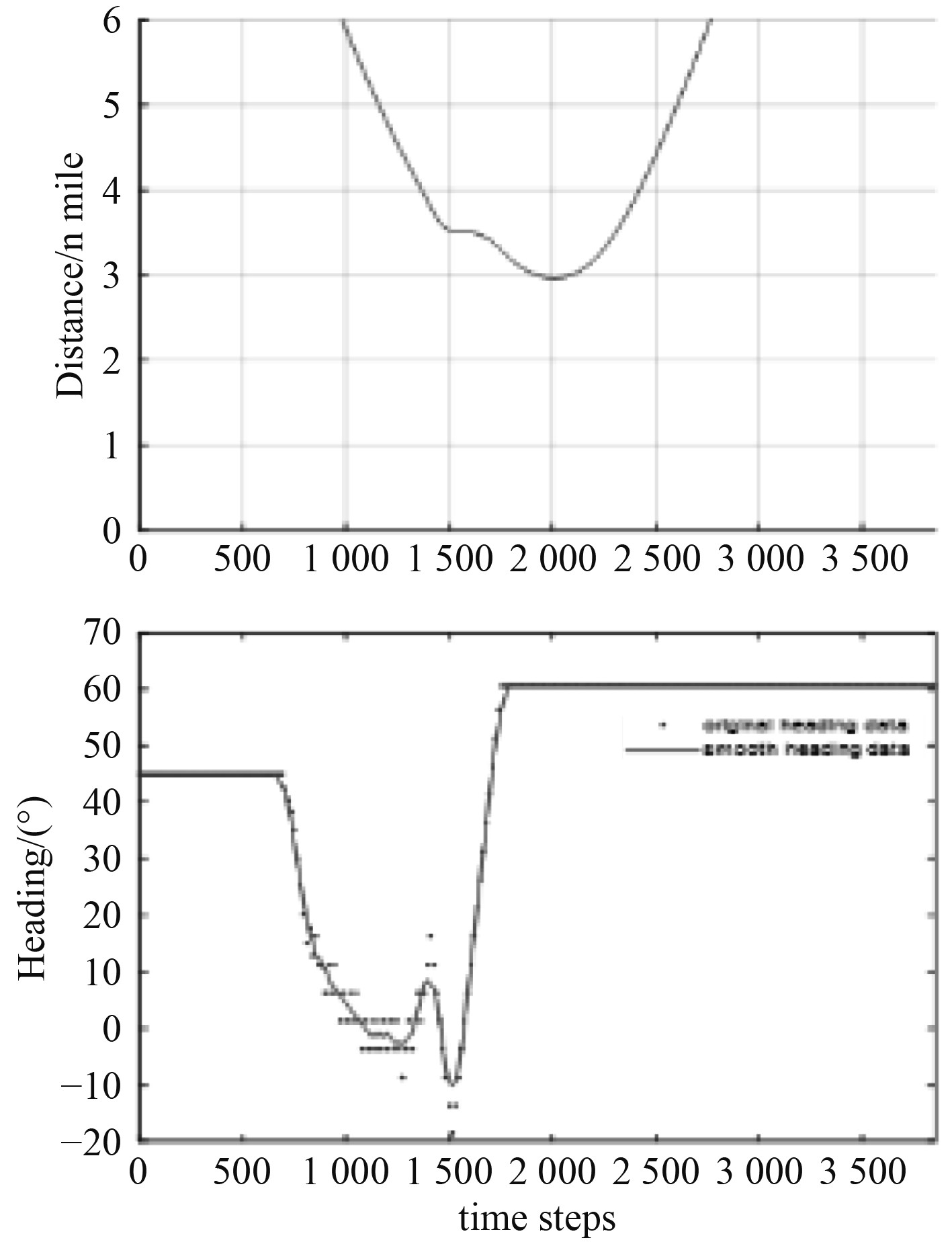
图5中，他船位置位于图1的A区，与本船构成交叉相遇局面。根据《规则》第十五条，本船为让路船，承担让路责任，需要避让他船，并尽量避免横越他船的前方。在第45步长时，两船的CRI超过0.5，我船采取右转45°进行避让，在第105步长时让请他船，在距他船2.8 n mile外驶过，满足《规则》第十六条要求，最终到达目标点。

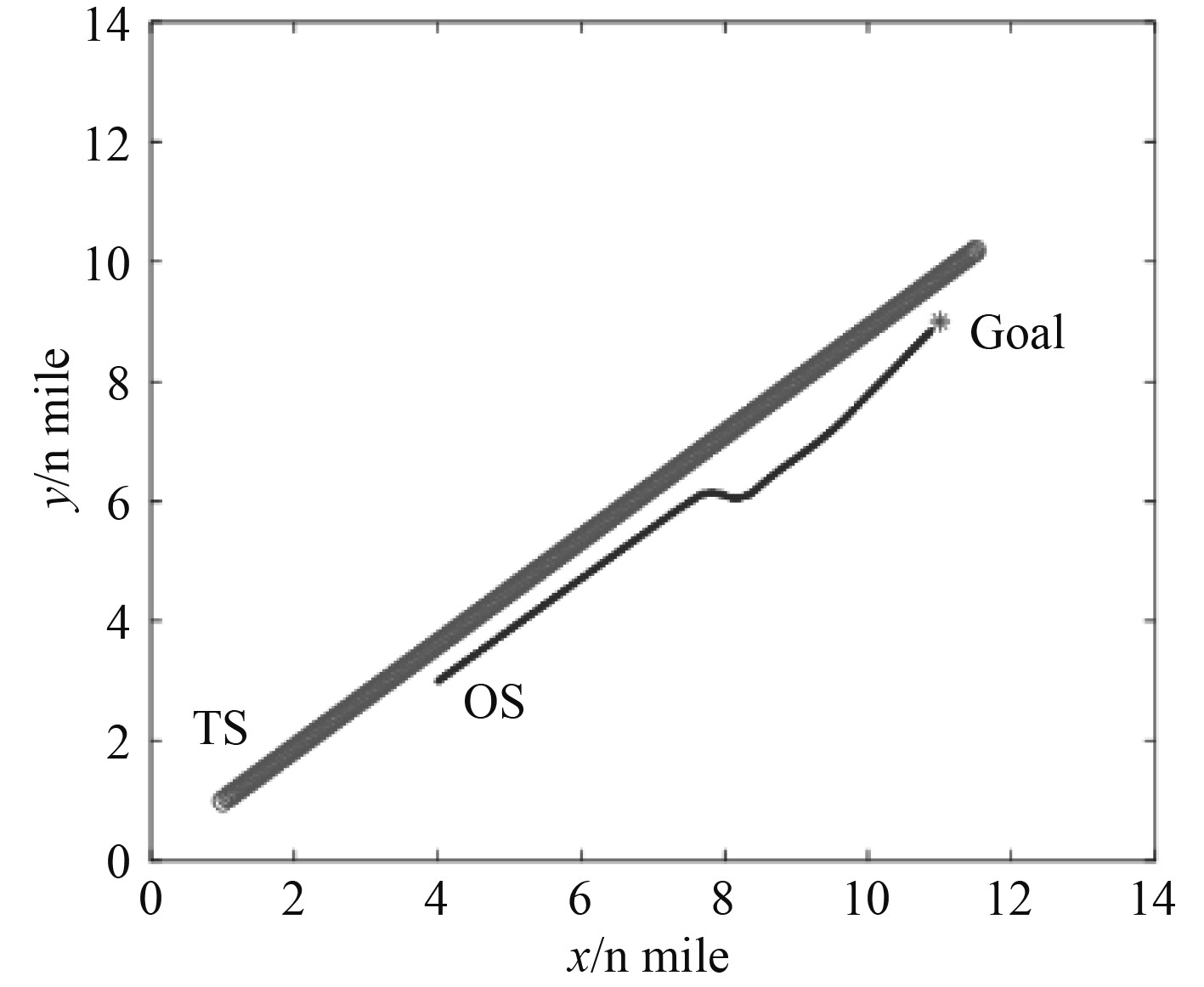
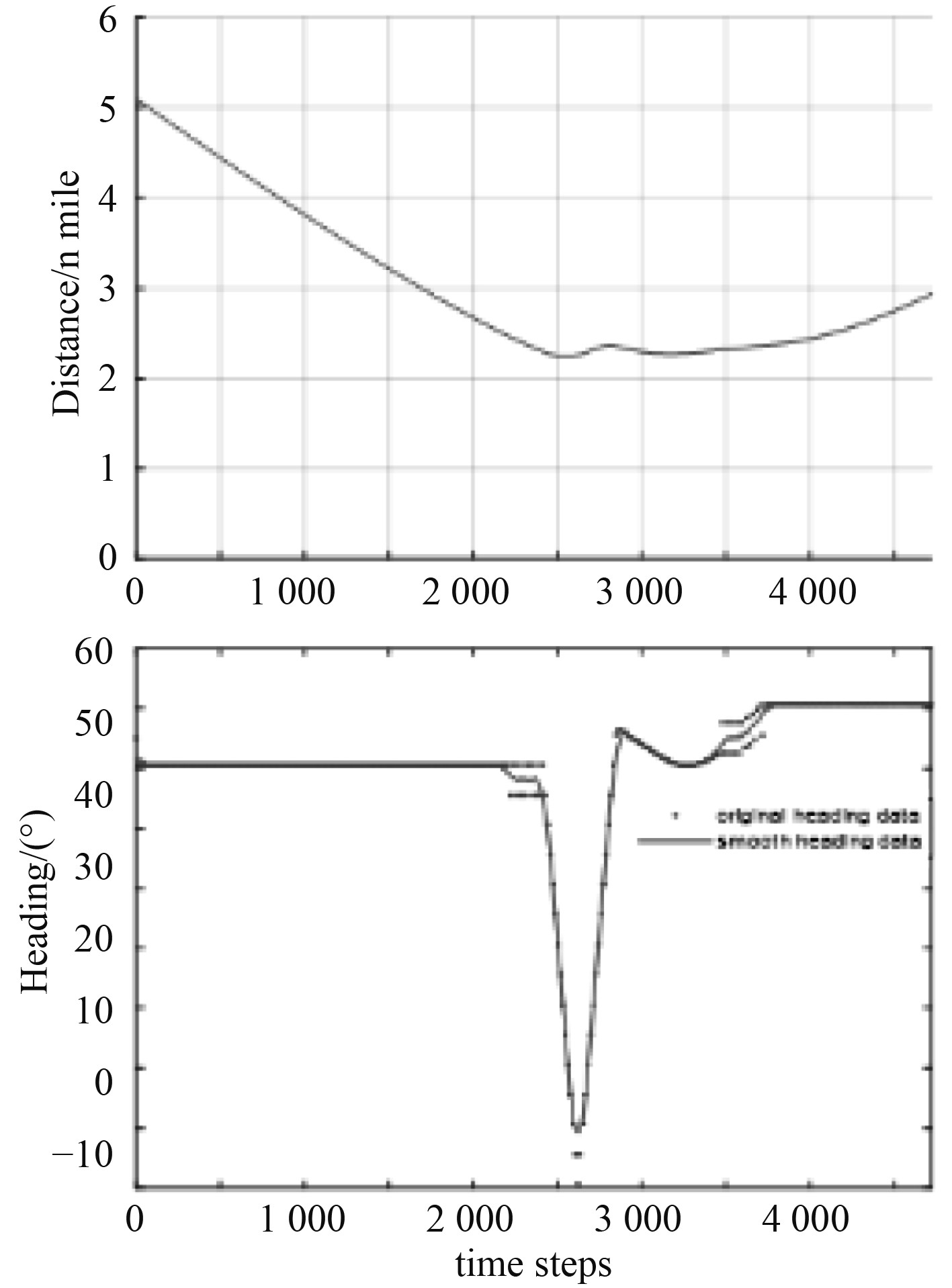
图7中，他船追越我船，位于C区，根据《规则》第十三条，本船为直航船，他船应给本船让路，我船在前期保向保速航行，并实时计算与他船的碰撞危险度，而他船并未采取任何避让措施，在第148步长时，两船的碰撞危险度超过0.9，距离为1.47 n mile，进入紧迫局面，根据《规则》第十七条，直航船此时应采取措施避免碰撞，本船采取右转60°进行避让，使两船在2.2 n mile外驶过，最终到达目标点。

仿真结果表明，本文设计的避碰模型可以准确地判断两船之间的会遇态势，并根据该态势分析出本船应承担的避碰责任，所规划的避碰措施符合《规则》第十四、十五、十六条的要求，安全地让清他船到达目标点。除此以外，在对遇局面仿真中，该模型能够针对他船不协调的避碰行为实时做出相应措施，说明该模型具有应急避碰的能力；在追越局面中，我船所采取的措施符合《规则》第十七条的要求，在他船没有采取相应避碰行动导致产生紧迫局面时，及时采取措施，避免碰撞，说明该模型具有判断是否产生紧迫局面的能力。

5 结　语

本文解决了传统人工势场法在船舶自动避碰应用中无法判断避让责任和紧迫局面的问题，设计的算法能够清晰地判断避让责任和紧迫局面，规划的船舶避让措施更加符合《规则》的要求。在船舶会遇时，通过本船与他船的相对方位来确定当前的会遇态势，进而判断本船的避让责任。仿真实验表明，本文算法可以清晰地判断出本船的避让责任，在对遇局面和交叉相遇局面下，本船有同等避让责任或为让路船，能够及时避让他船；在追越局面下，本船为直航船，能够保向保速航行直至产生紧迫局面。本文通过在算法中引入碰撞危险度，界定了何时产生紧迫局面。仿真实验表明，在追越局面中，他船未能采取合理的避让措施导致碰撞危险度增加，达到阈值，本船判定进入紧迫局面，采取相应避让行动避免碰撞。