2. 江苏科技大学 土木工程与建筑学院,江苏 镇江 212003
2. School of Civil Engineering and Architecture, Jingsu University of Science and Technology, Zhenjiang 212003, China
潜水器是海洋勘查与深海科研的重要工程装备。作为潜水器的组成部分,耐压壳体起着维护潜水器内部设备正常工作和保证人员安全的重要作用,耐压壳体通常为薄壳结构,在深水压强作用下必须具有较高的强度和结构稳定性,并具备良好的密封性能。对于薄壁结构,失效行为往往由失稳引起,所以结构稳定性问题在耐压壳体设计中被许多专家和学者所重视。崔维成等[1]通过对外压作用下耐压球壳屈曲问题的研究,分析并比较了常用的耐压球壳设计规范。马永前等[2]通过研究超椭球体壳在均匀压力作用下的屈曲,论证了厚球壳的实际屈曲载荷高于薄壳理论计算结果,薄壳理论存在局限性。罗凯等[3]通过某种改进的弧长算法对有限元模型迭代修正,然后对结构的屈曲现象进行分析。张建等[4]研究了蛋形耐压壳结构在不同壁厚条件下的非线性屈曲行为,结果表明蛋形耐压壳的屈曲载荷会随着壁厚的增加而呈线性增大趋势。Donnel等[5]通过多次试验研究发现壳体的初始几何缺陷会对薄壁圆柱壳的屈曲产生重要影响。Castro等[6]比较分析了不同类型初始几何缺陷对圆柱壳屈曲的影响,研究成果对缺陷敏感结构的设计极具参考意义。Huhne等[7]依据NASA-SP 8007设计规范,计算研究发现相比于模态缺陷,集中力引起的缺陷(FI)对结构屈曲的影响更大。Blachut等[8-9]发现不同位置的几何缺陷会对球壳稳性产生不同的影响。
相对于研究耐压壳的静力屈曲特性,结构在碰撞下产生的动力屈曲问题由于时间参数的引入变得更加复杂。目前关于碰撞下的动力屈曲问题研究较少,相应的研究方法也较少,研究主要集中在对结构的屈曲模式、临界载荷、临界屈曲时间等参数的分析上。本文通过Ansys/Ls-dyna软件构建钛合金耐压壳数值模型,并依据B-R动力屈曲准则,对耐压壳在碰撞下的动力屈曲展开有限元分析。
1 钛合金耐压壳有限元模型本文所选取的圆柱耐压壳结构参数为:内径2.0 m,长度21.5 m,壳厚35 mm。靶体设为礁石(近年以来,潜艇海底触礁事故频繁,所以有必要进行潜器与礁石碰撞的研究),礁石的形状为简化过后的球体形状,球体直径为4.0 m。耐压壳与礁石的碰撞模型如图1所示。外部静水压力取20 MPa,即工作水深取为2 km。

|
图 1 耐压结构碰撞模型 Fig. 1 model of pressure structure collision |
本文主要使用SHELL163薄壳单元和SOLID164实体单元进行网格划分,薄壳单元的算法为Belytschko-Tsay算法,该算法具有运算速度快,善于分析动态非线性问题的特点,是目前分析结构碰撞问题时较为常用的算法。采用Johnson-Cook模型定义钛合金材料(TC4),钛合金的材料参数如表1所示,网格大小选为50 mm×50 mm,礁石的材料通过Ansys/Ls-dyna中*MAT_JOHNSON_HOLMQUIST_CONCRETE模型表示。
|
|
表 1 钛合金(TC4)参数 Tab.1 Titanium alloy (TC4) parameters |
本文的动力屈曲判定准则以Budiansky-Roth动力屈曲准则为依据,该准则的观点是:如果所加载荷的微小增量导致结构的瞬态响应产生剧变,则认为动力屈曲发生。在本文的动力屈曲研究中,把撞击速度作为动力载荷的一种表现形式,结构在受到撞击作用时,当撞击速度增加至某一临界值时,几乎很小的增量就引起结构响应参数大幅度的变化,即动力载荷的微小增加导致结构的瞬态响应产生剧变,则认为此时结构发生动力屈曲,结构响应参数为圆柱形耐压壳撞击方向的位移。
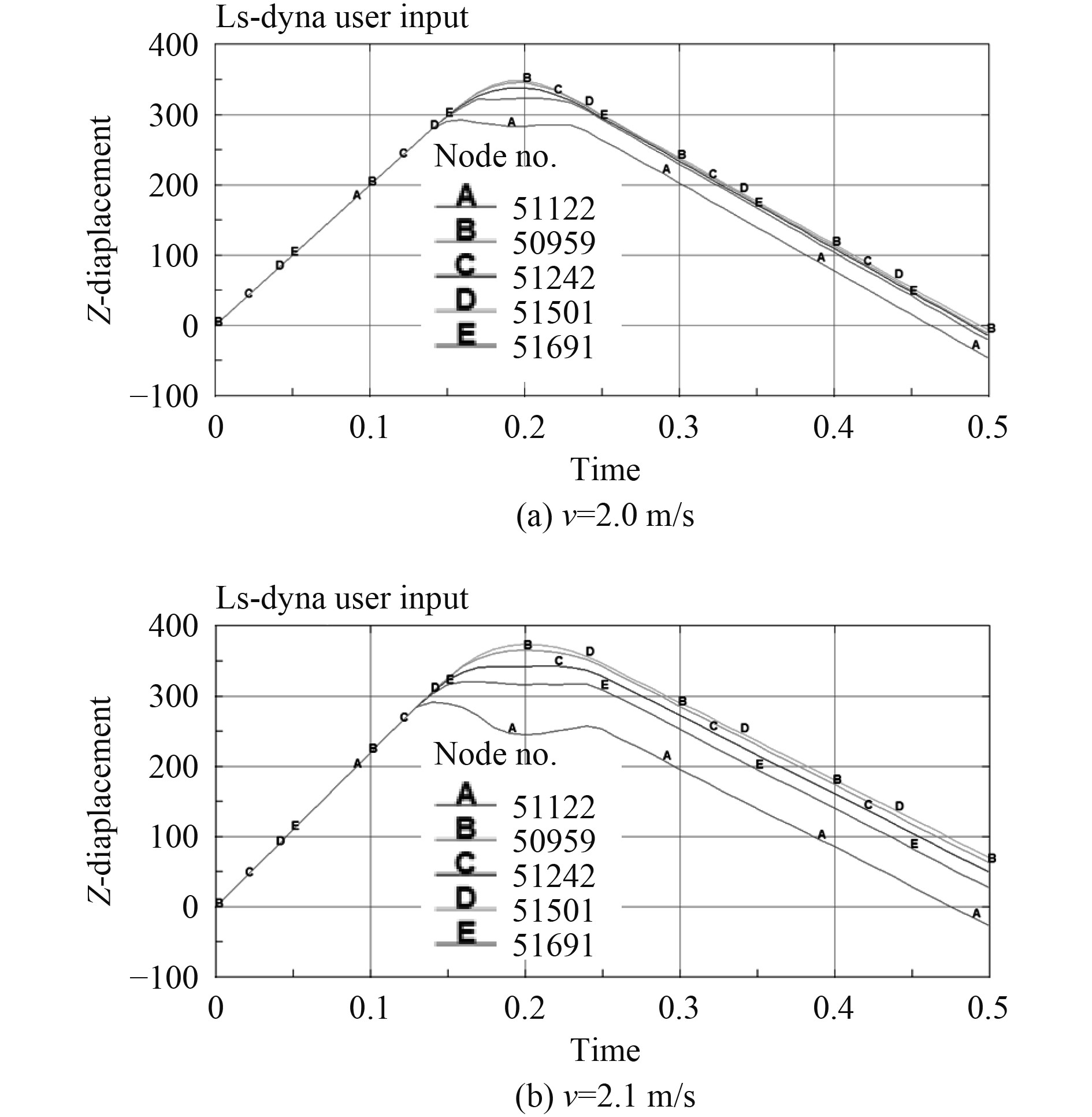
图2为耐压壳模型在撞击速度分别为2.0 m/s,2.1 m/s时,碰撞接触表面不同位置所选取节点的撞击方向位移-时间曲线。从图中可以发现,当耐压壳还未发生碰撞时,2种撞击速度下位移-时间曲线均呈斜线上升形态,当碰撞发生以后,曲线变化显然不同。当撞击速度为2.0 m/s时,曲线会呈对称式“返回”形态,而当撞击速度微增至2.1 m/s时,会有一小段下滑曲线,再呈斜线下降形态。
|
图 2 不同撞击速度下耐压壳位移-时间曲线 Fig. 2 Displacement-time curve of pressure shell under different impact speeds |
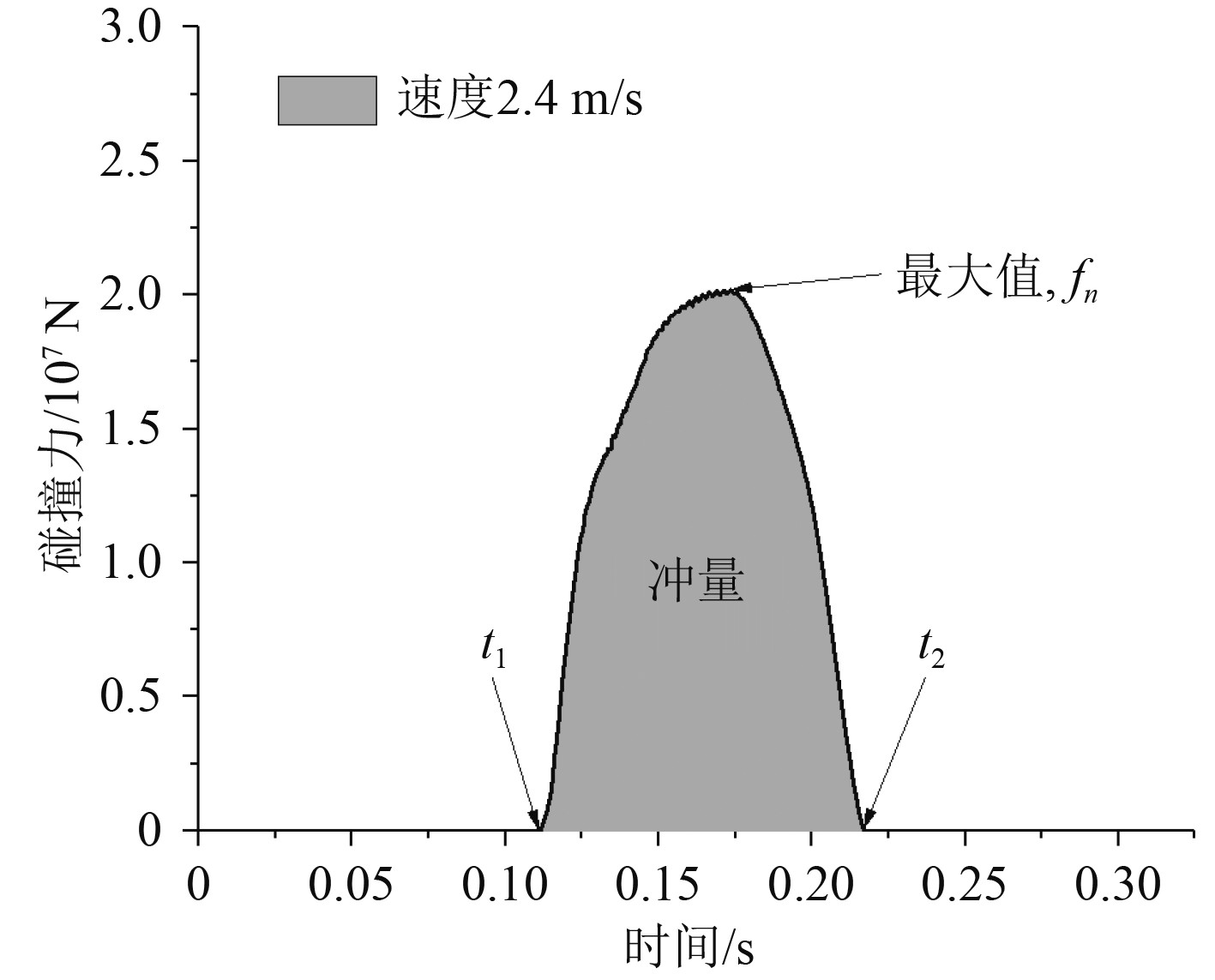
如图3所示,碰撞过程中的平均碰撞力可以通过下式计算得出:
|
图 3 碰撞力-时间曲线 Fig. 3 Collision force-time curve |
| $ I_{m}=\int_{t_{1}}^{t_{2}} f(t) {\rm{d}} t, f_{m}=I_{m} / \Delta t。$ | (1) |
式中:Im是冲量;
表2和表3分别为耐压壳厚度取35 mm,45 mm时不同撞击速度下碰撞力的相关数据,表中R为耐压壳半径,E为弹性模量,t为球壳厚度。最大碰撞力可通过有限元分析直接得出,平均碰撞力可通过式(1)求出,系数k1为最大碰撞力与平均碰撞力的比值,撞击速度的取值范围为1.2~2.8 m/s。
|
|
表 2 耐压壳厚度为35 mm时碰撞力数据 Tab.2 Collision force data when the pressure shell thickness is 35 mm |
|
|
表 3 耐压壳厚度为45 mm时碰撞力数据 Tab.3 Collision force data when the pressure shell thickness is 45 mm |
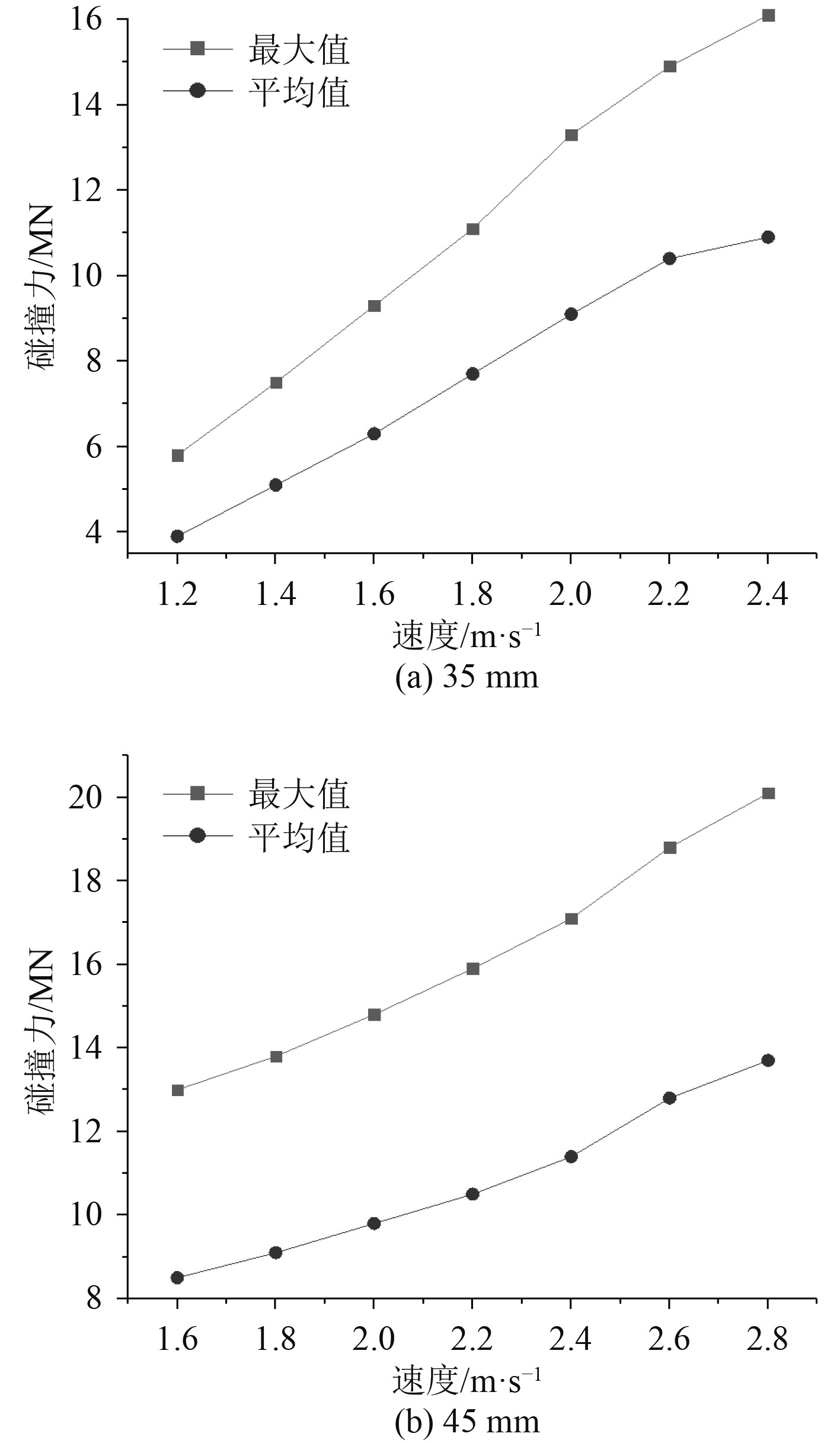
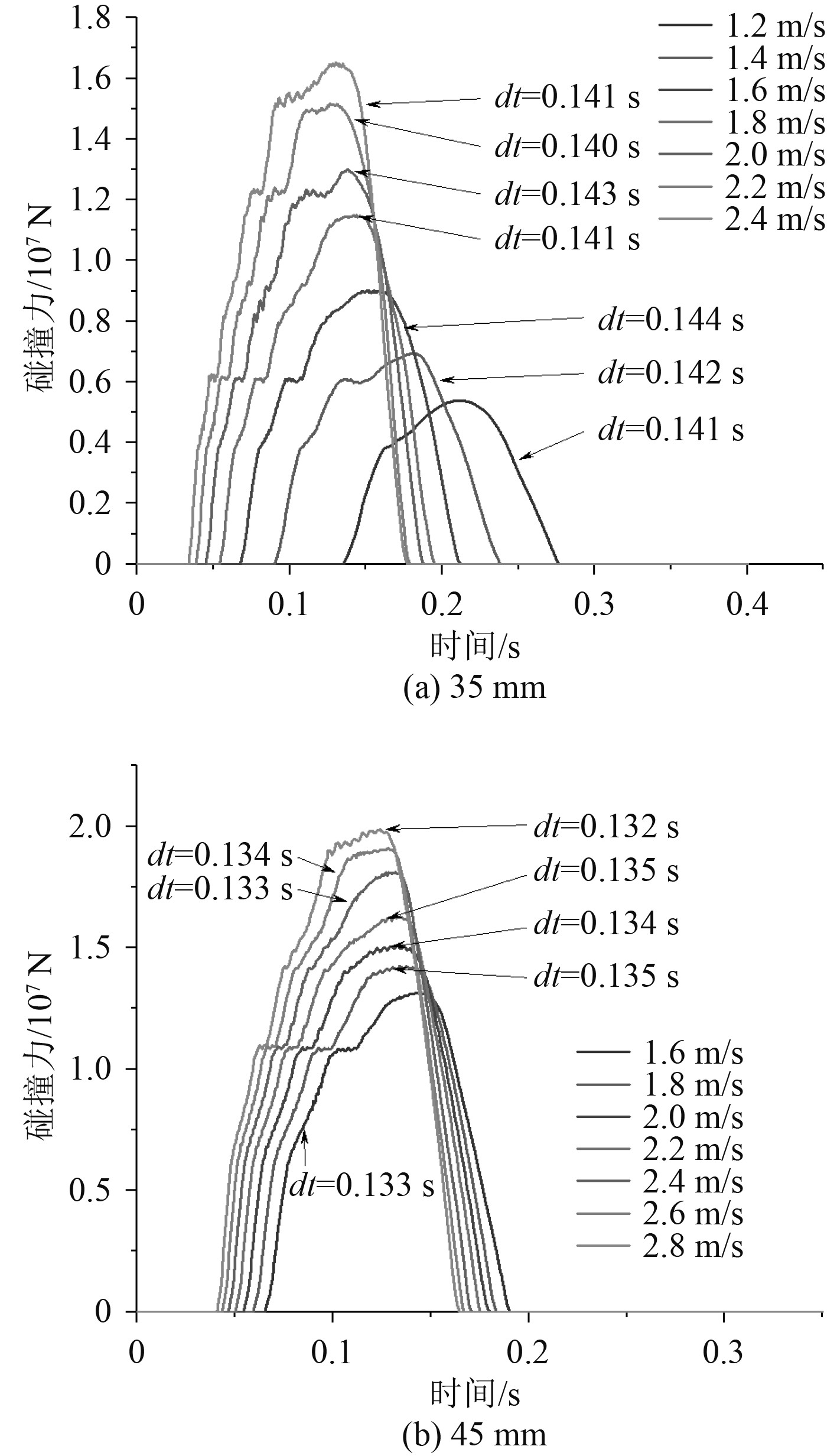
在本文中,若撞击速度微增至某一值时,结构刚好发生屈曲现象,则将该速度定义为碰撞的屈曲临界速度Va。图4为耐压壳厚度分别为35 mm,45 mm时碰撞力-速度关系图,图5为耐压壳厚度分别为35 mm,45 mm时不同撞击速度下的碰撞力-时间曲线。依据B-R动力屈曲判定准则,结合有限元分析结果,判断出当耐压壳的厚度分别为35 mm,45 mm时,其屈曲临界速度Va分别为1.8 m/s,2.4 m/s。
|
图 4 不同厚度下碰撞力-速度关系图 Fig. 4 Collision force-speed relationship under different thickness |
|
图 5 厚度分别为35 mm,45 mm时不同撞击速度下碰撞力-时间曲线 Fig. 5 Impact force-time curve at different impact speeds at 35 mm, 45 mm thickness |
结合图4与表2和表3可以发现:在撞击速度达到屈曲临界速度前,k1值基本不变,大约为1.50,即最大碰撞力与平均碰撞力的比值保持不变,撞击速度与最大碰撞力和平均碰撞力近乎呈线性关系,此线性关系成立的前提是不考虑其他因素(耐压壳的厚度,弹性模量,静水压力等)对碰撞力的影响;当撞击速度达到屈曲临界速度时,k1值会随撞击速度变化而发生改变,撞击速度与最大碰撞力和平均碰撞力之间的线性关系也不复存在。
由图5可知,保持其他参数不变,改变耐压壳的撞击速度,碰撞的持续时间基本不变,可能是因为耐压壳的撞击速度较小,速度变化也较小。当耐压壳的厚度分别为35 mm,45 mm时,碰撞的持续时间分别大约为0.141 s,0.134 s,即相同撞击速度下,厚度较大的耐压壳,碰撞的持续时间较短。
5 结 语本文研究得出以下结论:
1)在撞击速度达到使耐压壳发生屈曲前,碰撞过程中的最大碰撞力与平均碰撞力的比值可能不变。
2)在不考虑其他因素(耐压壳的厚度,弹性模量,静水压力等)对碰撞力的影响的前提下,撞击速度在达到使耐压壳发生屈曲前,与最大碰撞力和平均碰撞力近乎呈线性关系。
3)保持其他参数不变,厚度较大的耐压壳,碰撞的持续时间较短。
| [1] |
PAN B B, CUI W C. A comparison of different rules for the spherical pressure hull of deep manned submersible[J]. Journal of Ship Mechanics, 2011, 15(3): 276-85. |
| [2] |
马永前. 超椭球体壳在均匀压力作用下的屈曲问题研究[D]. 上海: 同济大学, 2009.
|
| [3] |
罗凯, 刘铖, 田强, 等. 薄膜结构的后屈曲分析[C]//可展开空间结构学术会议. 2014.
|
| [4] |
ZHANG J, WANG M, CUI W, et al. Effect of thickness on the buckling strength of egg-shaped pressure hulls[J]. Ships & Offshore Structures, 2017, 1-10. |
| [5] |
DONNELL L, WAN C C. Effect of imperfections on buckling of thin cylinders and columns under axial compression[J]. Journal of Applied Mechanice-Teanics-Transactions of the ASME, 1950, 17(1): 73-83. DOI:10.1115/1.4010060 |
| [6] |
CASTRO S G P, ZIMMERMANN R, ARBELO M A, et al. Geometric imperfections and lower-bound methods used to calculate knock-down factors for axially compressed composite cylindrical shells[J]. Thin-Walled Structures, 2014, 74(1): 118-132. |
| [7] |
CHRISTIAN H, RAIMUND R, JAN T. A new approach for robust design of composite cylindrical shells under axial compression[J]. 2005, 581: 141.
|
| [8] |
BŁACHUT J, JAISWAL O R. On the choice of initial geometric imperfections in externally pressurized shells[J]. Journal of Pressure Vessel Technology, 1999, 121(1): 71-76. DOI:10.1115/1.2883670 |
| [9] |
BŁACHUT J. Locally flattened or dented domes under external pressure[J]. Thin-Walled Structures, 2015, 97: 44-52. DOI:10.1016/j.tws.2015.08.022 |
 2021, Vol. 43
2021, Vol. 43
