2. 威海中远造船科技有限公司,山东 威海 264200
2. COSCO (Weihai) Shipbuilding Technology Co., Ltd., Weihai 264200, China
破冰船极地航行性能与船舶线型、推进功率、冰的物理特性等因素直接相关,其中推进功率的估算是破冰船初始设计阶段的一个重要环节,它直接关系到动力装置选型、推进系统设计等问题。同时,所估算的推进功率能否满足破冰性能的要求也是初始设计阶段需要考虑的问题
目前,推进功率评估分为经验公式直接估算和基于冰池模型阻力试验的间接估算两类。其中,各船级社规范均建立了相应的极地航行船舶推进功率经验公式直接估算方法[1-5],如俄罗斯船级社[1](RMRS)、芬兰—瑞典冰级规范[2](FSICR)、中国船级社[3]和美国船级社[4](ABS)等。但目前该方法均偏于保守,估算值与实船偏差的大小取决于经验公式收集的数据是否全面,实船装机功率仍然严重依赖于冰池试验,不利于破冰船初期研发。因此,有必要探索一套简便快捷估算推进功率、设计螺旋桨、估算破冰厚度以及分析推进功率与破冰性能之间匹配性的方法,用于破冰船初始设计,简化设计流程。
国内针对破冰船推进功率的研究主要包括最小推进功率与实船的对比、基于模式试验的推进功率理论估算等。吴蒙等[6]对比了RS,BV,ABS,DNV4家船级社的破冰船最小功率要求,其中ABS计算值与实船功率偏差最小;张东江[7]对比了FSICR规范、FSICR规范导则及ABS抗冰级船舶指导说明对主机功率的计算结果,计算结果均大于实船装机功率,实船主机应以冰池试验确定其冰阻力为准;季少鹏等[8]根据推力和阻力平衡原理,结合冰阻力模型试验结果,初步探索了大型极地运输船主机功率的评估,可满足大型极地运输船舶主机功率的评估;刁峰等[9]对比了不同冰阻力经验计算结果与模型试验结果,对冰阻力经验模型开展了参数研究;郑世博等[10]以RS规范计算的最小装机功率为基础,对同型船采用定距桨和吊舱推进系统的推进性能进行了实验对比分析,研究表明同一破冰航行要求情况下,吊舱推进系统配备的装机功率更小。但针对推进功率与所要求的破冰性能之间的匹配性研究相对较少。
本文以ABS规范估算的最小推进轴功率为基础,开展破冰工况螺旋桨设计,并考虑船体参数和推进功率,利用经验公式估算破冰厚度,最后分析了推进功率与破冰性能的匹配性。
1 最小推进功率估算 1.1 破冰船总体参数本研究以“泰梅尔”号、“北极”号、LK-60以及某破冰船总体和船型参数、三桨推进为基础开展最小推进功率与破冰能力匹配性分析,其主尺度和船型参数如表1所示。
|
|
表 1 破冰船总体和船型参数 Tab.1 Overall icebreaker and ship type parameters |
对比RS,BV,ABS,DNV船级社规范对于不同冰级破冰船最小轴功率的计算结果,ABS计算结果与实船轴功率偏差最小[6],因此,本研究选取ABS规范要求,作为最小推进轴功率的估算依据。
对于PC1到PC4级破冰船,最小推进轴功率N为[2]:
| $ N = kA{\left( B \right)^{0.8}}{\left( L \right)^{0.4}}[1 + m{e^{ - 5\Delta \times {{10}^{ - 6}}}}] \text{。}$ | (1) |
式中:系数k=0.735;A、m为系数,按表2取值。
|
|
表 2 A和m系数取值表 Tab.2 Value table of A and m coefficients |
4艘破冰船的最小推进轴功率如表3所示。
|
|
表 3 破冰船最小推进轴功率 Tab.3 Minimum propulsion shaft power of icebreaker |
破冰船具有2种典型的航行状态:敞水自航和冰区破冰工况,其中破冰工况作为破冰船的主要作业任务,螺旋桨设计应以破冰工况为主,兼顾敞水航行。因此,以系柱状态模拟破冰工况作为破冰船螺旋桨系统的实际设计条件。
考虑船宽限制、桨叶浸没深度、尾部线型以及船体空间对轴心距中纵剖面距离等因素限制,而且考虑俄罗斯核动力破冰船均采用1∶1∶1功率分配的4叶桨推进,针对以上4艘破冰船分别选取了3种不同螺旋桨直径方案,如表4所示。
|
|
表 4 不同螺旋桨直径的方案 Tab.4 Schemes of different propeller diameters |
为了使3个螺旋桨的工作负荷都处于较经济合理的状态,提高综合推进效率,既要使盘面比、螺距适宜,又要转速与功率匹配,使推进效率最佳。
选取重载负荷桨Kaplan,选取4叶桨、不同盘面比AE/AO(0.7,0.85,不同螺距比P/D(0.6,0.8,1.0)的螺旋桨[11],分别对以上4艘破冰船在3种螺旋桨直径下的系柱推力进行估算。
计算过程如下[12]:
1)计算不同轴功率分配、不同螺旋桨直径和转速下的KQ,计算公式为
| $ {K_Q} = \frac{Q}{{\rho {n^2}{D^5}}} = \frac{1}{{\rho {n^2}{D^5}}} \cdot \frac{{9\;550{P_D}}}{N} = \frac{{9\;550{P_D}}}{{\rho {n^2}{D^5}N}} \text{。}$ | (2) |
2)读取不同螺旋桨图谱[3]上进速系数J为0时的KQ对应的螺距比P/D和推力系数KT。
3)计算不同转速的系柱推力T,计算公式为
| $ T = \rho {n^2}{D^4}{K_T} \text{。}$ | (3) |
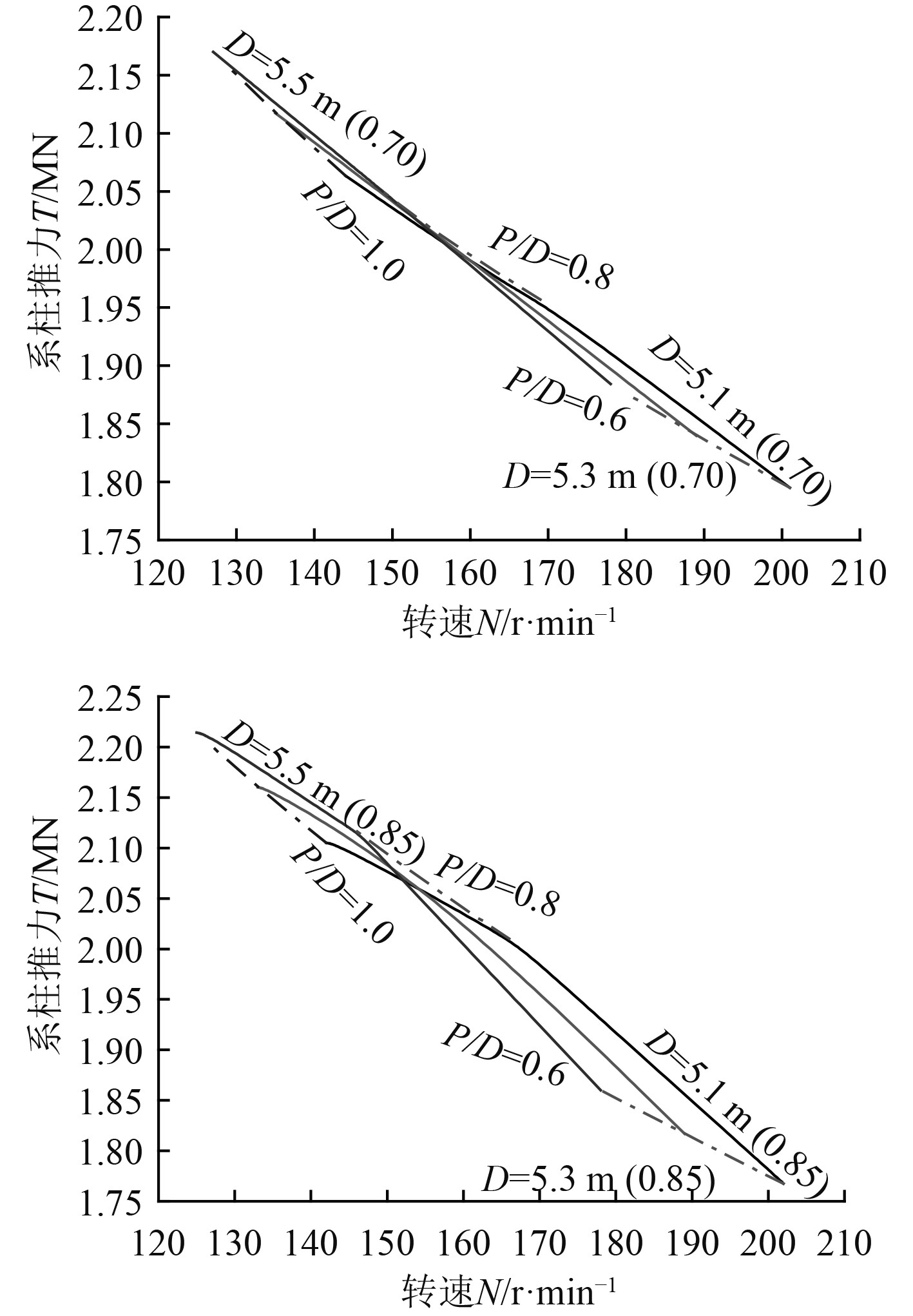
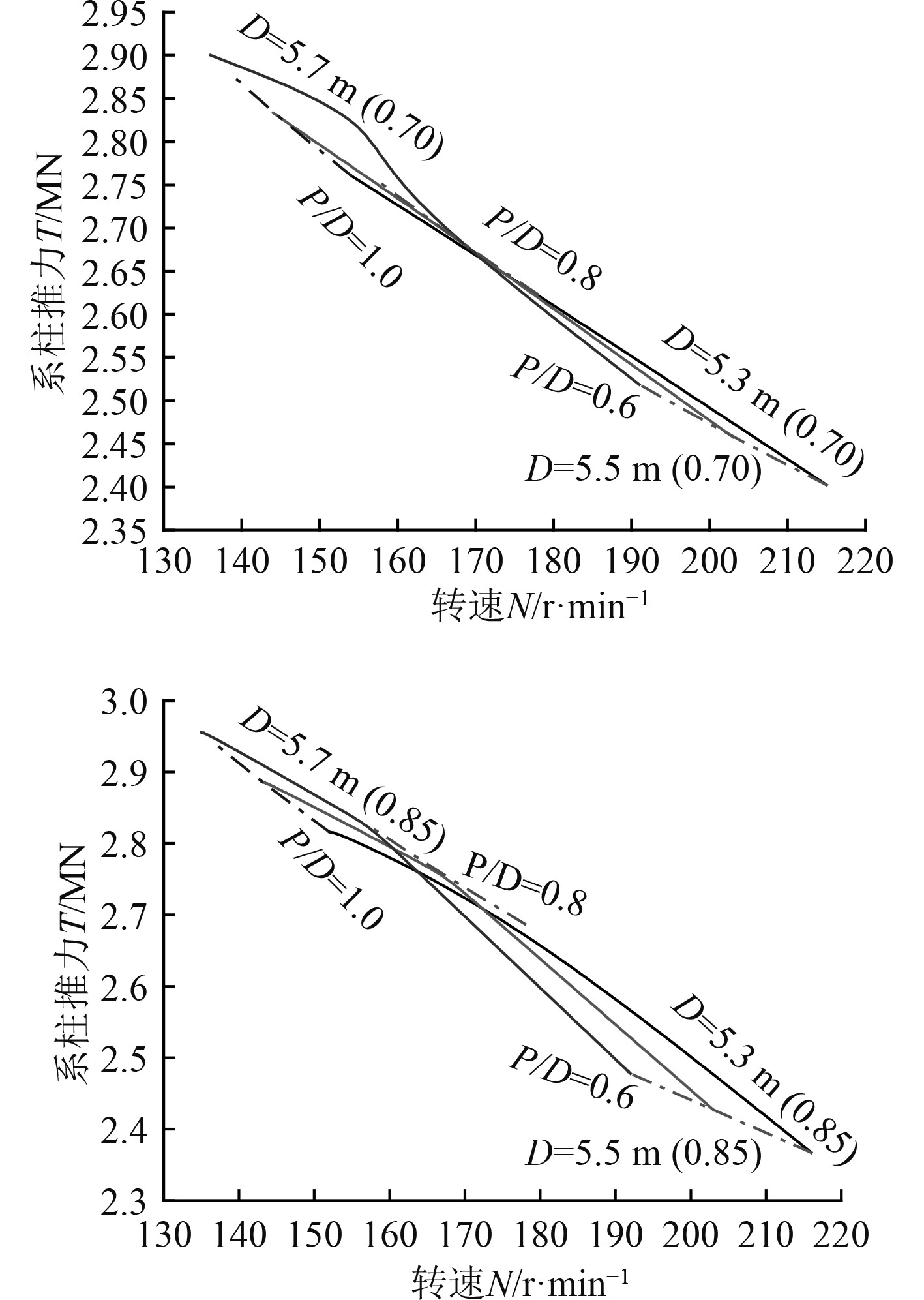
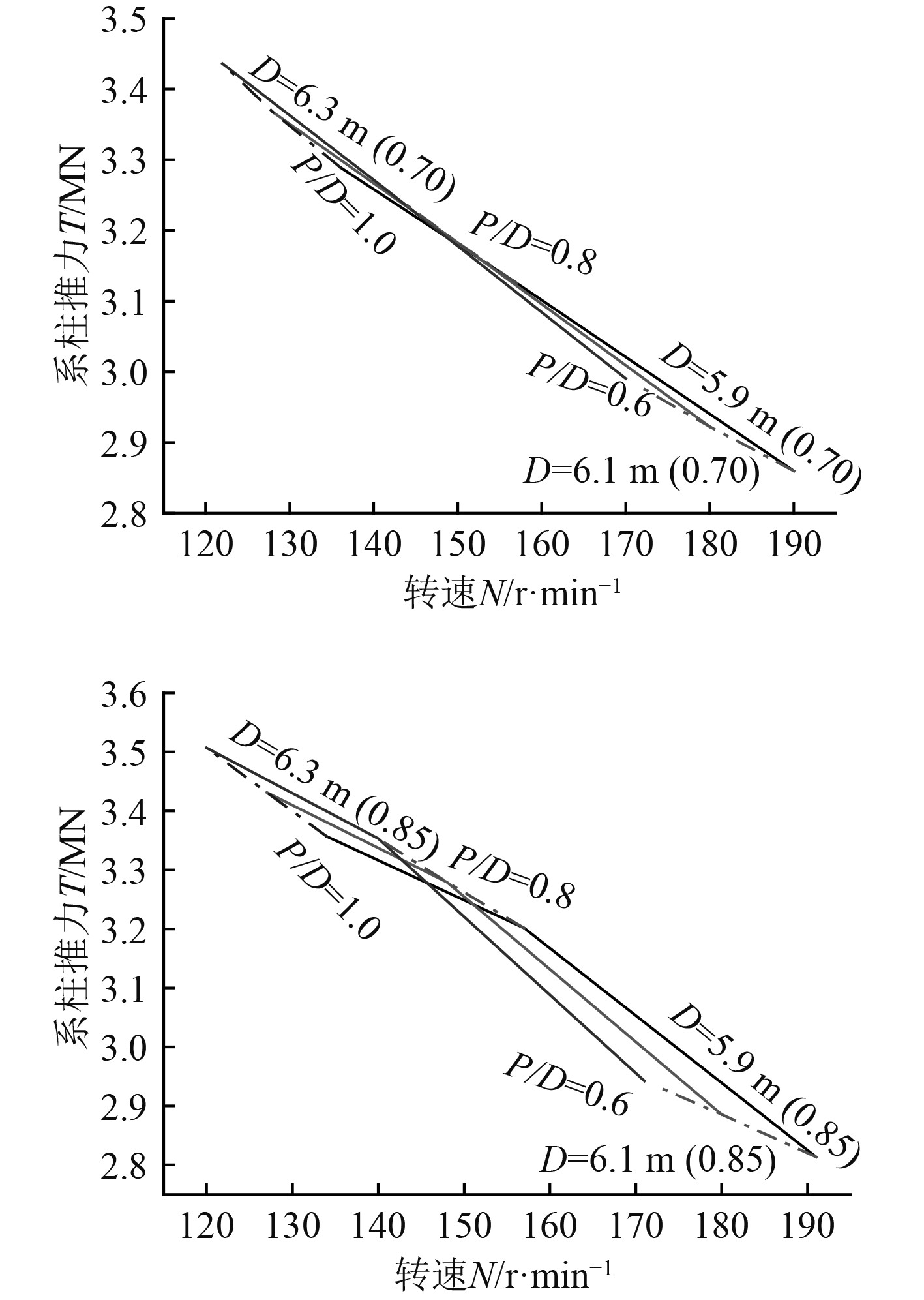
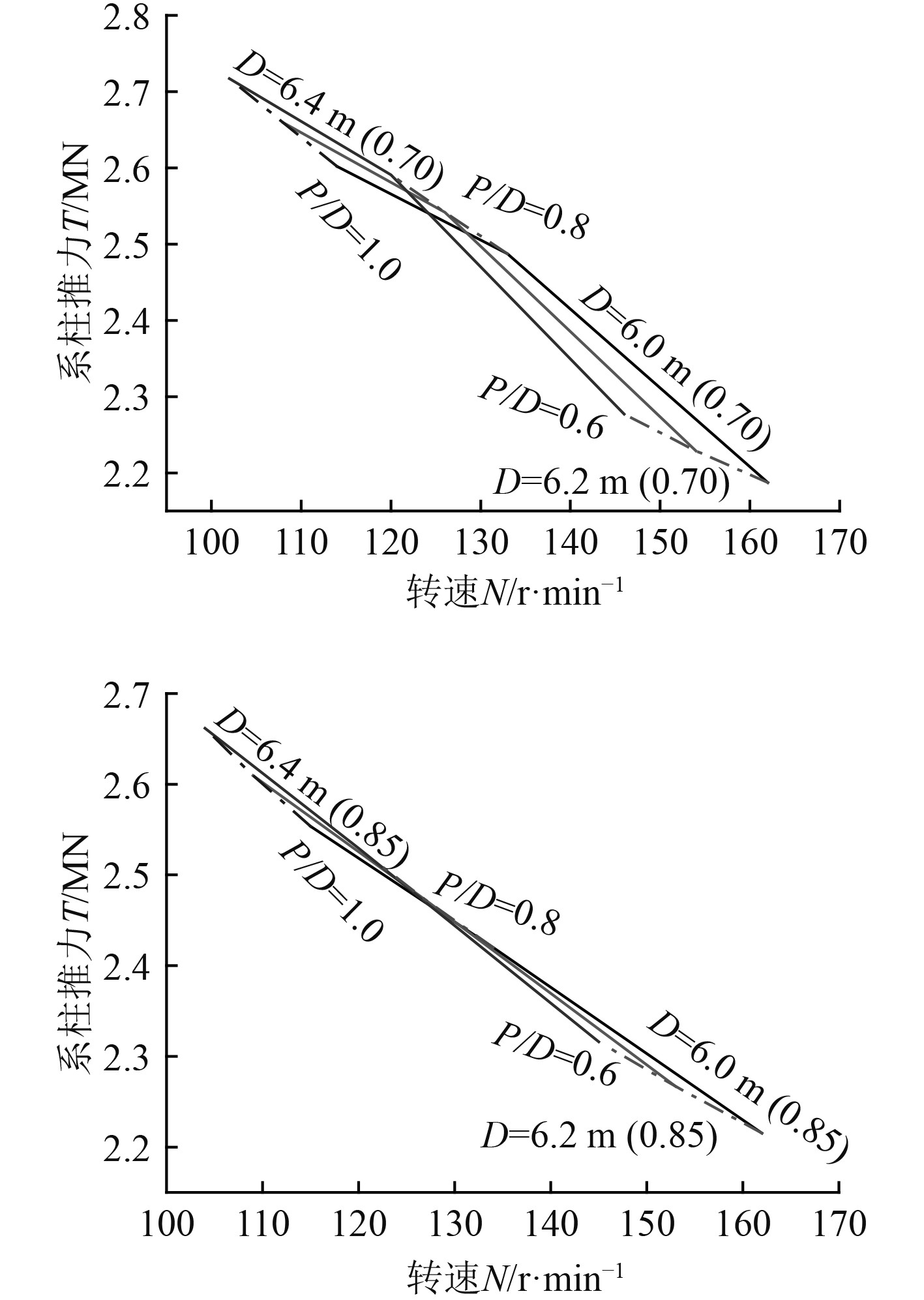
根据以上计算过程得出不同盘面比、直径以及转速下的系柱推力如图1~图4所示。
|
图 1 “泰梅尔”号单个螺旋桨系柱推力 Fig. 1 Bollard thrust of a single propeller of the Taymyr |
|
图 2 “北极”号单个螺旋桨系柱推力 Fig. 2 Bollard thrust of a single propeller of the North Pole |
|
图 3 LK-60单个螺旋桨系柱推力 Fig. 3 Bollard thrust of a single propeller of the LK-60 |
|
图 4 某破冰船单个螺旋桨系柱推力 Fig. 4 Bollard thrust of a single propeller of a self-developed |
选择最大系柱推力的螺旋桨参数作为破冰船工况螺旋桨设计参数,如表5所示。
|
|
表 5 基于最大系柱推力的单个螺旋桨设计参数 Tab.5 Design parameters of a single propeller based on the maximum bollard thrust |
由于破冰船螺旋桨负荷重、尾部流场因碎冰扰动不均匀,因此为确定破冰船螺旋桨可以实现预计推力,需对空泡现象进行校核。而且考虑舷侧桨和中心桨推进会相互干扰桨面处的流场,根据关于多桨推进干扰因子的研究,假定三桨推进中心桨和舷侧桨的推进因子如表6所示[13]。
|
|
表 6 破冰工况下螺旋桨设计推进因子参数 Tab.6 Propeller design propulsion factor parameters under ice breaking conditions |
进速
| $ {V_A} = (1 - b)(1 - w)V \text{,}$ | (4) |
船身效率
| $ {\eta _H} = \frac{{2{K_{T1}}\left( {1 - {t_1}} \right) + {K_{T2}}(1 - {t_2})}}{{2{K_{T1}}\left( {1 - {w_1}} \right)(1 - {b_1}) + {K_{T2}}\left( {1 - {w_2}} \right)(1 - {b_2})}} \text{。}$ | (5) |
其中下标1代表舷侧桨,下标2代表中心桨。
假设进速VA为3kn,利用柏利尔限界线[12]对表5各螺旋桨进行空泡校核,以上螺旋桨参数均不满足空泡校核要求。
为避免空泡产生,尽量减少系柱推力的降低,通过调节螺旋桨转速、螺距比获得满足空泡校核要求的螺旋桨设计参数。
|
|
表 7 考虑空泡的螺旋桨设计参数 Tab.7 Propeller design parameters considering cavitation |
目前,国际上在进行冰区航行性能的试验和计算时,通常以破冰船在弯曲强度为500 kPa、覆雪厚度为20 cm的均匀冰层中以3 kn稳定匀速航行的最大冰厚作为冰区航行性能评估的依据[14]。
Цай Л. Г基于模型试验和实船数据提出了考虑船首形状、船体参数、螺旋桨推力以及冰的物理性能等因素的破冰厚度半经验估算公式[14-15]:
| $ {h_{ice}} = \frac{{{\Delta ^{{1 \mathord{\left/ {\vphantom {1 4}} \right. } 4}}}}}{{\left( {42.6 - 3.7\dfrac{B}{T}} \right)F}}{\left( {\frac{{{P_e}}}{B}} \right)^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}} \text{。}$ | (6) |
式中,hice为破冰厚度,m;Δ为排水量,t;B为水线处船宽,m;T为吃水,m;Pe为螺旋桨推力,t;F为形状函数,如下式:
| $ F = {\left[ {2\left( {\cos \beta + {f_d}ctg\alpha } \right)\sin \alpha } \right]^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}} \text{。}$ | (7) |
式中:α为B/4处的水线倾角,(°);β为首肋骨外倾角,(°);fd为船体相对冰的动摩擦系数,取0.1。
根据上述经验公式估算本研究4艘破冰船的破冰船厚度hice如表8所示。
|
|
表 8 破冰厚度估算表 Tab.8 Estimation table of ice-breaking thickness |
总结以上4艘破冰船的实际与估算轴功率、螺旋桨推力、破冰厚度以及之间偏差如表9所示。
|
|
表 9 破冰性能实际值与估算值的对比表 Tab.9 Comparison table of actual value and estimated value of ice breaking performance |
对比分析可知:
1)与实际轴功率对比,基于ABS规范的最小推进轴功率估算值均偏高,并呈现高等级破冰船轴功率偏差减小的趋势,误差范围<20%;
2)本文设计的螺旋桨推力远大于实际螺旋桨推力,可能的原因是未考虑碎冰和冰盖等因素对螺旋桨流场的影响,或者选取的螺旋桨不适用于冰区航行;
3)与实际破冰能力对比,估算破冰厚度值均偏高,误差范围<30%,其主要原因是螺旋桨推力的计算偏差造成的,如替换实际螺旋桨推力,破冰厚度偏差<11.3%;
4)与其他破冰船相比,某破冰船形状系数F偏高,其船型有进一步优化的空间,提升破冰能力。
4 结论与展望1)本文初步探索了一套估算推进功率、设计螺旋桨、估算破冰厚度以及分析推进功率与破冰性能之间匹配性的闭环流程方法;
2)通过建立的分析方法,破冰船推进轴功率偏差<20%、破冰厚度偏差<30%,假如进一步优化螺旋桨设计结果,破冰厚度偏差可以<11.3%。
本文初步探索的破冰船推进功率与破冰性能匹配性分析方法具有一定的工程适用性,但其中设计得出的螺旋桨推力与实际值偏差过大,是否符合工程实际需要进一步研究,接下来还需要对冰区桨、破冰工况下螺旋桨的推进衰减等问题进一步研究。
| [1] |
FSICR. Finnish-swedish ice class rules[S]. 2008.
|
| [2] |
ABS. Rules for building and classing steel vessels[S]. 2010.
|
| [3] |
RMRS. Rules for building and classing steel vessels[S]. 2010.
|
| [4] |
中国船级社. 钢质海船入级规范[S]. 2016.
|
| [5] |
Guidelines for the application of the Finnish-Swedish Ice Class Rules[S]. 2005
|
| [6] |
吴蒙, 何炎平, 陈哲, 等. 不同冰级破冰船船级社最小功率要求分析[J]. 船海工程, 2019, 48(3): 128-131. DOI:10.3963/j.issn.1671-7953.2019.03.030 |
| [7] |
张东江. 北极航运及冰区船舶主机功率探讨[J]. 船舶, 2012, 23(4): 28-32. DOI:10.3969/j.issn.1001-9855.2012.04.006 |
| [8] |
季少鹏, 田于逵, 郝寨柳, 等. 大型极地运输船主机功率评估方法研究[J]. 船舶力学, 2019, 23(1): 1-8. DOI:10.3969/j.issn.1007-7294.2019.01.001 |
| [9] |
刁峰, 陈京普. 极地船舶冰阻力经验模型研究[J]. 中国造船, 2016, 57(2): 38-44. DOI:10.3969/j.issn.1000-4882.2016.02.005 |
| [10] |
郑世博, 索双武. 冰区加强大型商船推进系统研究[J]. 舰船科学技术, 2015, 37(5): 114-118. DOI:10.3404/j.issn.1672-7649.2015.05.024 |
| [11] |
盛振邦. 中国船用螺旋桨系列试验图谱[J]. 中国造船, 1983.
|
| [12] |
盛振邦. 船舶原理[M]. 上海: 上海交通大学, 2013.
|
| [13] |
毕俊颖. 多桨推进初步设计方法研究[D]. 大连: 大连理工大学, 2013: 76−87.
|
| [14] |
Цай Л. Г. Морские ледоколы, особенности проектирова-ния[J]. СПБМТУ СПб., 2003, 34-56. |
| [15] |
КЛИМАШЕВСКИЙ С. Н.. Расчет ледопроходимости ледоколов и судов ледового плавания, анализ параметров формы корпуса этих судов[J]. Судостроение, 2012(2): 11−16
|
 2021, Vol. 43
2021, Vol. 43
