2. 北京强度环境研究所,北京 100076
2. Beijing Institute of Structure and Environment Engineering, Beijing 100076, China
近年来,随着全球气候变暖,冰川融化,极地科考与极地运输的问题受到各个国家的高度重视,破冰船作为航行于极地区域的船舶,也逐渐进入大众的视野。破冰船在极地环境中航行相较于普通海况是大不相同的,破冰船不仅受到波浪载荷的影响,还会有冰载荷对其结构碰撞所产生的影响,且冰载荷多为随机交变载荷,造成船体结构疲劳损伤,因此研究破冰船在冰载荷作用下的疲劳问题显得极为重要.
目前国内外对于破冰船的疲劳强度分析主要分为有限元模拟和实船检测2种方法。张浩辉[1]采用基于直接计算法的船冰碰撞来预报破冰船的疲劳问题,但是受限于算法,其只计算了20 s的连续式破冰时历。Hwang Mi-Ran等[2-3]应用应变计测量系统测定韩国第1艘破冰研究船“阿龙”号船首推进器室侧壳的疲劳损伤和疲劳寿命,得出破冰船在水上航行过程中,受到冰的反复冲击和接触载荷作用,反复冰荷载引起的微裂纹可能导致疲劳失效,即冰致疲劳。Ito Hisashi等[4]采用直接计算方法对大型LNG船在冰荷载作用下的疲劳损伤进行了评估,对比分析了冰荷载引起的疲劳损伤与波浪荷载引起的疲劳损伤的关系。
由于非线性显式动力求解计算极为耗时耗力,并且对于计算机性能有很大的需求,目前对于有限元船冰碰撞计算都是基于短时间的计算。Jeong-Hwan Kim等[5]提出了一种基于长时历分析疲劳评估方法,该方法利用商业软件Abaqus进行数值分析碎冰场中冰对船体的影响。本文在此基础上提出一种基于长时历计算的船冰碰撞模拟方法,可以通过较长的时域数值模拟来获得船冰碰撞载荷的短期分布。通过船冰碰撞有限元模拟结果,筛选出的疲劳热点,运用雨流计数法对各个疲劳热点的应力时历曲线进行统计,得出应力循环下的均值和范围,并修正平均应力对于应力范围的影响,结合Palmgren-Miner线性累积损伤理论给出在设计寿命周期内的总损伤,进而进行破冰船结构冰致疲劳强度评估。
1 低温疲劳强度评估理论破冰船低温疲劳强度相较于常温疲劳强度有了较大的改变,从对应力时历曲线进行处理的雨流计数法、平均应力修正、低温疲劳S-N曲线和Palmgren-Miner线性累积损伤理论等4个方面进行阐述。
1.1 雨流计数法雨流计数法[6]是一种用于分析随机载荷谱的方法,可以同时考虑应力均值和应力幅值的影响,对于随机载荷谱作用下的疲劳分析问题十分适合。雨流计数法将时历曲线旋转,并取应力为x轴,时间为-y轴,载荷历程看成多层屋顶,计数程序沿着时历曲线从上向下流淌,假设从最大波峰(最大波谷)往下流,若没有屋顶阻拦,则雨滴将反向流淌,当流到下一波峰(波谷)时,此次第1次循环结束。开始下一轮雨流计数统计之前,会将上一次雨流计数统计出来的载荷谱进行删除,然后进行下一次雨流计数统计过程,持续这个过程直到随机载荷谱上的所有载荷都经过雨流计数统计。此时复杂的随机载荷谱已经分解为若干简单载荷循环,并提取处各个载荷循环的均值和幅值。
1.2 平均应力修正船体结构[7]在随机循环载荷的作用下,受到不同水平的平均应力Sm的影响,因此需要进行平均应力修正。工程上一般将应力幅值Sa和平均应力Sm进行归一化处理等寿命曲线,并将等寿命曲线处理成无量纲形式。
本文采用的是等寿命曲线修正中的Goodman直线修正法,其表达式如下:
| $ \frac{{{S_a}}}{{{S_{ - 1}}}} + \frac{{{S_m}}}{{{S_u}}} = 1。$ | (1) |
式中:Sa为应力幅值;S−1为对称循环下的应力幅值;Sm为平均应力;Su为材料抗拉强度。
1.3 低温疲劳S-N曲线钢材在低温下的力学性能相较于常温拥有较大的改变,根据研究结果表明船用钢材在低温下的各项力学性能都将会发生变化,其中钢材脆性加强,韧性下降,屈服强度以及弹性模量相较于常温下均增大,钢材的疲劳性能也因此发生改变。船级社给出的典型焊接接头常温S-N曲线并不适用于低温破冰船的强度校核,因此需要用试验的方法获得低温S-N曲线,通过规范[8]设计低温疲劳试验标准件,设计应力水平来进行不同应力范围下的疲劳试验,并对各组的疲劳试验数据进行统计分析,最终得出疲劳寿命的中值S-N曲线,S-N曲线的一般形式如下:
| $ \lg N = \lg A - m\lg S \text{。}$ | (2) |
文献[9-10]开展了DH36钢趾端焊接接头和十字焊接接头在−60°C的低温疲劳试验,求得DH36钢趾端焊接接头和十字焊接接头在置信度95%下的S-N曲线,趾端焊接接头S-N曲线如下式所示,十字焊接接头S-N曲线如下式:
| $ \lg N = {\text{12}}{\text{.883}} - {\text{3}}\lg S,$ | (3) |
| $ \lg N = {\text{13}}{\text{.057}} - {\text{3}}\lg S。$ | (4) |
破冰船的疲劳问题[11]针对整个设计寿命周期,但是采用非线性有限元模拟船冰碰撞时,是无法实现整个设计寿命周期的模拟,只能实现某一工况下一段时间的破冰过程,因此只能获得这一段时间内的损伤,这里采用线性累计损伤的方法获得破冰船在整个设计寿命周期内的疲劳累计总损伤。
考虑到浮冰、碎冰等工况的冰载荷要小于相同冰况的层冰载荷,本文将破冰船整个航行周期划分为不同的层冰破冰工况,设在破冰工况1内,一段时间t1内的某一热点得到若干的应力循环,设其中一个应力循环的应力幅值为第i级,平均应力值为第j级,且此时工作循环次数为nij,经过数据处理得到该结构在此应力范围内所能承受的最大寿命为Nij,其损伤可表示为:
| $ {D_{{t_1}ij}} = \frac{{{n_{ij}}}}{{{N_{ij}}}} ,$ | (5) |
根据线性累积损伤理论,在雨流计数法统计的时间段t1内,该热点的总损伤Dt1可表示为:
| $ {D_t}_{_1} = \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {{D_{{t_1}ij}}} } = \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {\frac{{{n_{ij}}}}{{{N_{ij}}}}} },$ | (6) |
设破冰工况1下的破冰航速为v1,则该热点在破冰工况1下单位海里的损伤度为:
| $ {D_t}_{_{\text{0}}}{\text{ = }}\frac{{{D_t}_{_1}}}{{{t_1}{v_1}}} = \frac{1}{{{t_1}{v_1}}}\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {{D_{{t_1}ij}}} } = \frac{1}{{{t_1}{v_1}}}\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {\frac{{{n_{ij}}}}{{{N_{ij}}}}} } ,$ | (7) |
设该热点在破冰工况1内的航行里程为S1,损伤度可表示为:
| $ {D_1} = {S_1}{D_{{t_0}}} = \frac{{{S_1}}}{{{t_1}{v_1}}}\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {\frac{{{n_{ij}}}}{{{N_{ij}}}}} },$ | (8) |
故该结构在整个设计寿命期内的总损伤度可表达为:
| $ \begin{split} D =& {D_1} + {D_2} + \cdots{D_x} + \cdots + {D_c} = \frac{{{S_1}}}{{{t_1}{v_1}}}\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {\frac{{{n_{ij}}}}{{{N_{ij}}}}} } + \\ & \frac{{{S_2}}}{{{t_2}{v_2}}}\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {\frac{{{n_{ij}}}}{{{N_{ij}}}}} } + \cdots + \frac{{{S_x}}}{{{t_x}{v_x}}}\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {\frac{{{n_{ij}}}}{{{N_{ij}}}} + \cdots} } + \\ & \frac{{{S_c}}}{{{t_c}{v_c}}}\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {\frac{{{n_{ij}}}}{{{N_{ij}}}}} } 。\end{split} $ | (9) |
采用破冰船作为算例船进行疲劳计算,由于破冰船采用首破冰方式,并考虑到已破碎的浮冰可能对后续舱室的影响,故船体模型截取128肋位之后的区域(即船首区域加一个舱室结构)完整壳单元建模,其他区域只设置船壳,并将调整质量分布与实船相同。破冰船主尺度参数如表1所示。
|
|
表 1 破冰船主尺度参数 Tab.1 Main dimension parameters of icebreaker |
假设破冰船航行在东西伯利亚海区域[12-13],参照破冰船设计工况要求,将海冰厚度以2.5 m为最大破冰厚度,破冰方式采用连续式破冰方式,计算冰厚取冰厚区间最大值,破冰航速取设计工况下的特定航速。破冰船的设计寿命为20年,在设计寿命内每年去东西伯利亚海区域科考10次,只考虑冰载荷对于破冰船的影响,海冰密集度取50%,则估算总航行里程为101424 n mile,海冰厚度分布[13]按照参考文献中给出的海冰厚度概率密度分布进行求取。破冰方式采用连续式破冰,破冰工况见表2。
|
|
表 2 破冰工况 Tab.2 Ice-breaking conditions |
采用弹塑性断裂模型作为船冰碰撞中的海冰材料模型,其材料属性如表3所示。文献[14]利用弹塑性断裂模型作为海冰材料模型与现有试验结果进行对比,验证了数值模拟方法可以模拟海冰的破坏情况。船体结构材料采用线性强化的弹塑性模型,其中应变率影响通过Cowper-Symonds模型考虑,
| $ {\sigma _y}\left( {{\varepsilon _{eff}}^P,{{\dot \varepsilon }_{eff}}^P} \right) = {\sigma _y}({\varepsilon _{eff}}^P)\left[ {1 + {{\left( {\frac{{{{\dot \varepsilon }_{eff}}^P}}{C}} \right)}^{\frac{1}{P}}}} \right] $ | (10) |
式中:C和P为应变率参数;
|
|
表 3 海冰模拟材料属性 Tab.3 Material properties of sea ice simulation |
|
|
表 4 船体结构材料属性 Tab.4 Material properties of hull structure |
本文对连续式破冰过程进行模拟,由于统计上收敛的冰载荷历史对于疲劳寿命计算十分重要,因此在时域中长时间的模拟是不可避免的,本文开展的连续式破冰模拟时间为800 s。由于冲击载荷的高频率,并考虑到时域冰-结构相互作用的模拟时长和破冰船航速,需要足够数量的冰单元,在这种情况下,建模、计算和后处理几乎不可能。本文采用周期性介质分析方法来解决这一问题。周期性介质分析方法(the periodic media analysis method)是一种用于分析重复结构的模型的计算机实现的方法,包括基于模型生成多个块,以使这些块首尾相连。
破冰船破冰时冰层区域假设分为3个部分:区域1,区域2,区域3,如图1所示。

|
图 1 周期性介质分析方法实例说明 Fig. 1 Illustration of periodic media analysis method |
当破冰船对区域1进行破冰时,区域2网格生成,以保证破冰过程的连续,当破冰船对区域3进行破冰时,由于破冰船已完全驶过区域1,此时区域1已经开辟出一条完整的航道,此时区域1已经对后续破冰船的疲劳计算不产生影响,因此区域1网格删除,以保证后续时间段有限元网格数控制在一定范围内,不响应后续的计算,如图2所示。

|
图 2 连续式破冰有限元模拟情况 Fig. 2 Finite element simulation of continuous ice-breaking |
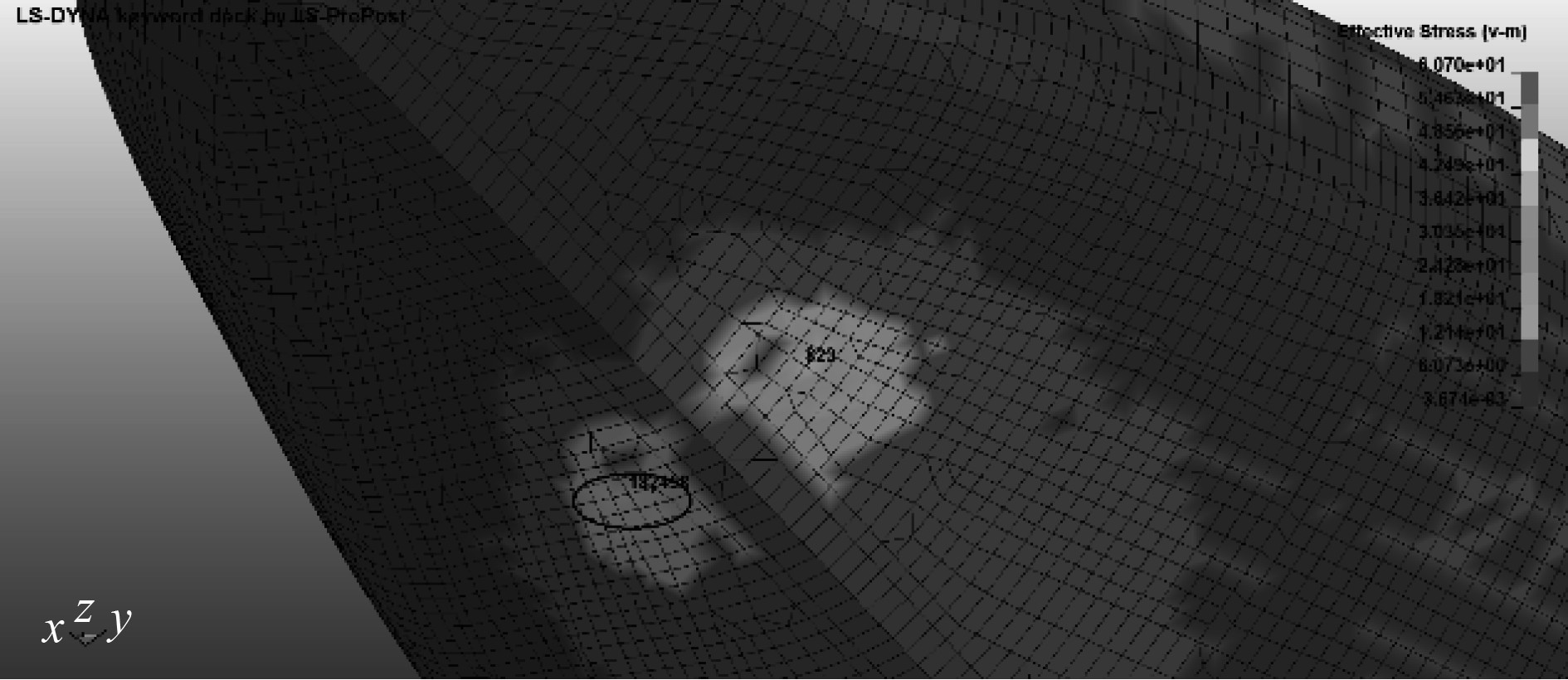
通过对破冰船有限元数值模拟结果分析,可以发现破冰船主要受力部位为船首外板冰带区域,其次当破冰船进行后续破冰时,船肩等部位也会受到已破碎海冰的影响,筛选出若干疲劳热点,如图3~图6所示,将图3~图6中的疲劳热点进行编号,依次为热点1、热点2、热点3、热点4。

|
图 3 船首与海冰初始碰撞点 Fig. 3 Initial collision point between bow and sea ice |

|
图 4 横舱壁与纵骨交界处 Fig. 4 Junction of transverse bulkhead and longitudinal |

|
图 5 船首外板碰撞点1 Fig. 5 Collision point 1 of bow outer shell plate |
|
图 6 船首外板碰撞点2 Fig. 6 Collision point 2 of bow outer shell plate |
由于前述有限元分析采用的是名义应力,而进行疲劳分析需要采用热点应力,表征结构几何突变所引起的热点应力与名义应力比值的热点应力集中系数可以按下式计算:
| $ f=\frac{\sigma_{{h}}}{\sigma_{{n}}} 。$ | (11) |
式中:σh为热点应力;σn为名义应力。
针对上述热点建立局部精细网格,网格的尺寸大小为t×t,获得粗细网格模型在同一载荷下的同一位置处的应力结果,并计算出应力集中系数。如表5所示,其中坐标参考点为船中剖面0肋位与船底交汇处。
|
|
表 5 应力集中系数汇总 Tab.5 Stress concentration factors summary |
选取破冰工况1进行说明,破冰工况1为连续式破冰工况,冰厚为2.5 m,破冰船航速为1.5 kn,连续式破冰的计算时间为800 s,破冰工况1疲劳热点应力时历曲线图如图7所示。可以看出,破冰船在有限元计算时间800 s内一直在进行连续式破冰模拟。在800 s的时历曲线下,破冰船的各个疲劳热点受到的应力幅值相差不大。
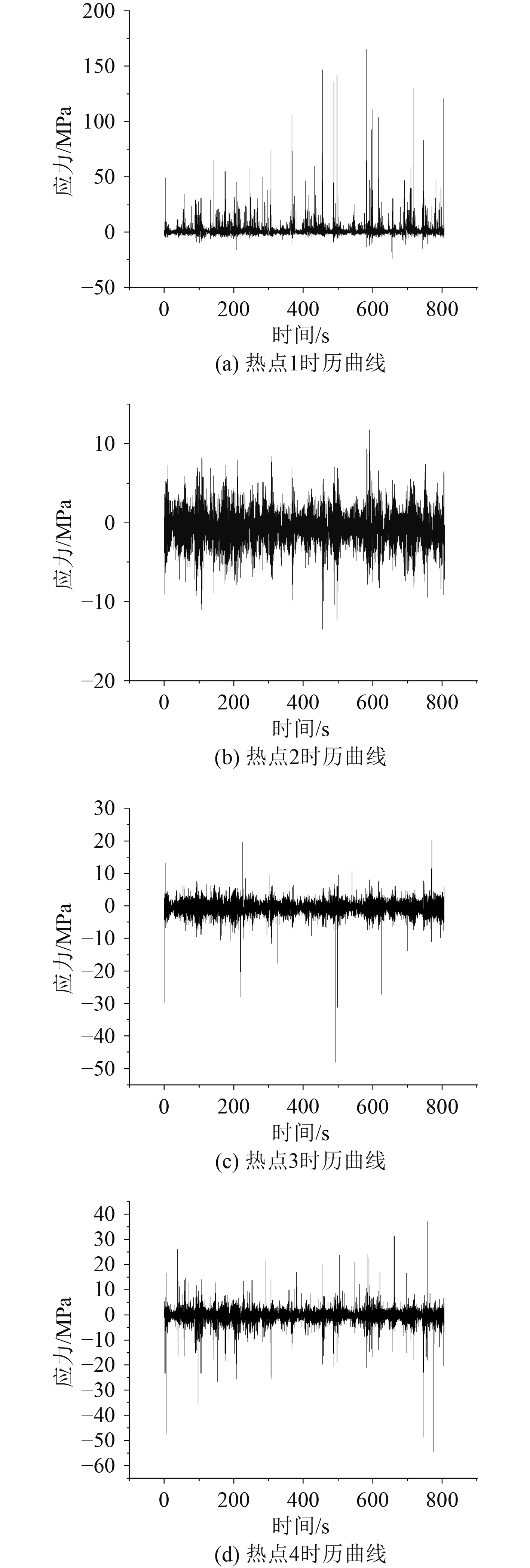
|
图 7 破冰工况1各疲劳热点应力时历曲线 Fig. 7 Time-history curves of stress in each fatigue hot spot in ice-breaking condition 1 |
在船体结构疲劳分析中,双参数Weibull分布可以很好的表示应力范围的长期分布,其概率密度和分布函数如下:
| $ {f_s}(S) = \frac{h}{q}{(\frac{S}{q})^{h - 1}}\exp \left[ { - {{\left( {\frac{S}{q}} \right)}^h}} \right] ,$ | (12) |
| $ {F_s}(S) = 1 - \exp \left[ { - {{\left( {\frac{S}{q}} \right)}^h}} \right]。$ | (13) |
式中:q为尺度参数;h为形状参数。
将各疲劳热点在各个工况下计算结果的应力范围按不同时长进行双参数Weibull分布拟合分析,讨论800 s过程中连续式破冰的稳定性。对破冰工况1下的应力分布结果进行分析,结果如图8所示。
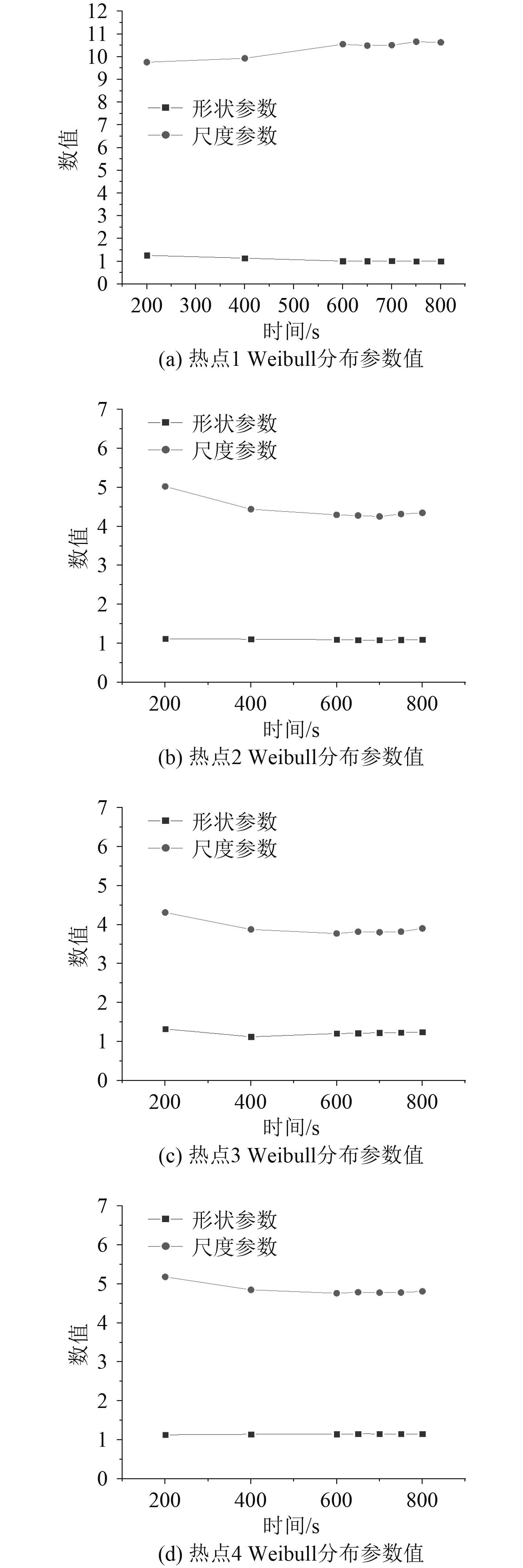
|
图 8 各热点不同时间段下Weibull分布参数值 Fig. 8 Weibull distribution parameters of hot spots in different time periods |
可以发现,连续式破冰过程中在前600 s的计算时间内,形状参数和尺度参数波动趋势较大,在600 s以后的计算过程中,形状参数和尺度参数逐渐趋于稳定,说明此时应力范围的Weibull分布趋于稳定,由此可以说明破冰船计算到800 s时应力时历曲线已经稳定,保证了计算结果的准确性。其他工况的现象也同破冰工况1相同。图9给出了各个疲劳热点下在破冰工况1中的应力范围概率分布曲线,表6给出了不同破冰工况下各热点Weibull参数。
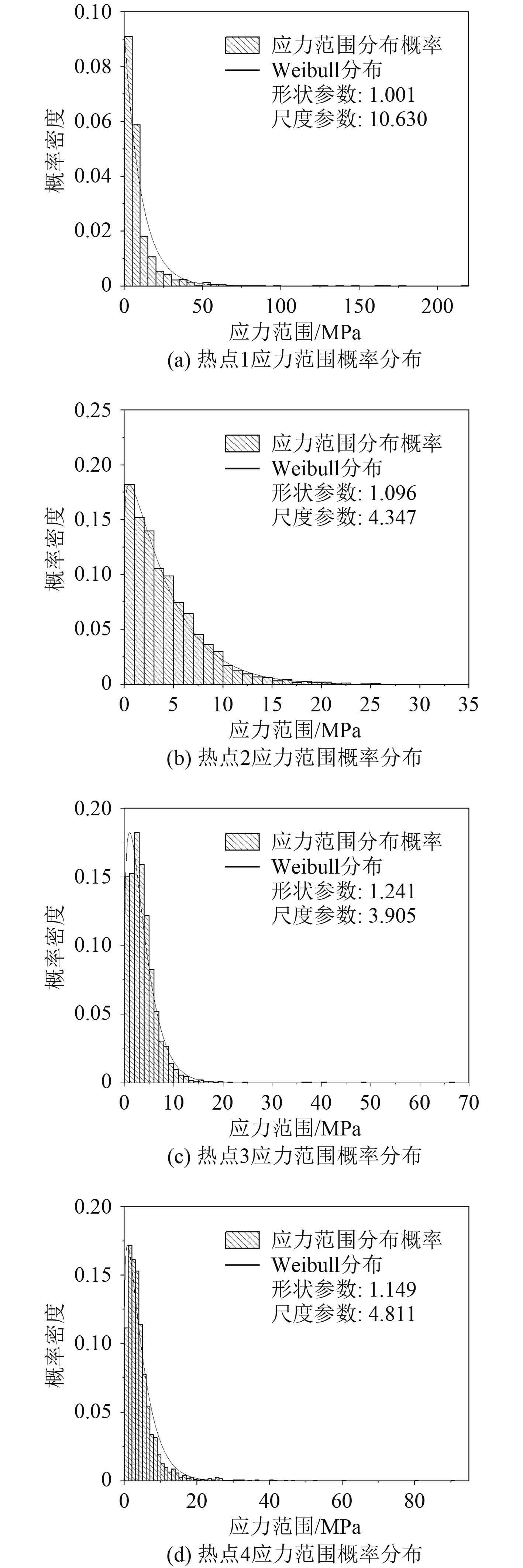
|
图 9 各热点应力范围概率分布 Fig. 9 Probability distribution of stress range for each hot spot |
|
|
表 6 不同破冰工况下各热点Weibull参数汇总 Tab.6 Weibull parameters summary of hot spots under different ice-breaking conditions |
在计算船体典型热点疲劳损伤时,采用疲劳热点应力S-N曲线,并根据热点的焊接形式选取。依据计算结果,热点1、热点4校核危险焊缝采用十字型焊接接头。热点2、热点3校核危险焊缝采用趾端型焊接接头。
按照前述的低温疲劳强度理论进行计算,运用雨流计数法对应力时历曲线进行统计,得出各个应力循环下的均值和幅值,并修正平均应力对于应力幅值的影响。最后结合Palmgren-Miner线性累积损伤理论和试验得出的低温S-N曲线得到各个热点的在雨流计数周期内的累积损伤度,并推导出各个工况单位海里下的总损伤度,给出在设计寿命周期内的总损伤。
从表7可以发现,各个热点的总损伤度均小于1,满足疲劳强度校核。通过分析发现,冰致疲劳与波浪载荷引起疲劳产生的疲劳位置略有不同,船冰碰撞所造成的高应力结构多发生在船体外板区域,船体外板不断与海冰发生碰撞,在交变载荷的作用下,易产生疲劳问题。进行破冰船疲劳强度校核时应该多着重考虑船体结构与海冰发生碰撞的区域。
|
|
表 7 各热点疲劳总损伤度 Tab.7 Total fatigue damage of each hot spot |
本文给出冰致疲劳分析理论,针对有限元计算得出的数据进行分析,包括对应力时历曲线进行处理的雨流计数法、平均应力修正、低温疲劳S-N曲线和Palmgren-Miner线性累积损伤理论。依据文献确定目标海域的冰厚分布情况,设定了3种破冰工况,确定了各个破冰工况下的计算破冰厚度、破冰航速、破冰方式、冰厚分布概率、破冰服役历程等关键参数。提出一种基于长时历计算的船冰碰撞模拟方法,可以较好地满足冰致疲劳载荷分析要求。连续式破冰采用周期性介质分析方法进行了800 s的船冰碰撞模拟,在600 s以后应力范围的Weibull分布趋于稳定,说明计算到800 s时应力时历可以较好体现破冰船疲劳应力范围分布,保证了计算结果的可靠性。通过分析发现,冰致疲劳与波浪载荷引起的疲劳产生的疲劳位置略有不同,船冰碰撞所造成的高应力结构多发生在船体外板区域,进行破冰船疲劳强度校核时应该多着重考虑船体结构与海冰发生碰撞的区域。
| [1] |
张浩辉. 极地船舶结构疲劳分析方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2018.
|
| [2] |
HWANG M R, LEE T K, KANG D H, et al. A study on ice-induced fatigue life estimation based on measured data of the ARAON[J]. Proceedings of the International Offshore and Polar Engineering Conference, 2016, 1262-1267. |
| [3] |
LEE J H, HWANG M R, KWON S W. Analysis of local ice load signals measured on an arctic voyage in 2013[J]. Proceedings of the International Conference on Port and Ocean Engineering under Arctic Conditions, POAC, 2015(1).
|
| [4] |
HISASHI I, YONGSUK S, KIBOK J, et al. Fatigue damage estimation of hull structure of large Arctic LNG carrier due to ice loads[C]// International Conference and Exhibition on Performance of Ships and Structures in Ice 2010, ICETECH, 2010: 233−238.
|
| [5] |
KIM J H, KIM Y. Numerical simulation on the ice-induced fatigue damage of ship structural members in broken ice fields[J]. Marine Structures, 2019, 66(7): 83-105. |
| [6] |
陈传尧. 疲劳与断裂[M]. 武汉: 华中科技大学出版社, 2013.
|
| [7] |
冯国庆. 船舶结构疲劳强度评估方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2006.
|
| [8] |
中国船级社. 极地船舶指南[S]. 北京: 人民交通出版社, 2016.
|
| [9] |
冯国庆, 刘文超, 赵伟栋, 等. DH36钢趾端焊接接头低温疲劳试验[J]. 船舶工程, 2020, 42(9): 93-98. |
| [10] |
ZHAO W, FENG G, LIU W, et al. Research on fatigue properties of typical welded joints of DH36 steel at 60 °C[J]. Applied Sciences, 2020, 10(11): 3742. DOI:10.3390/app10113742 |
| [11] |
胡毓仁, 陈伯真. 船舶及海洋工程结构疲劳可靠性分析[M]. 北京: 人民交通出版社, 1996.
|
| [12] |
IACS. Requirements concerning Polar Class[S]. 2007.
|
| [13] |
徐飞翔. 北极海冰变化及其对春季下行长、短波辐射通量变化的响应[D]. 上海: 上海海洋大学, 2018.
|
| [14] |
董斌, 钱源, 李元泰, 等. 船体(平台)渤海冰区作业安全性分析[J]. 中国舰船研究, 2020, 15(1): 145-151+169. |
 2021, Vol. 43
2021, Vol. 43

