0 引　言

船舶运动数学模型是船舶操纵性、船舶运动控制和航海仿真等研究的基础。2002年，国际海事组织（International Maritime Organization, IMO）通过MSC.137(76) “船舶操纵性标准”决议，提出“缩尺模型试验和/或用数学模型的计算机预测可用于在设计阶段测试其符合性^[1]”，明确规定可以利用船舶运动数学模型加计算机仿真的方法进行船舶操纵性研究。因此，建立准确的船舶运动数学模型具有重要的理论和实践意义，建立船舶运动数学模型的过程称为模型化，即船舶运动建模^[2]。

船舶运动是一个复杂的过程，受多变量耦合、多因素干扰、复杂流体动力学、随机不确定性等方面的共同作用^[3]。目前主要的船舶运动建模方法有船模试验、经验公式、机理建模以及系统辨识等。然而，船模试验建模的经济成本和时间成本高，经验公式方法的建模精度较低或者人工调试繁琐，机理建模应用耗费大量的计算资源、需要丰富的人工经验^[4]。系统辨识作为现代控制理论的重要分支，已成为一种建立被控对象数学模型的重要方法。尤其在船舶运动建模方面，系统辨识方法具有简洁高效、易于操作，并能够实现在线建模等优点，逐步成为船舶运动建模的重要研究方法。

本文从参数可辨识性、辨识模型、辨识算法和辨识数据等方面进行文献综述，分析当前该研究领域存在的问题，并对研究前景进行展望。

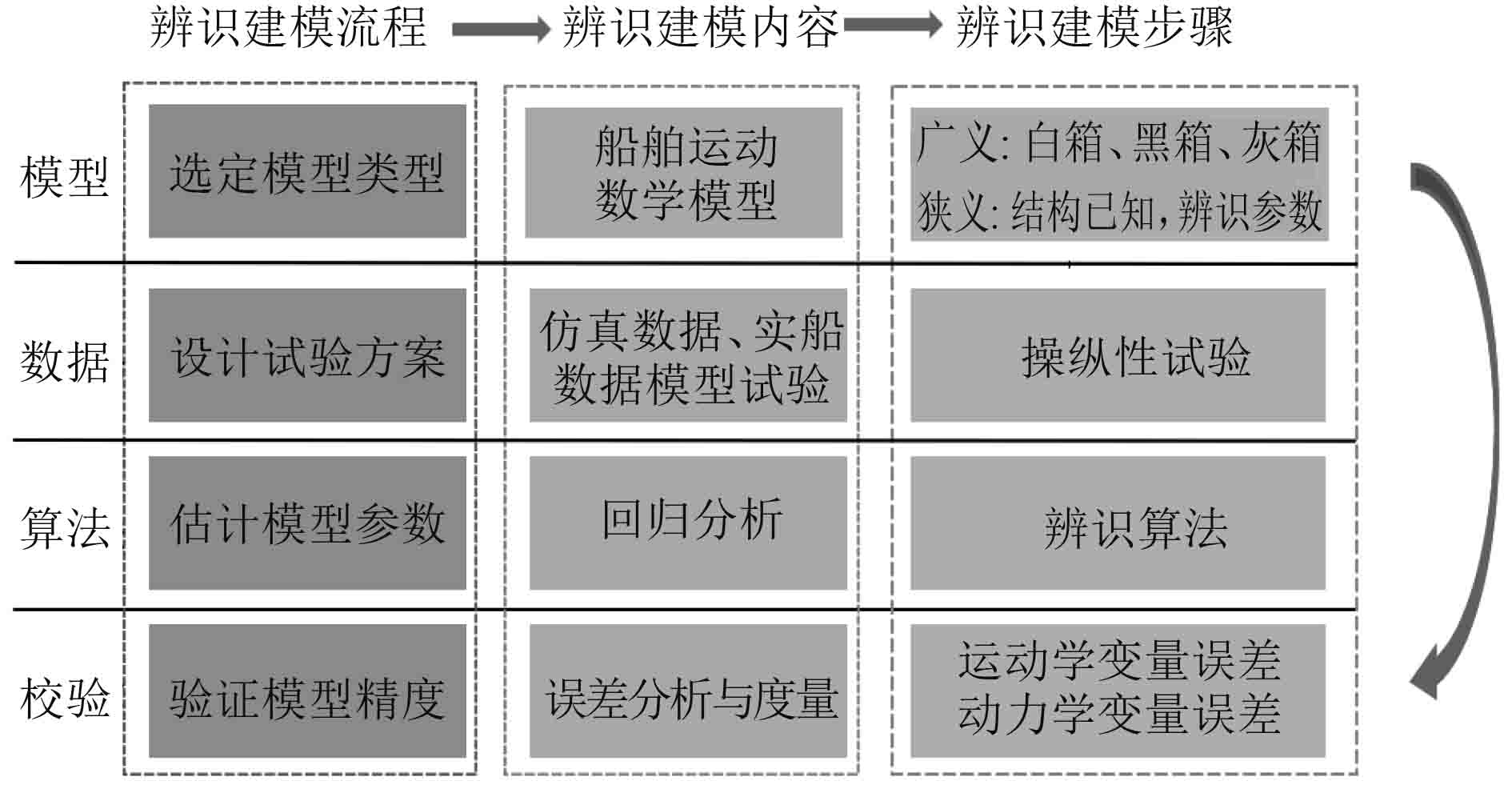
1 国内外研究现状

广义上，船舶运动辨识建模辨识分为白箱、黑箱和灰箱建模，以上分类是根据对模型结构和参数的了解程度确定的^[5]。白箱建模是指对模型结构和参数的意义完全了解，完全不了解的称为黑箱建模，介于二者之间的称为灰箱建模。狭义上，船舶运动辨识建模是指选定模型结构，通过辨识算法和数据确定参数，并具有一定泛化能力的建模方法，当前船舶模型结构方面的研究比较成熟，选定结构辨识参数，是目前主要的辨识建模方法。

如图1所示，船舶运动辨识建模主要包括模型、算法和数据等。目前主要的船舶运动数学模型主要包含响应型（Nomoto模型^[5]）、整体型（Abkowitz模型^[6]和Norrbin模型^[7]）和分离型（MMG模型^[8]）；比较常用的算法包括最小二乘法类算法(LS)、卡尔曼滤波（EKF）、支持向量机（SVM）、神经网络(NN) 、多新息算法（MI）等。辨识数据主要来源于实船试验数据、仿真数据、缩尺模型数据，以上数据大多以Z型试验和旋回试验等操纵性试验获得。

1.1 模型参数的可辨识性

将系统辨识应用于船舶运动建模，其思路将船舶运动视为一个动态的输入和输出系统，通过对数据的拟合和回归分析，确定模型中的参数。但在参数辨识过程中，不是所有的参数都可以通过辨识获得，即参数的可辨识性^[9]。Åström, K. J.首次在文献[10]中对模型参数的可辨识性进行了讨论，对于传递函数形式的响应型模型，如果没有零极点对消的情况，则各参数（K,T₁,T₂,T₃）均具有可辨识性。对于状态空间形式的模型，如该模型是可控的，则各参数也可辨识。此外，罗伟林等^[11]针对状态空间形式的模型的参数辨识，通过细长体理论或者经验公式方式预先设定附加质量矩阵P，再进行其他参数的辨识，辨识精度较高。在此基础之上，罗伟林在文献[12]中针对参数可辨识性的另外一个方面−参数漂移问题进行了讨论，即多重共线性问题，指辨识模型仅针对辨识所用数据表现出正确性，但不适用于其他情况。提出通过相关分析简化模型、模型差分、附加激励等措施解决这一问题。

1.2 辨识模型的选择

目前主要的船舶运动数学模型主要包括响应型、整体型和分离型。综述近年来船舶运动辨识建模的相关文献，响应型模型的参数辨识较为常见，一方面由于其参数的可辨识性强，另一方面其结构简单，参数较少。此外，相关研究中辨识建模常与船舶运动控制等研究结合，响应型模型便于控制器设计等。文献[13-21]中所涉及的辨识模型均为响应型，其中主要以一阶、二阶Nomoto模型为主。此外，以单一的模型辨识为主要研究内容的虽然占一定比例^[13-15]，但更多的是以模型辨识为基础，进行船舶的路径跟踪^[16,18]、减摇控制^[17]、航向保持^[19]等组合式研究，此外，在船舶运动辨识建模方面的研究中，也陆续出现了Abkowitz^[22-23]，MMG^[24-26]，Fossen^[27]等模型的辨识研究，取得了一定的研究成果，但是整体上来看还是以响应型模型辨识为主，并在辨识建模的基础上有进一步的延伸应用。

1.3 辨识算法的发展

船舶运动辨识建模算法中，最小二乘法（LS）作为一种基础性算法，有着广泛的应用。但是该算法存在着过度拟合和矩阵求逆的问题，其中矩阵求逆的可实施性和计算量是其主要限制。为此，递推最小二乘法(RLS)^[10]应运而生，该算法避免了矩阵求逆，可以实现在线辨识。其核心思想是利用当前误差（新息）对上一刻的估计值进行修正，随后出现了P型学习率^[13]和动态遗忘因子λ^[20]调节单个新息权重，多新息算法(MILS)^[15,21]对多个新息重复利用等，提高了辨识精度和收敛速度。卡尔曼滤波(KF)也被广泛的用于船舶模型的辨识中，出现了扩展卡尔曼滤波(EKF)^[28]和无迹卡尔曼滤波(UKF)^[29]等算法，该算法对于非线性系统的辨识效果较好，但也存在参数漂移和动力相消的问题。支持向量机(SVM)作为作为新一代的机器学习理论也被用于船舶模型辨识中，比较典型的有ε -支持向量机(ε -SVM)、最小二乘支持向量机(LS-SVM)^[17]及其他支持向量机类算法^[30-32]，该算法具有完备的理论推导、较强的泛化能力、全局最优等特点^[33]。神经网络(NN)是一种类似于人脑的人工智能算法，其显著特点就是良好的非线性函数逼近能力，为船舶的非线性动力学辨识提供了有效的途径，此外该算法更容易实现在线辨识^[34]，但神经网络应用于船舶模型辨识存在计算量较大的问题。此外，近年来出现一类多新息(MI)^[21]和非线性新息(N-MI)^[35]改进算法，通过对新息（误差信息）的处理，来提高辨识精度和收敛速度，取得了良好的效果，但其中新息长度和非线性系数的确定更多是靠经验公式进行调参。

1.4 辨识数据的来源

辨识数据是船舶运动辨识建模的核心和基础。目前，辨识数据的来源主要包括仿真实验、船模实验和实船试验数据。文献[17-20]对已知模型预设参数，并加入干扰进行仿真实验产生仿真数据，利用此数据进行模型参数辨识，以此来验证算法的有效性。该方法是获得辨识数据的主要方法。此外，船模实验也是产生辨识数据的重要方法。利用船模进行船舶操纵性实验，例如Z型实验和旋回实验^[14-16]产生辨识数据，辨识建模后再进行对应的操纵性仿真实验，对比二者符合度来验证辨识算法的有效性。以上2种辨识数据的产生方法，更多的是对辨识算法的验证性研究。而实船试验则是真正的以船舶运动建模为目的的试验方法，其主要包括缩尺模型^[21]、小型无人船^[25]和实船海试^[36]。利用缩尺模型的操纵性实验数据辨识从而获得原船舶的运动模型，其中缩尺效应会影响模型精度^[37]；利用小型无人船的相关实验数据辨识可较为准确的获得该船的运动模型，但此类实验对数据测量的准确性要求较高^[38]；实船海试的成本较高，可重复性差、数据处理繁琐，在实际应用中并不常见^[39-40]。

2 问题分析与展望 2.1 船舶运动辨识建模中存在的问题

1）辨识数据存在局限性

辨识建模是以数据驱动的建模方法。辨识数据是船舶运动辨识建模的核心和基础。现阶段的辨识建模数据主要来源于计算机仿真和静水中的船模实验，部分实船试验数据也是出自新船出厂时的标准操纵性实验。其辨识数据属于高质量（干扰少或者人为加入干扰）的持续激励信号，能够全面的激发模型特性，从而保证了辨识效果和泛化能力。但这也决定了辨识数据的局限性，尤其在线辨识中，存在外界干扰过大、持续激励不足、数据丢失或者不足等情况，将对辨识效果产生较大的负面影响。

2）辨识算法的理论支撑不足

当前，各类辨识算法层出不穷，既有传统的拟合类算法，也有神经网络类的智能算法。其算法的有效性、收敛性和泛化能力往往是通过仿真对比实验进行验证。但如前所述，高质量的辨识数据并不能全面验证算法性能，还需要充分的理论证明。目前辨识算法的理论证明更多是对收敛性的证明，对于其有效性、泛化能力以及算法的稳定性等方面的理论研究尚且不足。

3）辨识建模的工程应用不足

当前，对于船舶运动辨识建模的研究以辨识算法为主，但是高效的算法与工程应用之间缺乏有效的衔接。例如：利用仿真数据验证的辨识算法，如何保证其泛化能力；利用缩尺模型进行的相关实验，如何避免或减小缩尺效应对辨识效果的影响；实船试验过程中，各类传感器的标准能否满足高质量辨识数据的要求；在线辨识中船舶自有设备能否保证充分的计算能力等。船舶运动辨识建模的主要任务不仅是提出并验证有效的辨识算法，更应该从工程应用的角度出发，注重实用性。

2.2 研究展望

结合文献综述和问题分析，辨识建模将在以下几个方面有更广阔的研究空间和潜力：

1）注重辨识数据的获得、处理和应用。一方面是继续追求高质量辨识数据的获取，保证其可辨识性；另一方面，考虑工程应用，尤其在辨识数据不足或者丢失的情况下保证辨识效果等。

2）完善辨识算法的理论完备性。进一步探究各类辨识算法的理论基础，从算法的提出、构造到效果验证给出完整的理论证明。此外，从理论上探究机理建模与辨识建模之间的联系与区别也是一个值得研究的方向。

3）进一步深入非参数辨识的研究。参数辨识虽然能够充分利用当前成熟的模型结构，简化辨识建模问题。但是也存在着参数可辨识性和多重共线性等问题。脱离模型结构，进行非参数辨识，是辨识建模又一重要研究方向，可以进行深入的拓展型研究。

4）发展在线辨识更有工程应用价值。当前的辨识建模多为离线状态。随着智能船舶的发展，对船舶模型的精度要求越来越高，船舶在航行过程中外界环境和自身状态都在发生变化，在线辨识显得尤为重要，其中涉及在线辨识算法的动态调整、辨识数据的收集和处理等研究具有较强的工程实践意义。

3 结　语

近年来，随着智能船舶时代的到来，船舶运动数学模型的重要性日益凸显，其研究也逐渐深入和全面。其中船舶运动辨识建模因其高效简洁、易于操作等特点，逐渐成为建立船舶运动数学模型的主要方法。当前，船舶运动辨识建模成果丰硕，也必将在船舶操纵、船舶运动控制和航海仿真等领域发挥越来越重要的作用。