目前,很多导航系统都需要磁罗盘来提供辅助航向信息,本文提出基于磁通门传感器设计的磁罗盘应用于航空声呐浮标中,安装在浮标水下声系统定向探头内。航空声呐浮标空投入水后,水面漂浮气囊在海洋表面漂浮,水下声系统部分在海洋深处对潜艇进行测向、定位,当水下声系统探测到目标时需依靠磁罗盘来判断目标相对于磁北的真方位,最终通过水面漂浮气囊天线将目标信息发送出去,从而实现了声呐浮标对目标方位的实时探测。通常设计磁罗盘可以选用的测磁传感器为磁阻效应传感器、霍尔效应传感器和磁通门传感器。磁阻效应传感器应用范围广、测量方便,可以测量小梯度的非均匀磁场及快速时间变化磁场,但温度特性差,易受非线性关系限制[1]。霍尔效应传感器测量范围广、精度高、功耗小、尺寸小、易安装,适合于强磁场测量,但温度特性差,噪声大,灵敏度低[2]。磁通门传感器测量弱磁场范围宽、测量分辨力高、温度特性好、响应迅速、可靠性强,可以长期工作,能够满足声呐浮标的使用需要[3]。受浮标使用环境、体积、重量的限制,本文设计的磁罗盘,具有功耗低、尺寸小、重量轻、可靠性高、误差小的特点。
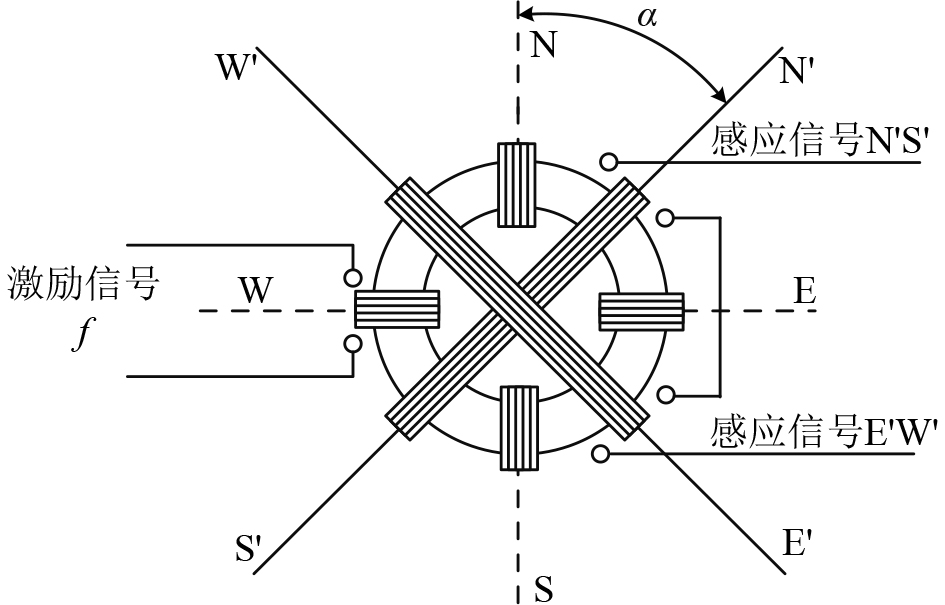
1 磁通门传感器工作原理磁通门传感器为磁饱和式传感器,其选取导磁率高的磁性材料做磁芯材料,在交变磁场的饱和激励下,磁场感应强度与磁场强度存在非线性关系,它是利用这种非线性关系来测量弱磁场的传感器。本文选用的环形正交磁通门传感器,其内部采用阻尼液使磁芯在一定情况下保持水平状态,增加传感器的稳定性,在其工作时激励磁场作用于磁芯上,两路正交的感应线圈将环境磁场调制成偶次感应电势,可用于地磁方位角测量。
环形正交磁通门传感器2组正交的N'S'向感应线圈和E'W'向感应线圈由同一个线圈激励,感应线圈感应环境磁场在其轴向的分量,产生与地磁方向有关的含多次谐波分量的信号,其中二次谐波分量稳定度最好,幅值最大,且其幅度与磁通门传感器N'S'方向偏离真地磁北方向的角度
|
图 1 磁通门传感器工作原理示意图 Fig. 1 Schematic diagram of the working principle of fluxgate sensor |
在一根铁芯上缠绕激励线圈和感应线圈,激励线圈经载流信号激励,根据法拉第电磁感应定律,感应线圈产生的感应电势为:
| $ e = - {10^{ - 8}}\frac{{\rm{d}}}{{{\rm{d}}t}}(W\mu HS)\text{。} $ | (1) |
式中:W为感应线圈匝数;µ为铁芯磁导率;H为载流激励线圈在铁芯上建立的激磁磁场强度;S为铁心横截面积。其中,S,N为不变量,铁芯远离饱和工作状态时,其磁导率µ近似为常数,则感应电势e仅与激磁磁场强度H有关。激磁磁场强度为:
| $ H = {H_m}\cos (2\text{π} {f_1}t) \text{,}$ | (2) |
式中:
| $ e = 2\text{π} \times {10^{ - 8}}{f_1}\mu WS{H_m}\sin(2\text{π} {f_1}t)\text{。} $ | (3) |
该式为变压器效应的理想数学模型。
由于铁芯磁化曲线存在非线性,激励磁场瞬时值变化会引起磁导率µ随之而变。所以,实际变压器效应的数学模型表达式为:
| $ \begin{split} e = &2\text{π} \times {10^{ - 8}}{f_1}\mu (t)WS{H_m}\sin(2\text{π} {f_1}t) -\\ &{10^{ - 8}}\frac{{{\rm{d}}\mu (t)}}{{{\rm{d}}t}}WSH\cos(2\text{π} {f_1}t) \text{。} \end{split} $ | (4) |
激励磁场瞬时值方向呈周期性变化,引起铁芯磁导率
| $ \begin{split} \mu (t) =& {\mu _{0m}} + {\mu _{2m}}\cos(4\text{π} {f_1}t) + {\mu _{4m}}\cos(8\text{π} {f_1}t) +\\ &{\mu _{6m}}\cos(12\text{π} {f_1}t) + \cdots \text{。} \end{split} $ | (5) |
式中:
由于变压器存在于环境磁场中,所以变压器铁芯的外加磁场有激励磁场和环境磁场。若环境磁场实际加在铁芯轴向的分量为
| $ \begin{split} e =& 2\text{π} \times {10^{ - 8}}{f_1}\mu (t)WS{H_m}\sin(2\text{π} {f_1}t) -\\ &{10^{ - 8}}\frac{{{\rm{d}}\mu (t)}}{{{\rm{d}}t}}WSH\cos(2\text{π} {f_1}t) - {10^{ - 8}}\frac{{{\rm{d}}\mu (t)}}{{{\rm{d}}t}}WS{H_0} \text{,} \end{split} $ | (6) |
将式(6)代入
| $ \begin{split} e({H_0}) = & - 2\text{π} \times {10^{ - 8}}{f_1}WS{H_0}(2{\mu _{2m}}\sin(4\text{π} {f_1}t) + \\ & 4{\mu _{4m}}\sin(8\text{π} {f_1}t) + 6{\mu _{6m}}\sin(12\text{π} {f_1}t) + \cdots )\text{。} \end{split} $ | (7) |
由式(7)可以证明,当铁芯磁导率
当铁芯处于周期性过饱和工作状态时,偶次谐波
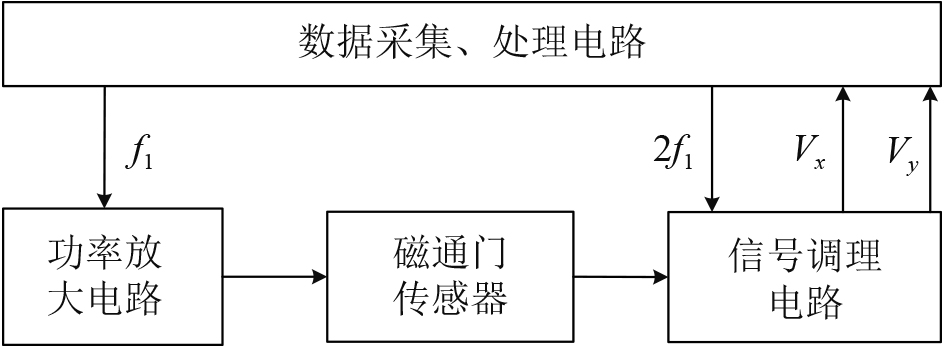
本文设计的磁罗盘组成包括功率放大电路、环形正交磁通门传感器、信号调理电路、数据采集、处理电路。其中信号调理电路由带通滤波电路、相敏检波电路组成,数据采集、处理电路主要包括激励信号及参考信号生成、AD采集和数据计算处理,组成框图如图2所示。
|
图 2 磁罗盘组成框图 Fig. 2 Block diagram of magnetic compass |
激励信号源的选择对磁罗盘性能有着决定性的作用,重点从频率稳定性、相位稳定性以及信号波形等几个方面考虑。磁通门传感器通过激励信号
功率放大电路的重要性能是增益、相移和电压波形,应具有足够的稳定度,且功率要求一定的裕度。FPGA器件对晶振分频输出
传感器感应线圈输出信号中的二次谐波分量表达式为:
| $ \text{N'S'感应信号}\;{H'_0}\cos (\alpha )\sin (4\text{π} {f_1}t)\text{,} $ | (8) |
| $ \text{ E'W'感应信号} \;{H'_0}\sin (\alpha )\sin (4\text{π} {f_1}t) \text{。}$ | (9) |
式中:
|
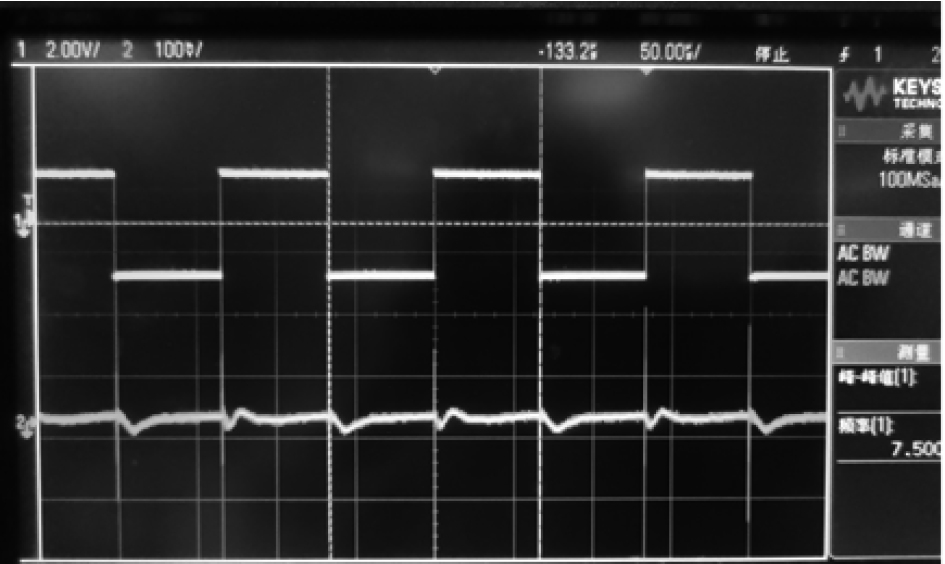
图 3 激励信号与感应信号对比图 Fig. 3 Comparison of excitation signal and induction signal |
调理电路将磁通门传感器N'S'与E'W'向感应输出信号分别经过带通滤波电路和相敏检波电路,彻底滤除所有感应信号中的脉动分量,最终得到仅包含有地磁方位角
1)带通滤波电路
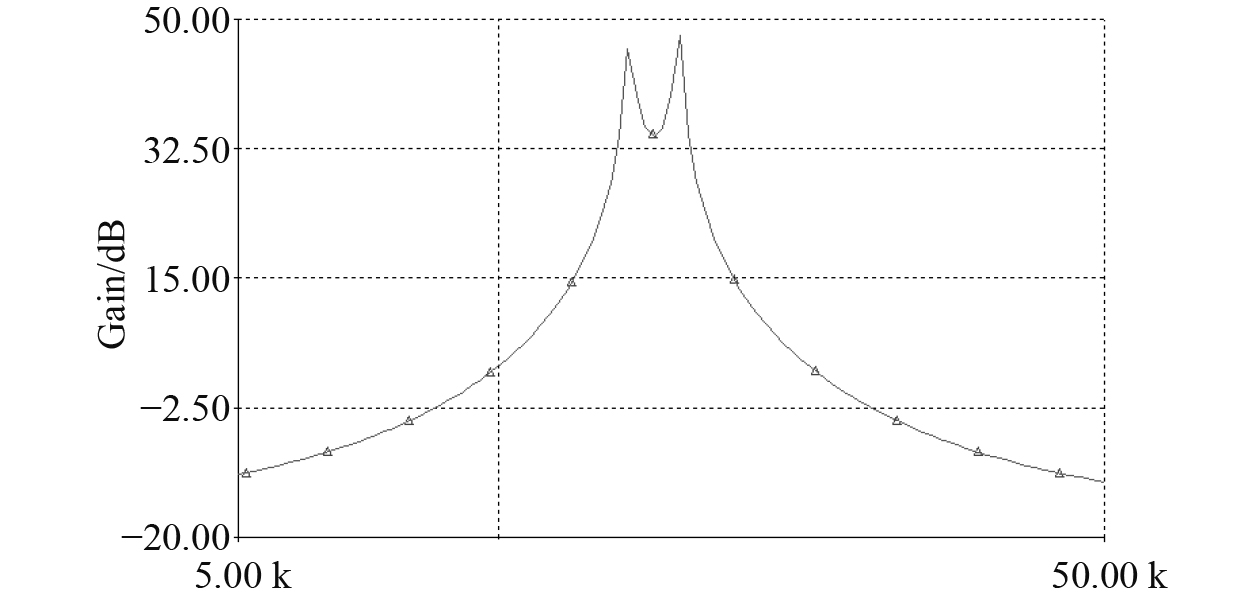
信号调理电路的带通滤波器,主要作用是对感应信号中磁感应信号的二次谐波分量频率信号进行选频,衰减其他多次谐波。本设计中的带通滤波器选用两级双T网络带通滤波器,其具有高Q值,滤波性能稳定,选频特性好的优点,频率响应特性如图4和图5所示。带通滤波器的第一级滤波器中心频率为
|
图 4 带通滤波器幅频特性 Fig. 4 Amplitudefrequency characteristics of a bandpass filter |
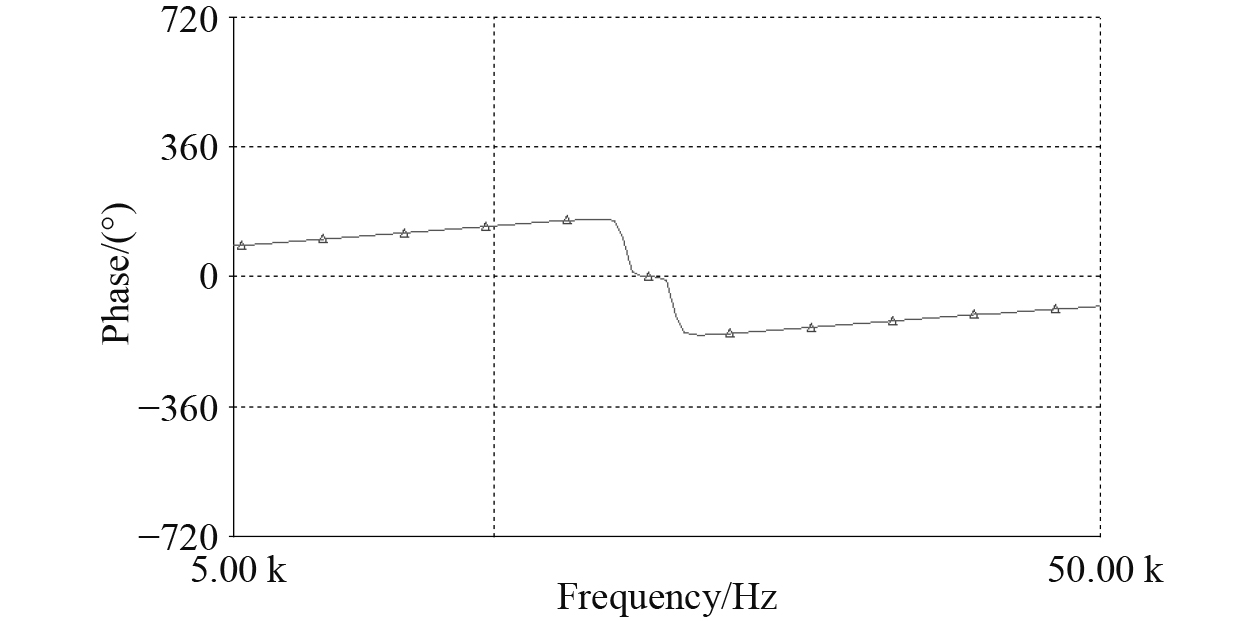
|
图 5 带通滤波器相频特性 Fig. 5 Phasefrequency characteristics of a bandpass filter |
2)检波电路
晶振分频输出
| $ \text{N'S'感应信号}\;{V_x} = {H''_0}\cos (\alpha )\text{,}$ | (10) |
| $ \text{E'W'感应信号}\;{V_y} = {H''_0}\sin (\alpha ) \text{。}$ | (11) |
FPGA控制AD采集磁罗盘两路感应输出信号
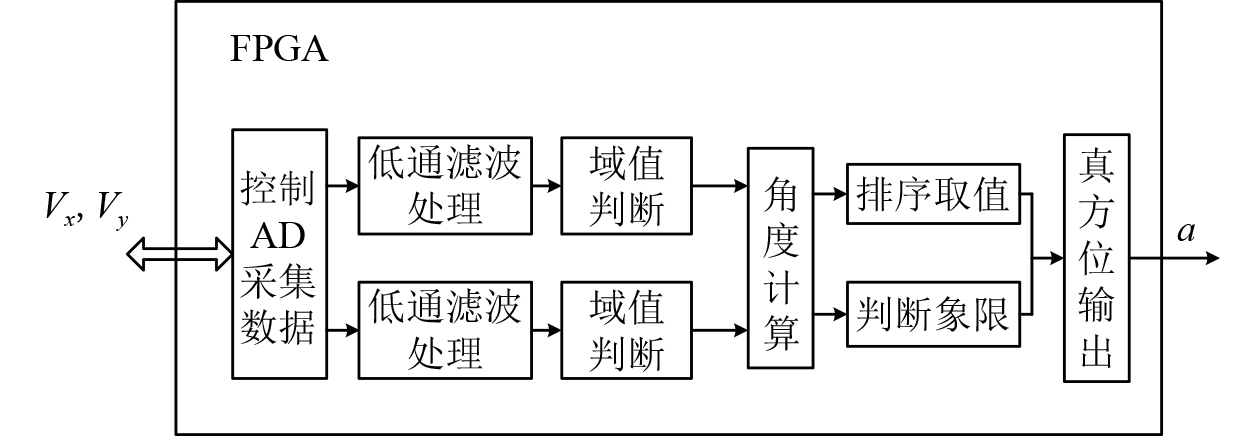
|
图 6 数字信号处理流程图 Fig. 6 Digital signal processing flowchart |
首先对两路感应信号进行低通滤波处理,去除两路感应信号波动或者毛刺产生的野点,同时增加对两路信号合法性判断,需满足:
| $ {G_L} \leqslant {({V_x})^2} + {({V_y})^2} \leqslant {G_H} \text{,}$ | (12) |
式中GL,GH为固定值门限,对于不满足该式的认为是野点,直接剔除。方位角计算式为:
| $ \left| \alpha \right| = \arctan ({{{V_y}}/{{V_x}}})\text{,} $ | (13) |
通过式(13)计算得到磁方位角,然后其值进入一个长队列,对该队列进行取平滑中值输出
| $ \left\{\begin{array}{*{20}{l}} \alpha = \arctan ({{{V_y}} /{{V_x}}})&{V}_{x} > 0\text{,}{V}_{y}\geqslant 0\text{,}\\ \alpha = 90 & {V}_{x}=0\text{,}{V}_{y} > 0\text{,}\\ \alpha = \arctan ({{{V_y}} / {{V_x}}}) + 180 & {V_x} < 0\text{,}\\ \alpha = 270 &{V}_{x}=0\text{,}{V}_{y} < 0\text{,} \\ \alpha = \arctan ({{{V_y}}/ {{V_x}}}) + 360 & {V}_{x} > 0\text{,}{V}_{y} < 0\text{。} \end{array}\right.$ | (14) |
利用测试夹具将磁罗盘安装在无磁转台上进行测试。为防止铁磁物质影响磁罗盘传感器,无磁转台以铝合金材料制作而成,其工作范围为0°~360°,航向精度为6′,航向分辨率为2′。利用指南针将无磁转台的零刻度与磁罗盘的北保持一致,将无转台分别转到10°,30°,60°,90°,120°,150°,180°,240°,270°,300°和330°,通过计算机串口读取磁罗盘方位角,并记录数据。图7为磁罗盘在不同方位上的测磁方位误差图,计算得到均方根误差为0.63°,其中最大偏差为0.96°。

|
图 7 磁罗盘测磁方位角误差曲线 Fig. 7 Magnetic azimuth error curve of magnetic compass |
此处均方根误差指的是每个测量点的实测值与无磁转台显示值的方位差值的均方根误差。计算式为:
| $ \Delta \alpha = \sqrt {{{({{(\Delta {\alpha _1}{\text{ - }}\bar \alpha )}^2} + {{(\Delta {\alpha _2}{\text{ - }}\bar \alpha )}^2} \cdots + {{(\Delta {\alpha _n}{\text{ - }}\bar \alpha )}^2})} \mathord{\left/ {\vphantom {{({{(\Delta {\alpha _1}{\text{ - }}\bar \alpha )}^2} + {{(\Delta {\alpha _2}{\text{ - }}\bar \alpha )}^2} \cdots + {{(\Delta {\alpha _n}{\text{ - }}\bar \alpha )}^2})} n}} \right. } n}}\text{。} $ | (15) |
式中:
引起磁罗盘测量误差的主要原因:1)磁通门传感器本身测磁引入的误差,主要与传感器铁心材料、探头加工装配误差等因素有关;2)信号激励源及参考信号可能存在的不稳定性引起的误差;3)外围电路不稳定引起的误差,其中滤波电路的稳定可靠是整个系统性能的关键;4)测量过程中,磁罗盘对北安装误差及环境杂散磁场引起的误差。综合考虑上述可能引起磁罗盘测磁方位误差的各个因素,在设计之初采取相应的可靠性设计,选用有效、适用于工程批生产的可行措施,将磁罗盘测磁方位误差降到最低。
5 结 语本文根据航空声呐浮标的实际使用需求,提出基于磁通门传感器的磁罗盘设计。该磁罗盘具有功耗低、尺寸小、重量轻、可靠性高、误差小等优点,满足航空声呐浮标性能需求,具有工程指导意义。
| [1] |
HAUSER H., STANGL G., HOCHREITER J. High-performance magnetoresistive sensors. Sensors and Actuators, A81, 2000: 27−31P
|
| [2] |
MAEANAKA K., OHGUSU T., ISHIDA M., et al. Integrated magnetic sensors detecting x, y and z component of the magnetic field. Transducers’87. 1987: 523−526P
|
| [3] |
张学孚, 陆怡良. 磁通门技术[M]. 北京: 国防工业出版社, 1995,
|
| [4] |
李希胜, 王家鑫, 汤程, 等. 高精度磁电子罗盘的研制[J]. 传感器技术学报, 2006, 19(6): 2441-2444. |
| [5] |
CARUSO M J, BRATLAN T, SMITH C H, et al. A new Perspective on Magnetic Sensors[J]. Sensors(USA), 1998, 15(12): 34-46. |
 2021, Vol. 43
2021, Vol. 43
