0 引　言

随着经济全球化时代的到来，从20世纪60年代开始，人类制造的水下噪声与日俱增，噪声问题日益突出，致使海洋生物处于十分危险的境地。因此为了减少航运业对海洋生物的影响，各个组织机构都在寻求解决水下噪声污染问题的方法。“商船水下辐射噪声对海洋生物影响”议题自从国际海事组织环保委员会第57次会议以来一直受到各国的广泛关注，并被列为优先考虑事项。2013年3月国际海事组织设计与备份委员会第57次会议批准了非强制性的“减少商船水下辐射噪声导则”，2014年3月IMO第66届MPC会议上正式审议通过该导则，并对外发布，目的是减小由商船产生的水下辐射噪声对海洋生物可能产生的短期或长期的负面影响，特别是对海洋哺乳动物的影响^[1]。

利用船舶水下辐射噪声水平指向性查找噪声源，分析其对周围海域影响，是控制船舶水下辐射噪声的有效技术手段。但船是个形状极其复杂的空间声源，要想从数学上严格求解形状不规则声源产生的声场是十分困难的，而实船测试是获得其水平指向性的最有效方法^[2]。罗雪峰^[3]提出一种基于线阵的舰船辐射噪声空问分布特性分析方法，刘宁^[4]提出一种基于单水听器的潜艇水下辐射噪声水平指向性测量方法，以上方法简单易行，可以满足船舶指向性测量的需求，但仍然面临2个困难：1）测量单元少，单程数量多，测量时间长，测量效率低，测量角度有限；2）海面布放的系统受风浪影响大，系统自身的抖动造成本底噪声高，低频测量能力弱，测量窗口期短。针对以上问题，本文提出了一种方便、快捷的船舶水平指向性测量方法，利用海底固定式辐射噪声测量系统，通过调节测量单元深度和合理规划船舶机动路径，可以得到水下不同深度平面辐射噪声分布情况，具有海底固定布放、测量单元位置固定、低频测量能力强、测量效率高，测量窗口期长等特点，能高效完成船舶水下辐射噪声水平指向性测量。

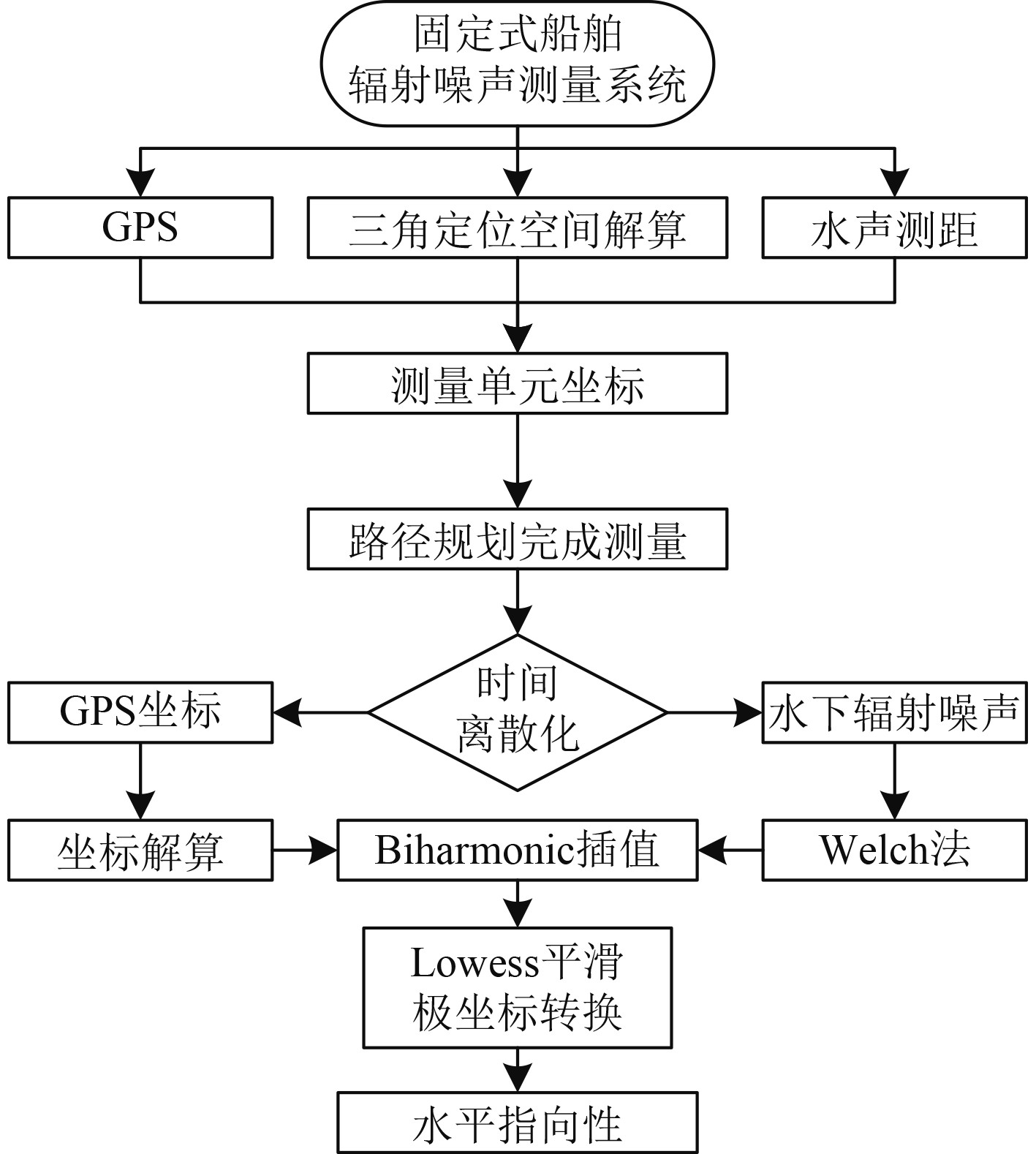
1 水平指向性测量方法

船舶水下辐射噪声水平指向性是指距离船舶等效声中心等距离处测得的辐射噪声级与舷角之间的关系^[5]。为此专门配置了海底固定式测量系统，来完成不同深度平面的辐射噪声测量，再辅以GPS系统和水下多频点三维定位系统，给出目标和测量单元间的空间位置关系，通过合理规划船舶机动路径，得到船舶周围平面内多点水下辐射噪声量级，对辐射噪声数据和位置信息进行同时基联合解算，实现船舶不同深度平面水平指向性测量。具体船舶水下辐射噪声水平指向性测量流程如图1所示。

1.1 测量单元绝对坐标测量

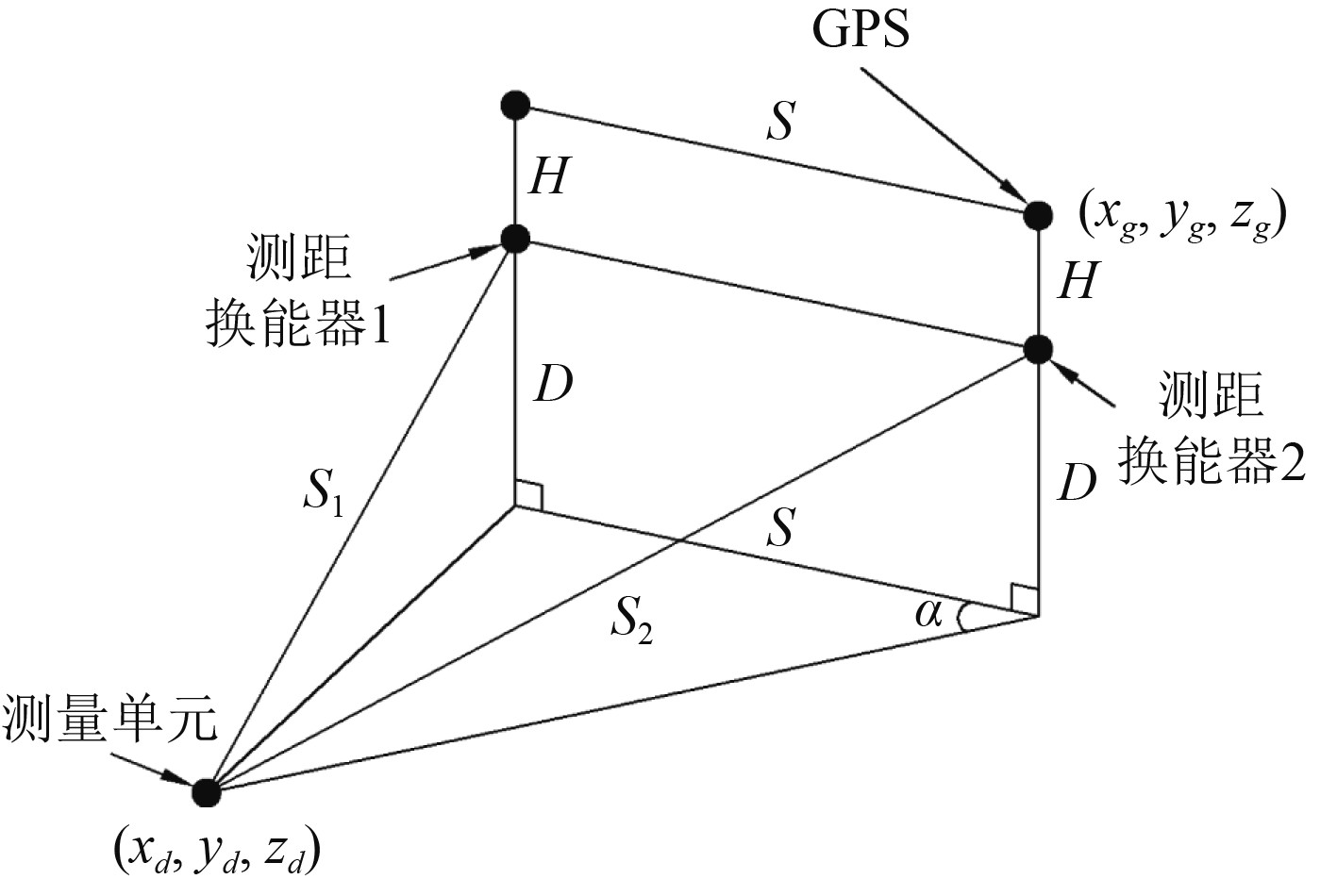
本文采用的空间位置测量原理是多频点测距得到相对位置坐标，再利用GPS得到绝对位置坐标，最后进行空间坐标转换，得到测量单元的大地绝对坐标，测量原理见图2。

在测量船首尾分别放置不同频率的高频换能器，两换能器间距S，在尾部换能器上方放置GPS，其坐标为w_g（x_g，y_g，z_g），换能器和GPS间距离为H，测量单元和测距换能器深度差为D。利用测距换能器可以到测量单元距尾部距离S₁，距首部距离S₂，再依据三角定位原理进行空间位置解算，即可获得测量单元的大地绝对坐标w_d（x_d，y_d，z_d），其坐标求解公式为：

$ \begin{split} & {x_d} = {x_g} \pm \frac{{{S^2} + {S_2}^2 - {S_1}^2}}{{2 \times S}}\text{，} \\ & {y_d} = {y_g} \pm \sqrt {{S_2}^2 - {D^2}} \times acos\left(\frac{{{S^2} + {S_2}^2 - {S_1}^2}}{{2 \times S \times \sqrt {{S_2}^2 - {D^2}} }}\right) \text{，}\\ & {z_d} = {z_g} - (H + D)\text{。} \end{split} $

(1)

1.2 机动路径规划

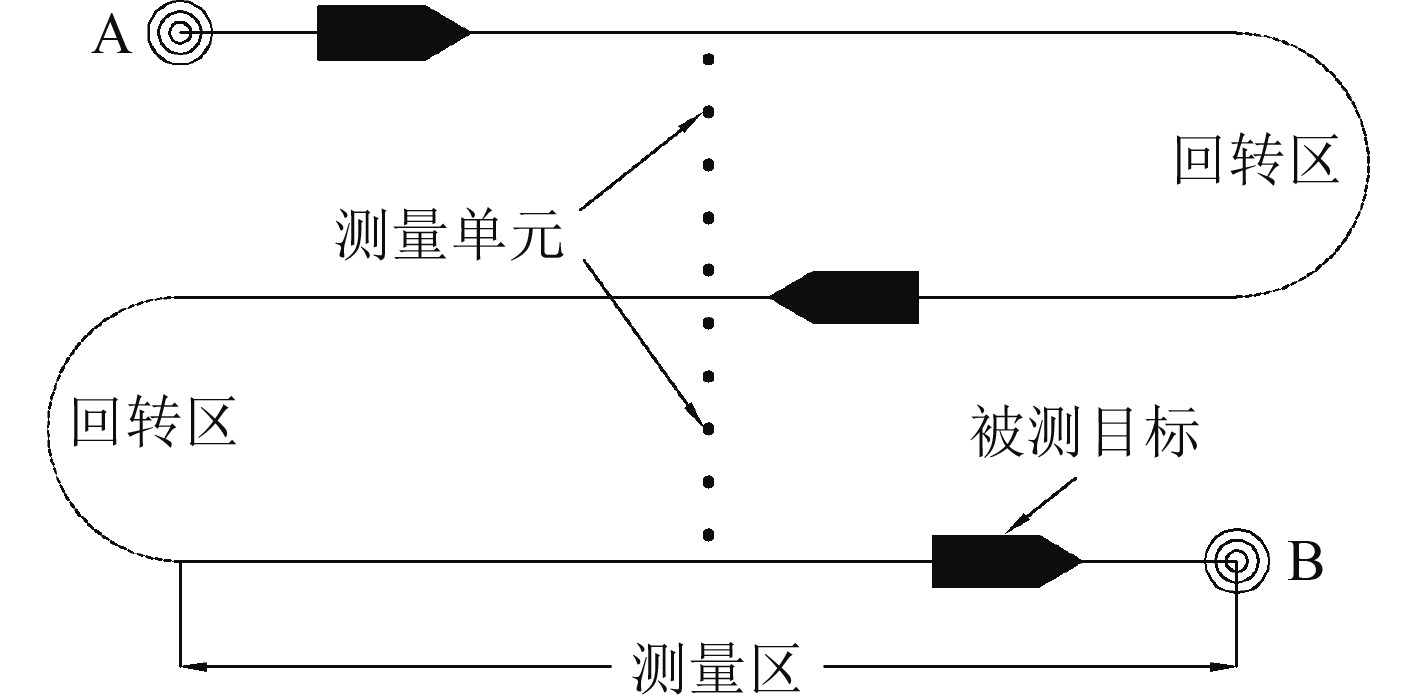
本文设计了一个“S”形船舶机动路径，可快速高效完成水平指向性测量，相对于传统方法具有工况少，时间短，简单可行等特点。如图3所示，在GPS引导下，船舶沿规划路径从A点机动至B点，在测量区保持匀速直线航行且全船设备处于工况设计的指定状态，根据水下辐射噪声概率分布特征，需要完成至少8个有效单程。新方法在测量某一工况时只需要穿越3次测量系统，相较于以往穿越6次测量系统的测量方法测量单程缩减一半，测量效率提高一倍。

1.3 位置解算

分析测量工况下的主要噪声源，确定噪声源位置，建立以噪声源为坐标原点的水平面笛卡尔坐标系，被测船船首为x方向，左舷为y方向，根据船上GPS位置信息w_s（x_s，y_s，z_s），可以解算得到测量单元坐标w_z（x_z，y_z，z_z），其求解公式为：

$ \begin{split} & {x_z} = ({x_s} + \Delta x) \pm {x_d} \text{，} \\ & {y_z} = ({y_s} + \Delta y) \pm {y_d} \text{，} \\ & {z_z} = ({z_s} + \Delta z) - {z_d} \text{。} \end{split} $

(2)

其中： $ \Delta x $ ， $ \Delta y $ ， $ \Delta z $ 为噪声源位置和船上GPS位置的距离差值。

根据工况航速和测量需求，设置水平指向性测量的时间分辨率 $ \Delta t $ ，即每隔 $ \Delta t $ 时刻，给出一组辐射噪声测量结果，则某一直航测量段测量单元位置信息分段处理后可表示为：

$ {W_{ai}} = [\begin{array}{*{20}{c}} {{w_{{z_{i1}}}}}&{{w_{{z_{i2}}}}}&{\cdots}&{{w_{{z_{in}}}}} \end{array}] \text{，}$

(3)

每一单程3个直航测量段，则某一单程测量单元位置信息可表示为：

$ {W_{\text{i}}}{\text{ = }}\left[ {\begin{array}{*{20}{c}} {{W_{{\text{a1}}}}} \\ {{W_{{\text{a2}}}}} \\ {{W_{{\text{a3}}}}} \end{array}} \right]{\text{ = }}\left[ {\begin{array}{*{20}{c}} {{w_{{z_{11}}}}}&{{w_{{z_{12}}}}}&{\cdots}&{{w_{{z_{1n}}}}} \\ {{w_{{z_{21}}}}}&{{w_{{z_{22}}}}}&{\cdots}&{{w_{{z_{2n}}}}} \\ {{w_{{z_{31}}}}}&{{w_{{z_{32}}}}}&{\cdots}&{{w_{{z_{3n}}}}} \end{array}} \right]\text{，} $

(4)

某一工况8个有效单程，则测量单元位置信息可表示为：

$ W{\text{ = }}\left[ {\begin{array}{*{20}{c}} {{W_1}}&{{W_2}}&{{W_3}}&{{W_4}}&{{W_5}}&{{W_6}}&{{W_7}}&{{W_8}} \end{array}} \right] \text{。}$

(5)

1.4 噪声数据处理

根据工况航速和测量需求，按水平指向性测量的时间分辨率 $ \Delta t $ 对数据进行分段计算，每一段中心时刻和位置信息中心时刻对齐，左右各取 $ \Delta t/2 $ 时长，记为 $ {x_k}(n) $ 。对每一段数据，采用Welch法再进行分段处理，以此降低测量结果的方差，则每一段数据 $ {x_k}(n) $ 的功率谱估计为^[6]：

$ \begin{split}{\widetilde{P}}_{PER}(\omega )=&\frac{1}{L}{\displaystyle \sum _{i=1}^{L}{P}_{PER}^{i}(\omega )}=\\ &\frac{1}{MUL}{{\displaystyle \sum _{i=1}^{L}\left|{\displaystyle \sum _{n=0}^{M-1}{x}_{k}^{i}(n){d}_{2}（n）}{e}^{-j\omega n}\right|}}^{2}\text{。}\end{split} $

(6)

式中： $ U={\displaystyle \sum {d}_{2}^{2}（n）}/M $ 为归一化因子，保证得到的谱是渐进无偏估计； $ {d}_{2}（n） $ 为所加窗函数，本文选择的是汉宁窗；M为 $ {x_k}(n) $ 再分段后每一小段长度；L为小段数量。

用分贝表示声压级为^[5]：

$ {L_{{x_k}}} = {L_P} = 10\lg \left(\frac{{{{\tilde{ P}}_{PER}}(\omega )}}{{{p_0}}}\right)\text{，} $

(7)

式中， $ {p_0} $ 为基准值，按国际标准选为1μPa。

则某一直航测量段水下辐射噪声信息可表示为：

$ {y_j} = [\begin{array}{*{20}{c}} {{L_{{x_{j1}}}}}&{{L_{{x_{j2}}}}}&{\cdots}&{{L_{{x_{jn}}}}} \end{array}] \text{，}$

(8)

每一单程3个直航测量段，则某一单程水下辐射噪声信息可表示为：

$ {Y_i} = \left[ {\begin{array}{*{20}{c}} {{y_1}} \\ {{y_2}} \\ {{y_3}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{L_{{x_{11}}}}}&{{L_{{x_{12}}}}}&{\cdots}&{{L_{{x_{1n}}}}} \\ {{L_{{x_{21}}}}}&{{L_{{x_{22}}}}}&{\cdots}&{{L_{{x_{2n}}}}} \\ {{L_{{x_{31}}}}}&{{L_{{x_{32}}}}}&{\cdots}&{{L_{{x_{3n}}}}} \end{array}} \right] \text{，}$

(9)

某一工况8个有效单程，则水下辐射噪声信息可表示为：

$ Y{\text{ = }}\left[ {\begin{array}{*{20}{c}} {{Y_1}}&{{Y_2}}&{{Y_3}}&{{Y_4}}&{{Y_5}}&{{Y_6}}&{{Y_7}}&{{Y_8}} \end{array}} \right]\text{。} $

(10)

1.5 绘制水平指向性曲线

通过以上计算得到时间点对齐的位置信息矩阵W和船舶水下辐射噪声信息距阵Y，但这些信息点在平面内散乱无规则，因此需要对测量得到的原始数据进行差值拟合。这里选择Biharmonic样条插值，该方法可以保持原始结果的本质结构和特征，而且算法计算量较小，效率较高^[7]。

通过测量得到了N个已知点的船舶水下辐射噪声声压级，Biharmonic样条插值即转化为解方程组：

$ \left\{\begin{array}{l}{\nabla }^{4}\omega （W）={\displaystyle \sum _{i=1}^{N}{\alpha }_{j}\delta （W-{W}_{j}）}\text{，}\\ \omega （{W}_{j}）={Y}_{j}\text{。}\end{array}\right. $

(11)

式中： $ {\nabla ^4} $ 为Biharmonic算子； $ \delta （W） $ 为单位冲击函数；W表示水平空间内的位置； $ \omega （W） $ 表示W处的声压级。式（11）的通解为：

$ \omega (W) = \sum\limits_{j = 1}^N {{\alpha _j}{\phi _m}(W - {W_j})} \text{，}$

(12)

其中， $ {\alpha _j} $ 满足线性方程：

$ {Y_i} = \sum\limits_{j = 1}^N {{\alpha _j}{\phi _m}({W_i} - {W_j})}\text{。} $

(13)

水平指向性是二维空间平面拟合，因而式（13）中Green函数采用 $ {\phi _m}(W) = {\left| W \right|^2}(\ln \left| W \right| - 1) $ ，利用测量得到的N个位置已知点的船舶水下辐射噪声声压级代入式（13）即可解得 $ {\alpha _j} $ ，从而通过式（12）能够得到任意位置W_j处的水下辐射噪声声压级Y_j。

完成以上插值处理，得到了8个有效单程数据绘制的水平声场分布结果，其中局部密集点的结果可以看做多次的重复测量，通过Lowess算法对结果进行适当的平滑，可以使特征更加明显，这里要注意窗口宽度的选取，过长的窗长容易造成结果失真^[8]。

最后按式（14）把笛卡尔坐标系转换为极坐标系，即可得到不同距离的水平指向性测量结果。

$\left\{\begin{array}{l}r=\sqrt{{x}^{2}+{y}^{2}}\text{，}\\ \theta =\mathrm{arctan}\left(\dfrac{y}{x}\right)\text{。}\end{array}\right. $

(14)

2 声源验证试验

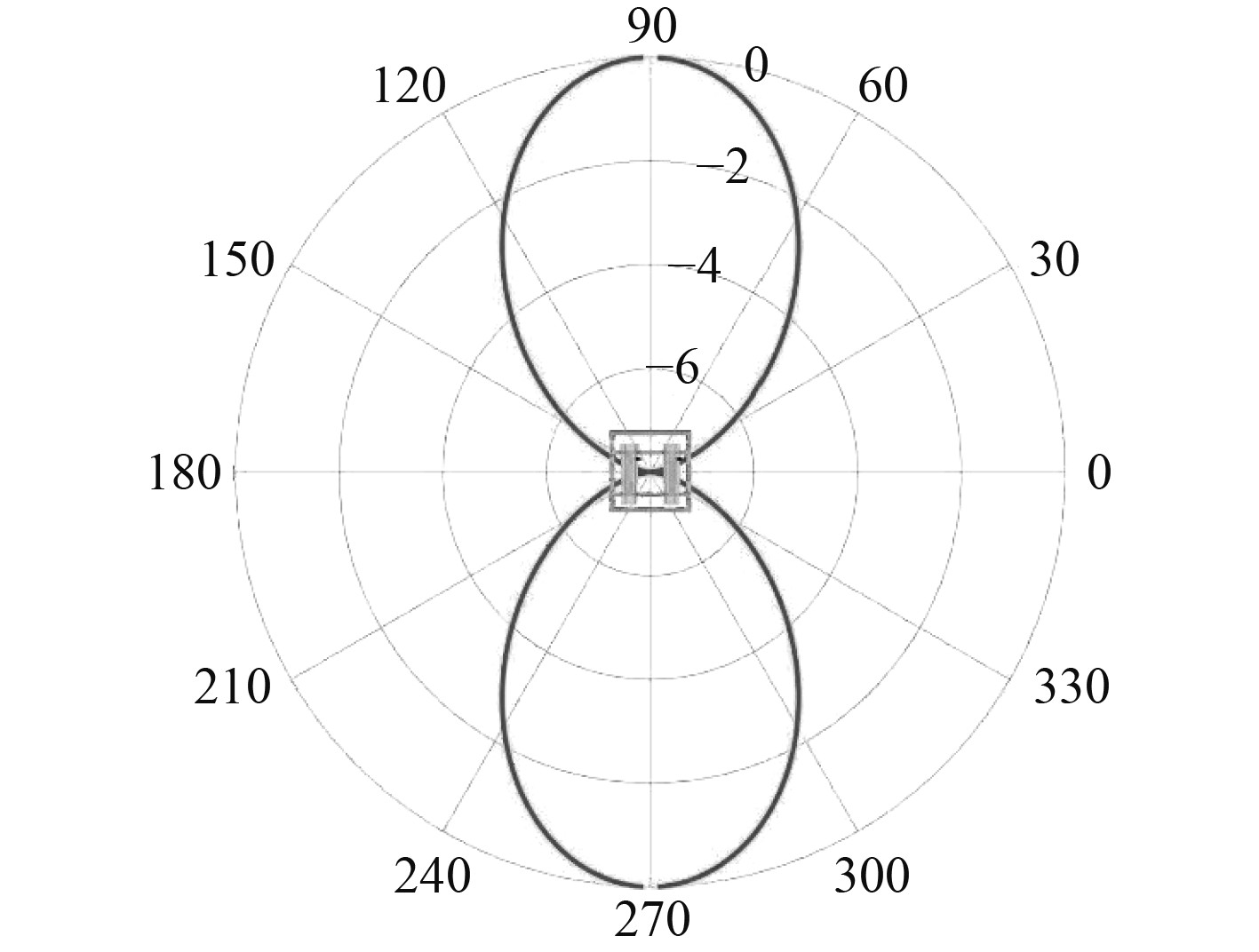
当2个相距1 m放置的点声源，同时发射半波长为1 m的单频信号时，会形成“8”字型水平指向性。以此设计了双声源试验，通过对比理论结果和测量结果验证测量方法的准确性。图4给出了相距1 m单频点源水平指向性理论计算结果。

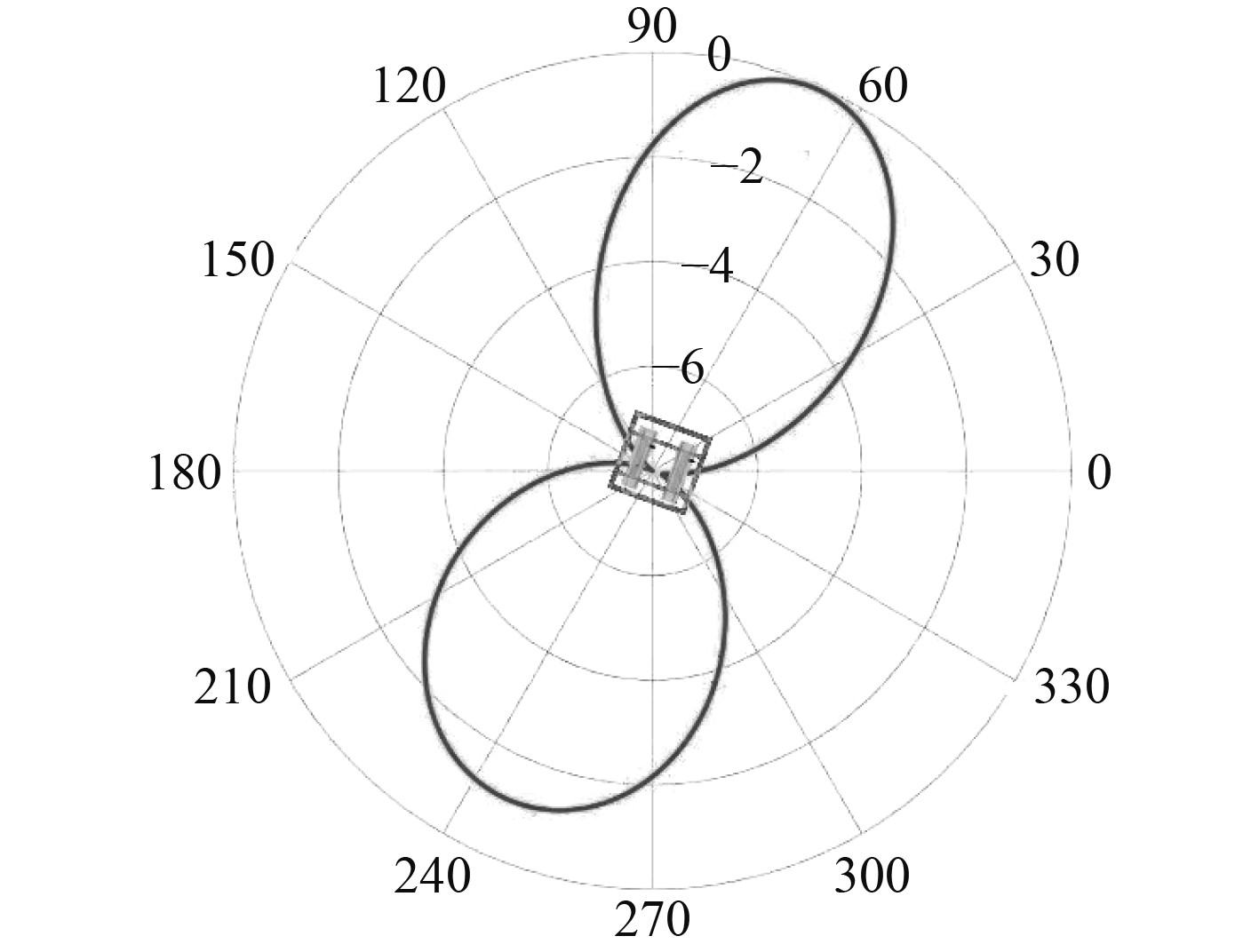
试验当日应用CTD测量试验海区声速为1 508 m/s，经计算754 Hz单频信号半波长为1 m，因此选其作为发射信号。通过渔船拖曳，按水平指向性测量方法完成8个有效单程，测量结果如图5所示。

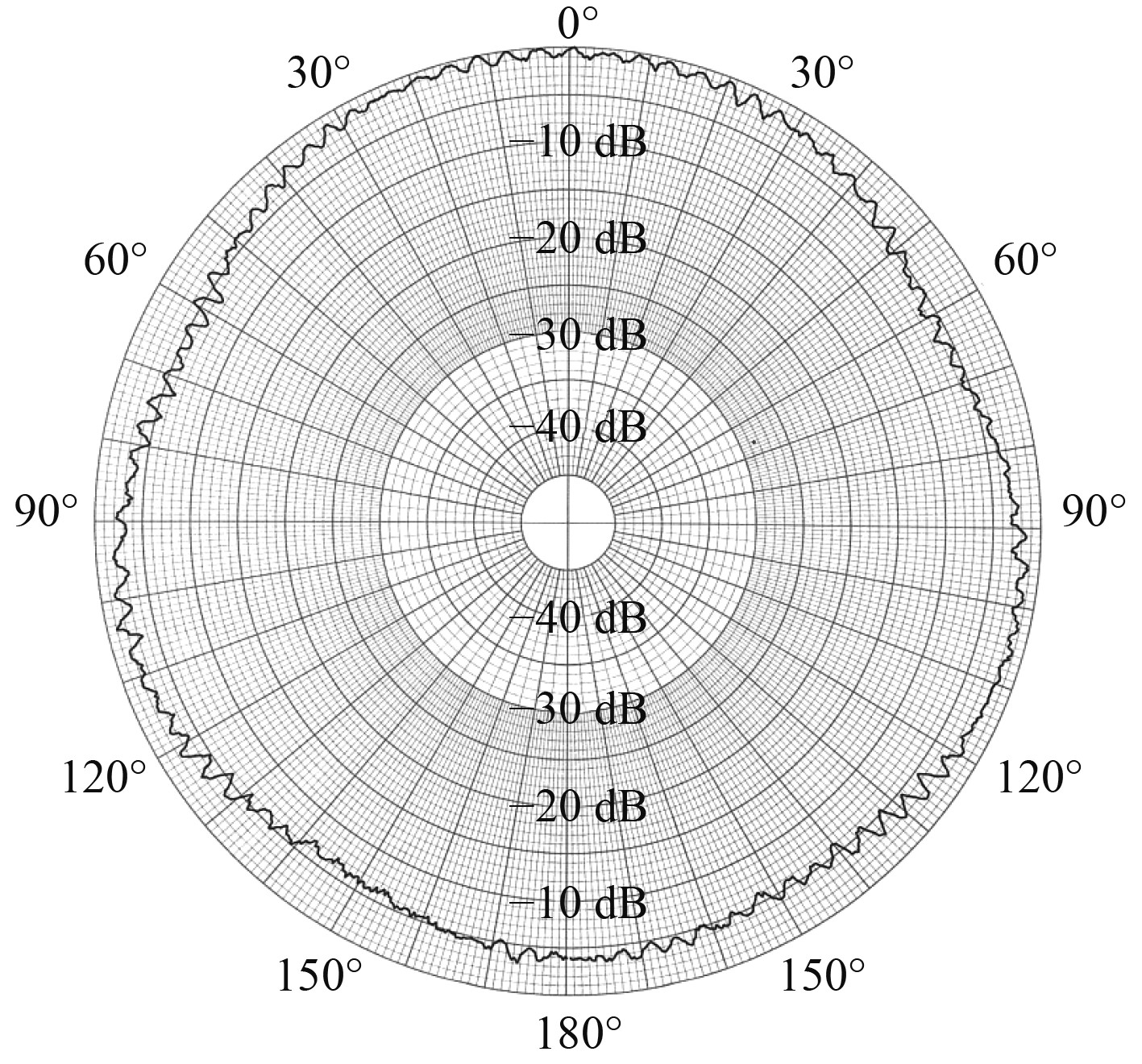
这里给出的是系统测量得到的双声源754 Hz单频信号半径50 m处水平指向性，从图中可以看出，实测结果和理论计算结果皆成“8”字型指向性，区别在于实测结果尾部旁瓣强度稍弱于首部旁瓣。为了进一步探究原因，查找了图6所示的声源800 Hz水平指向性出厂测试结果，声源在该频段具有首部强、尾部弱的指向性特点，与实测结果相吻合。因此，声源验证试验测量结果表明，基于固定式测量系统的船舶水下辐射噪声水平指向性测量方法合理可行，测量结果准确。

3 实船验证试验

为了验证水平指向性测量方法的工程实用性，设计了实船水平指向性测量试验。被测目标为5叶双桨交通艇，设计工况为直航6 kn （660 r/min），此时轴频为11 Hz，叶频为55 Hz。交通艇按水平指向性测量方法沿机动路径完成8个有效单程测量，测量结果如图7～图9所示。

从图7可以看出，在远距离时11Hz轴频信号依然明显，说明固定式测量相较于活动式测量在低频段测量能力明显提高。图中显示交通艇左舷存在明显噪声，上船查明是由于左舷轴系未对中引起的异常振动，造成其噪声量级高于右舷，存在的现象和测量结果相吻合。

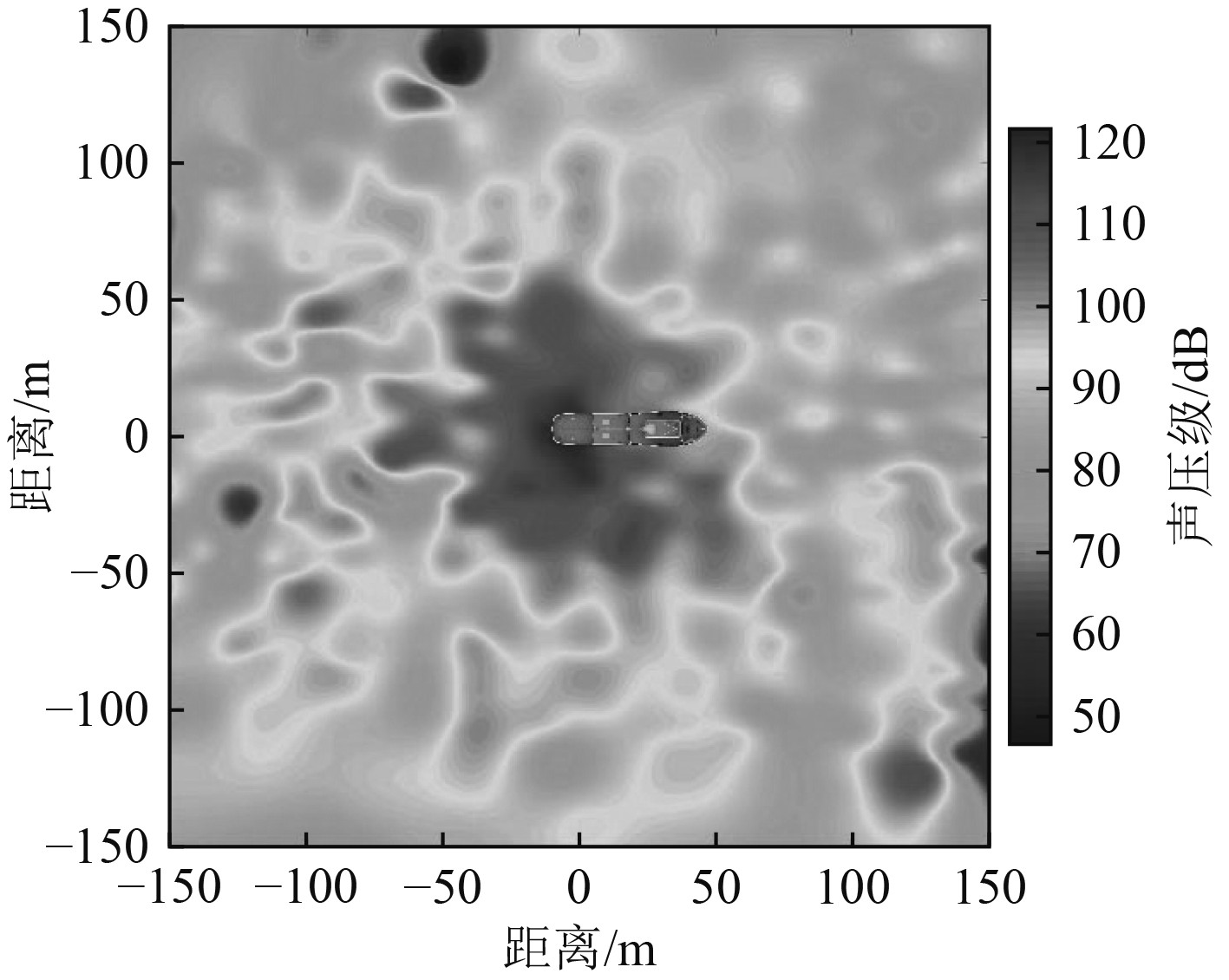
从图7和图8轴频和叶频的声场分布可以看出，单频信号随着距离由近及远具有时大时小的现象，且频率越高，现象越来越明显，说明轴频、叶频在传播的过程中具有波动性，且两桨之间存在相干现象。轴频噪声源位于船中靠后位置，叶频噪声源位于船尾部，和设备所处位置相同，说明通过水平指向性测量可以准确查找噪声源位置。

从图9宽带总声级声场水平空间分布图中可以看出，交通艇主要噪声源位于中部靠后位置，和轴频噪声源位置相同，说明6 kn直航工况主要噪声源为主机及轴系系统。因此，实船验证试验测量结果表明，基于固定式测量系统的船舶水下辐射噪声水平指向性测量方法具有工程实用性，低频测量能力突出，噪声源定位准确。

4 结　语

本文提出了一种基于固定式测量系统的船舶水下辐射噪声水平指向性测量方法，相比以往的方法，测量单程缩减一半，测量效率提高一倍。采用固定式测量系统，测量窗口期长，低频测量能力突出。通过开展2个相距1 m的754 Hz点源水平指向性测量试验，测量结果和理论计算结果相吻合，证明船舶水下辐射噪声水平指向性测量方法合理可行，测量结果准确。通过测量交通艇水下辐射噪声指向性，查明的低频噪声源位置和已知位置相吻合，说明本文提出的方法具备实船测量的工程实用性。