2. 中国科学院机器人与智能制造创新研究院,辽宁 沈阳 110169;
3. 辽宁省水下机器人重点实验室,辽宁 沈阳 110169;
4. 中国科学院大学,北京 100049
2. Institutes for Robotics and Intelligent Manufacturing Chinese Academy of Sciences, Shenyang 110169, China;
3. Key Laboratory of Marine Robotics, Liaoning Province, Shenyang 110169, China;
4. University of Chinese Academy of Sciences, Beijing 100049, China
水声目标识别技术为人类海洋经济与军事活动提供重要决策依据。随着海洋经济的快速发展和海洋开发活动的日益频繁,水声目标识别技术得到越来越多的应用[1]。水下机器人利用前视声呐检测并跟踪前方障碍物时,由于水下环境复杂且不均匀,易受到混响、环境及自噪声的干扰[2-3]。声呐接收的旁瓣信号会在主波束信号横向和纵向形成弧形亮斑干扰,旁瓣的干扰会使图像目标不明确[4]。复杂的环境噪声及障碍物目标成像的不连续性若得不到妥善处理,会影响水下机器人对障碍物目标的检测,进而影响其航行安全[5]。
大量文献调研表明,帧间差分法运算简单,易于实现,是一种实用性较强的运动目标识别方法[6]。差分法是通过对视频中相邻两帧或多帧图像做差分获得目标轮廓的方法[7-8]。针对多波束前视声呐图像中运动目标的检测问题,崔杰等[9]提出一种改进的帧间差分算法,获取视频序列中连续的三帧图像,相邻两帧图像做差分后,将得到的差分图像做或运算,经形态学处理后获得最终图像。然而将此算法实际应用到水下障碍物目标检测时,算法鲁棒性不足。本文针对障碍物检测过程中存在的高噪声、成像不连续的问题,将形态学算子与帧差法相融合,形成目标检测网络。相较于传统的差分法,本算法提高了目标检测的稳定性。同时,将帧间差分图像与当前帧图像进行适当的加权融合,进一步提高了目标障碍物检测的准确性和稳定性。由于水下机器人的运动速度较慢,经比较后选定Mean-shift算法用于对检测后得到的障碍物目标进行跟踪。实验结果表明,本算法在保证实时性的情况下,能够对障碍物目标进行稳定地检测与跟踪,具有广阔的应用前景。
1 基于帧差法的水声目标检测 1.1 二帧差分法获取视频序列中两帧的图像fk-1(x,y),fk(x,y) 将两帧图像进行差分,差分结果取绝对值后进行阈值处理,得到最终二值图像:
| $ {d_{k - 1,k}} = \left\{ \begin{split} & 255,\left| {{f_k}(x,y) - {f_{k - 1}}(x,y)}\right| \geqslant M\text{,}\\ & {0,\left| {{f_k}(x{\text{,}}y) - {f_{k - 1}}(x,y)} \right| < M}\text{。} \end{split} \right. $ | (1) |
其中,M是待选取的阈值。
1.2 三帧差分法获取视频序列中连续的三帧图像fk-1(x,y),fk(x,y),fk+1(x,y),中间帧图像依次与前后两帧图像进行差分,将差分结果取绝对值,并通过阈值分割进行二值化处理:
| $ {d_{k - 1,k}} = \left\{ \begin{split} & {1,\left| {{f_k}(x,y) - {f_{k - 1}}(x,y)} \right| \geqslant T}\text{,}\\ & {0,\left| {{f_k}(x,y) - {f_{k - 1}}(x,y)} \right| < T}\text{,} \end{split} \right. $ | (2) |
| $ {d_{k,k + 1}} = \left\{ \begin{split} & {1,\left| {{f_{k + 1}}(x,y) - {f_k}(x,y)} \right| \geqslant T}\text{,}\\ & {{0,\left| {{f_{k + 1}}(x,y) - {f_k}(x,y)} \right| < T}}\text{。} \end{split} \right. $ | (3) |
其中,T是待选取的阈值。
将差分后的图像进行“与”运算:
| $ B_k =d_{k-1,k} \cap d_{k,k+1} \text{,}$ | (4) |
| $ {f_k}(x,y) = \left\{ \begin{split} & {1,{B_k} = 1} \text{,}\\ & {0,{B_k} = 0}\text{。} \end{split}\right. $ | (5) |
按照式(5),当fk(x,y)=1时,取为前景,当fk(x,y)=0时,取为背景。
1.3 改进差分法在三帧差分法的基础上,为了保证障碍物目标检测的完整性,文献[8]按照式(6),将“与”运算改为“或”运算:
| $ B_k =d_{k-1,k}d_{k,k+1} \text{,}$ | (6) |
为消除零散的噪声与目标中的空洞,按照式(7)对二值图像fk(x,y)进行开闭滤波:
| $ f_k(x,y)={\rm{close}}({\rm{open}}(f_k(x,y)))\text{。} $ | (7) |
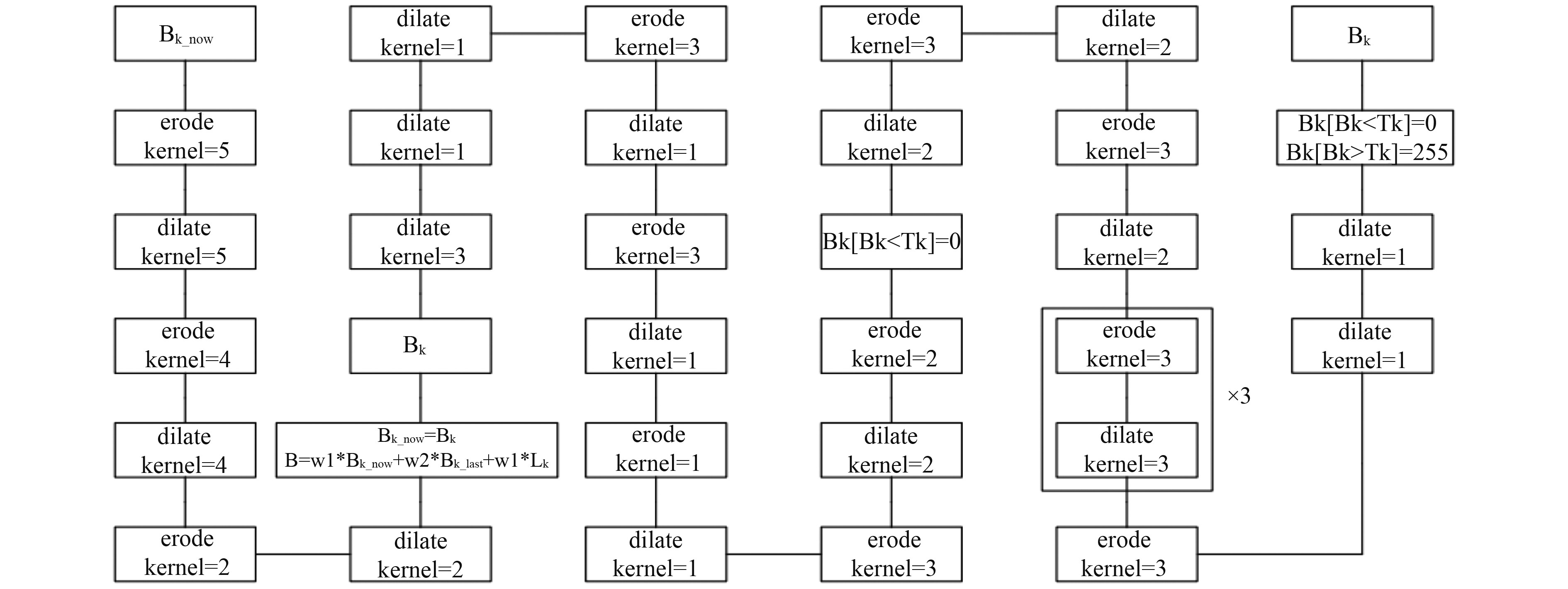
该算法充分利用帧间差分图像与当前帧图像所包含的不同特征信息,将二者按一定权重进行融合,提高了目标检测的稳定性。将形态学算子与上述算法相结合形成网络结构,将预处理后的图像送入此网络,并利用Mean-shift算法对网络输出后的结果进行跟踪。算法流程如图1所示。

|
图 1 算法流程图 Fig. 1 Algorithm flow chart |
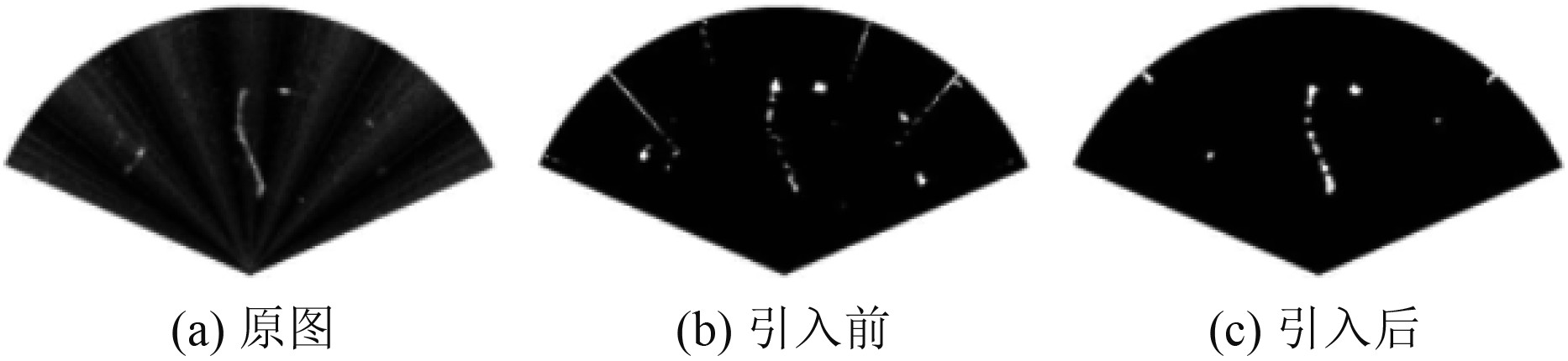
改进差分法[9]中所呈现的结果不尽如人意。针对环境噪声强烈,旁瓣噪声无法有效抑制2个问题进行研究。形态学滤波中,开运算可以过滤掉图像中存在的噪声,闭运算则可填补目标区域内部的空洞。此处将形态学算子视为特殊的卷积核,借鉴了深度神经网络中多层卷积核的思想,将不同大小的形态学算子按照层级进行相应的组合,通过反复的开闭运算,抑制不同程度的环境噪声和旁瓣噪声。因帧差法造成的目标区域内部空缺,也可经卷积核组成的网络,得到较为明显的填补。引入卷积核前后的效果对比如图2所示,可以看出卷积核网络有效抑制了旁瓣噪声和大部分的混响噪声。
|
图 2 卷积核融合效果对比图 Fig. 2 Convolution kernel fusion effect comparison chart |
本节中的“特征”指的是图像经过如差分、形态学算子滤波等运算后保留的信息,特征加权融合即是将图像经过不同运算后所保留的信息进行相应的融合,使得结果尽可能地符合目标检测的要求。
2.3.1 差分图像的融合考虑将当前得到的差分图像与上一时刻得到的差分图像进行适当的加权,以便获得更加完整、稳定的轮廓信息,公式如下:
| $ f_k(x,y)= w_1\times B_k+ w_2\times B_{k\_last} \text{。}$ | (8) |
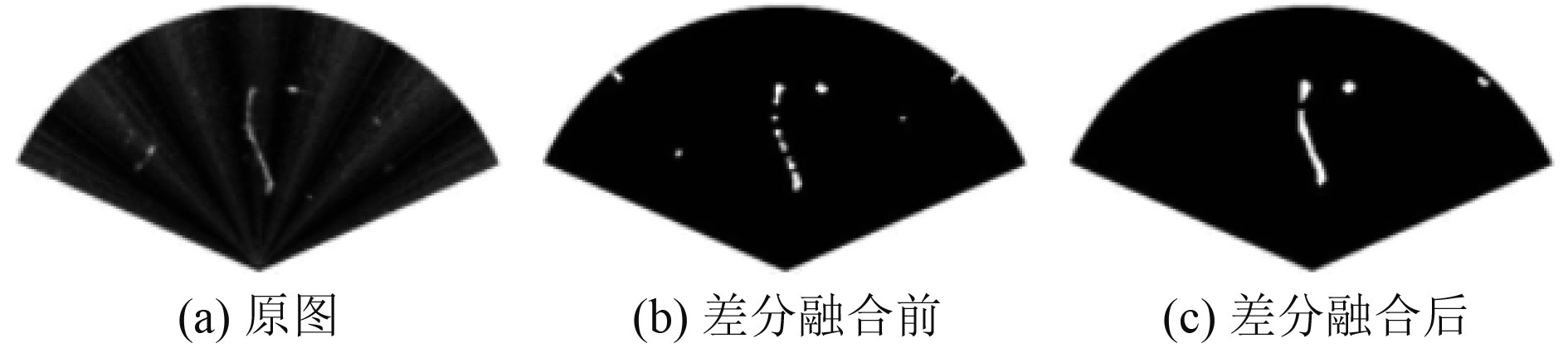
其中,Bk为当前帧的差分图像,Bk_last为上一时刻获得的差分图像,差分融合前后的效果对比如图3所示。从结果可以看出,差分融合使得障碍物目标的检测更加完整,且进一步抑制了混响噪声。
|
图 3 差分融合效果对比图 Fig. 3 Differential fusion effect comparison chart |
图3的结果表明,将2个连续不同时刻得到的差分图像进行融合,可以提高目标检测的完整性和稳定性。将当前帧图像中包含的特征信息也考虑进来,与图3中的差分融合后的图像c进行加权融合,进一步地提高目标检测的效果。公式如下:
| $ f_k(x,y)= w_1\times B_{k\_now}+w_2\times B_{k\_last}+w_3\times L_k \text{。}$ | (9) |
从图4的对比结果可以看出,将帧图像融合到算法中,可使障碍物目标检测得到的结果更加接近真实目标的形状。

|
图 4 帧图像融合效果对比图 Fig. 4 Frame image fusion effect comparison chart |
在差分法的基础上,综合考虑2.2和2.3节中的对比实验结果后,提出本文障碍物目标检测的完整算法,算法流程如下:
步骤1
Lk-2,Lk-1,Lk为包含障碍物目标的连续三帧图像,设定阈值Tk-2,Tk-1,Tk分别为Lk-2,Lk-1,Lk帧图像的灰度像素的均值[10],低于阈值的像素取为0。
Lk-2[Lk-2<Tk-2]=0,
Lk-1[Lk-1<Tk-1]=0,
Lk[Lk<Tk]=0。
步骤2
将相邻两帧图像相减,利用式(10)和式(11)分别得到帧间差分图像dk-2,k-1(x,y),dk-1,k(x,y):
| $ d_{k-2,k-1}(x,y)=|L_{k-1}(x,y)-L_{k-2}(x,y)| \text{,}$ | (10) |
| $ d_{k-1,k}(x,y)=|L_k(x,y)-L_{k-1}(x,y)| \text{。}$ | (11) |
步骤3
取帧间差分图像进行“或”运算:
| $ B_{k\_now}=d_{k-2,k-1}|d_{k-1,k} \text{。}$ | (12) |
步骤4
采用不同大小的椭圆形算子,如表1所示。
|
|
表 1 椭圆形算子名称及大小 Tab.1 Ellipse operator name and size |
将步骤3得到的Bk_now送入加权融合的连续帧差分网络中,得到初步的Bk,,如图5所示。
|
图 5 特征融合网络 Fig. 5 Feature fusion network |
步骤5
| $ B_k=w_1\times B_{k\_now}+w_2\times B_{k\_last}+w_3\times L_k \text{。}$ | (13) |
式中:将当前时刻的差分图Bk_now、上一时刻的差分图Bk_last、当前帧Lk图像进行加权融合得到更加鲁棒的
Mean-shift算法[11-12]采用颜色直方图作为目标的特征,颜色直方图被划分为M个区间,用特征空间中概率密度函数的形式描述特征空间中的目标模板[13],如下式:
| $ q=\{q_m\}_{m=1,\cdots,M} \text{,}$ | (14) |
| $ {q_u} = C\sum\limits_{i = 1}^N {k\left( {{{\left\| {\frac{{{x_0} - x_i^*}}{h}} \right\|}^2}} \right)} \delta [b(x_i^* - u)] \text{。}$ | (15) |
其中:N为目标框中像素的个数;q为目标模板概率密度分布的向量;{xi*}i=1,···,M是框中像素的位置信息;k(x)为核函数;C为归一化常数;h为半径,也称带宽函数,大小等于跟踪框宽度的一半。b(xi*)是将像素点映射到颜色直方图对应的区间,δ为单位脉冲函数。
待跟踪目标映射到特征空间以后,在之后的图像序列中选定可能包含待跟踪目标的区域,也将其映射到特征空间,用概率密度函数的形式描述,p为向量表达形式,pu表示其第u个分量,如下式:
| $ p(y)=\{p_u(y)\}_{u=1,\cdots ,M} \text{,}$ | (16) |
| $ {p_u}(y) = {C_h}\sum\limits_{i = 1}^{{n_h}} {k\left( {{{\left\| {\frac{{y - {x_i}}}{{{h_h}}}} \right\|}^2}} \right)} \delta [b({x_i} - u)] \text{。}$ | (17) |
其中:y表示候选区域的中心坐标;pu(y)为候选区域的第u个特征的概率;hh是带宽;Ch是归一化常量
3.2 相似性度量目标模型与候选模型间以距离公式定义相似度,如下式:
| $ d(y) = \sqrt {1 - \rho [p(y),q]}\text{,} $ | (18) |
| $ \rho [p(y),q] = \sum\limits_{u = 1}^M {\sqrt {{p_u}(y){q_u}} }\text{。} $ | (19) |
其中,d(y)的值越小,候选目标与待跟踪目标的相似性越大。目标是找到一个相似程度最大的候选目标,认定其为跟踪的目标。
3.3 目标跟踪y0是初始的匹配位置,即上一帧图像中的待跟踪目标位置。利用泰勒公式对p(y)在y0处进行泰勒展开,如下式:
| $ \rho [p(y),q] = \frac{1}{2}\sum\limits_{i = 1}^M {\sqrt {{p_0}({y_0}){q_u}} } + \frac{{{C_h}}}{2}\sum\limits_{i = 1}^{{n_h}} {wik} \left( {{{\left\| {\frac{{y - {x_i}}}{{{h_h}}}} \right\|}^2}} \right)\text{,} $ | (20) |
| $ wi = \sum\limits_{u = 1}^M {\sqrt {{q_u}/{p_u}({y_0})} } \delta [b({x_i} - u)] \text{。}$ | (21) |
最大化公式(20),即最大化其第二项。在这个过程中,核函数的值移动到当前帧的目标中心:
| $ {y_1} = \frac{{\displaystyle\sum\limits_{i = 1}^{{n_h}} {{x_i}{w_i}g\left( {{{\left\| {\dfrac{{y - {x_i}}}{{{h_h}}}} \right\|}^2}} \right)} }}{{\displaystyle\sum\limits_{i = 1}^{{n_h}} {{w_i}g\left( {{{\left\| {\dfrac{{y - {x_i}}}{{{h_h}}}} \right\|}^2}} \right)} }} \text{。}$ | (22) |
为了检验特征融合网络算法的有效性,将本算法与二帧差分法、改进差分法进行实验结果的对比。采用4个不同的图像序列进行实验效果展示,其中,序列1是航行器直线航行时所获取障碍物的连续5帧场景(从上至下),序列2是转动航行时所获取障碍物的连续5帧场景(从上至下),序列3与序列4为其余2种障碍物目标的连续5帧场景(从上至下)。选择4组包含不同目标形状、不同运动状态的图像序列可以比较彻底地检测算法的有效性,对比结果如图6~图9所示。a1~a5是原声呐图像序列,b1~b5是经二帧差分法得到的检测结果,c1~c5是改进差分法检测结果,d1~d5为本算法目标检测结果。

|
图 6 序列1 Fig. 6 Sequence one |

|
图 7 序列2 Fig. 7 Sequence two |

|
图 8 序列3 Fig. 8 Sequence three |

|
图 9 序列4 Fig. 9 Sequence four |
从抑制混响噪声的程度评价:二帧差分法与改进差分法一定程度上抑制了混响噪声,然而这2种算法受背景环境影响较大,仍有许多混响噪声未被很好地抑制,在混响噪声变化复杂时这一现象更加明显,如序列3所示。相较于前2种算法,本算法对于混响噪声有较好的抑制效果。
1)从抑制旁瓣噪声程度评价
如序列1、序列4中第四、第5帧图像所示,二帧差分法与改进差分法对旁瓣噪声的抑制能力不足,会产生虚检的情况。本算法对于旁瓣噪声有很好的抑制效果。
2)从目标障碍物检测的完整性评价
水下航行器航行时,由于潜器速度较慢,二帧法表现很差,不能完整地检测出障碍物,且帧与帧之间,障碍物形态变化剧烈,如序列3、序列4所示;改进差分法相对于二帧差分法,检测障碍物的完整性有了一定提升,但是依然存在边缘过渡剧烈、内部出现空洞等现象,并且帧与帧之间障碍物形态变化依然明显,如序列1中第4帧与第5帧图像所示。本算法对于障碍物目标的形态能够较好被检测出来,并且使其在帧与帧之间过渡平缓自然。
总的来说,当背景噪声复杂、目标移动速度较慢时,二帧差分法几乎失效;改进差分法保留了障碍物的大致轮廓,但是也使障碍物检测的完整程度被严重破坏;本算法使障碍物检测的完整性得到很好的保证。
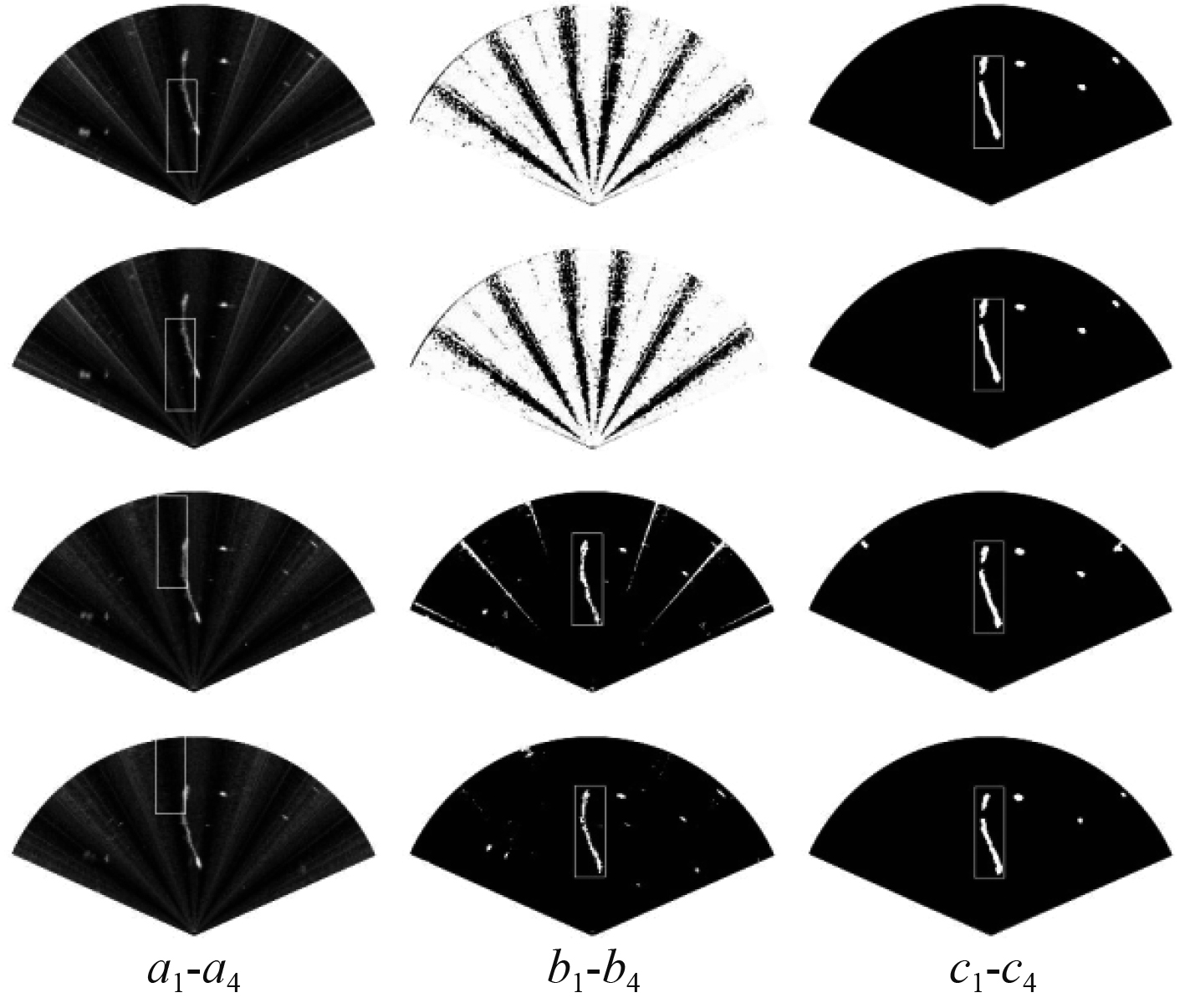
4.2 目标跟踪结果与分析利用Mean-shift算法对障碍物目标进行跟踪,每隔固定时长,截取一帧,作为跟踪结果。以跟踪结果作为检验加权融合特征网络算法有效性的标准。对比结果如图10所示。
|
图 10 跟踪效果对比图 Fig. 10 Track effect comparison chart |
其中,a1~a4是利用Mean-shift算法在原视频序列中直接进行跟踪的结果,b1~b4是利用改进差分法[8]进行目标检测后,再利用Mean-shift跟踪的结果,c1~c4是利用本算法进行目标检测后的跟踪结果。
从结果可以看出,由于大量噪声的存在,Mean-shift在原视频上跟踪失效;改进差分法提升了跟踪目标的有效性,但是由于目标检测及抑制噪声的不稳定性,导致在一些图像帧中目标跟踪失败;本算法由于稳定地检测了目标及有效地抑制了噪声,使得Mean-shift算法能够稳定地跟踪目标。
5 结 语从4个序列的实验对比结果可以看出,传统差分法不适合运动速度较慢的目标检测,并且当目标区域的灰度值在大范围内相似时,目标区域内部会出现空洞。本文提出了加权融合的差分网络算法,较好地解决了传统差分法在水下目标运动缓慢、高噪声场景下存在的问题。针对不同的运动场景、不同的障碍物目标,本算法均显示出良好的抑制噪声、检测障碍物目标的能力。基于实航图像的实验结果验证了本文提出方法的可行性和有效性。
| [1] |
方世良, 杜栓平, 罗昕炜, 等. 水声目标特征分析与识别技术[J]. 中国科学院院刊, 2019, 34(3): 297-305. FANG Shi Liang, DU Shuan Ping, LUO Xin Wei, et al. Feature analysis and recognition technology of underwater acoustic target[J]. Bulletin of Chinese Academy of Sciences, 2019, 34(3): 297-305. |
| [2] |
孙亚晶. 基于深度学习的声呐图像目标识别技术研究[D]. 南京: 东南大学, 2019. SUN Ya Jing. Research of Sonar Image Target Recognition Technology Based On Deep Learning[D]. Nanjing: Southeast University, 2019. |
| [3] |
李庆武, 霍冠英, 周妍. 声呐图像处理[M]. 北京: 科学出版社, 2015: 18−22.
|
| [4] |
温永媛. 合成孔径声呐成像旁瓣抑制算法研究[D]. 昆明: 云南大学, 2016. WEN Yong Yuan. Sidelobe suppression algorithm of synthetic aperture sonar imaging[D]. Kunming: Yunnan University, 2016. |
| [5] |
徐从营, 裴承艳. 基于分区自适应阈值的声呐障碍物检测算法研究[J]. 数字海洋与水下攻防, 2018, 1(2): 1-5. XU Cong Ying, FEI Cheng Yan. Research on obstacle detection algorithm of sonar based on partition adaptive threshold[J]. Digital Ocean & Underwater Warfare, 2018, 1(2): 1-5. |
| [6] |
屈晶晶, 辛云宏. 连续帧间差分与背景差分相融合的运动目标检测方法[J]. 光子学报, 2014, 43(7): 219-226. QU Jing Jing, XIN Yun Hong. Combined continuous frame difference with background difference method for moving object detection[J]. Acta Photonica Sinica, 2014, 43(7): 219-226. |
| [7] |
郭戈, 王兴凯, 徐慧朴. 基于声呐图像的水下目标检测、识别与跟踪研究综述[J]. 控制与决策, 2018, 33(5): 906-922. GUO Ge, WANG Xing Kai, XU Hui Pu. Survey of research on underwater target detection, recognition and tracking based on sonar images[J]. Journal of Control and Decision, 2018, 33(5): 906-922. |
| [8] |
S. Yu, T. Kim, G. Marani and S. K. Choi, Real-Time 3D sonar image recognition for underwater vehicles[C]//2007 Symposium on Underwater Technology and Workshop on Scientific Use of Submarine Cables and Related Technologies, Tokyo, 2007, 142−146, doi: 10.1109/UT.2007.370843.
|
| [9] |
崔杰, 胡长青, 徐海东. 基于帧差法的多波束前视声呐运动目标检测[J]. 仪器仪表学报, 2018, 39(2): 169-176. CUI Jie, HU Chang Qing, XU Hai Dong. Moving target detection for multi-beam forward-looking soanr based on frame-difference method[J]. Chinese Journal of Scientific Instrument, 2018, 39(2): 169-176. |
| [10] |
张俞鹏, 刘志, 任静茹, 等. 基于多波束前视声呐的水下障碍物检测及避障算法[J]. 工业控制计算机, 2020, 33(3): 6-8. ZHANG Yu Peng, Liu Zhi, Ren Jing Ru, et al. Underwater obstacle detection and avoidance based on multi-beam forward-looking sonar[J]. Industrial Control Computer, 2020, 33(3): 6-8. |
| [11] |
陈双叶, 王善喜. 基于五帧差分和改进的Meanshift算法的运动目标跟踪[J]. 计算机科学, 2016(S1): 203-206. CHEN Shuang Ye, WANG Shan Xi. Moving object tracking based on five frame difference and improved meanshift algorithm[J]. Computer Science, 2016(S1): 203-206. |
| [12] |
J. K. Suhr, H. G. Jung, G. Li and J. Kim, Mixture of Gaussians-Based Background Subtraction for Bayer-Pattern Image Sequences[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2010, 21(3): 365−370.
|
| [13] |
张少娜. 基于均值漂移的目标跟踪算法研究[D]. 南京: 南京邮电大学, 2013. ZHANG Shao Na. Research on mean shift based object tracking algorithm[D]. Nanjing: Nanjing University of Posts and Telecommunications, 2013. |
 2021, Vol. 43
2021, Vol. 43
