2. 华中科技大学 能源与动力工程学院, 湖北 武汉 430074
2. School of Energy and Power Engineering, Huazhong University of Science and Technology, Wuhan 430074, China
据统计,全世界约有1/2~1/3的能源由于摩擦而被消耗。与此同时,摩擦引起的磨损也是造成机械设备及零件失效的主要原因之一[1]。随着全世界对节能减排及可靠性的日益关注,科研工作者不断探索减少摩擦、降低磨损的方法与措施。纳米流体是指将少量纳米尺度颗粒(直径小于100 nm)加到水、乙二醇或润滑油等传统基液中所形成的悬浮液,于1995年由Choi[2]提出。有研究表明,相比于传统流体,纳米流体具有较好的导热、减摩等性能。
A.K. Rasheed等[3]对纳米润滑油进行了内燃机台架试验。测试结果表明,在润滑油中加入石墨烯纳米颗粒可使发动机传热速率提升70%,同时活塞组件的磨损也有所降低。高传平等[4]对Fe3O4纳米润滑油进行了摩擦实验。实验结果表明,在纳米润滑油作用下摩擦副表面生成了一层或多层抗摩擦自修复膜,一定程度上起到了抗磨减摩的作用;Hu等[5]采用分子动力学方法,研究得出纳米流体在高载荷下具有减摩特性。
目前,国内外对纳米润滑油的研究大多集中在纳米颗粒对基础油物性参数影响规律及其抗磨减摩性能测试等方面,而采用数值计算方法对纳米润滑油润滑特性的研究则相对较少。本文将纳米润滑油视为一单相流体,基于相关研究所提出的油基纳米流体物性参数模型,以某型16V柴油机为对象,研究CuO纳米颗粒的加入对曲轴主轴承最小油膜厚度、最大油膜压力以及摩擦损失功率等润滑特性的影响,为纳米润滑油的研究及应用提供参考依据。
1 流体润滑基础理论 1.1 基本控制方程基于一定假设,由N-S方程和连续方程可推导出通用Reynolds方程。在此基础上,进一步考虑表面粗糙度的影响,可得到平均Reynolds方程[6],如下式:
| $ \begin{split} & \frac{\partial }{{\partial x}}\left( {{\phi _x}\frac{{\rho {h^3}}}{\eta }\frac{{\partial \bar p }}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {{\phi _y}\frac{{\rho {h^3}}}{\eta }\frac{{\partial\bar p }}{{\partial y}}} \right) = 6U\frac{{(\partial \bar {{h_T})} }}{{\partial x}} + \\ & 6U\sigma \frac{{\partial (\rho {\phi _s})}}{{\partial x}} + 12\frac{{\partial (\rho \bar {{h_T})} }}{{\partial t}} \text{。} \end{split} $ | (1) |
式中:x和y分别表示曲轴主轴承圆周方向和轴向坐标;ρ为润滑油密度;η为润滑油动力粘度;h为名义油膜厚度;σ为表面综合粗糙度;
采用Greenwood/Tripp粗糙接触模型[7],粗糙接触压力如下式:
| $ p_{asperity}= \frac{16\sqrt {2} }{15}\pi (\eta \beta \sigma )^2E'\sqrt {\frac{\sigma }{\beta }} F_{\frac{5}{2}}(H) \text{。}$ | (2) |
式中:H为膜厚比;η,β分别为表面微凸体的密度和曲率半径。
2 纳米流体物性参数模型 2.1 密度模型纳米流体密度采用Pak等[8]提出的数值模型,如下式:
| $ {\rho _{nf}} = {\rho _p}\phi + {\rho _{bf}}(1 - \phi )\text{。} $ | (3) |
式中:ϕ为纳米颗粒体积浓度。下标nf,bf,p分别代表纳米流体、基础液和纳米颗粒。该模型理论计算值与M. Saeedinia等[9]测得的CuO纳米润滑油实验值较为一致。
2.2 比热容模型文献[10]提出一种纳米流体比热容模型,如下式:
| $ {(\rho {C_p})_{nf}} = (1 - \phi ){(\rho {C_p})_{bf}} + \phi {(\rho {C_p})_p} \text{。}$ | (4) |
将式(4)代入式(5),经整理可得:
| $ {C_{{p_{nf}}}} = \frac{{(1 - \phi ){{(\rho {C_p})}_{bf}} + \phi {{(\rho {C_p})}_p}}}{{{\rho _p}\phi + {\rho _{bf}}(1 - \phi )}} \text{。}$ | (5) |
式中,Cp为比热容。
2.3 粘度模型在对纳米流体粘度进行分析时,Krieger等[11]考虑到颗粒的聚集作用,提出了以下数值模型:
| $ \frac{{{\eta _{nf}}}}{{{\eta _{bf}}}} = {\left(1 - \frac{\phi }{{{\phi _m}}}\right)^{ - [\eta ]{\phi _m}}}\text{。} $ | (6) |
式中:ϕm为最大颗粒浓度;[η]为特征粘度。
Chen等[12]考虑到颗粒聚集体内部密度的不一致性,对Kriegere-Dougherty模型作进一步修正,如下式:
| $ \frac{{{\eta _{nf}}}}{{{\eta _{bf}}}} = {\left(1 - \frac{\phi }{{{\phi _m}}}{\left(\frac{{{a_a}}}{a}\right)^{3 - D}}\right)^{ - [\eta ]{\phi _m}}} \text{。}$ | (7) |
式中:aa,a分别为纳米聚集体和纳米颗粒的等效半径;D为不规则指数。
Kole等[13]在对CuO纳米润滑油粘度特性进行研究时,ϕm,[η],D值分别取0.5,2.5和1.7。通过粘度对比和动态光散射(DLS)分析验证,取aa=7.15a。考虑到柴油机轴承润滑油剪切率较高,ϕm取0.605[14]。因此,本文所采用的CuO纳米润滑油粘度模型如下式:
| $ \frac{{{\eta _{nf}}}}{{{\eta _{bf}}}} = {\left(1 - \frac{\phi }{{0.605}} \times {7.15^{1.3}}\right)^{ - 1.51}}\text{。} $ | (8) |
采用由Sadegh.A等[15]建立的纳米润滑油热传导模型,如下式:
| $ \begin{split} {K_{bf}} =& (3.9 \times {10^{ - 5}} - 0.0305){\phi ^2} + (0.086 - \\ & 1.6 \times {10^{ - 4}}T) \times \phi + {\kern 1pt} 3.1 \times {10^{ - 4}}T + \\ & 0.129 - 5.77 \times {10^{ - 6}}{K_{np}} - 40 \times {10^{ - 4}} \text{。} \end{split} $ | (9) |
式中:T为纳米流体平均温度。该模型是基于最小二乘法对多组实验数据拟合而成,相比其他模型更加适用于油基纳米流体热传导系数的计算。
2.5 物性参数值基于上述纳米流体物性参数模型,以体积分数为2.0%的CuO纳米润滑油为例,其主要物性参数如表1所示。
|
|
表 1 CuO、SAE40及纳米润滑油主要物性参数表 Tab.1 Main physical properties of nano-CuO oil |
以某型16V柴油机为原型,开展CuO纳米润滑油对曲轴主轴承摩擦润滑特性影响研究。该型柴油机主要结构参数如表2所示,标定工况下缸内压力如图1所示。
|
|
表 2 某型16V柴油机主要结构参数表 Tab.2 Main structure parameter of the 16V diesel engine |
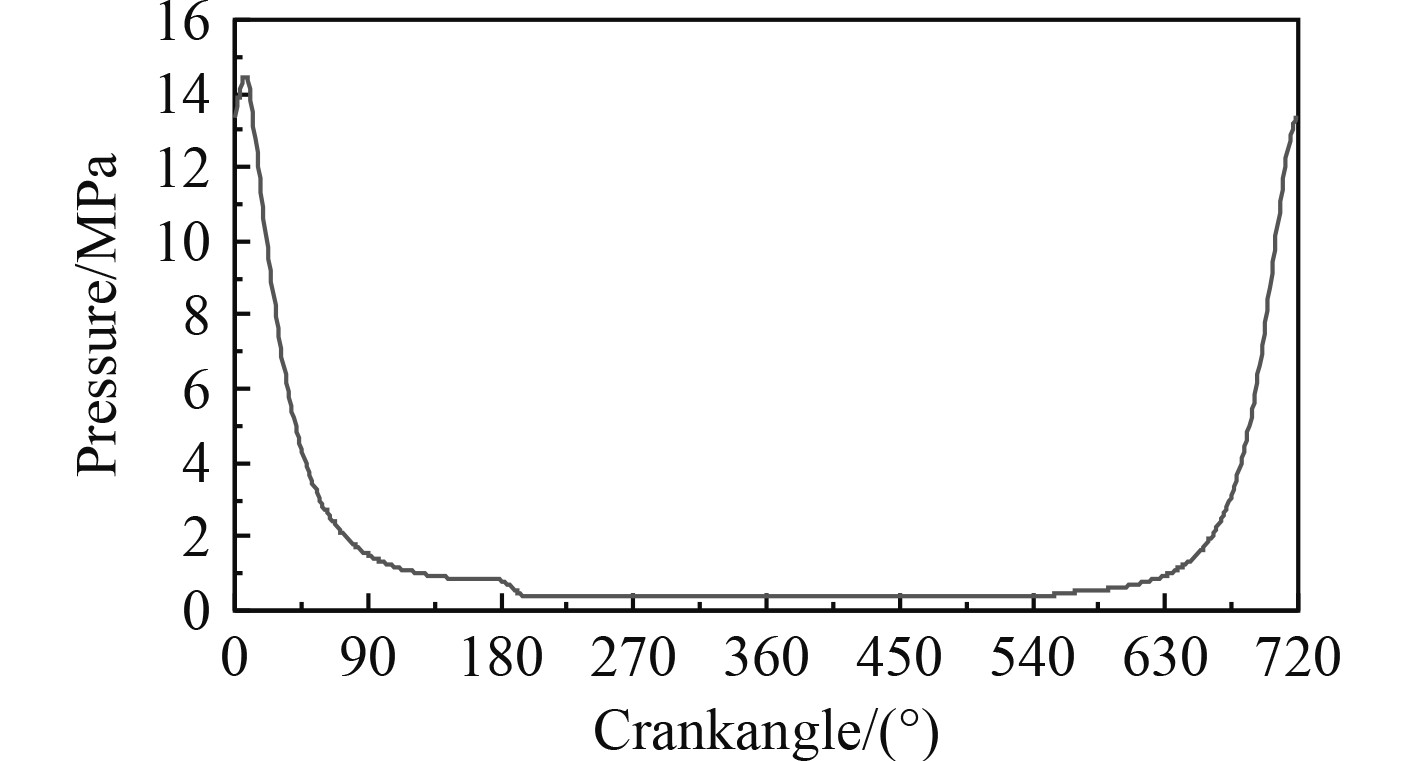
|
图 1 标定工况下缸内压力示功图 Fig. 1 Cylinder pressure under the calibration condition |
基于AVL EXCITE,建立该型柴油机曲柄连杆机构动力学模型,主要包括体单元(活塞、连杆、曲轴、轴承座等)和连接单元(活塞-缸套连接、轴承连接等),如图2所示。
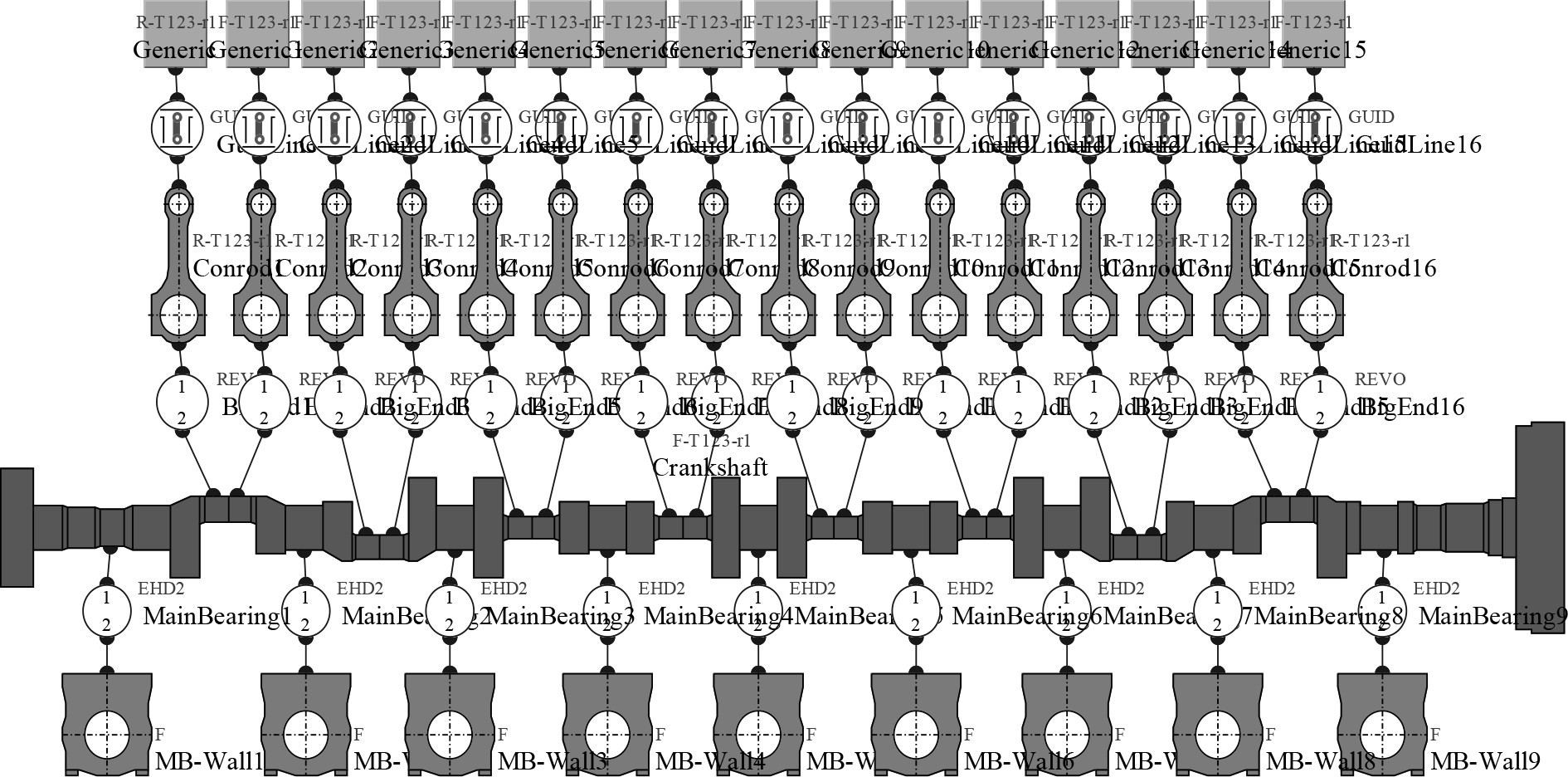
|
图 2 某型16V柴油机曲柄连杆机构虚拟样机模型 Fig. 2 Virtual prototype model of crank and rod mechanism |
对模型中的单元属性进行定义,并根据需要设置柴油机全局参数和载荷工况等。在Hypermesh中对曲轴及轴承座等部件进行网格划分,通过子结构缩减计算获得所需的节点质量、刚度等信息。最终,建立曲柄连杆机构三维动力学数值模型,如图3所示。

|
图 3 16V柴油机曲柄连杆机构三维动力学模型 Fig. 3 3D dynamic model of crank and rod mechanism |
采用弹流动压润滑连接单元,考虑表面粗糙度和温度的影响,对曲轴主轴承润滑特性进行仿真分析。曲轴主轴承润滑性能计算参数如表3所示。
|
|
表 3 曲轴主轴承润滑计算参数 Tab.3 Main bearing lubrication calculation parameters |
标定工况(1 050 r/min)下,基于SAE40润滑油进行曲轴主轴承润滑性能分析,各主轴承载荷、最小油膜厚度及摩擦损失功率如图4所示。
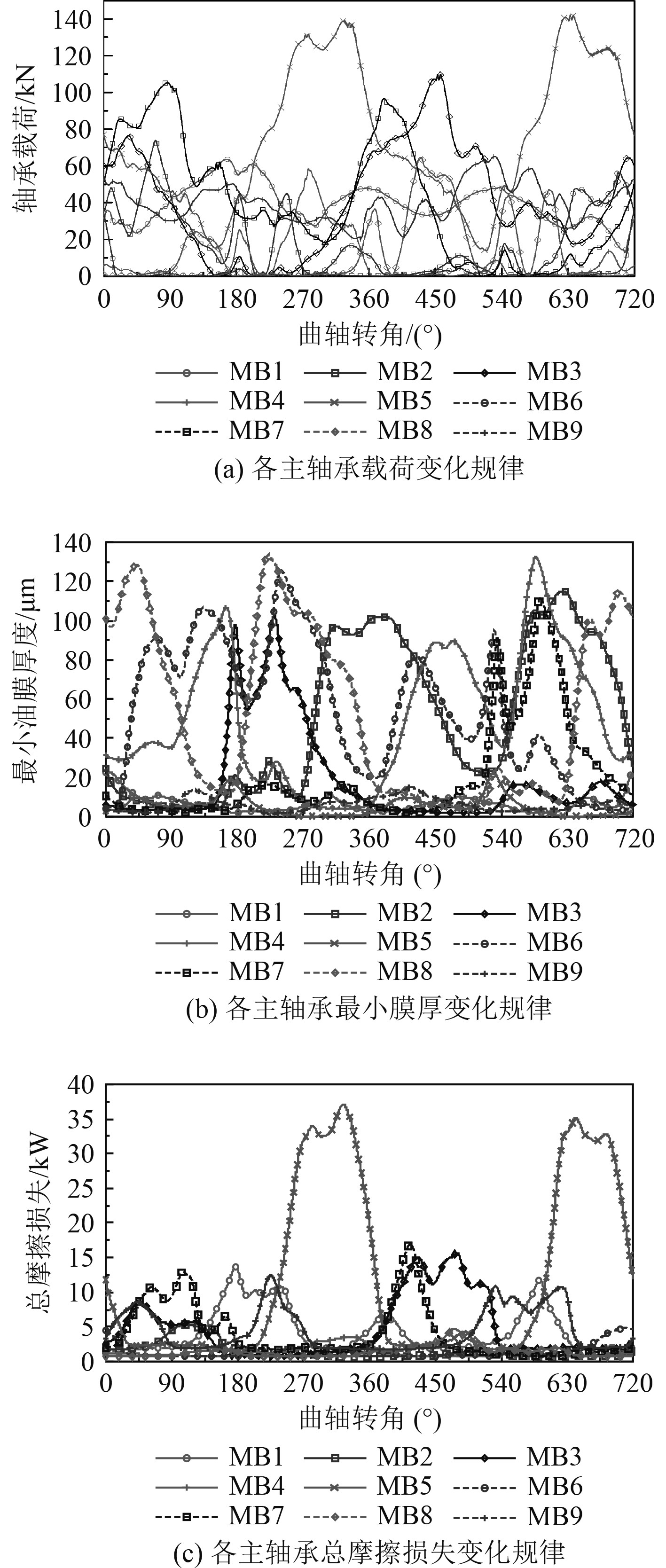
|
图 4 标定工况下各主轴承润滑特性 Fig. 4 Lubrication characteristics under the calibration condition |
通过对比可知,标定工况下第5主轴承最大轴承载荷及总摩擦功率损失均为最大,而最小油膜厚度最薄,仅为0.5 μm。由此可知,与其余主轴承相比,第5主轴承工作状况最为恶劣,润滑性能最差。
4.2 纳米润滑油对主轴承润滑性能影响分析由于第5主轴承润滑性能最为恶劣,以第5主轴承为研究对象,对比分析不同体积分数纳米润滑油对曲轴主轴承润滑性能的影响。
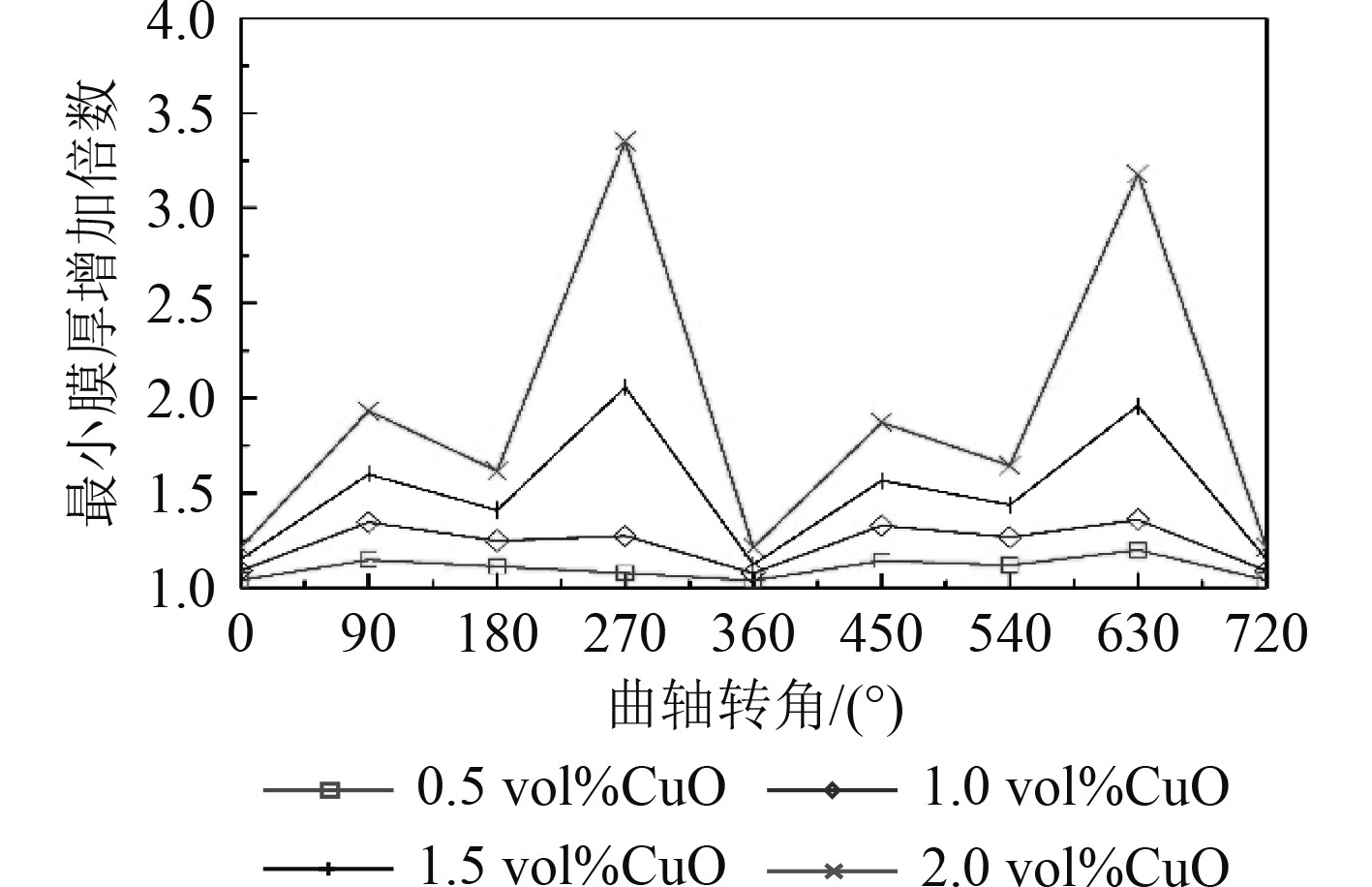
采用不同体积分数CuO纳米润滑油时,以第5主轴承最小油膜厚度随曲轴转角变化如表4及图5所示。可以看出,采用纳米润滑油后,在整个工作循环内第5主轴承最小油膜厚度均得到了提升,且随着纳米颗粒体积分数的增加,最小油膜厚度也随之增大。特别是在轴承负载较大时,纳米CuO颗粒的加入对最小油膜厚度的影响更加显著。例如,当曲轴转角为270CA和630CA时,体积分数为2%的纳米润滑油相比于SAE40润滑油,其最小膜厚分别增加了3.4倍和3.2倍(见图6)。其最主要的原因是纳米颗粒的加入增加了润滑油的粘度,提高了润滑油的承载能力。
|
|
表 4 不同体积分数CuO纳米润滑油最小油膜厚度(μm) Tab.4 Minimum film thickness of nano-CuO oil (μm) |
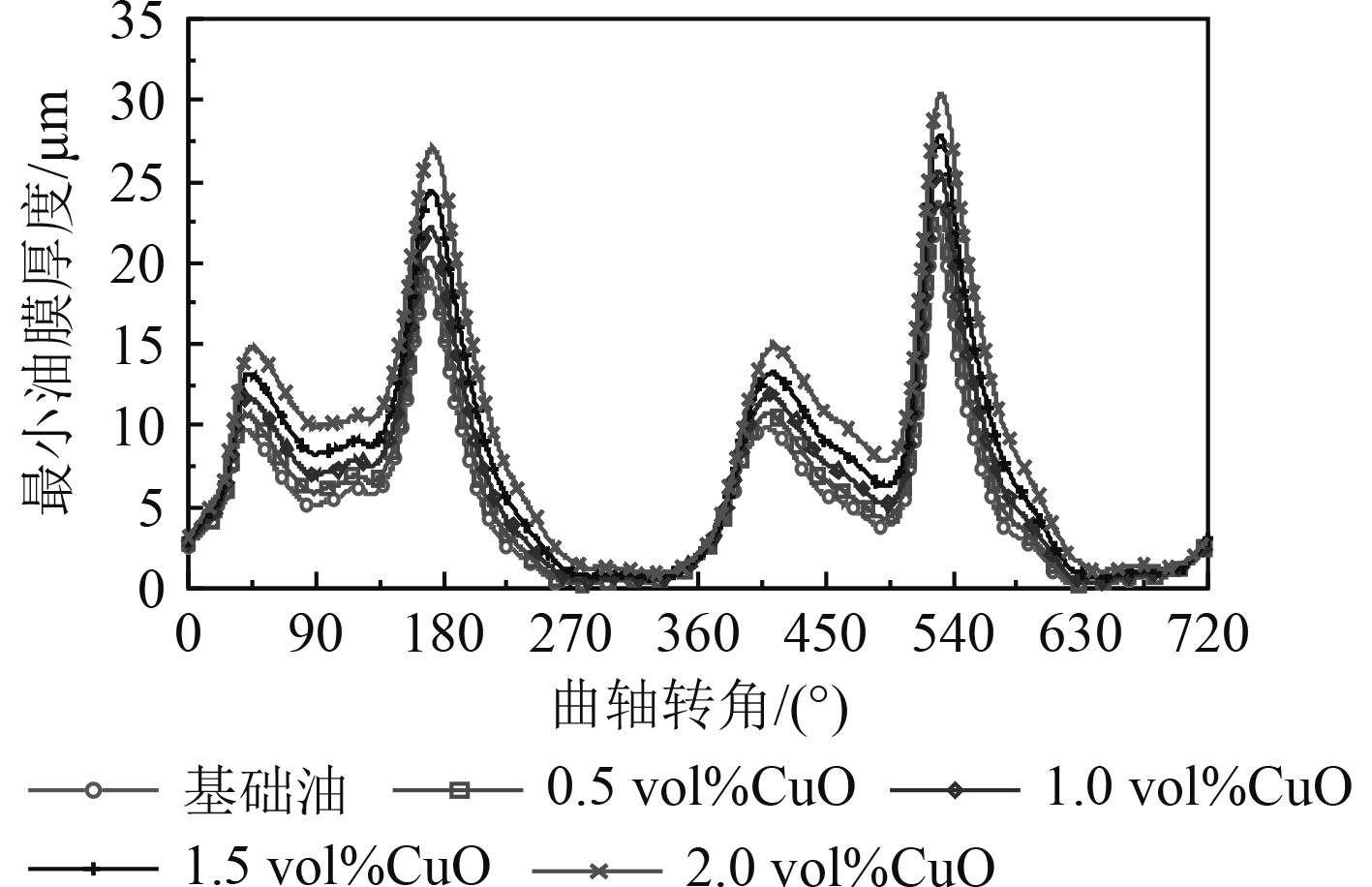
|
图 5 不同体积分数纳米润滑油对最小油膜厚度的影响 Fig. 5 Effect of volume fraction on the minimum oil film thickness |
|
图 6 不同体积分数纳米润滑油最小油膜厚度增加率 Fig. 6 The minimum oil film thickness increase rate of nano-lubricating oil with different volume fractions |
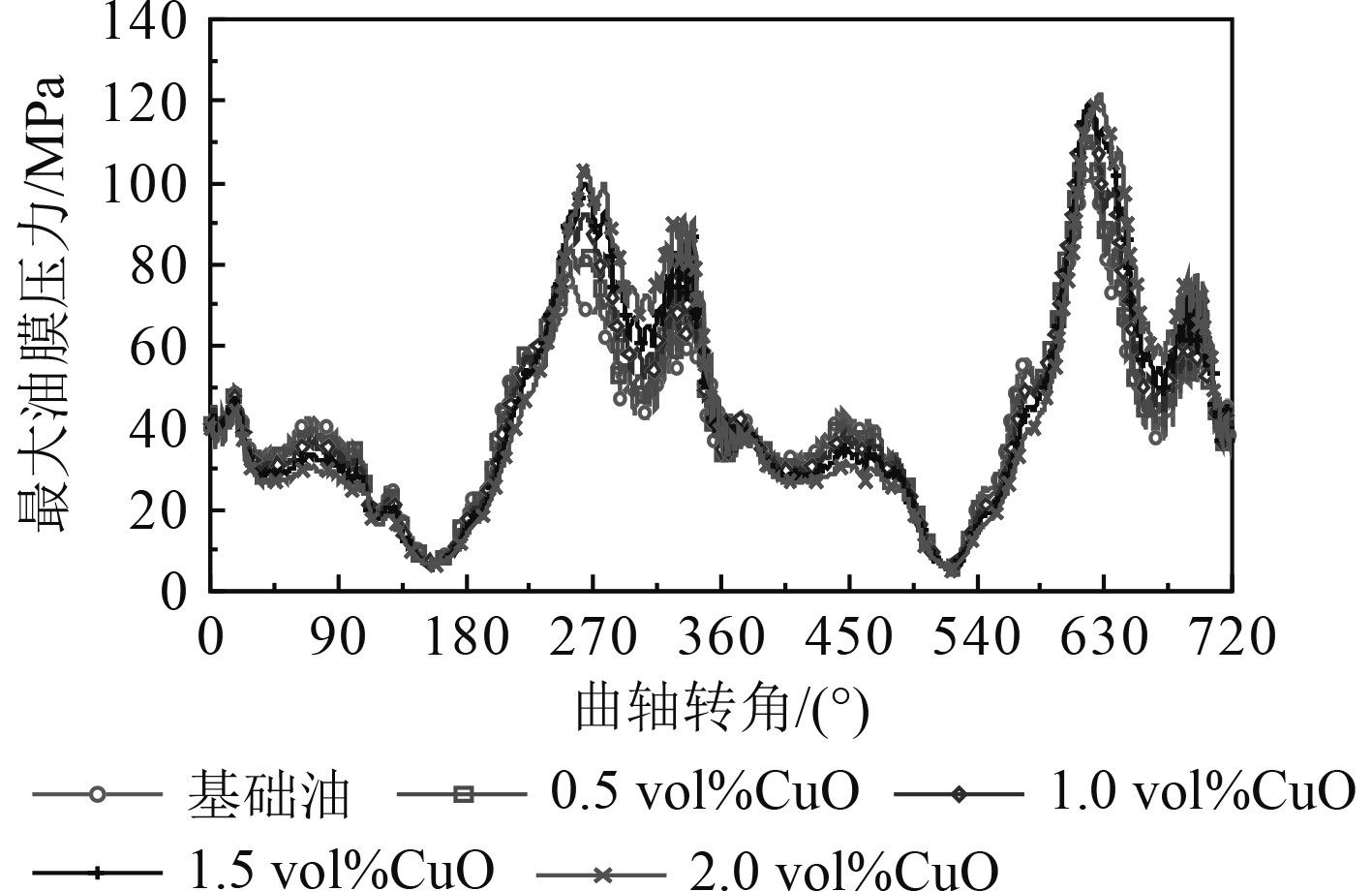
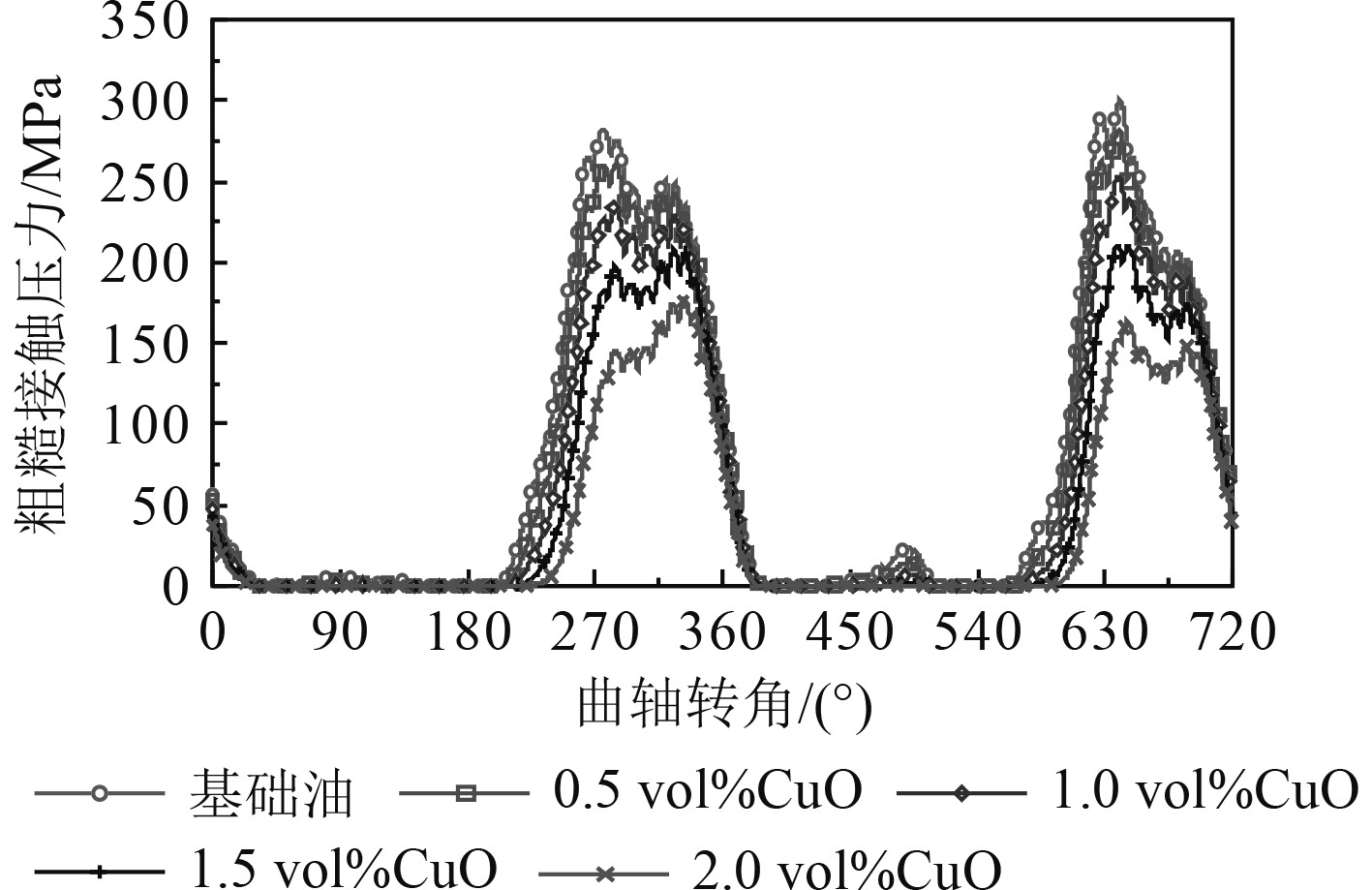
不同体积分数CuO纳米润滑油在不同曲轴转角下的最大油膜压力如图7所示。从图中可以看出,当第5主轴承负载较大时,纳米润滑油相比于基础油,能明显提高主轴成最大油膜压力。而在其余转角下,纳米润滑油最大油膜压力有所降低。分析其原因,主要是因为纳米颗粒的加入,增加了润滑油粘度,提高了油膜承载能力。在主轴承负载较高时,纳米润滑油能产生更大的油膜压力,支撑曲轴主轴颈的旋转运动,减少润滑表面粗糙峰的接触,降低摩擦力。且随着纳米颗粒体积分数的增加,油膜承载能力越强,产生的最大油膜压力越大。不同体积分数纳米润滑油对第5主轴承粗糙接触压力的影响如图8所示。其影响规律与图7相对应,较好地验证了上述分析结论。而在载荷较小时,主轴承处于流体润滑状态,主要靠润滑油膜承载。纳米润滑油具有更好的承载能力,在相同载荷作用下,形成相对较厚的最小油膜厚度,产生较小的油膜压力。
|
图 7 不同体积分数纳米润滑油对最大油膜压力的影响 Fig. 7 Effect of nano lubricating oil with different volume fractions on maximum oil film pressure |
|
图 8 不同体积分数纳米润滑油对粗糙接触压力的影响 Fig. 8 Effect of nano lubricating oil with different volume fractions on rough contact pressure |
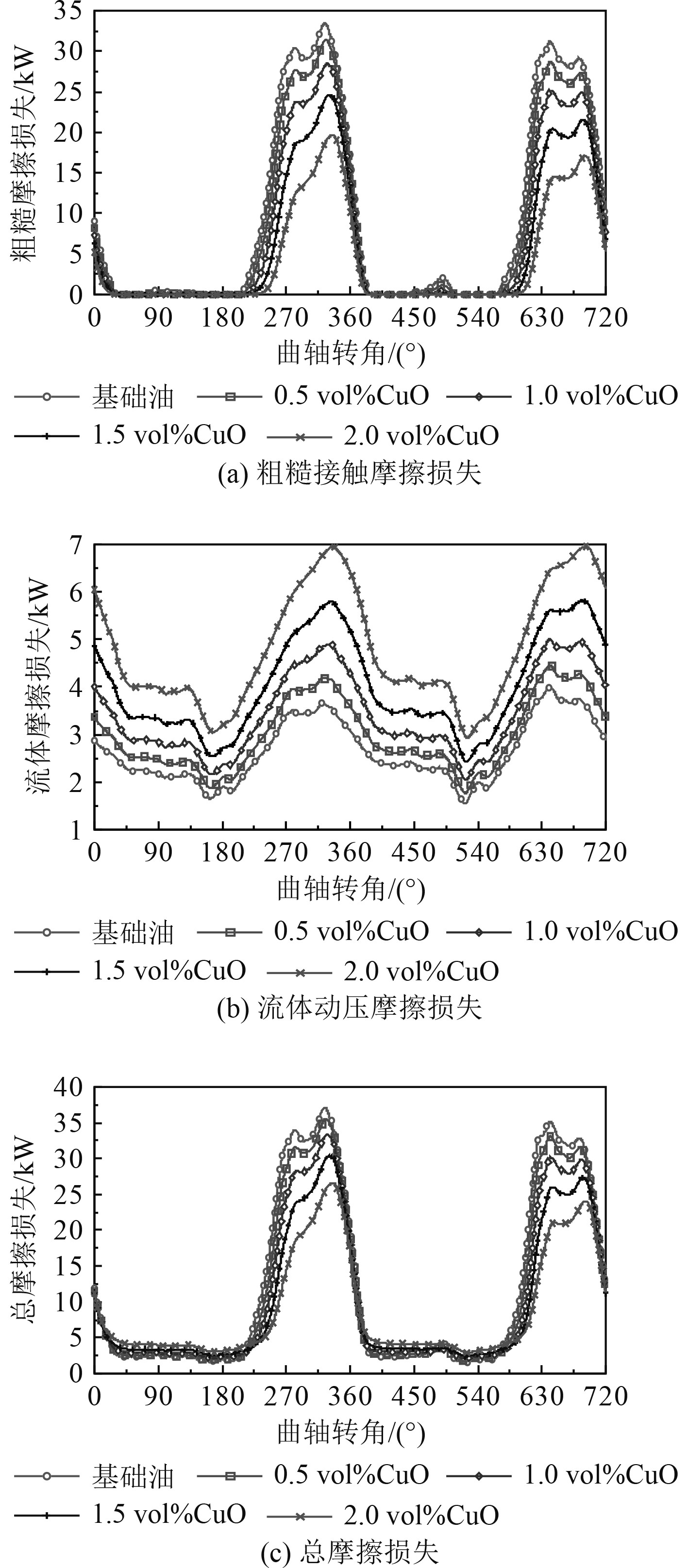
图9分别为标定转速下采用不同体积分数CuO纳米润滑油时第5主轴承流体动压损失、粗糙峰接触摩擦损失及总摩擦损失随曲轴转角的变化规律。从图中可以看出,纳米颗粒的加入提高了润滑油粘度,增加了润滑油膜流体剪切损失,但同时降低了润滑表面粗糙峰接触摩擦损失。因此,纳米润滑油对主轴承摩擦损失的影响作用主要取决于主轴承润滑状态。通过对总摩擦损失进行积分,得到不同体积分数纳米润滑油时第5主轴承在一个工作循环内的总摩擦损失,如表5所示。可见,纳米润滑油相比于基础油降低了主轴承总摩擦损失。
|
图 9 不同体积分数纳米润滑油对摩擦损失的影响 Fig. 9 Effect of nano lubricating oil with different volume fractions on friction loss |
|
|
表 5 第5主轴承总摩擦损失(单位:J) Tab.5 Total friction loss of the 5th main bearing (J) |
为进一步分析不同体积分数纳米润滑油对16V柴油机曲轴主轴承整体摩擦润滑特性的影响,对曲轴主轴承总摩擦损失进行积分求和,其结果如表6所示。
|
|
表 6 曲轴主轴承总摩擦损失(单位:J) Tab.6 Total friction loss of crankshaft main bearing (J) |
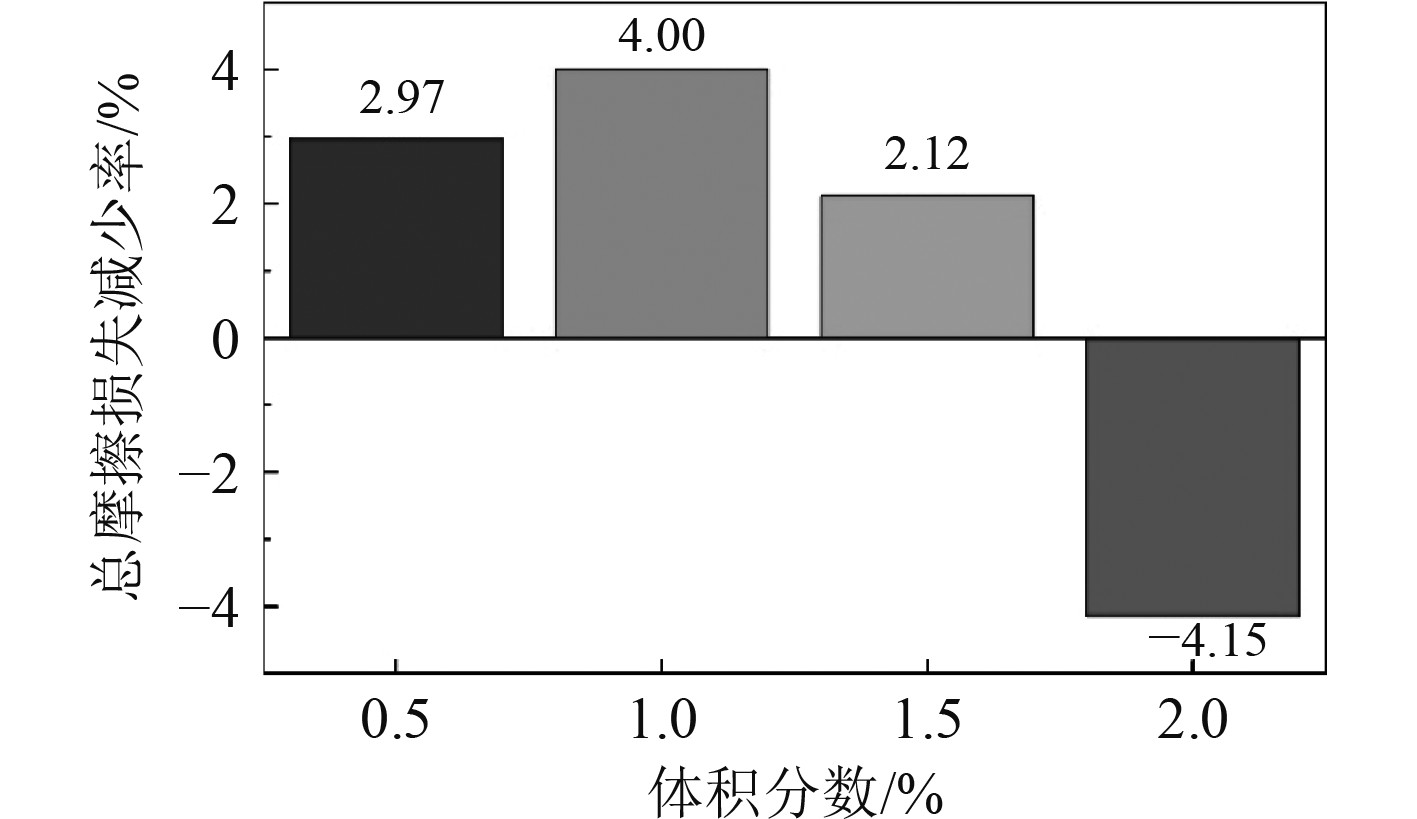
相比基础油,不同体积分数纳米润滑油对曲轴主轴承总摩擦损失减少率如图10所示。从图中可见,纳米颗粒的体积分数并非越高越好,而是存在一最优值。当摩擦副负载较大,油膜较薄,处于混合润滑时,纳米颗粒的加入能降低粗糙峰接触摩擦损失;当处于流体动压润滑时,由于纳米润滑油粘度增加,从而造成流体剪切摩擦损失也会相应增大。最终,总摩擦损失取决于两者的综合影响。文献[16]也给出了相似的结论。
|
图 10 不同体积分数纳米润滑油总摩擦损失减少率 Fig. 10 Total friction loss reduction rate of nano-lubricating oil with different volume fraction |
本文以某型16V柴油机为研究对象,通过建立曲轴主轴承流体润滑模型,开展了不同体积分数CuO纳米润滑油对曲轴主轴承润滑特性影响分析,得出以下主要结论:
1)与其余主轴承相比,第5主轴承负载最大,润滑性能最为恶劣。纳米润滑油能明显增加第5主轴承最小油膜厚度。当体积分数为2%时,最小油膜厚度最大增加了3.4倍,使第5主轴承润滑状况得到了明显改善。
2)纳米颗粒的加入提高了润滑油承载能力,增加主轴承油膜厚度。在高负荷时,降低了主轴承粗糙接触压力;在低负荷时,降低了最大油膜压力。
3)相比于基础油,当工作状况较为恶劣时,纳米润滑油能明显减少主轴承总摩擦损失,且随着纳米颗粒体积分数增加这种效果更为明显。
4)通过对曲轴主轴承进行整体分析时发现,纳米润滑油体积分数并非越高越好,而是存在一最优值。纳米润滑油对曲轴主轴承摩擦损失的影响取决于主轴承润滑状态。当主轴承处于混合或边界润滑时,纳米润滑油的抗磨减摩效果更为明显。否则,则反而增加主轴承摩擦损失。
| [1] |
温诗铸, 黄平. 摩擦学原理[M]. 北京: 清华大学出版社, 2008.
|
| [2] |
CHOI S U S, EASTMAN J A. Enhancing thermal conductivity of fluids with nanoparticles[J]. ASME Fed, 1995, 231(1): 99-105. |
| [3] |
RASHEED A K, KHALID M, JAVEED A, et al. Heat transfer and tribological performance of graphene nanolubricant in an internal combustion engine[J]. Tribology International, 2016, 103: 504-515. DOI:10.1016/j.triboint.2016.08.007 |
| [4] |
高传平, 王燕民, 向龙华, 等. 片状Fe3O4纳米颗粒在润滑油中的摩擦化学性质[J]. 硅酸盐学报, 2013(10): 1339-1346. |
| [5] |
HU C, BAI M, LV J, et al. Molecular dynamics simulation on the friction properties of nanofluids confined by idealized surfaces[J]. Tribology International, 2014, 78(4): 152-159. |
| [6] |
PATIR N, CHENG H S. Application of average flow model to lubrication between rough sliding surfaces[J]. ASME J. Lubr. Technol, 1979, 101: 220-229. DOI:10.1115/1.3453329 |
| [7] |
GREENWOOD J A, TRIPP J H. The contact of two nominally flat rough surfaces[J]. ARCHIVE:Proceedings of the Institution of Mechanical Engineers 1847-1982 (vols 1-196), 1970, 185(1970): 625-634. |
| [8] |
PAK B C, CHO Y I. Hydrodynamic and heat transfer study of dispersed fluids with submicron metallic oxide particles[J]. Experimental Heat Transfer, 1998, 11(2): 151-170. DOI:10.1080/08916159808946559 |
| [9] |
SAEEDINIA M, AKHAVAN-BEHABADI M A, RAZI P. Thermal and rheological characteristics of CuO–Base oil nanofluid flow inside a circular tube[J]. International Communications in Heat & Mass Transfer, 2012, 39(1): 152-159. |
| [10] |
XUAN Y, ROETZEL W. Conceptions for heat transfer correlation of nanofluids[J]. International Journal of Heat and Mass Transfer, 2000, 43(19): 3701-3707. DOI:10.1016/S0017-9310(99)00369-5 |
| [11] |
KRIEGER I M, DOUGHERTY T J. A mechanism for non‐newtonian flow in suspensions of rigid spheres[J]. Transactions of the Society of Rheology, 2000, 3(1): 137-152. |
| [12] |
CHEN H, DING Y, HE Y, et al. Rheological behaviour of ethylene glycol based titania nanofluids[J]. Chemical Physics Letters, 2007, 444(4-6): 333-337. DOI:10.1016/j.cplett.2007.07.046 |
| [13] |
KOLE M, DEY T K. Effect of aggregation on the viscosity of copper oxide–gear oil nanofluids[J]. International Journal of Thermal Sciences, 2011, 50(9): 1741-1747. DOI:10.1016/j.ijthermalsci.2011.03.027 |
| [14] |
CHEN H, DING Y, TAN C. Rheological behaviour of nanofluids[J]. New Journal of Physics, 2007, 9(10): 367. DOI:10.1088/1367-2630/9/10/367 |
| [15] |
ABEROUMAND S, JAFARIMOGHADDAM A, MORAVEJ M, et al. Experimental study on the rheological behavior of silver-heat transfer oil nanofluid and suggesting two empirical based correlations for thermal conductivity and viscosity of oil based nanofluids[J]. Applied Thermal Engineering, 2016, 101: 362-372. DOI:10.1016/j.applthermaleng.2016.01.148 |
| [16] |
SHAHMOHAMADI H, RAHMANI R, RAHNEJAT H, et al. Thermohydrodynamics of lubricant flow with carbon nanoparticles in tribological contacts[J]. Tribology International, 2016, 113: 50-57. |
 2021, Vol. 43
2021, Vol. 43

