由于通过技术要求使柴油机满足排放的要求已经不能满足实现,陈永军[1]提出了关于混动力系统的设计,从串联、并联以及串并混联3种结构说明研究现状,提出新型混合动力设计并采用了自动切换控制系统。文献[2]中对固体氧化物燃料电池以及微型燃气轮机混合动力系统进行建模仿真分析,并提出了新的控制方法,对燃油和空气流量以及进出口温度具有良好的控制效果,一定程度上提高了系统对燃料的利用率,提高了混合动力船舶的推进效率。针对系统控制的问题,蔡英凤等[3]在汽车混合动力领域提出了补偿滑模控制,从转矩的角度控制系统的传动过程,控制系统的稳定性。文献[4]中对混合动力船的具体改造进行优化设计,从方案、施工等各个环节进行设计,提出了新型的改造方案。对上述文献中的内容进行研究发现,首先从混合动力船的结构角度优化混合动力的结构,其次从燃料和混合动力的效率出发,如何控制系统的利用率以及增强系统的燃料电池的效率,总体缺乏系统控制以及整体运行性能的研究。文献[5]中针对燃料电池寿命的问题以及电能质量问题,提出了一种小波变换的船舶能量管理策略,以此提高电池寿命以及电能质量。文献[6]以无人船为对象,采用了智能的深度网络算法对系统的能量管理进行分析,对系统混合动力系统的使用情况进行非常详细的分析与说明,对本文关于控制策略的研究具有很好的参考价值。文献[7-8]从能量管理的角度,使用模糊控制策略以及粒子群优化算法对混合动力系统进行优化控制,实现船舶动力的绿色发展。文献[9]在北斗系统导航基础上对混合动力船舶进行研究,实现如何节能减排,提高混合动力船舶的推进能力以及系统的稳定性,以此实现节能减排的目的。文献[10]为混合动力船舶设计了基于瞬时优化船舶机电电机混合动力控制系统,由柴油机和发电机构成混合动力系统的硬件,利用模块分化的方法设计系统软件,系统设计完成后,通过对比试验进行耗能效果验证。结果表明,混合动力控制系统较传统动力控制系统节约油耗5.5 L,以此实现了节能减排的目标。文献[11]针对燃料燃料电池混合储能的尺寸进行了设计,对燃料电池转化时的频率进行优化。文献[12-13]对系统建立模型仿真分析系统的动力性能以及氮氧化物的排放,定量分析系统的改善状况,并对锂电池组和永磁同步发电机进行系统运行分析,模拟锂电池的投入与切断。
综上所述,混合动力船舶主要对燃料电池和锂电池的混合动力、发电机与蓄电池的混合动力等常见的混合动力系统模型进行仿真分析研究,从燃料电池的利用率以及锂电池的使用寿命和电能质量的角度,分析系统中混合动力的稳定性,其中缺少相应的具体分析。本文通过使用改进的RBF自适应滑模控制策略对蓄电池组与发电机组的转换控制,提高蓄电池组混合动力系统的效率以及电能质量,并且通过Matlab/Simulink进行仿真分析实验,进一步证明控制策略的有效性。
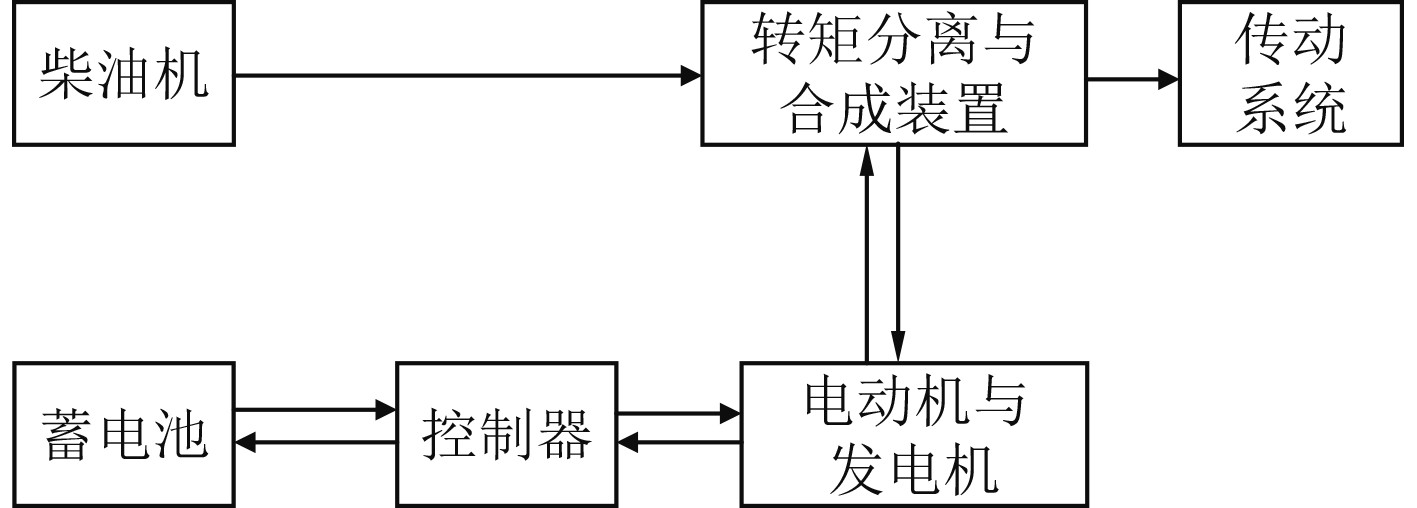
1 蓄电池组混合动力模型船舶混合动力推进是将传统的柴油发电机与清洁能源包括太阳能电池、风电等组合使用的动力系统,两者有着不同的工作性能,相互补充,控制船舶动力能够达到更好的效果,其中目前常见蓄电池组是一种可充电的锂电池组。混合动力系统有串联、并联、串并混合3种架构形式,本文将使用并联结构模型,其模型结构图如图1所示。
|
图 1 混合动力系统并联结构图 Fig. 1 Parallel structure diagram of hybrid power system |
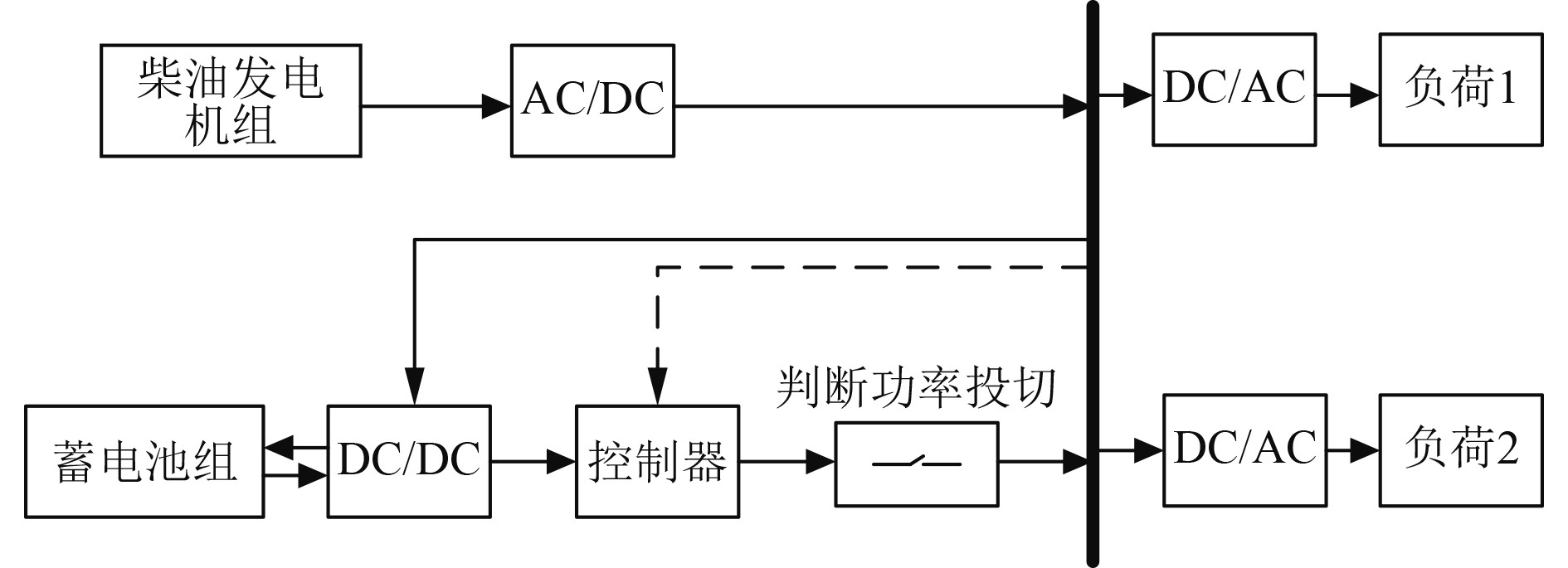
如何合理控制蓄电池的使用使得效率最大化是控制研究的重点。对系统发电机和蓄电池进行结构细化,包括蓄电池组、柴油发电机组以及逆变结构,针对不同的负荷采用不同的逆变参数。其结构图如图2所示。
|
图 2 混合动力系统电力部分结构示意图 Fig. 2 Schematic diagram of the electric power part of the hybrid power system |
对蓄电池与发电机组的混合动力系统电能质量与功率效率进行着重分析。以无人船为例[6],假设混合动力船舶的参数如表1所示。
|
|
表 1 船舶电力参数 Tab.1 Ship electrical parameters |
此船推进系统中传动部分耗电量为主要部分,以及系统控制部分耗电,没有大型的日用耗电损耗,相比较而言,负载简单,有利于系统理论仿真控制研究。
2 混合动力系统建模在本文混合动力系统研究中,针对蓄电池控制分析将以功率P为控制目标,假设 P1为发电机输出的功率,P2为蓄电池提供的功率,关于发电机P1在系统没有投入P2时,发电机可以进行调节满足系统功率需求,在P2投入时进行控制操作。其中满足功率关系如下式:
| $ p = {p_1} + {p_2}\text{。}$ | (1) |
其中,取P1和P2的计算分别为
此处的滑模控制为控制混合动力系统的效率最优化以及功率的及时投入,因此采取对系统输出的功率以及负载实际功率对比优化,判断系统是否需要将蓄电池组投入使用,因此采取对综合负载误差进行控制分析,误差值如下式:
| $ e = p - {p^*}\text{。}$ | (2) |
式中:e为混合动力系统负载功率误差;P为负载实际功率;P*为系统提供的实际功率。
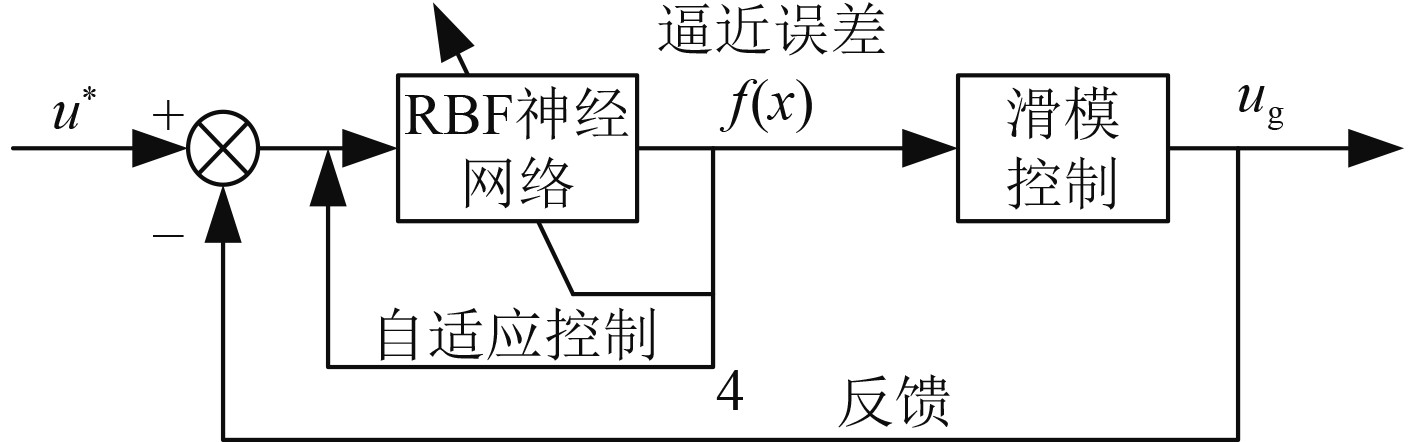
2.2 RBF结构及理论本文采用RBF神经网络自适应滑模控制,控制系统简要过程如图3所示。利用RBF网络的万能逼近特性,逼近滑模控制误差f(x),进行误差反馈及补偿,达到系统的稳定。其中,自适应律和滑模h趋近律共同保证系统的稳定。
|
图 3 神经网络控制结构简图 Fig. 3 Schematic diagram of neural network control structure |
网络算法为:
| $ f = {W^*}^Th\left( x \right) + \varepsilon\text{,}$ | (3) |
其中,h为网络的高斯基函数输出,W*为网络的理想权值,ɛ为网络的逼近误差,ɛ≤ɛN。
网络输入取x=[e e’]T,则网络输出为:
| $ \hat f\left( x \right) = {\hat W^{\rm{T}}}h\left( x \right) \text{,}$ | (4) |
根据式(3)和式(4)可得:
| $ f\left( x \right) - \hat f\left( x \right) = {W^{*{\rm{T}}}}h\left( x \right) + \varepsilon - {\hat W^{\rm{T}}}h\left( x \right) = {\tilde W^{\rm{T}}}h\left( x \right) + \varepsilon \text{。}$ | (5) |
改进传统滑模面切换函数s=ce+e′,选取滑模面切换函数:
| $ s = {k_1}e + {k_2}\int {e{\rm{d}}t} \text{,}$ | (6) |
其中:k1,k2分别为滑模面切换函数的比列系数和积分系数。
对函数s求导,得
| $ \dot s = {k_1}\dot e + {k_2}e \text{,}$ | (7) |
根据滑模控制理论,当系统工作在滑面时,s′=0,得
| $ \dot s = slaw \text{,}$ | (8) |
其中,slaw表示趋近律,通过改进等速趋近律,采用分数阶滑模趋近律,本质未变,通过逼近的方法增加了可调系数。
| $ {D^\alpha }s = - \zeta {sgn} s \text{,}$ | (9) |
其中,0<α<1,ζ>0。
变换得:
| $ \dot s = {D^{1 - \alpha }}\left( { - \zeta {sgn} s} \right) \text{。}$ | (10) |
证明:
为了证明控制系统稳定性,将李亚普若夫函数定义为
| $ \begin{split} \dot {V} =& s\dot{ s} + \frac{1}{\gamma }{{\tilde {W}}^T}\dot {\hat {W}} = s\left( {k_1}\dot e + f\left( x \right) +\right. \\ &\left.{k_2}\left( {u - ui - {{{u^2}}/r} - {p^*}} \right) \right) + \frac{1}{\gamma }{{\tilde {W}}^T}\dot{ \hat {W} } \end{split} \text{,}$ | (11) |
其中,
| $u = - \frac{{{k_1}}}{{{k_2}}}\dot e - \frac{1}{{{k_2}}}\hat f\left( x \right) + \frac{{ui + {{{u^2}} \mathord{\left/ {\vphantom {{{u^2}} r}} \right. } r}}}{{{k_2}}} + \frac{1}{{{k_2}}}{p^*} + \frac{1}{{{k_2}}}slaw \text{,}$ | (12) |
根据式(15)和式(8),可得:
| $ \begin{split} \dot {V} = &s\left( {f\left( x \right) - \hat {f}\left( x \right) + slaw} \right) + \frac{1}{\gamma }{{\tilde {W}}^{\rm{T}}}\dot {\hat {W}}= \\ & s\left( { - {{\tilde {W}}^{\rm{T}}}h\left( x \right) + \varepsilon + slaw} \right) + \frac{1}{\gamma }{{\tilde {W}}^{\rm{T}}}\dot {\hat {W }} =\\ &\varepsilon s + slaw \cdot s + {{\tilde {W}}^{\rm{T}}}\left( {\frac{1}{\gamma }\dot{ \hat {W}} - sh\left( x \right)} \right) \text{。} \end{split} $ | (13) |
取自适应律为
| $ \begin{split} \dot V =& \varepsilon s + slaw \cdot s = s\left( {\varepsilon + {D^{1 - \alpha }}\left( { - \zeta {sgn} s} \right)} \right)= \\ & \varepsilon s - \left| s \right|{D^{1 - \alpha }}\zeta \leqslant \left| {{\varepsilon _N}} \right|\left| s \right| - \left| s \right|{D^{1 - \alpha }}\zeta \leqslant \\ & - \left( {{D^{1 - \alpha }}\zeta - \left| {{\varepsilon _N}} \right|} \right)\left| s \right| \text{。} \end{split} $ | (14) |
根据式(14),当D1-αζ>|ɛN|时,则V’<0。可见控制律中的趋近律具有克服神经网络逼近误差的作用,以保证系统能够达到稳定的状态。根据李亚普若夫稳定性判据,可以判断控制系统在平衡点处是渐近稳定的,系统可以在有限的时间内到达滑模面,并能够在滑模面上运动。
3 仿真分析为研究和分析本文所采用的改进的滑模控制策略对混合动力船的有效性以及可靠性,通过Matlab/Simulink仿真平台设计380 V/60 Hz的混合动力无人船模型,对缓和动力船系统的电能转换和分配进行仿真,分析功率效率以及混合动力船的电能质量,判断通过此方法对系统的电能混合动力控制的可靠性,并与一般PI控制下的效果进行对比。对系统电压以及频率等电能质量进行定量分析,分析控制策略的优越性,以及不足之处。仿真时长设置为5 s,关于蓄电池组的投切过程依据系统仿真实际变化进行控制,部分图形取仿真2.95~3.05 s的仿真图。系统仿真的主要参数如表2所示。
|
|
表 2 混合动力船舶系统电力参数 Tab.2 Electric parameters of hybrid power ship system |
根据表2进行仿真参数设置,其中LCL参数设计应该满足滤波参数的原则10f<fres<f开关/2。在仿真系统中关于电动机负载的额定参数[12],所采用的参数如表3所示。
|
|
表 3 电动机额定参数 Tab.3 Motor rated parameters |
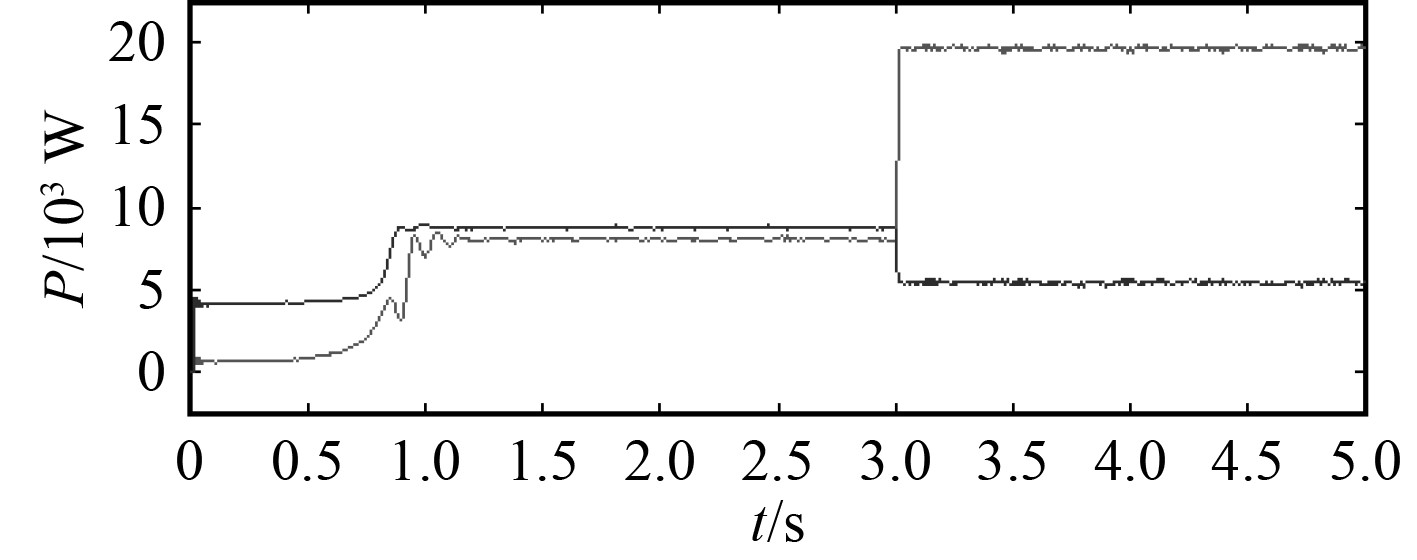
对本文所采用的控制方式进行仿真。首先分析系统功率分配投入的状态,从蓄电池组和柴油发电机的功率变化状况进行分析,关于蓄电池组和柴油发电机功率投入变化分别如图4和图5所示。
|
图 4 蓄电池组功率变化图 Fig. 4 Change chart of battery pack power |
|
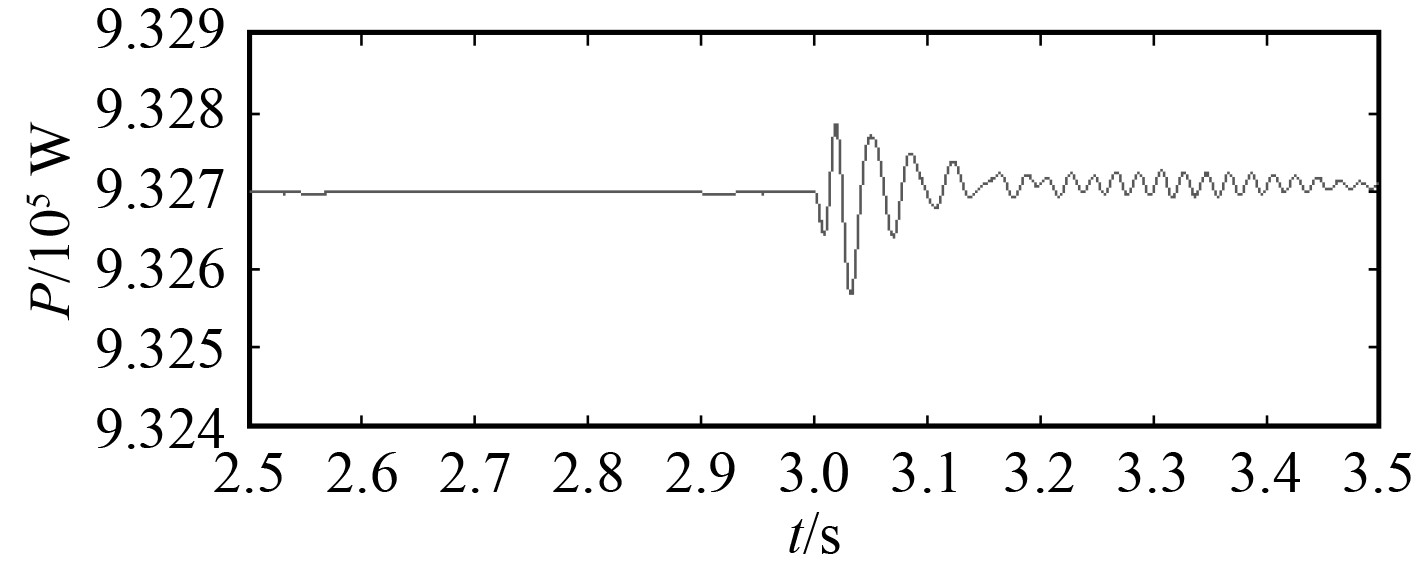
图 5 发电机功率变化图 Fig. 5 Change diagram of generator power |
由图4可以看到,初期投入缓慢,投入的负载是没有在柴油发电机供电的负载,同时无功功率大于有功功率,说明系统中感性负载较多,直至系统达到稳定状态之后,检测发现系统中发电机的功率不能完全满足电机以及其他容性负载的需要,因此在3 s时刻投入蓄电池组进行补充供电,随着其他容性负载的进入系统有功功率增加,同时无功功率减少。
由图5可以看到,系统柴油发电机稳定供电时,稳定供电负载没有变化,当在3 s时蓄电池并入通过蓄电池组进行补偿,系统柴油发电机功率首先得到缓解,在没有满载的情况下,系统功率可进行调节。当满载之后,通过蓄电池组进行稳定供电时,柴油发电机输出的功率同样可以稳定在初始功率0.924 MW,功率会在此上下波动,但是功率波动范围较小。
3.2 功率效率分析对系统功率的效率进行分析,蓄电池组的投入是否可以有效提高系统的使用效率。系统蓄电池组和发电机有功功率效率的仿真图如图6和图7所示。
|
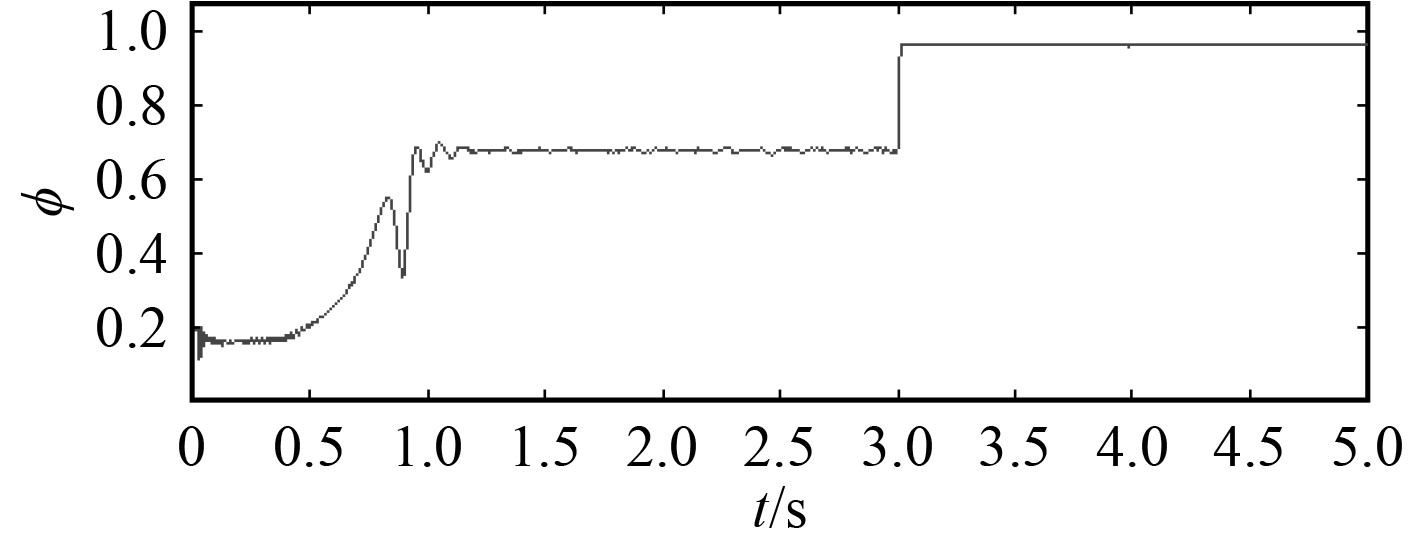
图 6 蓄电池组功率投入的效率 Fig. 6 Efficiency of battery pack power input |
|
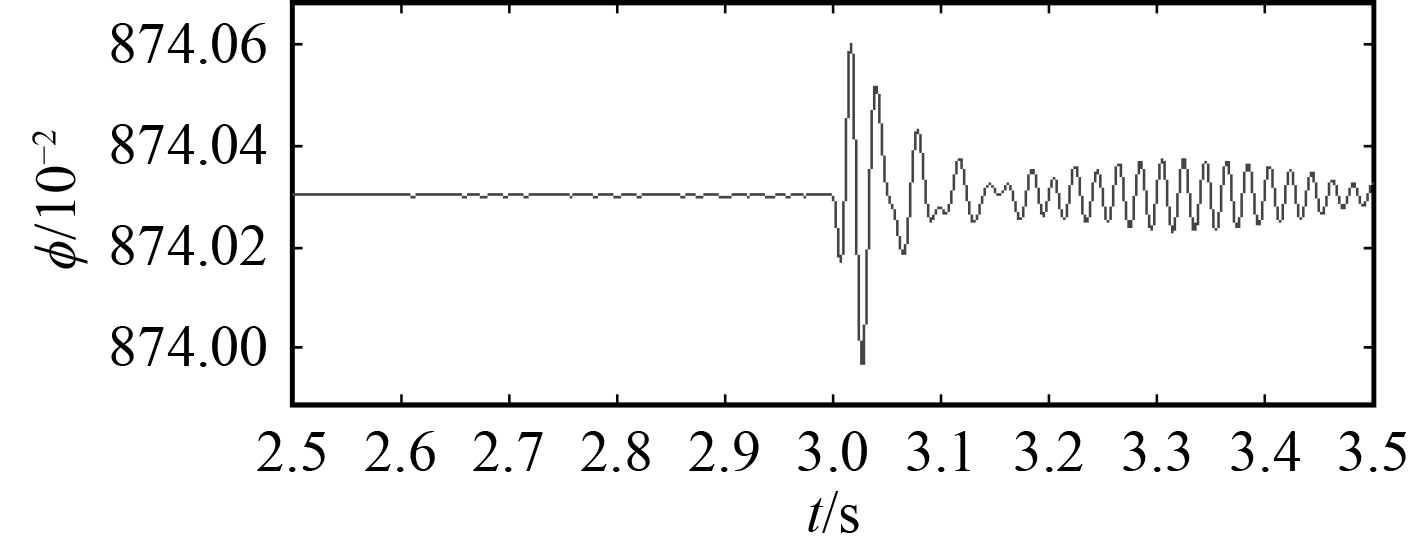
图 7 发电机组功率投入效率 Fig. 7 Efficiency of generating set power input |
通过功率的投入发现蓄电池组投入的有功功率增大,其中无功变化相对较小。随着有功投入增大,系统的效率增大,当3 s发电机组完全投入之后效率达到98%。由图7可以看到,柴油发电机组的功率效率稳定在87.4%左右基本无变化,如果采用发电机进行供电,其效率无法达到98%,同时发电机中铁损和铜损也相应增大。当系统采用蓄电池组时,其基本完全投入使用,通过百分之百的投入使用,可以有效提高系统功率效率,提高船舶推进以及负载供电的效率。
4 结 语本文通过改进的滑模控制理论,对混合动力船舶的供电进行控制仿真分析,将改进传统滑模控制策略用于岸电并网的电压控制,采用PI形式的滑模面与分数阶滑模控制律来控制混合动力进行控制,同时抑制了系统采用滑模控制的抖振现象。仿真实验验证了传统滑模控制策略的有效性,相比之下改进传统滑模控制策略具有更好的稳定性和可靠性,能够有效地抑制系统本身产生的抖振,但是不能完全消除。通过仿真研究发现,本文所采用的控制方法可以有效实现混合动力船蓄电池和柴油发电机的综合控制,提高船舶供电系统电能的利用率。
| [1] |
陈勇军. 一种新型船用混合动力系统设计[J]. 装备制造技术, 2018(7): 47-50. CHEN Yongjun. Design of a new type of marine hybrid power system[J]. Equipment Manufacturing Technology, 2018(7): 47-50. DOI:10.3969/j.issn.1672-545X.2018.07.016 |
| [2] |
刘运新, 马川. 一种新型船用燃料电池混合动力系统的建模[J]. 中国航海, 2016, 39(1): 13-16+21. LIU Yunxin, MA Chuan. Modeling of a new type of marine fuel cell hybrid power system[J]. Navigation of China, 2016, 39(1): 13-16+21. DOI:10.3969/j.issn.1000-4653.2016.01.004 |
| [3] |
蔡英凤, 窦磊, 陈龙, 等. 基于补偿滑模控制的混合动力汽车协调控制[J]. 汽车工程, 2020, 42(4): 431-438. CAI Yingfeng, DOU Lei, CHEN Long, et al. Hybrid electric vehicle coordinated control based on compensating sliding mode control[J]. Automotive Engineering, 2020, 42(4): 431-438. |
| [4] |
史志赛, 刘亮清, 赛军杰, 等. 柴电混合动力改造轴系复装方案[J]. 船舶工程, 2020, 42(1): 63-67. SHI Zhisai, LIU Liangqing, SAI Junjie, et al. Diesel-electric hybrid retrofit shafting reinstallation plan[J]. Ship Engineering, 2020, 42(1): 63-67. |
| [5] |
张泽辉, 陈辉, 高海波, 等. 基于实时小波变换的燃料电池混合动力船舶能量管理策略[J]. 中国舰船研究, 2020, 15(02): 127-136. ZHANG Zehui, CHEN Hui, GAO Haibo, et al. Energy management strategy for fuel cell hybrid ships based on real-time wavelet transform[J]. China Ship Research, 2020, 15(02): 127-136. |
| [6] |
陈剑龙, 刘俊峰, 王振刚, 等. 基于DRL的无人船混合动力系统能量管理策略研究[J]. 中国测试, 2020, 46(02): 9-15. CHEN Jianlong, LIU Junfeng, WANG Zhengang, et al. Research on energy management strategy of unmanned ship hybrid power system based on DRL[J]. China Measurement and Test, 2020, 46(02): 9-15. |
| [7] |
YANG Rui, YUAN Yupeng, YING Rushun, et al. A novel energy management strategy for a ship’s hybrid solar energy generation system using a particle swarm optimization algorithm[J]. Energies, 2020, 13(6).
|
| [8] |
韩北川. 基于模糊控制的混合动力船舶能量管理策略研究[J]. 机电工程技术, 2019, 48(7): 84-87. HAN Beichuan. Research on energy management strategy of hybrid power ship based on fuzzy control[J]. Mechanical and Electrical Engineering Technology, 2019, 48(7): 84-87. DOI:10.3969/j.issn.1009-9492.2019.07.030 |
| [9] |
王永鼎, 程湘裕. 基于BDS的混合动力船舶节能研究[J]. 全球定位系统, 2020, 45(2): 112-118. WANG Yongding, CHENG Xiangyu. Research on energy saving of hybrid power ships based on BDS[J]. Global Positioning System, 2020, 45(2): 112-118. |
| [10] |
李书舟, 容慧, 彭勇. 基于瞬时优化的船舶机电电机混合动力控制系统研究[J]. 舰船科学技术, 2018, 40(12): 91-93. LI Shuzhou, RONG Hui, PENG Yong. Research on ship electromechanical motor hybrid power control system based on instantaneous optimization[J]. Ship Science and Technology, 2018, 40(12): 91-93. |
| [11] |
高以康, 张新塘, 徐达. 内河船舶液化天然气发动机-蓄电池混合动力系统性能仿真[J]. 内燃机工程, 2020, 41(1): 42-48+56. GAO Yikang, ZHANG Xintang, XU Da. Performance simulation of inland watercraft LNG engine-battery hybrid power system[J]. Internal Combustion Engine Engineering, 2020, 41(1): 42-48+56. |
| [12] |
赵福海, 王锡淮. 燃料电池锂电池混合动力船舶建模与仿真[J]. 船电技术, 2019, 39(10): 33-36+41. ZHAO Fuhai, WANG Xihuai. Modeling and simulation of fuel cell lithium battery hybrid power ship[J]. Ship Electric Technology, 2019, 39(10): 33-36+41. DOI:10.3969/j.issn.1003-4862.2019.10.009 |
| [13] |
CHEN Hui, ZHANG Zehui, GUAN Cong, et al. Optimization of sizing and frequency control in battery/supercapacitor hybrid energy storage system for fuel cell ship[J]. Energy, 2020, 197. |
 2021, Vol. 43
2021, Vol. 43
