2. 上海交通大学,上海 200240
2. Shanghai Jiaotong University, Shanghai 200240, China
根据世界上诸多大国,如美国,俄罗斯等对北极地区的勘测调查,得出了北极地区的石油与天然气资源十分丰富,约有世界上尚未探明资源的四分之一[1]。除此之外,极地地区还蕴含着许多其他的矿物以及渔业稀有资源。物探船是一种调查船,主要用于海洋地球物理勘探,分为海洋调查船、科学考察船、水文测量船、工程勘查船等。不同类型的物探船采用不同的物探方法。极地物探船上装备了许多精密专业的勘测设备与仪器,可以独立完成复杂困难的海域开发勘测与数据采集的任务。
电力系统是船舶的重要组成部分,是船舶实现安全航行和可靠运行功能的必要保证[2]。但是,无论是极地地区的地理位置还是其自然生态环境,都是十分恶劣的,对于极地物探船的运行以及设备操作人员,紧急维护人员等都十分不利。这就要求极地物探船上的电力系统设备与运行能够承受住极地的恶劣环境同时保证其运行的稳定性与可靠性,防止电力系统发生故障损坏等问题导致极地物探船工作出现问题。所以,极地物探船必须配备一套可靠性高并且操作性强的电力系统设备,同时考虑成本、环境、可靠性等因素,有利于保证极地物探船连续不间断的工作运行,同时节约造船成本以及对保护极地环境做出一些贡献。
目前,国内外关于极地物探船动力系统最优配置的研究相对较少,也没有关于向极地物探船增添新能源可行性的研究。由于极地环境十分恶劣,极地航行气象条件和海况极为恶劣,涉及海冰、低温、风雪、海雾等,这些因素不仅会影响新能源的发电效果,更会影响新能源装置设备的安全,导致有些新能源会无法在极地环境中使用。所以,必须对在极地物探船上加入新能源的可行性进行分析,并通过实例论证加入新能源后,船舶动力系统得到了可靠性与经济性的双重优化。
国内外船舶的研究者以及电力能源的研究者对于船舶动力系统的新能源应用,物探船的发展以及极地物探船的关键技术已经开展了大量的研究工作。有的学者对新能源在船舶上的应用进行研究,文献[3-4]针对船舶动力系统中应用清洁能源的关键技术和优化方案进行分析研究,结合了燃料电池、锂离子电池、超级电容和柴油发电机等新能源,提出了混合动力系统优化配置方法从而提高船舶整体能放水平。文献[5]针对应用于船舶的风力发电系统进行了研究,分析了风力发电原理以及其工作特点,讨论其在船舶上应用的可能性。有的学者对物探船的发展与特点进行研究,文献[6-7]在整体上分析了物探船的关键技术和主要特点,分析了物探船在总布置、性能指标、谐波控制、水下噪声等方面的技术难点。文献[8-10]研究了物探船几种动力系统推进方式的特点,包括混合动力推进系统与电力推进系统,说明了物探船对动力系统的要求以及各种动力系统的技术优点。文献[11-13]给出了物探船的典型实例“海洋石油”760号分析,并且提出物探船动力系统的配置与优化方案,给出了物探船的部分参数指标。有的学者对极地环境的物探船进行了研究,文献[14-17]对极地物探船的发展和未来的研究趋势进行了研究分析,为以后的极地物探船的科研工作指明了方向。但是,针对极地物探船上利用新能源的研究还比较少。
本文首先对极地物探船上新能源利用进行研究,分析了极地中恶劣的气象环境对新能源使用的影响,讨论新能源在极地环境中应用的可行性。最后利用NSGA-II遗传算法,分析在船舶动力系统的电力推进模式中加入光伏发电的优势。在船舶动力系统中加入新能源,有利于减少船舶动力系统推进成本,减少碳的排放量并且提高了船舶运行的可靠性,使得这一套电力系统更加符合极地物探船对电力系统的要求,大大提高对极地地区资源的开发与利用。
1 极地环境对新能源的影响 1.1 极地环境对风力发电的影响1)极地的低温环境会对风机的机叶装置产生严重影响。在极地的超低温环境下,风机的风扇叶片 会结晶,导致粗糙度增大,叶片翼型的气动性能随之降低。同时,由于低温环境的影响,原本风扇驱动系统中的一些部件可以承受的冲击载荷变得无法承受,可能会发生脆性断裂的情况。因此,在风速过高、温度过低时,风机设备难以进行高载荷的工作运行。
2)极地的低温对风机上不同种类的零部件具有较大影响,许多风机当中的金属零件会由于负荷形式不同产生不同的问题。例如,传动系统中的齿轮箱和主轴承受冲击载荷后发生低温脆性断裂的问题。因此,需要提高材料和构件的多重抗冲击性能,这会大大增加风机的制造成本与难度。
3)风机材料的化学成分,晶粒尺寸等重要因素都要考虑极地环境下低温的影响,可能会导致风机的冲击韧性降低以及影响风机的冷脆转变温度等。
通过上述影响的分析可得结论,由于风机设备不适应极地的各种恶劣环境,所以暂时不考虑将风力发电设备作为主要新型能源加入极地船舶的动力系统中来提供发电动力。
1.2 极地环境对光伏能源的影响光伏电池的输出功率大小主要受到光照强度和温度的影响,当光照强度一定时,光伏电池组件的开路电压,短路电流与环境温度都有一定的关系。
相比于风机,光伏发电系统则更加适用于极地的低温环境,因为低温环境不仅不会对光伏电池产生负面影响,随着温度的降低,光伏电池的最大输出功率会略有增加,更适合在极地环境中应用。同时发现,在光强和温度不变的情况下,光伏电池总是有一个最大输出功率点,这就要求光伏发电系统具有跟踪最大功率点的能力,以提高发电效率。在这种低温情况下的光伏发电系统甚至比正常地区温度下的发电效率要高,同时由于光伏能源为新能源,光伏系统的安装对于极地物探船的可靠性、环保性以及发电成本等都是有利的。
但是,极地环境对光伏发电系统也有一定的硬性要求,比如选择的光伏板需要体积小、重量轻、安装方便等特点来克服极地环境中设备安装遇到的问题;选用的光伏板要求交联度高,粘接强度高,表面钢化玻璃透光率高,强度高,才可用于极地科研应对极地的恶劣环境。考虑到供电系统对负载的需求,需要一定的额定功率才可以有效提高负载的续航能力,需要可以采用MPPT的最大功率追踪技术达到这一功率。
因为光伏发电与极地的低温环境较为适合,所以可以尝试将光伏发电系统加入极地物探船的动力系统中,作为电力推进系统中的二级或者备用供电的发电设备。
2 基于遗传算法的船舶动力系统优化 2.1 遗传控制算法原理遗传算法(Genetic Algorithm,GA)最早由美国的John holland于20世纪70年代提出,该算法是根据大自然中生物体进化规律而设计提出,是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。
目前,在解决多目标优化这样的实际问题中,多考虑Pareto最优解集,而非支配排序遗传算法(Nondominated Sorting Genetic Algorithm, NSGA-II)是最常用的算法之一, 它比一代的NSGA算法的改进之处在于,采用了快速的非支配排序方法,将算法的时间复杂度降为O(MN2),且在NSGA-II中使用了排挤算法和精英策略来代替共享函数算法,保留了种群中个体多样性。
2.2 船舶电力推进动力系统的优化模型将光伏系统作为主要的新能源加入极地物探船的动力系统中,并对加入新能源的极地物探船动力系统进行遗传算法的优化计算,观察新能源加入后对极地物探船动力系统各方面的影响。
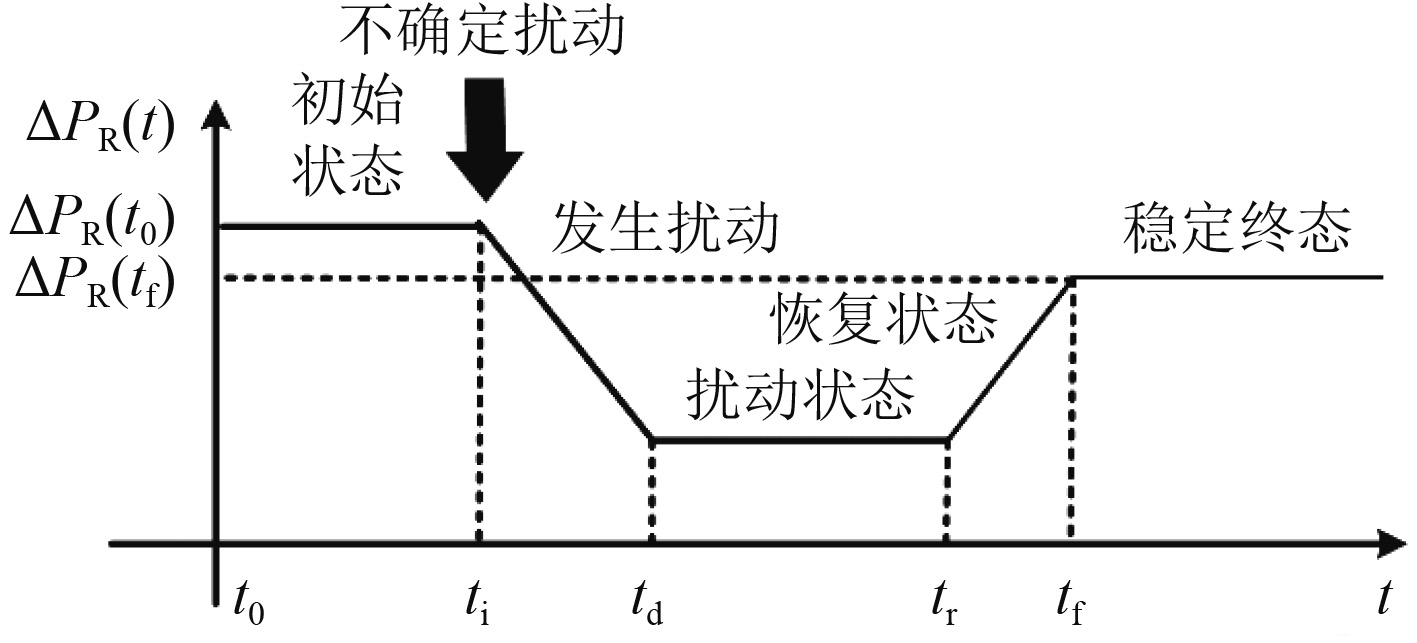
2.2.1 优化模型目标函数[18]首先考虑极地环境中的恶劣气候条件对船舶电力系统的稳定性与可靠性的影响,针对电网受扰动恢复到平衡的过程,本文提出了弹性系数这个概念[18]。在借鉴国内外学者对弹性指标的量化方法后,可得弹性系数就是指电网或者电力系统受到扰动后从故障状态恢复到平衡状态的一种能力。图1为电网受到扰动故障后恢复到平衡的一个过程图。t0时刻为系统初始状态,ti时刻为系统开始受到扰动,td时刻扰动结束,系统进入故障状态,tr时刻系统开始逐步恢复,tf时刻系统恢复到稳定状态。
|
图 1 电力系统在扰动后运行状态曲线 Fig. 1 Operation curve of DN under the incident |
弹性系数为实际恢复功率不平衡程度与总损失功率不平衡程度之比。将弹性系数的表达式作为极地物探船电力系统的可靠性目标函数,如下式:
| $ R(t) = \frac{{\Delta {P_{\text{R}}}(t) - \Delta {P_{\text{R}}}({t_{\text{d}}})}}{{\Delta {P_{\text{R}}}({t_0}) - \Delta {P_{\text{R}}}({t_{\text{d}}})}},t \geqslant {t_{\text{r}}}\text{。}$ | (1) |
同时,需要考虑极地物探船电力系统的经济性。为此可以以最小成本为目标建立一个目标函数来反映电力系统优化的经济效益。它由传统发电机组的发电成本和光伏电源组成,本文为光伏电源的发电成本等组成,如下式:
| $ \begin{split} C(t) =& \sum\limits_{p \in {\text{PV}}} {(C_{p,t}^{{\text{SU}}} + C_{p,t}^{{\text{SD}}} + C_{p,t}^{\text{G}}({{\tilde P}_{p,t}}))}+\\ &\sum\limits_{g \in G} {(C_{g,t}^{{\text{SU}}} + C_{g,t}^{{\text{SD}}} + C_{g,t}^{\text{G}}({P_{g,t}}))} +\\ &\sum\limits_{e \in {\text{ESS}}} {(C_{e,t}^{{\text{ch}}} + C_{e,t}^{{\text{dch}}})} \text{。} \end{split}$ | (2) |
其中:
同时,考虑极地物探船电力系统的环保性,可以以污染排放物为目标建立一个目标函数来反映电力系统优化的环保性。由于光伏能源属于清洁能源,本文忽略其污染排放量。当船舶电力系统在系统发生一定故障时,电力系统中的主要污染排放物为燃料消耗。所以本文以CO2和NO2的排放量为例,来表示本文中污染物的排放程度。根据以上分析,CO2和NO2的排放量可以用式(3)来进行计算:
| $ W(t) =\sum\limits_{g \in {\text{G}}} ({\omega _{{\rm{CO_2}}}}{P_{g,t}} + {\omega _{{\rm{NO}}_2}}{P_{g,t}})\text{。}$ | (3) |
其中:
该优化运行模型的最终目标可以表示为式(4),其中kR,kC,kP表示各个目标的优先级。
| $ \min \sum\limits_t {( - {{k}_{{{R}}}}R(t) + {k_C}C(t) + {K_W}W(t))}\text{。}$ | (4) |
船舶电力系统优化的约束条件主要包括等式约束和不等式约束,等式约束主要是潮流方程的约束。
1)潮流约束
| $ \begin{split}&\left\{ {\begin{array}{*{20}{c}} {{P_{{\text{G}}i}}{\text{ + }}{P_{Ni}} - {P_{{\text{D}}i}}{\text{ = }}{U_i}\displaystyle\sum\limits_{j \in i} {} {U_j}({G_{ij}}\cos {\delta _{ij}} + {B_{ij}}\sin {\delta _{ij}}) = 0} \text{,}\\ {{Q_{{\text{G}}i}}{\text{ + }}{{\text{Q}}_{Ni}} - {Q_{{\text{D}}i}}{\text{ = }}{U_i}\displaystyle\sum\limits_{j \in i} {} {U_j}({G_{ij}}\sin {\delta _{ij}} + {B_{ij}}\cos {\delta _{ij}}) = 0} \text{,} \end{array}} \right.\\ &i,j \in {{\text{S}}_{\text{B}}}\text{。}\\[-13pt] \end{split}$ | (5) |
其中:
而不等式约束包含了节点电压约束、线路支路容量约束、传统机组与新能源发电机组的出力限制约束。
2)节点电压约束
| $ {U_{i\_\min }} \leqslant {U_i} \leqslant {U_{i\_\max }},i \in {S_B}\text{,}$ | (6) |
其中:
3)支路容量功率约束
| $ - {P_{ij\_\max }} \leqslant {P_{ij}} \leqslant {P_{ij\_\max }},i,j \in {S_B}\text{,}$ | (7) |
其中:
4)传统发电机组出力约束
式(8)表示传统机组出力大小约束,而式(9)则表示在一定时间尺度下的传统发电机的爬坡约束。
| $ P_g^{\min } \leqslant P_{g,t}^{} \leqslant P_g^{\max },\begin{array}{*{20}{c}} {}&{} \end{array}\forall g \in G\text{,}$ | (8) |
| $ - \Delta P_g^{{\rm{RD}}} \leqslant P_{g,t} - P_{g,t - 1}\leqslant \Delta P_g^{{\text{RU}}},\forall g \in {\text{G}}\text{。}$ | (9) |
其中:
5)光伏电源出力约束
与传统发电设备不同的是,光伏发电出力具有很大的波动性,一般使用光伏发电出力标准值的最大波动量来约束新能源出力情况,如下式:
| $ P_p^{{\text{nom}}} - \hat P_p^{} \leqslant \tilde P_{p,t}^{} \leqslant P_p^{{\text{nom}}} + \hat P_p^{},\begin{array}{*{20}{c}} {}&{} \end{array}\forall p \in {\text{PV}}\text{。}$ | (10) |
其中:
为了验证所提出的在极地物探船上应用光伏新能源的优化模型的可行性和优越性,本文根据某物探船电力系统结构与数据为典型算例进行仿真论证分析。
传统物探船的电力系统中共有5个直流电源,3个交流电源以及应急发电机和停泊发电机。
各个可控单元即发电机具体数据参数参考表1。
|
|
表 1 可控单元的约束参数 Tab.1 Parameters of the controllable sources |
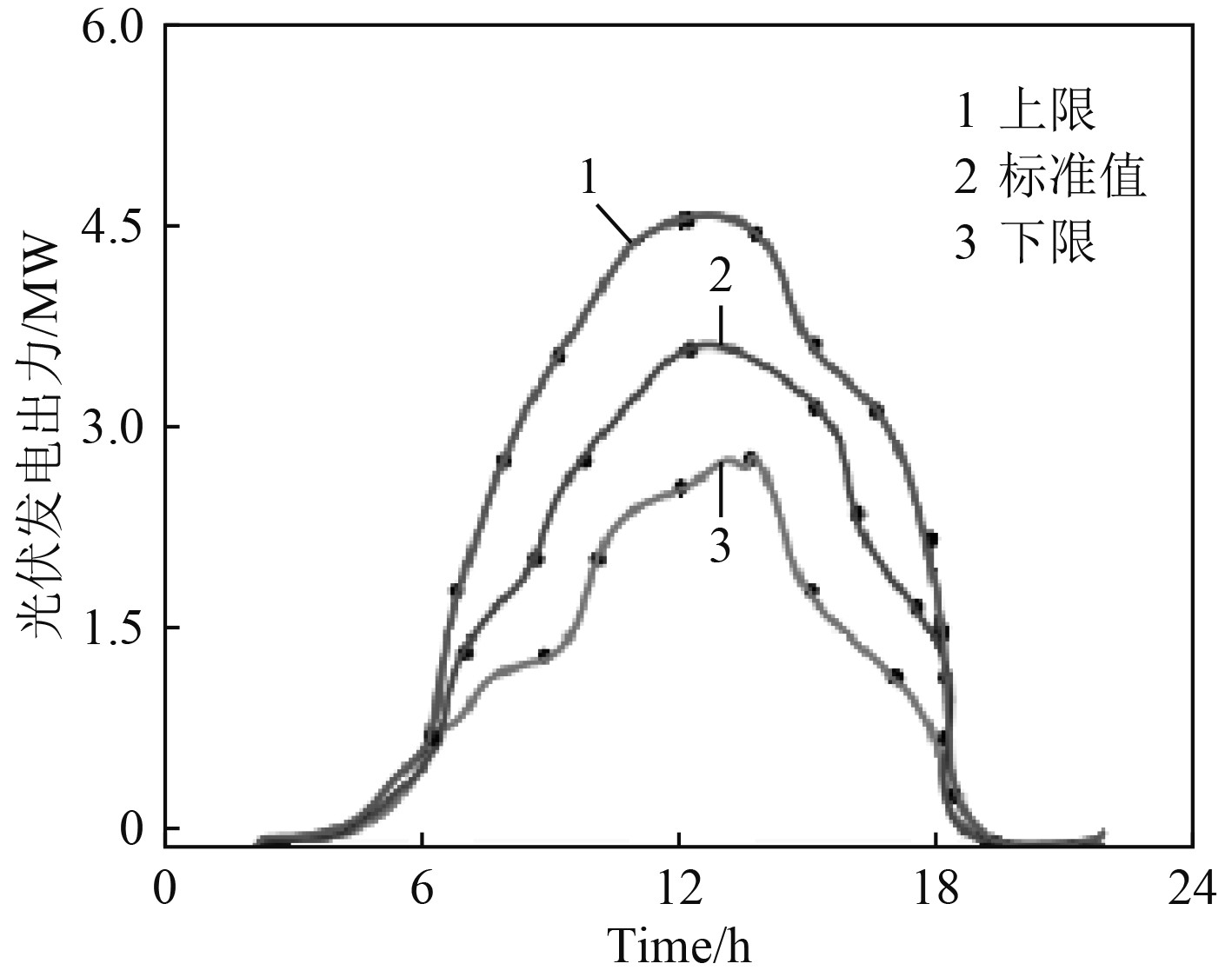
对于光伏出力及负荷情况,采用其在典型日24 h内的出力及负荷曲线作为输入,如图2所示(数据采用IEEE算例中新能源的出力情况)。
|
图 2 典型日不确定变量曲线 Fig. 2 Curve of uncertain variables in a typical day |
由于本文所提出优化模型的总目标由3个具有不同优先级参数的目标函数组成,因此最终计算得到的含新能源的极地物探船动力系统优化方案在一定程度上由权重参数kR,kC和kP决定。所以必须选取合适的权重参数使得3个目标函数的数量级一致,才可以进行优化运算。经过多次运算与测试后,本文选取kR = 2500, kC = 0.3, kP = 1.5,既符合数量级要求,又使得优化方案最优。
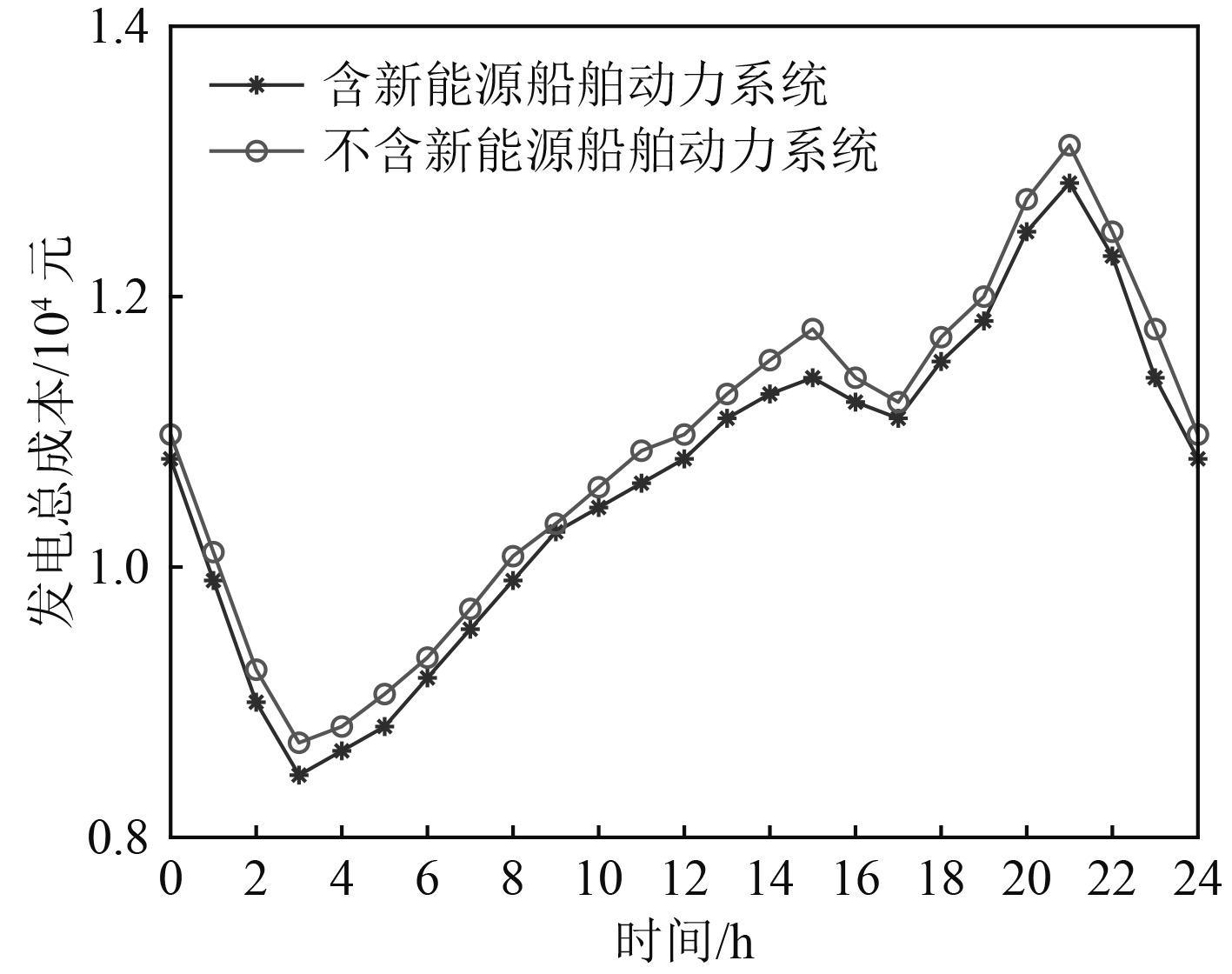
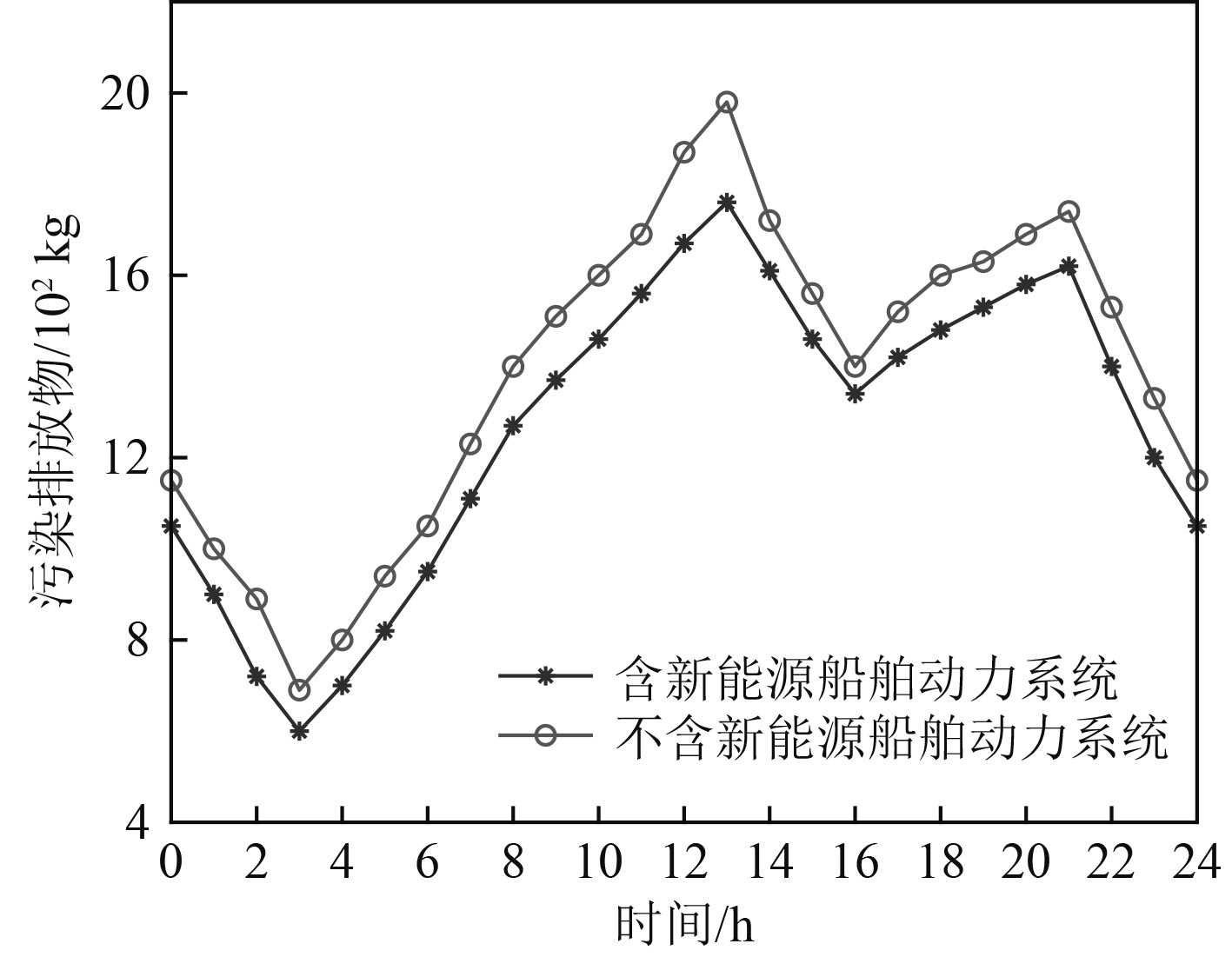
分别对含有新能源光伏发电机的物探船动力系统以及不含新能源光伏发电机的物探船动力系统进行计算,将2种情况下优化算法后的结果进行比较,最后从运行成本、船舶电力系统的可靠性、污染物的排放这3点进行对比分析。考虑极地物探船在恶劣环境下遇到干扰的情况下24 h运行周期,以优化经济和环保指标作为目标。同时,以35 min为周期,以弹性系数即可靠性指标作为目标。包含新能源与不含新能源的物探船动力系统优化计算结果如图3~图5所示。
|
图 3 总运行成本优化结果 Fig. 3 The optimal results of total cost |
|
图 4 总污染物排放优化结果 Fig. 4 The optimal results of total pollutant emissions |
|
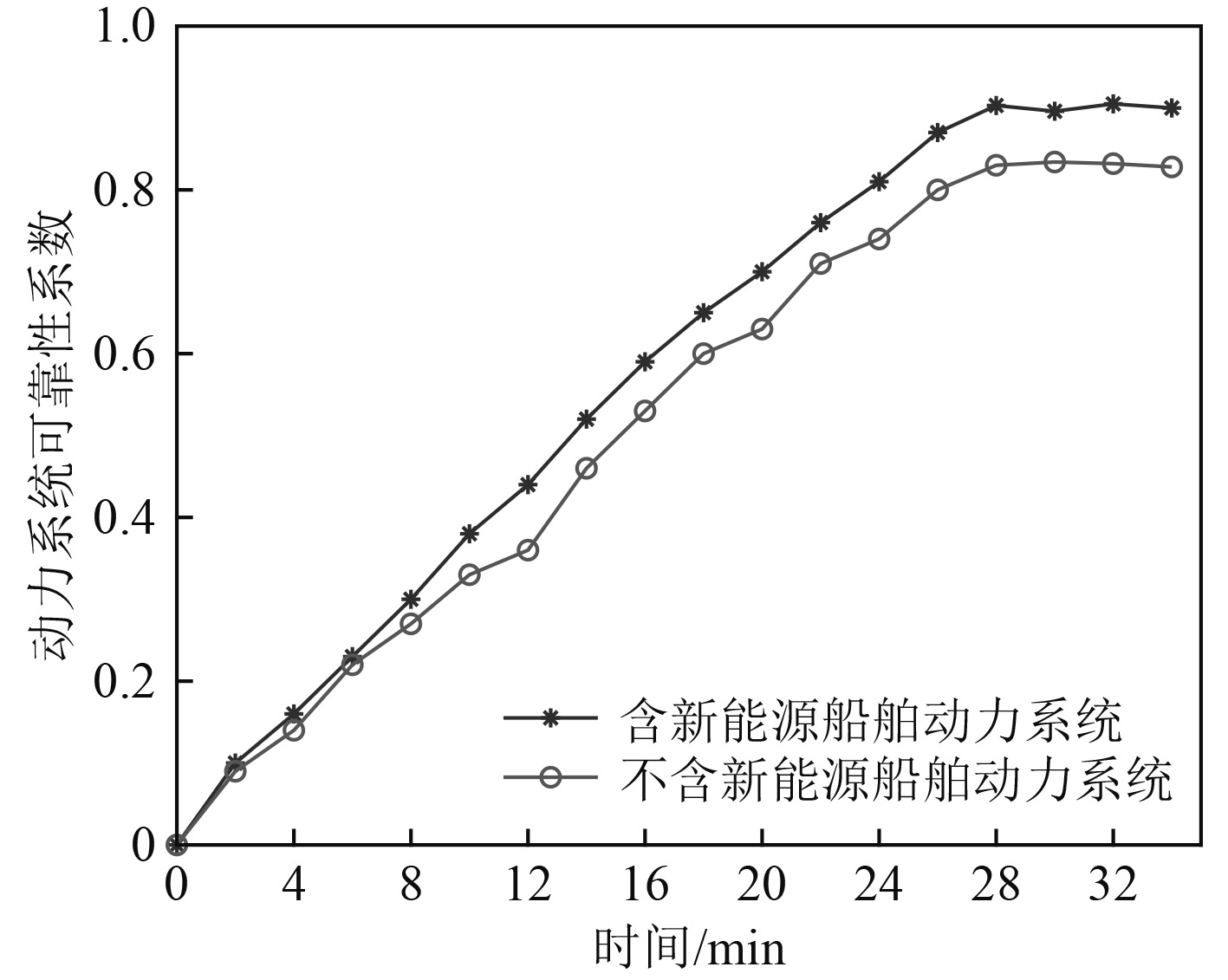
图 5 可靠性优化结果 Fig. 5 The optimal results of reliability |
优化计算结果表明,在权重参数选取kR = 2500, kC = 0.3, kP = 1.5的情况下,通过对比包含新能源的船舶动力系统优化结果与不包含新能源的船舶动力系统优化结果,可以发现本文所提出的对极地物探船电力推进动力系统加入新能源的优化方案是可行的,并且船舶动力系统总体水平得以改进,加入了新能源后总运行成本和污染物总排放量都会降低,而可靠性指数则会提高。在应用含新能源和不含新能源2种不同的极地物探船动力系统能源配置方案后,通过计算可知含新能源动力系统的总成本、污染物排放量、系统的可靠性都优于不含新能源的动力系统。
4 结 语本文将含有新能源的极地物探船动力系统与不含新能源的极地物探船动力系统分别进行遗传算法的优化计算,通过对比计算结果,可以发现本文所提出的对极地物探船电力推进动力系统加入新能源的优化方案是可行的,并且船舶动力系统总体水平得以改进,加入了新能源后总运行成本和污染物总排放量都会降低,而系统的可靠性指数则会提高。
| [1] |
吕宝刚. 北极航行的环境因素及冰区航行安全措施研究[D]. 大连: 大连海事大学, 2012.
|
| [2] |
贠廷军, 李京伟, 王晓雷. 船舶动力系统现状及发展趋势[J]. 船舶物资与市场, 2020(8): 1-2. |
| [3] |
王凯, 卢博闻, 李仁祥, 等. 船舶多清洁能源混合动力系统及其关键技术[J]. 舰船科学技术, 2020, 42(17): 6-11. WANG Kai, LU Bowen, LI Renxiang, et al. Ship multi-clean energy hybrid power system and its key technologies[J]. Ship Science and Technology, 2020, 42(17): 6-11. |
| [4] |
王凯, 卢博闻, 李宇奇, 等. 船舶多清洁能源混合动力系统优化设计方法[J]. 船舶工程, 2020, 42(4): 8-14+108. |
| [5] |
段树华. 应用于船舶的自动化风力发电系统研究[J]. 舰船科学技术, 2016, 38(2): 40-42. DUAN Shuhua. Research on automatic wind power generation system applied to ships[J]. Ship Science and Technology, 2016, 38(2): 40-42. |
| [6] |
夏侯命胜, 李志雨, 王东, 等. 物探船关键技术及发展趋势[J]. 船舶工程, 2019, 41(10): 16-23. |
| [7] |
付学辉, 李铭. 大型深水物探船关键技术研究[C]//第十七届中国科协年会——分6 中国海洋工程装备技术论坛论文集, 2015: 6.
|
| [8] |
吴泽奇, 曹锋, 严晨刚. 混合推进方式在物探船上的应用[J]. 科技创新与应用, 2015(26): 37. |
| [9] |
池波, 翁爽. 直流配电技术电力推进系统在物探船上的应用[J]. 舰船科学技术, 2014, 36(11): 108-111. CHI Bo, Weng Shuang. Application of DC power distribution technology electric propulsion system in geophysical exploration ship[J]. Ship Science and Technology, 2014, 36(11): 108-111. DOI:10.3404/j.issn.1672-7649.2014.11.021 |
| [10] |
张舒蓉. 12缆物探船电力推进系统研究[J]. 船舶与海洋工程, 2012(2): 47-52. ZHANG Shurong. Research on the electric propulsion system of the 12-cable geophysical prospecting ship[J]. Ship and Ocean Engineering, 2012(2): 47-52. DOI:10.3969/j.issn.1005-9962.2012.02.012 |
| [11] |
王波, 饶广龙, 李铭, 等. 高性能物探船推进动力系统配置分析[J]. 船舶, 2016, 27(2): 58-65. DOI:10.3969/j.issn.1001-9855.2016.02.011 |
| [12] |
“海洋石油760”号南海深水二维物探船[J]. 船舶, 2016, 27(1): 116.
|
| [13] |
叶锦文, 金余. 高性能物探船的设计和建造[C]//2012年中国造船工程学会优秀学术论文集, 中国造船工程学会, 2013: 8.
|
| [14] |
蔡梅江, 曹伟, 胡冰. 北极东北航道经济性及未来发展趋势分析[J]. 交通信息与安全, 2020, 38(3): 105-111+147. DOI:10.3963/j.jssn.1674-4861.2020.03.014 |
| [15] |
岳宏, 吴笑风, 赵宇欣. 极地船舶发展现状及研制趋势[J]. 中国船检, 2020(7): 58-64. DOI:10.3969/j.issn.1009-2005.2020.07.016 |
| [16] |
白雪梅. 极地船舶发展及相关建议[J]. 中国远洋海运, 2020(2): 68-70. |
| [17] |
张俊武, 吴清伟, 赵旭. 极地冰区船舶发展分析[J]. 船舶工程, 2016, 38(11): 1-5+57. |
| [18] |
王俊, 郑晓冬, 邰能灵, 等. 弹性导向的配电网鲁棒优化运行策略[J]. 太原理工大学学报, 2019, 50(5): 660-666. |
 2021, Vol. 43
2021, Vol. 43
