过去一二十年中,AUV的轨迹跟踪控制系统的设计方法一直是研究的热点之一。Yuh等[1]对此进行了全面而细致的研究。同时,各类生产活动对AUV的自主能力要求越来越高,例如使用AUV定期检查海上平台的圆柱形桩基,往往需要AUV沿螺旋线下沉以提高作业效率。欠驱动机器人轨迹跟踪主要的难点在于缺少能够对全自由度直接进行控制的独立推进器。因此,欠驱动机器人受漂移力或波浪力等非线性时变扰动的影响更大。Nakamura等[2]较早开展了对欠驱动AUV非线性控制方法的研究,但是其动力学模型比较粗糙,没有考虑强非线性和强耦合的离心力、科氏力项的影响。
随着非线性控制理论的发展,有很多专家学者基于更为完整的动力学模型对欠驱动AUV的运动控制稳定性和控制律进行了广泛的研究,包括轨迹跟踪[3-5]、路径点跟踪[6]、水下管道跟踪[7-8]、水下入坞控制、水下避障[9]等,但是这些运动控制研究通常基于三自由度的全驱动或欠驱动AUV动力学模型,着重关注AUV三自由度的运动特性,忽略了其他的运动特性。如Xiang等[10]基于反步法和李雅普诺夫直接法设计了AUV水平面运动控制器。Xu等[11]针对欠驱动AUV的水平面轨迹跟踪问题设计了自适应动态滑模控制器。也有一些研究者直接基于五或六自由度AUV动力学模型进行控制器设计,如Khoshnam等[12]设计了神经网络自适应鲁棒控制器,进行了海流扰动下AUV三维轨迹跟踪运动仿真,取得了较好的跟踪效果。王宏健等[13]设计了滤波反步法控制器,完成了水下三维曲线轨迹的跟踪运动仿真。贾鸣鹤等[14]设计了神经网络自适应反馈控制器,完成了AUV对三维螺旋下潜轨迹的跟踪。
本文首先给出了欠驱动六自由度AUV动力学模型和大部分该AUV的水动力导数。之后,通过虚拟目标法建立了欠驱动AUV的轨迹跟踪误差方程,并设计了DRNN-S控制器。最后,本文在Matlab平台上进行了欠驱动AUV三维曲线轨迹跟踪运动仿真,展示了轨迹跟踪过程中的AUV姿态变化、AUV舵角响应、推力响应。仿真结果显示,DRNN-S控制器可用于欠驱动AUV的三维轨迹跟踪控制。
1 AUV动力学模型水下机器人六自由度动力学与运动学方程[15]如下:
| $ \begin{split} &{\boldsymbol{M}}\dot \varsigma + {\boldsymbol{C}}\left( \varsigma \right)\varsigma + {\boldsymbol{D}}\left( \varsigma \right)\varsigma + {\boldsymbol{G}}\left( \eta \right) = \tau + f\text{,} \\ &\dot \eta = {{{J}}_\Theta }\left( \eta \right)\varsigma \text{。} \end{split} $ | (1) |
式中:
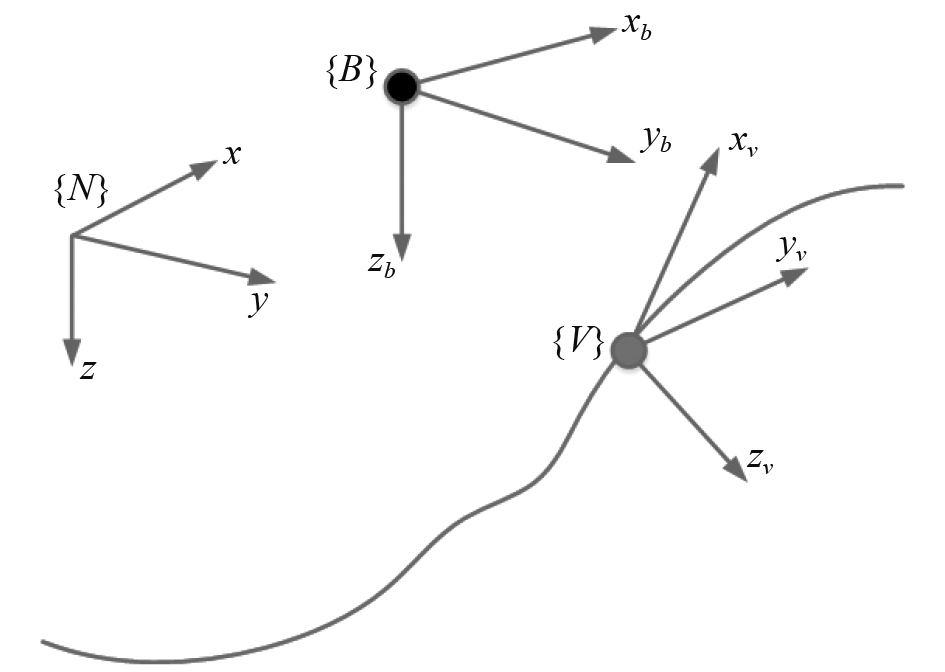
如图1所示,{N}为固定坐标系,{B}为艇体坐标系,{V}为跟踪轨迹上的虚拟坐标系。要保证AUV能够实时跟踪三维曲线轨迹,{B}应与{V}一直保持重合。
|
图 1 {N},{B},{V}坐标系 Fig. 1 {N}, {B} and {V} coordinate system |
定义{N}坐标系下的跟踪误差为
| $ {\varepsilon _e} = {\boldsymbol{R}}_b^{n{\rm{T}}}{\eta _e}\text{,}$ | (2) |
其中,
| $ {\boldsymbol{R}}_b^{nT} = \left[ {\begin{array}{*{20}{c}} {\cos \psi \cos \theta }&{\sin \psi \cos \theta }&{ - \sin \theta } \\ { - sin\psi }&{\cos \psi }&{\text{0}} \\ {\cos \psi \sin \theta }&{\sin \psi \sin \theta }&{\cos \theta } \end{array}} \right]\text{,} $ | (3) |
对式(2)微分可得:
| $ {\dot \varepsilon _e} = \dot {\boldsymbol{R}}_b^{n{\rm{T}}}{\eta _e} + {\boldsymbol{R}}_b^{n{\rm{T}}}{\dot \eta _e} \text{。}$ | (4) |
展开式(4)可化简如式(5)所示,经以上述变换后得到{B}坐标系下的误差方程以及误差微分方程。之后,将根据运动误差方程,针对欠驱动AUV设计DRNN-S控制器,控制器输出轴向驱动力
| $ \left\{ {\begin{array}{*{20}{l}} {{\dot x}_e} = u - q{z_e} + r{y_e} - {{\dot x}_d}\cos \left( \theta \right)\cos \left( \psi \right) -\\ \qquad {{\dot y}_d}\cos \left( \theta \right)\sin \left( \psi \right) + {{\dot z}_d}\left( \theta \right) \text{,}\\ {{{\dot y}_e} = v - r\left( {{x_e} + \tan \left( \theta \right){z_e}} \right) + {{\dot x}_d}\sin \left( \psi \right) - {{\dot y}_d}\cos \left( \psi \right)} \text{,}\\ {{\dot z}_e} = w + q{x_e} + r\tan \left( \theta \right){y_e} - {{\dot x}_d}\sin \left( \theta \right)\cos \left( \psi \right) -\\ \qquad {{\dot y}_d}\sin \left( \theta \right)\sin \left( \psi \right) - {{\dot z}_d}\cos \left( \theta \right) \text{。} \end{array}} \right. $ | (5) |
由于欠驱动AUV动力学模型的强非线性和耦合性,三维轨迹跟踪运动中使用线性控制器往往无法取得较好的跟踪效果。本文设计了DRNN-S控制器,使用混合控制器可以避免DRNN在线迭代学习过程中不容易发散,而神经网络又能补偿S面控制器的输出,提高S面控制器的鲁棒性。S面控制器是一种非线性无模型控制器,类似模糊PD控制器,对于非线性系统有较好的效果,得到了大量的应用和改进。李岳明等[18]在S面基础上改进提出了自适应S面控制器,并基于李雅普诺夫稳定性理论进行了稳定性分析。仿真表明自适应S面控制可以显著减小超调、加速收敛。自适应S面位置跟踪方程如下[18]:
| $ {u_s} = \frac{2}{{1 + \exp \left( {\left( { - {k_1}e - {k_2}\dot e} \right)} \right)}} - 1{\text{ + }}\Delta f \text{,}$ | (6) |
| $ \Delta f = S\left( {\Delta e,0} \right) \text{,}$ | (7) |
| $ \Delta e = \gamma \left( {1 - \delta } \right){e_t} + \delta {\alpha _t}{\beta _t}\sum\limits_{i = t - n}^t {{e_i}} \text{。}$ | (8) |
式中:
| $ {k_1} = \left[ {\begin{array}{*{20}{c}} {20}&0&0 \\ 0&6&0 \\ 0&0&1 \end{array}} \right],{k_2} = \left[ {\begin{array}{*{20}{c}} {0.01}&0&0 \\ 0&{0.001}&0 \\ 0&0&{0.001} \end{array}} \right]\text{。} $ | (9) |
DRNN是一种3层在线学习神经网络,相对于传统的前馈神经网络,该网络对非线性系统有更好的拟合效果。DRNN的性能指标函数如下:
| $ E\left( k \right) = \frac{1}{2}{\left( {{u_t}\left( k \right) - {u_d}\left( k \right)} \right)^2} = \frac{1}{2}{\left( {{u_s}\left( k \right)} \right)^2} \text{。}$ | (10) |
其中混合控制器总输出
仿真实验在Matlab平台上进行。仿真使用的流线型AUV动力学方程如式(1),AUV驱动方式为尾部单螺旋桨推进器和尾部十字形舵。方程所用到的系数如表1所示,包括了AUV全部惯性类水动力系数和部分粘性类水动力系数。动力学模型中的不确定部分使用下式模拟:
|
|
表 1 AUV水动力系数表 Tab.1 The hydrodynamic coefficients for an AUV |
| $ {f_w} = {c_{w1}}w + {c_{w2}}\left| w \right|w + {c_{w3}}{w^3},w = u,v,w,p,q,r \text{。}$ | (11) |
其中,
AUV质量属性为特征长度L=2.38 m,m=167 kg,Ixx = 4.73 kg·m2,Iyy = 70.27 kg·m2,Izz = 71.38 kg·m2。忽略AUV非对角转动惯量。
三维曲线轨迹方程如下:
| $ \left\{ {\begin{array}{*{20}{l}} {x(t) = t} \text{,}\\ {y(t) = 200 \cdot \cos \left( {\dfrac{\text{π} }{{200}}t} \right) - 200} \text{,}\\ {z(t) = 0.1t} \text{。} \end{array}} \right. $ | (12) |
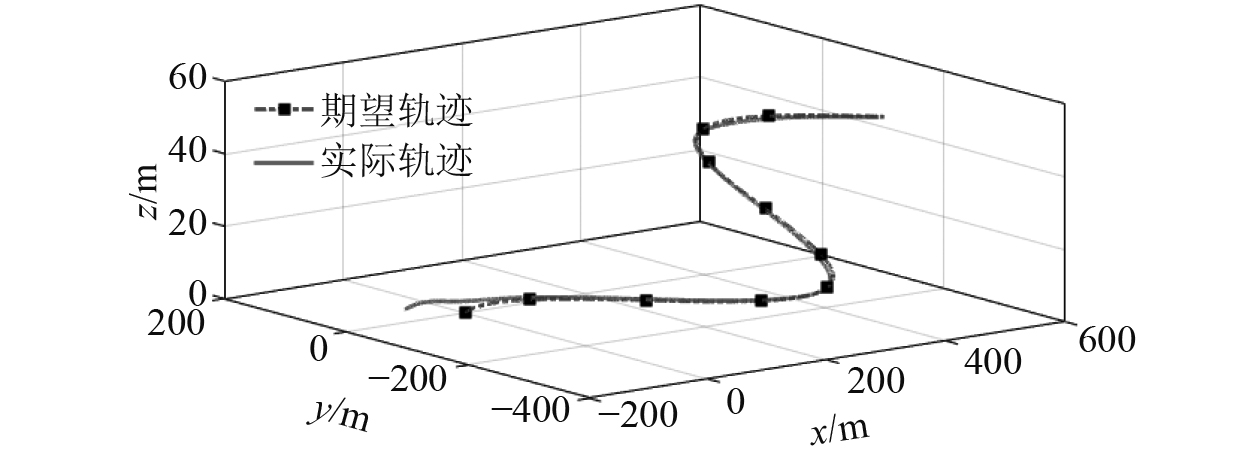
图2~图4为了欠驱动AUV三维轨迹跟踪效果。图2中,AUV从[−50 50 0]位置出发,开始跟踪三维曲线轨迹,轨迹起点为
|
图 2 AUV三维轨迹跟踪 Fig. 2 Three-dimensional trajectory tracking for an AUV |
|
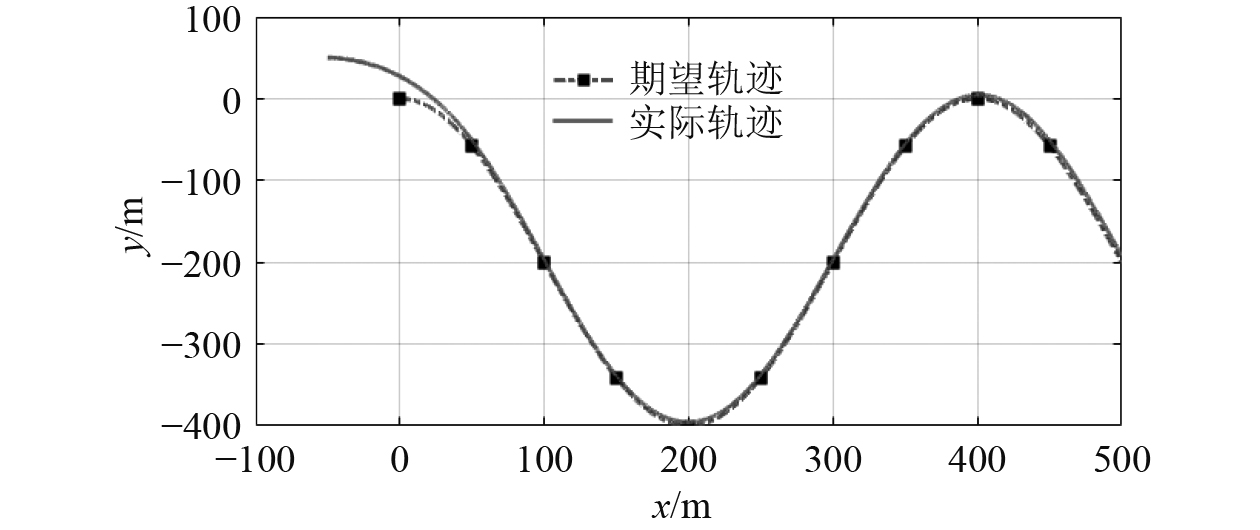
图 3 三维轨迹跟踪x-y平面投影 Fig. 3 XY plane prejection for three-dimensional trajectory tracking |
|
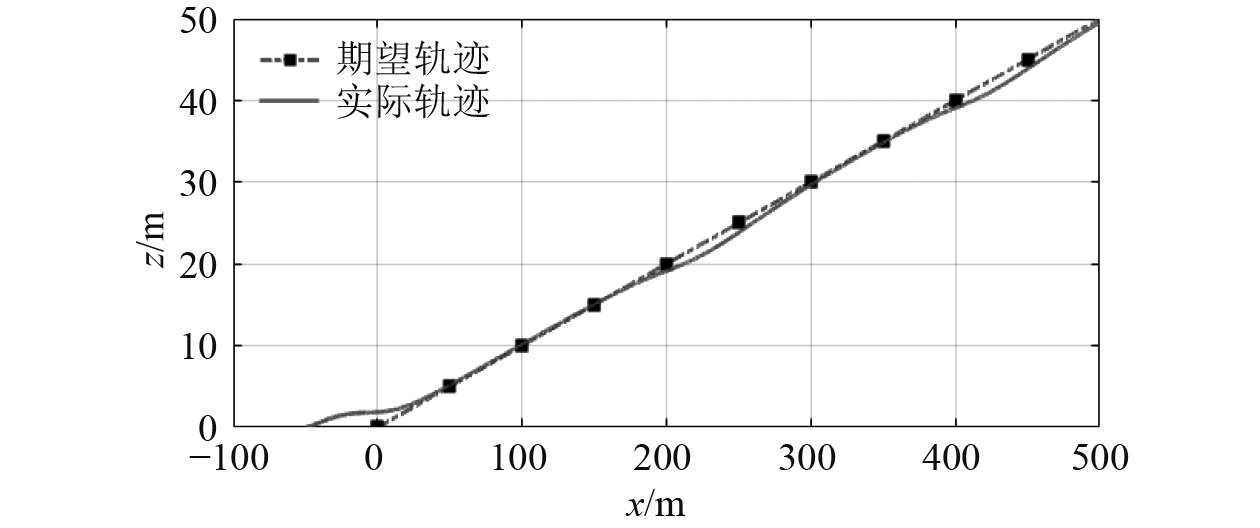
图 4 三维轨迹跟踪x-z平面投影 Fig. 4 XZ plane prejection for three-dimensional trajectory tracking |
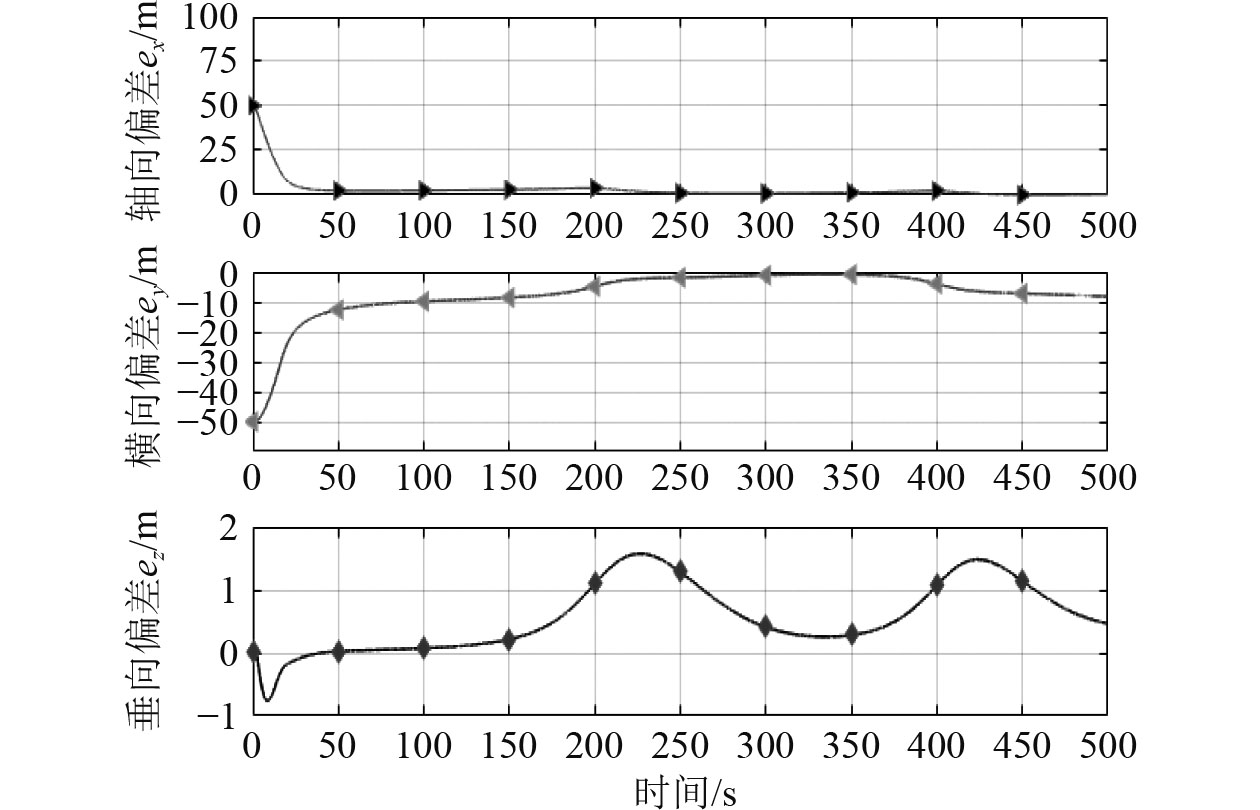
|
图 5 位置跟踪偏差 Fig. 5 Tracking errors |
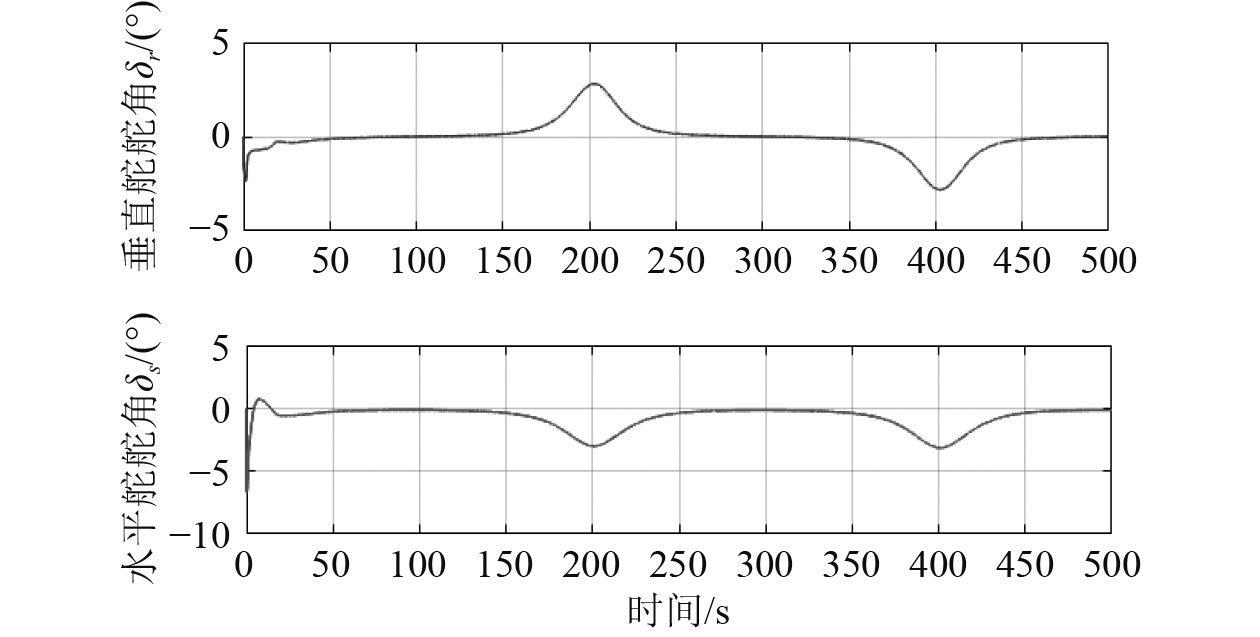
|
图 6 舵角响应 Fig. 6 Rudder response |

|
图 7 轴向速度跟踪偏差 Fig. 7 X-axis velocity error |
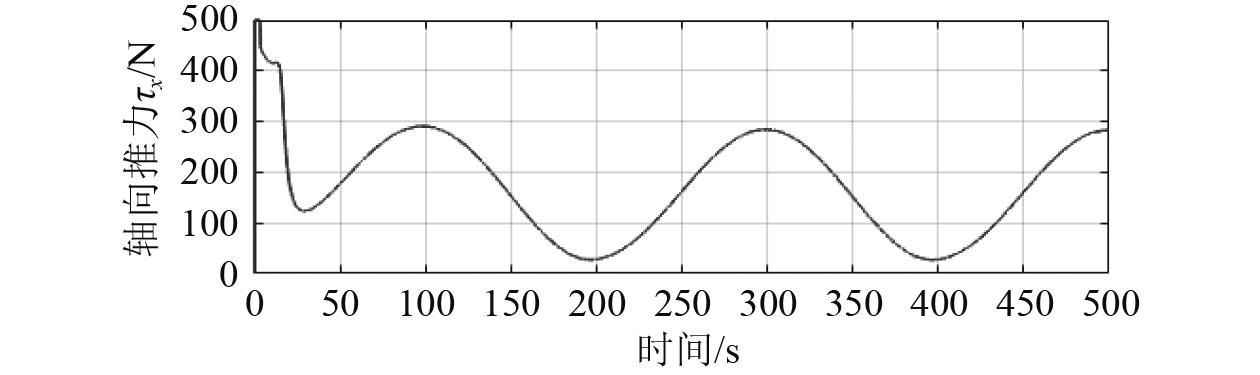
|
图 8 推力响应 Fig. 8 Thrust response |
综上,基于DRNN-S自适应控制器,欠驱动AUV能以较小误差实时跟踪三维曲线轨迹。
5 结 语本文通过在Matlab平台进行仿真,验证了DRNN-S非线性无模型控制器在欠驱动AUV三维轨迹跟踪任务中有良好的控制效果,基于虚拟目标法建立的跟踪误差方程,AUV能保持较小的跟踪误差对曲线轨迹进行实时跟踪。通过组合DRNN与自适应S面控制器,建立了DRNN-S混合控制器。通过组合两种非线性鲁棒控制器,一方面提高了神经网络对非线性强耦合动力学模型的拟合效果,克服了神经网络直接拟合动力学模型时容易发散的问题。另一方面,由于DRNN在线学习后可以补偿S面控制器的输出,减少了手动调整S面控制器增益参数的工作量。
| [1] |
YUH J. Design and control of autonomous underwater robots: A survey[J]. Autonomous Robots, 2000, 8(1): 7-24. DOI:10.1023/A:1008984701078 |
| [2] |
NAKAMURA Y, SAVANT S. Nonlinear tracking control of autonomous underwater vehicles[C]// Robotics and Automation, 1992. Proceedings, 1992 IEEE International Conference, 1992(3): A4-A9.
|
| [3] |
夏国清, 杨莹, 赵为光. 欠驱动AUV模糊神经网络L_2增益鲁棒跟踪控制[J]. 控制与决策, 2013(3): 351-356. |
| [4] |
万磊, 崔士鹏, 张国成, 等. 欠驱动水下机器人航迹跟踪控制[J]. 电机与控制学报, 2013, 17(2): 103-111. DOI:10.3969/j.issn.1007-449X.2013.02.016 |
| [5] |
张勋, 边信黔, 唐照东, 等. AUV均衡系统设计及垂直面运动控制研究[J]. 中国造船, 2012, 53(1): 28-36. |
| [6] |
陈东, 向先波, 郑金荣, 等. 欠驱动AUV三维轨迹跟踪控制[C]// 第三十二届中国控制会议, 2013: 6.
|
| [7] |
曾文静, 徐玉如, 万磊, 等. 自主式水下机器人的光视觉管道探测跟踪系统[J]. 上海交通大学学报, 2012(2): 178-183+189. |
| [8] |
唐旭东. 智能水下机器人水下管道检测与跟踪技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2011.
|
| [9] |
张汝波, 李建军, 杨玉. 基于改进蚁群算法的 AUV 航路避障任务规划[J]. 华中科技大学学报(自然科学版), 2015(s1): 428-430. |
| [10] |
XIANG X, LAPIERRE L, JOUVENCEL B J R. Smooth transition of AUV motion control: From fully-actuated to under-actuated configuration[J]. Robotics Autonomous Systems, 2015, 67: 14-22. DOI:10.1016/j.robot.2014.09.024 |
| [11] |
XU J, WANG M, QIAO L. Dynamical sliding mode control for the trajectory tracking of underactuated unmanned underwater vehicles[J]. Ocean Engineering, 2015, 105: 54-63. DOI:10.1016/j.oceaneng.2015.06.022 |
| [12] |
SHOJAEI K, DOLATSHAHI M. Line-of-sight target tracking control of underactuated autonomous underwater vehicles[J]. Ocean Engineering, 2017, 133: 244-252. DOI:10.1016/j.oceaneng.2017.02.007 |
| [13] |
王宏健, 陈子印, 贾鹤鸣, 等. 基于滤波反步法的欠驱动AUV三维路径跟踪控制[J]. 自动化学报, 2015(3): 631-645. |
| [14] |
贾鹤鸣, 张利军, 齐雪, 等. 基于神经网络的水下机器人三维轨迹跟踪控制[J]. 控制理论与应用, 2012, 29(7): 56-62. |
| [15] |
FOSSEN T I. Handbook of Marine Craft Hydrodynamics and Motion Control[M]. 2011.
|
| [16] |
BREIVIK M, FOSSEN T I: Guidance-based path following for autonomous underwater vehicles[J]. Oceans, 2005(1-3): 2807−2814.
|
| [17] |
BREIVIK M, FOSSEN T I, Ieee: A unified control concept for autonomous underwater vehicles[J]. American Control Conference, 2006(1-12): 4920.
|
| [18] |
李岳明, 庞永杰, 万磊. 水下机器人自适应S面控制[J]. 上海交通大学学报, 2012(2): 195-200+206. |
 2021, Vol. 43
2021, Vol. 43

