自主式水下航行器(AUV)水动力参数的辨识成为对其运动研究和运动控制器设计的关键所在[1]。在工程应用中,对水动力系数求取的主要方法有:经验公式估算方法、数值模拟方法、模型试验方法以及基于实航数据的参数辨识方法。经验公式估算方法具有较好的经济性和可行性,但其精确性难以保证。数值模拟方法大多采用流体计算(CFD)软件,但计算量较大,且计算结果容易受到模型网格划分质量和边界条件的影响[2];模型试验方法虽然对水动力参数的求取精确度较高,但其成本较高,花费时间较长,会不可避免的受到传感器及操作误差的影响[3];基于实航数据的参数系统辨识方法成本较低,能更好地反映航行器在真实环境中的水动力参数,适用性和精确性较好。
现阶段的AUV水动力参数系统辨识方法有很多,但大多数辨识所用到的数据来源或辨识方程为AUV的水平面运动或竖直平面运动甚至单自由度运动等,未考虑完整的六自由度运动方程。一些辨识方法在遇到数据掺杂噪声时辨识结果较差,往往需要对数据预先进行滤波消噪处理,加大了参数辨识的工作量。例如参数辨识中的牛顿—拉夫逊算法对数据初值极为敏感[4],也会导致辨识工作变得复杂。为完善或避免上述问题,本文采用自适应粒子群优化算法和最小二乘[5-6]准则相结合的方式对AUV水动力参数进行辨识。建立所需辨识的AUV六自由度动力学方程。系统介绍自适应粒子群优化算法和最小二乘准则。基于自适应粒子群优化算法和最小二乘准则建立AUV水动力参数的辨识方法。进行AUV水动力参数辨识的仿真计算。
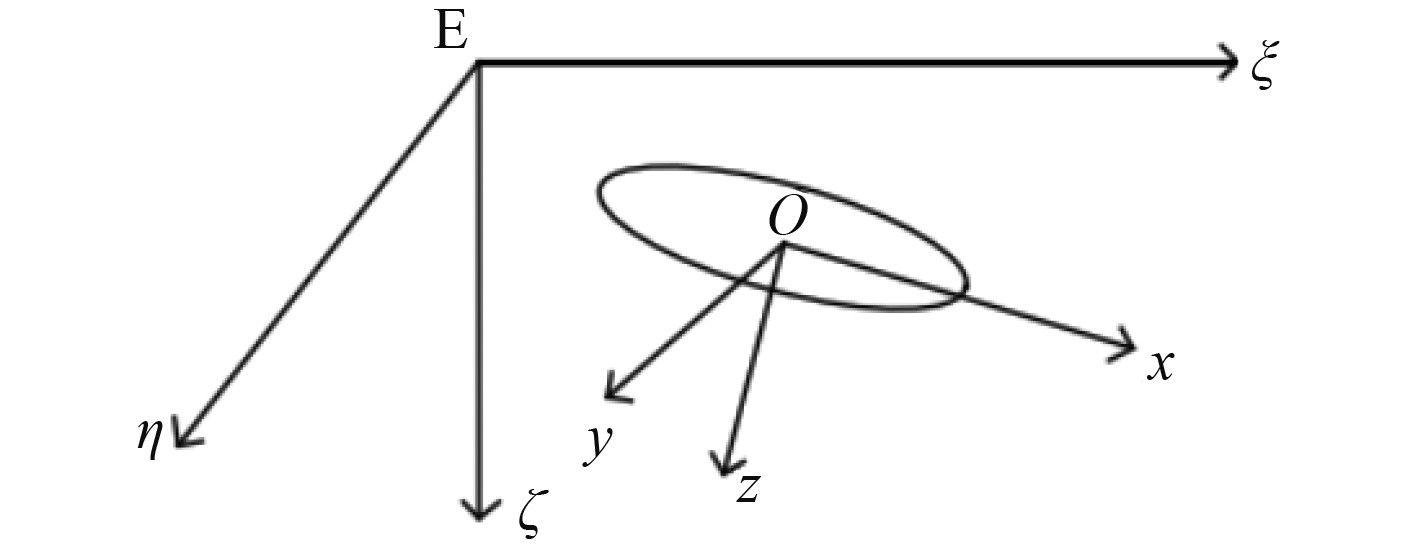
1 AUV数学模型对于AUV的水动力参数辨识,需要先建立AUV运动的数学模型。为描述AUV的运动,采用如图1所示的固定坐标系
|
图 1 固定和运动坐标系 Fig. 1 Fixed and moving coordinates |
根据本文所辨识的AUV[8]具有外形左右、上下、前后对称的结构特征,此时运动坐标系原点选为AUV重心,对AUV动力学方程进行系统辨识,得到AUV六自由度运动动力学方程如下式:
| $ \begin{split} & m(\dot u - vr + wq) + (W - B)\sin \theta - X = {X_{\dot u}}\dot u + {X_u}u +\\ & {X_{u\left| u \right|}}u\left| u \right| + {Z_{\dot w}}wq - {Y_{\dot v}}vr{\text{,}} \end{split} $ | (1) |
| $ \begin{split} & m\left( {\dot v - wp + ur} \right) - (W - B)\cos \theta \sin \varphi - Y = {Y_{\dot v}}\dot v + {Y_v}v + \\ & {Y_{v\left| v \right|}}v\left| v \right| - {Z_{\dot w}}wp + {X_{\dot u}}ur{\text{,}} \end{split} $ | (2) |
| $ \begin{split} & m(\dot w + vp - uq) - (W - B)\cos \theta \cos \varphi - Z =\\ & {Z_{\dot w}}\dot w + {Z_w}w + {Z_{w\left| w \right|}}w\left| w \right| + {Y_{\dot v}}vp - {X_{\dot u}}uq {\text{,}} \end{split}$ | (3) |
| $ \begin{split} & {I_x}\dot p + {I_z}rq - {I_y}qr + {y_b}B\cos \theta \cos \varphi - {z_b}B\cos \theta \sin \varphi - K = \\ & {K_{\dot p}}\dot p + {K_p}p + {K_{p\left| p \right|}}p\left| p \right| + {Z_{\dot w}}wv - {Y_{\dot v}}vw + {N_{\dot r}}rq - {M_{\dot q}}qr{\text{,}} \end{split} $ | (4) |
| $ \begin{split} & {I_y}\dot q - {I_z}rp + {I_x}pr - {z_b}B\sin \theta - {x_b}B\cos \theta \cos \varphi - M = \\ & {M_{\dot q}}\dot q + {M_q}q + {M_{q\left| q \right|}}q\left| q \right| - {Z_{\dot w}}wu + {X_{\dot u}}uw - {N_{\dot r}}rp + {K_{\dot p}}pr{\text{,}} \end{split} $ | (5) |
| $ \begin{split} & {I_z}\dot r + {I_y}qp - {I_x}pq + {x_b}B\cos \theta \sin \varphi + {y_b}B\sin \theta - N = \\ & {N_{\dot r}}\dot r + {N_r}r + {N_{r\left| r \right|}}r\left| r \right| + {Y_{\dot v}}vu - {X_{\dot u}}uv + {M_{\dot q}}qp - {K_{\dot p}}pq{\text{。}} \end{split} $ | (6) |
|
|
表 1 固定坐标系主要运动参数定义 Tab.1 Definition of main motion parameters in fixed coordinate system |
|
|
表 2 运动坐标系主要运动参数定义 Tab.2 Definition of main motion parameters in motion coordinate system |
对于所给定的AUV来说,以式(1)为例,可变换形式如下式:
| $ \begin{split} & m(\dot u - vr + wq) + (W - B)\sin \theta - X =\\ & {X_{\dot u}}\dot u + {X_u}u + {X_{u\left| u \right|}}u\left| u \right| + {Z_{\dot w}}wq - {Y_{\dot v}}vr{\text{。}} \end{split} $ | (7) |
式(7)左侧不包含辨识参数,右侧各组成部分均含有辨识参数。式(T)可写成式(8),T满足关系式(9)。
| $ T = \left[ {\begin{array}{*{20}{c}} {\dot u}&u&{u\left| u \right|}&{wq}&{ - vr} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{X_{\dot u}}} \\ {{X_u}} \\ {{X_{u\left| u \right|}}} \\ {{Z_{\dot w}}} \\ {{Y_{\dot v}}} \end{array}} \right]{\text{,}} $ | (8) |
| $ T = m(\dot u - vr + wq) + (W - B)\sin \theta - X {\text{。}}$ | (9) |
由式(8)可知,当测量数据采样点数大于等于所需辨识水动力参数个数时,即可利用方程关系解出水动力参数。但式(8)涉及到测量参数的微分项,高次项等,当其存在噪声引起误差时,即使该误差很小,也会导致水动力参数的求解出现病态结果,并且由式(1)~式(6)可知,水动力参数之间存在耦合作用,很难直接用理论或实验的方法较为准确的获得全部参数。因此本文将AUV的水动力参数辨识转化为最优化问题,基于粒子群算法对复杂的非线性模型方程是否连续、可微等不做要求及其自身特点,利用最小二乘法准则和自适应粒子群算法实现对该问题的求解。
2.1 最小二乘法准则式(1)~式(6)一般形式如下:
| $ \dot x(t) = f(x(t),u(t),\theta ){\text{,}} $ | (10) |
式中,
由式(10)可知,当输入
因此,要想实现对水动力参数的辨识,可采用最小二乘准则,其具体形式如下:
| $ J(\theta ) = \sum\limits_{i = 1}^N {{{\left( {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }_i} - {x_i}(\theta )} \right)}^{\rm{T}}}} \left( {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }_i} - {x_i}(\theta )} \right) {\text{。}}$ | (11) |
式中,
因此,AUV水动力参数的辨识问题可转化为改变参数
粒子群优化(PSO)算法是一种进化计算方法,具有随机性和继承性的特点。它起源于对鸟类捕食行为的研究,最早由Eberhart博士和Kennedy博士发明[9-10]。粒子群算法的原理如下:
首先初始化一定量的随机粒子,作为随机解。假设搜索空间为d维,种群规模为M,第i个粒子的位置和速度分别为
| $ {v_{i,j}}(t + 1) = k{v_{i,j}}(t) + {c_1}{r_1}[{p_{i,j}} - {x_{i,j}}(t)] + {c_2}{r_2}[{p_{g,j}} - {x_{i,j}}(t)] {\text{,}}$ | (12) |
| $ {x_{i,j}}(t + 1) = {x_{i,j}}(t) + {v_{i,j}}(t + 1) {\text{。}}$ | (13) |
其中,
粒子群算法[12-13]的计算性能很大程度上取决于算法的控制参数,例如惯性权重、学习因子、粒子数、最大速度、适应度计算公式等。
1)惯性权重
对于惯性权重而言,当其数值较大时,利于跳出局部极小点,便于全局搜索[14],当其数值较小时,便于对当前区域进行精确局部搜索,利于算法收敛。充分考虑粒子群算法存在的早期容易陷于局部最优解以及后期容易在全局最优解附近产生振荡的问题,为平衡其全局搜索能力和局部改良能力,采用动态惯性权重更新公式(14),实现惯性权重的自适应变化。
| $ k = \left\{ {\begin{aligned} & {{k_{\min }} + \frac{{({k_{\max }} - {k_{\min }})*(f - {f_{\min }})}}{{({f_{avg}} - {f_{\min }})}},f \leqslant {f_{avg}}} {\text{,}}\\ & {{k_{\max }},f > {f_{avg}}} {\text{。}} \end{aligned}} \right. $ | (14) |
式中:
2)学习因子
学习因子
3)种群规模
种群规模的大小根据问题的复杂程度进行选择,一般种群规模越大,粒子群算法的寻优结果越好。
4)粒子范围
在条件允许的情况下,可对粒子范围进行预估,以促进粒子群算法的寻优进程。
5)最大速度
为了减少搜索空间的可能性,可根据粒子范围设定粒子的速度范围。
6)适应度值
粒子群优化算法的迭代过程中,粒子的位置和速度不断更新,而适应度值是确定粒子群优化是否符合要求的判断依据。
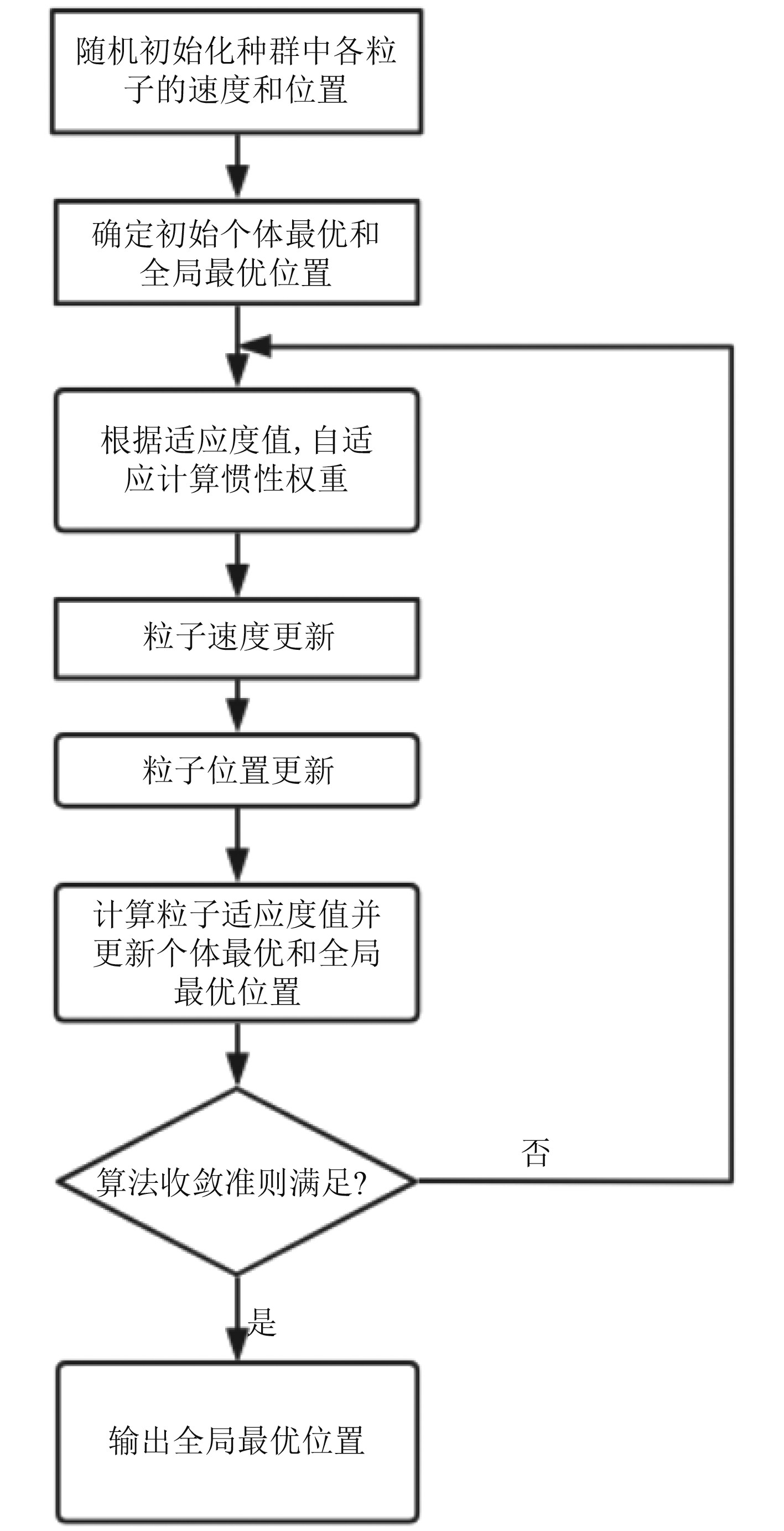
图2为自适应粒子群算法的流程图。
|
图 2 自适应粒子群算法流程 Fig. 2 Flow of adaptive particle swarm optimization algorithm |
本文设计的参数辨识算法思想是将粒子的位置意义定为待辨识的水动力参数。首先,利用给定的水动力参数求得理论运动参数值后叠加噪声,选取其中的N个作为式(11)中的实际观测数据
根据图2所显示的流程,最小二乘准则和自适应粒子群算法在AUV水动力参数辨识中的计算流程具体如下:
1)随机初始化各粒子,确定初始个体最优和全局最优
根据AUV水动力参数为负的特点,可设定初始化粒子位置为负数,初始速度采用1以内随机数。然后利用随机得到的粒子位置作为水动力参数代入所建立的AUV模型中进行仿真,仿真的其他条件设置同实际观测数据获取时的一致。选取仿真得到的AUV运动参数中对应实际观测参数时间点的参数作为
2)进入迭代,更新惯性权重,更新个体最优和全局最优位置
每次迭代采用上一次迭代所获取的各个粒子适应度值(初次迭代采用步骤1中得到的数据),对式(12)中所需要用到的惯性权重依据式(14)进行更新,然后根据式(12)和式(13)更新粒子的速度和位置,并用所设定的粒子范围和速度范围对更新后的数据进行约束。每次迭代中,当得到第n个粒子更新后的速度和位置,将粒子位置代入AUV水动力模型中进行仿真计算,然后选取仿真得到的AUV运动参数中对应实际观测参数时间点的参数作为
3)迭代指定步数,输出全局最优位置
算法收敛准则定为达到指定迭代次数,然后输出此时的全局最优粒子位置,也就是所需辨识的AUV水动力参数。
4 模拟仿真为检验自适应粒子群算法的可行性,采用模拟仿真进行验证。
已知本文所研究的AUV的几何参数及其水动力参数,为贴近AUV实际运动特性和确定所需辨识的水动力参数,采用系统辨识出的六自由度运动方程(1)~方程(6)作为其运动方程,在确定的初始状态
根据辨识算法设计,分别运用粒子群算法和自适应粒子群算法对水动力系数进行辨识。考虑AUV运动具有的强耦合、非线性、参数时变性等特点,将采样数据个数N定为100,粒子数取为50,
|
|
表 3 PSO和自适应PSO辨识结果 Tab.3 The identification results of PSO and Adaptive PSO |
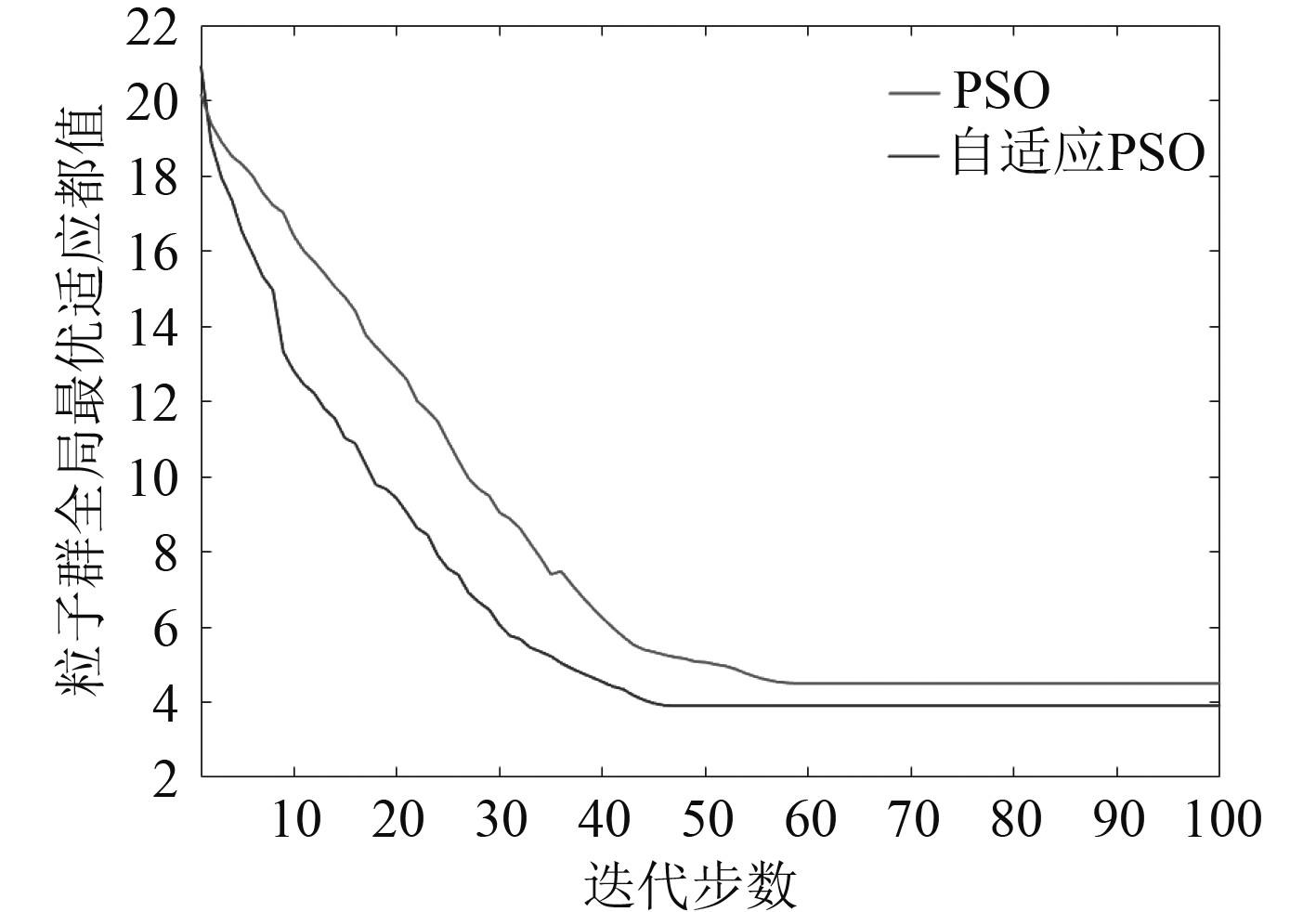
|
图 3 PSO与自适应PSO辨识收敛曲线 Fig. 3 Identification convergence curves of PSO and adaptive PSO |
由辨识结果对比以及图3辨识收敛曲线可知,在其他参数设置相同的条件下,自适应粒子群算法对AUV水动力系数的辨识速度和精度均优于粒子群算法。究其原因,自适应粒子群算法中,惯性权重的自适应设置使得各微粒的适应度值趋于一致或者趋于局部最优时,惯性权重增加,而各微粒的适应度值比较分散时,惯性权重减小。同时对于适应度值优于平均适应度值的微粒,其对应的惯性权重因子较小,从而保护了该微粒。反之对于目标适应度值差于平均适应度值的微粒,其对应的惯性权重因子较大,使得该微粒向较好的搜索区域靠拢。相比于惯性权重为定值的粒子群算法,自适应粒子群算法更好的平衡了全局搜索能力和局部改良能力,在保护适应度值较小粒子的同时,实现适应度较大粒子向较好区域的搜索,提升收敛速度和精度。
此外,为检验该方法对噪声的敏感性,在不同数据观测高斯白噪声的标准差值和相同的算法参数设置下,依据设计的辨识算法实现对AUV水动力参数的辨识,采用辨识50次取平均值的方法对结果进行修正。并将最终结果同仿真过程中的实际水动力参数进行比较。以式(1)中的水动力参数辨识为例,其结果如表4所示。
|
|
表 4 AUV水动力参数辨识结果 Tab.4 Identification results of hydrodynamic parameters |
由计算流程以及表4结果可得到以下结论:
1)辨识过程自始至终采用的为AUV六自由度方程,充分保留了其运动方程非线性、参数时变性、强耦合等特点,贴近实际,整体辨识结果较好,说明自适应粒子群算法的适用性较好。表4虽然只辨识了式(1)中所涉及到的AUV水动力参数,但该方法对于辨识参数的维度不敏感,因而对于其他水动力参数的辨识可类似进行。
2)当实际观测数据引入的噪声标准差从1%~7%变化时,AUV的水动力参数辨识的相对误差不超过3.27%,辨识结果较好,充分体现了自适应粒子群算法在AUV水动力参数辨识中对数据所掺杂噪声敏感性较低的特点;
3)辨识中并未对数据初值做特殊要求,可看出该方法对初值的敏感度较低,适应性较好;
4)表4中不同噪声水平下的AUV水动力参数辨识中,所运用的自适应粒子群算法参数设置均相同,意在控制变量,突出考察该方法对不同噪声的鲁棒性。在实际情况下,可对自适应粒子群算法中的参数进行调整,以获得更好的结果。
5 结 语本文针对AUV水动力参数辨识中所存在的一些问题,提出自适应粒子群算法和最小二乘准则相结合的辨识方法,用该方法实现了对AUV水动力参数的辨识,并将其同粒子群算法的辨识结果进行了比较,检验了该方法对噪声的敏感性。最终结果表明,该方法在AUV水动力参数辨识中具有可行性、可靠性以及鲁棒性,并且在辨识精度、收敛速度上均优于粒子群算法。
| [1] |
李庆梅, 刘平, 等. 基于NSGA-Ⅱ算法的水下机器人水平面运动参数辨识[J]. 上海第二工业大学学报, 2016, 33(2): 141-145. LI Qing-mei, LIU Ping, et al. Hydrodynamic coefficients identification for the horizontal plane motion of the underwater vehicle using NSGA-II algorithm[J]. jouranl of shanghai polytechinc university, 2016, 33(2): 141-145. DOI:10.3969/j.issn.1001-4543.2016.02.011 |
| [2] |
李迎华, 吴宝山, 张华. CFD动态网格技术在水下航行体非定常操纵运动预报中的应用研究[J]. 船舶力学, 2010, 14(10): 1100-1108. LI Ying-hua, WU Bao-shan, ZHANG Hua. Research on application of prediction for unsteady maneuvering motion of underwater vehicle by dynamic mesh technique in CFD[J]. Journal of Ship Mechanics, 2010, 14(10): 1100-1108. DOI:10.3969/j.issn.1007-7294.2010.10.004 |
| [3] |
KIM J Y, KIM K H, CHOI H S, et al. Estimation of hydrodynamic coefficients for an AUV using nonlinear observers[J]. IEEE Journal of Oceanic Engineering, 2002, 27(4): 830-840. DOI:10.1109/JOE.2002.805098 |
| [4] |
陈玮琪, 颜开, 王宝寿. 辨识航行体水动力参数的智能方法[J]. 船舶力学, 2011, 15(4): 359-363. CHEN Wei-qi, YAN Kai, WANG Bao-shou. Intelligent identification of hydrodynamic parameters of navigating body[J]. Journal of Ship Mechanics, 2011, 15(4): 359-363. DOI:10.3969/j.issn.1007-7294.2011.04.005 |
| [5] |
RIDAO P, BATLLE J, CARRERAS M. Model identification of a low-speed UUV[C]//Proceedings of the 1st IFAC workshop on guidance and control of underwater vehicles, Glasgow, Scotland, UK: IFAC, 2003: 47−52.
|
| [6] |
林子淇. 水下机器人动力学建模与系统辨识技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2015. LIN Ziqi. Research on dynamic modeling and techniques of system identification of underwater Vehicle[D]. Harbin: Harbin Engineering University, 2015. |
| [7] |
王绍宾. 基于鲁棒控制的自主水下航行器控制方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2018. WANG Shaobin. Research on control method of autonomous underwater vehicle based on robust control[D]. Harbin: Harbin Engineering University, 2018. |
| [8] |
SILPA C. Autonomous underwater robot: vision and control.[D]. Australian National University, Australia, 2001.
|
| [9] |
Kennedy J, Eberhart R. Particle swarm optimization[C]//IEEE Int’l Confon Neural Networks. Perth, Australia, 1995: 1942−1948.
|
| [10] |
SHI Y H, EBERHART R C. A modified particle swarm optimizer[J]. IEEE international conference on evolutionary computation, anchorage alsaka, 1998, 69-73. |
| [11] |
沈智鹏, 代昌盛. 欠驱动船舶路径跟踪的强化学习迭代滑模控制[J]. 哈尔滨工程大学学报, 2017(5). SHEN Zhipeng, DAI Changsheng. Iterative sliding mode control based on reinforced learning and used for path tracking of under-actuated ship[J]. Journal of Harbin Engineering University[J], 2017(5). |
| [12] |
罗彩君. 基于粒子群算法的欠驱动船舶航向控制研究[J]. 舰船科学技术, 2019, 41(10): 25-27. LUO Cai-jun. Research on underactuated ship heading control based on particle swarm optimization[J]. ship science and technology, 2019, 41(10): 25-27. |
| [13] |
韦波. 粒子群优化的RBF神经网络在海上运输事故预测中的应用[J]. 舰船科学技术, 2016, 38(4): 181-183. WEI Bo. Application of RBF neural network in the prediction of sea transportation accidents in the particle swarm optimization[J]. ship science and technology, 2016, 38(4): 181-183. |
| [14] |
方淡玉, 黄橙, 等. 基于船舶六自由度运动的船舶航行安全实时监控系统研究[J]. 数字技术与应用, 2013(6). FANG Dan-yu, HUANG Cheng, et al. Research on real-time monitoring system of ship navigation safety based on ship's six degrees of freedom movement[J]. Digital Technology and Application, 2013(6). |
 2021, Vol. 43
2021, Vol. 43
