2. 中国科学院机器人与智能制造创新研究院,辽宁 沈阳 110169;
3. 辽宁省水下机器人重点实验室,辽宁 沈阳 110169;
4. 中国科学院大学,北京 100049
2. Institutes for Robotics and Intelligent Manufacturing, Chinese Academy of Sciences, Shenyang 110169, China;
3. Key Laboratory of Marine Robotics, Liaoning Province, Shenyang 110169, China;
4. University of Chinese Academy of Sciences, Beijing 100049, China
海洋中深度大于 6500 m 的海域被称为“深渊”,深渊区域大深度、超高压的工作环境对于水下机器人是十分严峻的挑战,因此人类对深渊的认知还在初级阶段[1]。面向深渊探测,全海深自主遥控水下机器人(ARV) 应运而生。ARV 作为一种混合型水下机器人,其融合了自主水下机器人(AUV)和遥控水下机器人(ROV)的部分技术。相较于传统 ROV,ARV 的作业范围增大、对母船支持要求降低但作业能力也相应减弱。相较于AUV,其特点为巡航作业时可进行实时监控,一旦发现兴趣点,即可切换为 ROV 模式利用机械手完成作业[2]。作业能力是 ARV 的一项重要能力,当 ARV 进行悬浮作业时,由于机械臂对载体的耦合作用,会导致载体姿态发生较大变化,反过来又会影响机械臂作业。因此载体在机械臂扰动下的姿态稳定控制对于顺利完成水下作业十分重要。
目前已经有很多控制算法被应用于水下机器人的控制中,如 PID 控制[3]、预测控制[4-5]、模糊逻辑控制[6-7]、基于神经网络的控制[8-9]、滑模控制(SMC)[10-14]等。其中滑模控制对满足匹配条件的干扰和摄动具有较强鲁棒性,且算法简单易于工程实现,在水下机器人上得到了广泛应用。SMC的主要缺点在于存在抖振问题。对于水下机器人而言,抖振会增加推进器能耗甚至损坏推进器。在抖振抑制方面,高阶滑模控制近年来受到了广泛关注,其将不连续项隐藏到高阶导数中,经过积分器的滤波作用,抖振得到了很大抑制。高阶滑模中的超螺旋算法 (Super-Twisting Algorithm,STA) 是其中最流行的算法,因为其不需要知道滑模变量的导数信息。STA 在保持滑模控制鲁棒性的同时具有良好的抖振抑制能力,然而它的离散实现多采用显式欧拉法,其在无扰动时也会引发额外的抖振现象,称为离散化抖振,而且离散化抖振会随着采样周期或控制增益值的增大而加剧[15]。为了抑制SMC采用显式离散化引发的抖振,隐式(后向)欧拉离散法近年来得到了发展[16],理论和实验都验证了其可有效抑制离散化抖振[17-18]。隐式法最近也被用到了STA上[19-20],仿真与实验结果显示基于隐式离散化的STA有效抑制了离散化抖振且对采样周期和过高的控制增益不敏感。
为了稳定机械臂扰动下的载体姿态,本文首次将隐式离散化后的STA[19]应用到全海深ARV在悬浮作业时的姿态稳定控制上。
1 系统建模ARV的运动学和动力学模型涉及到2个坐标系,一个固定的大地坐标系{e}用于确定ARV在流场中的位置,一个体坐标系{b}固定于ARV上并随其一起运动, 如图1所示。

|
图 1 ARV坐标系 Fig. 1 The coordinate frames of ARV |
ARV六自由度动力学模型在文献[21]中进行了详细的说明。由于机械臂运动主要影响的是横倾和纵倾这2个自由度,因此仅对这2个自由度的控制进行研究。考虑机械臂扰动,未知环境扰动和未建模动力学后的纵倾和横倾自由度的运动学和动力学模型如下:
1)横倾力矩方程
| $ \begin{split} & {I_x}\dot p + ({I_z} - {I_y})qr - (\dot r + pq){I_{zx}} + ({r^2} - {q^2}){I_{yz}} + \\ & (pr - \dot q){I_{xy}} + m[{y_G}(\dot w - uq + vp) - {z_G}(\dot v - wp + ur)]= \\ & {K_v}v + {K_w}w + {K_p}p + {K_{\dot v}}\dot v + {K_{\dot w}}\dot w + {K_{\dot p}}\dot p + {K_{u\left| w \right|}}u\left| w \right| + \\ & \left( {{y_G}W - {y_B}B} \right)\cos \theta \cos \phi - \left( {{z_G}W - {z_B}B} \right)\cos \theta \sin \phi +\\ & \Delta {f_\theta } + {d_{m,\theta }} + {d_{u,\theta }} + {u_\theta } {\text{,}} \end{split} $ | (1) |
| $ \dot \phi = p + \sin \phi \tan \theta q + \cos \phi \tan \theta r{\text{。}} $ | (2) |
2)纵倾力矩方程
| $ \begin{split} & {I_y}\dot q + ({I_x} - {I_z})rp - (\dot p + qr){I_{xy}} + ({p^2} - {r^2}){I_{zx}} + (qp - \dot r){I_{yz}} + \\ & m\left[ {{z_G}(\dot u - vr + wq) - {x_G}(\dot w - uq + vp)} \right] ={M_u}u + {M_w}w + \\ & {M_q}q + {M_{uw}}uw + {M_{\dot u}}\dot u + {M_{\dot w}}\dot w + {M_{\dot q}}\dot q + {M_{w\left| w \right|}}w\left| w \right| +\\ & {w^2}\left[ {{M_{{\delta _s}{\delta _s}}}{{\left( {{\delta _s} - \frac{{\text π} }{2}\frac{{{\delta _s}}}{{\left| {{\delta _s}} \right|}}} \right)}^2}\frac{w}{{\left| w \right|}} + {M_{{\delta _s}}}\left( {{\delta _s} - \frac{{\text π} }{2}\frac{{{\delta _s}}}{{\left| {{\delta _s}} \right|}}} \right)} \right] - \\ & \left( {{x_G}W - {x_B}B} \right)\cos (\theta )\cos (\phi ) - \left( {{z_G}W - {z_B}B} \right)\sin (\theta ) + \\ & \Delta {f_\theta } + {d_{m,\theta }} + {d_{u,\theta }} + {u_\theta } {\text{,}} \\[-10pt] \end{split} $ | (3) |
| $ \dot \theta = \cos \phi \,q - \sin \phi \,r {\text{。}}$ | (4) |
其中:m为载体的质量,W为重力大小,B为浮力大小, [xG yG zG]T 表示重心在体坐标系中的坐标,浮心坐标为[xB yB zB]T, [Ix Iy Iz]T 和 [Ixy Iyz Izx]T分别表示惯性矩和惯性积,
由于横倾自由度和纵倾自由度分析完全类似,因此这里仅取横倾自由度进行分析。为了便于控制器设计,式(1)可简化为:
| $ \dot p = {\left( {{I_x} - {K_{\dot p}}} \right)^{ - 1}}\left( {{u_\phi } + {{\hat f}_\phi } + \Delta {f_\phi } + {d_{m,\phi }} + {d_{u,\phi }}} \right) {\text{。}}$ | (5) |
其中:
| $ \begin{split} {{\hat f}_\phi } =& {K_v}v + {K_w}w + {K_p}p + {K_{\dot v}}\dot v + {K_{\dot w}}\dot w + {K_{u\left| w \right|}}u\left| w \right| + \\ & \left( {{y_G}W - {y_B}B} \right)\cos \theta \cos \phi - \left( {{z_G}W - {z_B}B} \right)\cos \theta \sin \phi - \\ & ({I_z} - {I_y})qr + (\dot r + pq){I_{zx}} - ({r^2} - {q^2}){I_{yz}} - (pr - \dot q){I_{xy}} -\\ & m[{y_G}(\dot w - uq + vp) - {z_G}(\dot v - wp + ur)]{\text{。}}\\[-10pt] \end{split} $ | (6) |
联立式(5)和式(2), 可以得到惯性坐标系下横倾自由度的动力学方程:
| $ \ddot \phi = {b_\phi }\left( {{u_\phi } + {{\hat f}_\phi } + \Delta {f_\phi } + {d_{m,\phi }} + {d_{u,\phi }}} \right)\, + {f_{c,\phi }}{\text{。}} $ | (7) |
其中:
| $ \begin{gathered} {f_{c,\phi }} = \cos \phi \,\tan \theta q\dot \phi + \sin \phi {\sec ^2}\theta q\dot \theta + \sin \phi \,\tan \theta \dot q -\\ \quad \quad \sin \phi \tan \theta r\dot \phi + \cos \theta {\sec ^2}\theta r\dot \theta + \cos \phi \tan \theta \dot r {\text{。}} \end{gathered} $ |
为了便于控制器设计,横倾和纵倾自由度的动力学方程不失一般性地可写成如下通用形式:
| $ \ddot x = b\left( {u + \hat f + \Delta f + {d_m} + {d_u}} \right)\, + {f_c}{\text{。}} $ | (8) |
其中
为了得到STA的离散化形式,需要回顾STA在连续域下的设计。为了在水下机器人这个2阶系统上应用STA,首先要进行滑模面设计,使得控制输入出现在滑模变量的1阶导上。为了简便,这里选择如下的线性滑模面:
| $ s = \dot e + \lambda e {\text{,}}$ | (9) |
其中:
滑模趋近率采用STA:
| $ \begin{split} & \dot s = - {k_1}{\left| s \right|^{\tfrac{1}{2}}}sign(s) + \varpi {\text{,}} \\ & \dot \varpi = - {k_2}sign(s) {\text{,}} \end{split} $ | (10) |
其中:
对滑模变量微分可得:
| $ \dot s = b\left( {u + \hat f + \Delta f + {d_m} + {d_u}} \right)\, + {f_c} - {\ddot x_d} + \lambda \dot e{\text{,}} $ | (11) |
比较式(11)和式(10), 在连续域下的控制器可设计为:
| $ \left\{ {\begin{split} & {u = {b^{ - 1}}( - {k_1}{{\left| s \right|}^{\tfrac{1}{2}}}sign(s) + \varpi + {{\ddot x}_d} - \lambda \dot e)} {\text{,}}\\ & {\dot \varpi = - {k_2}sign(s)} {\text{。}} \end{split}} \right. $ | (12) |
为了测试算法的鲁棒性以及降低控制器对模型的依赖,控制器并没有使用名义动力学模型信息
为了抑制离散化引发的抖振,采用隐式欧拉法对式(12)进行离散化。
对于式(11),其可改写成如下紧凑的形式:
| $ \left\{ {\begin{array}{*{20}{l}} {\dot s = bu - {{\ddot x}_d} + \lambda \dot e + \varphi (t)}{\text{,}} \\ {\dot \varphi (t) = \Delta (t)} {\text{。}} \end{array}} \right. $ | (13) |
其中:
式(13)的离散化模型为:
| $ \left\{ {\begin{array}{*{20}{l}} {{s_{k + 1}} = {s_k} + hb{u_k} + h(\lambda {{\dot e}_k} - {{\ddot x}_{d,k}}) + h{{\bar \varphi }_k}}{\text{,}} \\ {{\varphi _{k + 1}} = {\varphi _k} + h{{\bar \Delta }_k}}{\text{。}} \end{array}} \right. $ | (14) |
其中:h为采样周期;
针对式(14), 采用隐式欧拉法的STA控制器可设计为[19]:
| $ \left\{ {\begin{aligned} &{{u_k} = {b^{ - 1}}[ - {k_1}{{\left| {{{\tilde s}_{k + 1}}} \right|}^{\tfrac{1}{2}}}sgn({{\tilde s}_{k + 1}}) + {v_{k + 1}} + {{\ddot x}_{d,k}} - \lambda {{\dot e}_k}]} {\text{,}}\\ &{{v_{k + 1}} \in {v_k} - h{k_2}sgn({{\tilde s}_{k + 1}})} {\text{。}} \end{aligned}} \\[-10pt]\right. $ | (15) |
其中:
不同于显式欧拉法使用的单值符号函数,式(15)的
| $ {N_K}(x) = \{ w \in {\mathbb{R}^n}|\left\langle {w,y - x} \right\rangle \leqslant 0,\forall y \in K\} $ | (16) |
对于
| $ {N_{[ - 1,1]}}(x) = \left\{ {\begin{array}{*{20}{l}} {{\boldsymbol{R}^ - }}{\text{,}}&{x = - 1}{\text{,}} \\ {\{ 0\} }{\text{,}}&{x \in ( - 1,1)} {\text{,}}\\ {{\boldsymbol{R}^ + }}{\text{,}}&{x = 1} {\text{。}} \end{array}} \right. $ | (17) |
根据凸分析,
| $ {\tilde s_{k + 1}} = {s_k} + hb{u_k} + h(\lambda {\dot e_k} - {\ddot x_{d,k}}) {\text{,}}$ | (18) |
式(18)表示无扰动名义系统,
将控制输入式(15)代入式(18)中,可得到无扰动虚拟闭环系统:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\tilde s}_{k + 1}} = {s_k} - h{k_1}{{\left| {{{\tilde s}_{k + 1}}} \right|}^{\tfrac{1}{2}}}{\rm{sgn}}({{\tilde s}_{k + 1}}) + h{v_{k + 1}}}{\text{,}} \\ {{v_{k + 1}} \in {v_k} - h{k_2}\,{\rm{sgn}}({{\tilde s}_{k + 1}})} {\text{。}} \end{array}} \right. $ | (19) |
式(19)可写成如下的等价形式:
| $ {\tilde s_{k + 1}} + h{k_1}{\left| {{{\tilde s}_{k + 1}}} \right|^{\tfrac{1}{2}}}sgn({\tilde s_{k + 1}}) - {s_k} - h{v_k} \in - {h^2}{k_2}sgn({\tilde s_{k + 1}}) {\text{。}}$ | (20) |
注意到
广义方程式(20)可写成如下紧凑的形式:
| $ g({\tilde s_{k + 1}}) \in - {h^2}{k_2}sgn({\tilde s_{k + 1}}) {\text{,}}$ | (21) |
其中:
定义变量
| $ f(y) = {g^{ - 1}}(x) = \left\{ {\begin{split} & {{{\left[ {\frac{{ - b + \sqrt {{b^2} - 4({c_k} - y)} }}{2}} \right]}^2},}&{y \geqslant {c_k}}{\text{;}} \\ & { - {{\left[ {\frac{{b - \sqrt {{b^2} + 4({c_k} - y)} }}{2}} \right]}^2},}&{y < {c_k}} {\text{。}} \end{split}} \right. $ | (22) |
最终可得到如下广义方程:
| $ f( - {h^2}{k_2}{\xi _{k + 1}}) \in {N_{[ - 1,1]}}({\xi _{k + 1}}){\text{。}} $ | (23) |
定理1:广义方程式(23)和式(21)仅有唯一解
证明:注意到函数
| $ 0 \in f({\vartheta _{k + 1}}) + {N_{[ - {h^2}{k_2},{h^2}{k_2}]}}({\vartheta _{k + 1}}) {\text{,}}$ | (24) |
可以验证对于所有
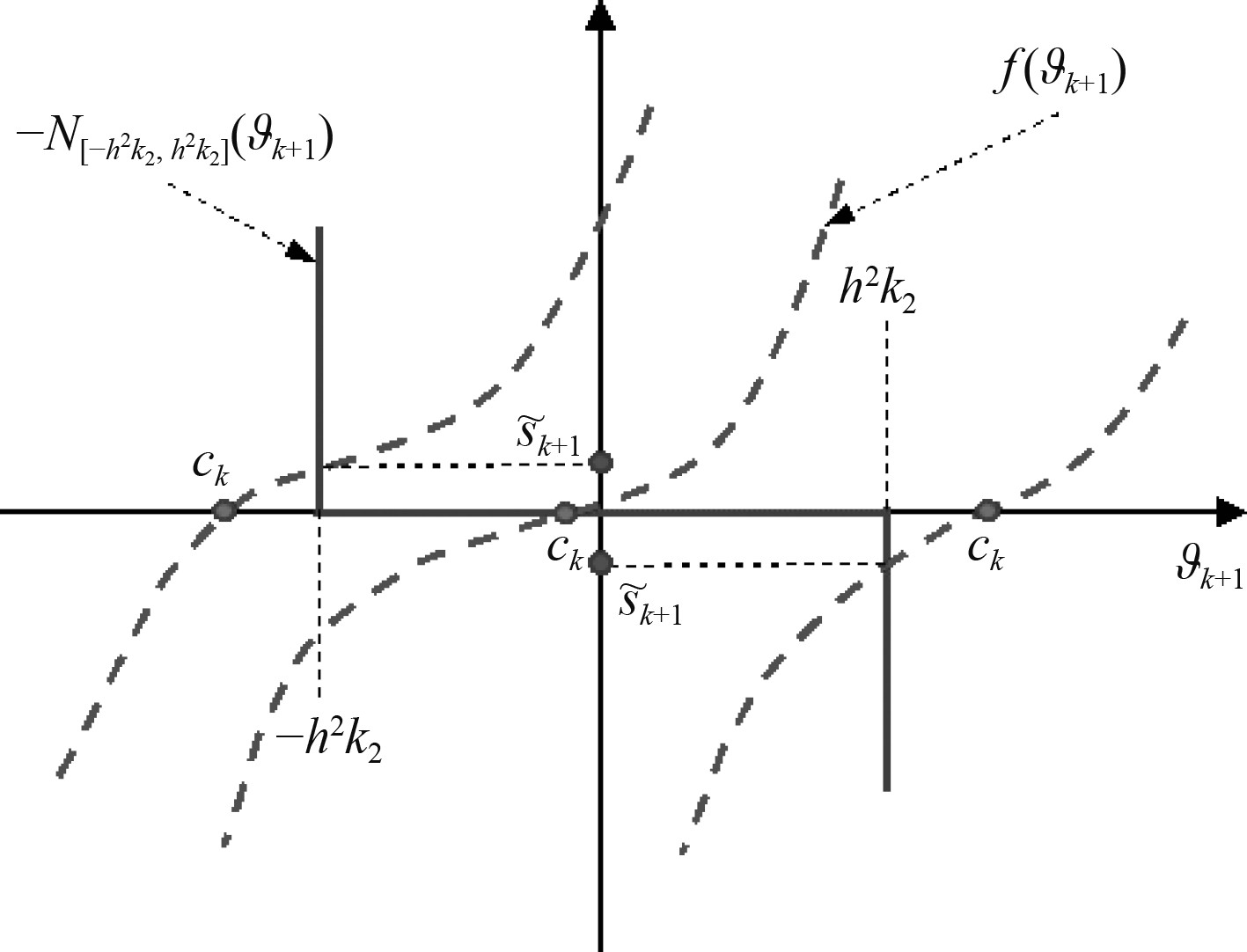
|
图 2 广义等式(24)的图解 Fig. 2 Graphical interpretation of the generalized equation (24) |
由于式(21)中的2个映射为式(23)中相应副本的逆,因此它们的交点也是唯一的。这意味着在
为了求解
1)
| $ {\vartheta _{k + 1}} = - {h^2}{k_2} \to {\xi _{k + 1}} = 1 \to {\tilde s_{k + 1}} > 0{\text{,}} $ |
2)
| $ {\vartheta _{k + 1}} = {c_k} \in [ - {h^2}{k_2},\;\;{h^2}{k_2}] {\text{,}}$ |
| $ {\xi _{k + 1}} = {{{\vartheta _{k + 1}}} \mathord{\left/ {\vphantom {{{\vartheta _{k + 1}}} { - {h^2}{k_2}}}} \right. } { - {h^2}{k_2}}} \in [ - 1,1] \to {\tilde s_{k + 1}} = 0{\text{,}} $ |
3)
| $ {\vartheta _{k + 1}} = {h^2}{k_2} \to {\xi _{k + 1}} = - 1 \to {\tilde s_{k + 1}} < 0 {\text{。}}$ |
分类1和分类3中的
为了验证所提出控制算法的有效性和优越性,在Matlab/Simscape环境下进行仿真实验。
3.1 任务描述仿真中载体和机械臂的部分参数如表1所示。为了问题的简化及排除其他因素的影响,仿真中忽略推进器动力学特性,传感器获取的信号假设是理想的。在仿真过程中,机械臂进行运动,规划的关节轨迹如3所示。与此同时载体则依靠自身的控制维持姿态的稳定。控制器分别采用显式欧拉法和隐式欧拉法离散的STA,且仅考虑横倾和纵倾这2个自由度的控制。其中载体的初始位姿和速度均设置为0,纵倾角和横倾角的目标值也设置为0。为了测试控制算法的鲁棒性,模型参数假设存在30% ~ 40%的不确定性,施加的时变外部扰动如下:
|
|
表 1 ARV部分参数值 Tab.1 Partial parameter values of the ARV |
| $ \left\{ {\begin{array}{*{20}{l}} {{d_{u,\phi }} = 25 + 16\sin (0.2t){\rm{N}} \cdot {\rm{m}}}{\text{,}} \\ {{d_{u,\theta }} = 30 + 15\sin (0.2t + {{\text π} \mathord{\left/ {\vphantom {{\text π} 4}} \right. } 4}){\rm{N}} \cdot {\rm{m}}} {\text{。}} \end{array}} \right. $ | (25) |
为了研究采样周期对2种离散化方法的影响,仿真中的采样周期分别设置为0.001 s,0.01 s和0.1 s。
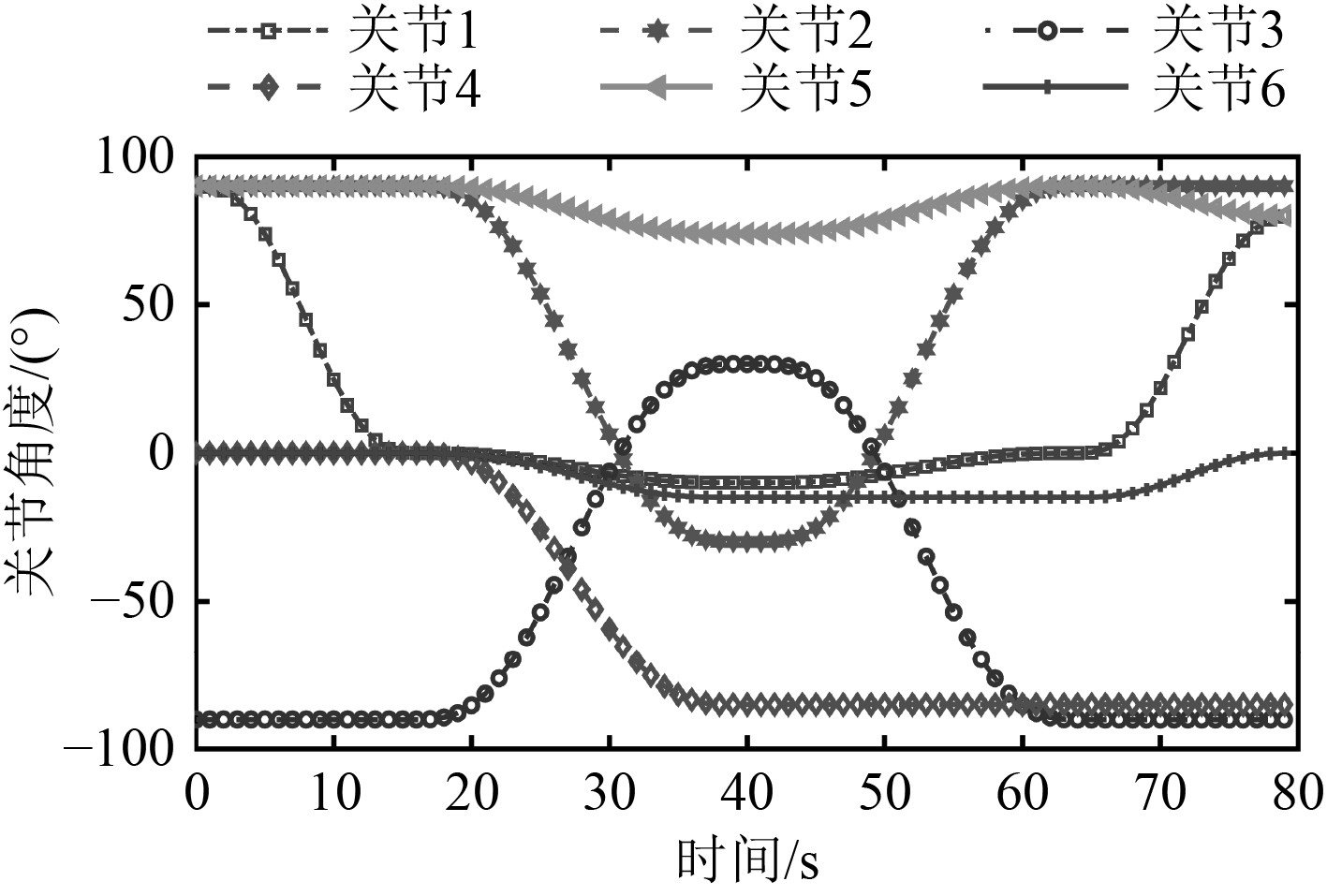
|
图 3 规划的关节轨迹 Fig. 3 Planned joint trajectories |
为了排除参数选择对控制性能的影响,确保对比仿真实验的公平性,采用多目标优化算法进行控制参数调优。
为了评价控制参数的优劣,引入如下2个目标函数:
| $ RMSE = \sqrt {\frac{1}{N}\sum\limits_{k = 0}^{N - 1} {e_k^2} } {\text{,}}$ | (26) |
| $ CHAT = \frac{1}{N}\sum\limits_{k = 0}^{N - 1} {\left| {u({t_{k + 1}}) - u({t_k})} \right|} {\text{。}}$ | (27) |
第1个目标函数计算误差的均方根,用来评价姿态的稳定控制性能;第2个目标函数计算了控制输入的平均变化值,可用来衡量控制输入的抖振大小。这2个目标函数值都是越小越好。
待优化的参数是
| $ \begin{split} & {{\lambda _\phi } \in [0,\;5]}{\text{,}}\quad{{k_{1,\phi }} \in [0,\;10]}{\text{,}}\quad{{k_{2,\phi }} \in [0,\;10]} {\text{,}}\\ & {{\lambda _\theta } \in [0,\;5]}{\text{,}}\quad{{k_{2,\theta }} \in [0,\;10]}{\text{,}}\quad{{k_{2,\theta }} \in [0,\;10]} {\text{。}} \end{split} $ | (28) |
为了避免推进器饱和,控制输入也限定在一定范围内:
多目标优化采用Matlab中Global Optimization Toolbox中的gamultiobj函数实现。
3.3 仿真结果与分析图4为不同采样周期下经多目标优化得到的Pareto前沿, Pareto前沿上的点称为Pareto最优解。可以发现隐式法对应的Pareto最优解CHAT值总体来看远小于显式法,且集中在一个较小值, 这表明隐式法有效地抑制了离散化抖振。显式法的Pareto最优解CHAT值则分布在一个较大范围内,表明显式法容易引发较大的抖振。对比RMSE值可发现显式法可达到更小的值,代价是产生了更大的抖振。对比不同采样周期的Pareto前沿,发现随着采样周期的增加,显式法和隐式法对应的Pareto前沿均向右移动,然而隐式法Pareto最优解的CHAT值增加较小,仍然集中在一个较小值。显式法Pareto最优解对应的CHAT值分布范围明显扩大,这说明显式法对采样周期的增加较敏感,采样周期的增加明显增大了离散化抖振。
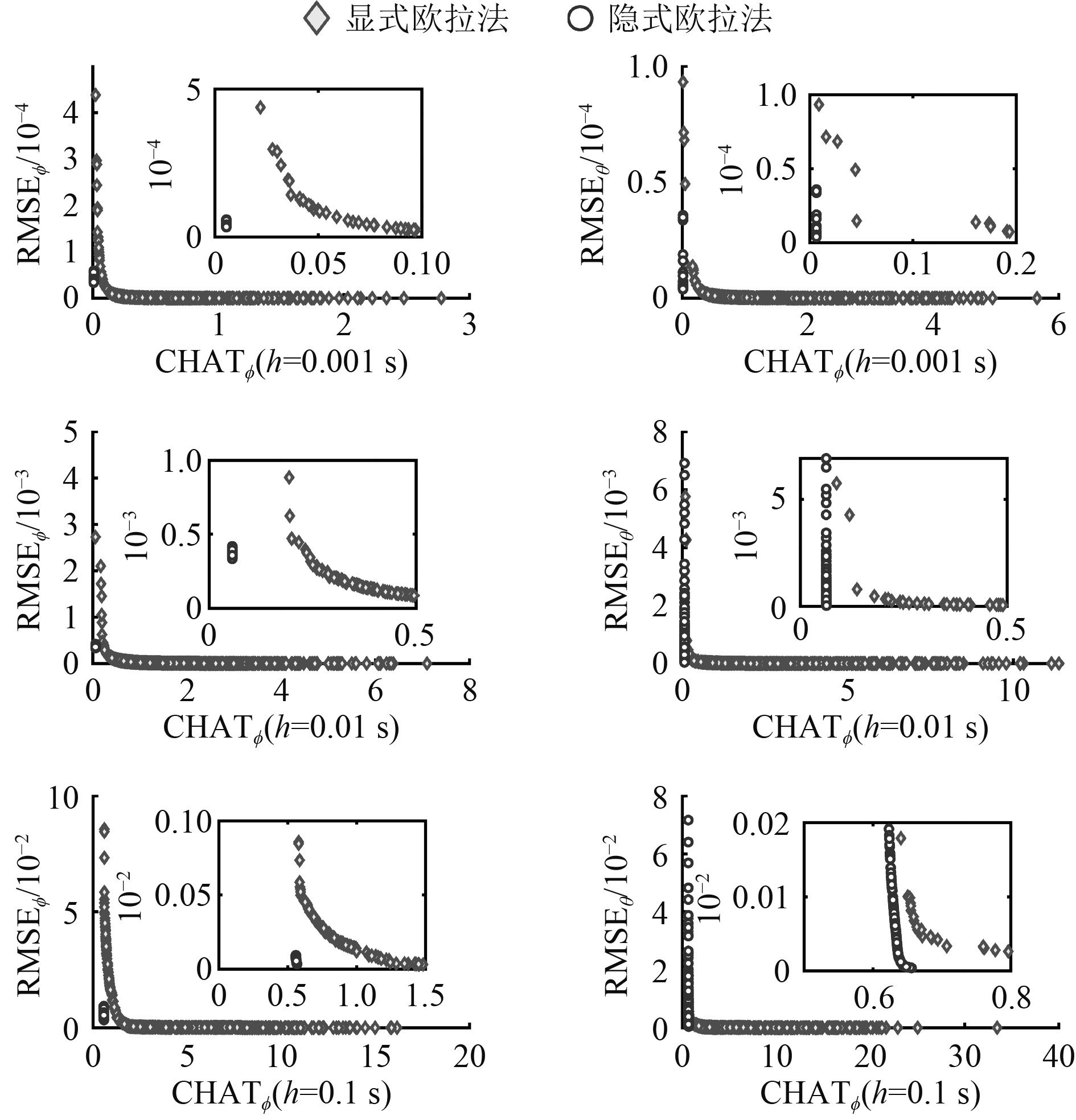
|
图 4 不同采样周期对应的Pareto前沿 Fig. 4 Pareto fronts for different sampling time |
为了分析2种离散化方法对增益的敏感性,图5给出了采样时间周期为0.1 s时得到的Pareto最优解对应的设计变量值分布图,即控制器参数值分布图。从图5可以发现,显式法的滑模面增益
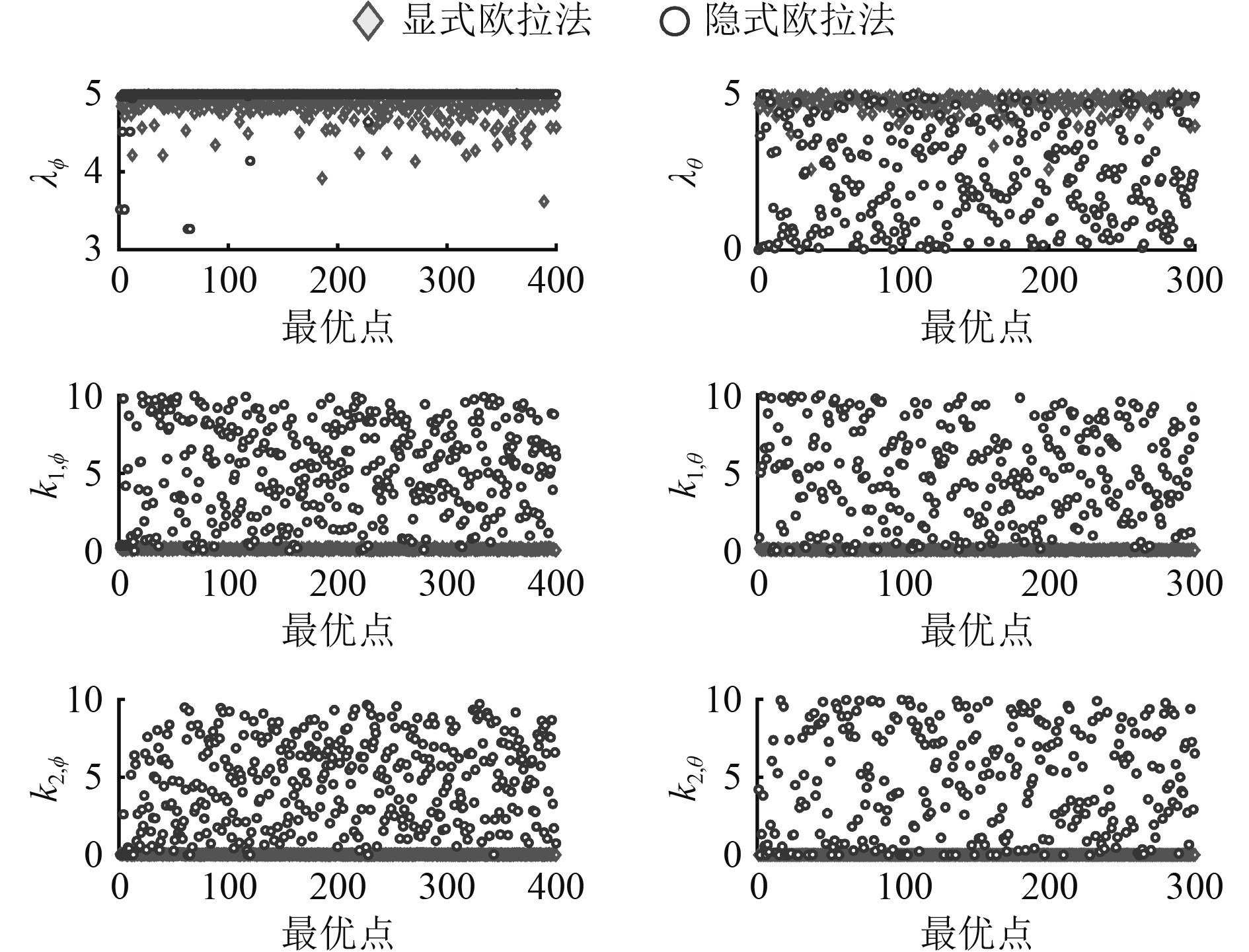
|
图 5 设计变量分布图 Fig. 5 The scattergram of design variables |
为了更加直观地展示隐式法相对显式法的区别和优势, 在采样周期0.1s对应的 Pareto 前沿上选择最优设计点进行仿真实验。为了确保公平的对比,在 RMSE 值相似的情况下选取对应的最优点,选取的 Pareto 最优设计点对应的目标函数值如表2所示,相应的设计变量值如表3所示。
|
|
表 2 选取的最优设计点目标函数值 Tab.2 Objective function values for selected optimum design points |
|
|
表 3 选取的设计变量值 Tab.3 The selected design variable values |
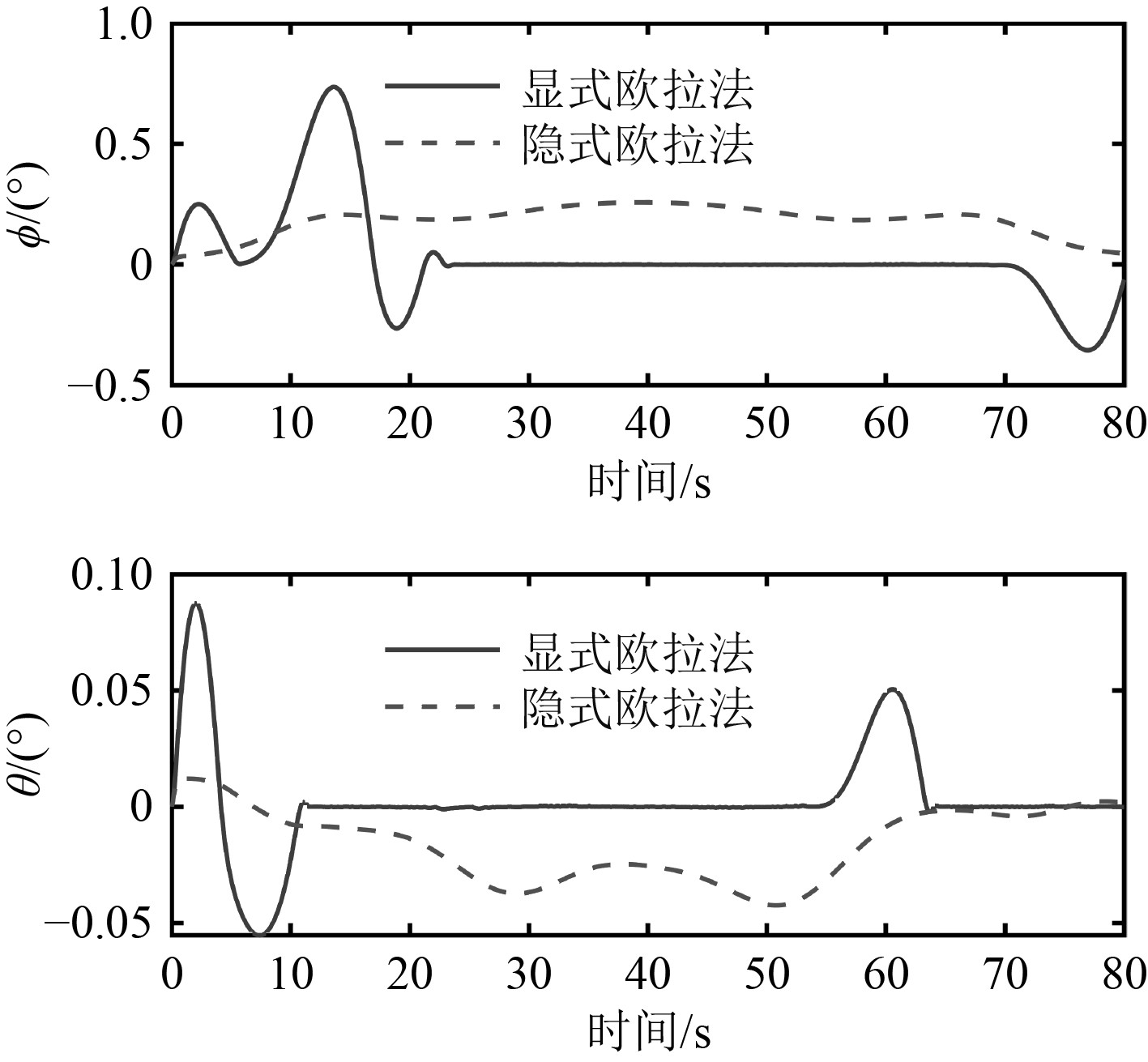
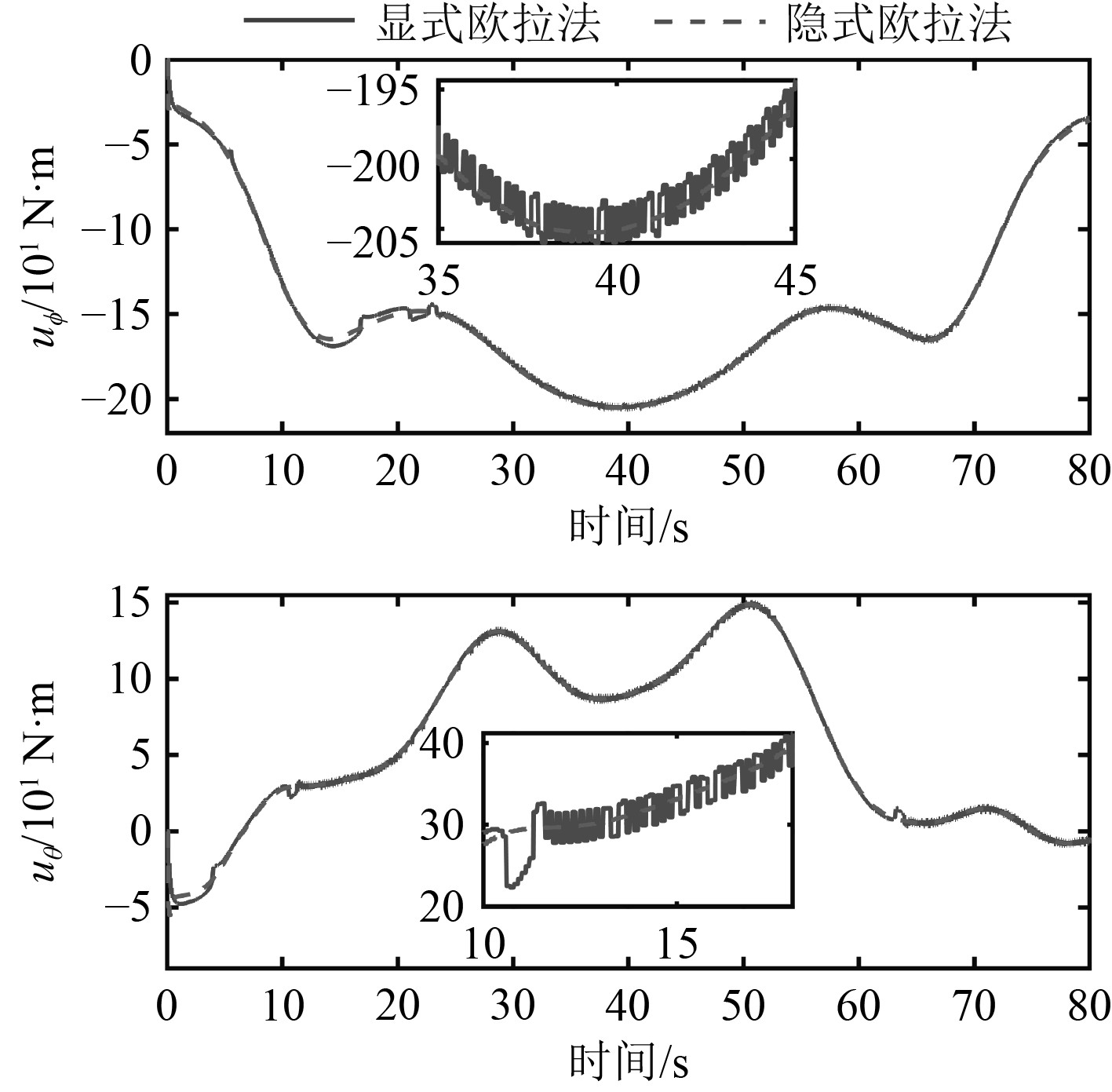
图6为横倾角和纵倾角随时间变化曲线图。由于选择了相似的RMSE值,可看到两者的控制性能大致相当。显式法对应的姿态角在初始阶段振荡较大,不过可实现较小的稳态误差,隐式法对应的姿态角则比较平滑,但稳态误差较大,不过根据RMSE的性能指标,两者可认为大致相当。图7为控制输入随时间变化曲线图,从图中的放大视图可以发现显式法对应的控制输入存在明显的抖振现象,隐式法则得到平滑的的控制输入。
|
图 6 横倾角和纵倾角随时间变化曲线 Fig. 6 Time trajectories of the roll angle and pitch angle |
|
图 7 控制输入随时间变化曲线 Fig. 7 Time trajectories of control inputs |
本文针对具有作业能力的全海深ARV悬浮作业时载体的姿态控制问题提出了一种隐式离散化广义超螺旋算法,并基于多目标优化算法完成了控制器参数优化。仿真结果表明,所提出的算法有效抑制了STA离散化带来的抖振,且控制算法对采样周期和过高控制增益不敏感。未来的工作包括将隐式离散化方法扩展到广义超螺旋算法[24]以及进行水池实验。
| [1] |
唐元贵, 王健, 陆洋, 等. “海斗号”全海深自主遥控水下机器人参数化设计方法与试验研究[J]. 机器人, 2019, 41(6): 697-705. |
| [2] |
陆洋, 唐元贵, 王健, 等. 全海深ARV浮力配平计算方法[J]. 机器人, 2021, 43(1): 74-80. |
| [3] |
YAN J, GAO J, YANG X, et al. Tracking control of a remotely operated underwater vehicle with time delay and actuator saturation[J]. Ocean Engineering, 2019, 184, 299–310.
|
| [4] |
YAN Z, GONG P, ZHANG W, et al. Model predictive control of autonomous underwater vehicles for trajectory tracking with external disturbances[J]. Ocean Engineering, 217, 78−84.
|
| [5] |
SHEN C, SHI Y, BUCKHAM B. Trajectory Tracking Control of an Autonomous Underwater Vehicle Using Lyapunov-Based Model Predictive Control[J]. IEEE Trans. Ind. Electron. , 65, 5796–5805.
|
| [6] |
KHODAYARI M. H, BALOCHIAN S. Modeling and control of autonomous underwater vehicle (AUV) in heading and depth attitude via self-adaptive fuzzy PID controller[J]. J. Mar. Sci. Technol. , 2015(20): 559–578.
|
| [7] |
XIANG X, YU C, LAPIERRE L, et al. Survey on Fuzzy-Logic-Based Guidance and Control of Marine Surface Vehicles and Underwater Vehicles[J]. Int. J. Fuzzy Syst, 2018(20): 572–586.
|
| [8] |
ZHANG J, XIANG X, ZHANG Q, et al. Neural network-based adaptive trajectory tracking control of underactuated AUVs with unknown asymmetrical actuator saturation and unknown dynamics[J]. Ocean Engineering., 2020(218): 108−193.
|
| [9] |
ELHAKI O, SHOJAEI K: A robust neural network approximation-based prescribed performance output-feedback controller for autonomous underwater vehicles with actuators saturation[J]. Eng. Appl. Artif. Intell, 2019(88): 103−382.
|
| [10] |
RANGEL M. A. G, MANZANILLA A, A. E. SUAREZ Z, et al. Adaptive Non-singular Terminal Sliding Mode Control for an Unmanned Underwater Vehicle: Real-time Experiments[J]. Int. J. Control Autom. Syst, 2020(18).
|
| [11] |
BORLAUG I. -L. G, PETTERSEN K. Y, GRAVDAHL J. T. Comparison of two second-order sliding mode control algorithms for an articulated intervention AUV: Theory and experimental results[J]. Ocean Engineering, 2020, 222: 108−480.
|
| [12] |
PATRE B, LONDHE P, WAGHMARE L, et al. Disturbance estimator based non-singular fast fuzzy terminal sliding mode control of an autonomous underwater vehicle[J]. Ocean Engineering, 2019, 159: 372–387, 2018.
|
| [13] |
LEE S. -D, HONG PHUC B. XU D, X, et al. Roll suppression of marine vessels using adaptive super-twisting sliding mode control synthesis[J]. Ocean Engineering , 2019(195): 106−724.
|
| [14] |
GUERRERO J, TORRES J, CREUZE V, et al. Trajectory tracking for autonomous underwater vehicle: An adaptive approach[J]. Ocean Engineering, 2019(172): 511–522.
|
| [15] |
KOCH S, REICHHARTINGER M, HORN M. On the Discretization of the Super-Twisting Algorithm[C]. 2019 IEEE 58th Conference on Decision and Control (CDC), Nice, France, Dec. 2019: 5989–5994.
|
| [16] |
BROGLIATO B, POLYAKOV A. Digital implementation of sliding-mode control via the implicit method: A tutorial[J]. Int. J. Robust Nonlinear Control, 2020(9): 51−21, Sep. 2020.
|
| [17] |
HUBER O, ACARY V, BROGLIATO B. Lyapunov Stability and Performance Analysis of the Implicit Discrete Sliding Mode Control[J]. IEEE Trans. Autom. Control, 2018(61).
|
| [18] |
HUBER O, ACARY V, BROGLIATO B, et al. Implicit discrete-time twisting controller without numerical chattering: Analysis and experimental results[J]. Control Eng. Pract., 2016(46): 129–141.
|
| [19] |
BROGLIATO B, POLYAKOV A, EFIMOV D. The Implicit Discretization of the Supertwisting Sliding-Mode Control Algorithm[J]. IEEE Trans. Autom. Control, 65(8): 8.
|
| [20] |
KOCH S, REICHHARTINGER M. Discrete-time equivalents of the super-twisting algorithm[J]. Automatica, 2019(107): 190–199.
|
| [21] |
刘金夫, 王亚兴, 唐元贵, 等. 全海深ARV动力学建模及简化研究[J]. 海洋技术学报, 2019, 38(2): 21-29. |
| [22] |
SHTESSEL Y. B, MORENO J. A, PLESTAN F, et al. Super-twisting adaptive sliding mode control: A Lyapunov design[C]// 49th IEEE Conference on Decision and Control (CDC), Atlanta, GA, USA, Dec. 2010: 5109–5113.
|
| [23] |
FACCHINEI F, PANG J. -S. Finite-dimensional variational inequalities and complementarity problems. New York: Springer, 2003.
|
| [24] |
CASTILLO I, FRIDMAN L, J. MORENO A. “Super-twisting algorithm in presence of time and state dependent perturbations[J]. Int. J. Control, 91(11):11.
|
 2021, Vol. 43
2021, Vol. 43
