2. 海军工程大学 舰船与海洋学院,湖北 武汉 430033
2. College of Ships and Oceans, Naval University of Engineering, Wuhan 430033, China
舰船机械设备的稳定运转是产生机械振动的主要因素之一,为了减小机械设备的振动幅度,一般采用在基础与被隔振物体之间设置隔振器。准零刚度隔振系统因其特有的高静低动刚度特性在减振降噪方面应用广泛,在参数设置理想的情况下能展现出很好的隔振性能,而且相比传统线性隔振器,其在低频隔振领域应用广泛。然而在实际工程中,受环境等因素的影响,系统元器件的参数会发生一定的改变,对这些参数的变化并非能够随时随地的掌握。与此同时,准零刚度隔振系统属于非线性系统,含有三次方项,参数的改变可能使系统从小振幅运动状态变换到大振幅运动状态,不利于机械设备的正常工作。设计一种控制器,使准零刚度隔振系统在参数发生扰动的情况下仍然能够控制被隔振设备运行在小振幅运动状态是本文研究的主要内容。
自适应控制经过近几年的发展,能很好地融入到各种控制系统并取得很好的控制效果,梁翠香等[1]将其应用在Qi系统的混沌控制,在参数受到较大扰动的情况下仍使系统保持渐近稳定。陈学菲等[2]将其应用在参数不确定的非自治混沌系统,并证明了误差系统是指数稳定的。程春蕊等[3]基于自适应滑模控制方法,对非线性混沌系统在模型不确定和外部扰动的情况下的同步问题进行研究,得到一类带有模型不确定性和外部扰动项的整数阶及分数阶非线性混沌系统的同步。刘梓豪[4]基于SD振子理论,建立一种载荷自适应的准零刚度隔振系统,解决了振动过程中载荷质量变化的问题。姚立强[5]针对一类随机非线性系统,引入辅助子系统设计控制器,并验证了控制策略的有效性和可行性。李国军等[6]提出了一种带有修正偏差功能的自适应控制策略,解决了控制过程中的颤振问题。
本文延续自适应控制算法在非线性控制领域的广泛应用,针对两自由度准零刚度隔振系统参数受到扰动的情况,首先对隔振系统进行动力学建模得到系统的动力学方程,对系统的动力学特性进行分析,利用数值仿真的方法得到系统的分岔图,然后设计基于系统变量为观测量的参数自适应控制器,并利用直接方法证明受控系统的全局稳定性。最后通过数值仿真证明所设计的控制器的有效性。
1 两自由度准零刚度隔振系统建模两自由度准零刚度隔振系统一阶形式无量纲动力学微分方程[7]为:
| $ \left\{ \begin{array}{l} {{\dot x}_1} = {y_1}\text{,} \\ {{\dot y}_1} = - {\xi _1}({y_1} - {y_2}) - ({x_1} - {x_2}) + \gamma {({x_1} - {x_2})^2} -\\ \qquad {({x_1} - {x_2})^3} + f\cos \omega t \text{,} \\ {{\dot x}_2} = {y_2} \text{,} \\ {{\dot y}_2} = - w{\xi _2}{y_2} - w{k_2}{x_2} + w{\xi _1}({y_1} - {y_2}) + w({x_1} -\\ \qquad {x_2}) - w\gamma {({x_1} - {x_2})^2} + w{({x_1} - {x_2})^3} \text{。} \end{array} \right. $ | (1) |
其中:
对系统刚度
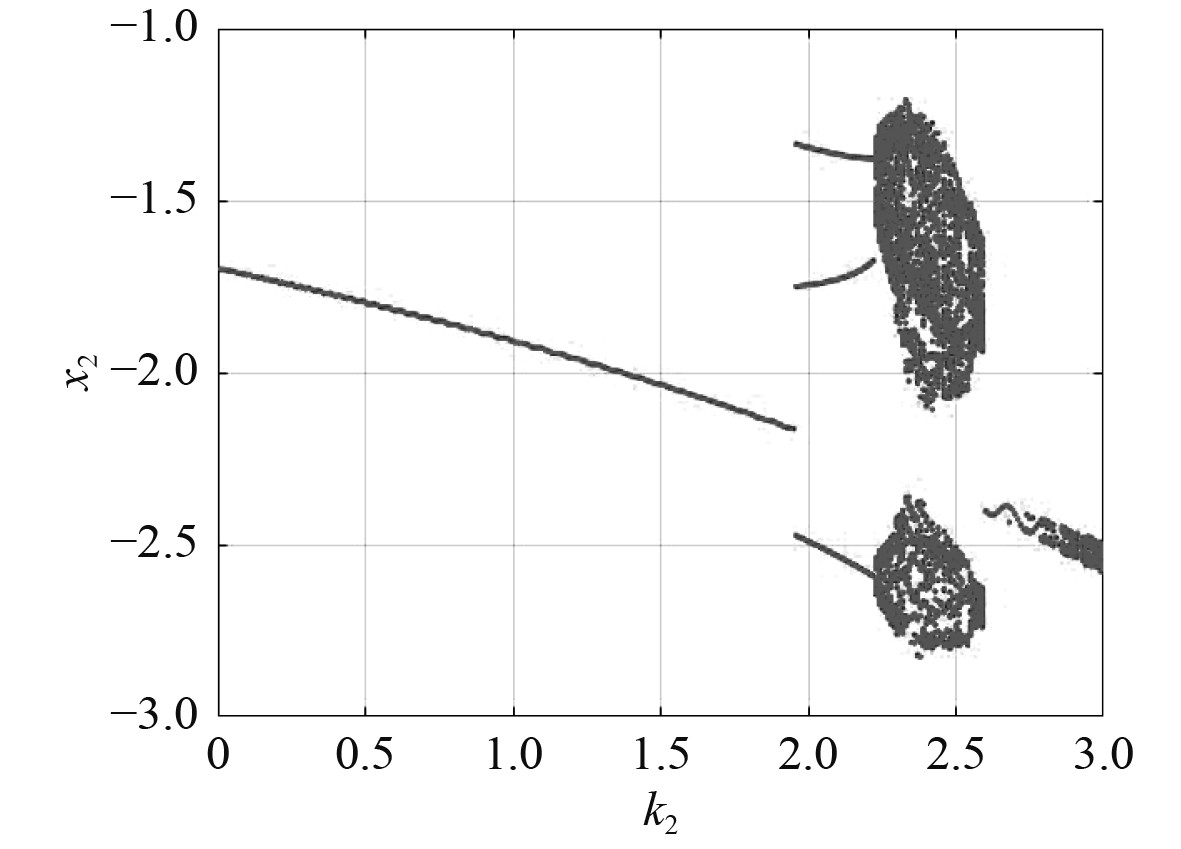
|
图 1
|
图1表明当

|
图 2
|

|
图 3
|
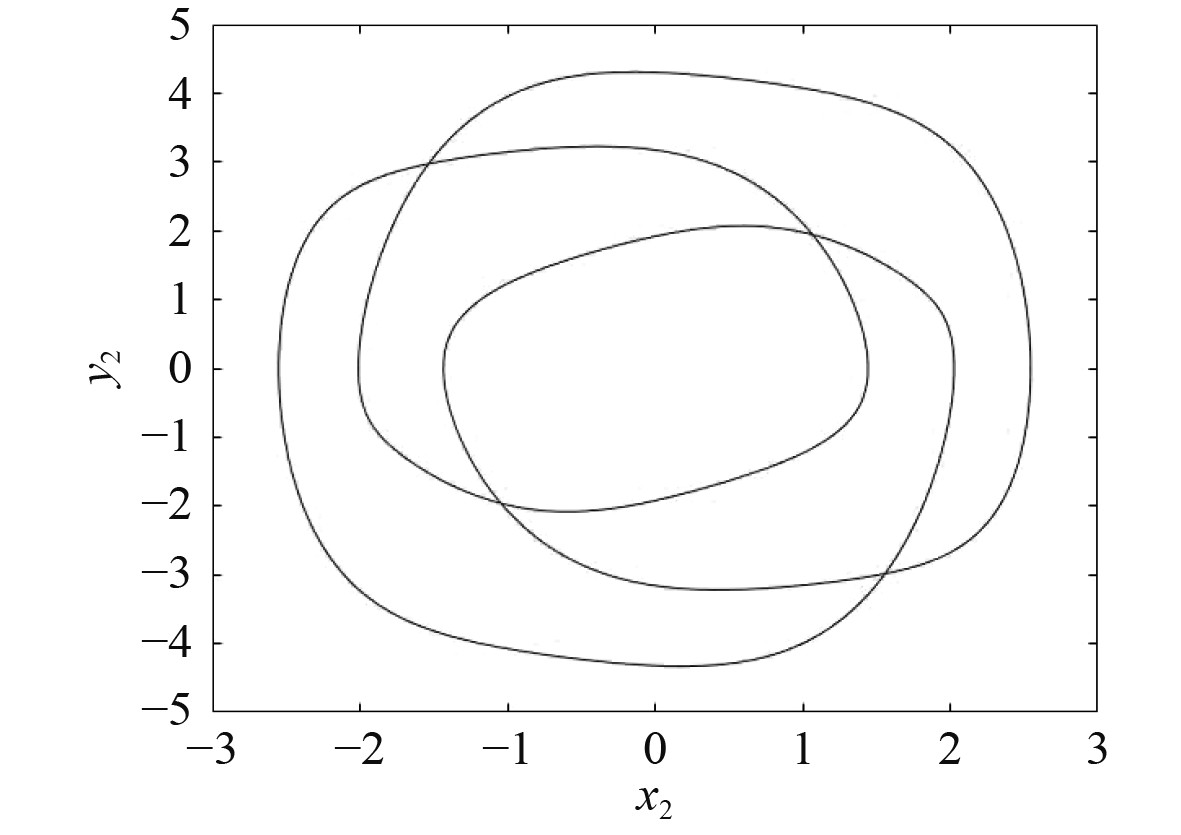
|
图 4
|

|
图 5
|

|
图 6
|
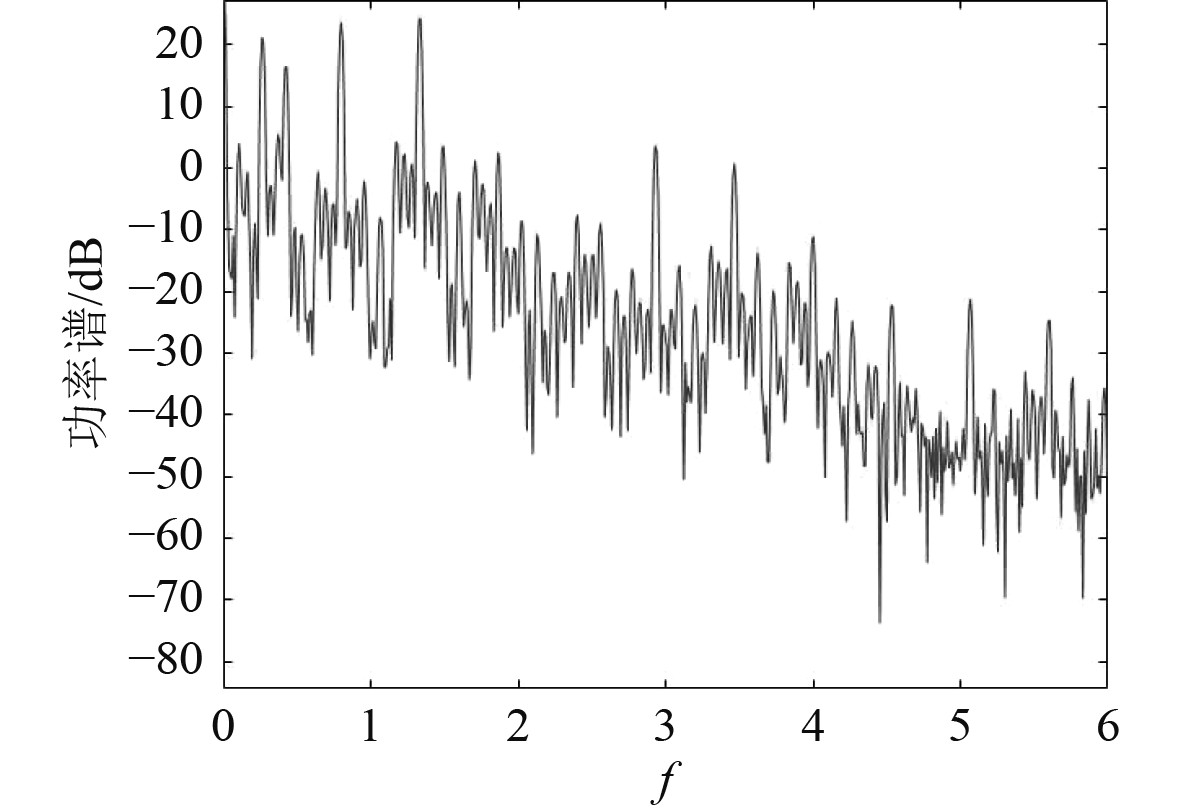
|
图 7
|
选取隔振系统结构参数
| $ \left\{ \begin{array}{l} {{\dot x}_1} = {y_1}\text{,} \\ {{\dot y}_1} = - {\text{0}}{\text{.1}}({y_1} - {y_2}) - ({x_1} - {x_2}) + {\text{2}}{({x_1} - {x_2})^2} -\\ \qquad{({x_1} - {x_2})^3} + {\text{6}}{\text{.8}}\cos {\text{1}}{\text{.6}}t \text{,} \\ {{\dot x}_2} = {y_2} \text{,}\\ {{\dot y}_2} = 0.5( - {\text{0}}{\text{.1}}{y_2} - {k_2}{x_2} + {\text{0}}{\text{.1}}({y_1} - {y_2}) +\\ \qquad({x_1} - {x_2}) - {\text{2}}{({x_1} - {x_2})^2} + {({x_1} - {x_2})^3}) \text{。} \end{array} \right. $ | (2) |
设式(2)的参考模型为:
| $ \left\{ \begin{array}{l} {{\dot x}_1} = {y_1} \text{,} \\ {{\dot y}_1} = - {\text{0}}{\text{.1}}({y_1} - {y_2}) - ({x_1} - {x_2}) + {\text{2}}{({x_1} - {x_2})^2} -\\ \qquad{({x_1} - {x_2})^3} + {\text{6}}{\text{.8}}\cos {\text{1}}{\text{.6}}t \text{,} \\ {{\dot x}_2} = {y_2} \text{,} \\ {{\dot y}_2} = 0.5( - {\text{0}}{\text{.1}}{y_2} - 0.1{x_2} + {\text{0}}{\text{.1}}({y_1} - {y_2}) + \\ \qquad({x_1} - {x_2}) - {\text{2}}{({x_1} - {x_2})^2} + {({x_1} - {x_2})^3})\text{,} \end{array} \right. $ | (3) |
当参数
| $ {\dot k_2} = - \left( {{k_2} - 0.1} \right){\left( {{x_1} - {x_2}} \right)^2} \text{,}$ | (4) |
则式(2)变为:
| $ \left\{ \begin{array}{l} {{\dot x}_1} = {y_1} \text{,}\\ {{\dot y}_1} = - {\text{0}}{\text{.1}}({y_1} - {y_2}) - ({x_1} - {x_2}) + {\text{2}}{({x_1} - {x_2})^2} -\\ \qquad{({x_1} - {x_2})^3} + {\text{6}}{\text{.8}}\cos {\text{1}}{\text{.6}}t \text{,}\\ {{\dot x}_2} = {y_2} \text{,}\\ {{\dot y}_2} = 0.5( - {\text{0}}{\text{.1}}{y_2} - {k_2}{x_2} + {\text{0}}{\text{.1}}({y_1} - {y_2}) +\\ \qquad({x_1} - {x_2}) - {\text{2}}{({x_1} - {x_2})^2} + {({x_1} - {x_2})^3}) \text{,}\\ {{\dot k}_2} = - \left( {{k_2} - 0.1} \right){\left( {{x_1} - {x_2}} \right)^2} \text{。} \end{array} \right. $ | (5) |
为证明所设计控制器的稳定性,根据李雅普诺夫稳定性定理,首先构造Lyapunov函数:
| $ V\left( t \right) = \frac{1}{2}{\left( {{k_2} - 0.1} \right)^2}\text{,} $ | (6) |
求导得:
| $ \begin{split} \dot V\left( t \right) =& \left( {{k_2} - 0.1} \right){{\dot k}_2} = \left( {{k_2} - 0.1} \right)\left( { - \left( {{k_2} - 0.1} \right){{\left( {{x_1} - {x_2}} \right)}^2}} \right) =\\ & - {\left( {{k_2} - 0.1} \right)^2}{\left( {{x_1} - {x_2}} \right)^2} \leqslant 0\text{,} \\[-12pt] \end{split} $ | (7) |
由式(6)和式(7)可知
| $ \underset{t\to \infty }{\mathrm{lim}}{\displaystyle \int_{t}^{0}\dot{V}\left(t\right){\rm{d}}t=}V\left(\infty \right)-V\left(0\right)=\text{有限值,} $ | (8) |
式(8)表明当
| $ \mathop {\lim }\limits_{t \to \infty } \dot V\left( t \right) = 0 \text{,}$ | (9) |
由于式(7)中
| $ \mathop {\lim }\limits_{t \to \infty } \left( {{k_2} - 0.1} \right) = 0\text{。} $ | (10) |
由此证明受控系统是渐进稳定的,实现了两自由度准零刚度隔振系统在参数受到扰动情况下的稳定控制。
3.2 数值仿真采用Matlab对所设计的自适应控制算法进行数值仿真,当准零刚度隔振系统中的参数
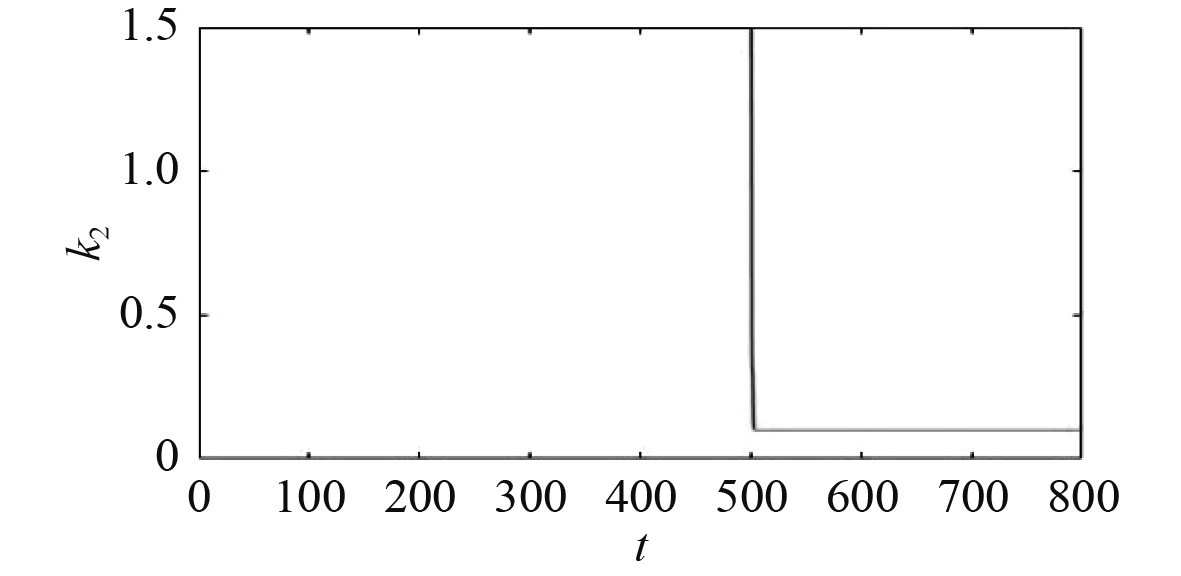
|
图 8
初始参数
|

|
图 9
初始参数
|
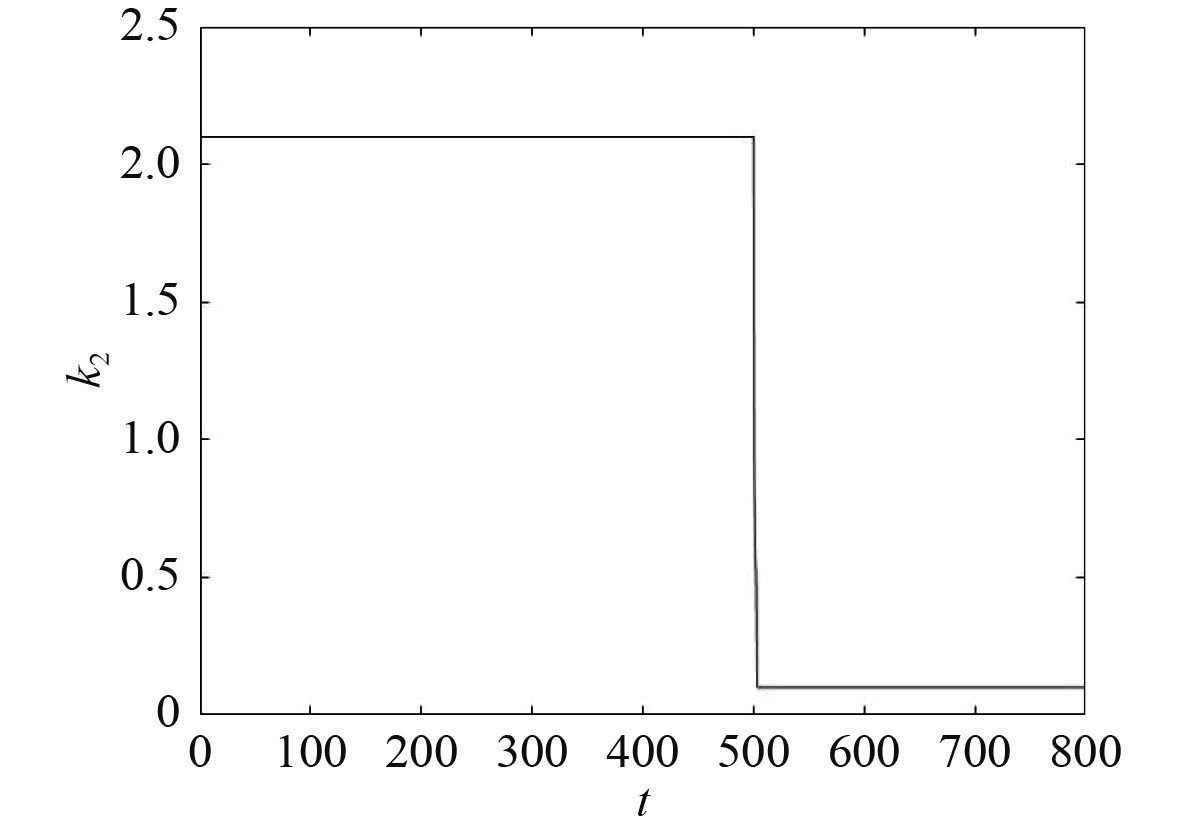
|
图 10
初始参数
|

|
图 11
初始参数
|
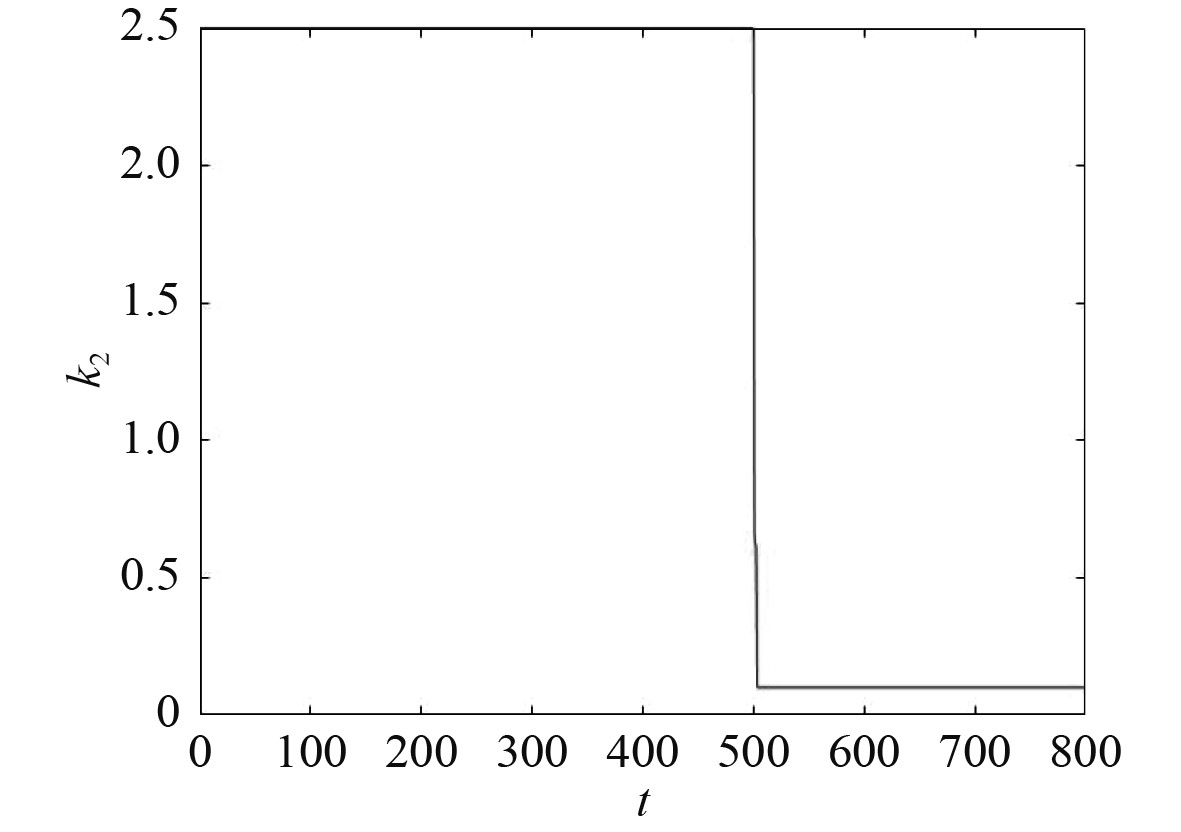
|
图 12
初始参数
|

|
图 13
初始参数
|
准零刚度隔振系统的动力学微分方程含有三次方项,系统参数微小的改变都有可能会使系统的运动状态发生变化,对其动力学行为的控制比较复杂,本文基于参数自适应控制方法,设计参数自适应控制器,使系统在参数发生变化情况下仍能运行到期望的小振幅运行状态,得出结论如下:
准零刚度隔振系统动力学模型随结构参数的改变,表现出丰富的动力学特性。
设计的控制器能使准零刚度隔振系统在参数(刚度)发生变化的情况下能很快恢复到期望值,并且系统的运动状态也能维持在理想的小振幅运动状态。
在隔振器结构参数(刚度)不断发生改变的情况下所设计的控制器仍能保证准零刚度隔振系统运行于小振幅运动状态,说明所设计的自适应控制器在一定范围内是有效的。
| [1] |
梁翠香, 唐驾时, 萧寒. 四维Qi系统的参数自适应控制[J]. 振动与冲击, 2010, 29(9): 126-128+150+247. DOI:10.3969/j.issn.1000-3835.2010.09.029 |
| [2] |
陈学菲, 刘辉昭. 参数不确定非自治混沌系统的自适应指数同步[J]. 应用数学和力学, 2021, 42(3): 316-322. |
| [3] |
程春蕊, 毛北行. 一类非线性混沌系统的自适应滑模同步[J]. 山东大学学报(工学版), 2020, 50(5): 1-6. |
| [4] |
刘梓豪. 基于准零刚度特性的载荷自适应隔振系统设计与研究[D]. 哈尔滨: 哈尔滨工业大学, 2020.
|
| [5] |
姚立强. 几类随机非线性系统稳定性与自适应控制研究[D]. 青岛: 山东科技大学, 2020.
|
| [6] |
李国军, 陈东杰, 董齐芬, 等. 带有修正项的非线性系统自适应学习控制[J]. 信息与控制, 2020, 49(3): 343-350+364. |
| [7] |
柴凯, 楼京俊, 朱石坚, 等. 两自由度非线性隔振系统的吸引子迁移控制[J]. 振动与冲击, 2018, 37(22): 10-16. |
 2021, Vol. 43
2021, Vol. 43

