2. 武汉理工大学 交通学院,湖北 武汉 430063
2. School of Transportation, Wuhan University of Technology, Wuhan 430063, China
邮轮舱室进行设计的主要目的是利用现有的各种技术方法,通过人为措施对舱室内部的各种环境因素进行控制,最终创造出一个相对比较合适的工作和居住环境[1-2]。建立科学系统的人-机-环境评价体系进而实现对邮轮客舱设计方案的定量分析与评价[3],对推动我国邮轮设计行业的不断发展有着非常重要的作用。邮轮舱室在家具布局设计方面由于没有特别严格的要求所以使得最终的设计效果依赖于设计者本身的经验是否丰富,进而使得设计效果具有很强的模糊性与主观性;再者,影响最终设计效果的因素有很多定性和定量的方面,例如空间合理性、美观性、人-机-环境协调性等,这些影响评价结果的因素数量不仅众多,相互之间关联的关系也比较复杂,还会涉及到许多不定性信息的处理[4],传统的专家决策方法存在一定的主观性[5],由于这些原因导致难以对设计效果做出精准的评估。因而在舱室设计之初,需要一套客观科学的方案评价方法。
模糊综合评价法应用模糊数学理论,适合用于解决人机工程不定性信息的处理和综合评估问题并能够将一些模糊的因素确定化;层次分析法是一种定性与定量分析相结合的多准则决策方法,对于处理多层次复杂系统的综合评估问题具备优势。综上,本文结合层次分析法和模糊综合评价法,提出一种模糊层次分析综合评价法,使邮轮客舱舱室人-机-环境评价更加合理。
1 邮轮客舱模糊层次分析综合评价 1.1 确定评价的关键因素集设第1层指标中评价对象有
| $ U{\text{ = \{ }}{u_1},{u_2},{u_3} \cdot \cdot \cdot {u_i}, \cdot \cdot \cdot {u_m}\} {\text{,}}$ | (1) |
由于评价因素集
| $ {u_i} = \left\{ {{u_{i1}},{u_{i2}}, \cdots {u_{ij}}, \cdots ,{u_{in}}} \right\},(j = 1,2, \cdots ,n) {\text{,}}$ | (2) |
设评价结果的个数为
| $ V = \left\{ {{v_1},{v_2}, \cdots ,{v_k}, \cdots ,{v_p}} \right\} {\text{。}} $ | (3) |
评估指标体系建立后,可通过主观或客观权重法逐一确定当前目标层中的指标在上一层中所占的比重,也称其为权重。权重的大小能够直接反映出评价指标在整个评价体系的重要程度,也会对评估结果最终实现量化起着关键的作用。
邮轮舱室设计指标往往会有很强的主观性和模糊性,为了使得赋权的过程与结果尽可能满足要求,通常由适用性较强的AHP法确定。
1.2.1 建立递阶层次结构模型将复杂问题进行条理化、层次化分析,构建出层次分析结构模型如图1所示。
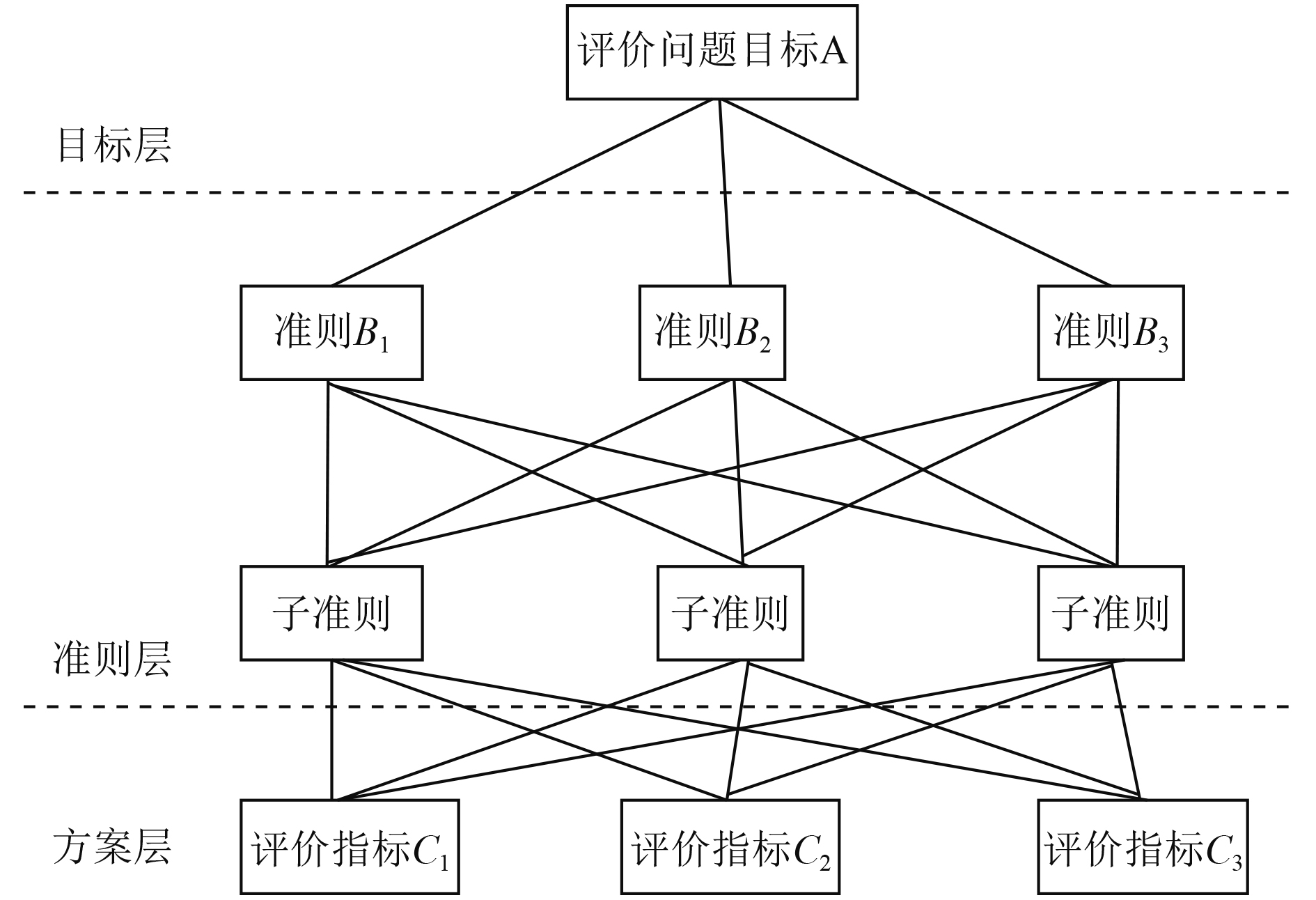
|
图 1 层次分析结构图 Fig. 1 Hierarchical analysis structure diagram |
为获取元素间的相对重要性,按照层次结构将同层次的元素两两比较,构造出比较判断矩阵并按相应的比例标度将评价定量化,如表1和表2所示。如果有
|
|
表 1 判断矩阵形式 Tab.1 Judgment matrix form |
|
|
表 2 比例标度及其含义 Tab.2 Proportional scale and its meaning |
判断矩阵C性质如下:
1)
2)
3)
| $ CI = \frac{{{\lambda _{\max }} - n}}{{n - 1}} {\text{,}} $ | (4) |
计算随机一致性比例为:
| $ CR = \frac{{CI}}{{RI}} {\text{。}} $ | (5) |
式中:
如果
如图1所示,设准则层B层有
设C层C1,C2 ,C3对上一层(B层)中的因素
| $ CR = \frac{{{b_1}C{I_1} + {b_2}C{I_2} + \cdots + {b_m}C{I_m}}}{{{b_1}R{I_1} + {b_2}R{I_2} + \cdots + {b_m}R{I_m}}} {\text{。}}$ | (6) |
当
评估隶属度表示对因素集中的每一子因素
| $ {{{r}}_i} = \left( {{r_{i1}},{r_{i2}} \cdots {r_{im}}} \right){\text{,}} $ | (7) |
m个单因素评价集构造出一个总的评价矩阵即为隶属度矩阵R,表示如下:
| $ {\boldsymbol{R}} = {\left( {{{{r}}_{ij}}} \right)_{m \times n}} = \left[ \begin{array}{*{20}{c}} {r_{11}}&{{{r}}_{12}}& \cdots &{{{r}}_{1n}} \\ {r_{21}}&{{{r}}_{22}}& \cdots &{{{r}}_{2n}} \\ \vdots &\vdots& \vdots & \vdots \\ {r_{31}}&{{{r}}_{m2}}& \cdots &{{{r}}_{mn}} \end{array} \right]{\text{。}} $ | (8) |
各级评价指标权重集表示为:
一级指标权重集
| $ B = \{ {B_1}, \cdot \cdot \cdot {B_i} \cdot \cdot \cdot {B_m}\}{\text{,}} $ | (9) |
二级指标权重集
| $ {C_i} = \{ {C_1},{C_2}, \cdots {C_j}, \cdots ,{C_n}\} ,(j = 1,2, \cdots ,n) {\text{。}}$ | (10) |
主观赋权根据资深专家的经验主观判断得到初始权重值,然后用贝叶斯后验分布来进行修正,得到最终合成权重值。权重集为:
| $ A = \left( {{{\text{a}}_1},{a_2} \cdots {a_m}} \right) {\text{。}}$ | (11) |
式中:满足
确定单因素权重集和单因素评价矩阵
| $ {L}_{i}=A·R=\left[{a}_{i1}\;\;{a}_{i2}\;\;\cdots {a}_{in}\right]·\left[\begin{array}{l}{r}_{i1}\\ {r}_{i2}\\ \;\;\vdots\\ {r}_{in}\end{array}\right]=\left[{l}_{i1}\;\;{\text{l}}_{i2}\;\;\cdots \;\;{\text{l}}_{ik}\;\;\cdots\;\; {\text{l}}_{ip}\right] {\text{。}}$ | (12) |
式中:
本文运用模糊层次分析综合评价法,以某邮轮居住舱室的综合环境为例进行评价。
2.1 邮轮客舱设计评价指标体系建立由于邮轮更加注重对相关娱乐旅游功能、设计美感、居住舒适度的要求,以及需满足舱室居住者、家居设备和室内环境三者之间的人-机-环境协调的特性。同时考虑到邮轮的航行条件,在对邮轮客舱舱室的设计方案进行评价时涉及到多个因素,需要按照多角度多层次的步骤来建立评价体系,只有这样才能最终准确实现客舱舱室人-机-环境系统性能。本文主要研究舱室环境舒适性,将邮轮舱室设计效果的影响因素进行分类,并将现有的数据资料结合相关专家的建议,选取室内结构和空间环境2个典型关键因素,最终建立邮轮客舱舱室设计评估指标体系,如图2所示。
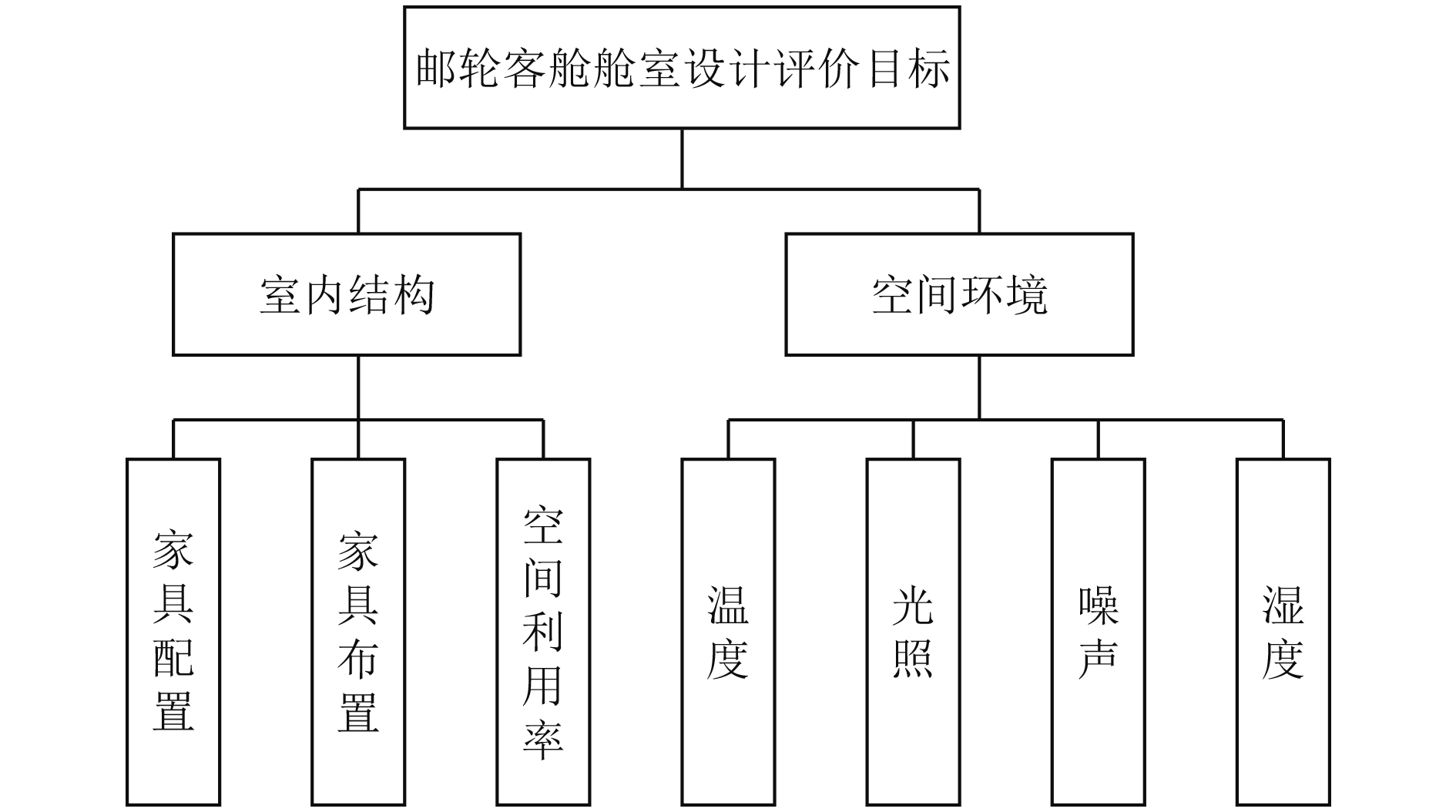
|
图 2 邮轮客舱舱室设计评估指标体系 Fig. 2 Evaluation index system of cruise cabin design |
结合图2所示的邮轮客舱舱室设计评价指标体系,确定以下评价因素集:第1层评价指标
本文构建的评价集为
建立层次结构模型,将与评价问题相关元素按照目标层、准则层、方案层3个层次进行分解,得到评价指标体系层次结构如图3所示。
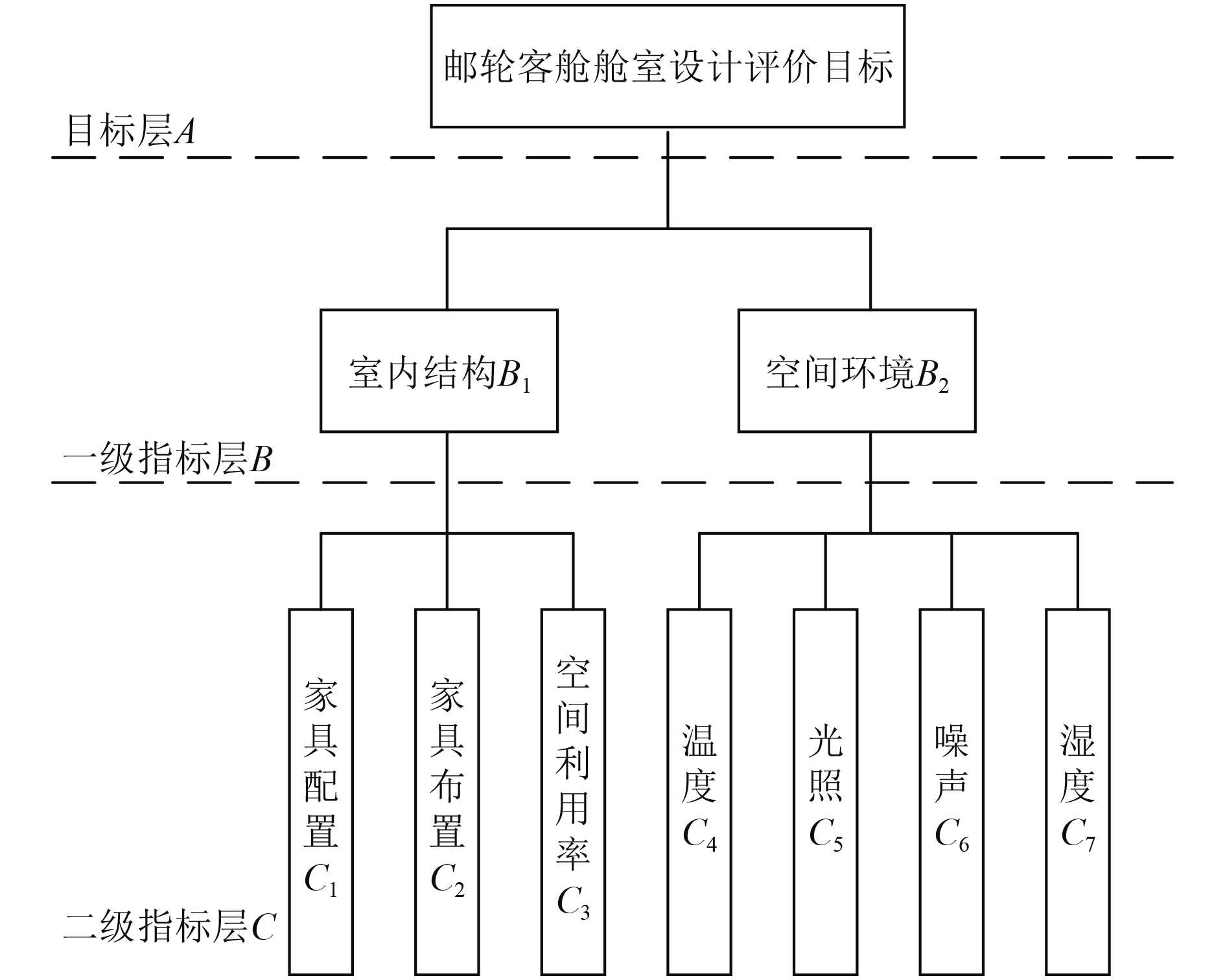
|
图 3 评价指标体系层次结构 Fig. 3 Evaluation index system hierarchy |
各级评价指标权重集表示为:
一级指标权重集
| $ B = \{ {B_1},{B_2}\} {\text{,}}$ | (13) |
二级指标权重集:
| $ {C_i} = \{ {C_1},{C_2}, \cdots {C_j}, \cdots ,{C_7}\} ,(j = 1,2, \cdots ,7){\text{。}} $ | (14) |
由于一级指标的上一层只有一个目标,所以这一层级有1组权重,同理二级指标层的上一层有2个目标所以这一层有2组权重。为了区分这2组权重,分别用b和w来表示,通过逐层分析,最终确定权重排序分析与计算结果,如表3~表5所示。
|
|
表 3 B层权重排序分析 Tab.3 B layer weight ranking analysis |
|
|
表 4 C层权重排序分析(1) Tab.4 Ranking analysis of C-layer weight (1) |
|
|
表 5 C层权重排序分析(2) Tab.5 Ranking analysis of C-layer Weight (2) |
得到判断矩阵如下:
对于此矩阵,由计算可得出:
说明判断矩阵D通过一致性检验,层次单排序的结构符合一致性要求。
得到判断矩阵如下:
对于此矩阵,由计算可得出:
由一致性检验的结果来看,层次单排序的结构符合一致性要求。
得到判断矩阵如下:
对于此矩阵,由计算可得出:
由一致性检验的结果来看,这种层次单排序的结构符合一致性要求。
综合上面计算得出的结果来看,层次单排序的结构都符合一致性要求,原先初步给各层次赋予的权重值有效。
2.3.2 确定评价指标合成后的权重完成对单一层次的赋权后,结合图3所示的评价指标体系层次结构,即可构建总体的合成权重计算模型:
| $ {w_i} = \sum\limits_{j = 1}^m {{b_j}{w_j}} ,{\text{ }}(j = 1,2, \cdots ,n) {\text{。}}$ | (15) |
式中:
按照式(15)可以计算出二级评价指标C相对于目标A的最终合成权重,其中
|
|
表 6 二级评价指标C相对于目标A的合成权重 Tab.6 The synthetic weight of the second-level evaluation index C relative to target A |
得到判断矩阵如下:
对于此矩阵,由计算可得出:
由一致性检验的结果来看,这种层次总排序的结构符合要求。
2.4 确定单因素评价矩阵式(8)为室内结构指标评价矩阵
|
|
表 7 室内结构指标评价结果统计 Tab.7 Indoor structural index evaluation results statistics |
依据专家的评价意见室内结构定性指标隶属度为:
| $ {{{r}}_{1jk}} = \frac{{{N_{1jk}}}}{N} {\text{。}}$ | (16) |
式中:
而空间环境这类评价指标通常属于定量指标,据热、光、声环境的要求和限制得出标准如表8所示。
|
|
表 8 空间环境指标评价标准 Tab.8 Evaluation criteria of space environment index |
这些定量指标往往有着明确的相关隶属度确定规则来计算出最终的隶属度
| $ {r}_{21}\left({x}_{1}\right)=\left\{\begin{array}{*{20}{l}} 0&{x}_{1}<10,{x}_{1}>35\\ \left(\dfrac{1.0-0.5}{14-10}\right)\times \left({x}_{1}-10\right)+0.5&{10}\leqslant {x}_{1}<14\\ \left(\dfrac{1.0-0.8}{18-14}\right)\times \left({x}_{1}-14\right)+0.8&{14}\leqslant {x}_{1}<18\\ 1&18\leqslant {x}_{1}\leqslant 24\\ \left(\dfrac{1.0-0.5}{29-24}\right)\times \left({x}_{1}-24\right)+0.5&{24}<{x}_{1}\leqslant 29\end{array}\right\} {\text{,}}$ | (17) |
| $ {r}_{22}\left({x}_{2}\right)=\left\{\begin{array}{*{20}{l}}\left(\dfrac{1.0-0.8}{75-25}\right)\times \left({x}_{1}-25\right)+0.8&{25}<{x}_{2}<75\\ 1&75\leqslant {x}_{2}\leqslant 100\\ \left(\dfrac{1.0-0.8}{150-100}\right)\times \left({x}_{1}-100\right)+0.8&{100}<{x}_{2}<150\\ \left(\dfrac{1.0-0.5}{200-150}\right)\times \left({x}_{1}-200\right)+0.5&{150}<{x}_{1}\leqslant 200\\ 0&{x}_{1}> 200\end{array}\right\} {\text{,}}$ | (18) |
| $ {r_{23}}\left( {{x_3}} \right) = \left\{ \begin{array}{*{20}{l}} 1&{x_3} < 45 \\ \left( {\dfrac{{1.0 - 0.8}}{{60 - 45}}} \right) \times \left( {{x_3} - 45} \right) + 0.8&{\text{45}} \leqslant {x_3} \leqslant 60 \\ \left( {\dfrac{{1.0 - 0.6}}{{70 - 60}}} \right) \times \left( {{x_3} - 60} \right) + 0.6&{{60}} \leqslant {x_3} \leqslant 70 \\ 0&{x_3} > 70 \end{array} \right\} {\text{,}}$ | (19) |
| $ \begin{split}&{r}_{24}\left({x}_{4}\right)=\\ &\left\{\begin{array}{*{20}{l}}\left(\dfrac{1.0-0.8}{50\text{%}-45\text{%}}\right)\times \left({x}_{4}-45\text{%}\right)+0.8&\text{45\%}\leqslant {x}_{4} <50\text{%}\\ 1&\text{50\%}\leqslant {x}_{4}\leqslant 65\text{%}\\ \left(\dfrac{1.0-0.8}{\text{70\%}-65\text{%}}\right)\times \left({x}_{4}-65\text{%}\right)+0.8&\text{65\%} <{x}_{4}\leqslant 70\text{%}\\ \left(\dfrac{1.0-0.5}{90\text{%}-70\text{%}}\right)\times \left({x}_{4}-70\text{%}\right)+0.5&\text{70\%}\leqslant {x}_{4}\leqslant 90\text{%}\\ 0&{x}_{4} > 90\text{%}\end{array}\right\}\end{split} {\text{。}}$ | (20) |
式中:
定量指标由于能够给出具体的值则不需要专家进行模糊评价,根据具体的数值直接计算出指标隶属度
由式(16)以及表6可以得到评价向量
| $ {R_1} = \left[ \begin{array}{*{20}{c}} {r_{111}}&{r_{112}}& \cdots &{r_{114}} \\ {r_{121}}&{r_{122}}& \cdots &{r_{124}} \\ {r_{131}}&{r_{132}}& \cdots &{r_{134}} \end{array} \right] = \left[ \begin{array}{*{20}{c}} 0&0.4&0.5 &0.1\\ 0.2 & 0.5 & 0.3 & 0\\ 0.3 & 0.6 & 0.1 & 0 \end{array} \right] {\text{。}}$ |
在本文中,邮轮客舱舱室的定量指标如表9所示。
|
|
表 9 邮轮客舱舱室的定量指标 Tab.9 Quantitative index of cruise cabin |
由式(17)~(20)以及表9可以得到评价向量
| $ {R_2} = \left[ \begin{array}{c} {r_{21}} \\ {r_{22}} \\ {r_{23}} \\ {r_{24}} \end{array} \right] = \left[ \begin{array}{c} 1 \\ 0.9 \\ 1 \\ 0.88 \end{array} \right] {\text{。}}$ |
1)计算一级模糊综合评价最终结果
在本文中一级评价定性指标
| $ {B_1} = \left[ {0.319\;6,0.558\;4,0.122\;0} \right]{\text{,}} $ |
单因素模糊评价向量为:
| $ \begin{split} {L_1} =& \left[ {0.316\;9\;\;\; 0.558\;4 \;\;\; 0.122\;0} \right] \times \left[ \begin{array}{*{20}{c}} 0& 0.4 & 0.5 & 0.1 \\ 0.2 & 0.5 & 0.3 & 0\\ 0.3 & 0.6 & 0.1 & 0 \end{array} \right] =\\ & \left[ {0.148\;3\quad 0.479\;2 \quad 0.339\;5 \quad 0.031\;7} \right] {\text{。}} \end{split} $ |
在本文中一级评价定性指标
| $ {B_2} = \left[ {0.384\ 9,0.384\ 9,0.087\ 4,0.142\ 8} \right]{\text{,}} $ |
单因素模糊评价向量为:
| $ {L_2} = \left[ {0.384\ 9,0.384\ 9,0.087\ 4,0.142\ 8} \right] \times \left[ \begin{array}{c} 1 \\ 0.9 \\ 1 \\ 0.88 \end{array} \right] = 0.944\;4 {\text{。}}$ |
确定完定性模糊评价向量和定量模糊评价向量,最终的综合评价结果还需要对其进行相应的加权与转换计算。
2)评价结果最终实现
采用模糊综合评价法(FCA)进行评价的最终目标是把得到的定性指标和定量指标进行合成,最终给出一种综合评价结果。在构建评价集的过程中为了能够直观地显示评价效果所以采用的是五分制的评语集
| $ {W}_{1}={L}_{1}·V {\text{,}}$ | (21) |
| $ {W}_{2}={L}_{2}·V {\text{,}}$ | (22) |
| $ W=\left[{\text{b}}_{1}\quad{\text{b}}_{2}\right]\cdot\left[\begin{array}{l}{W}_{1}\\ {W}_{2}\end{array}\right] {\text{。}}$ | (23) |
定性指标的最终评价分数为:
| $ \begin{split}{W}_{1}=&{L}_{1}\cdot V=\left[0.148\;3\quad0.479\;2\quad 0.339\;5\quad 0.031\;7\right]\times\\ &{\left[5\quad 4\quad 3\quad 2\right]}^{{\rm{T}}}=3.740\;2{\text{,}} \end{split}$ |
定量指标的最终评价分数为:
| $ {W}_{2}={L}_{2}\cdot V=0.944\;4\times 5=4.722\;0 {\text{,}}$ |
设计评价总目标的最终分数为:
| $ \begin{split}W=&\left[{\text{b}}_{1}\quad{\text{b}}_{2}\right]\cdot\left[\begin{array}{l}{W}_{1}\\ {W}_{2}\end{array}\right]=\left[0.5\quad \text{0}\text{.5}\right]\times\\ &\left[\begin{array}{l}3.740\;2\\ 4.722\;0\end{array}\right]=\text{4}\text{.231\;1}{\text{。}}\end{split} $ |
3)模糊综合评价结果分析
设计总目标得出的评价分数4.2311介于评价集4~5之间可以看出,模糊评价等级为优秀。
3 结 语目前,随着邮轮业的不断发展,邮轮对功能、美感、居住舒适度的要求越来越高。本文针对邮轮客舱舱室人-机-环境评价问题提出一种模糊层次分析综合评价法。
1)将邮轮客舱舱室评价指标体系分成层次结构,利用层次分析法确定各个评价指标的权重值,分层次利用模糊综合评价方法,最终得出总的评价结果。
2)采用该评价方法对某邮轮客舱舱室进行综合评估,结果表明该方法具有一定的可行性。
3)该方法结合主观与客观因素,评估过程中提高了针对性和精确性。本文的评价方案能够为邮轮客舱舱室后续调整和优化提供有意义的参考价值。
| [1] |
李晓文, 朱兆一, 熊云峰, 等. 基于信息集成算子的舰船舱室设计方案评估[J]. 大连理工大学学报, 2018, 58: 357-361. DOI:10.7511/dllgxb201804004 |
| [2] |
胡莹颖, 张祥瑞, 林壮, 等. 船舶区域舱室复合环境综合评价方法研究[J]. 船舶, 2018, 29(02): 19-26. |
| [3] |
陈武, 彭飞, 牟金磊, 等. 舰艇舱室居住性指标体系及其模糊关联评估优化研究[J]. 武汉理工大学学报(交通科学与工程版), 2015, 39(6): 1263-1268. |
| [4] |
施红, 王均毅, 陈佳敏, 等. 船舶舱室综合环境质量评价方法[J]. 江苏科技大学学报(自然科学版), 2019, 33(1): 32-38. |
| [5] |
张阔远, 陈辉, 商蕾. 综合评价方法在船舶驾驶舱设计的应用[J]. 武汉理工大学学报(交通科学与工程版), 2011, 35(5): 1077-1080. DOI:10.3963/j.issn.1006-2823.2011.05.048 |
 2021, Vol. 43
2021, Vol. 43

