2. 上海交通大学 高新船舶与深海开发装备协同创新中心,上海 200240;
3. 中国船舶及海洋工程设计研究院,上海 200011
2. Collaborative Innovation Center for Advanced Ship and Deep-sea Exploration, Shanghai Jiaotong University, Shanghai 200240, China;
3. Marine Design and Research Institute of China, Shanghai 200011, China
轮印载荷是船舶营运过程中常见的载荷类型,具有局部集中分布、位置不固定的特点,对船舶设计工作有较高的要求。在轮印载荷作用下,甲板的承载能力会影响船舶结构的安全性能。船舶甲板是典型的加筋板结构,因此,轮印载荷作用下加筋板承载能力的研究工作对于船舶结构设计有着十分重要的意义。
国内外许多学者已经对轮印载荷进行了大量的研究,LING Zhu等[1]以橡胶块代替轮胎进行了加筋板强度试验,进而研究了在重型车辆及直升机轮载作用下加筋板结构的极限承载能力和塑性变形规律,并提出了加筋板板厚的弹塑性设计方法。LIN Hong等[2]从局部侧向载荷下矩形板破坏模式入手,结合塑性屈服线理论提出了“双钻式”破坏模式以及考虑薄膜力的甲板厚度设计方法,其结果与IACS规范吻合较好。Burak Can Cerik[3]通过数值方法研究了侧向载荷产生的塑性变形对钢板纵向对压行为的影响,其研究结果表明,侧向载荷引起的塑性变形会降低板破坏前的刚度和纵向极限强度。A. Aalberg等[4]通过铝合金加筋板纵向对压试验研究了加筋板纵向极限强度和崩溃模式,其结果表明,加筋板屈曲方向不一定与初始缺陷的方向一致,同时通过与欧洲铝合金结构设计准则对比板刚度发现,试验所用加筋板刚度均超过了设计准则值。Jeom Kee Paik等[5]提出了考虑侧向载荷情况下的加筋板纵向极限强度表达式,将加筋板破坏模式分成6种,然后通过试验和数值仿真对所提表达式进行验证,证明了其合理性。陈彦廷等[6]作了船体板和加筋板极限强度问题的研究综述,目前通过试验法对于加筋板结构强度的研究工作中,大多是单轴向压缩试验,考虑侧向压力或双轴向压缩的试验比较少。刘春正等[7]研究了初始挠度对加筋板纵向极限承载能力的影响,提出了初始挠度对极限载荷影响的影响因子及其计算方法。其研究结果表明,随着初始挠度的幅值和半波数的增加,加筋板极限承载力逐渐减小。刘聪等[8]通过在橡胶块上加压的方式模拟轮印载的方式研究了轮印载荷在加筋板上的载荷分布特性,其研究结果表明,加强筋上均布轮印载荷为接触面上均布轮印载荷的1.279 倍。同时研究了多种参数对该分布规律的影响。王维舟等[9]研究了各船级社对车辆甲板厚度设计规范的差异,以及塑性承载能力利用水平。研究结果表明,规范中部分板格的最大应力值超过了材料的屈服应力。谭开忍等[10]作了船体结构极限强度的研究综述,介绍了加筋板、船体板和船体梁极限强度的计算方法以及相关的试验研究成果。
以上研究多以橡胶块代替轮印载荷来研究其分布特点和加筋板的应力响应。对加筋板极限承载能力的研究多着眼于加筋板纵向极限承载力,而对于加筋板在轮印载荷作用下的极限承载能力进行研究的文献还比较少。本文以铝合金加筋板为例,通过试验和仿真结合的方式对加筋板在轮印载荷作用下的极限承载力进行研究。
1 试验方案 1.1 试验模型及测点布置为确定轮印载荷作用下加筋板上的承载能力,本文设计了如图1所示的试验模型,模型材料为铝合金。其中,模型的长度为1400 mm,宽度为1400 mm,纵骨间距为200 mm,纵骨跨距为400 mm和600 mm。横梁高度为200 mm。为了模拟固支边界条件,在模型四周增设了厚度为20 mm的带孔围板,以此与四周工装件栓接。
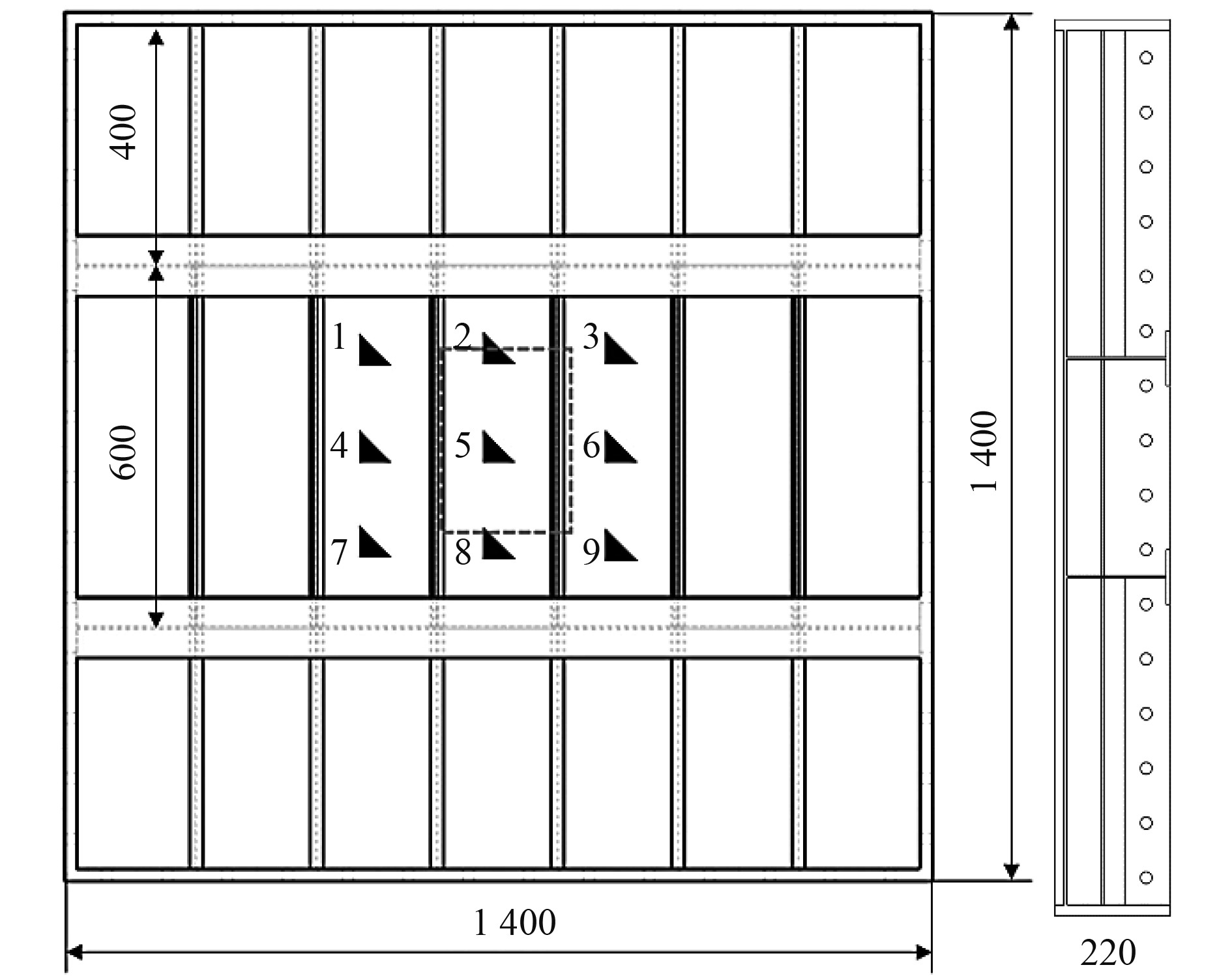
|
图 1 试验模型及测点布置示意图 Fig. 1 Experimental model and test points |
为获取模型应变、加筋板垂向位移和加载块位移等数据。模型面板上共布置了9个三向应变测点和1个单向应变测点,三向片布置情况如图1所示,单向片位于加载区所骑纵骨的腹板处。共布置1个位移测点,位于5号应变测点旁边,如图2中U所示。通过线位移计来测量加载块的位移,该位移计布置于加载油缸处。
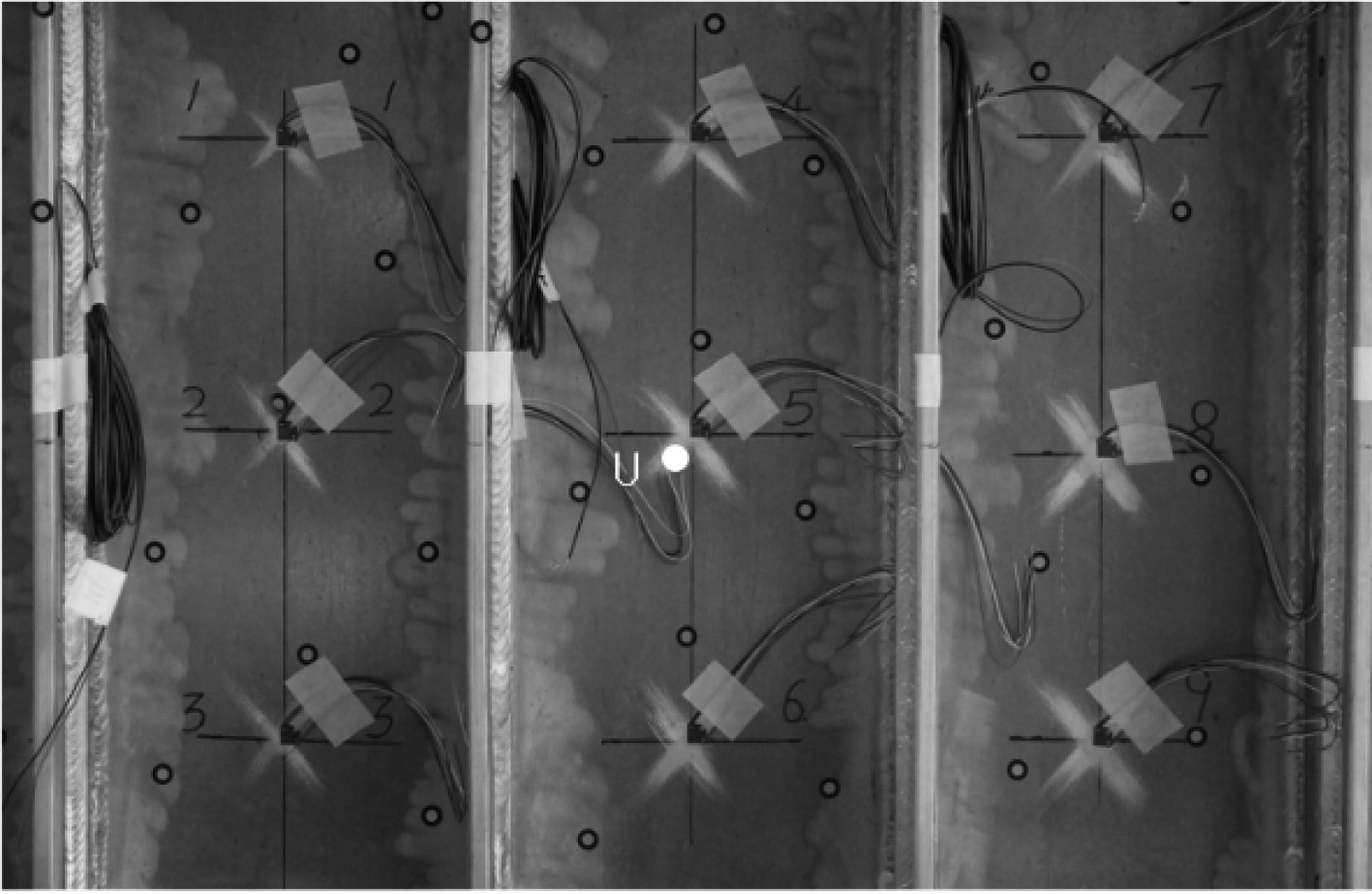
|
图 2 试验应变位移测点布置 Fig. 2 Experimental test points of strain and displacement |
为了获得试验模型的材料性能参数,根据规范GBT228-2002要求制定了相应的拉伸试件并进行了单轴拉伸试验。材料应力-应变曲线如图3所示,其弹性模量为68 GPa,名义屈服应力为168 MPa,泊松比为0.33,断裂应变为0.18,比例极限为131MPa左右。所得到的材料性能参数用于数值仿真计算。
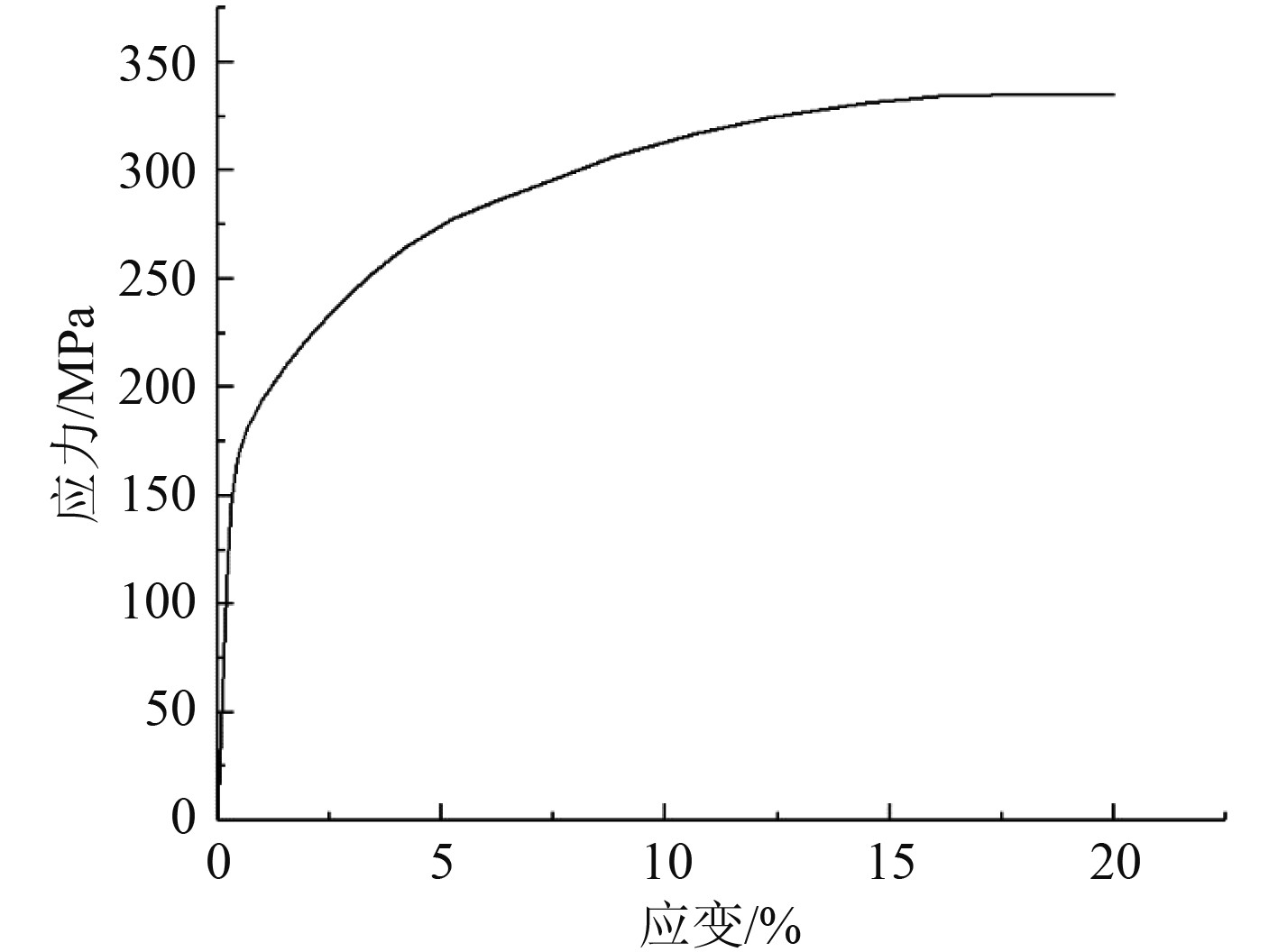
|
图 3 材料应力-应变曲线 Fig. 3 Tensile curve of material |
为更好模拟轮印载荷的特征,选用加载钢块和橡胶垫叠加的方式进行加载,根据某型号轮胎的轮印尺寸确定钢块尺寸为220 mm×320 mm,橡胶垫厚度约10 mm。同时为防止应力集中对试验结果的影响,对加载钢块的下侧面进行了倒角处理。加载位置如图1中虚线框所示,该位置紧靠纵骨一侧,为试验前通过数值仿真确定的危险位置。模型安装完毕后,首先通过加载油缸进行预加载以确保加载块与模型充分接触,将数据采集装置清零后进行正式加载试验。加载过程缓慢匀速进行,直至模型失去承载能力。
2 试验结果 2.1 应力-载荷曲线根据胡克定律将试验模型各应变测点数据转换为Mises应力,模型各测点应力达到屈服极限以前的应力-载荷曲线如图4所示。可以看出,加载初期各测点应力与载荷有较好的线性对应关系,当载荷达到约50 kN时单向测点出现非线性变化,此时对应的应力为110 MPa左右。该非线性现象产生的原因一是因为材料比例极限到屈服极限之间的非线性变化而产生,二是因为该测点所在位置的应力分布比较复杂,应变片只能测出一个方向的应变,难以反映该区域真实应力情况。在载荷达到6.5 t(65 kN)左右时,位于加载区域下方的加强筋应力达到屈服应力σs,模型产生塑性变形,此时可以认为变形达到了模型弹性状态的终点。因此,模型弹性承载能力取为6.5 t,对应的压力为0.87 MPa。
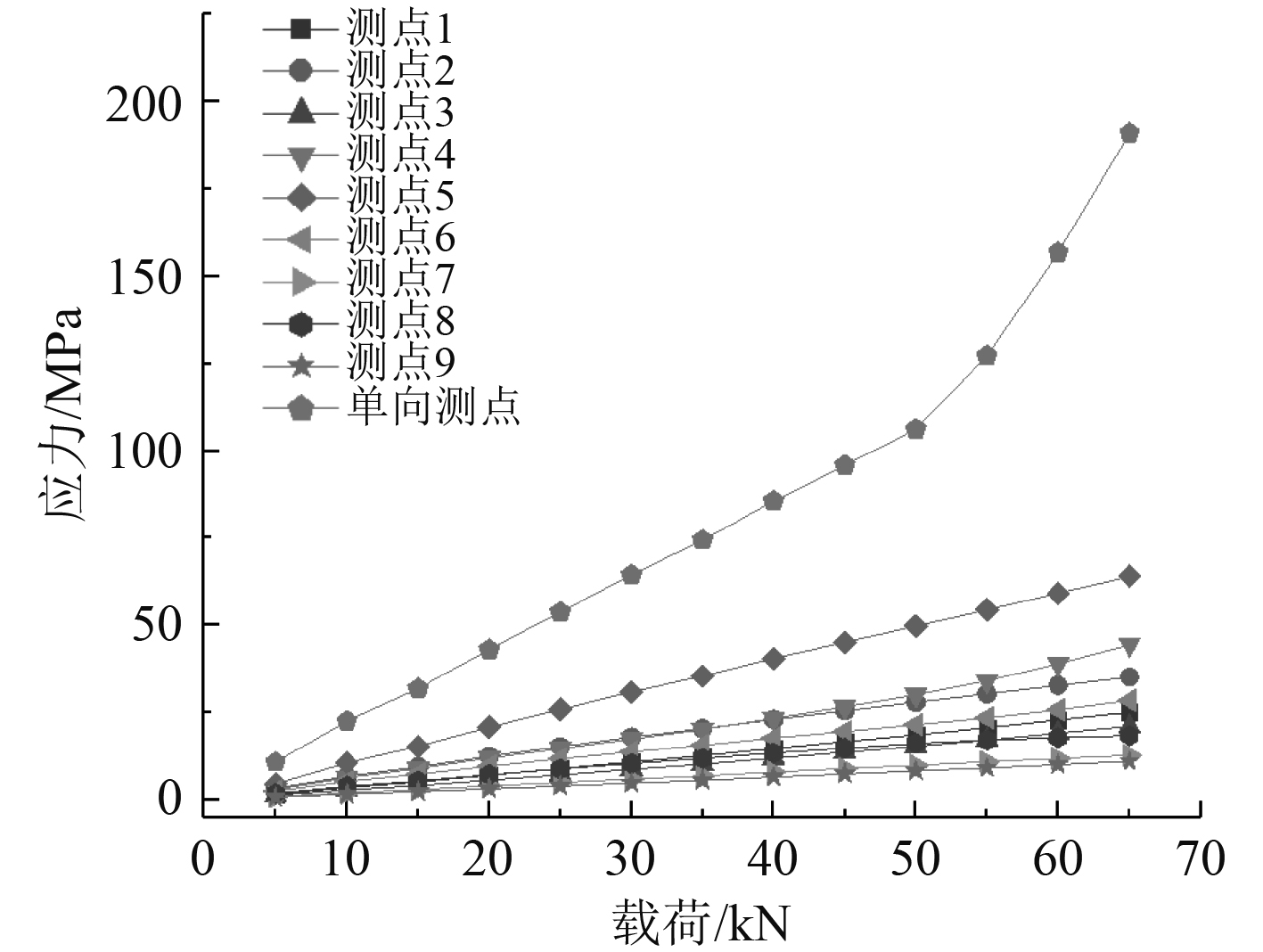
|
图 4 应力-载荷曲线 Fig. 4 Stress-load curves |
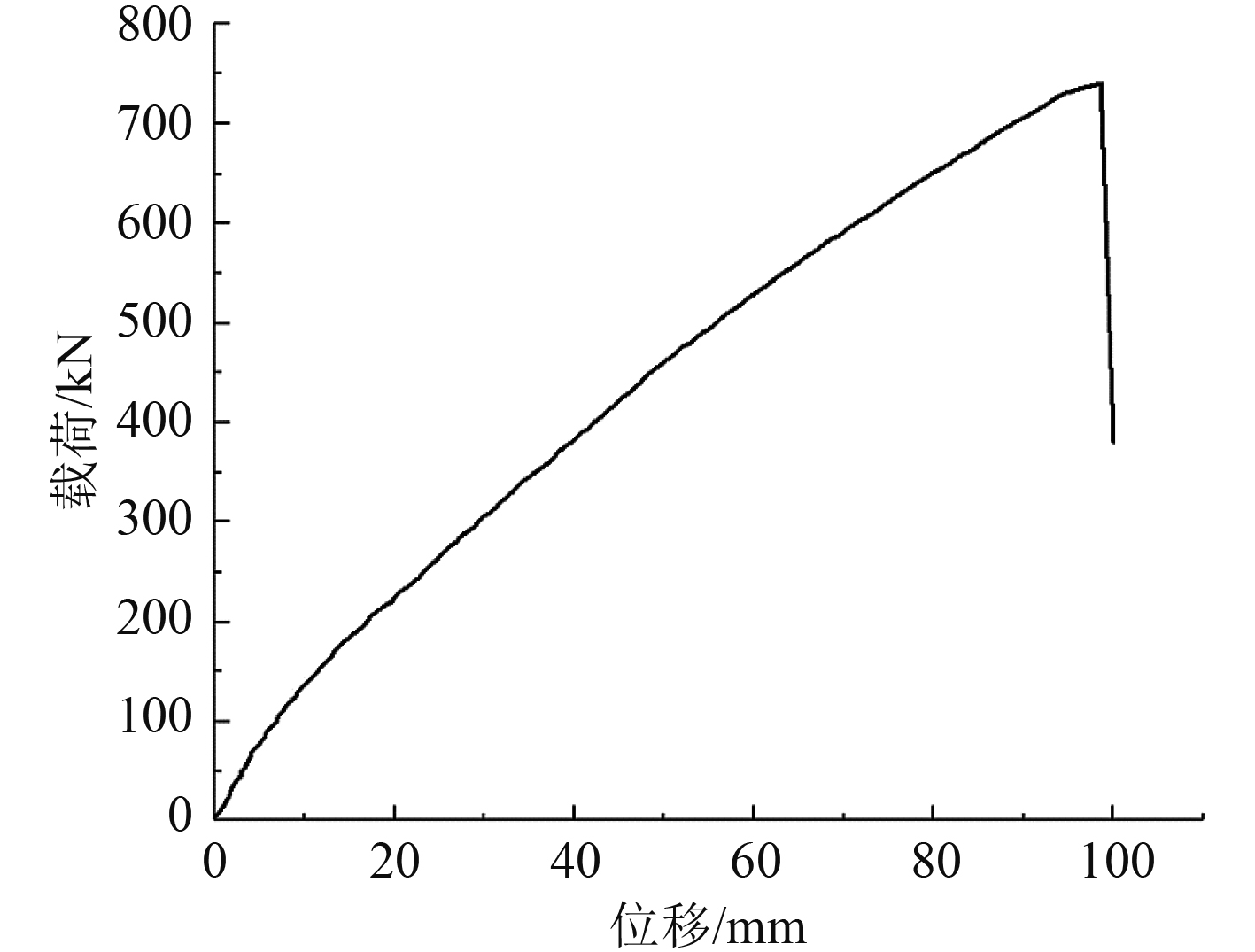
随着加载的进行,模型垂向位移逐渐增加,当垂向位移达到约98.6 mm时,模型面板突然破裂,加筋板随即丧失承载能力,此时对应的加筋板侧向承载能力约74.2 t(742 kN)左右,对应的压力为9.79 MPa左右,即为该加筋板的极限承载能力。整个加载过程的载荷-位移曲线如图5所示。可以看出,模型侧向极限承载能力是其弹性承载能力的11.4倍左右。一般情况下,设计载荷与弹性最大承载能力接近,这说明了相对设计载荷来说,该结构具有较大的安全裕度。
|
图 5 载荷-位移曲线 Fig. 5 Load-displacement curve |
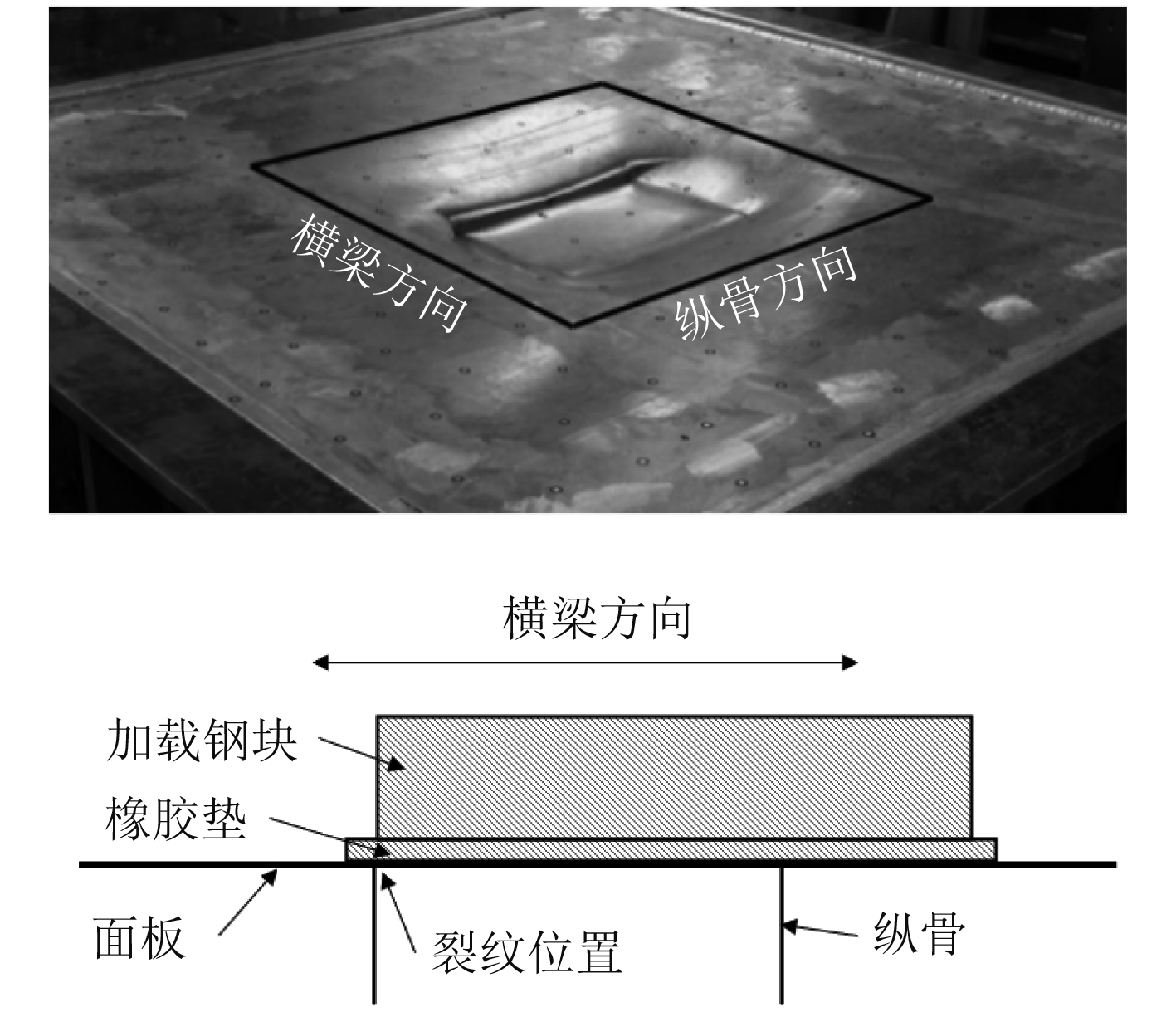
卸载并拆除加载装置以后,模型整体破坏情况如图6所示,产生的裂纹位于加载钢块相邻纵骨一侧的面板上,整个加载区域下陷量达98.6 mm,下陷区域主要集中在加载区域及其附近3个板格内。断裂面整齐,略长于钢块边长,未超出钢块部分的裂纹与钢块平行,超出钢块部分的裂纹方向与钢块边呈45°角向外延伸。破坏原因应是加载钢块与加筋板纵骨的剪切力作用。
|
图 6 模拟破坏情况 Fig. 6 Model destruction result |
根据图7所示的模型尺寸建立有限元模型,数值模型包括围板结构和加筋板。模型整体单元类型为S4R,单元边长为10 mm。为模拟试验模型的边界条件,在螺栓位置处以点约束代替螺栓的固定作用,按照式(1)对各点进行约束。材料参数由拉伸试验确定,由于拉伸试验得到的结果为工程应变和工程应力的关系,仿真时按照式(2)将工程应力应变转换为真实应力应变参与计算,式中

|
图 7 有限元模型 Fig. 7 FME model |
| $ {R_x} = {R_y} = {R_z} = U{R_x} = U{R_y} = U{R_z} = 0 {\text{,}} $ | (1) |
| $ \left\{ \begin{array}{l} {\varepsilon _{true}}{\text{ = }}\ln (1 + {\varepsilon _{eng}}) {\text{,}}\\ {\sigma _{true}}{\text{ = }}{\sigma _{eng}}(1 + {\varepsilon _{eng}}) {\text{。}} \end{array} \right. $ | (2) |
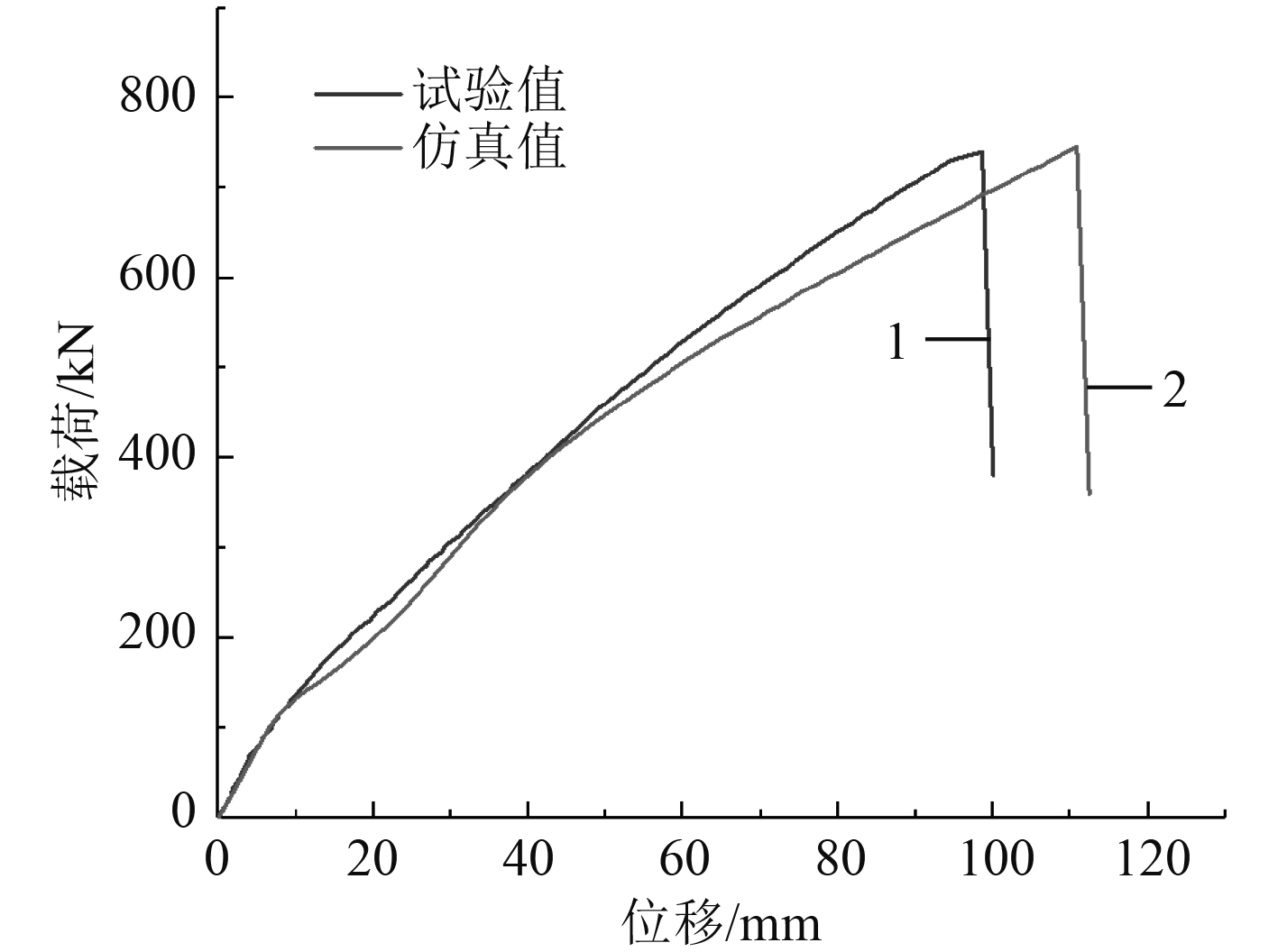
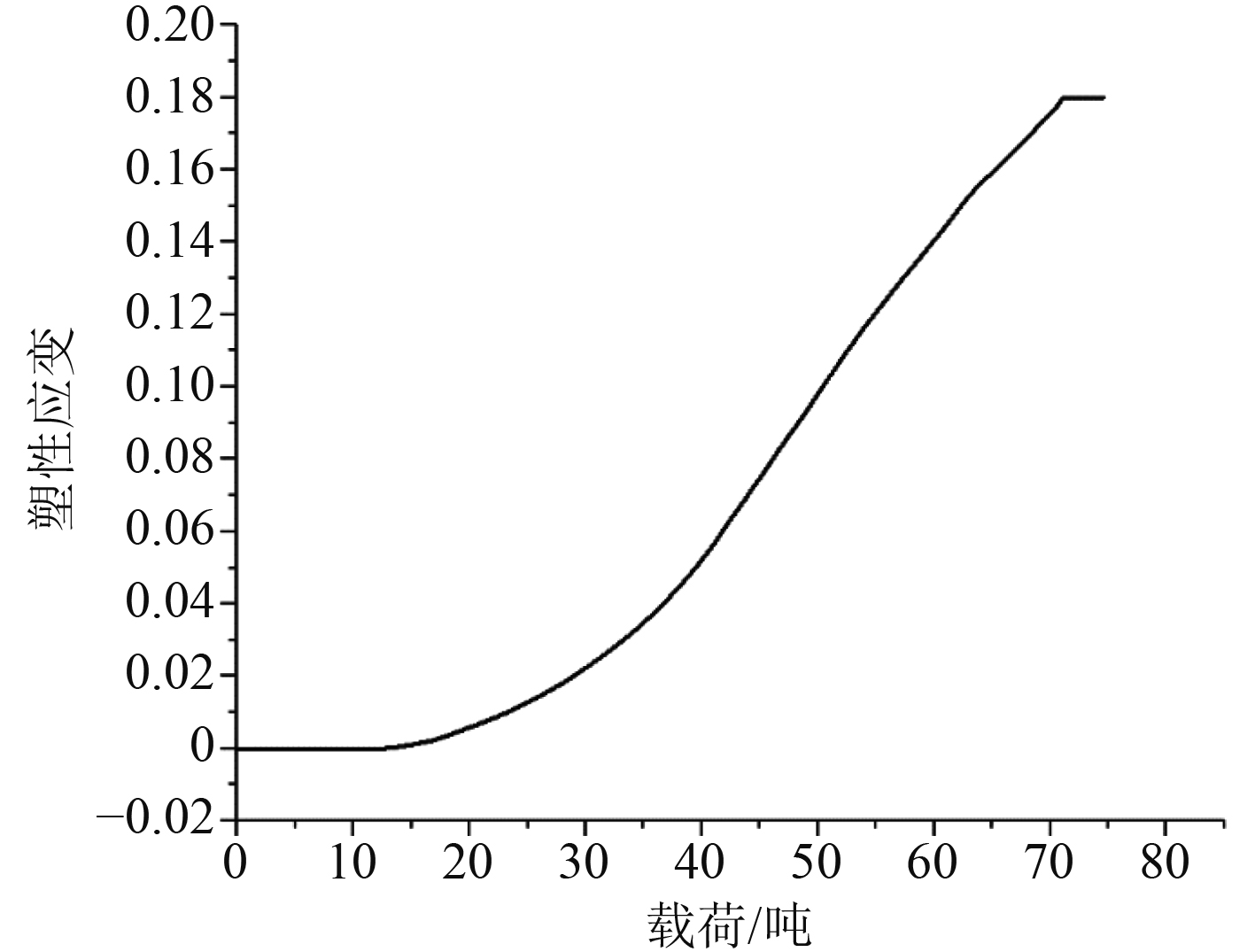
通过仿真计算,得出的模型极限强度在74.6 t(746 kN)左右,如图8所示。可以看出,仿真模型与试验模型的载荷-位移曲线吻合较好,极限载荷值相差不大,但极限载荷值对应的位移有所区别,主要原因可能有模型残余应力的影响和初始变形的影响等。模型加载区角部单元的塑性应变与载荷关系如图9所示,当塑性应变达到材料失效应变时即产生裂纹,如图10(a)所示。模型达到极限状态以后,加载块毗邻纵骨一侧的面板破裂,试验模型与仿真模型面板破裂情况的对比如图10(b)所示。破坏渐进过程对应的平均塑性应变分布云图如图11所示,从加筋板整体破坏过程Ⅰ~Ⅲ上看,仿真结果与试验结果的初始裂纹段与试验结果一致,但裂纹延伸段与试验结果有差异,这是由于失效准则的选取与材料本身性质共同导致的。
|
图 8 载荷-位移曲线试验仿真对比 Fig. 8 Comparison of load-displacement curves |
|
图 9 塑性应变-载荷曲线 Fig. 9 Curve of plastic strain-load |

|
图 10 破坏情况试验仿真对比 Fig. 10 Comparison of model destruction result |

|
图 11 破坏渐进过程 Fig. 11 Progressive process of destruction |
船舶设计过程中,对于甲板等结构,一般通过弹性理论进行设计,但允许一部分塑性变形。结合试验结果和加载区域的面积可知,加筋板弹性最大承载能力为6.5 t,对应的压力为 0.872MPa,加筋板极限承载能力为74.2 t,对应的压力为9.79 MPa。试验所用加筋板侧向极限承载能力是其弹性承载能力的11.4倍左右,可见加筋板在侧向承载能力方面具有很大的安全裕度。
通过试验位移数据可知,轮印载荷作用下,铝合金加筋板达到极限承载力对应的位移为98.6mm。加筋板达到极限状态后,由于钢块与纵向加强筋的局部剪切作用引起的加筋板面板局部剪切破坏。该破坏发生后,加筋板立即失去承载能力。
此外,由于侧向加载达到极限状态时对应的侧向位移量很大,因此在考虑该工况下加筋板失效准则时,最好同时结合加筋板功能性失效准则和结构破坏失效准则来综合判断。
5 结 语通过轮印载荷作用下加筋板极限承载力试验和相应的数值仿真研究,本文得出如下结论:
1)轮印载荷作用下,加筋板对应的弹性承载力为6.5 t(0.872 MPa),侧向极限承载力为73 t(9.79 MPa),可见结构具有很大的安全裕度。
2)轮印载荷作用下,加筋板的失效模式为面板局部剪切破裂,面板破裂后结构立即失去承载能力。
3)加筋板达到侧向极限状态时对应的侧向位移较大,在判断加筋板是否失效时,应同时考虑结构的功能性失效模式和结构破坏失效模式。
| [1] |
LING Zhu, WEI Cai, PAUL A. Frieze. Design method for steel deck plates under quasi-static patch loads with allowable plastic deformations [J]. Marine Structures, 2020, 71: 102702.
|
| [2] |
LIN Hong, JORGEN A. Plastic design of laterally patch loaded plates for ships [J]. Marine Structures, 2007, 20: 124−142.
|
| [3] |
BURAK C C. Ultimate longitudinal compressive strength of steel plates with lateral patch load induced plastic deformation [J]. Thin-Walled Structures, 2018, 122: 416−424.
|
| [4] |
AALBERG A, LANGSETH M, LARSEN P. K. Stiffened aluminium panels subjected to axial compression [J]. Thin-Walled Structures, 2001, 39: 861−885.
|
| [5] |
JEOM K P, BONG J K. Ultimate strength formulations for stiffened panels under combined axial load, in-plane bending and lateral pressure: a benchmark study [J]. Thin-Walled Structures, 2002, 40: 45−83.
|
| [6] |
陈彦廷, 于昌利, 桂洪斌. 船体板和加筋板的屈曲及极限强度研究综述[J]. 中国舰船研究, 2017, 12(1): 54-62. DOI:10.3969/j.issn.1673-3185.2017.01.009 |
| [7] |
刘春正, 吴梵, 牟金磊. 含初始挠度加筋板的极限承载能力分析[J]. 舰船科学技术, 2017, 39(5): 10-15.
|
| [8] |
刘聪, 程远胜, 张攀等. 加筋板轮印载荷分布特性的试验与数值分析[J]. 海洋工程, 2017,35(4): 84-93.
|
| [9] |
王维舟, 刘俊, 陈锋. 轮载下车辆甲板塑性承载能力利用程度研究[J]. 舰船科学技术, 2016,38(2): 49−53.
|
| [10] |
谭开忍, 李小平. 船体结构极限强度研究进展[J]. 船舶, 2006, 5: 19−25.
|
 2021, Vol. 43
2021, Vol. 43
