船舶在高速行驶过程中产生的阻力会导致更多的燃料损耗,更严重的是,船舶在大风浪中会导致失速现象,从而造成重大的海难事故[1],随着船舶设计体型的日益增大,船舶在高速航行过程中产生的波浪增阻可以达到静水阻力的10%~30%[2],所以,研究在静水以及波浪状态下的船舶阻力性能具有重要的意义。
本文主要对双体船在自航下的静水阻力和总阻力系数进行计算,通过二因次换算法[3]、三因次换算法[4]将对船模的计算结果换算成实船的阻力以及总阻力系数,并将其和使用STAR-CCM+实尺度法[5]计算的实船阻力和总阻力系数进行对比,通过对3种计算方法的结果进行对比,计算双体船在波浪下航行的波浪增阻随波长变化的规律,通过计算得出的数据可以对双体船在满足船舶能效指数[6]要求的基础上对双体船的船型优化提供数据支持。
船舶阻力计算通常使用船模实验的方法,通过对船模的阻力和总阻力系数进行计算,并使用二因次换算法和三因次换算法把船模阻力换算成实船的阻力和总阻力系数。随着计算机技术和船舶计算流体力学的发展,采用CFD方法研究船舶的性能成为一种重要的手段,Blanca Pena[7]使用STAR-CCM+软件将实尺度计算流体模拟的结果与实尺度直接测量数据进行对比,证明船舶CFD实尺度模拟的可行性。
1 双体船的换算和建模将双体船模型尺度和实船尺度按照1∶16.2缩小到3 m的船模进行静水航行阻力计算,实船和船模尺度的换算结果如表1所示。
|
|
表 1 实船和船模尺度 Tab.1 Principal dimensions of the catamaran and catamaran model |
船模和实船的航速换算按照重力相似原则,换算结果如表2所示。
|
|
表 2 船模和双体船速度换算 Tab.2 Speed conversions of the catamaran model and catamaran |
双体船船模主尺度如表3所示。
|
|
表 3 Delft-372双体船主尺度表 Tab.3 Principal dimensions of Delft-372 Catamaran |
使用CFD软件STAR-CCM+对双体船实尺度计算,需要选取相应的计算域和划分具有足够精度的网格,如图1所示。本文所选取的计算域如图1(a)所示,为了保证大部分区域的计算性能,本文对双体船网格的主要运用Trim网格,并对船体周围、自由面上下一定范围内和船型变化较大的部位进行加密,网格的生成利用对称边界条件和以半模的方式生成网格。其网格划分的结果如图2(b)~图2(d)所示。

|
图 1 双体船计算域以及网格划分 Fig. 1 Catamaran computational domain and grid partition |
采用STAR-CCM+对双体船不同航速下的静水阻力数值计算,共选取双体船从低速到高速一共7个不同的航速进行计算,湍流模型选取带旋转修正的Realizable k-ε模型,不同航速对应的雷诺数和傅汝德数如表4所示。
|
|
表 4 静水阻力的计算工况 Tab.4 Working condition of the calm water resistance |
使用STAR-CCM+计算得出的双体船静水总阻力与通过船模试验得出的结果进行对比,计算结果和对比图如表5和图2所示。
|
|
表 5 总阻力计算结果 Tab.5 Total drag calculation |
|
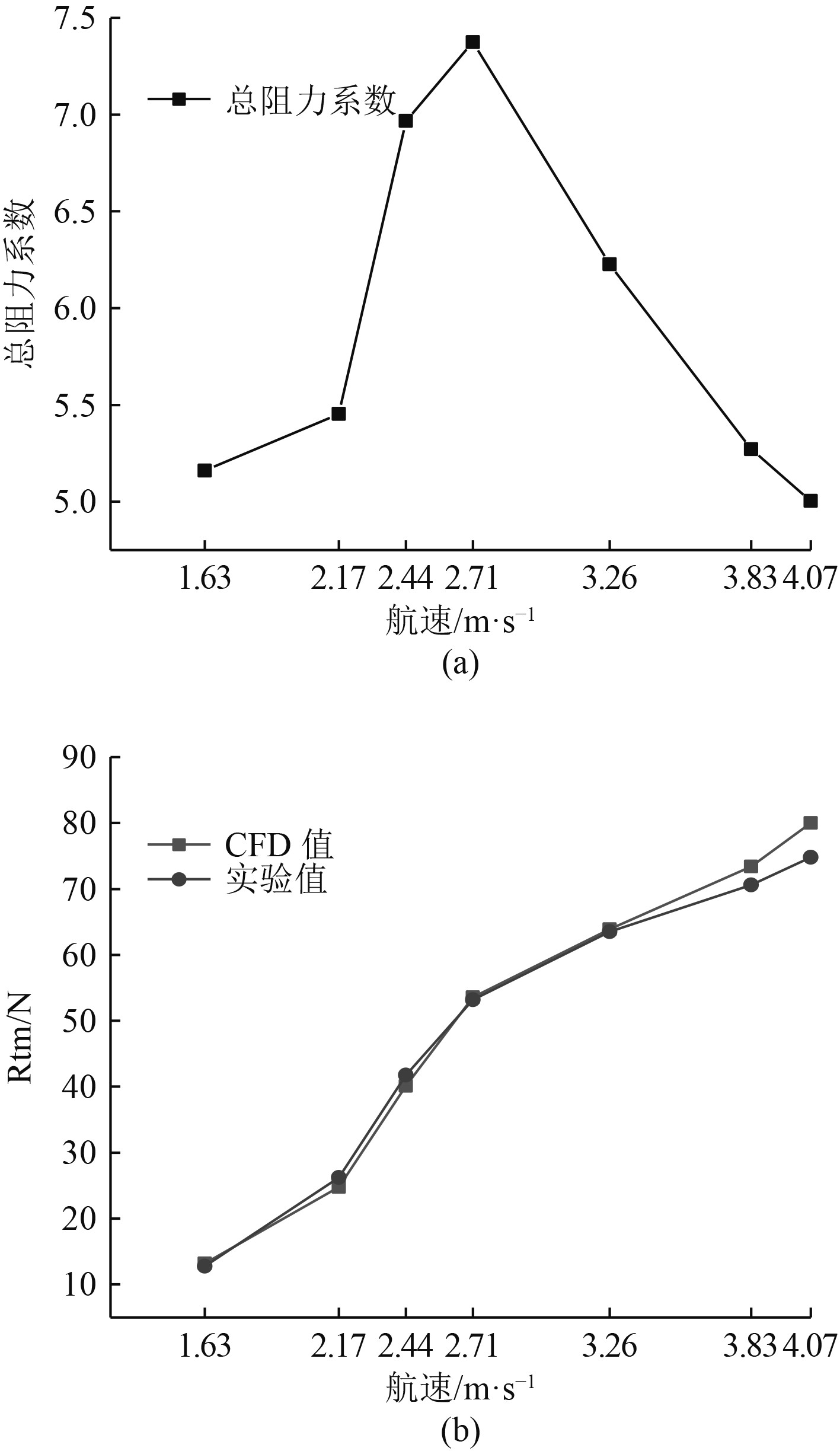
图 2 总阻力系数与航速的关系和CFD数值计算结果与实验计算的对比 Fig. 2 Effect of velocity on total drag coefficient and comparison of experimental and CFD calculated values |
由表5可知,通过CFD计算双体船的船模总阻力与通过试验的方法计算的双体船总阻力结果误差较小,计算的误差最大为6.9%,说明使用CFD软件STAR-CCM+软件计算船舶阻力的可靠性。通过图2(b)可以看出,CFD数值计算的结果和试验计算结果的变化趋势较为一致,根据图2(a),在双体船航速Vm=2.71 m/s时,总阻力系数达到峰值,之后随着航速的增加而逐渐减小,也表明双体船在高航速下具有良好的阻力性能。
2.2 实尺度法计算船舶阻力实尺度法计算双体船的总阻力,选取表2中双体船的航速进行计算,通过使用STAR-CCM+软件,以及二因次换算法和三因次换算法对双体船的总阻力和总阻力系数计算。
由于船模和实船不能同时满足雷诺数和傅汝德数相等,所以船舶阻力仅仅在保持傅汝德数相等的情况下进行计算,并做出适当假定进行计算[8];由于二因次换算法(傅汝德法)将粘压阻力(Rpv)和兴波阻力(Rw)两种不同的性质的力合并进行计算,但对于肥大的船将出现ΔCf为负值等问题,因此休斯20世纪50年代提出了三因次换算法[8]。经过20多年的发展,在实用上已趋于完善,在1978年的ITTC会议上推荐为标准的换算方法。
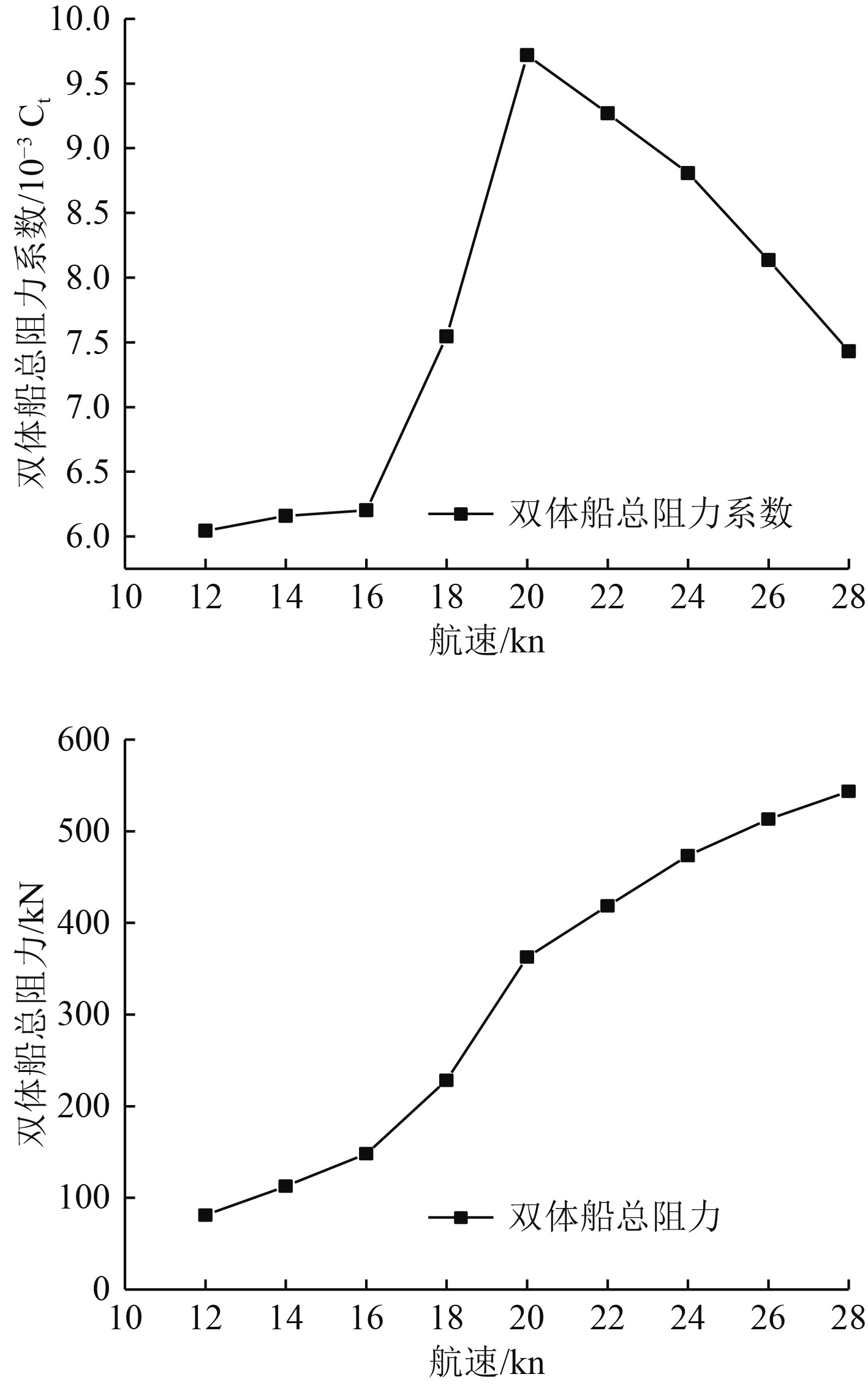
使用STAR-CCM+实尺度法计算双体船总阻力和总阻力系数与航速的关系如图3所示。
|
图 3 实尺度法计算的双体船总阻力系数和总阻力与航速的关系 Fig. 3 Catamaran total drag coefficient and total drag versus for catamaran by full-scale calculation |
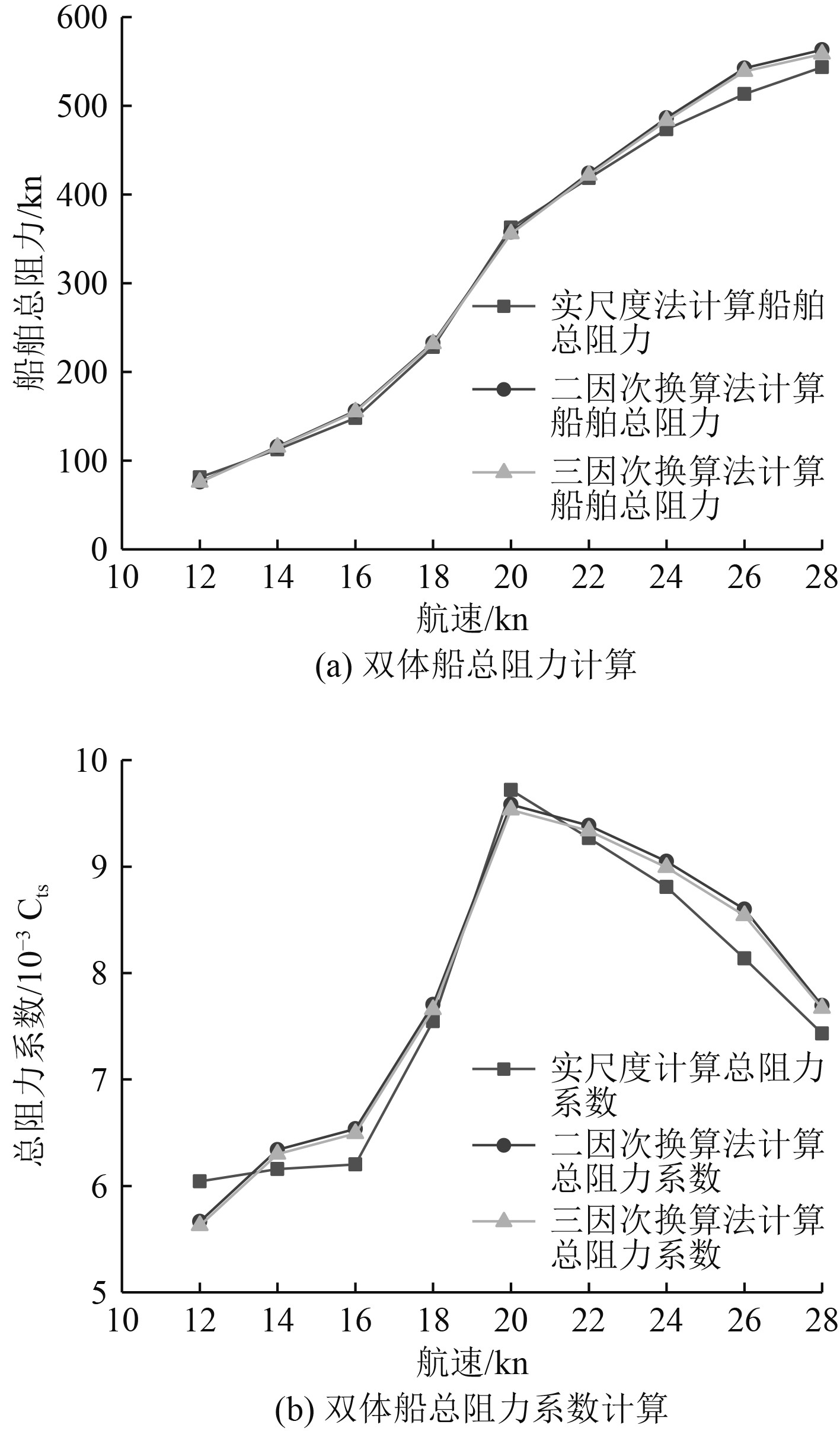
使用二因次换算法、三因次换算法和实尺度法计算双体船在不同航速下的总阻力与总阻力系数的关系进行对比,其关系如图4所示。
|
图 4 总阻力系数和总阻力与航速的关系 Fig. 4 Total drag coefficient and total drag versus velocity |
由图4(a)可知,双体船总阻力的计算结果满足工程上的计算精度的要求。由图4(b)可以看出,双体船的总阻力系数在Vs=20 kn时总阻力系数达到峰值,随后随着航速的增大而逐渐减小,表明双体船在高航速情况下阻力性能的优越性。
工程上多运用二因次换算阻力的结果为准,使用三因次换算法和STAR-CCM+计算的结果与二因次换算法计算结果的对比保证了使用STAR-CCM+对双体船阻力预报结果的准确性。
3 基于STAR-CCM+的双体船波浪增阻系数计算根据已有的研究表明[9],影响波浪中阻力的增加值的因素主要有船型和波浪两方面,本文主要对不同波长与垂线间长之比(
某一瞬时自由面波形图如图5所示,所取波幅h=0.55m(λ/L=0.5)。

|
图 5 波幅0.55 m时的自由液面波形图 Fig. 5 Free surface waveform at h=0.55 m |
双体船在计算工况下的阻力和波浪增阻系数的计算结果如表6所示。
|
|
表 6 阻力值和总阻力系数计算结果 Tab.6 Calculation of the drag values and the total drag coefficient |
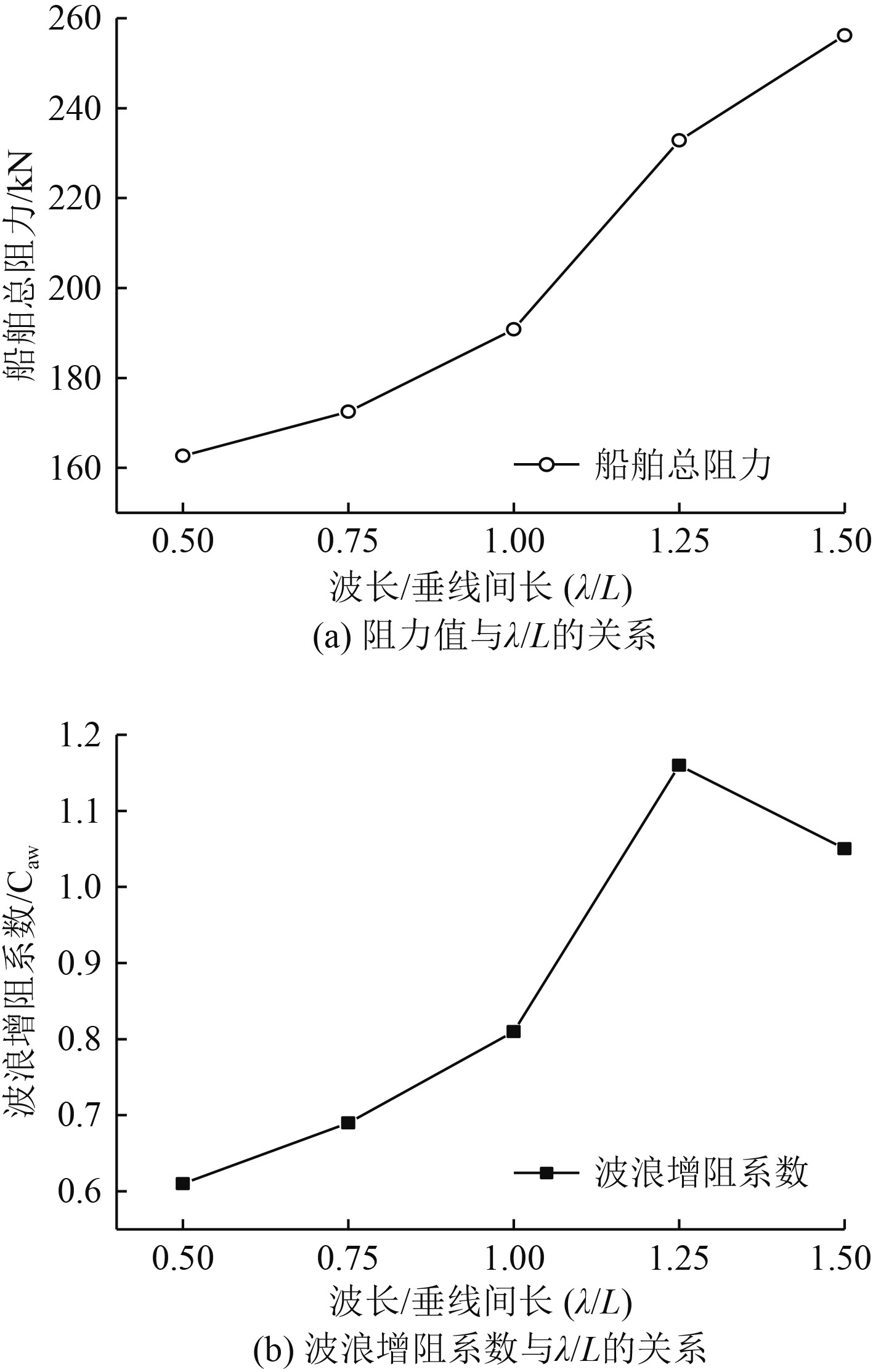
由图6可以看出,在双体船航速一致的情况下,波浪增阻系数随着波长的增加而增加,在λ/L=1.25时,其波浪增阻系数达到峰值,在之后的1.25
|
图 6 双体船波浪阻力值及阻力系数变化曲线 Fig. 6 Curves of wave resistance value and resistance coefficient |
本文通过二因次换算法、三因次换算法以及基于CFD的STAR-CCM+方法对双体船在静水航行的总阻力和阻力系数进行计算,并对规则波下的双体船的波浪增阻进行计算,得出如下结论:
在双体船总阻力系数和阻力的计算上,二因次换算法和三因次换算法在计算的差别上相差不大,基于STAR-CCM+的双体船总阻力系数计算上,其增长趋势与二因次换算法和三因次换算法相同,总阻力系数的计算误差在7%以内;在总阻力的计算上,3种方法计算的结果大致相同;在双体船波浪增阻的计算上,其波浪增阻系数在λ/L=1.25时达到峰值。
通过计算表明,使用基于CFD的STAR-CCM+软件对双体船的阻力性能进行计算具有计算速度快、计算精度高的特点,可以在双体船阻力估算中推广应用,并在双体船得船型优化上提供数据支持。
| [1] |
张进峰,石志超,项勇. 寒潮大风浪中船舶失速数值计算[J]. 大连海事大学学报, 2014, 40(2): 39-42. ZHANG Jin-feng, Shi Zhi-chao, Xiang Yong. Numerical calculation of ship speed loss in rough seas with cold wave[J]. Journal of Dalian Maritime University, 2014, 40(2): 39-42. |
| [2] |
CHUANG Zhenju, STEEN Sverre. Speed loss of a vessel sailing in oblique waves[J]. Ocean Engineering, 2013, 64. |
| [3] |
HIDEO O, HIDEAKI M. Evaluation of added resistance in regular incident waves by computational fluid dynamics motion simulation using an overlapping grid system[J]. Journal of Marine Science and Technology, 2003, 8(2). |
| [4] |
蒋志鹏. 耙吸挖泥船航速与拖力预报研究 [D].上海上海交通大学, 2012. JIANG Zhi-peng. Study of ship speed & drag force prediction on trailing suction hopper dredger[D]. Shanghai: Shanghai Jiao Tong University, 2012. |
| [5] |
魏可可, 高霄鹏. 基于STAR-CCM+对5415船模的阻力预报[J]. 兵器装备工程学报, 2016, 37(9): 157-161. WEI Ke-ke, GAO Xiao-peng. Resistance prediction of 5415 ship model based on STAR-CCM+[J]. Journal of Ordnance Equipment Engineering, 2016, 37(9): 157-161. |
| [6] |
程红蓉, 李百齐. 关于 EEDI 衡准方法的比较研究[J]. 中国造船, 2012, 53(3): 103-109. CHENG Hong-rong, LI Bai-qi. Comparison about EEDI criterion methods[J]. Shipbuilding of China, 2012, 53(3): 103-109. |
| [7] |
BLANCA P, MUK-PAVIC E, PATRICK F. Detailed analysis of the flow within the boundary layer and wake of a full-scale ship[J]. Ocean Engineering, 2020, 218(2020): 108022.
|
| [8] |
盛振邦, 刘应中. 船舶原理[M].上海: 上海交通大学出版社, 2004.
|
| [9] |
谢云平, 高天敏, 谢蔚刚, 等. M型风电运维船船型设计与波浪增阻及耐波性能[J]. 船舶工程, 2020, 42(6): 26-31. XIE Yun-ping, GAO Tian-min, XIE Wei-gang, et al. Hull form design, added resistance in wave and wave resistance performance of M-type wind power maintenance vessel[J]. Ship Engineering, 2020, 42(6): 26-31. |
 2021, Vol. 43
2021, Vol. 43
