严重的波浪砰击大概率会造成船体外飘结构的损伤,传统的二维切片法与三维局部船首入水往往不能考虑船舶相对运动特性,对砰击载荷进行较为准确的预报。Karman[1]最先对二维楔形体结构入水进行研究,Wagner[2]在Karman[1]的基础上发展为近似平板理论,Gavrilenko[3]和Kubenk[4]在考虑流体的可压缩性方面作了不同程度的研究,Vinje等[5]研究了结构三维外形会对砰击压力的影响,杨凡[6]对美国船级社ABS[7]给出的三维修正因C3D进行了公式倒推与数值仿真验证。虽然三维方法使得结果得到了精进,但其预报出的砰击载荷数值,及载荷分布规律与真实航行过程中船舶监测到的波浪砰击差异较大。传统的楔形体简化,局部船首垂直入水模拟等方法不能较好的解释波浪翻卷、破碎以及波浪间的相互作用等问题,需要考虑砰击发生时复杂的非线性因素。
1973年Ochi等[8]根据冲量理论,提出一种基于试验值回归采用保角变换法计算砰击压力系数的方法。Kapsenberg[9]对随浪试验和顶浪模型试验的结果进行了比较,田喜民等[10]采用三维Rankine源法求解船体在不规则波中的砰击压力峰值。Ley[11]基于砰击模型试验对游艇的分段模型在规则波以及极限不规则波工况下甲板上浪载荷进行了研究;Ole等[12]对Ro-Ro船的首部拍击荷载的直接计算方法进行了研究,与试验结果一致性较高,由于理论方法在解决实际工程问题时具有一定的局限性,而试验研究的成本相对较高,因此数值计算在砰击问题研究中越来越受到重视。司海龙等[13]将船舶运动时域预报方法与CFD流体数值计算技术相结合,研究了船波相对位置对砰击载荷的影响。Kwang-Jun Paik等[14]使用CFD方法计算了船体在规则波中的运动载荷,并使用单向和双向流固耦合方法计算了结构响应。陈月[15]基于STAR-CCM+与Abaqus进行外部耦合,联合仿真,研究了流体-结构弹性耦合相互作用对波浪砰击载荷下船首船尾结构响应的影响。
本文基于STAR-CCM+软件的重叠网格方法,嵌入六自由度结构刚性运动模型,即DFBI(Dynamic Fluid Body Interaction,DFBI)运动;只考虑5阶斯托克规则波下首外飘型船舶纵摇及垂荡2个自由度运动,以劳氏船级社规范海况为蓝本设计了3组工况,对规则波作用下的首外飘型船舶波浪砰击载荷CFD预报,并研究不同海况下在外飘结构上砰击载荷特性与分布规律。应用VOF方法根据各时刻的流体所占空间与网格空间的比函数α构造和捕捉自由液面。本文方法可考虑船舶航行中非线性的波浪环境因素,对船体砰击荷载进行预报。
1 CFD理论公式 1.1 六自由度运动方程质心的平移方程将根据全局惯性坐标系设定,表达式为:
| $ \frac{{{\rm{d}}\left( {{m_B}{{\bf{v}}_C}} \right)}}{{{\rm{d}}t}} = {{\boldsymbol{F}}_B}{\text{。}} $ | (1) |
3个角动量方程为:
| $ \frac{{{\rm{d}}\left( {{{\boldsymbol{I}}_C} \cdot {w_B}} \right)}}{{{\rm{d}}t}} = {{\boldsymbol{M}}_C} {\text{,}}$ | (2) |
力和力矩为:
| $ {F_B} = \int\nolimits_S {\left( {T - pI} \right) \cdot n{\rm{d}}S + } {m_B}g{\text{,}} $ | (3) |
| $ {M_C} = \int\nolimits_S {\left( {r - {r_c}} \right) \times \left( {\left( {T - pI} \right) \cdot n} \right){\rm{d}}S} {\text{。}}$ | (4) |
式中:mB为结构质量;vC为物体质心处的速度;IC为物体的惯性矩;wB为角速度;FB和MC为作用在结构上的力和力矩。
1.2 流体控制方程对于粘性的三维流动,假定流动由RANS方程控制,其中湍流效应包括涡流模型和粘性模型。
质量守恒:
| $ \frac{{\text{d}}}{{{\text{d}}t}}\int\nolimits_V {\rho {\text{ d}}V + \int\nolimits_S {\rho ({\boldsymbol{{{v}}}} - {{{{\boldsymbol{{v}}}}_b}}) \cdot {\boldsymbol{{{n}}}}{\text{ d}}S = 0} }{\text{,}} $ | (5) |
动量守恒:
| $ \begin{split} & \frac{{\text{d}}}{{{\text{d}}t}}\int\nolimits_V {\rho {\boldsymbol{v}}{\text{ d}}V + } \int\nolimits_S {\rho {\bf{v}}({\boldsymbol{v}} - {{\boldsymbol{v}}_b}) \cdot {\boldsymbol{n}}{\text{ d}}S = }\\ & \int\nolimits_S {({\boldsymbol{{T}}} - p{\boldsymbol{I}}) \cdot {\boldsymbol{n}}{\text{ dS}}} + \int\nolimits_V {\rho {\boldsymbol{b}}{\text{ d}}{V}}{\text{。}} \end{split} $ | (6) |
式中:
STAR-CCM+软件采用的附加阻尼项是基于非线性粘性阻尼消波项:
| $ S_Z^{\text{d}} = \rho \left( {{f_1} + {f_2}{\text{|}}\omega {\text{|}}} \right)\frac{{{e^k} - 1}}{{e - 1}}\omega {\text{,}}$ | (7) |
| $ {{k}} = {\left( {\frac{{x - {x_{sd}}}}{{{x_{ed}} - x}}} \right)^{n\delta }}{\text{。}} $ | (8) |
其中:
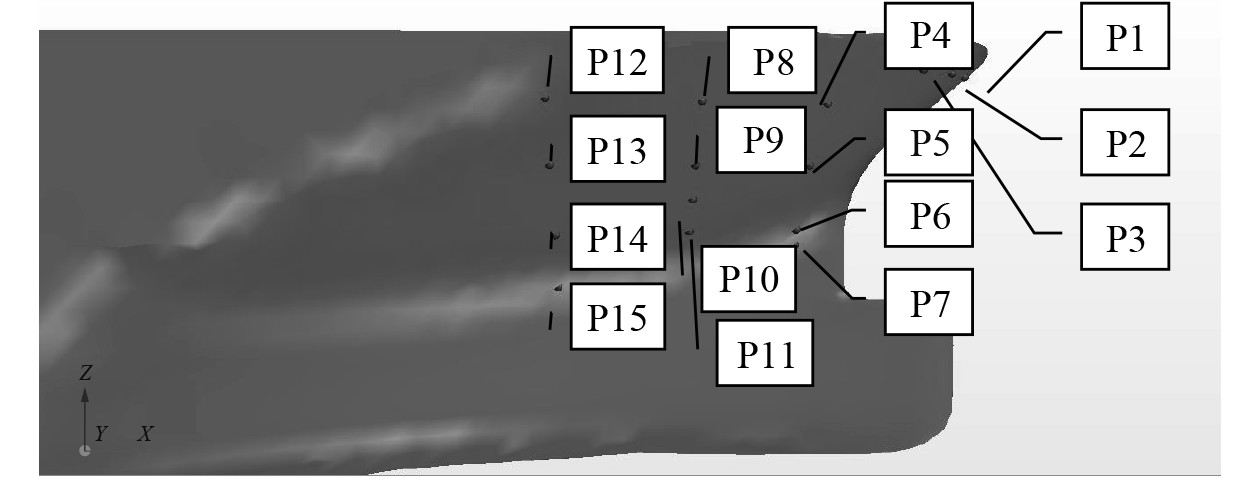
以3800 PCTC船作为研究对象,船型参数如表1所示,3800 PCTC如图1所示,监测点如图2所示。
|
|
表 1 船型参数 Tab.1 Ship type parameters |

|
图 1 3800 PCTC全船湿表面模型图 Fig. 1 3800 PCTC full ship wet surface model diagram |
|
图 2 监测点局部布置示意图 Fig. 2 Schematic diagram of local layout of monitoring points |
|
|
表 2 计算工况参数 Tab.2 Calculation conditions parameters |
图3 (a)为工况1中(船首顶端)P1砰击载荷时历曲线与船体监测点垂向运动速度曲线,其速度曲线近似正弦曲线,且速度幅值也较小。此时砰击的发生,对船体运动速度的改变近乎为零。图3 (b)为工况2中P1测点砰击压力和速度的时间变化对比曲线。其载荷曲线与速度曲线均产生了较大变化;在船舶运动到15 s时,船首部发生了明显的砰击现象,其压力值为400 kPa,随后砰击压力迅速降低,且有一段较长时间的稳定低载荷,而后船体首部也有明显的负压现象,在负压极值处也有一段平滑值。相较于工况1,速度曲线略为陡峭,但垂向速度最大值处速度曲线仍较平缓。图3 (c)为工况3中P1测点砰击压力和速度的时间变化对比曲线。从图中可知,由于工况3的海况更为恶劣,载荷曲线与速度曲线更为陡峭砰击发生时,压力值较工况1、工况2下的压力值都有所增大,P1测点的压力峰值为580 kPa,随后砰击压力同样在逐渐降低,也具有延时现象。各监测点速度曲线在船体入水极大值后,速度有了肉眼可见的极大畸形,说明高海况对船体运动状态产生了不可忽视的影响。

|
图 3 船首P1点砰击压力和运动速度对比曲线 Fig. 3 Comparison curve of slamming pressure and speed at P1 point of bow |
基于LR规范,波浪砰击载荷Pbf根据下式计算:
| $ P_{b f}=0.5\left(K_{k f} V_{b f}^{2}+K_{r \nu} H_{r v} V_{r v}^{2}\right){\text{,}} \quad \mathbf{k N} / \mathbf{m}^{2}{\text{。}} $ | (9) |
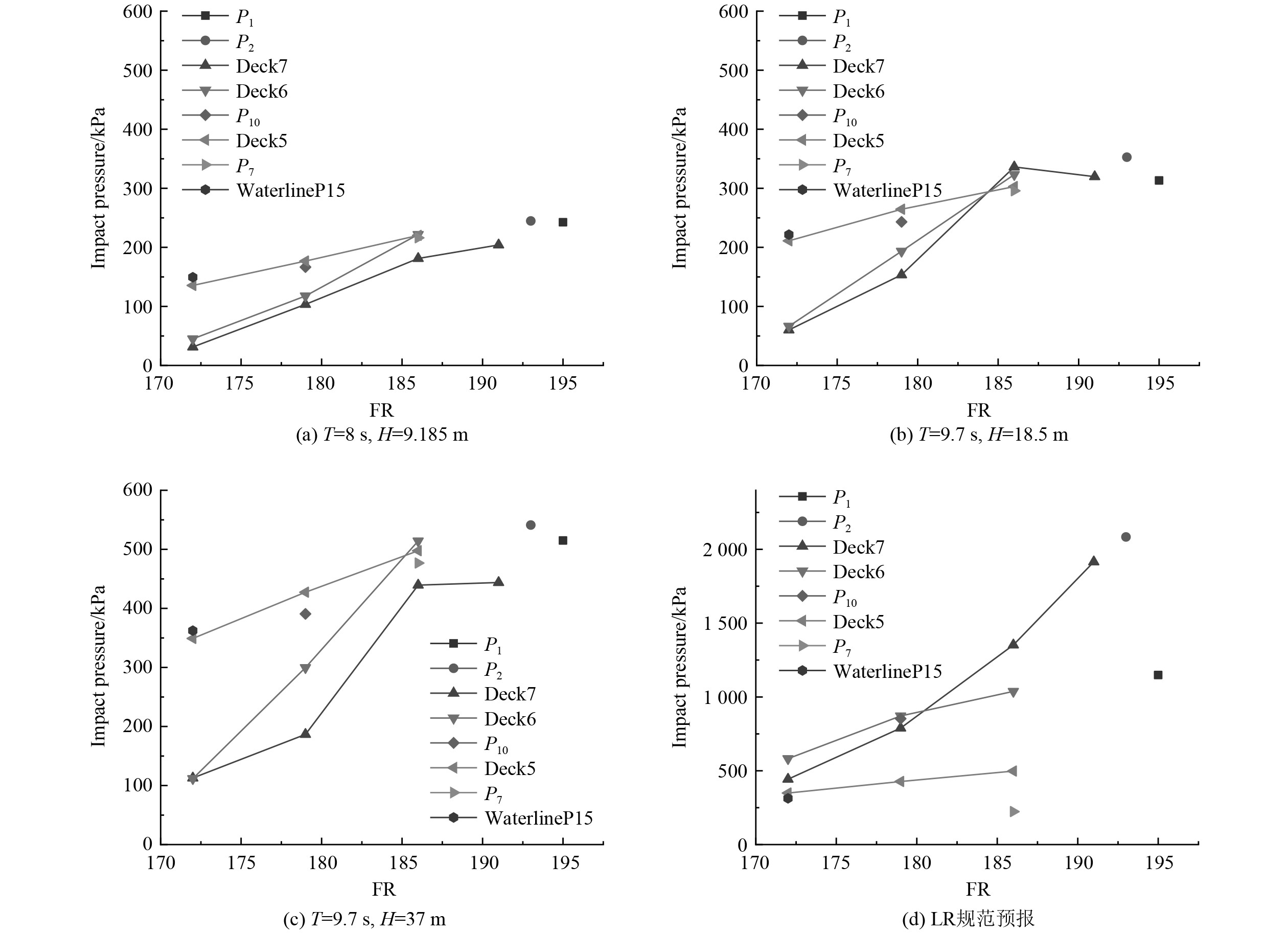
图4(a)所示低海况为T=8 s,H=9.185 m时,FR170~190站位,Deck7,Deck6以及Deck5层甲板监测点压强峰值分布,P1,P2,P7不在甲板与站位交界处,故单独列点;监测点压强峰值均随着监测点距离船首距离的增加而减小,距离船首越近,砰击载荷峰值越大;但同一站位,底层甲板砰击载荷大于高层甲板监测点;说明此时低层甲板砰击载荷受水平受动水波压力影响越大。图4(b)所示中等海况波浪为T=9.7 s,H=18.5 m时,FR170-190站位,Deck7,Deck6以及Deck5层甲板监测点压强峰值曲线。相似于T=8 s,H=9.185 m时同层甲板,各监测点压强峰值均随着监测点距离船首距离的增加而减小,距离船首越近,砰击载荷峰值越大。但同一站位,底层甲板砰击载荷低于高层甲板监测点,说明此时FR186站位监测点砰击载荷水平受动水波压力影响开始减小,监测点与水面垂向船波相对运动对砰击载荷开始增大。图4(c)所示高等海况波浪为T=9.7 s,H=37 m时,FR170-190站位,Deck7,Deck6以及Deck5层甲板监测点压强峰值曲线。不同于T=9.7 s,H=18.5 m时同层甲板,各监测点压强峰值呈现出更为强烈的非线性趋势。同一层甲板随着监测点距离船首距离的增加而减小,距离船首越近,砰击载荷峰值越大。以FR186站位监测点砰击载荷极值为例:Deck6介于Deck7与Deck5之间,受船波垂向相对砰击与水平动水波压力综合响应,情况更为复杂,非线性更为强烈。但同一站位,低层甲板砰击载荷呈现出一定的线性关系,而高层甲板Deck7呈现出强烈的非线性趋势。由表3可知,P7,P15两个点在较高海况下砰击载荷反而比规范值要大,这可归因于复杂的船波相对运动,结构校核时应比规范要保守才能保证结构安全。
|
图 4 各层甲板监测点砰击载荷极值分布 Fig. 4 Distribution of slamming load extreme value of monitoring points on each deck |
|
|
表 3 砰击载荷汇总 Tab.3 Summary of slamming load |
船波垂向相对运动对砰击载荷至关重要。本文基于LR规范,对垂向砰击相对速度进行预报。
| $ {V_{{\text{bf}}}}{\text{ = }}\sqrt {V_{thbf}^2 + 2{m_1}\ln ({N_{bf}})} {N_{{\text{bf}}}} > 1{\text{,}} $ | (10) |
| $ V_{{\rm{bf}}}=0{\text{,}} \qquad {N}_{\text {bf }}<1{\text{,}} $ | (11) |
同时,根据垂向砰击入水简化公式(11),以P1点为例,求出砰击系数,以此来验证滑动砰击载荷Ps与垂向砰击载荷Pi的关系:
| $ K{\text{ = }}\frac{P}{{0.5\rho {V^2}}} {\text{。}}$ | (12) |
|
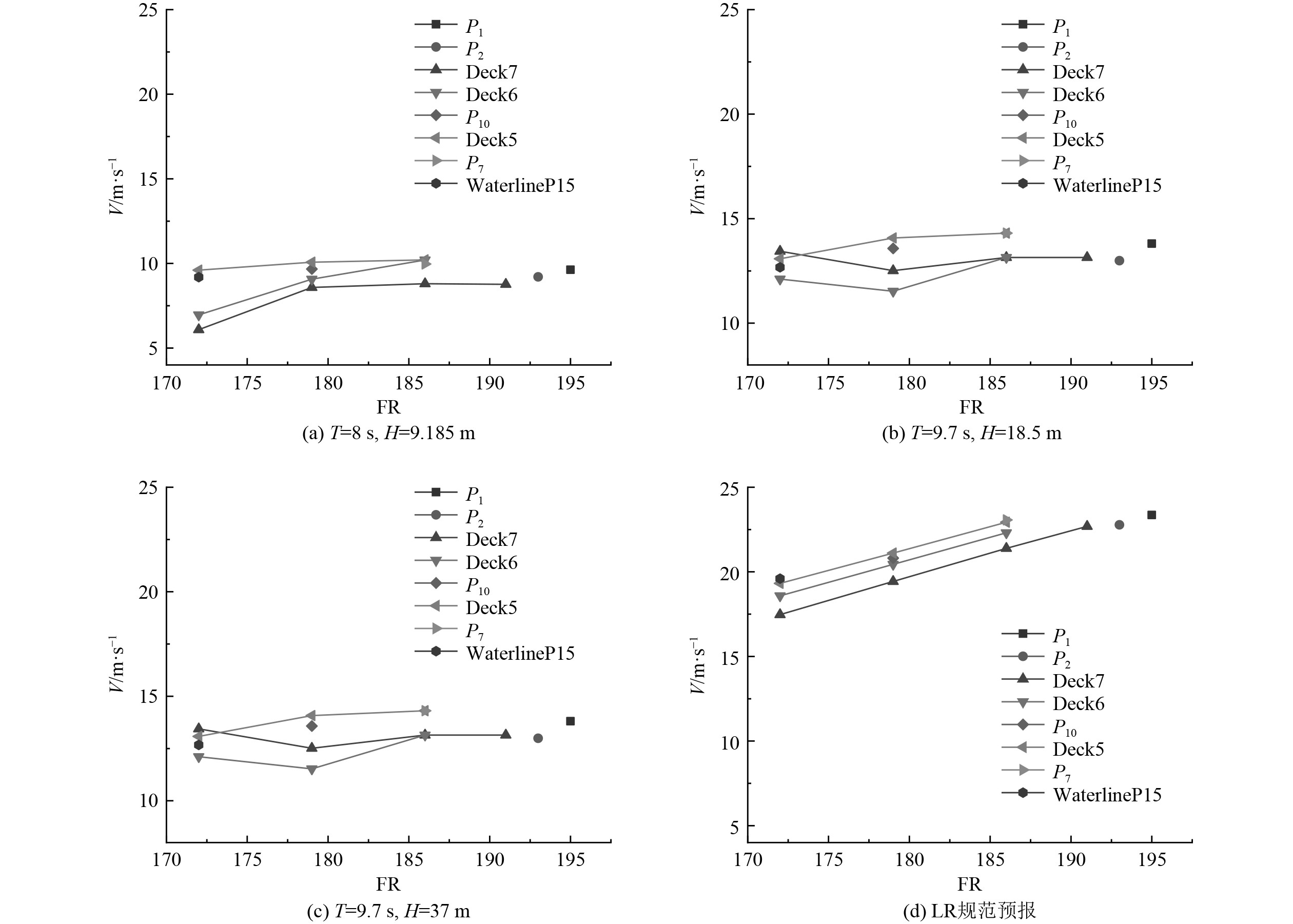
图 5 各层甲板监测点砰击发生垂向船波相对速度极值Vbf分布 Fig. 5 Distribution of the extreme value of Vbf from the slamming of the monitoring points |
|
|
表 4 P1砰击系数K Tab.4 Slam coefficient K for P1 |
1)LR 规范值沿船长方向呈线性增加,而本文中砰击发生速度极值呈非线性规律:中高海况时的高层甲板增加率为先减小后增大,最终趋于平稳;而低海况时,增长较平稳,其分布规律与规范较为吻合。
2)根据砰击公式,对垂向砰击系数进行求解,随着海况的增加,砰击载荷与垂向砰击相对速度均增大,但垂向砰击载荷系数随之减小,极限海况下的砰击系数更接近三维修正理论系数0.71[7]修正后的LR-Pi值。
3)低海况时,FR172~FR186砰击发生时设计速度都是沿船高方向减小。其原因是低海况时,对船体运动状态改变较小,而此时的船舶垂向相对运动较小,砰击载荷中的水平滑动载荷Ps所占比重较高海况要大。
4)高海况时,本文计算结果比LR 规范值略小。当计算点高度相同时,越靠近船首差异较明显;除却受负压与甲板上浪影响较为严重的P12点,规范值均大于本文值。
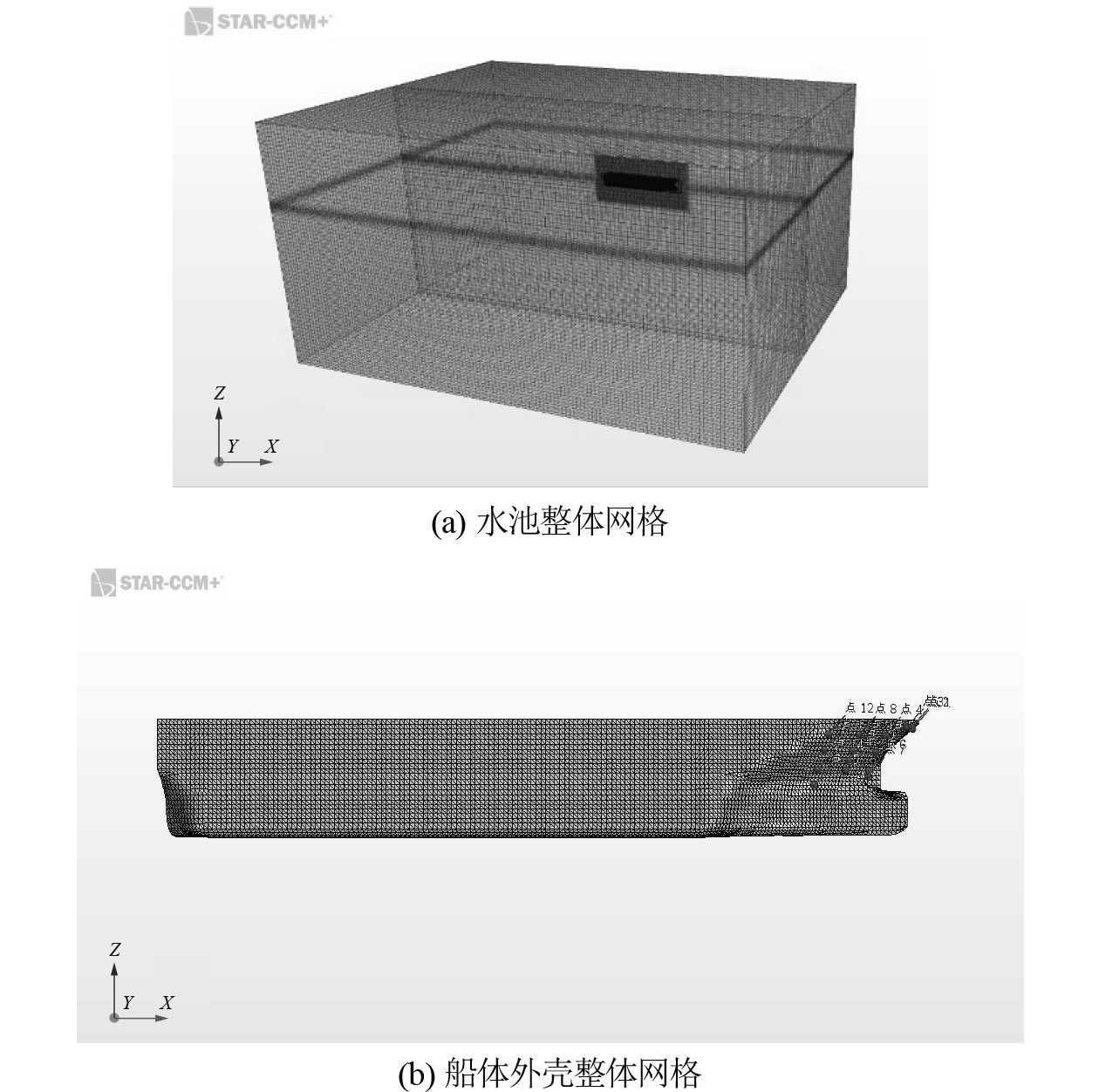
4 网格收敛性验证本文选取实尺度模型进行建立砰击载荷预报,该三维数值水槽的模型示意图,边界条件如图6所示。设定坐标原点位于船首FR186基线对称中心处。X轴正向与波浪传播方向相反,Y轴正方向与船体横向方向一致,Z轴沿的吃水方向。数值波浪水池1000 m,宽800 m,高520 m,静水面以上的高度为170 m,入口边界位于X= 300 m位置处,尾部消波区从压力出口沿x正方向300 m,在水池试验区域的x=0处位置设置一虚拟浪高仪来获取波浪的时历。

|
图 6 三维数值水槽的模型示意图 Fig. 6 Schematic diagram of the three-dimensional numerical water tank model |
本文首先选取劳氏船级社给出的设计工况,以波高为9.185 m,周期为8 s为输入参数对斯托克斯5阶规则波进行造波测试,采用3种密度由疏到密的网格划分方式对该波浪进行了数值模拟,网格参数如表5所示。3条波形曲线非常接近,此时网格密度的增加并不能显著提高计算精度,因此本文选取尺寸A对数值波浪水池网格划分,波形验证曲线如图7所示。
|
|
表 5 测试网格分类 Tab.5 Mesh Type |

|
图 7 网格收敛性验证曲线 Fig. 7 Verification curve of grid convergence |
本文3800 PCTC计算模型网格划分如图8所示。背景区域基础尺寸设为8.0 m,网格生成器类型选为:表面重构,自动表面修复,切割体网格网格单元且为各相同性;液面附近进行两层液面网格加密,x:y:z=4:4:1,第1层水面加密最小z向尺寸同波形验证一样,设为0.5 m,第2层加密z=1 m,运动加密区域,采用最小液面加密区相同尺寸;为减小网格间运动插入变量产生错误,重叠区域网格尺寸与运动加密区尺寸一致,减运算区域基础尺寸设为0.5 m,船体最小表面尺寸取0.005 m,相较于背景区域网格生成器多选棱柱层网格生成器,厚度为0.1 m,时间步长为0.01 s。
|
图 8 网格示意图 Fig. 8 Schematic diagram of grid |
当砰击发生时,自由液面会有波浪破碎,液面飞溅等强烈的非线性波面环境,会使水质点以更快的相对速度与外飘结构发生砰击。同时,自由液面的非线性变化也会使外飘结构砰击位置发生改变,结构应力集中现象也会随之改变;所以有必要对波浪砰击中,自由液面的变化特征进行研究。然而,传统的波浪砰击研究方法很难实现,对水质点,自由液面变化的监测,而本文所使用的CFD方法,可以较好对二者进行监测。T=8 s,H=9.185 m海况下的自由液面如图9~图11所示。

|
图 9 工况1自由液面形态时刻图t=4~6 s(外飘入水) Fig. 9 Condition 1 Free liquid surface shape time chart t=4~6 s (outside floating into water) |
|
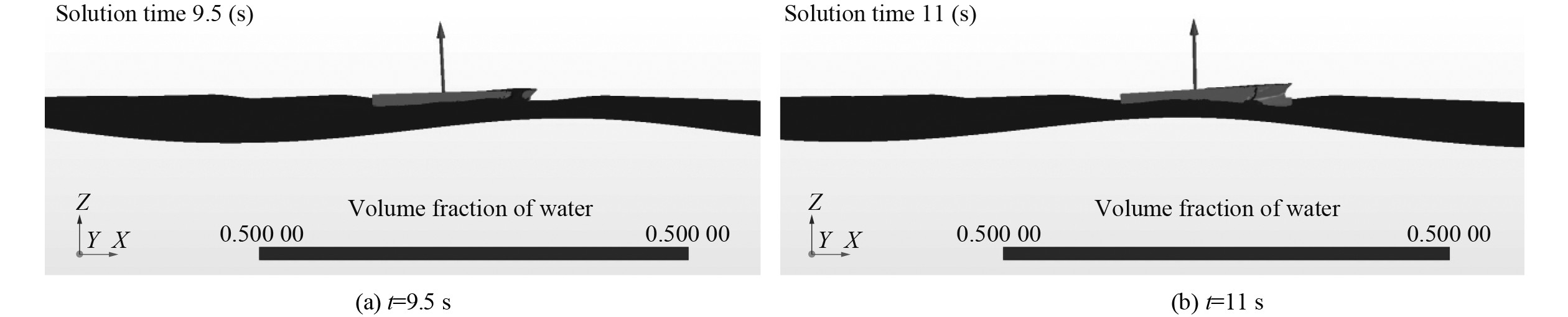
图 11 工况1自由液面形态时刻图t=9.5~11 s (船首抬升-完全出水) Fig. 11 Condition 1 Free liquid surface shape time chart t = 9.5~11 s (the bow is raised-full water) |
|
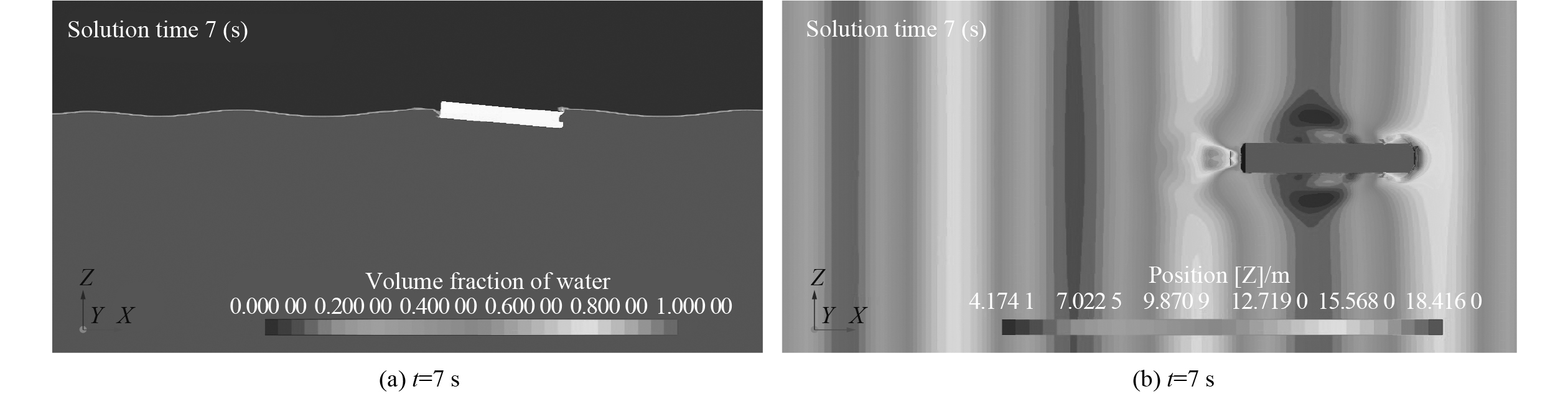
图 10 工况1自由液面形态时刻图t=7 s(入水砰击-甲板上浪) Fig. 10 Condition 1 Free liquid surface shape time diagram t=7 s (water slamming-wave on deck) |
t =9~11 s时,在迎浪航行中船首已经发生甲板上浪,此时船首抬升。靠近平行中体监测点,如P12遭受的波浪载荷主要为甲板上浪砰击,特点为数值较小,载荷曲线较缓和,但之后会有较大的负压现象,与P1~P3等监测点不同,此时的负压值大于正压砰击(正压31.31 kPa,负压−61.65 kPa),在传统的砰击理论研究中,这种现象难以进行解释与载荷预报。
4.2 船首外飘砰击压力云图图12为T=8 s,H=9.185 m海况下船首外飘砰击压强云图。在t=4 s和t=11 s时下层甲板的载荷分布明显中间有一个载荷较小区间,再一次证实前文中关于监测点压强沿甲板高度与船长方向的分布规律。

|
图 12 T=8 s,H=9.185 m时船首外飘压强云图 Fig. 12 Strong cloud image of floating pressure outside the bow at T=8 s and H=9.185 m |
t =4~6 s时,船体经历纵倾最大角度到外飘船首入水发生砰击;t =7 s时发生甲板上浪现象;t =9~11 s时船体穿浪而出,船首开始抬升,而此时靠近船首尾部的P12,P13开始承受较大的动水压力与负压。3组海况中,正压与负压分别为31.31 kPa,60.06 kPa,112.73 kPa和−61.65 kPa,−96.46 kPa,−183.94 kPa,故在结构校核时应特别考虑这几个点的负压。
5 结 语本文对规则波作用下船首外飘波浪砰击载荷特性进行研究,通过选取LR规范中设计海况与极限海况的有义波高设计了3组( 低、中、高)规则波来进行计算,对船首外飘在波浪环境中砰击过程,自由液面变化,砰击载荷在外飘结构上分布以及载荷极值速度极值等非线性现象进行了分析,结论总结如下:
1)LR规范计算时并没有考虑球首等结构因素,船波相对运动状态等因素的影响。CFD数值仿真方法可以考虑更多的非线性因素,预报出砰击发生时的船波相对速度。
2)通过对比可知,LR仅考虑了某种极限海况,不能适用于每种海况。在低海况船舶高速或全速航行工况应重点关注滑行载荷Ps;在高海况下应重点关注垂向砰击载荷Pi,但在中海况则需要综合考虑,以往单一的考虑某单一方向,往往会导致较大的误差。
3)高海况时本文计算结果与规范预报较接近,但总体来说比LR规范值略小。当计算点高度相同时,越靠近船首差异较明显,随着到船首距离的增加,差异逐渐减小;除却受负压与甲板上浪影响较为严重的P12
4)通过本文方法预报波浪作用于船首外飘的砰击载荷,相较于势流方法可以准确描述高度非线性自由液面流动,还可以得到详细的流场数据如速度场、压力场等,可视化特性较强。
| [1] |
KARMAN V. The iMP act onseaplane floats during landing[M]. NACA, No. 321, 1929.
|
| [2] |
WAGNER V H. Phenomena associated with landing and sliding on liquid surfaces[J]. National Advisory Committee for Aeronautics, 1929, 321: 145-162. |
| [3] |
GAVRILENKO V N, KUBENKO V D. Plane problem of rigid body penetration intoa CoM pressible fluid. soviet applied meehanies[C]//International Applied Mechanics, 1985, 12(4): 345−352.
|
| [4] |
KUBELLKO V D, GAVRILENKO V N. Axsymmetric Problemofthe Penetration of rigid bodies into a coM Pressible fluid[J]. Soviet Applied Meehanies, 1987, 23(23): 152-158. |
| [5] |
VINJE T. BREVIG, NOULINEAR P. Two-dimensional ship motions[J]. ShipRes. Inst. Norway, 198l: 112-81.
|
| [6] |
杨凡. 大外飘船舶砰击载荷与结构强度研究[D]. 哈尔滨: 哈尔滨工程大学, 2017.
|
| [7] |
Guide for slamming loads and strength assessment for vessels [S]. American Bureau of Shipping, 2011.
|
| [8] |
OCHI M K, MOTTER L E. Prediction of slamming characteristics and hull responses for ship design[J]. Transactions SNAME, 1973, 81: 144-177. |
| [9] |
KAPSENBERG G K, VAN’T VEER A P, HACKETT J P, et al. Afterbody slamming and whipping loads[C]// SNAME Annual meeting. San Fransisco, 2003: 213−232.
|
| [10] |
田喜民, 邹早建, 王福花. 大型船舶外飘砰击压力计算研究[J]. 中国造船, 2014, 55(1): 1-10. DOI:10.3969/j.issn.1000-4882.2014.01.001 |
| [11] |
LEY J, OBERHAGEMANN J, AMIAN C, et al. Green water loads on a cruise ship [C]//Proc. 32th Int. Conf. on Ocean, Offshore and Arctic Engineering. 2013.
|
| [12] |
Mingkang Wu, HERMUNDSTAD O A. Time-domain simulation of wave-induced nonlinear motions and loads and its applications in ship design[J]. Marine Structures, 2002, 15(6).
|
| [13] |
司海龙, 陈震. 船首底部砰击压力概率预报方法研究[J]. 中国造船, 2012(1): 9-16. |
| [14] |
Kwang-Jun Paik, Pablo M. Carrica, Donghee Lee, Kevin Maki. Strongly coupled fluid–structure interaction method for structural loads on surface ships[J]. Ocean Engineering, 2009, 36(17).
|
| [15] |
陈月. 基于VOF法的波浪砰击载荷下大型船体结构耦合响应研究[D]. 镇江: 江苏科技大学, 2019.
|
| [16] |
Rules and Regulations for the classification of ships [S]. London: Lloyd's Register, 2014.
|
 2021, Vol. 43
2021, Vol. 43
