2. 中国人民解放军92474部队,海南 三亚 572018;
3. 海军装备部驻沈阳地区军事代表局,辽宁 沈阳 110015
2. No.42474 Unit of PLA, Sanya 572018, China;
3. Military Representative Bureau of Naval Armament Department Stationed in Shenyang Area, Shenyang 110015, China
伴流场的不均匀性是螺旋桨桨叶上不定常流现象的根源,在主艇体确定以后,尾操纵面决定着操纵性能并直接影响流场的均匀性[1],从尺寸上与主艇体相比,尾操纵面较小,但其与推进器的距离更近,潜艇尾流场和螺旋桨的进流面受其影响更直接。潜艇尾操纵面的建筑形式有多种,十字形尾舵是现代潜艇常见的布置形式,一般都由稳定翼和舵翼组成;还有一种“X”形尾操纵面,是指4个尾翼呈“X”形正交布置,舵轴中心线与艇体的中纵对称面成45°夹角的操纵面,其可动部分为X舵,在采用X舵的潜艇中一般仅有舵没有稳定翼,即全动舵[2]。德国设计的“海豚”级潜艇在尾操纵面的水平方向上加设了稳定翼,“海豚改”则是在垂向上布置了一个稳定翼。这为本文接下来研究的舵翼分离型尾操纵面提供了思路,从考虑操纵性和尾流场的均匀性出发,可以将传统的十字舵稳定翼和转动舵在空间分离,变为全动舵的X舵尾操纵面,或者X舵+稳定翼尾操纵面,并简单分析这3种尾操纵面潜艇的水动力和尾流场。
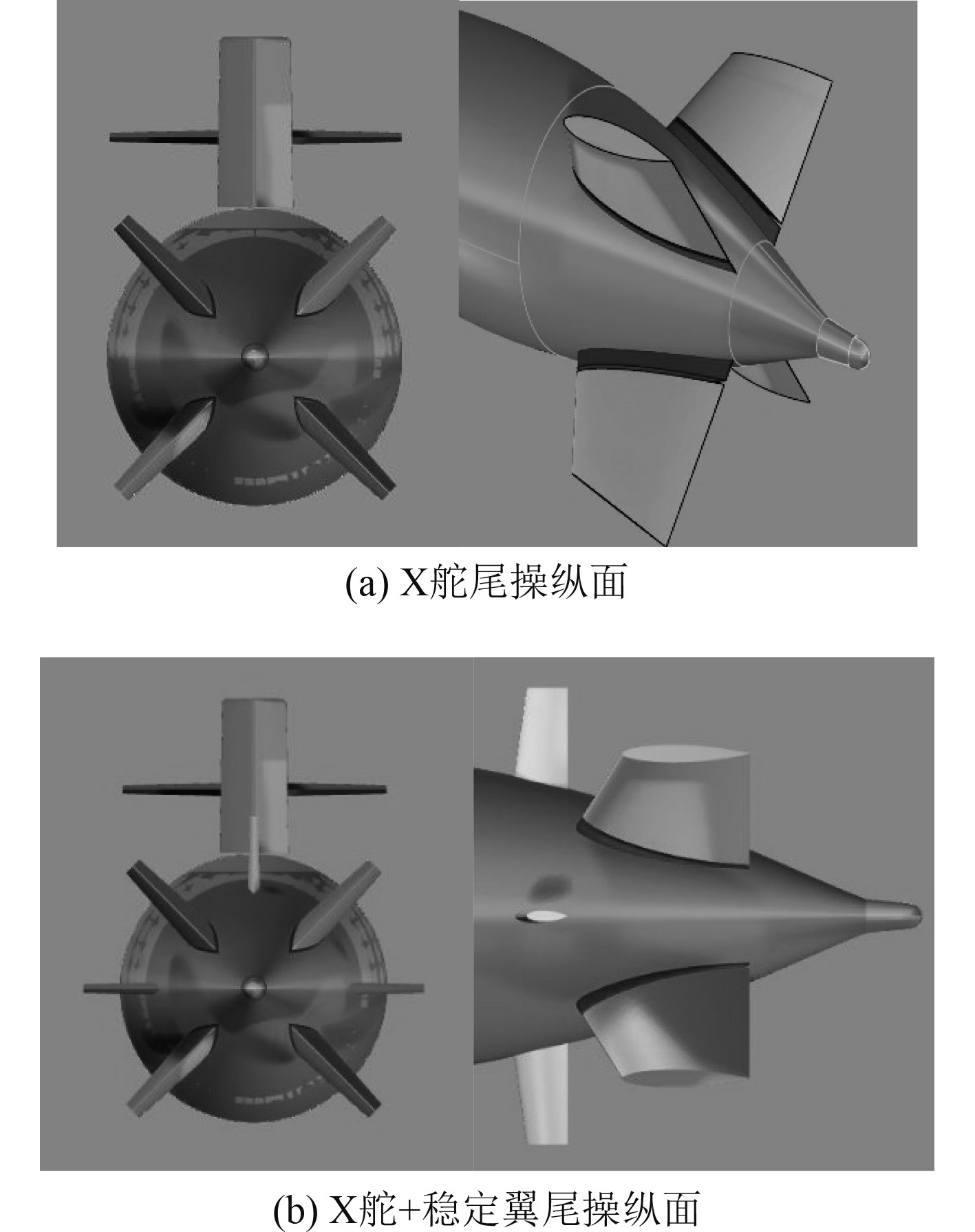
1 舵翼分离型尾操纵面原理第1种舵翼分离的方式为:在不改变舵型的基础上将带稳定翼的十字舵变成全动的X舵,并保证X舵的舵面积和原来十字舵的舵面积相等。第2种分离方式则是在X舵的基础上增加稳定翼,在设计稳定翼时,主要考虑了几个原则:1)不额外增加舵翼面积,因为舵与稳定翼的面积对潜艇稳定性和水动力性能的影响较大;2)不移动原操纵面的纵向布置位置,保持尾舵与水动力中心的距离大致不变。基于以上考虑,选择使全动舵面积的一部分“转化”为稳定翼面积,其中每一个稳定翼面积为原舵面积的20%,X舵面积缩减为原来的80%;稳定翼的翼型与舵翼型相同,翼展与舵翼的展长相等;为了避免稳定翼的水动力效果与舵发生重叠,将稳定翼完全置于舵前,投影面积恰好不重叠;3)从稳定性的角度考虑,潜艇在水平面内的动稳定性应比垂直面的动稳定性要求低,因此垂直面只设置了上稳定翼,在水平面设置2个稳定翼。传统的十字舵如图1所示,改进后的X舵如图2所示。舵翼分离型尾操纵面的布置形式如图3所示,X舵的舵轴位置是将原十字舵的舵轴在艇横剖面上旋转45°而得到的,稳定翼与X舵不是在同一圆周上的,而是将其错开分布,安装于水平面与垂直面处。

|
图 1 十字舵示意图 Fig. 1 Schematic diagram of cross rudder |

|
图 2 全动X舵示意图 Fig. 2 Schematic diagram of full motion X rudder |
|
图 3 舵翼分离型尾操纵面布置形式 Fig. 3 Arrangement of rudder wing separated tail control surface |
湍流是流体运动中常见的现象,计算潜艇流场必然会涉及到湍流。在CFD数值模拟中处理湍流问题,有很多有效的方法如DNS,LES,RANS等,本文采用RANS方法。
2.1 控制方程在求解潜艇在水下的运动时,控制方程为质量守恒方程(或称为连续性方程)和动量守恒方程(Navier-Stokes方程):
| $ \frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} + \frac{{\partial w}}{{\partial z}} = 0 {\text{,}}$ | (1) |
| $ \rho \frac{{\partial {u_i}}}{{\partial t}} + \rho {u_j}\frac{{\partial {u_i}}}{{\partial {x_j}}} = - \frac{{\partial p}}{{\partial {x_j}}} + \mu \frac{\partial }{{\partial {x_j}}}\left(\frac{{\partial {u_i}}}{{\partial {x_j}}}\right) + {f_i}{\text{。}} $ | (2) |
式中:
李世强等[3]通过采用不同的湍流模型分析潜艇绕流的速度场、涡量场,发现SSTk-
| $ \frac{\partial(\rho k)}{\partial t}+\frac{\partial\left(\rho u_{j} k\right)}{\partial x_{j}}=\frac{\partial}{\partial x_{j}}\left[\left(\mu+\sigma_{k} \mu_{1}\right) \frac{\partial z}{\partial x_{j}}\right]+P_{k}-\beta^{*} \rho \omega^{2}{\text{,}} $ | (3) |
| $ \begin{split}{l} \frac{\partial(\rho \omega)}{\partial t}+\frac{\partial\left(\rho u_{j} \omega\right)}{\partial x_{j}}=&\frac{\partial}{\partial x_{j}}\left[\left(u+\sigma_{a} \mu_{2}\right) \frac{\partial \omega}{\partial x_{j}}\right]+ \frac{y \rho}{\mu_{t}} P_{k}-\\ &\beta \rho \omega^{2}+2 \rho\left(1-F_{1}\right) \frac{\sigma_{\omega 2}}{\omega} \frac{\partial k}{\partial x_{j}} \frac{\partial \omega}{\partial x_{j}}{\text{。}} \end{split} $ | (4) |
其中,
选取的计算对象为某潜艇模型,模型主要参数如表1所示,X舵与X舵+稳定翼尾操纵面潜艇几何模型如图4和图5所示。
|
|
表 1 某潜艇主要参数 Tab.1 Main parameters of a submarine |

|
图 4 X舵潜艇模型 Fig. 4 X-rudder submarine model |

|
图 5 X舵+稳定翼潜艇模型 Fig. 5 X rudder + stabilized wing submarine model |
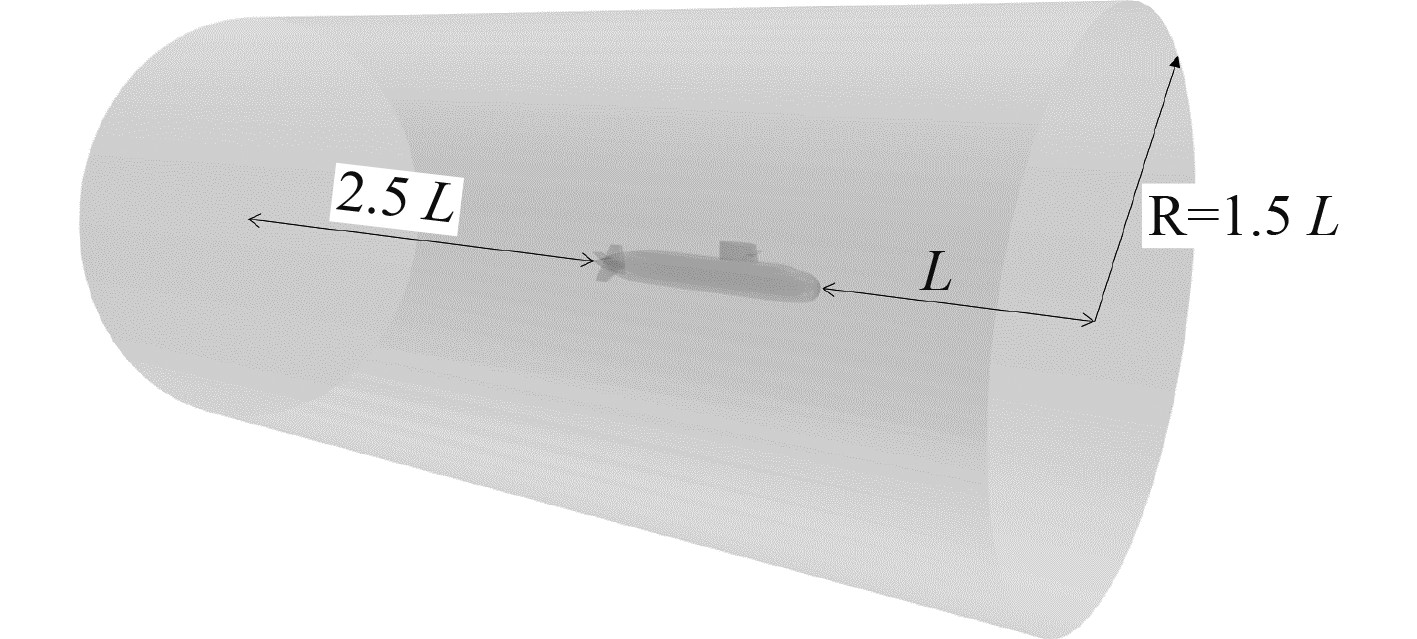
模型建成以后在其外部建立一个圆柱形区域作为计算域,如图6所示。潜艇到计算域周向距离为1.5 L(L为艇的长度),计算域进口到艇艏的距离为1.5 L,潜艇尾部到计算域出口的距离为2.5 L。在潜艇的围壳处,尾操纵面处适当地建立加密块。
|
图 6 计算域 Fig. 6 Computational domain |
网格是数值模拟的核心,网格质量在很大程度上决定数值模拟结果的精度和结果能否收敛,不同的试验对网格的要求也不一样,本文主要研究舵翼分离型为操纵面的水动力及尾流场,因此对尾部的网格要求较高。基于商用软件STAR-CCM+自带的网格生成器,计算域内采用切割体网格,切割体网格生成器可以针对复杂的网格问题生成高质量的网格。潜艇尾部的曲率变化大,可通过切割体网格加密尾流以捕捉出现在艇体后的湍流和瞬态流体情况,即可以更好地捕捉尾流场。潜艇表面与计算域连接处使用棱柱层网格进行划分,棱柱层网格可直接求解粘性子层(低y+~1),对于更粗糙的网格,它可以更精确地拟合壁面函数(高 y+ > 30)。由于潜艇表面的摩擦应力不同,艇体表面的位置不同,y+的取值也不同,但一般可取中部的y+值作为代表,y+值一般为25~170之间[5]。为了提高现有表面的整体质量并针对体网格模型进行优化,本文使用表面重构对潜艇表面进行三角形化,并对附体处进行了体积加密。艇体表面附近网格划分如图7所示,离艇体越远的地方网格越稀疏,越靠近艇体网格越密集。对于边界条件的设置,迎流面及计算域柱面设为速度入口,柱形计算域艇后方横截面为压力出口,艇体表面为壁面无滑移边界。

|
图 7 艇体表面附近网格图 Fig. 7 Grid near hull surface |
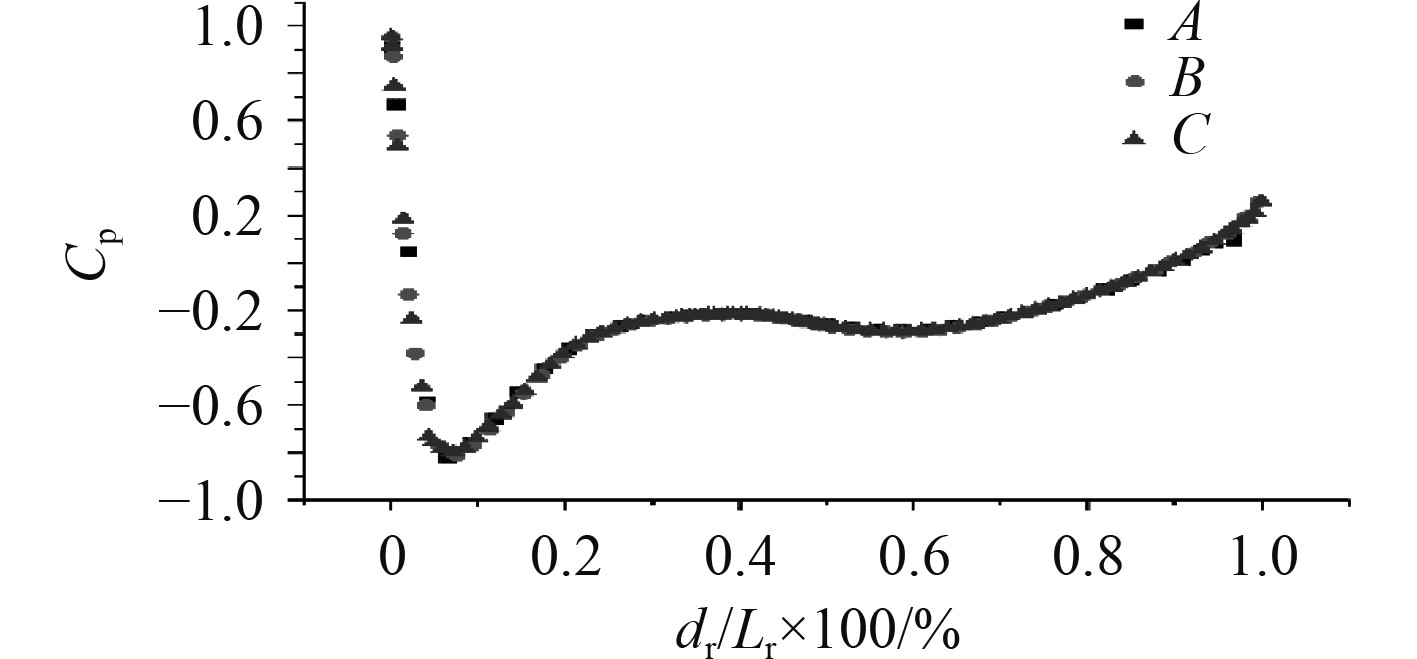
从理论上说,增加网格节点数通常有利于提高模拟结果的精度,但是,考虑到计算机资源的制约,网格节点数过大会导致计算成本增加。因此,在保证计算精度的前提下,在数值模拟的前期尽可能减少网格节点数。网格无关性检验是解决上述问题的常用方法[6]。以美国泰勒舰船研究中心(DTRC)设计的Suboff AFF-8潜艇为计算模型,在保证其他网格参数相对于基准值不变的前提下,按网格增长因子1.141仅改变网格生成中的基础尺寸设置3套不同数量的网格,分别为A(100万)、B(145万)、C(265万),采用RANS方法监测指挥台围90%高度截线处的压力系数和距艇首部端点x/L=0.978的桨盘面处无因次轴向速度等值线的分布,计算结果如图8所示。图中dr为围壳截线上的点到计算高度处截线前缘点的轴向距离,Lr为计算高度处尾翼截线弦长的长度。
|
图 8 90% 指挥台围壳高度截线处压力系数 Fig. 8 Pressure coefficient at the intercept line of 90% height of command platform enclosure |
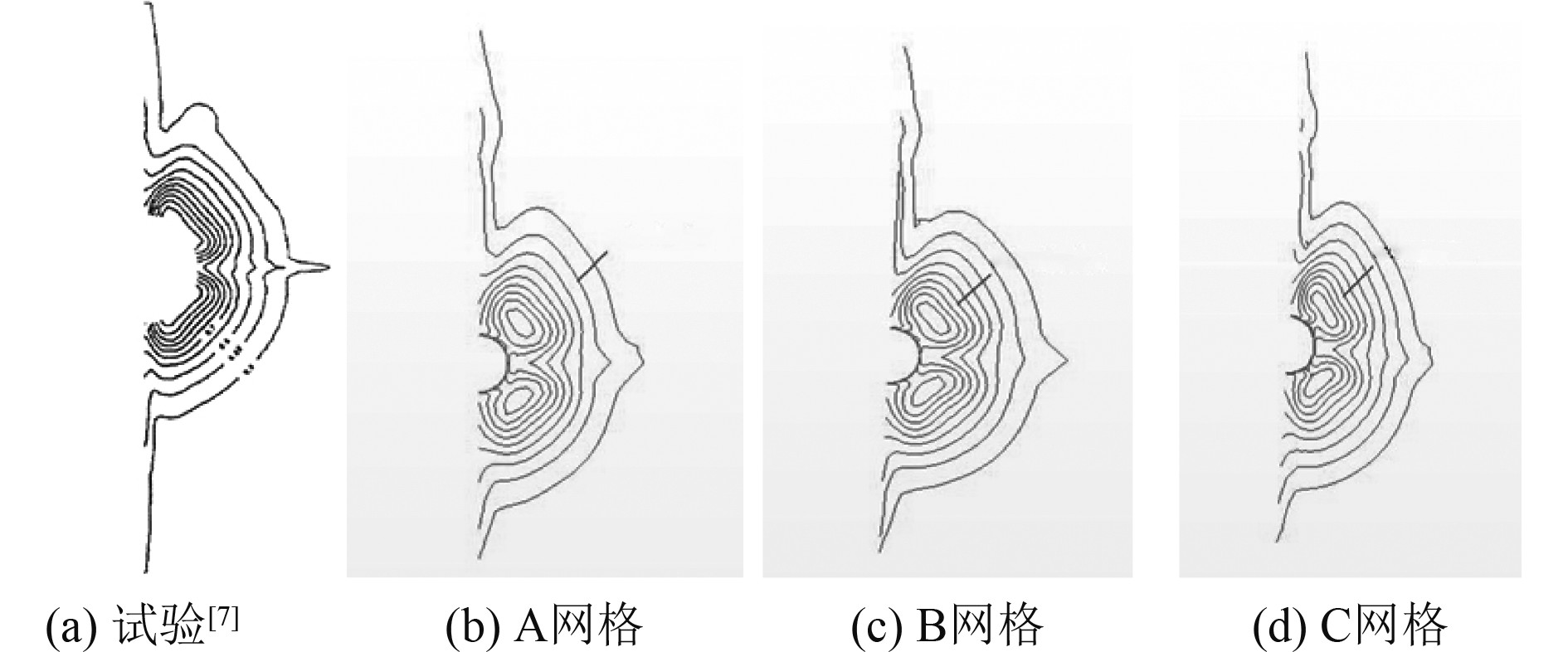
从图9的计算结果可以看出这3套不同数量的网格模拟出的桨盘面无因次轴向速度等值线分布与试验结果很相近,只是在水平舵处的轴向速度有微小的差异,说明这3套网格参数的设置是满足计算要求的,再增加网格量对计算收益不大,为了节约计算资源和更好地捕捉尾流场细节,本文采用B网格的设置参数开展接下来的计算分析。
|
图 9 桨盘面无因次轴向速度等值线分布图 Fig. 9 Isoline distribution of dimensionless axial velocity on propeller disk |
假设来流均匀,设置5种初始速度,舵角、攻角和漂角均为零,表2为3种不同尾操纵面潜艇计算的阻力值。
|
|
表 2 不同速度下定常直航阻力计算结果 Tab.2 Calculation results of steady direct sailing resistance at different speeds |
从表2可以看出,3种不同尾操纵面在低速航行时,X舵+稳定翼潜艇的总阻力最大,其次是X舵潜艇,十字舵潜艇的总阻力最小;在高速航行时,X舵的总阻力最小,其次是X舵+稳定翼,而十字舵的总阻力反而是最大的。由于X舵和X舵+稳定翼都是在保持十字舵在垂直面和水平面正投影面积不变的情况下进行设计的,因此3种尾操纵面的湿表面积相差不大,摩擦阻力相差也不大;X舵+稳定翼尾操纵面在布局位置上是周向错开的,与X舵尾操纵面潜艇相比相当于增加了附体,而粘性压差阻力主要是由于艇体首部、尾部的压力差而产生的[8],其值与艇体、特别是尾操纵面形状有关,所以X舵+稳定翼尾操纵面潜艇的粘性压差阻力比其他2种尾操纵面潜艇都大。
5.2 变漂角试验数值模拟对十字舵、X舵、X舵+稳定翼3种尾操纵面潜艇进行变漂角斜航试验数值模拟,设置来流速度为2.5 m/s,漂角变化范围(−10°,10°),舵角为零,得到无因次侧向力Y`以及首摇力矩N`同无因次速度V`的关系,如图10所示。可以看出3种尾操纵面潜艇Y`,N`相差不大。

|
图 10 侧向力与首摇力矩系数模拟值 Fig. 10 Simulation value of lateral force and yaw moment coefficient |
将3种尾操纵面潜艇侧向力与首摇力矩系数进行三次多项式拟合可以求得水平面位置水动力导数Yv'、Nv',相关计算结果如表3所示。
|
|
表 3 水平面位置导数CFD计算结果 Tab.3 CFD calculation results of horizontal position derivative |
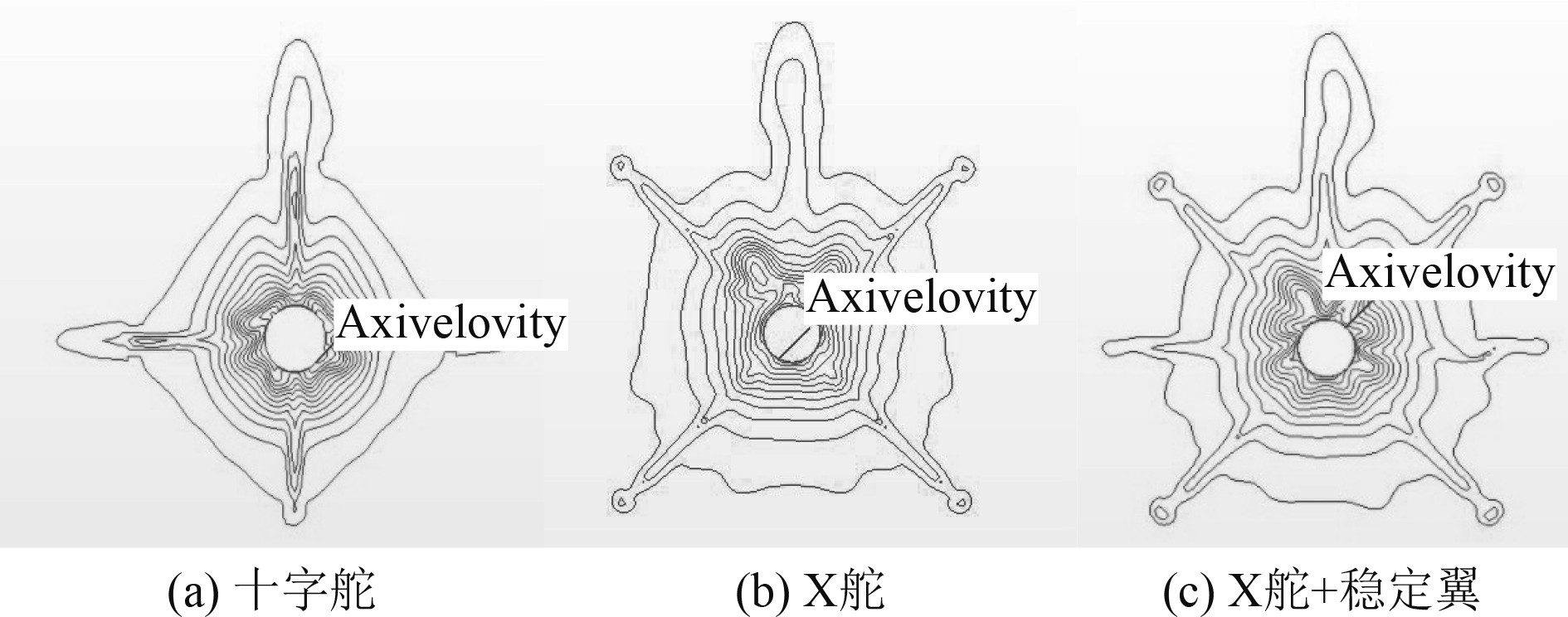
为了对3种不同尾操纵面潜艇的尾流场品质进行定性分析,V=2.5 m/s非定常直航情况下,监测3种尾操纵面潜艇桨盘面横截面处的轴向速度分布等值线,如图11所示。可以看到,稳定翼对速度等值线的影响较为明显,在稳定翼安装处速度等值线有较为明显的隆起,说明此处速度波动较大。对比3种尾操纵面的速度等值线分布可以看出,指挥台围壳对桨盘面处的速度等值线分布影响明显,十字舵尾操纵面和X+稳定翼尾操纵面潜艇由于稳定翼的加入,反而使上半部分的速度分布更为均匀,X舵尾操纵面垂直面上没有稳定翼,可以看出此处的速度等值线较为弯曲和密集。可能是舵翼根部的涡系导致,而周向其他位置速度变化比较均匀。加装稳定翼之后,稳定翼所在的水平方向速度出现波动,而上垂直稳定翼与围壳在周向位置是重合的。从图11可以看出,上垂直稳定翼与X舵的共同作用,可以缓和围壳涡系对尾流场的影响。说明垂直面的稳定翼可以改善由于指挥台围壳导致的桨盘面处轴向速度不均匀度。
|
图 11 桨盘面处轴向速度分布等值图 Fig. 11 Contour map of axial velocity distribution on propeller disk |
图11只能定性地描述速度分布情况,为了进一步定量地描述3种尾流场的均匀性,提出流场速度分量不均匀度系数的表达式:Ui=(Uimax-Uimin)/Uo,Uimax为流体速度分量峰值,Uimin为流体速度分量谷值,Uo平均速度。由于潜艇的螺旋桨直径一般不超过主艇体最大直径的40%,因此监测桨盘面处r/R=0.25,r/R=0.3,r/R=0.4三处的轴向速度,R为主艇体的最大半径,r为桨盘面上所取的圆周半径。
从图12和表4可以看出,在桨盘面有意义半径内,随着半径的增大,十字舵的不均匀度在增大,而X舵和X舵+稳定翼尾操纵面潜艇的桨盘面处的轴向速度均匀度相对较好。这是因为潜艇围壳和围壳舵产生的涡会发展延伸到桨盘面处,造成速度波动明显,而X舵在周向上是与围壳舵成45°的,再加上稳定翼在周向上与围壳重合,对围壳以及围壳舵产生的涡起到削减的作用,从而提高了螺旋桨的进流品质 ,可以减小螺旋桨桨叶的非常力变化范围。

|
图 12 桨盘面轴向速度变化曲线的比较 Fig. 12 Comparidson of axial velocity curves of the paddle disk |
|
|
表 4 桨盘面轴向速度不均匀度比较 Tab.4 Comparidson of axial velocity unevenness of the paddle disk |
图13为十字舵、X舵、和X舵+稳定翼尾操纵面潜艇在均匀来流下的涡强分布(Q-Criterion=15 s−2)。图中可以清晰地看到十字舵潜艇在舵翼的根部有较大的涡系,X舵尾操纵面潜艇上侧2个舵根部也有较明显的涡系,而下侧面2个舵根部涡系明显减少,可能和舵翼根部的马蹄涡和指挥台围壳涡系有关;在加装稳定翼后,上侧舵翼根部的涡系明显减少,稳定翼的梢部也出现了一些涡,但是结合图13和图14分析可知,对于螺旋桨入流面来说,十字舵尾操纵面的涡强最大,X舵尾操纵面潜艇在上侧2个舵翼间的涡强相对较大,下侧2个舵翼间的涡强相对弱一些,而X舵+稳定翼尾操纵面潜艇流入桨盘面的涡强明显减小,且涡强的分布也较均匀。涡流较强会导致舵升力性能变差,还会引起涡激振动,从而加剧螺旋桨的振动。结果表明,稳定翼的加入虽然会对舵的水动力性能产生类似艇体伴流场的影响,但是其对螺旋桨的振动与噪声水平起到了一定的改善作用,因此可以认为,X舵+稳定翼尾操纵面可以在一定程度上改善潜艇尾流场的品质。

|
图 13 三种不同为操纵面潜艇涡强图 Fig. 13 Vortex intensity diagram of submarine with three different control surfaces |

|
图 14 r/R=0.7桨盘面处涡量幅值 Fig. 14 R / r = 0.7 vorticity amplitude on the disc |
本文通过STAR-CCM+商用软件,在均匀来流的条件下,对分离型尾操纵面潜艇直航以及变漂角斜航运动的模拟,分析了传统的十字舵尾操纵面潜艇与X舵、X舵+稳定翼尾操纵面潜艇的阻力以及尾流场均匀性,由计算结果可以得到以下结论:
1)由于3种尾操纵面的湿表面积相差不大,三者的摩擦阻力基本相同;但是随着航速的提高,十字舵尾操纵面的总阻力比其他两种尾操纵面潜艇的总阻力大;而稳定翼与X舵在周向上错开,相当于增加了附体,所以X舵+稳定翼尾操纵面潜艇的粘压阻力要稍大于其他2种尾操纵面潜艇的粘压阻力。
2)桨盘面上十字舵的4个舵翼处速度等值线的分布较为密集且不均匀,由于受指挥台围壳的影响,X舵的上侧舵翼处轴向速度不均匀度较为明显,X舵+稳定翼可以减小指挥台围壳对尾流场的影响;在桨盘面有意义的半径范围内,随着半径增大,舵翼分离型尾操纵面的尾流场的不均匀度降低,说明舵翼分离型尾操纵面可以改善螺旋桨进流面流场品质。
3)桨盘面处,十字舵尾操纵面越靠近艇体表面的地方涡强越大且变化显著,X舵尾操纵面则是在上侧两翼根处出现较强的涡,X舵+稳定翼尾操纵面的涡强显著减小且涡强分布较为均匀。说明X舵+稳定翼尾操纵面对螺旋桨的振动与噪声水平起到改善作用。
| [1] |
盛振邦, 刘应中. 船舶原理(下册) [M]. 上海: 上海交大出版社, 2005.
|
| [2] |
施生达. 潜艇操纵性[M]. 北京: 国防工业出版社, 1995.
|
| [3] |
李士强, 肖昌润, 曹植珺. 基于STAR-CCM+的潜艇尾流场及水动力数值分析[J]. 中国舰船研究, 2018, 13(z1): 29-35. |
| [4] |
MENTER, F. R. Two-equation eddy-viscosity turbulence modeling for engineering applications[J]. AIAA Journal, 1994, 32(8): 1598-1605. DOI:10.2514/3.12149 |
| [5] |
叶金铭, 张凯奇, 于安斌. 基于STAR-CCM+的全附体潜艇尾流场数值分析[J]. 海军工程大学学报, 2017, 29(4): 53-58. |
| [6] |
冯静安, 唐小琦, 王卫兵. 基于网格无关性与时间独立性的数值模拟可靠性的验证方法[J]. 石河子大学学报:自然科学版, 2017(35): 56. |
| [7] |
BULL P. The validation of CFD predictions of nominal wake for the SUBOFF fully appended geometry[C]// Proceedings of 21st Symposium on Naval Hydrodynamics. Trondheim, Norway, 1996.
|
| [8] |
柏铁朝, 卢锦国. 附体对潜艇阻力及尾部伴流场的影响[J]. 舰船科学技术, 2013, 35(3): 47-51. |
 2021, Vol. 43
2021, Vol. 43
