水平圆柱在复合式浮式防波堤中是一种常见的结构,海域中结构物所受的外力作用很多,波与流是其中的2种。由于波流的长期作用,结构物容易产生疲劳与坍塌,所以研究波流与结构物的作用对结构物设计和生产安全有着重要的现实意义。
早期针对波浪对非完全水平淹没圆柱体已经有了大量的研究,其中大部分采用了理论分析和物理实验的方法。Dixon等[1]考虑圆柱轴心和低于静水面的情况,改变波浪频率和圆柱的淹没深度对水平圆柱体上的波浪力进行实验研究。随着流体计算的发展,对部分淹没水平圆柱体上波浪力的数值模拟研究也不断开展。Westpahlen等[2]采用有限体积法等CFD方法对波浪与非淹没水平圆柱的作用问题进行数值模拟,计算水平圆柱所受的垂向力,发现计算结果与Dixon的实验结果较为接近。Hu等[3]基于黏性流理论建立了数值波浪水槽,在线性波作用下对半淹没水平圆柱体进行受力计算,其数值结果与Dixon的实验值和Westpahlen计算值能够较好吻合。刘必劲等[4]改进Morison方程对水平圆柱浮子所受波浪力进行准确预测,研究得出淹没深度对圆柱体所受波浪力有影响。毛鸿飞等[5]改变部分淹没水平圆柱体的垂向位置与波浪幅值,得出水平圆柱体所受波浪力随着垂向位置升高而增大。
相对于波,波流对水平圆柱体的研究较少。Xiao等[6]研究了波流作用下圆柱体的受力情况,发现圆柱体所受的波流力大于波浪力与流体力的简单求和。胡克等[7]研究波流作用下的水动力特性,得出流速与浸没深度的增加能够同时增加附加水质量系数和拖曳力系数。柏君励等[8]研究波流与不同淹没深度下的水平圆柱的影响时发现,波浪反射与阻塞作用共同影响水平圆柱所受波流力的大小。Bai等[9]通过修正Morsion方程与实验值比较发现,在部分淹没的情况下,测得值比理论值大,相反,在完全淹没的情况下,测得值相对较低。
在此基础上,本文对不同波幅、周期与圆柱淹没深度对波流力特征的影响进行数值计算。基于STARCCM+软件建立数值模型,采用的基本方程为Navier-Stokes(N-S)方程,数值离散方法为Finite Volume Method(FVM),湍流模型为Renormalization-group(RNG)k-w模型,捕捉自由表面用Volume of Fluid(VOF)方法,造波使用Fenton[10]的五阶波浪理论,采用速度边界法造波及阻尼消波。使用该模型,首先对半淹没水平圆柱体的波流力进行数值验证,验证该模型对结构物受力的准确性。然后应用该模型对不同工况下的水平圆柱体进行波流力的数值计算,分析波幅、淹没深度和波周期对水平圆柱体波流力的影响以及波流与圆柱相互作用时波浪的反射情况,为在波流作用下的结构物设计提供参考。
1 数值模型 1.1 控制方程对于不可压缩的黏性流体流动问题,可分别用如下张量形式表示连续方程和动量守恒方程:
| $ \frac{{\partial \rho {\mu _i}}}{{\partial {x_i}}} = 0{\text{,}} $ | (1) |
| $ \frac{{\partial \rho {\mu _i}}}{{\partial t}} + \frac{{\partial p{\mu _i}{\mu _j}}}{{\partial {x_j}}} = - \frac{{\partial p}}{{\partial {x_i}}} + \mu \frac{\partial }{{\partial xj}}\left( {\frac{{\partial {\mu _i}}}{{\partial {x_j}}} + \frac{{\partial {\mu _j}}}{{\partial {x_i}}}} \right) + \rho g {\text{。}}$ | (2) |
式中:
用VOF方法对数值模型的自由表面进行捕捉。
| $ \alpha =\left\{\begin{array}{*{20}{c}}0{\text{,}}&\text{气相}{\text{,}}\\ 0\sim 1{\text{,}}&\text{自由表面}{\text{,}}\\ 1{\text{,}}&\text{液相}{\text{。}}\end{array} \right. $ | (3) |
混合流体的密度和黏性系数计算式为:
| $ \rho {\text{ = }}\alpha {\rho _w} + \left( {1 - \alpha } \right){\rho _a} {\text{,}}$ | (4) |
| $ \mu {\text{ = }}\alpha {\mu _w} + \left( {1 - \alpha } \right){\mu _a}{\text{。}} $ | (5) |
其中,下标w表示液相,a表示气相。
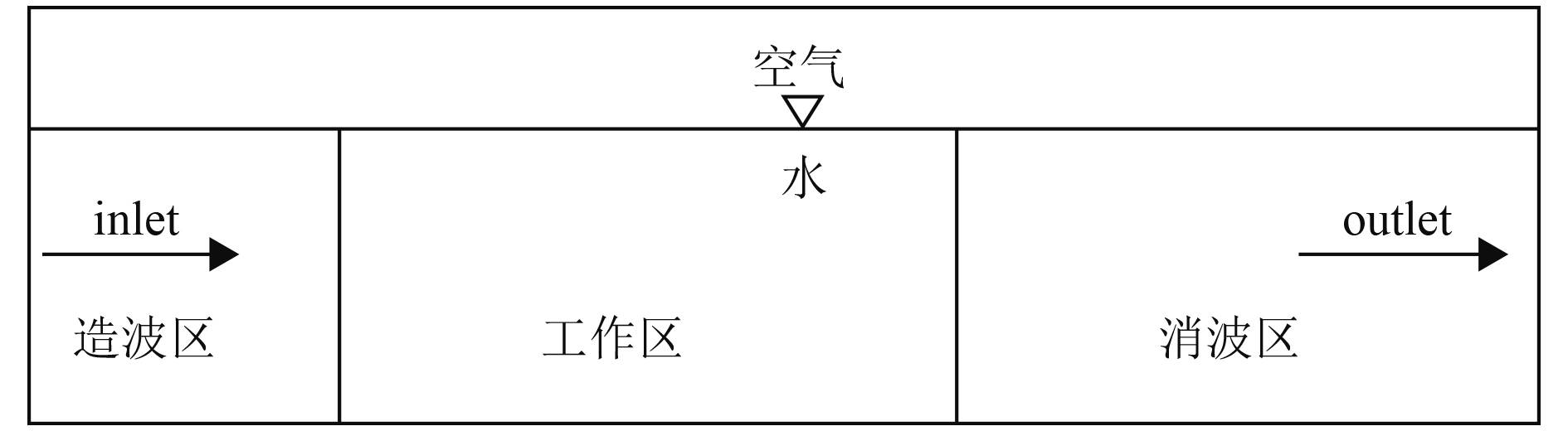
1.3 边界条件数值波浪水槽模型及其平面图如图1所示。在水槽入口处给定边界条件为速度入口,即造波采用的方法速度边界法;顶部边界只允许空气离开或进入区域,因此给定压力出口边界;出口处采用阻尼消波,并给定压力出口的边界条件。水槽的底部边界为不可滑移的固定边界。其中造波区设置在水槽前端,其目的是协助生成波浪和吸收反射波浪;消波区设置在水槽末端,其功能是把出口边界的波浪反射消除。
|
图 1 数值波浪水槽的示意图 Fig. 1 Sketch of numerical wave flume |
用下列方程计算结构物上的流体作用力:
| $ F = {F_p} + {F_\nu } = - \int {pn{\rm{d}}s + \int {\tau S{\rm{d}}s} } {\text{。}}$ | (6) |
式中:Fp和Fv分别是压力和黏性切力;n为单为法向量;s单位切向量;
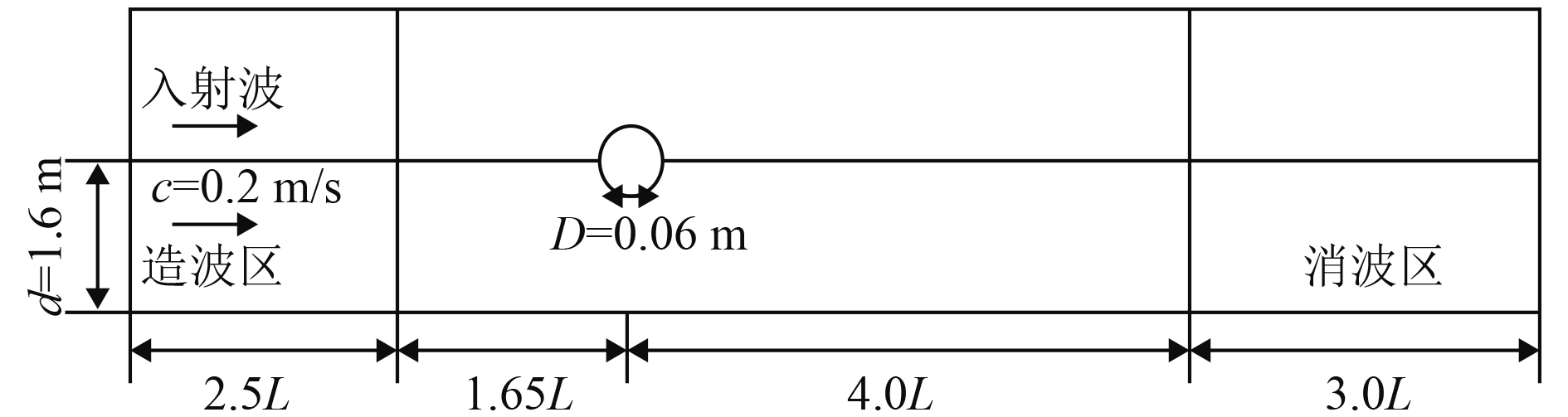
参照Bai等[9]的物理实验值,验证半淹没水平圆柱体上所受的流体作用力,计算设置如图2所示。水平圆柱淹没在水中一半,圆柱直径D=0.06m,水深d=1.6m,流速c=0.2m/s,为了减少计算的工作量,造波理论采用了Fenton[10]提出的Stokes五阶波理论,入射波周期T=0.7s,波高H=0.03m。
|
图 2 数值水槽模拟的示意图 Fig. 2 The computation domain of water channel |
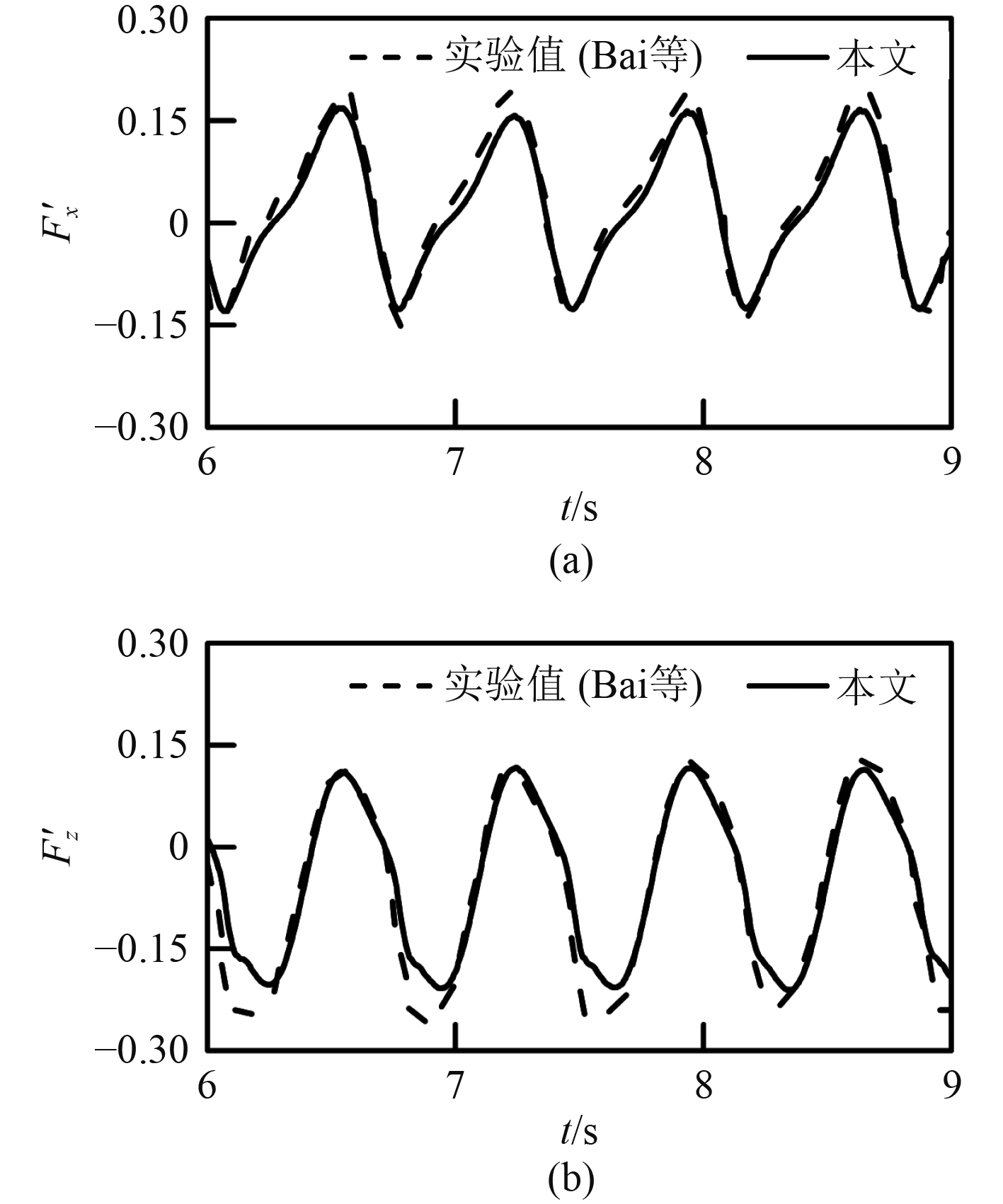
将圆柱所受作用力的数值结果选取其中几个周期与实验结果作比较,如图3所示。本文所有的受力数据均采用圆柱完全淹没时的浮力进行无量纲处理,其中垂直作用力Fz为扣除初始时刻静浮力后的值,如下式:
|
图 3 水平圆柱上的波流力 Fig. 3 Wave-current forces on a horizontal cylinder |
| $ {F_x}' = \frac{{{F_x}}}{\rho g\text{π} {D^2}l {\vphantom {{\rho g\text{π} {D^2}l} }}/4} {\text{,}}$ | (7) |
| $ {F_z}' = \frac{{{F_z}}}{{{\rho g\text{π} {D^2}l {\vphantom {{\rho g\text{π} {D^2}l} }}}/4}}{\text{。}} $ | (8) |
通过观察发现与已有文献的实验数据吻合良好,证明该模型非完全淹没水平圆柱体所受波流作用力计算有着良好的计算精度。本文的流体力在波浪循环初期,升沉力占主导地位。在通过峰值后,力在减小,并在相对波周期的一半后变为负值。当波流进一步传播,水位上升时,向下的力减小。
3 数值计算与结果分析 3.1 算例设置和计算参数数值计算中,圆柱体的水平位置及造波区及工作区长度与验证的算例相同,其中水深d=1 m,圆柱半径r=0.05 m以及流速c=0.25 m/s保持不变。选取多个波高A=0.012 5~0.05m,取值间隔为0.012 5 m;多个垂向位置为0~0.1 m,取值间隔为0.025 m,其中垂向位置的距离是圆心与静水面的距离值S;选取多个周期T=0.69 s,0.99 s,1.29 s,1.59 s。
3.2 网格收敛性验证选取3种不同的网格验证网格的收敛性,分别对3种水平圆柱上所受的波浪力进行计算,网格参数如表1所示。计算参数为r=0.05 m,S=0 m,T=1.29 s。
|
|
表 1 网格参数 Tab.1 Mesh parameters |
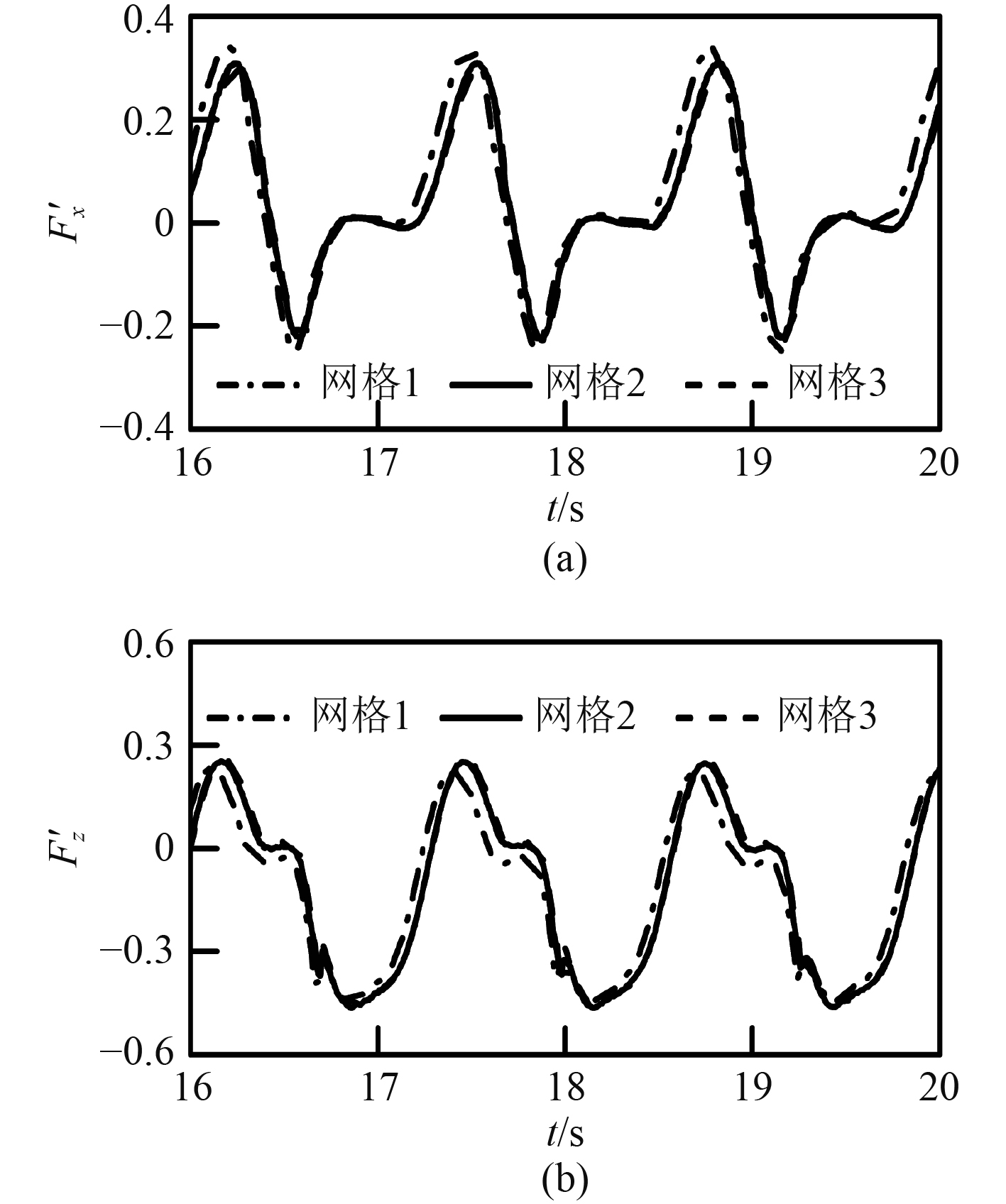
对比不同网格划分下的圆柱所受的波流力,如图4所示。由图可见,网格2与网格3对应的数值尤为接近,而较稀疏的网格1与较密的网格相比较有些误差。综合以上3种网格,网格2是既符合精度要求又符合减少计算量的要求,因此后文以网格2的设置条件开展计算。
|
图 4 不同网格下的圆柱水平波流力时间历程 Fig. 4 Time-series of horizontal wave-current forces on a cylinder with different mesh |
对不同的波幅、淹没深度及周期下的波流作用力进行计算并在圆柱上游2D和下游2D处监测波高,分析波幅等对波反射与波阻塞的影响。
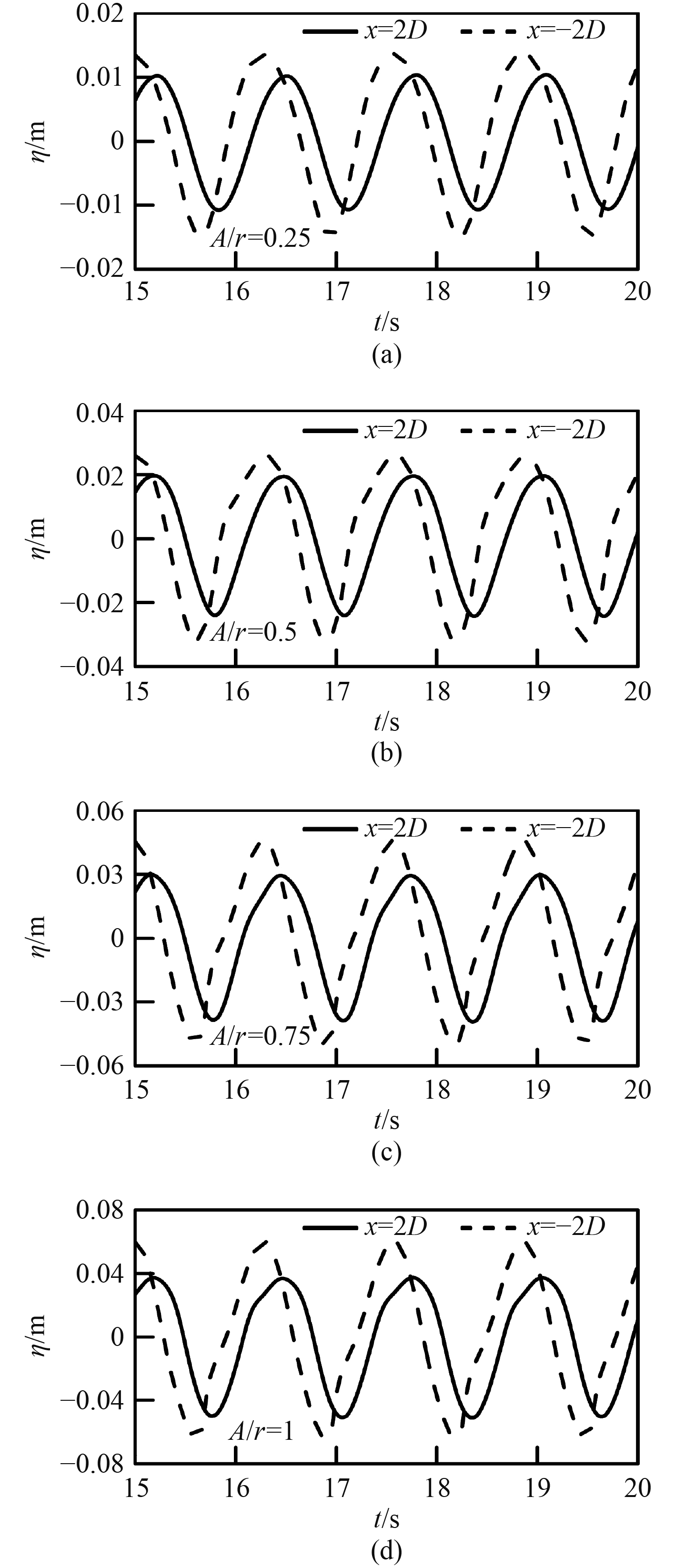
3.3.1 波流与水平圆柱体相互作用时的自由表面变形图5为S=0 m,T=1.29 s下几个不同波幅工况的时历曲线,此时圆柱圆心在水平面上。从圆柱上游2D和下游2D处的波高历时曲线对比发现,在波流情况下,圆柱处于部分淹没时会形成显著的波反射和波浪阻塞,随着波幅的增大,波浪反射与波浪阻塞明显增加。在圆柱处于半淹没时波浪反射比波浪阻塞的作用要大。
|
图 5 不同波幅下圆柱上游2D与下游2D的时间历时曲线 Fig. 5 Time-series curves of 2D upstream and 2D downstream of cylinder under different wave amplitudes |
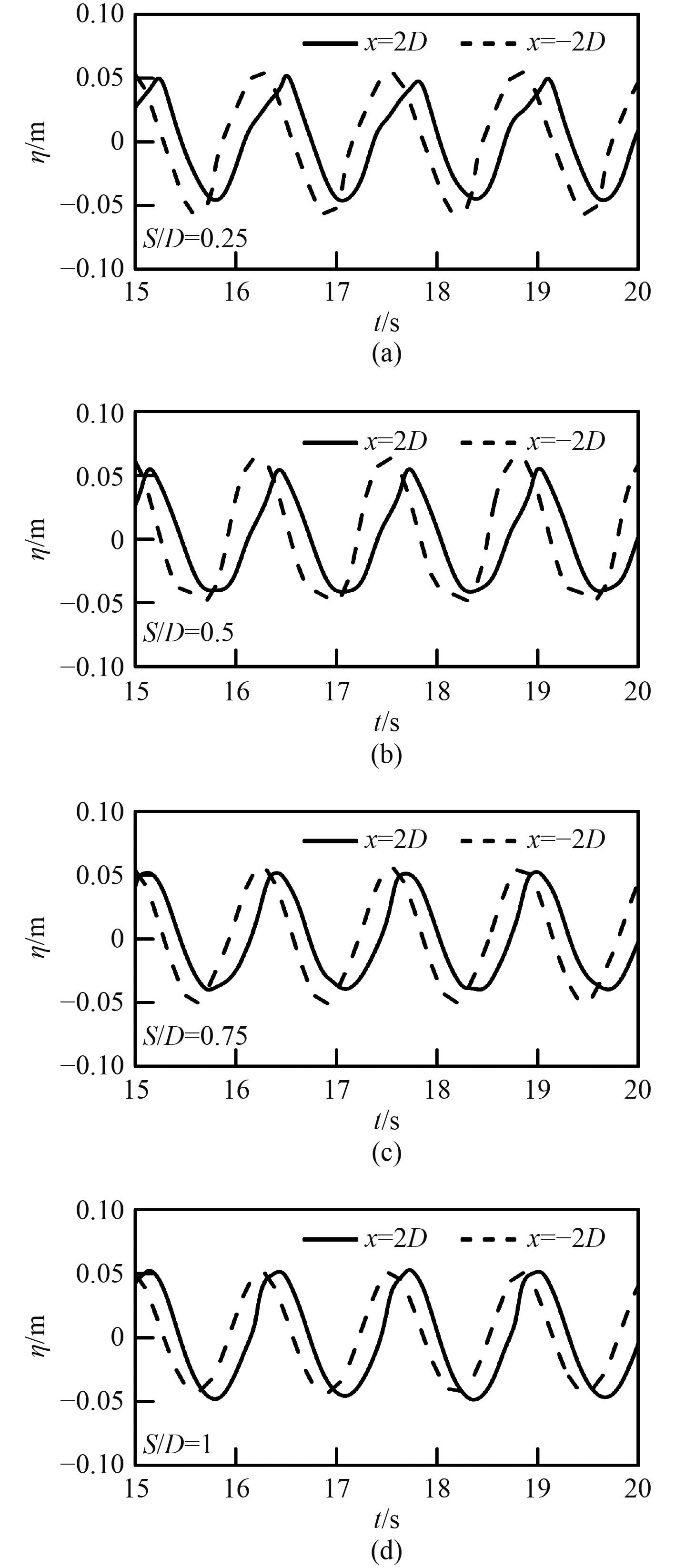
图6为A=0.05 m,T=1.29 s下几个不同深度工况的时历曲线。对比圆柱上游2D和下游2D处的波高历时曲线发现,随着淹没深度的增加,波浪反射在减小,波浪阻塞在增加,波浪阻塞渐渐大于波浪反射的作用。
|
图 6 不同深度下圆柱上游2D与下游2D的时间历时曲线 Fig. 6 Time-series curves of 2D upstream and 2D downstream of cylinder under different wave amplitudes |
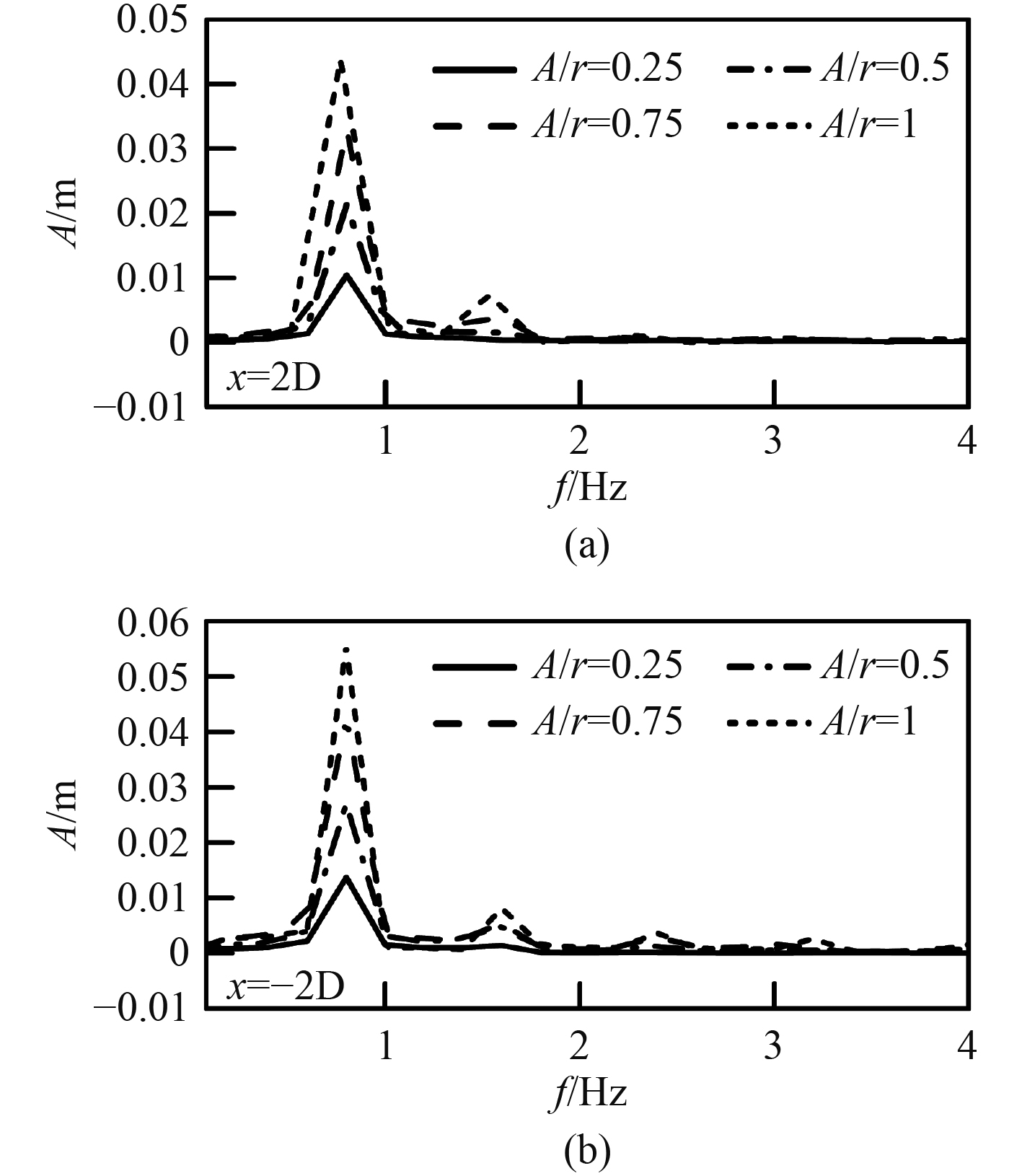
对图5各波高曲线进行傅里叶变换,如图7所示。和图5类似,当圆柱部分淹没流速不变时,上游2D处会形成明显的反射波,并与入射波叠加使得圆柱上游的水面振幅显著上升,并随着波幅的增大,波反射越明显。在下游2D处会形成明显的波阻塞效应,随着波幅的增大,波阻塞越明显。与图5对比来看,圆柱对波的反射作用比阻塞作用明显更大,此时波浪反射作用占主导。此外,还可以看出,在半淹没状态下,此时波流与圆柱相互作用时,波浪的高阶成分非常多,自由液面的非线性很大。
|
图 7 不同波幅下圆柱上游2D与下游2D处自由液面的傅里叶谱对比 Fig. 7 Comparison of Fourier spectra of free surface at 2D upstream and 2D downstream of cylinder under different wave amplitudes |
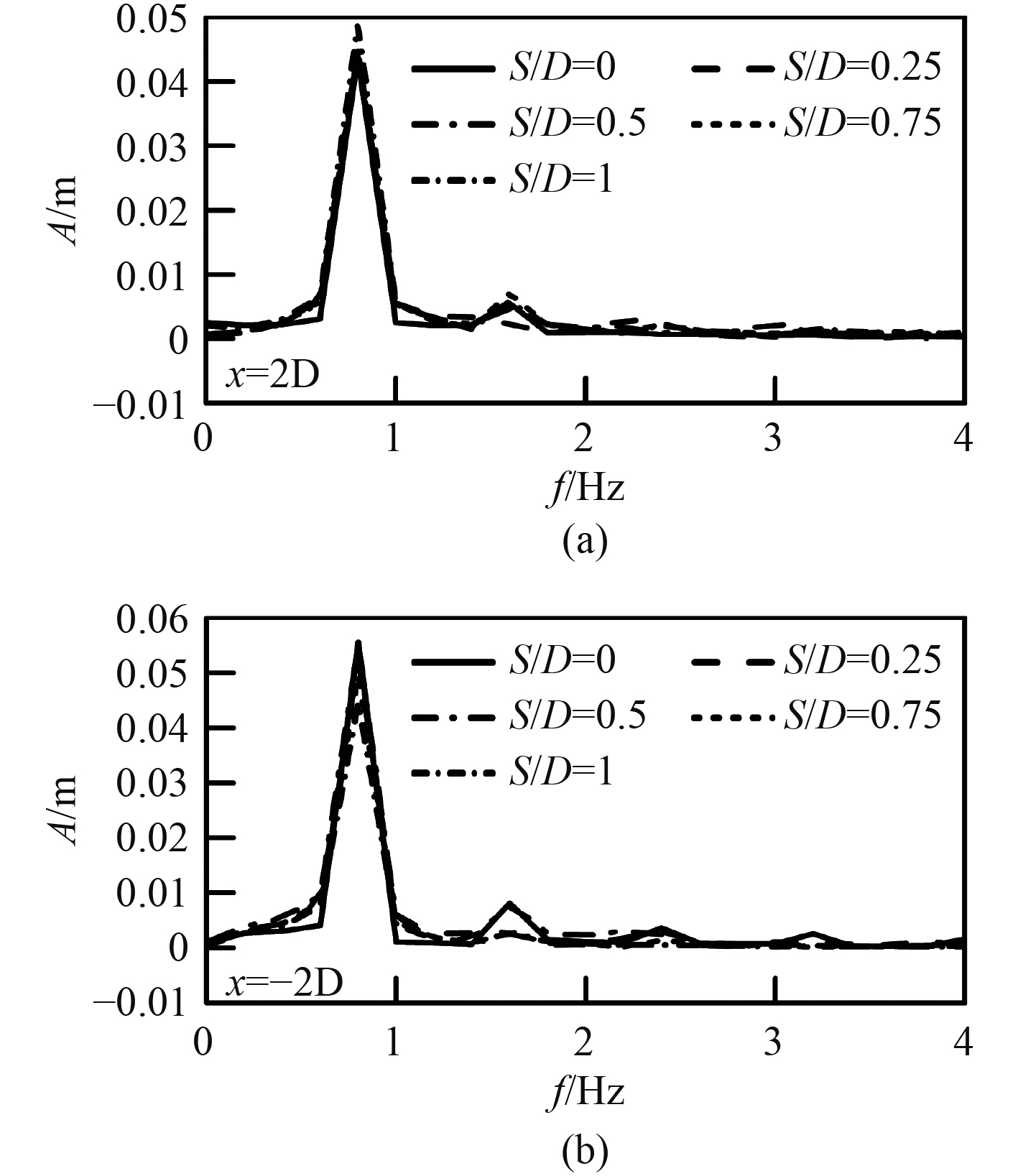
对图6各波高曲线进行傅里叶分析,如图8所示。和图6类似,随着淹没水深的增加,波浪阻塞在增加,波浪反射在全部淹没时减小,波浪阻塞渐渐占主导作用。
|
图 8 不同垂向位置下圆柱上游2D与下游2D处自由液面的傅里叶谱对比 Fig. 8 Comparison of Fourier spectrum of free surface at 2D upstream and 2D downstream of cylinder at different vertical positions |
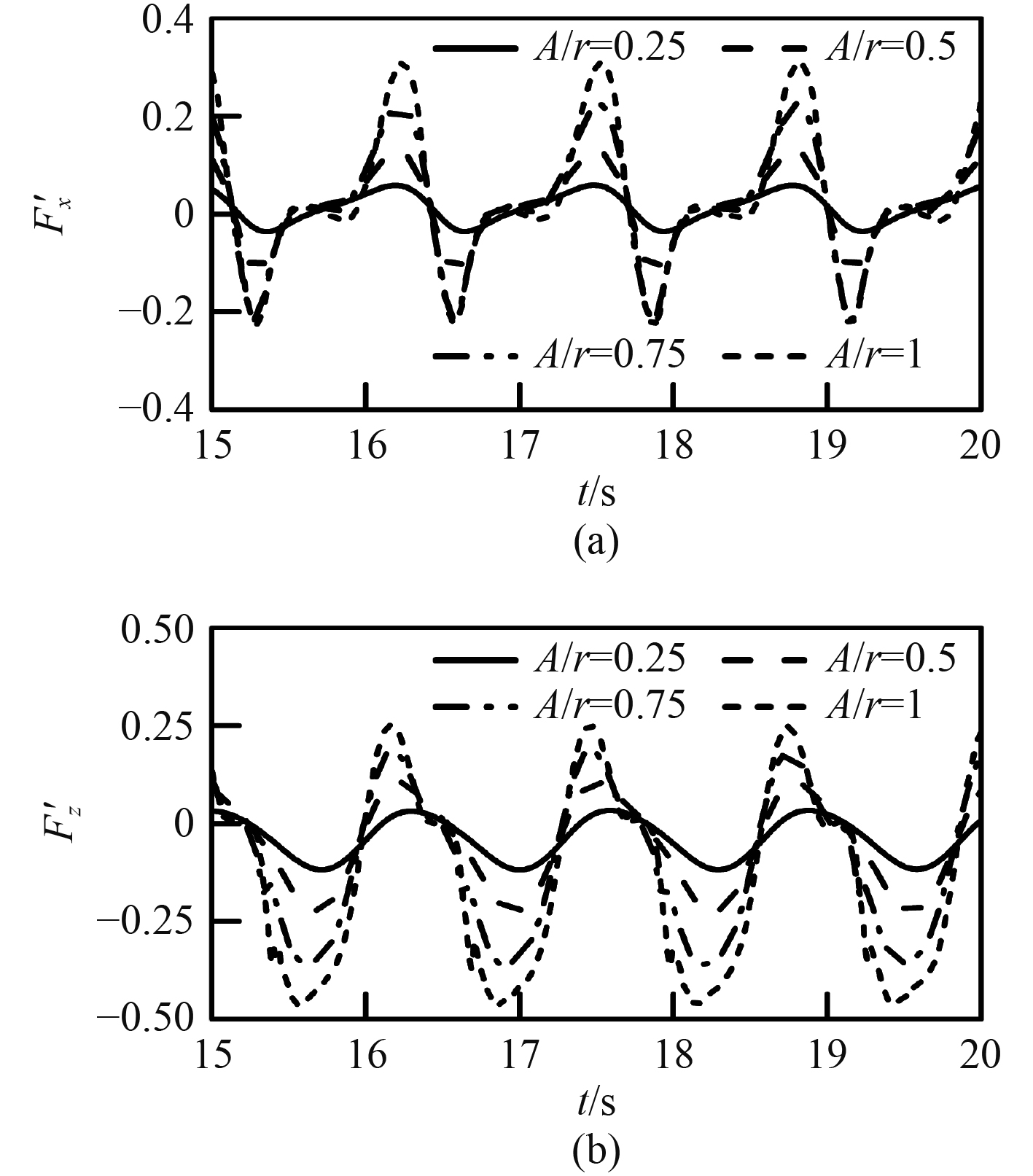
图9为工况T=1.29 s,S=0 m下,几个不同波幅下的圆柱所受波流水平作用力与垂向作用力的时间历程结果。图10为工况T=1.29 s,S=0 m,A=0.05 m下的涡量图。由图9可知,波幅较小的情况下,作用力曲线比较平滑;随着波幅的增大,流体力曲线变得粗糙。这是由于波幅的增大,波浪能够逐步爬高到圆柱最高点。随着波幅增大,圆柱所受的波流作用力也随之增大。水平作用力的正值随着波幅的增加,变化幅度逐渐减少,垂向力的正向幅值变化也逐渐减小;圆柱所受力的不对称越发明显,且水平力的正方向数值逐渐大于负方向,垂向力的负方向数值逐渐大于正方向,这是由于随着波幅的增加,波浪反射在增加,圆柱上游振幅增加使得垂直于波向的投影面积与排开水的体积增大。由图10可知,在部分浸没的情况下,波流与圆柱的作用时,圆柱迎浪面的液面先升高,进而带动背浪面水深增高,波流力为正。经过一段时间后,圆柱迎浪面水体下降,这时背浪面高于迎浪面,此时水平波流力方向与之前相反。
|
图 9 波流力时间历程 Fig. 9 Time-series of wave-current force |

|
图 10 波流下的涡量场分布图 Fig. 10 Distribution of vorticity field under wave-current |
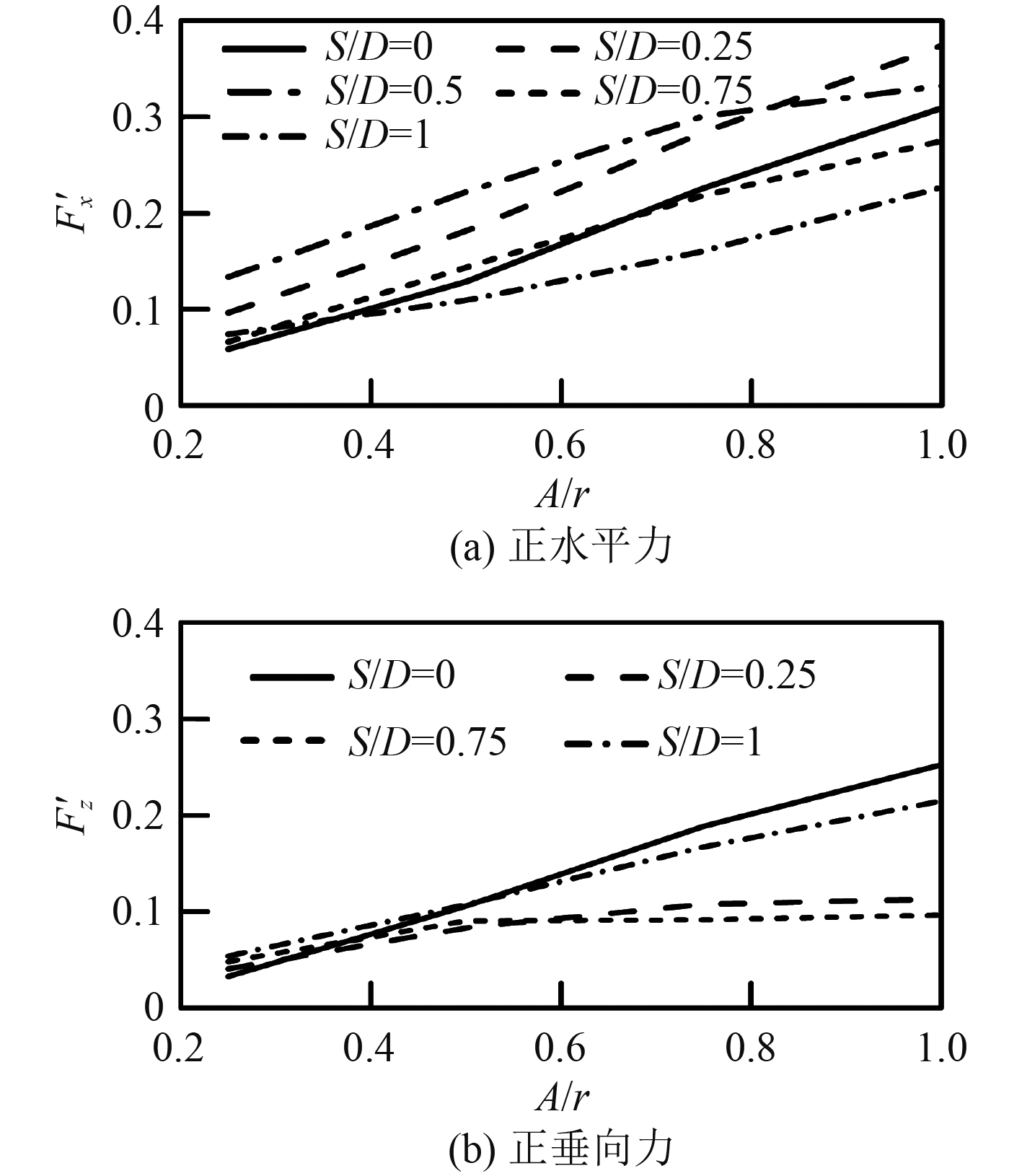
不同的S/D下正向水平力和垂向波流力随A/r的变化特征如图11所示。随着波幅的增加,波流力在总体上呈现上升的趋势。随着淹没深度的增加,波流力呈现出不同的发展趋势。在部分浸没时,随着深度的增加,正向水平力呈现上升的趋势,正向垂向力随着波幅的增加呈现着下降的趋势。随着波幅和垂向位置的增加,圆柱对波流的反射作用越强,使得上游的振幅增加,叠加波波峰越高波谷越低,所以圆柱的受力峰值在增加。在完全浸没时,正水平力随着浸没深度增加而呈现下降趋势,正向垂向力随着浸没深度的增加而上升,此外在刚好完全淹没的时候,正垂向力没有正值。这是由于当圆柱处于完全淹没时,波反射作用迅速减小。随着淹没深度的增加,浮力的影响较小,但随着波幅和水深的增加,波流的阻塞作用越强。当圆柱处于S/D=0.5时,圆柱顶部与自由液面刚好相切,此时的波浪反射很大,大于阻塞作用,类似前面分析。此时圆柱的受力峰值在增加,所以正水平力很大,又由于完全淹没,使得浮力对垂向力的影响小,所以垂向力很小。
|
图 11 不同S/D下正向波流力随A/r的变化对比 Fig. 11 Comparison of forward wave-current force with A/r under different S/D |
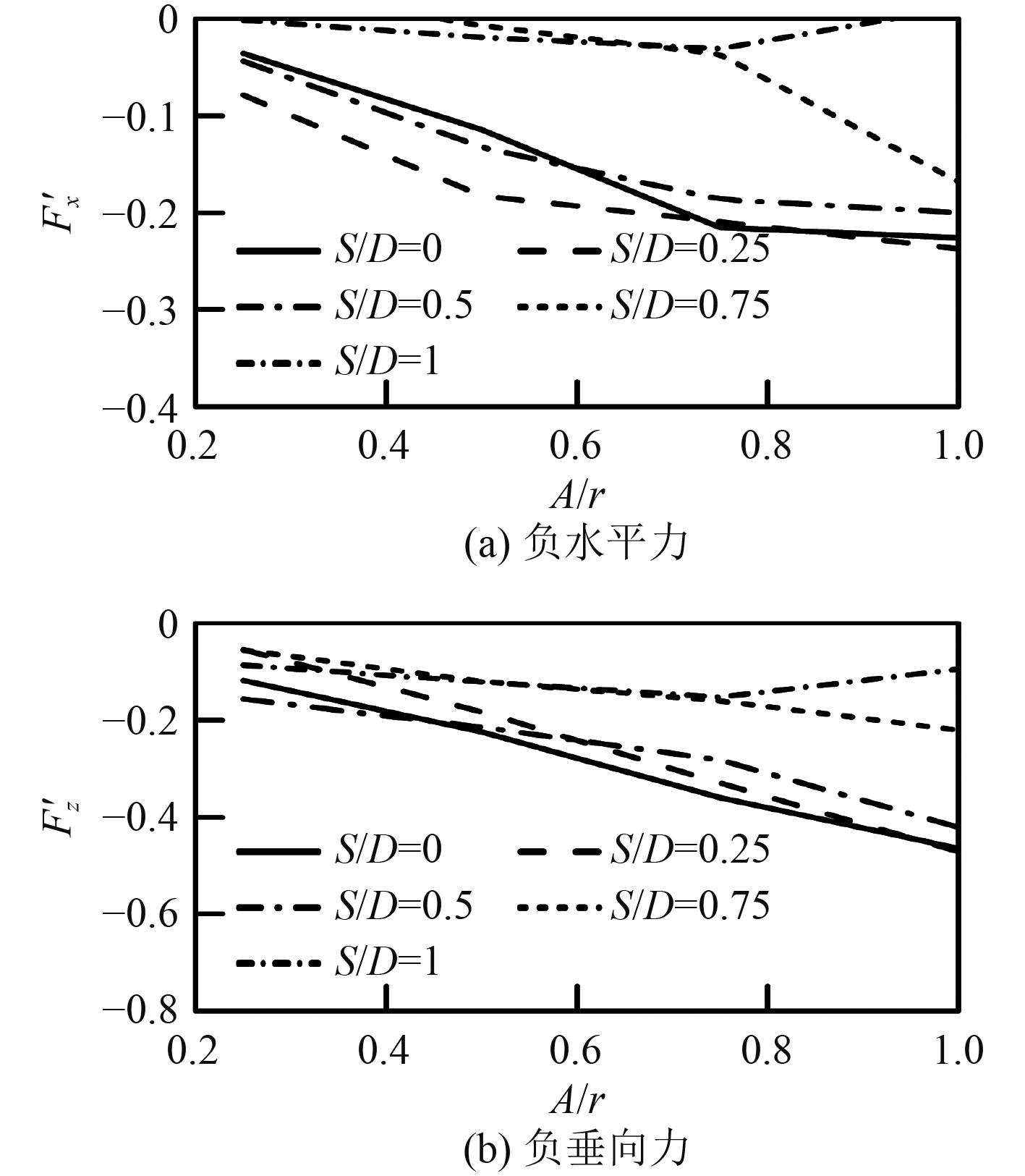
不同的S/D下负向水平和垂向波流力随A/r变化特征如图12所示。垂向力(负的极值以绝对值比大小)在部分淹没的情况下,随着淹没深度与波幅的增加,负水平力与垂向力的大小在增加;随着波幅的增加,不同深度下的水平力与垂向力的大小趋于一个值。在图11全部浸没的情况下,随着淹没深度的增加,负水平力的大小随之减小,负垂向力也随之减小。这是由于全部淹没时,波浪阻塞大于波浪反射,波浪阻塞降低了圆柱周围水的速度和加速度,从而减小了圆柱所受的波流力。
|
图 12 不同S/D下负波流力随A/r的变化对比 Fig. 12 Comparison of negative wave-current force with A /r under different S/D |
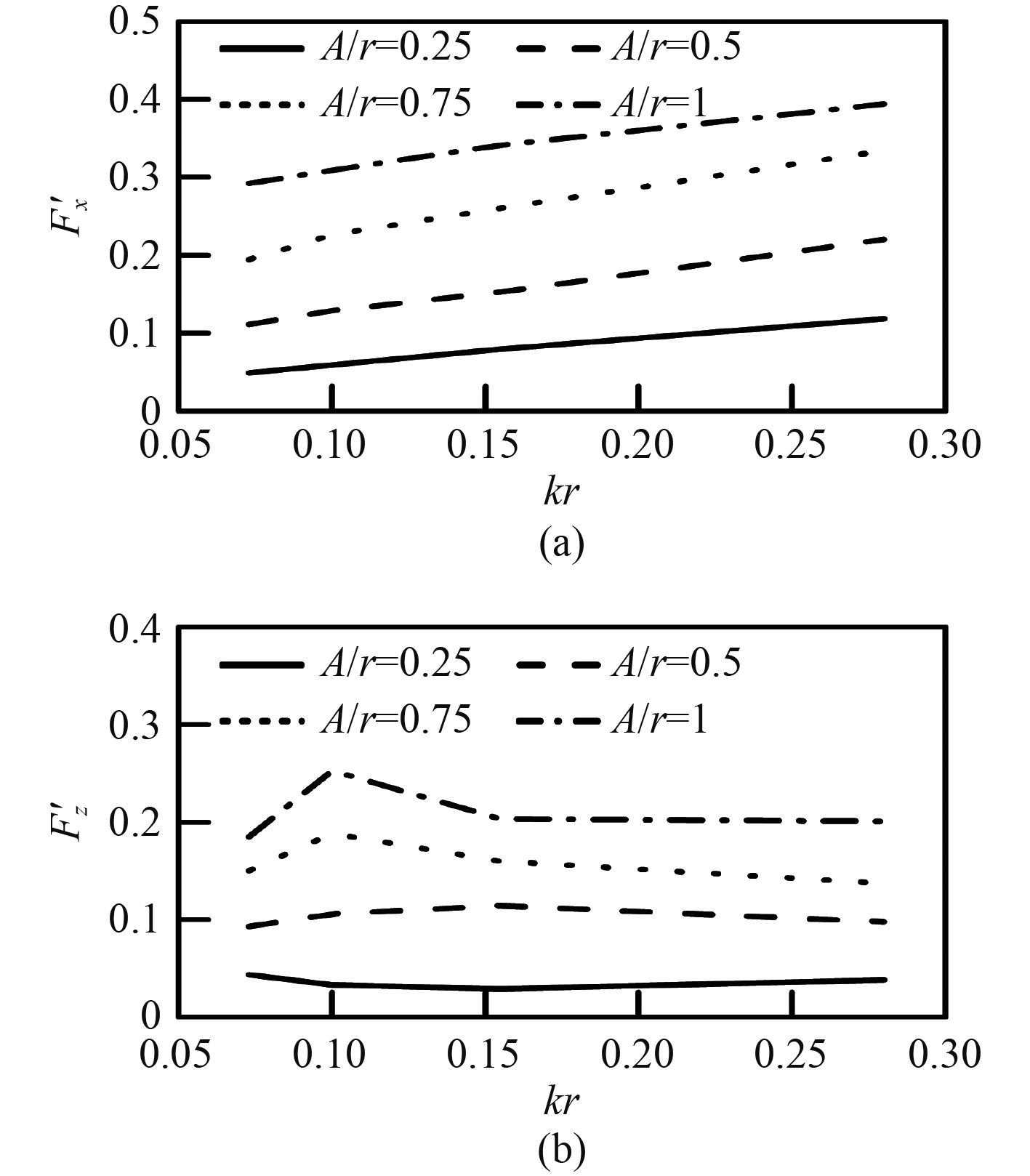
图13为S=0 m时不同波幅下的正向波流力随着频率的变化特征。随着频率和波幅的增大,水平波流力也随之增大;垂向波浪力的变化在频率较小时,变化幅度稍微大一些,随着频率的增加,垂向波流力的大小趋于平缓,接近一个特定值,并随着波幅的增大,这一值也随之增大。
|
图 13 不同A/r下正向波流力随频率的变化对比 Fig. 13 Comparison of forward wave-current force with frequencies at different A/r |
本文对水平圆柱体在波流下所受的力开展数值模拟。首先用前人的实验数据验证数学模型的有效性,其次对不同工况下的波流力进行分析,如下:
1)在水平圆柱体部分淹没时,随着波幅的增加,波浪的反射与阻塞作用都在增加,但波浪反射大于阻塞作用;圆柱在完全淹没时,随着淹没深度的增加,波浪反射作用减小,阻塞作用增大且大于反射作用,所以波幅与垂向位置对于圆柱所受波流力的研究有着极大的影响。
2)水平圆柱所受的波流力随波幅的增大而增大,在部分浸没时,波流力随着波幅的增大,正负方向的力开始变得不对称起来,水平力正方向的大小逐渐大于负方向,负垂向力的大小逐渐大于正垂向力的数值,这主要受波浪反射和阻塞的影响。
3)随着波幅与垂向位置的改变,圆柱所受的波流力也呈现了一些规律。在部分淹没的情况下,随着波幅的增加和垂向位置的增加,水平波流力的大小在增加,垂向波流力的大小在减小;在完全淹没的情况下,水平波流力的大小在减小,正垂向波流力在增加,负垂向波流力的大小在减小,这是波浪的反射与阻塞共同作用下的结果。
4)在部分浸没下,随着频率的增加,水平圆柱所受的波流正向垂向力趋于平缓接近一个特定值。
| [1] |
DIXON A G, GREATED C A, SALTER S H. Wave forces on partially submerged cylinders[J]. Journal of the Waterway Port Coastal and Ocean Division, 1979, 105(4): 421-438. DOI:10.1061/JWPCDX.0000165 |
| [2] |
WESTPHALEN J, GREAVES D M, WILLIAMS C K, et al. Extreme wave loading on offshore wave energy devices using CFD: a hierarchical team approach [C]//The 8th European Wave and Tidal Energy Conference. Uppsala, Sweden, 2009.
|
| [3] |
HU Z Z, CAUSON D M, MINGHAM C G, et al. Numerical simulation of floating bodies in extreme free surface waves[J]. Natural Hazards and Earth System Sciences, 2011, 11: 519-527. DOI:10.5194/nhess-11-519-2011 |
| [4] |
刘必劲, 傅丹娟, 张友权, 等. 浅浸没水平圆柱浮子波浪力计算研究[J]. 海洋工程, 2019(4).
|
| [5] |
毛鸿飞, 陈洪洲. 非完全淹没水平圆柱上波浪力特征的数值模拟[J]. 水科学进展, 2019(5).
|
| [6] |
XIAO H, HUANG W, TAO J, et al. Numerical modeling of wave–current forces acting on horizontal cylinder of marine structures by VOF method[J]. Ocean Engineering, 2013, 58-67. |
| [7] |
胡克, 付世晓, 许玉旺, 等. 不同浸没深度下水平圆柱体的水动力特性试验研究[J]. 船舶力学, 2017, 21(10)1198. |
| [8] |
BAI J, MA N, GU X, et al. Study of interaction between wave-current and the horizontal cylinder located near the free surface[J]. Applied Ocean Research, 2017, 44-58. |
| [9] |
柏君励, 马宁, 顾解忡. 波流对不同淹没深度水平圆柱的载荷分析[J]. 上海交通大学学报(自然版), 2018, 52(8): 938-945. |
| [10] |
FENTON J D. A fifth-order Stokes theory for steady waves[J]. Journal of Waterway, Port, Coastal and Ocean Engineering, 1985, 111: 216-234. DOI:10.1061/(ASCE)0733-950X(1985)111:2(216) |
 2021, Vol. 43
2021, Vol. 43
