0 引　言

水下航行体是一种重要的装备^[1]。针对水下航行体的探测技术研究受到了极大的关注^[2]。在海洋环境中，海水密度分层的层间密度值小，海洋内部较微弱的扰动也能激发大振幅的内波，且分层密度差值小、回复力弱，自生内波周期长、波长长^[3]。水下航行体航行过程中所激发的水动力尾迹是一种难以消除的物理场信息。

为了深入理解尾迹产生的物理机理及其与随机海面的相互作用特性，国内外开展了许多工作。对于潜体水动力尾迹的产生机理、传播特性以及水面特征，国外学者进行了大量的实验和仿真研究^[4-17]。赵先奇等^[11]在密度连续分布的3层流体中，对细长条运动生成的内波问题进行了实验研究。研究结果表明，运动细长体产生的内波可以分为排水体积产生的Lee波和旋涡和湍流效应产生的尾迹波，在F_r = 4.0时Lee波会转变为尾迹波。魏岗等^[12]对半球体的内波转换的实验研究发现，在Froude数为1.6时，Lee波就开始向尾迹波转变。通过目前的实验研究方法可以获得较为准确的结果，但是无法捕获整个流场的演化过程，不利于深入理解尾迹形成的机理和传播过程。近年来计算流体力学技术得到了迅速发展，逐渐成为研究水动力尾迹的主要方式。孟庆杰等^[15]通过数值模拟的方式，对在均匀流体以及强分层流体中运动的Suboff模型的流场和尾迹特征进行了解析。研究发现，两类工况下Suboff的表面尾迹都呈现开尔文波系，但在强分层流体中Suboff自由面尾迹的横波效应显著加强。Change等^[16]使用了RANS方法和VOF模型模拟Suboff在不同Froude数的双层流体中运动所产生的内波。结果表明，随着Froude的增加，内波波长增大，而开尔文角减小。

目前，国内外针对潜体兴波的数值仿真研究相对较少，已有的研究都是在海水密度保持不变或者密度强分层的假设下进行的^[15-17]。本文将采用RANS方法以及VOF方法对密度连续分层环境下全尺度的Suboff产生的自由面尾迹进行数值模拟。通过对流场结构和尾迹特征进行详细的解析，研究密度连续分层以及潜深等参数对尾迹形成和传播的影响。

1 数值方法 1.1 控制方程

基于雷诺平均N-S方程(RANS方程)，不可压缩流动的控制方程为：

$ \frac{{\partial \overline {{u_i}} }}{{\partial {x_i}}} = 0, $

(1)

$ \rho \frac{{\partial \overline {{u_i}} }}{{\partial t}} + \rho \overline {{u_j}} \frac{{\partial \overline {{u_i}} }}{{\partial {x_j}}} = \rho \overline {{F_i}} - \frac{{\partial \overline p }}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left(\mu \frac{{\partial \overline {{u_i}} }}{{\partial {x_j}}} - \rho \overline {u'_iu'_j} \right){\text{。}} $

(2)

式中： $ \overline {{u_i}} $ 与 $ u'_i $ 为雷诺平均速度和脉动速度； $ \ \rho \overline {u'_i u'_j} $ 为雷诺应力项； $ \overline {{F_i}} $ 为质量力； $ \ \rho $ 为流体密度。

1.2 湍流模型

RANS方程组中有关湍流脉动值的雷诺应力项 $ \rho \overline {u'_i u'_j} $ 是未知的。为了使方程封闭，选用Realizable k-ε湍流模型对雷诺应力项进行建模，湍动能k及耗散率ε输运方程分别为：

$\begin{split} \frac{\partial }{\partial t}(\rho k)+\frac{\partial }{\partial {x}_{j}}(\rho k{u}_{j})=&\frac{\partial }{\partial {x}_{j}}\left[\left(\mu +\frac{{\mu }_{t}}{{\sigma }_{k}}\right)\frac{\partial k}{\partial {x}_{j}}\right]+\\ &{P}_{k}+{P}_{b}-\rho ϵ-{Y}_{M}+{S}_{k} {\text{，}} \end{split} $

(3)

$ \begin{split}\frac{\partial }{{\partial t}}(\rho \varepsilon ) + \frac{\partial }{{\partial {x_j}}}(\rho \varepsilon {u_j}) =& \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] +\rho {\mkern 1mu} {C_1}S\varepsilon - \\ &\rho {\mkern 1mu} {C_2}\frac{{{\varepsilon ^2}}}{{k + \sqrt {\nu \varepsilon } }} + {C_{1\varepsilon }}\frac{\varepsilon }{k}{C_{3\varepsilon }}{P_b} + {S_\varepsilon }{\text{，}} \end{split} $

(4)

其中， $ {C_1} = \max \left[ {0.43,\dfrac{\eta }{{\eta + 5}}} \right] $ ， $\eta = S\dfrac{k}{\varepsilon }$ ， $S = \sqrt {2{S_{ij}}{S_{ij}}} $ 。式中： $ {P_k} $ 表示由于平均速度梯度而产生的湍流动能； $ {P_b} $ 为由浮力引起的湍流动能； $ {C_2} $ 和 $ {C_{1\varepsilon }} $ 为常数（ ${C_2} = 1.9 $ ， ${C_{1\varepsilon }}{\text{ = }} 1.44$ ）； $ {\sigma _k} $ 和 $ {\sigma _\varepsilon } $ 分别为湍动能和耗散率的湍流普朗特数， ${\sigma _k} = 1.0$ ， ${\sigma _\varepsilon } = 1.0$ ； ${\mu _t} = \rho {C_\mu }\dfrac{{{k^2}}}{\varepsilon }$ 。其中， ${C_\mu } = \frac{1}{{{A_0} + {A_s}\dfrac{{k{U^*}}}{\varepsilon }}}$ ， $ {U^*} \equiv \sqrt {{S_{ij}}{S_{ij}} + {{\tilde \Omega }_{ij}}{{\tilde \Omega }_{ij}}} $ ， ${\tilde \Omega _{ij}} = {\Omega _{ij}} - 2{\varepsilon _{ijk}}{\omega _k}$ ， ${\Omega _{ij}} = \overline {{\Omega _{ij}}} - $ ${\varepsilon _{ijk}}{\omega _k} $ ， $ \overline {{\Omega _{ij}}} $ 为旋转坐标系中角速度 $ {\omega _k} $ 的平均旋转速率张量。常数 $ {A_0} $ 和 $ {A_s} $ 分别为：

$ {A_0} = 4.04,\;\;{A_s} = \sqrt 6 \cos \phi\text{，} $

(5)

$ \phi =\frac{1}{3}{\mathrm{cos}}^{-1}(\sqrt{6}W),W=\frac{{S}_{ij}{S}_{jk}{S}_{ki}}{{\tilde{S}}^{3}}\text{，} $

(6)

$ \tilde{S}=\sqrt{{S}_{ij}{S}_{ij}},{S}_{ij}=\frac{1}{2}\left(\frac{\partial {u}_{j}}{\partial {x}_{i}}+\frac{\partial {u}_{i}}{\partial {x}_{j}}\right)\text{。} $

(7)

1.3 VOF方法

本文采用VOF(Volume of Fluid)方法对潜体激发的自由面尾迹进行追踪。此方法引入了一个流体体积分数的输运方程，通过求解该输运方程可以得出每个网格单元内互不掺混流体的体积分数，以此来确定交界面的位置。

假设第q种流体在单元中的体积分数为 ${\alpha _{{q}}}$ ，对第q种流体有：

$ \frac{{\partial {\alpha _{\text{q}}}}}{{\partial t}} + {u_i}\frac{{\partial {\alpha _{\text{q}}}}}{{\partial {x_i}}} = 0 {\text{，}}$

(8)

流体的体积分数之和需要满足：

$ \sum\limits_{q = 1}^n {{\alpha _q}} = 1{\text{，}} $

(9)

单元内流体的密度为：

$ \rho = \sum\limits_{q = 1}^n {{\alpha _q}} {\rho _q} {\text{。}}$

(10)

式中: $ {u_i} $ 为微元的速度。本文自由面均用 $ {\alpha _{air}} = 0.5 $ 的等值面来表示。

1.4 计算设置 1.4.1 研究对象

选用全尺度Suboff标模作为研究对象，该模型的示意图如图1所示。总长度L = 100 m，最大直径D = 11.662 m，附体长度L_w = 8.448 m，附体高度H_w = 5.094 m。

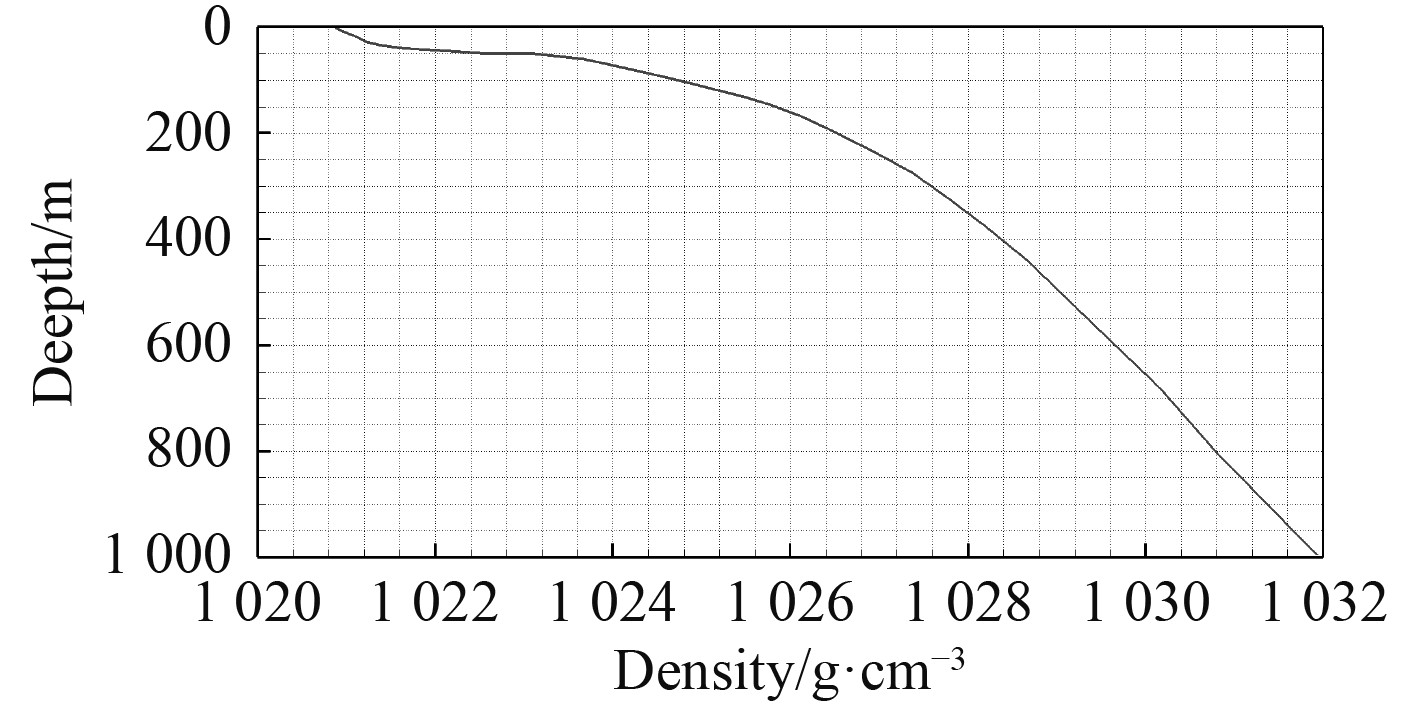
当前的研究考虑了实际海水中密度的连续分层效应，真实工况下海水密度随深度变化的趋势如图2所示。为了实现密度的连续变化，使用VOF方法。液体进口处根据Fluent中的用户自定义函数（User Defined Function，UDF）定义不同深度处轻重液体的体积分数，根据式（7）轻重液体密度与体积分数配比实现密度的连续变化。

1.4.2 计算域与边界条件

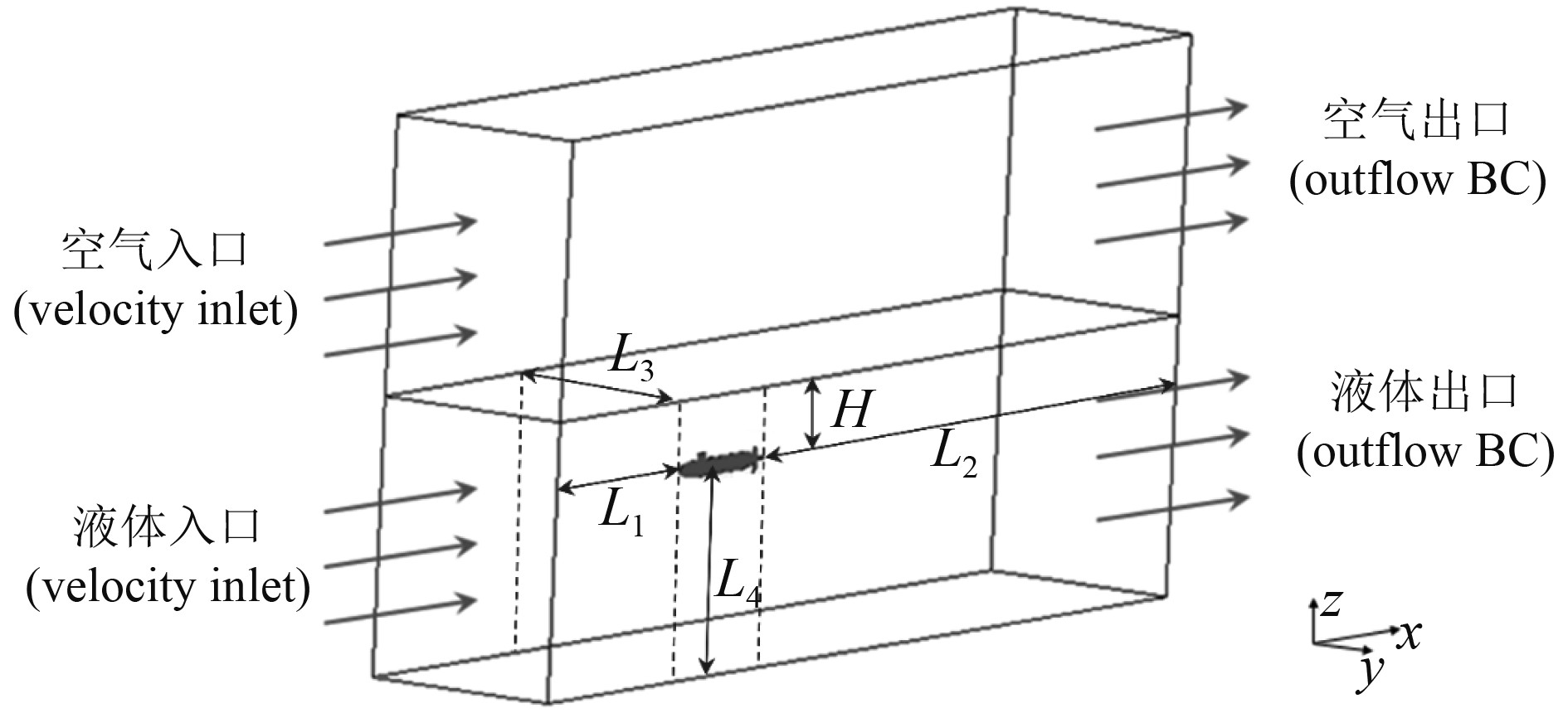
为了提高计算的效率，根据当前流场的对称性特征，只对一半的流场进行计算，中间的对称面使用对称边界条件。计算域的示意图如图3所示。考虑到计算域的大小对尾迹捕捉精度的影响，在整个计算过程中，始终保持入口处距离潜体头部约1.5 L（L为Suboff潜体的全长，在当前计算中潜体长度为100 m）；出口处距离潜体尾部约4～5 L；计算域底部距离潜体中心处约1.5～2.0 L；计算域的侧面距离对称面约1.5 L。如图3所示，空气和液体的入口均采用速度入口边界条件，出口均采用Outflow出口边界。计算域的上下方设置为可滑移壁面边界条件，而艇体周围为无滑移壁面边界。计算域的左右侧面均为零梯度的对称边界条件。

1.4.3 计算网格

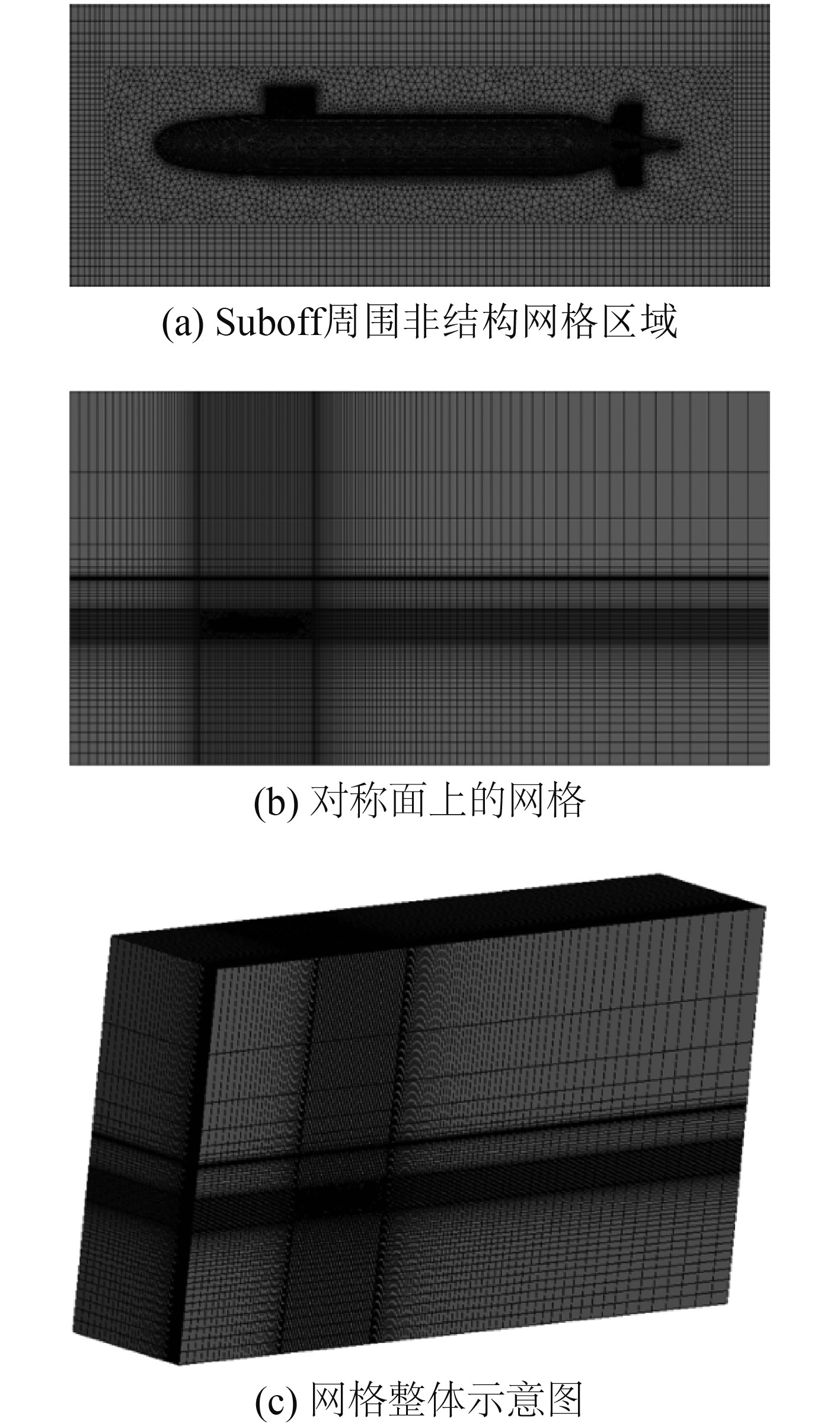
考虑到当前计算模型几何外形的复杂性，为了减少网格数量，同时提高计算效率，本文采用了混合网格的方法对流场进行网格划分。其中，Suboff周围使用了非结构网格，远离艇体的区域使用了结构网格。当前计算使用的网格所图4所示，图4(a)为Suboff周围的非结构网格区域，图4(b)为对称面上的网格，图4(c)为整个计算域内的网格示意图。非结构网格与结构网格通过interface进行关联。为了更好捕捉自由面上的尾迹特征，在气液交界面附近的网格进行了局部加密。

2 结果分析 2.1 数值模型验证

为了验证当前数值模型的可靠性，将本文计算的自由面尾迹与文献[18]中的进行比对。图5为文献[18]和本文计算所得的自由面尾迹波高图。图5(a)和图5(b)中的Suboff的潜深为20 m，航速为30 kn。由图5可知，2种工况下的自由面尾迹均呈现出明显的Kelvin波系特征，两者的波形夹角约为24^o。2种工况下表面波的波形基本一致，波长基本相同，最大波谷都是出现在水下航行体尾部对应的水面。由于当前2种工况下水下航行体的尺度存在差异，所以自由面尾迹的最大波高出现了一定的差异。文献[18]中艇长为85.22 m水下航行体在自由面激发尾迹的最大波高为2.77 m，当前计算的结果为3.35 m，两者的相差约为1.1倍，这与水下航行体尺寸的比例一致。根据以上的对比分析，认为当前的计算结果可靠。

2.2 流体分层的影响

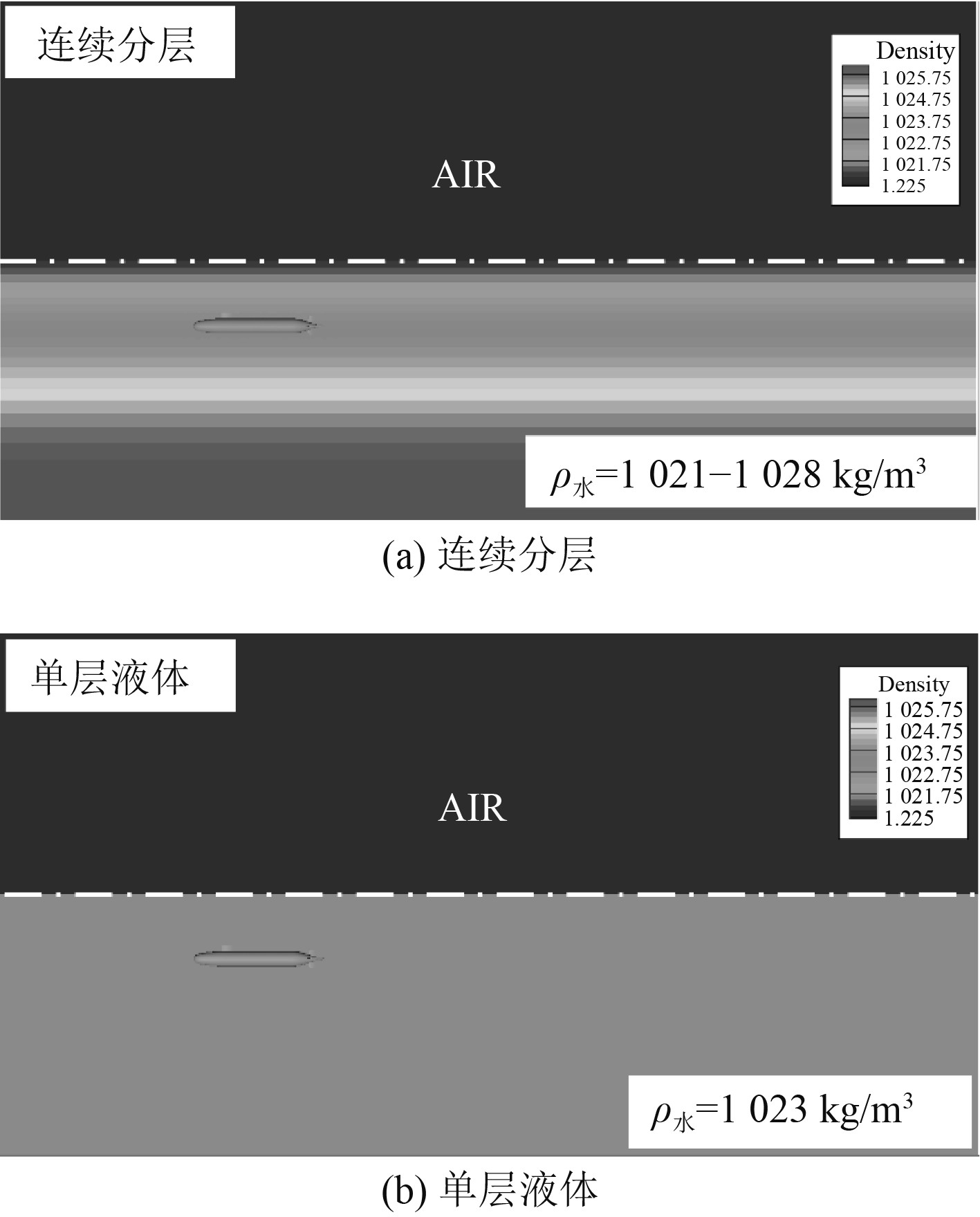
为了考察真实环境中流体分层作用对Suboff周围流场的影响，将航速为30 kn的Suboff分别置于密度连续变化和密度恒定的水中，采用数值仿真的方式求解Suboff周围的流场。根据图2海水密度随深度变化的曲线可知，连续分层算例中海水的密度将在1 021～1 028 kg/m³之间连续变化。而对于单层液体工况下的算例，密度将设定为1 023 kg/m³。图6为2种工况下海水在深度方向的密度变化。。

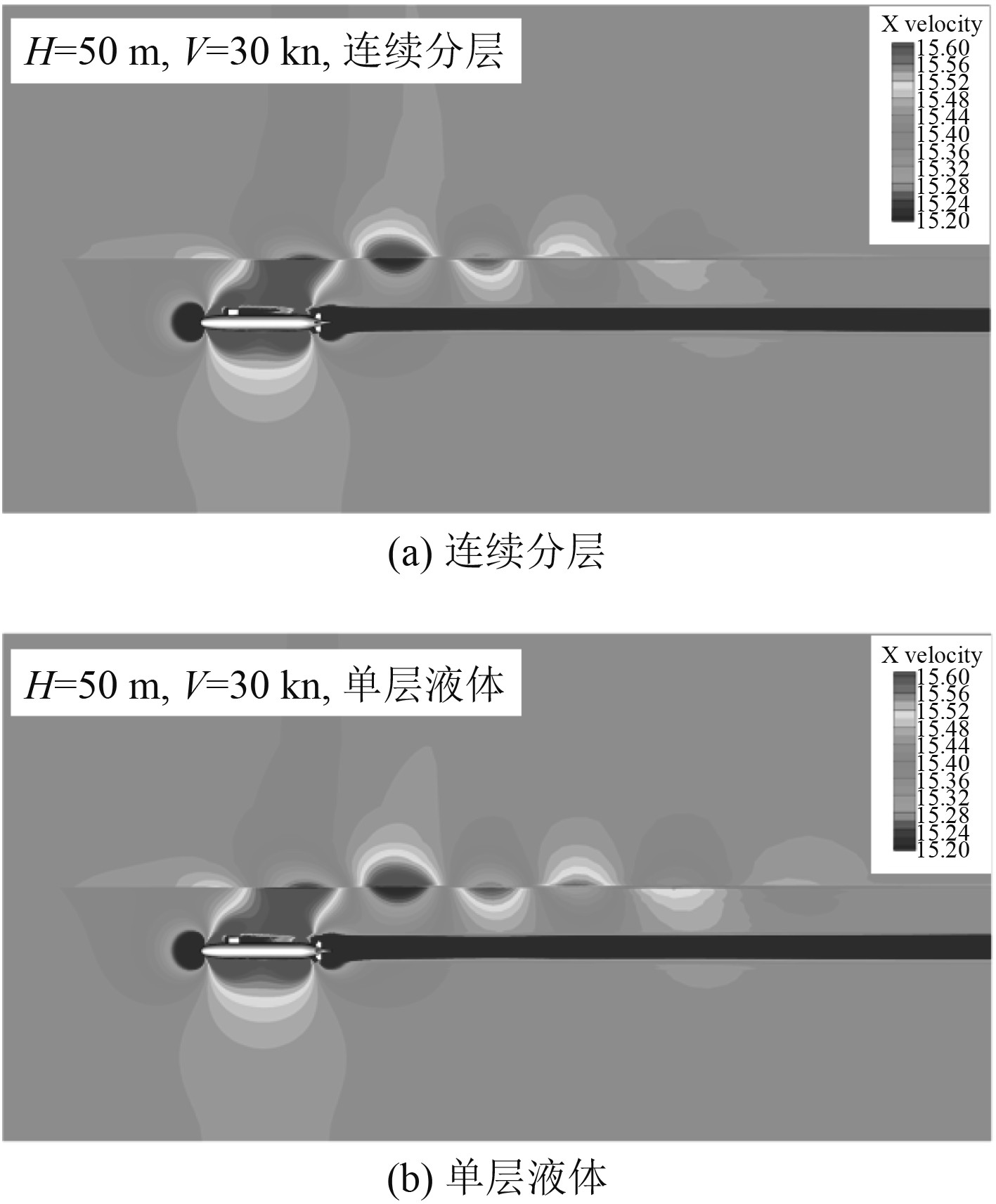
表1为潜深对自由面尾迹的最大波高的影响，其中水下航行体的航行速度均为30 kn。为了考察密度分层对自由面尾迹特征的影响，在表1中将连续分层与单层液体2种工况下自由面尾迹的最大波高进行了比较。由表1可知，2种状态下自由面尾迹的最大波高都基本保持一致。图7为潜深50 m、航速30 kn时Suboff在x/L=0.3和x/L=0.9切面上x速度以及压力的分布，其中每个云图左侧为连续分层环境中的流场，右侧为单层液体环境中的流场。由图7（a）可知，x/L=0.3处为附体正后方，由于附体对流动有一定的阻碍作用，附体后方出现了一个低速区域。而x/L=0.9处为Suboff尾舵的切面，液体流过后舵面时速度增加，压力减小。如图7可知，在当前2个典型的位置处，连续分层环境中Suboff周围的流场与单层液体环境中的流场表现出完全一样的特征，密度的连续变化不会改变Suboff周围的流场结构。根据流体的波动理论可知，流体受到扰动后，在恢复力的作用下，会产生使运动恢复平衡的倾向，由于流体的惯性和恢复力的互相制约，就会形成流体的波动。图8为2种工况下Suboff对称切面上的x速度分布。可知，Suboff的存在改变了原有的流动状态。艇前的水流速度减小，但是流过艇身时流体速度增加，速度增加的区域一直向上扩展至自由面，这会给自由面带来一定的扰动。由于自由面两侧流体的密度存在较大的差异，自由面的扰动使得表面一侧的液体穿过平衡分界面进入另一侧的气体中，因此在原先的平衡位置上就存在2种流体。为了达到平衡状态，重力和浮力将不断互相作用，因此自由面就会形成波动。自由面的变形会使得流体内部同一表面上出现压力波动，使得表面的波动向外传播，这就是水下航行体在自由面激发尾迹的物理机制。如图8所示，自由面附近的流体出现了明显的速度波动，并且会一直往后传播。连续分层与单层液体的速度剖面基本保持一致，速度的大小以及分布几乎完全相同，但与连续分层环境相比当前工况下单层液体环境中自由面的速度波动传播的更远。

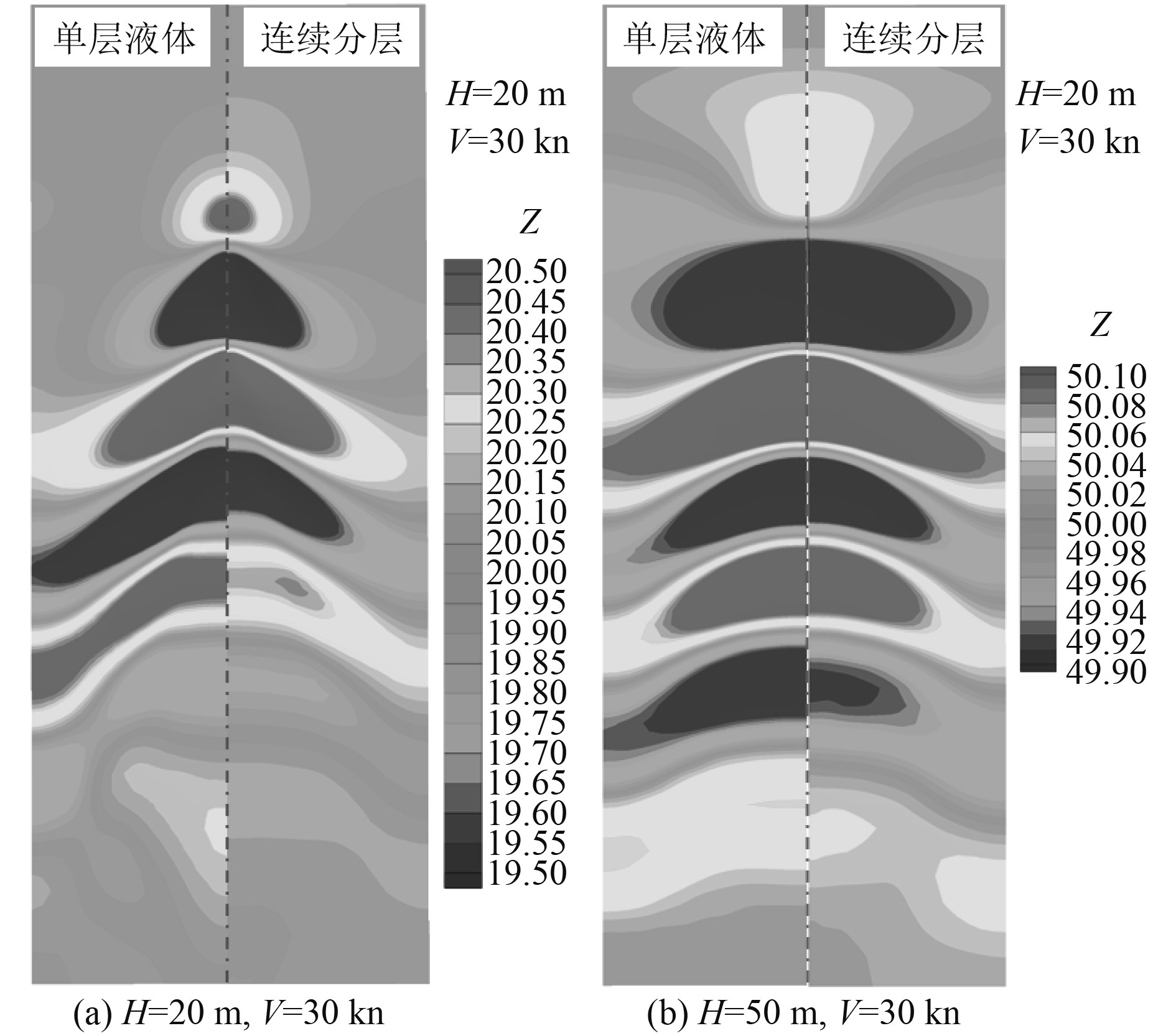
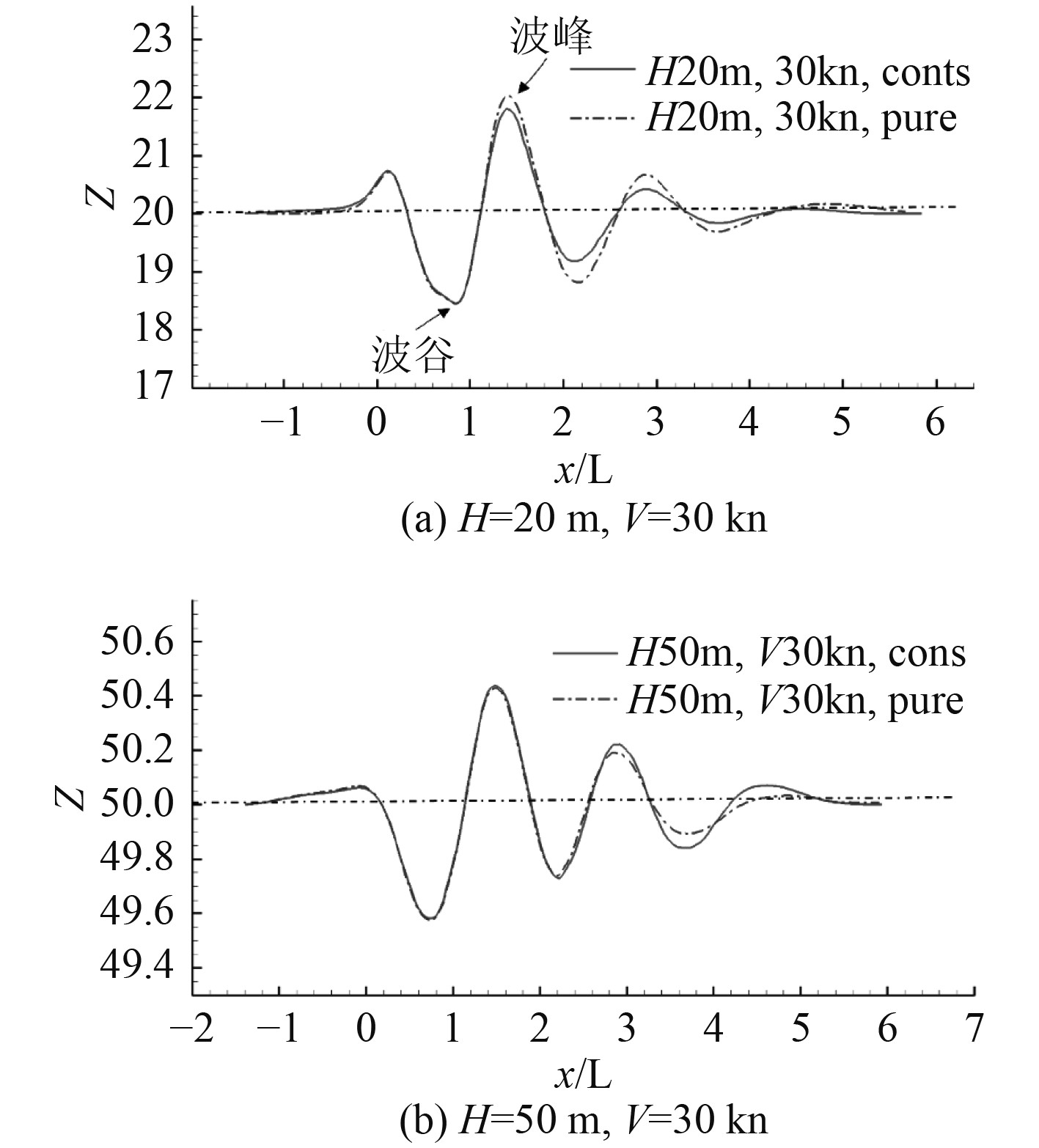
图9为2种不同潜深下单层液体和连续分层环境中的水下航行体产生的自由面尾迹对比。从图中可以发现，2种工况下水下航行体激发的自由面尾迹的形状基本上保持一致，都呈现出非常显著的开尔文波系特征。在前3个波长的尾迹中，两者的特征基本相同。在第4个波长后，连续分层环境中的尾迹特征迅速衰退，而单层环境中的尾迹特征仍然十分明显。图10为当前2种工况下连续分层和单层液体环境中表面波的波形。在潜深为20 m和50 m时，2种工况中表面波的波峰/谷位置、波长基本一致。在x/L=0处即潜体头部会出现一个较小的波峰，表面波最大的波谷出现在x/L=0.8处，最大波峰出现在x/L=1.5，波长约为1.5L。整个表面兴波约在3个波长后开始衰弱，影响范围可达到船后约500 m范围。由图9和图10可知，连续分层和单层液体环境中表面波的波形几乎完全重合，波形、波长、波高基本保持一致。

2.3 潜深对尾迹的影响

为了研究潜深对自由面尾迹的影响，对航速为30 kn，潜深为20 m，50 m，80 m和100 m的Suboff激发的流场进行详细的数值模拟。由表1可知，在潜深为20 m时，最大波高达到3.35 m。随着潜深的增加，自由面尾迹的最大波高逐渐减小。潜深为100 m时，最大波高已经减小至0.127 m。表2为不同潜深下航行速度为30 kn的Suboff产生自由面尾迹的最大波速。在潜深为20 m时，自由面尾迹的波速最大，为16.26 m/s。自由面尾迹的波速会随着潜深的增加而减小，当潜深为100 m时，波速只有15.47 m/s，这与航行速度为15.43 m/s时基本相当。通过对尾迹特征的分析发现，潜深对自由面尾迹有非常显著的影响。

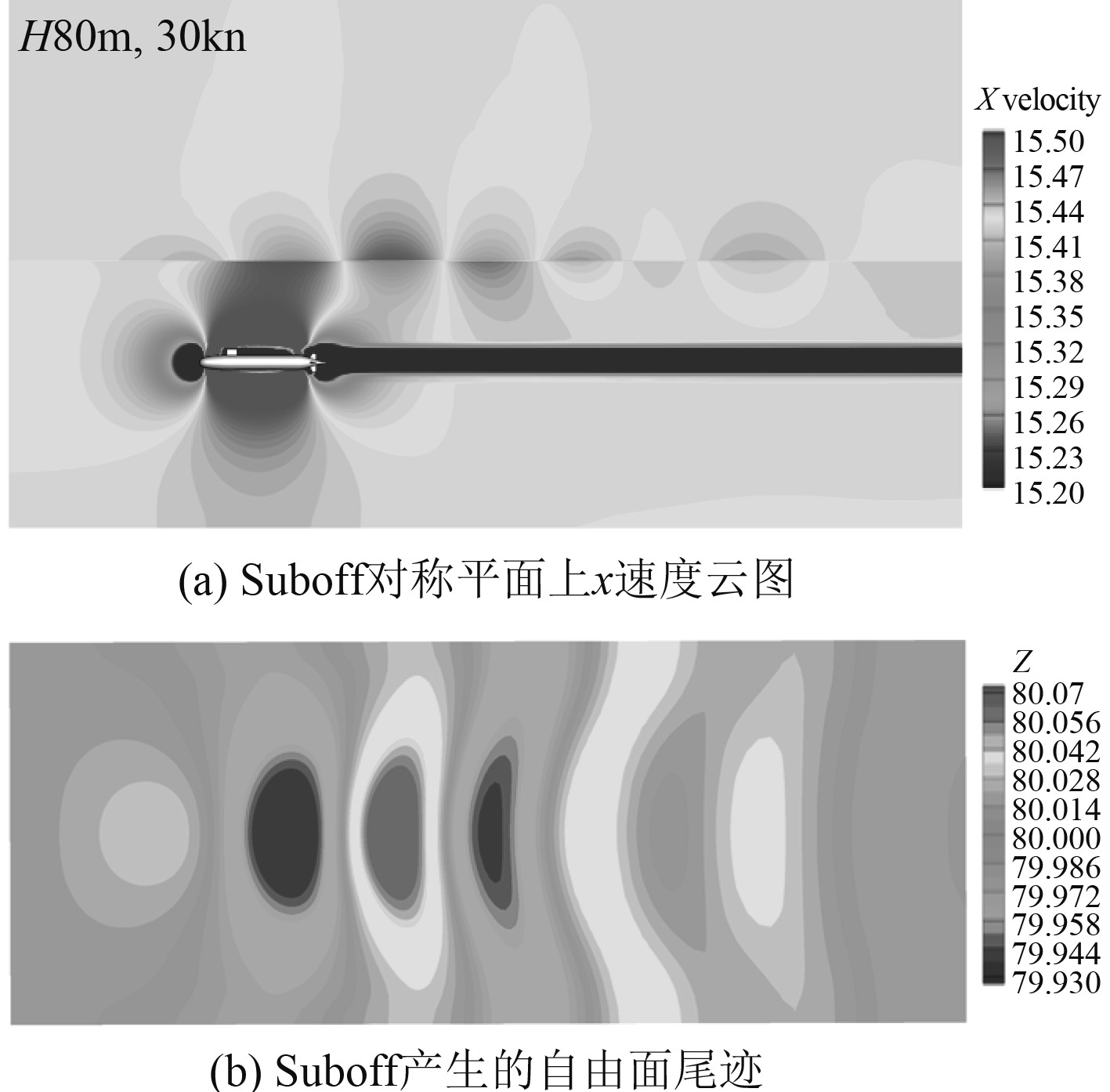
为了探明潜深对自由面尾迹特征影响的过程，对不同潜深的Suboff周围的流场进行分析。图11、图12以及图13分别为3种不同潜深条件下Suboff对称切面上x速度云图和对应的自由面尾迹。根据2.1节中的分析可知，水下航行体的运动使得艇身上方的液体速度增加，这种速度扰动一直会传播至自由面。自由面附近流体密度差异较大，速度扰动使得2种流体互相穿越自由面，这打破了原有的平衡。由图11(a)、图12(a)和图13(a)可知，在不同潜深的条件下，Suboff对称切面的x速度场出现了显著的差异。潜深为20 m时，自由面附近流体的速度出现了明显的大幅度波动，而潜深为80 m时自由面的速度波动相比而言变得十分微弱。水下航行体的运动会使得艇身周围的流体加速，但是随着潜行深度的增加，水下航行体对自由面附近流体的加速作用减小，水下航行体运动对自由面产生的扰动逐渐变得微弱。

由图11(b)、图12(b)和图13(b)可知，3种条件下的自由面尾迹均呈现明显的开尔文波系结构，且水下航行体头部处对应的自由面为上凸，而艇身处对应的自由面是下凹的。在潜深为20 m时，尾迹呈现明显的后掠形态。随着潜行深度的增加，自由面尾迹的波形角逐渐变大。

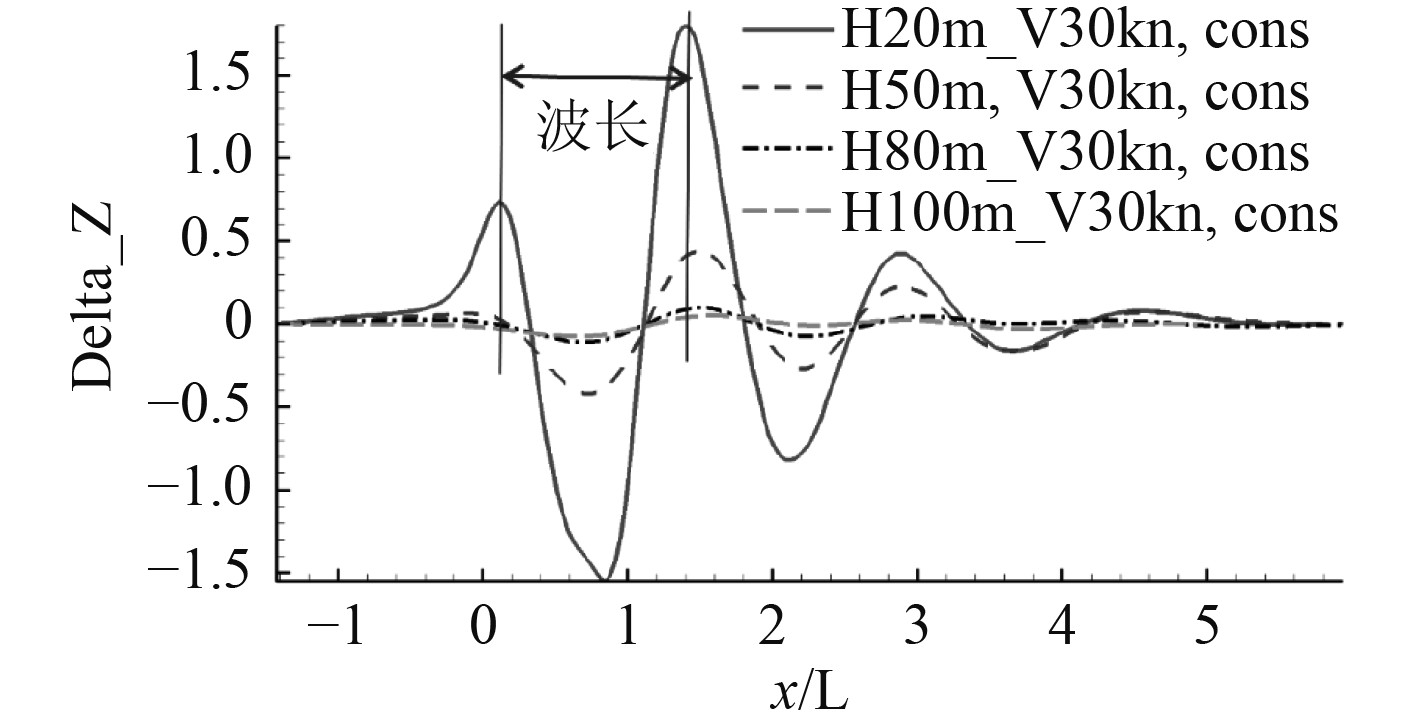
图14为航速为30 kn时不同潜深下自由面尾迹的波形图。可知，4种工况的自由面上第一个波峰均出现在x/L=0处（即潜体头部），最大波谷和最大波峰分别位于x/L=0.8和x/L=1.5处。不同潜深下，表面波的波长基本保持一致，约为1.5L。对于航速为30 kn，潜深为20 m的工况而言，表面波的最大谷值约为1.52 m，最大峰值约为1.80 m。随着潜深的增加，表面波波峰高度显著减小。

3 结　语

本文以全尺度的Suboff模型为研究对象，基于非定常雷诺平均N-S方程（URANS），结合k-ε湍流模型和Volume of Fluid(VOF)方法，对连续分层环境中运动的Suboff模型周围的流场以及自由面尾迹的特征进行了数值仿真研究。

1）考察了密度连续分层环境对自由面尾迹的影响。通过对连续分层和单层液体2种工况下流场结构以及尾迹特征进行详细的对比研究发现，密度的变化不会对Suboff周围的流场产生较大的影响。在2种工况下，自由面尾迹均呈现出明显的开尔文波系结构，且波形、最大波高以及最大波速基本保持相同。通过对流场的深入分析发现，潜体的运动会对周围的流场产生扰动，这种扰动会一直传播至自由面。由于自由面附近流体密度的差异较大，受到扰动后会导致原来的平衡位置出现两种不同密度的流体。为了恢复平衡，自由面附近流体重力和浮力会互相作用，使得液面出现波动。在这2种工况下，扰动源完全相同，所以自由面尾迹的特征基本相同。

2）对不同潜深下Suboff产生的自由面尾迹进行了研究。研究表明，随着潜航深度的增加，自由面尾迹的最大波高和波速急剧减小，尾迹特征减弱。通过对Suboff周围流场进行详细的解析发现，由于粘性作用的存在，随着潜深的增加，潜体对自由面附近流体的加速作用减小，自由面附近受到的扰动逐渐变小，所以激发的尾迹变得更加微弱。