水下航行体因其极强的隐蔽性与突袭性而在军用领域占有重要地位,其中以潜艇最具代表性[1]。近年来,受益于光电技术的飞速发展,红外探测设备的分辨率、精度和抗干扰能力大大提高,红外探潜作为一种重要的非声探潜措施,以其探测范围大、昼夜工作、被动探测等优点而被广泛关注[2-4]。水下航行体在航行过程中,其动力系统产生的废热会被冷却水吸收,并随冷却水排放到海水中。这些冷却水的温度明显高于周围水体的温度,在密度差的驱使下向上浮升,有可能在海面形成温度异常的红外特征。
目前,相关学者针对密度分层对热射流流动的影响进行了大量研究,并取得了一系列成果。江传富等[5]提出了热尾流不同发展阶段的物理模型,分析了其在密度均匀和分层流体中的浮升规律;张昊春等[6]建立了温度分层环境和均匀介质环境中的射流模型,计算得到了热尾流的温度分布特性及浮升扩散过程中的衰减规律;杨立等[7]通过对线性密度分层流体中热尾流的浮升过程研究,发现了流体的分层会抑制热尾流的浮升。
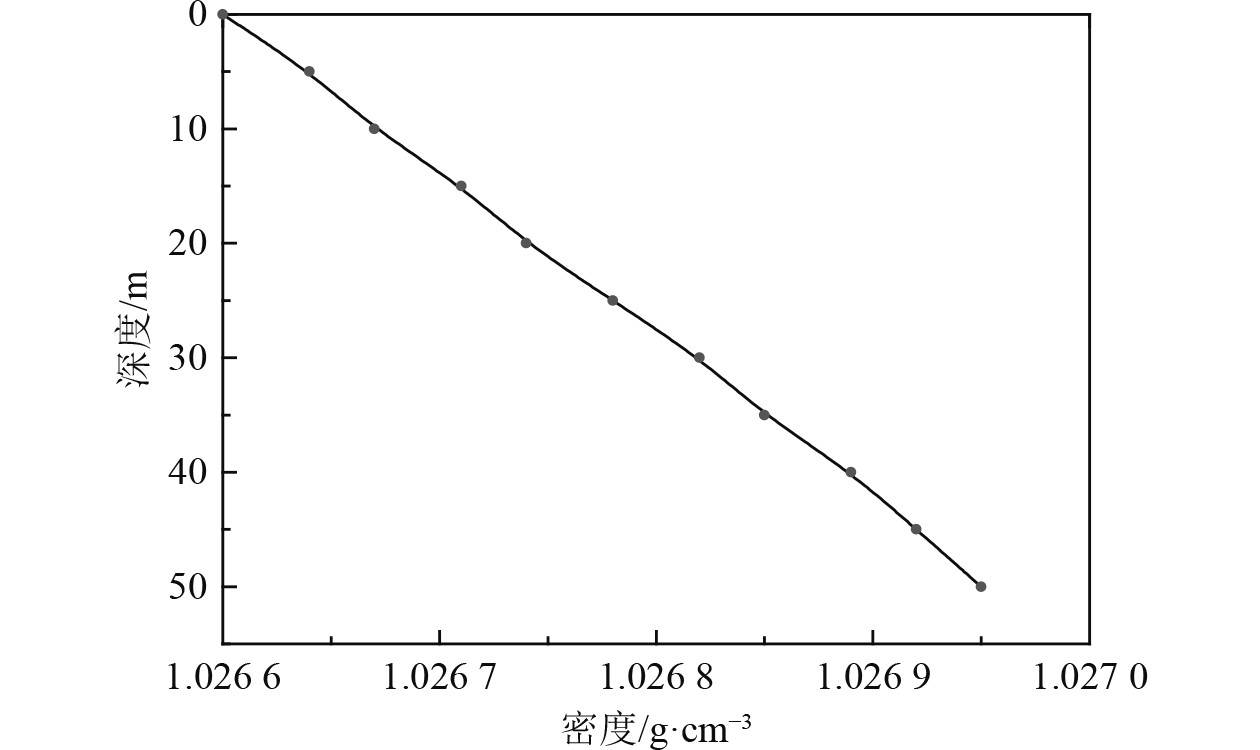
海水的温度分布受诸多因素的影响,如深度、地理位置、季节、太阳辐射和海洋大气热交换等。海水温度随深度的增加而显著递减,根据NOAA(National Oceanic and Atomspheric Administration)数据库WOD(World Ocean Database)可得海水温度沿着深度方向的变化规律[8],不同纬度地区海水总体温度变化值约在30℃左右;同一地区,在50 m深度范围内,海水温度变化范围约在1℃~2℃,靠近海平面处(深度20 m以内)温度沿深度变化不明显,原因为海上风浪大,海平面处海水运动剧烈,不同深度海水之间对流混合,温度趋于一致;深度大于20 m后水温迅速下降。海水盐度是指海水中全部溶解固体与海水质量之比,也会随深度的变化而发生改变。根据海水温度、盐度在深度方向上的变化情况,总结了40° N附近50 m深度内,密度变化规律,如图1所示。在深度方向上,海水的密度为线性增加,50 m深度下密度的增长幅度为0.35‰。需要指出的是,大量文献中对表层海水密度分层的处理方式也是线性的,与图1中的规律有一致性[9,10]。
|
图 1 40° N海水密度分层的典型变化规律 Fig. 1 Typical variation law of seawater density stratification at 40°N latitude |
本文在海水密度沿深度方向变化规律的基础上,使用数值仿真手段模拟热射流在密度分层海水中的运动,探究密度分层对热射流流动的具体影响关系,矫正未分层情况下数值仿真的预测结果,增加数值仿真预测结果的可靠性。
1 数学模型数值仿真采用流体连续介质模型假设,其流动受纳维斯托克斯(N-S)方程控制[11]。N-S方程的张量形式如下:
| $ \begin{split}&\frac{{\partial \left( {\rho {u_i}} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_i}{u_j}} \right)}}{{\partial {x_j}}} = - \frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left( {\mu \frac{{\partial {u_i}}}{{\partial {x_j}}}} \right) + f_i\text{,} \\ &\left( {i, j = 1,2, 3} \right)\text{,}\end{split} $ | (1) |
| $ \frac{{\partial \left( {{u_j}} \right)}}{{\partial {x_j}}} = 0 {\text{。}}$ | (2) |
式中:
以温度形式表达的能量方程为:
| $ \frac{{\partial T}}{{\partial t}} + \frac{{\partial T}}{{\partial {x_j}}} = \frac{\partial }{{\partial {x_j}}}\left( {\alpha \frac{{\partial T}}{{\partial {x_j}}}} \right),\qquad\left( {i, j = 1, 2,3} \right) ,$ | (3) |
其中
密度与温度的关系式为:
| $ \rho=\rho_{\mathcal{R e f}}\left[1-\beta\left(T-T_{\text {Ref }}\right)\right] {\text{,}}$ | (4) |
式中:
密度不分层情况下,Boussinesq假设参考密度
| $ G=\rho_{R{\rm{ef}}}[1-\beta(T-T_{R{\rm{ef}}})]g{\text{,}} $ | (5) |
所受浮力为:
| $ F={\rho }_{R\text{ef}}g{\text{。}}$ | (6) |
式(6)与式(5)相减,得到浮力与重力的合力大小为:
| $ {F}_{\text{i}}={\rho }_{R\text{ef}}[\beta (T-{T}_{R\text{ef}})]g {\text{。}}$ | (7) |
由于数值仿真软件设置的实际需要,参考密度
| $ \beta^{\prime}=\frac{\rho(h)}{\rho_{\text {Ifof }}} \beta {\text{。}}$ | (8) |
其中:
数值仿真的计算区域如图2所示,整个计算区域x方向(航行方向)长为120 m,z方向宽为80 m,y方向(垂直方向)高为70 m。喷嘴(即热射流出口)离顶端自由液面高度为50 m,距离入口平面长度为5 m。整个计算区域划分为1,2,3三个区域。根据计算精度的需要,分别对这3个计算区域划分了疏密不同的网格,其中,喷嘴位于计算区域1中,其网格质量将会影响整个热射流流场的分布,因此对该区域的网格进行了加密处理,尤其在喷嘴周围使用了高密度的O型网格。

|
图 2 计算区域 Fig. 2 Computational region |
计算区域左侧面设置为入口边界条件,入口海水温度为15℃;喷嘴也设置为入口边界条件,热射流的速度大小为0.33m/s。右侧面设置为出口边界条件,其余外侧面均为自由滑移壁面。计算区域内部的接触面设置为interfaces。
2.2 工况计算图1定量描绘了40° N海域,50 m水深海水密度的典型分布,不难发现其变化范围极小。因此,定义海水的密度分层值
| $ \varphi=\frac{\left(\rho_{50}-\rho_{0}\right)}{\rho_{0}} {\text{。}}$ | (9) |
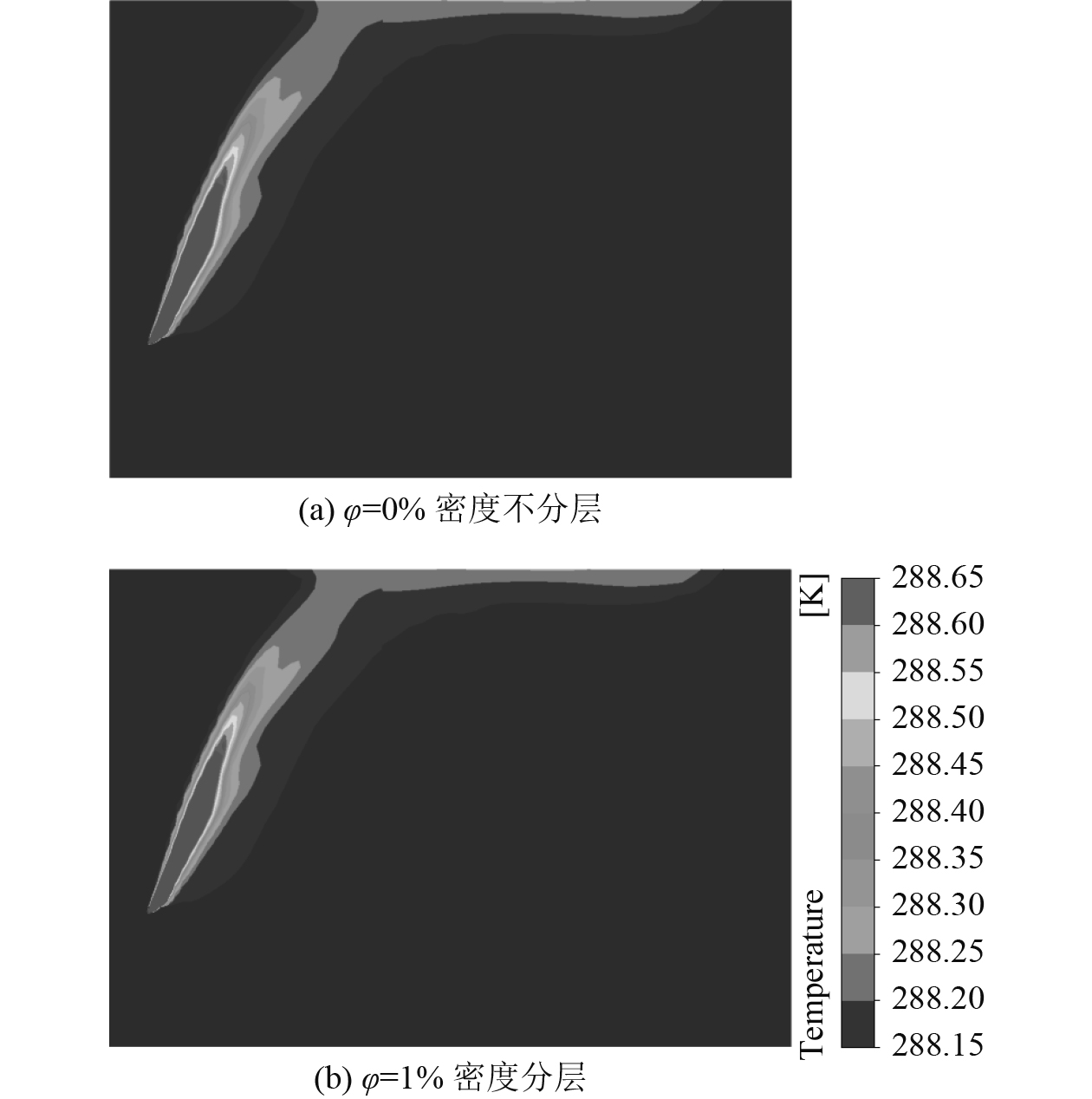
图3给出了相同时刻,密度不分层
|
图 3 t=16min,xy截面温度云图 Fig. 3 xy section temperature nephogram in 16 min |
为了在数值计算结果中体现密度分层对热射流的影响,需使密度分层的影响远大于数值计算误差,因此数值仿真计算选取水下航行体航速V为0 kn,0.1 kn,0.2 kn,密度分层值
采用热射流高度H作为衡量热射流影响的指标,假设海水温度为15℃,若受热射流影响使温度上升0.01℃,图4给出了热射流某时刻温度15.01℃的等值面图,任意时刻热射流高度H定义为此时喷嘴中心到T=15.01℃温度等值面顶端的垂直距离。

|
图 4 15.01℃等值面 Fig. 4 15.01 °C isosurface |
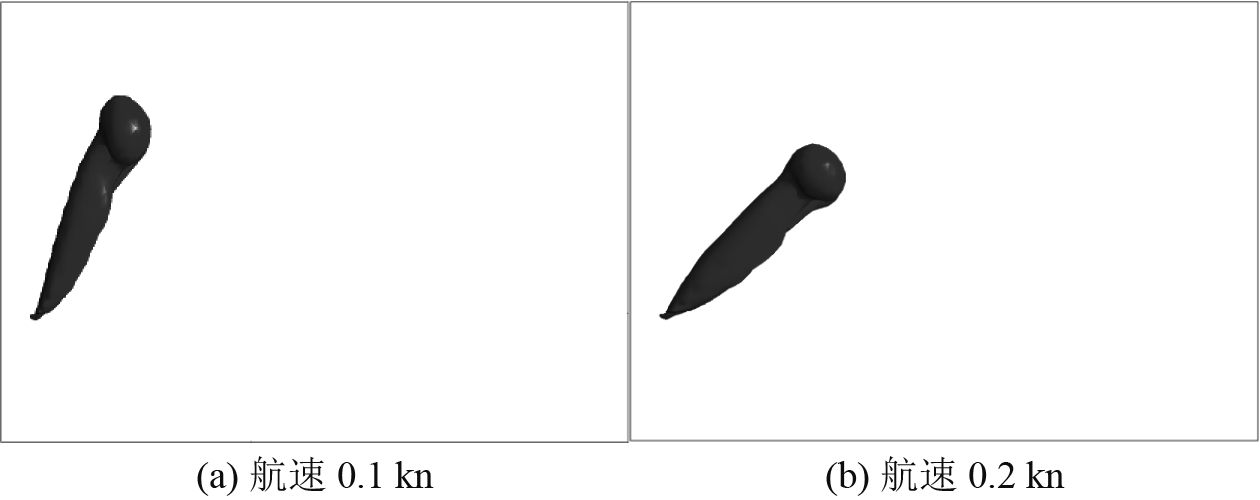
密度不分层情况下,随着航速增加,相同时刻热射流的高度H逐渐降低;随着热射流温度的提高,相同时刻热射流的高度H逐渐升高。图5与图6对比了相同密度分层值=50%情况下,水下航行体航速、热射流温度对热射流流场的影响,结果表明上述规律依然成立。由图5可知,在热射流出口温度为45℃情况下,航速0.2 kn相对于航速0.1 kn,其热射流15.01℃等值面顶端较低,即热射流高度H较低;由图6可知,在航速0.1 kn情况下,热射流出口温度55℃相较于出口温度45℃,其热射流高度H较高。
|
图 5 t=4 min,热射流15.01℃等值面 Fig. 5 Hot jet 15.01 °C isosurface at 4 min |

|
图 6 t=4 min,热射流15.01℃等值面 Fig. 6 Hot jet 15.01 °C isosurface at 4 min |
由
为了体现密度分层影响对热射流流场的影响,引入密度分层影响的修正系数
| $ \omega = \frac{{{H_\varphi }}}{{{H_0}}} \text{,}$ | (10) |
其中:H0为密度不分层(即
| $ {H_\varphi } = \omega {H_0}\text{。}$ | (11) |
图7(a)列出了

|
图 7
|
图8列出了

|
图 8
|
图9列出了V=0.1 kn,

|
图 9
V=0.1 kn, |
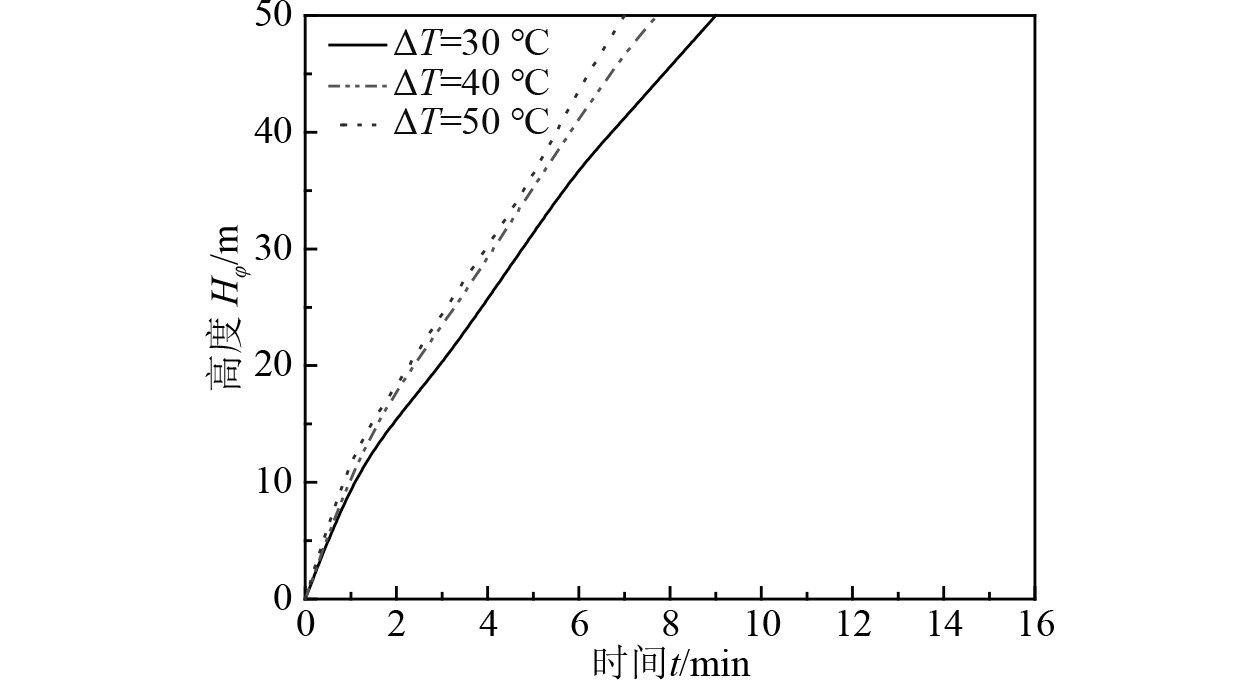
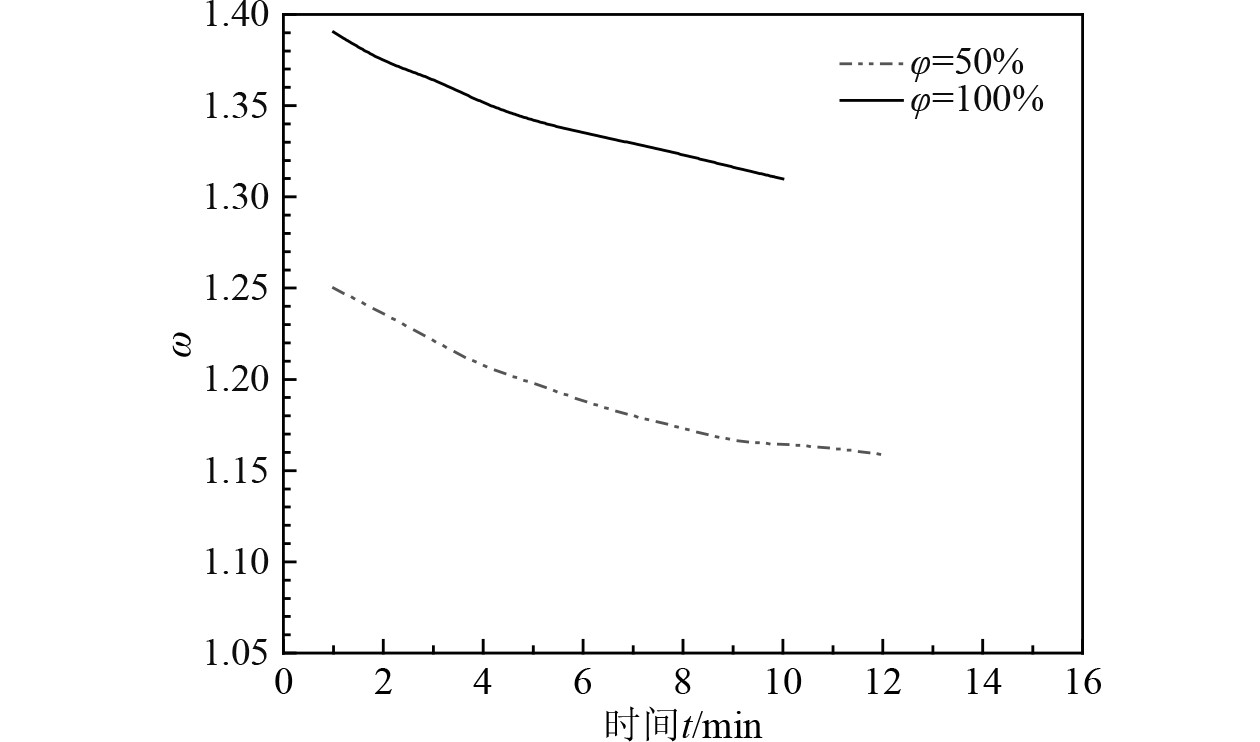
图10~图14分别列出了改变密度分层值
|
图 10
|
|
图 11
|

|
图 12
|
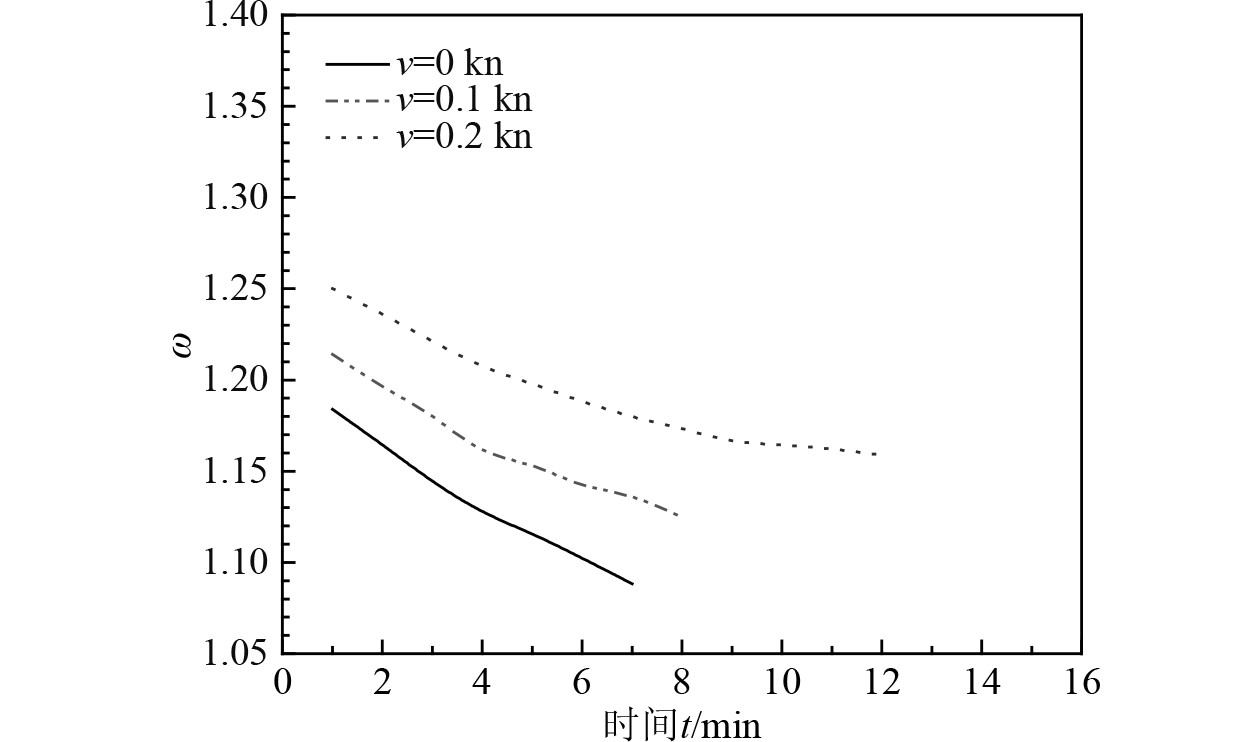
|
图 13
|
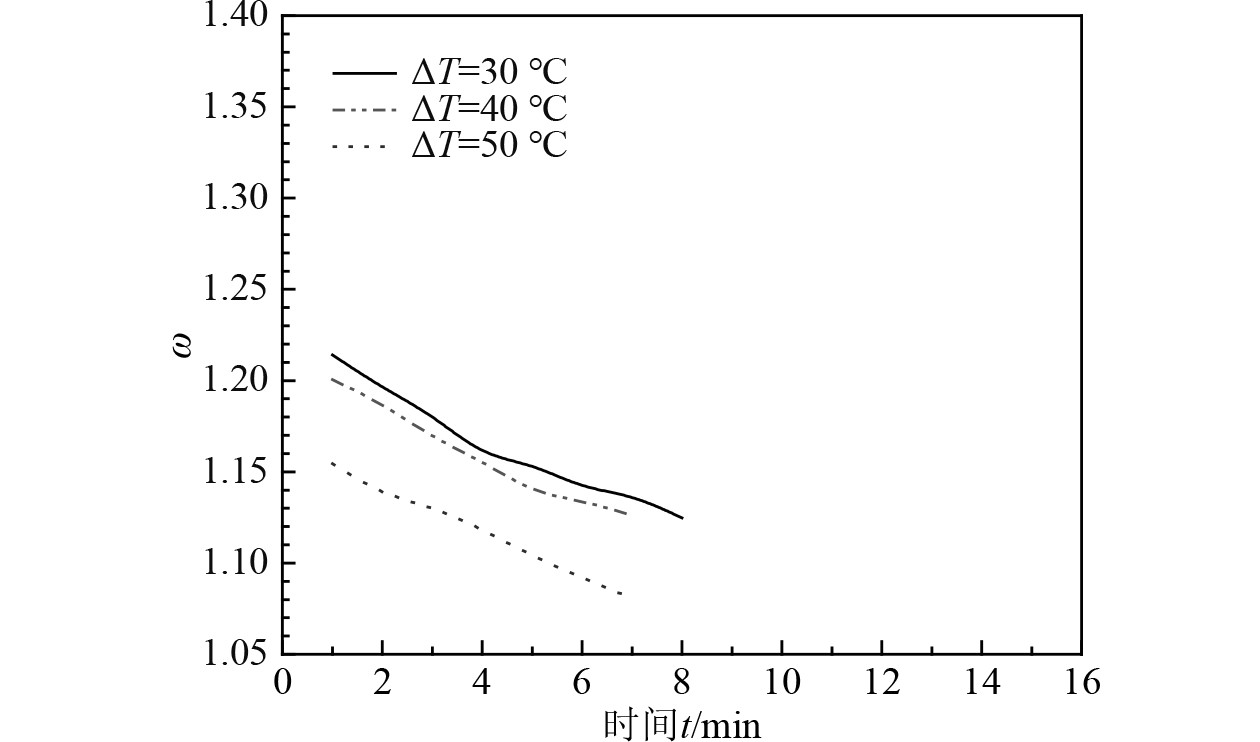
|
图 14
V=0.1 kn, |
由图10~图14可知,密度分层值
| $ \omega = 1 + a{(1 + V)^b}{\varphi ^c}\Delta {T^d}{{{t}}^e}\text{,}$ | (12) |
当
| $ \omega = 1 + 2.214\;5{(1 + V)^{2.711\;5}}{\varphi ^{0.784\;5}}\Delta {T^{-0.598\;5}}{{{t}}^{- 0.224\;0}}\text{。}$ | (13) |
该式的验证范围是:0 kn
该拟合关联式的计算结果与数值仿真结果对比,误差在6%以内,且绝大部分数据点的误差都在1%以下。因此在确定密度分层值
水下航行体航行过程中,其动力系统的废热以冷却水的形式向外界直接排出,在密度差的作用下向海面浮升。实际海洋环境下,海水密度随水深是变化的,而热射流浮升力的大小受海水密度的影响。基于此,本文研究了密度分层对热射流流场的影响,结论如下:
1)随着海水深度的增加,海水的盐度上升,温度下降,这两者均会造成海水密度随深度的增加而增大;
2)所得到的拟合关联式计算结果与数值仿真结果对比,误差在6%以内,且绝大部分数据点的误差都在1%以下。
| [1] |
杨卫平, 张志龙, 李吉成. 水下缩比航行体热尾流的红外探测实验[J]. 国防科技大学学报, 2016(4): 107-112. YANG Wei-ping, ZHANG Zhi-long, LI Ji-cheng. Experimental test system design for thermal wakes of submerged vehicle based on scale model[J]. Journal of National University of Defense Technology, 2016(4): 107-112. |
| [2] |
张旭升, 郭亮, 胡日查, 等. 潜艇热尾流的浮升扩散规律及海表温度特性[J]. 红外技术, 2016, 38(8): 678-682. ZHANG Xu-sheng, GUO Liang, HU Ri-cha, et al. Buoyancy diffusion law and ocean-surface temperature characteristic of submarine thermal wake[J]. Infrared Technology, 2016, 38(8): 678-682. |
| [3] |
MAY, D, GRAEME G WREN. Detection of submerged vessels using remote sensing techniques[J]. Australian Defence Force Journal, 1997, 127(11): 9-15. |
| [4] |
ZOU Nan, ARYE Nehorai. Detection of ship wake using an airborne magnetic transducer[C]//Conference Record of Thirty-Second Asilomar Conference on Signals, Systems and Computers. IEEE, 1998(2): 1316−1321.
|
| [5] |
江传富, 王江安, 杨坤涛, 等. 水下航行器热尾流浮升及分布研究[J]. 激光与红外, 2005, 35(12): 932-934. JIANG Chuan-fu, WANG Jiang-an, YANG Kun-tao, et al. Study on floating and distributing rule of submarines thermal wake[J]. Laser and Infrared, 2005, 35(12): 932-934. DOI:10.3969/j.issn.1001-5078.2005.12.007 |
| [6] |
张昊春, 吉宇, 马锐. 水下航行体热尾流浮升特性研究[J]. 舰船科学技术, 2015, 37(7): 24-28. ZHANG Hao-chun, JI Yu, MA Rui. Buoyant characteristics of thermal wakes discharged by underwater vehicles[J]. Ship Science and Technology, 2015, 37(7): 24-28. DOI:10.3404/j.issn.1672-7649.2015.07.006 |
| [7] |
杨立, 华顺芳, 杜先之. 水下航行器热尾流在稳定分层环境中的浮升规律[J]. 工程热物理学报, 1991, 12(1): 74-77. YANG Li, HUA Shun-fang, DU Xian-zhi. Floating law of thermal wake of underwater vehicle in stable stratified environment[J]. Journal of Engineering Thermophysics, 1991, 12(1): 74-77. |
| [8] |
World Ocean Database 2018 Updates [EB/OL].https://www.ncei.noaa.gov/access/ world-ocean-database/wod-updates.html
|
| [9] |
熊英, 关晖, 吴锤结. 黏性分层流中椭球体俯仰振荡研究[J]. 应用数学和力学, 2018, 39(8): 900-912. XIONG Ying, GUAN Hui, WU Chui-jie. Study on prolate spheroid pitching oscillation in viscous stratified flow[J]. Applied Mathematics and Mechanics, 2018, 39(8): 900-912. |
| [10] |
郝英泽, 何斌. 海水密度变化对潜艇悬停垂向运动的影响仿真研究[J]. 船海工程, 2008, 37(2): 117-119. DOI:10.3963/j.issn.1671-7953.2008.02.033 |
| [11] |
刘沛清, 赵芸可. 伯努利方程对流体力学理论建立的历史贡献[J]. 力学与实践, 2020, 42(2): 258-264. LIU Pei-qing, ZHAO Yun-ke. Historical contribution of bernoulli equation to the establishment of fluid mechanics theory[J]. Mechanics and Practice, 2020, 42(2): 258-264. DOI:10.6052/1000-0879-19-179 |
 2021, Vol. 43
2021, Vol. 43
