海洋中有规则波、不规则长峰波和短峰波、畸形波(freak wave)以及其他一些奇特的波浪等,一些非常规的波浪环境,由于其出现的偶然性和巨大的破坏性,以及对其缺乏充分的认识,对船舶和海洋工程结构物航行安全构成了极大的威胁。
图1给出了典型的方形波浪示意,这种波浪现象还称“十字海”(Cross sea),在海面出现时呈现出方形和网格状。方形波的产生是由于不同的天气模式使海洋产生了2个方向不同的海浪系统,当它们相遇时就可能会形成十字交叉,形成方形波浪。

|
图 1 典型的方波示意图 Fig. 1 Typical cross wave |
最早关于船舶遭遇这种交叉海浪的研究开始于Toffoli等[1],他们分析了类似方形波浪这种交叉海浪对船舶航行事故发生的影响。Onorato[2]研究了2组畸形波在交叉相遇时的不稳定现象。McAllister[3]在实验室研究了“新年波”在交叉相遇时的波浪破碎特征,Brennan[4]研究了交叉海浪下的非线性交互特征。Li[5]通过SAR传感器等测试工具,分析了2个相聚很远的风暴在海面上相遇交叉的现象。Renaud[6]基于水池模型试验和势流理论计算研究了某LNG船在双向组成的单色规则波中的运动响应及二阶波浪力。目前,船舶在波浪中运动的研究多是基于单向波浪进行的,忽略了波浪方向分布的影响,由于方形波是由2组波浪以一定角度交叉形成的,波浪间的相互叠加影响,使得波峰、波谷会出现明显的变化,船舶在方形波浪中的航行相比单向规则波也会更加危险。
随着CFD模拟技术和重叠网格技术的发展,使得船舶在方形波浪这种非典型波浪中的运动可以得到有效模拟,本文建立的船舶在方形波浪中运动模拟方法以及非线性运动特性研究,可为后续船舶在这种畸形波浪下的性能评估和安全航行提供参考。
1 数值计算方法及研究对象 1.1 计算模型采用RANS方程模拟波浪中船体运动,通过有限体积法使用控制体求解积分形式的质量和动量守恒方程,水和空气的体积分数,以及湍流模型方程。分离迭代求解方法基于SIMPLE算法,采用二阶迎风格式离散求解RANS方程中的对流项,利用二阶欧拉隐式格式进行时间积分。采用流体体积分数法VOF(Volume of Fluid)求解自由面流动。本文采用涡粘性模型中的
采用重叠网格的计算方法,将计算域分为背景域和重叠区域,只需要船体周围有限的重叠网格区域进行运动,然后通过边界插值完成与外部整体计算域的数值信息交换,从而可以有效地求解各种大幅运动。
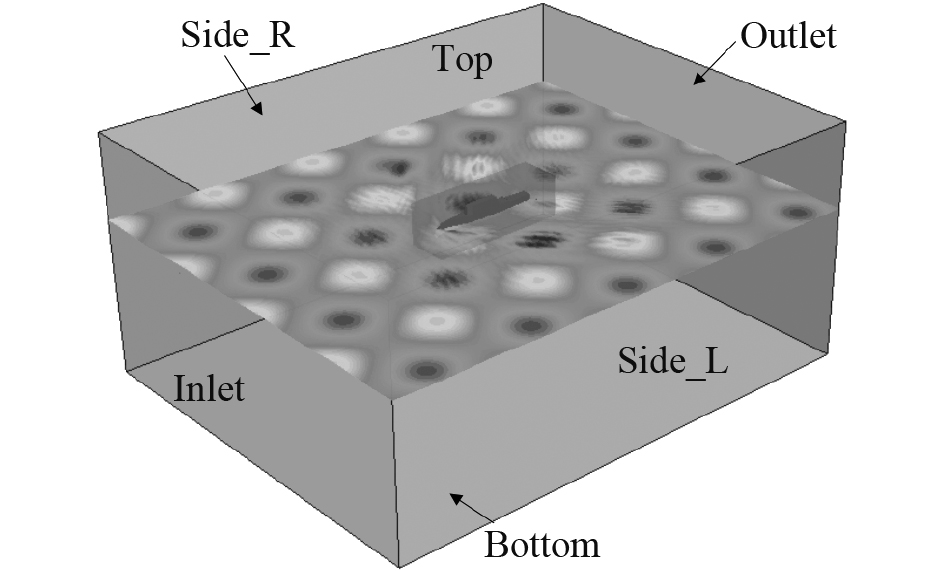
计算域如图2所示,其边界范围包括:入口(Inlet)(模型首部前约2 Lpp)、出口(Outlet)(模型尾部后约2 Lpp)、侧边界(Side_L&Side_R)(模型侧方约2Lpp)、上边界(Top)(水线以上约0.8 Lpp)、下边界(Bottom)(水线以下约1.5 Lpp)。
|
图 2 计算域示意图 Fig. 2 Computational domain |
背景域中上边界设置为压力出口,其他边界均设置为速度入口。重叠域边界设置为重叠网格条件。在Inlet,Outlet,Side边界施加波浪强制模型防止波浪反射的干扰,以均匀波浪场作为数值计算的初始条件。
计算域生成切割体网格(Trimmed Mesh),在船体壁面周围生成边界层网格。网格划分过程中:船模首部、尾部和舭龙骨附近网格适当加密;在模型表面附近网格加密,其中第1层网格间距根据y+确定(y+平均约为50~100);自由表面附近网格根据波高和波长的值也适当加密,图3为网格划分的拓扑结构示意图。

|
图 3 计算域网格拓扑结构示意图 Fig. 3 Topology structure of mesh |
本文计算采用的是东京2015 CFD workshop的标准船型ONR内倾船,计算模型带有舭龙骨,船模缩尺比为1∶48.935。ONR内倾船的三维模型如图4所示,模型主尺度参数如表1所示。

|
图 4 ONR内倾船三维几何模型图 Fig. 4 3D geometric model of ONRT |
|
|
表 1 ONR内倾船主尺度 Tab.1 The main parameters of ONRT |
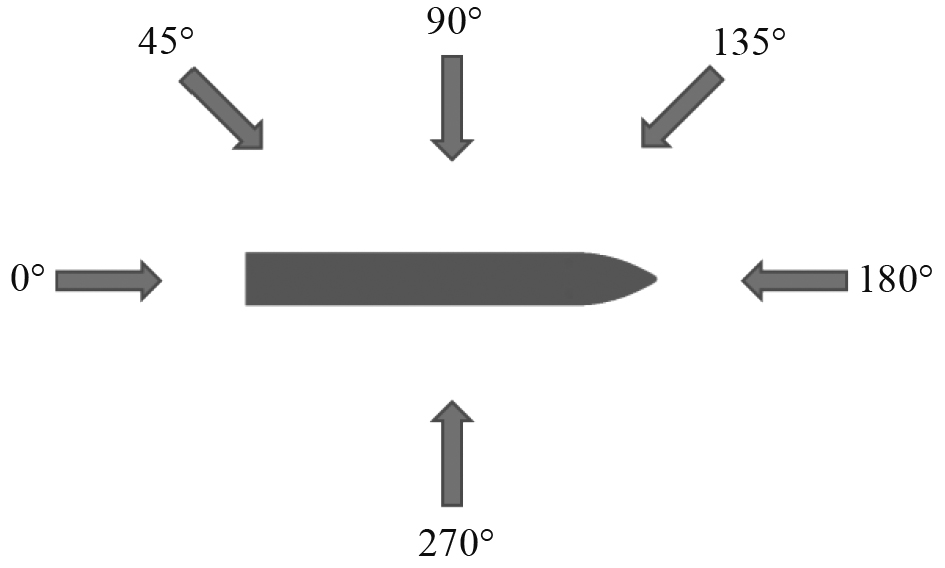
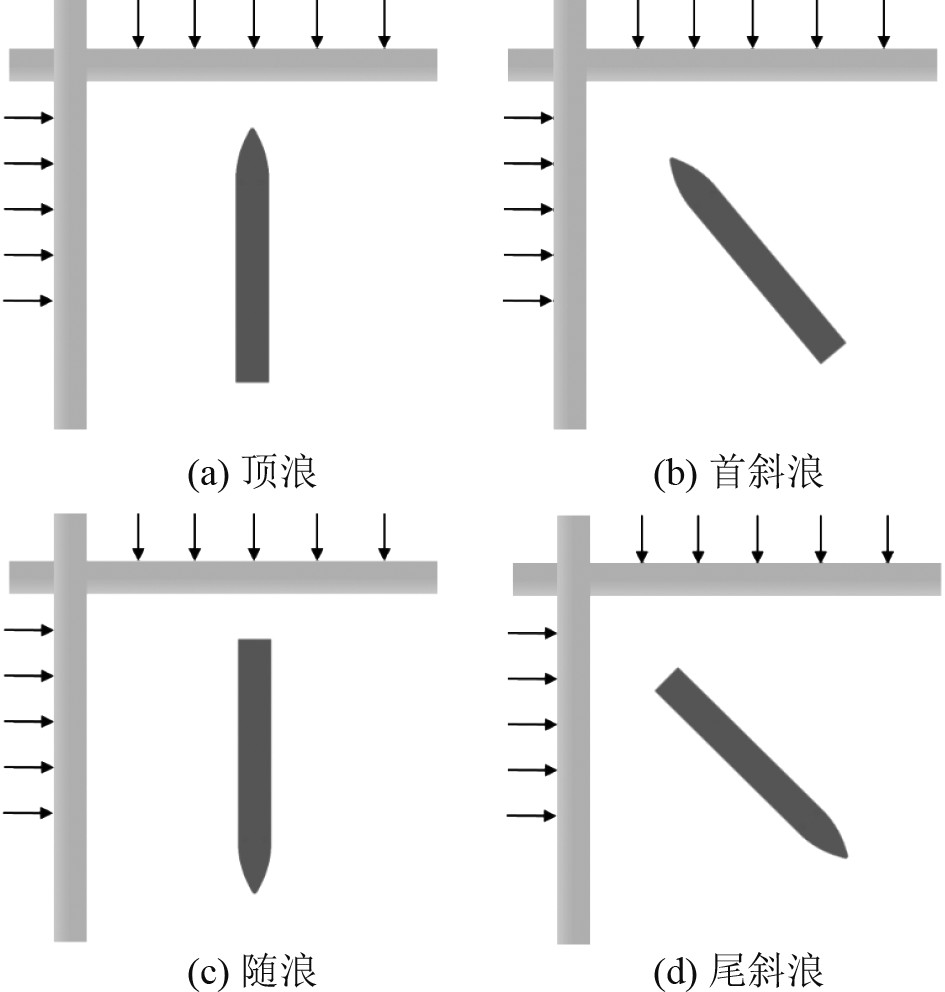
单向规则波和方形波浪中相应的浪向角定义如图5和图6所示。方形波由2个正交的规则波叠加而成,本文仅考虑2个波高和波长相同、且相位差为0°的2个规则波的叠加情况。
|
图 5 单向规则波浪向角定义图 Fig. 5 Heading angle of regular wave |
|
图 6 方形波浪浪向角定义图 Fig. 6 Heading angle of cross wave |
首先针对方形波浪进行数值模拟分析,计算工况条件为
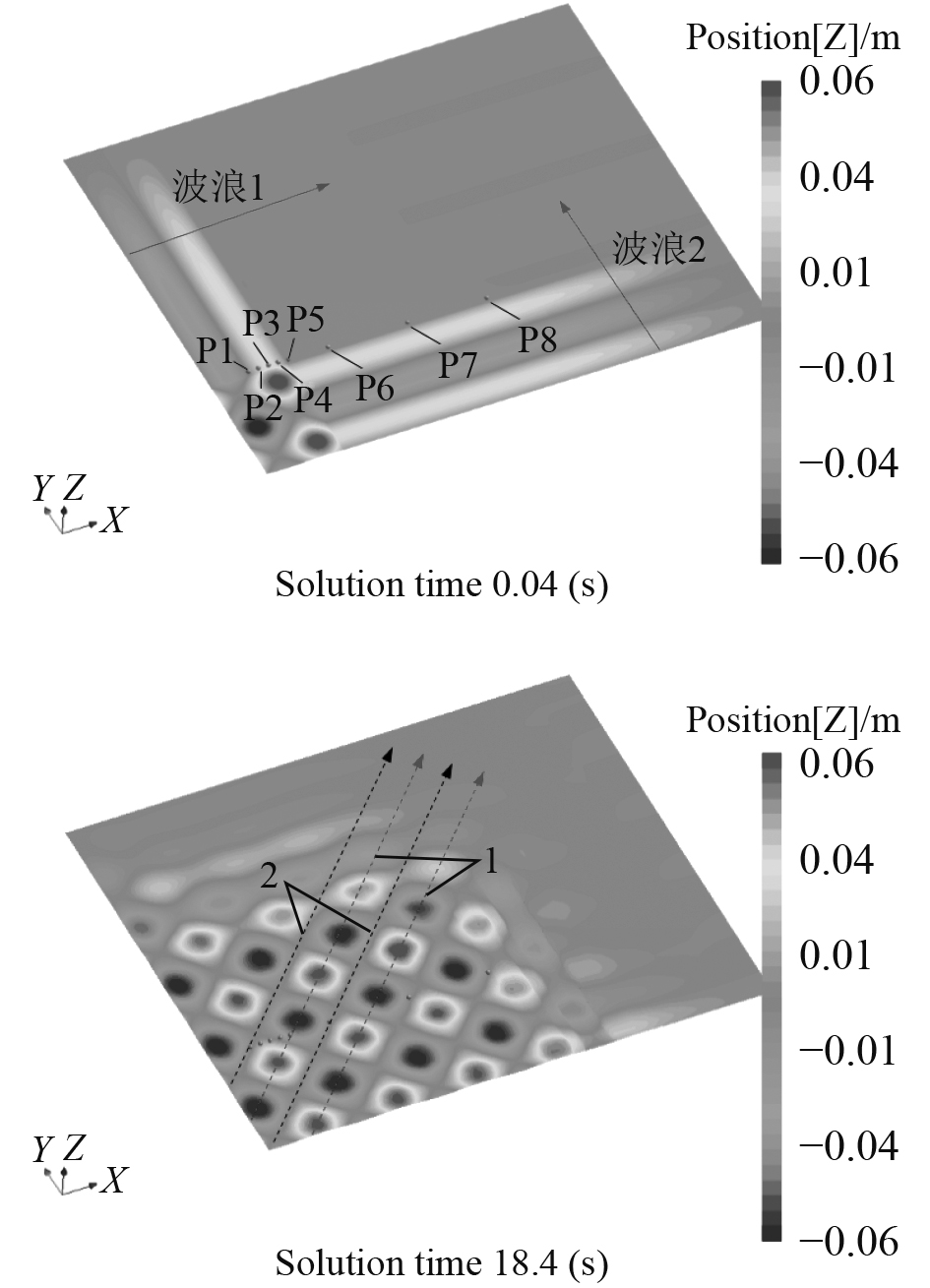
设置8个波高监控点,各监控点距离波浪1造波入口距离分别为0.5 Lpp,0.625 Lpp,0.75 Lpp,0.875 Lpp,1 Lpp,1.5 Lpp,2.5 Lpp和3.5 Lpp,通过这些监控点监视相应位置的波面时间历程。其中,监控点5位于2组波浪波峰波谷叠加能量最大的位置。图7为各监测点的位置示意以及波浪行进示意图,从图中可以看出波浪1和波浪2相遇后叠加的波峰、波谷会按照箭头1所示的方向向前移动,箭头2所示的行进路线上由于波浪1波峰与波浪2波谷能量相互抵消,波浪幅值接近0。
|
图 7 方形波浪监测点及波峰、波谷位置示意图 Fig. 7 The monitors of cross wave and the position of wave crest and trough |
考虑到监控点5是波峰、波谷叠加能量最大的位置点,表2给出了波陡
|
|
表 2 方形波浪波幅数值模拟误差(Monitor 5) Tab.2 The simulation error of cross wave amplitudes |
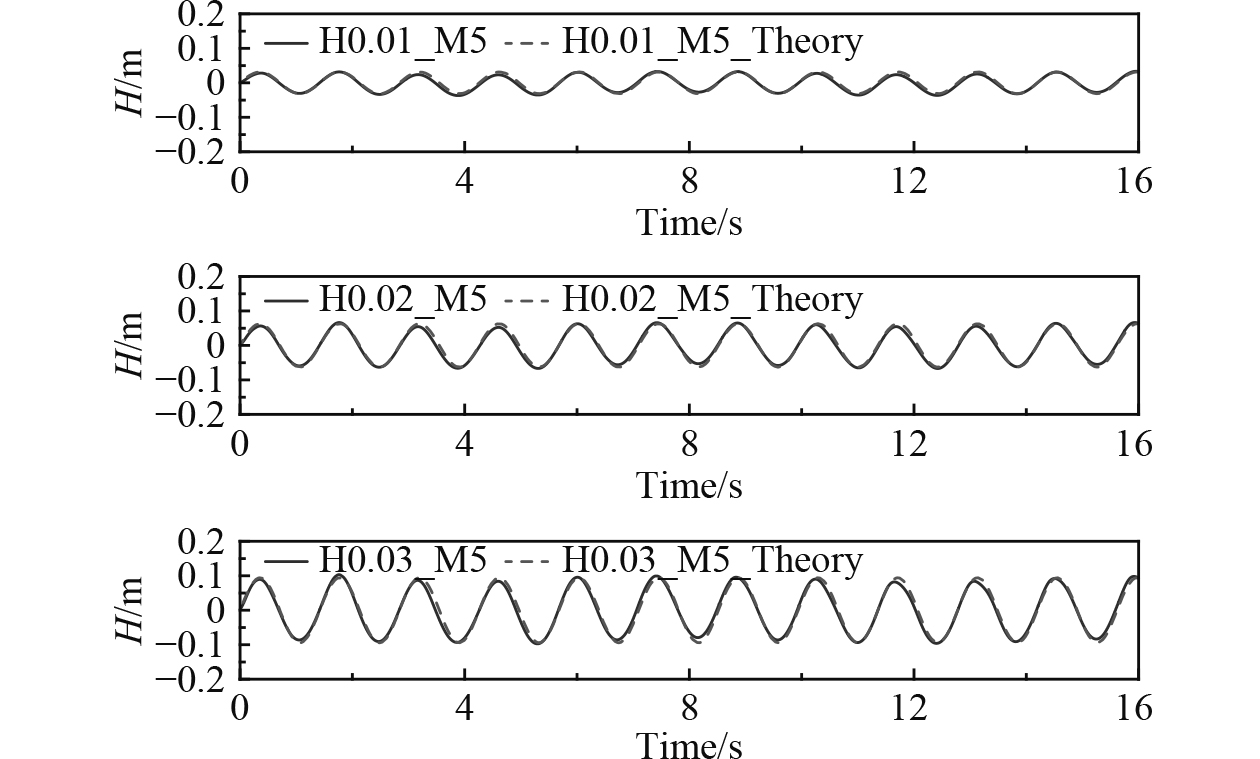
|
图 8 不同波高下方形波浪数值模拟与理论结果对比图(Monitor 5) Fig. 8 The comparison of simulations and theory solutions in different wave heights(Monitor 5) |
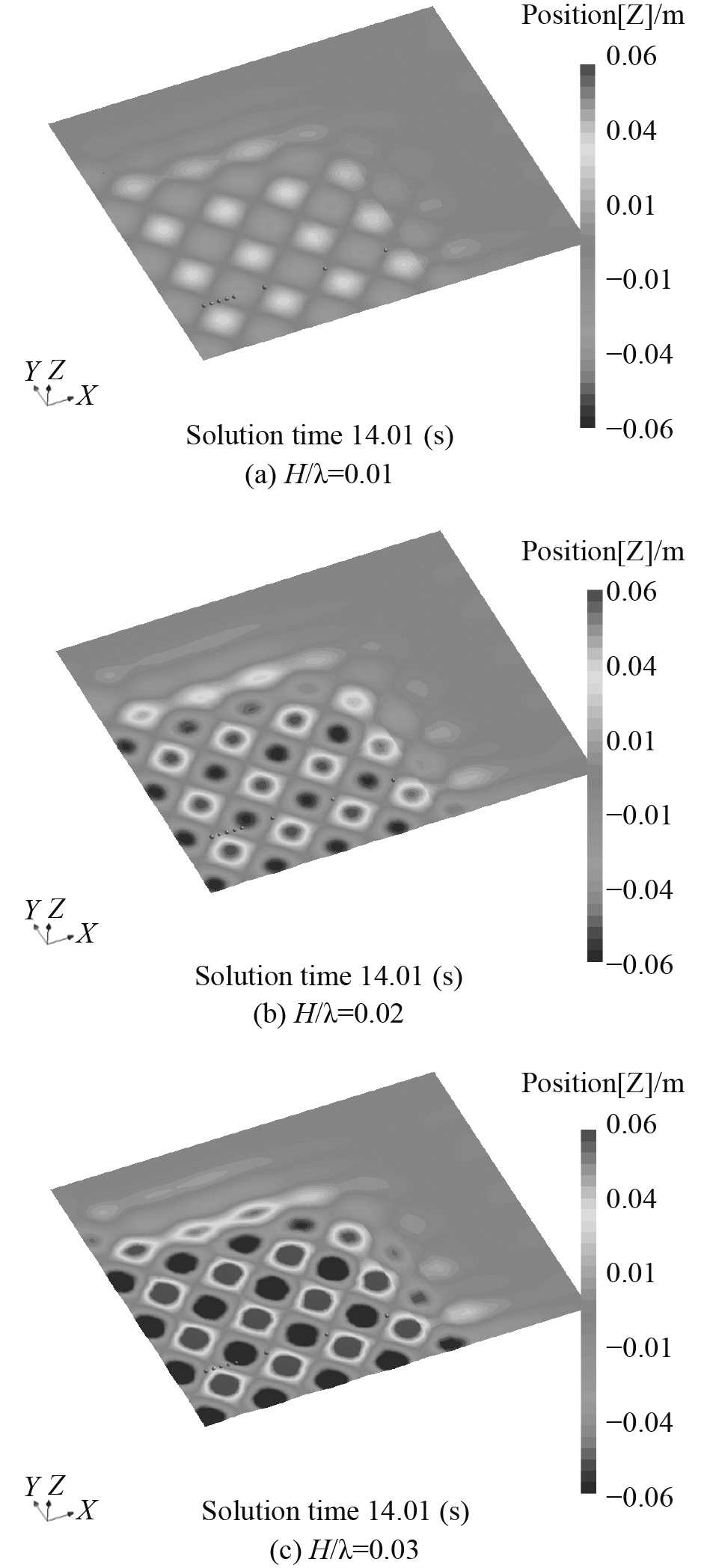
|
图 9 不同波高下方形波浪自由面波形图 Fig. 9 The free surface wave pattern in different wave heights |
模拟船舶在波浪中运动时,由于在非对称的波浪作用下,如果不施加额外的舵控制,船舶很难保持原有的航向,所以计算中仅考虑垂荡、横摇和纵摇三自由度的耦合运动。
3.1 不同浪向下运动响应分析图10为Fn=0.0时,不同浪向下船舶在方形波和单向规则波中的垂荡、横摇和纵摇时历曲线。图10中SWa,SWb,SWc,SWd分别对应图6中方波顶浪、首斜浪、随浪和尾斜浪,180°和135°对应图5中单向规则波的顶浪和首斜浪。当船舶航行在方形波浪中SWb和SWd浪向,以及单向规则波顶浪状态(180°)时,船舶遭遇的是对称的波浪作用。当在航行在方形波浪中SWa和SWc浪向,以及单向规则波首斜浪状态(135°)时,船舶遭遇的是非对称的波浪作用。
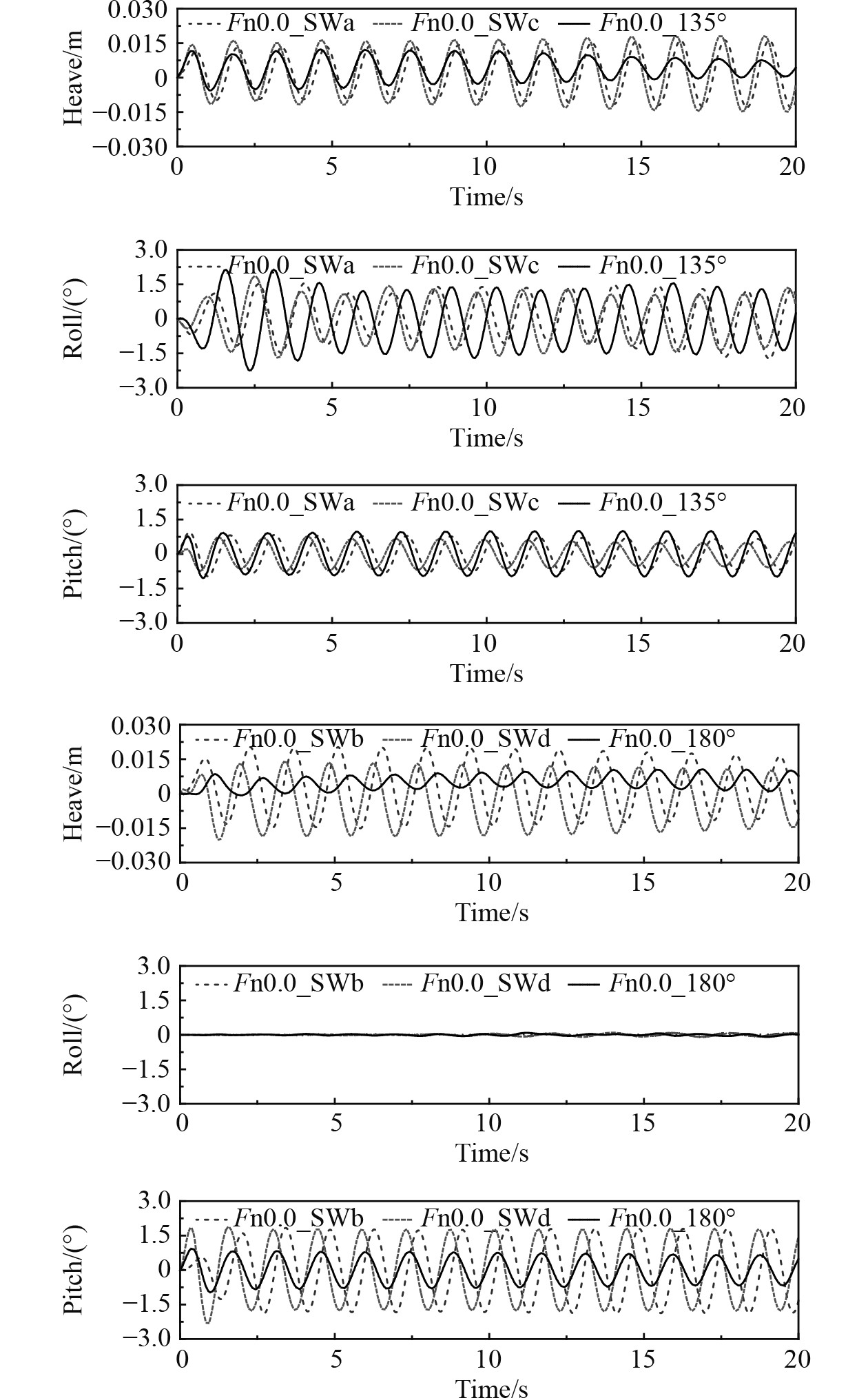
|
图 10 方形波浪和单向规则波中不同浪向下垂荡、横摇、纵摇运动时历曲线(Fn=0.0) Fig. 10 The time history of heave、roll and pitch in different heading angles with regular wave and cross wave(Fn=0.0) |
从运动时历曲线可以看出,对于方形波浪条件,在Fn=0.0时,考虑非对称波浪条件(SWa,SWc),2组波浪条件间的运动幅值差异很小。同样,对称波浪条件下(SWb,SWd)也一样。在对称波浪作用下,方形波浪中船舶的运动幅值要大于单向规则波下的运动幅值。在非对称波浪下,船舶会有明显的横摇。在方形波浪非对称波浪力作用下的纵摇运动要大于对称波浪力下的纵摇运动。
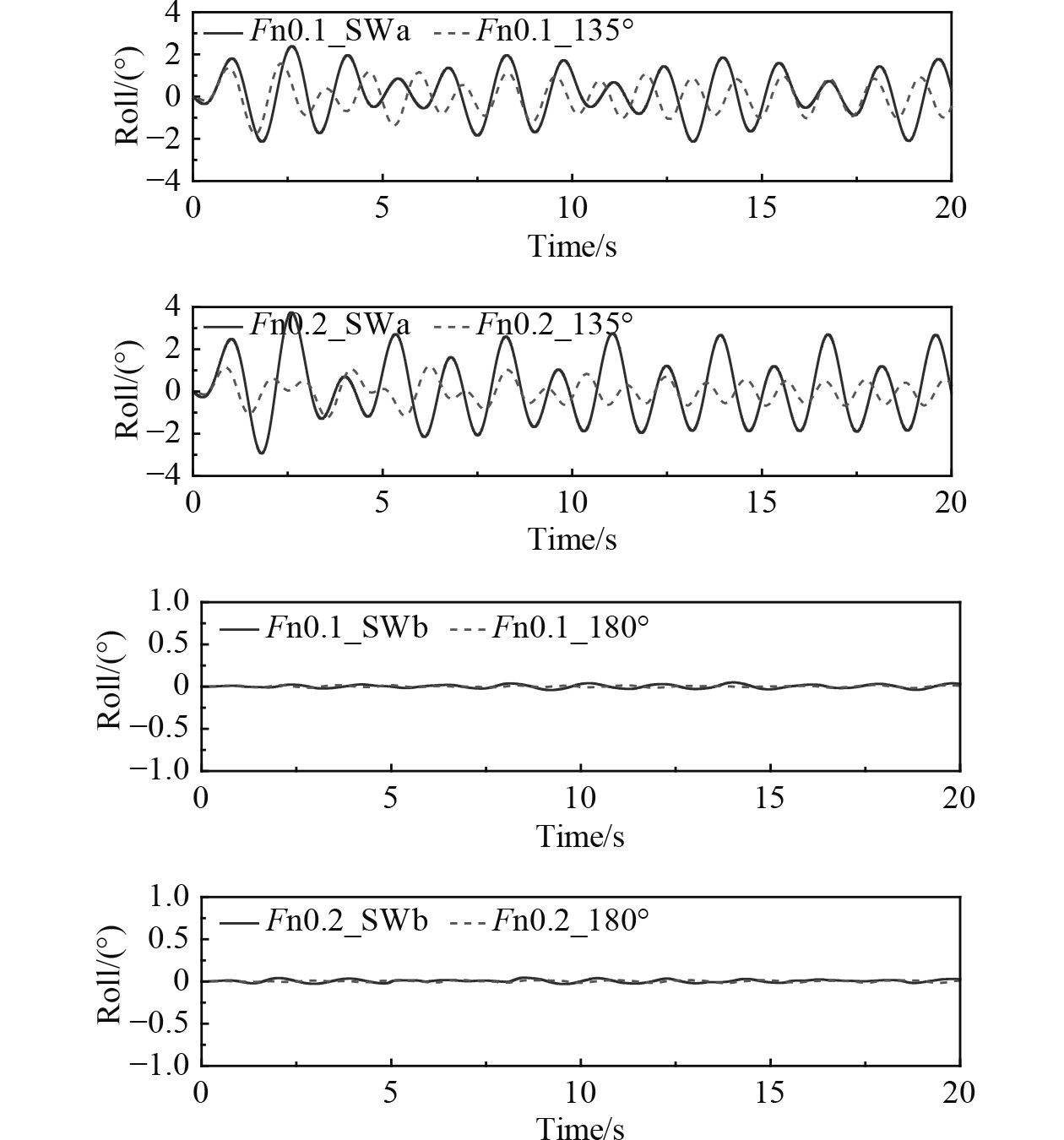
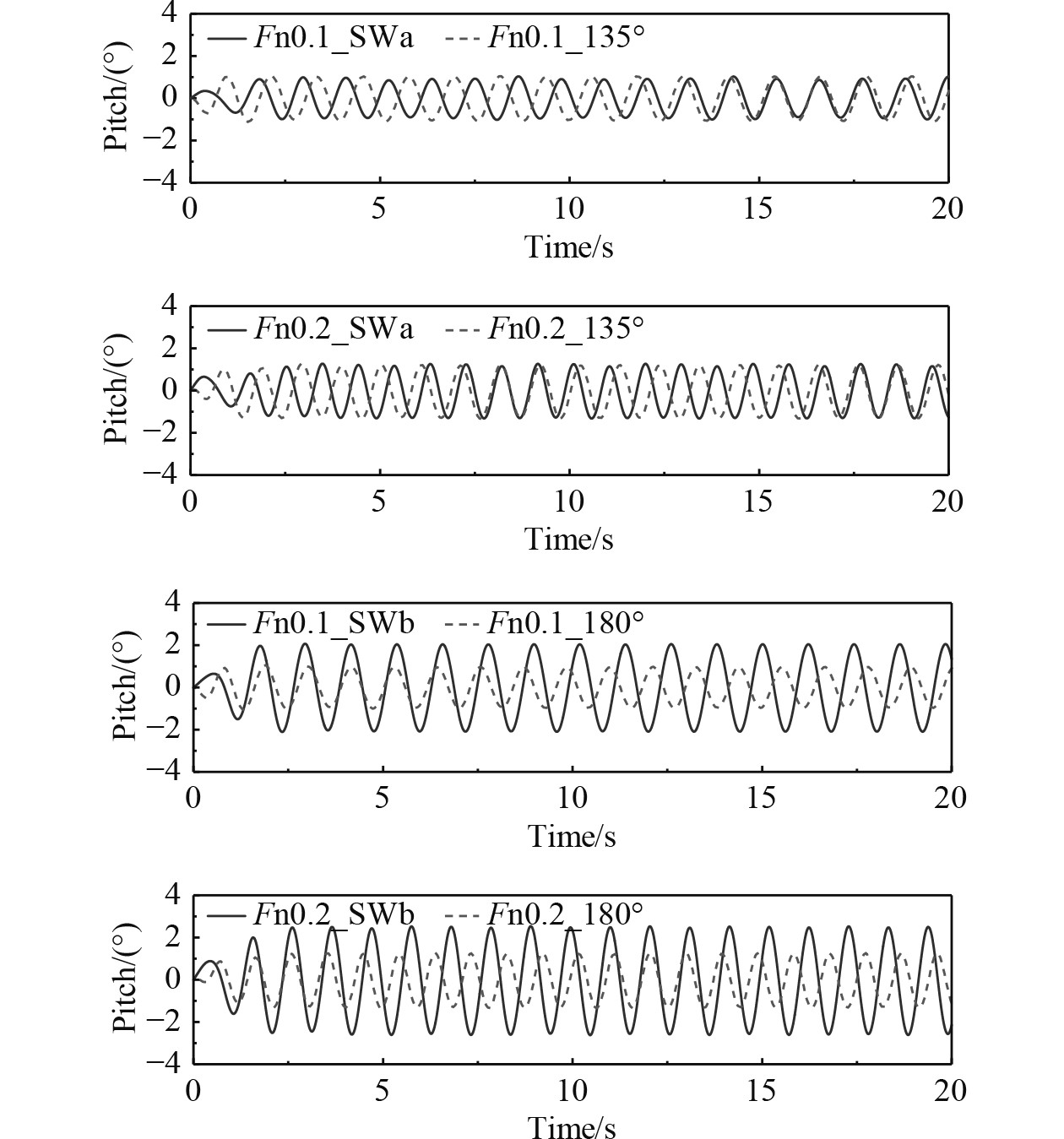
3.2 不同航速下运动响应分析从图11~图13可以看出,随着航速的增加,运动幅值也在增加。除纵摇运动外,方形波浪下的运动幅值要大于规则波下的运动幅值。在对称的波浪作用下,船舶不会发生明显的横摇运动。方形波对称波浪作用下,船舶的垂荡和纵摇呈规律的正弦运动,但是在非对称的波浪作用下,垂荡和横摇呈不规则的周期性运动,这是因为两成分规则波周期性非对称作用在船体的结果。在航速Fn=0.1时,SWa波浪条件横摇运动呈现先增大后减小的周期性运动,在航速Fn=0.2时,呈现出单边横摇幅值一大一小的周期性变化。
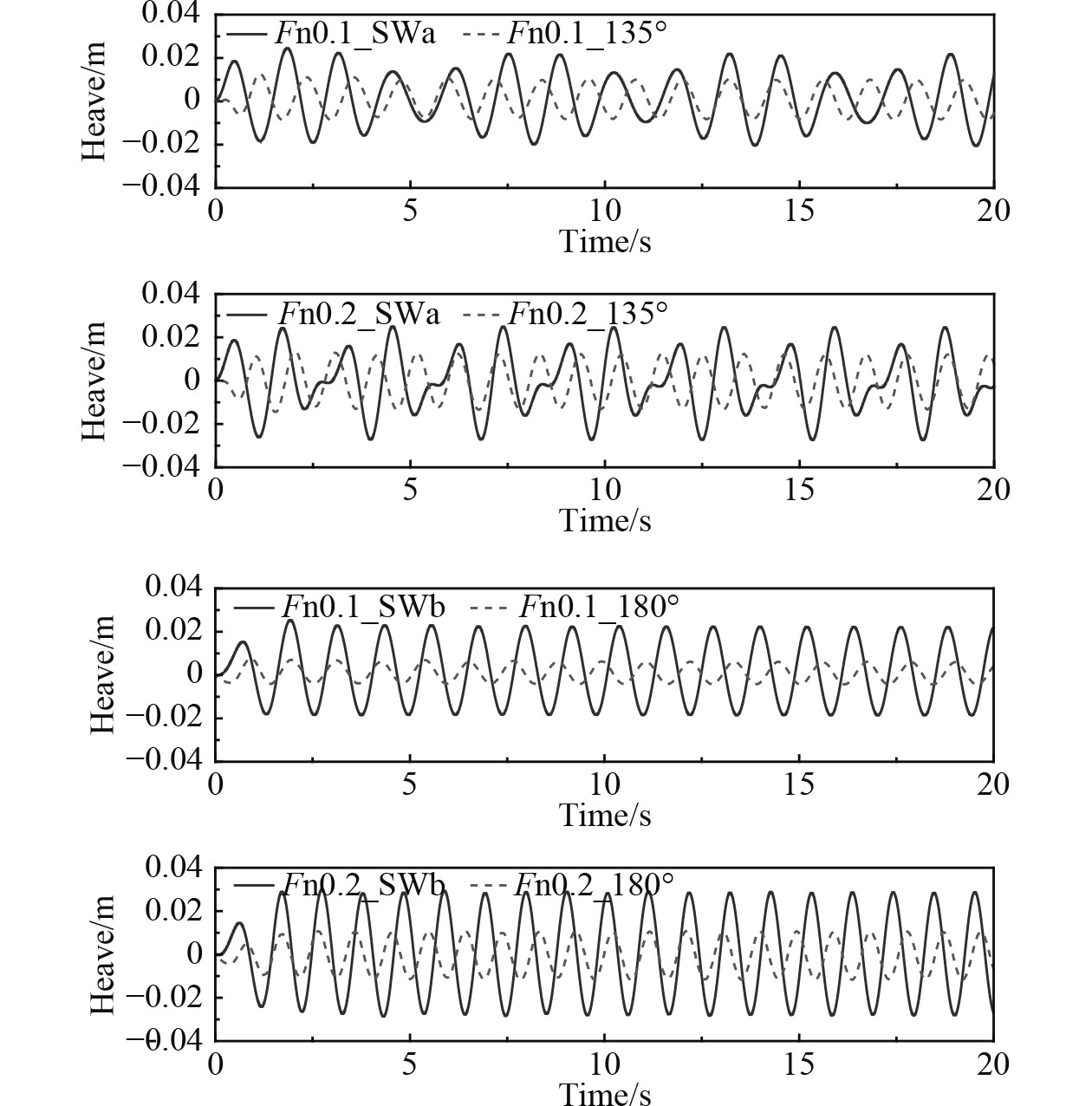
|
图 11 方形波浪和单向规则波中不同航速下垂荡运动时历曲线 Fig. 11 The time history of heave in different speed with regular wave and cross wave |
|
图 12 方形波浪和单向规则波中不同航速下横摇运动时历曲线 Fig. 12 The time history of roll in different speed with regular wave and cross wave |
|
图 13 方形波浪和单向规则波中不同航速下纵摇运动时历曲线 Fig. 13 The time history of pitch in different speed with regular wave and cross wave |
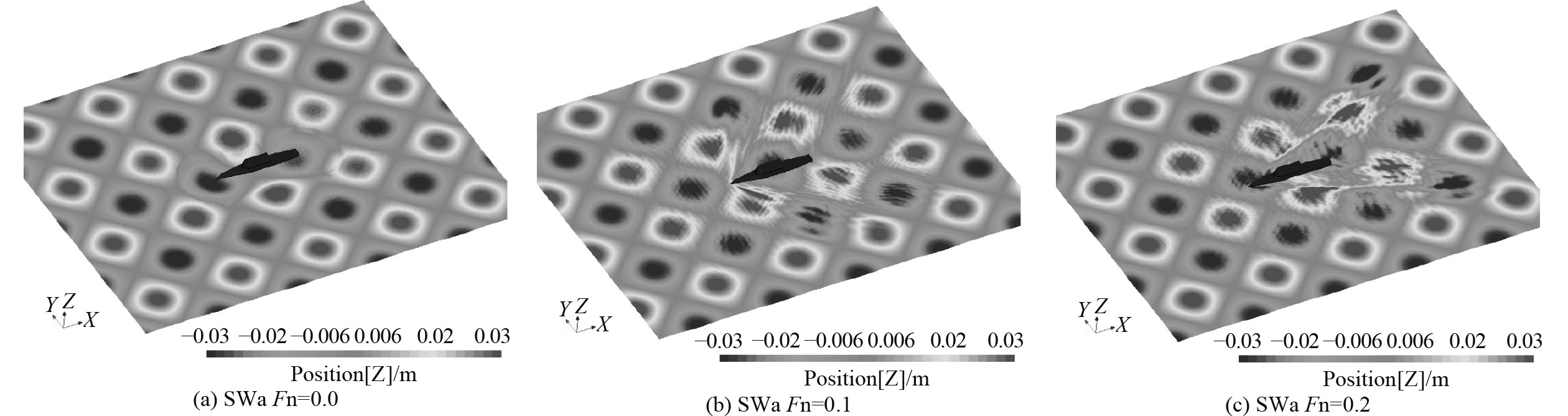
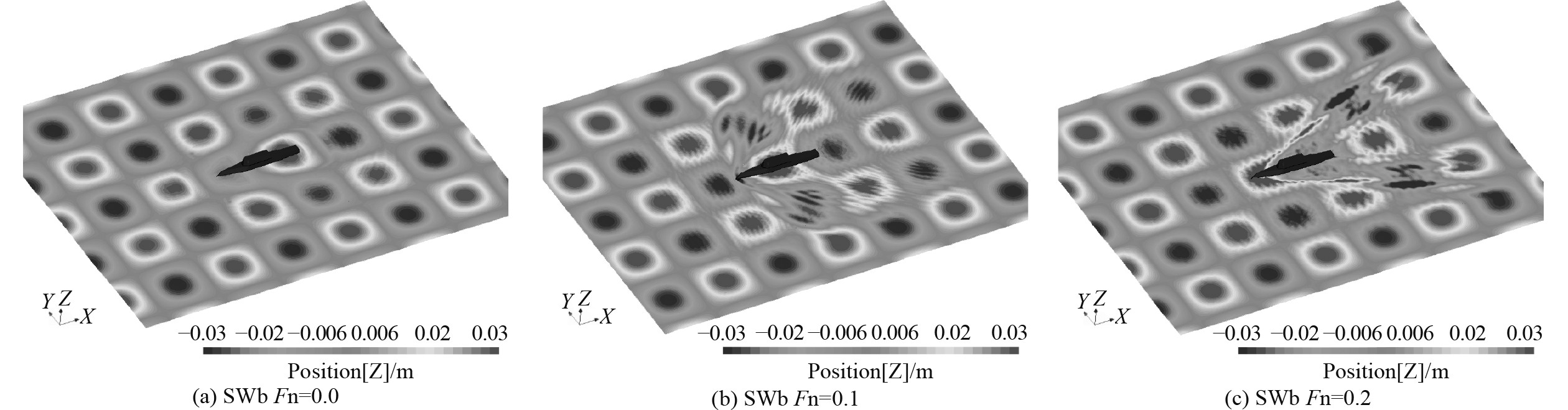
图14和图15为方形波浪中对称和非对称波浪作用下不同航速自由面波形图。从图14中可以看出,在对称波浪作用下船体兴波呈现对称分布,从图15可以看出,由于横向波浪的影响,船体辐射的波浪与来波相互作用,船体周围的兴波呈非对称分布,随着航速的增加会表现得更加明显。
|
图 14 方形波浪中非对称波浪作用下不同航速自由面波形图 Fig. 14 The free surface wave pattern of asymmetric cross wave in different speed |
|
图 15 方形波浪中对称波浪作用下不同航速自由面波形图 Fig. 15 The free surface wave pattern of symmetric cross wave in different speed |
图16为Fn=0.2、波陡H/
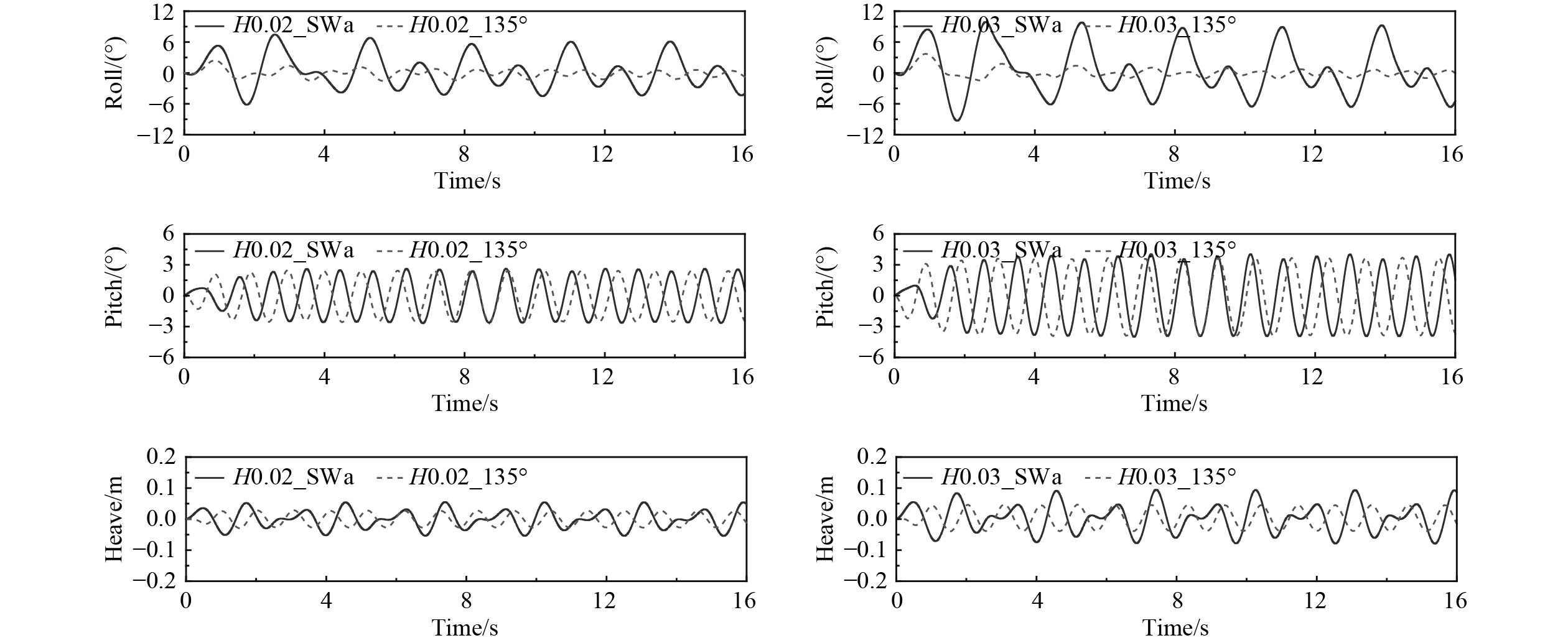
|
图 16 方形波浪和单向规则波中不同波陡下运动时历曲线(Fn=0.2) Fig. 16 The time history of motion in different wave steepness with regular wave and cross wave (Fn=0.2) |
从计算中也发现,在航速Fn为0.01,波陡为0.03时,船舶在方形波浪中出现了甲板上浪的非线性现象。图17展示了方形波浪中一个波浪遭遇周期内甲板上浪过程,虽然本文中的模拟对象为ONR内倾船型,有着穿浪的船型特征,但是可以看出,由于方形波浪中叠加后的波浪有着较高的峰值,当波峰到达船首时,船舶出现了明显的埋首现象。这样使得船舶甲板有了上浪现象。在波陡为0.03的条件下,船舶本身伴随着明显的横摇运动,这些都加剧了船舶上浪现象的发生。在波浪继续行进的过程中,船首遭遇波谷,船舶本身的纵摇运动又使得船舶抬首,甲板上的水会顺着甲板到达上层建筑的位置,然后沿着船侧内倾的干舷滑落。当遇到下一个波峰时船舶继续发生埋首,然后再发生下一周期的甲板上浪。

|
图 17
方形波浪中一个波浪遭遇周期内甲板上浪示意图(Fn=0.01, |
1)考虑非对称波浪作用的情形
以方形波浪条件(SWa)和规则波首斜浪(135°)进行对比分析,图18为波陡H/
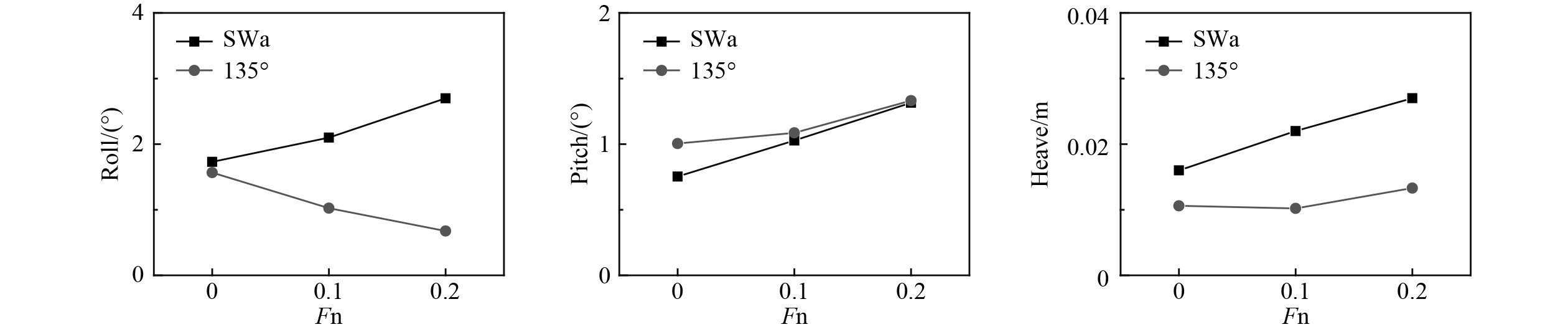
|
图 18 非对称波浪作用下方形波浪和单向规则波中运动幅值对比(H/λ=0.01) Fig. 18 The comparison of motion amplitudes with cross wave and regular wave by asymmetric wave force (H/λ=0.01) |
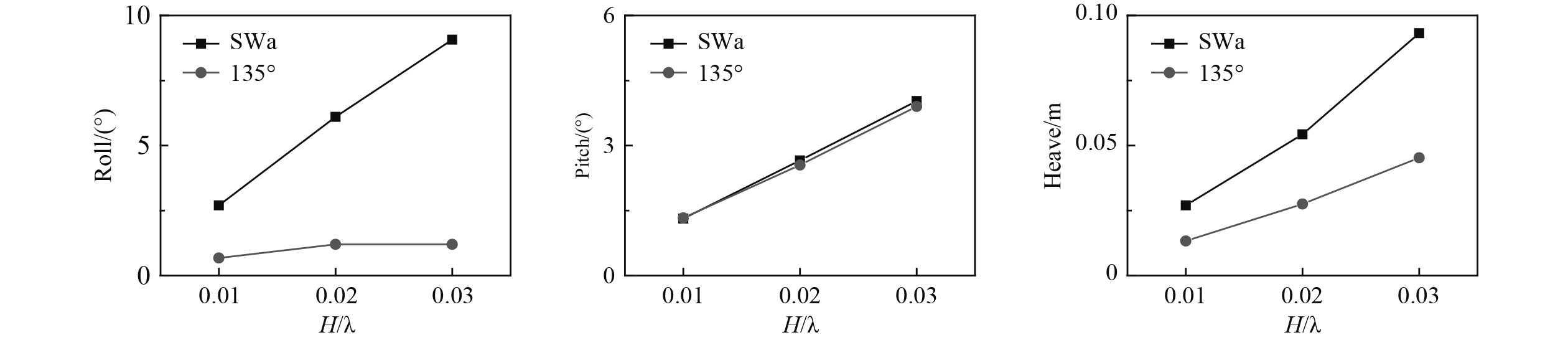
|
图 19 非对称波浪作用下方形波浪和单向规则波中运动幅值对比(Fn=0.2) Fig. 19 The comparison of motion amplitudes with cross wave and regular wave by asymmetric wave force(Fn=0.2) |
2)考虑对称波浪作用的情形
图20为波陡H/
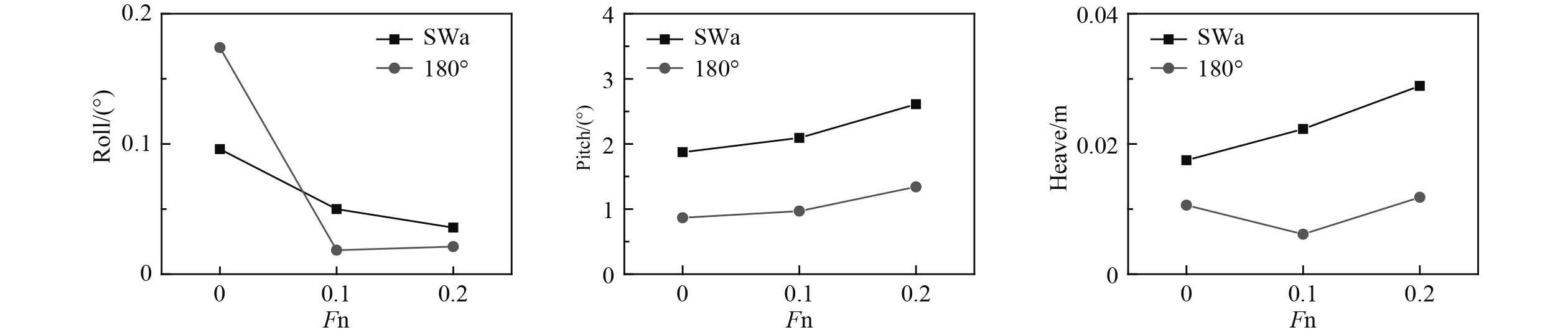
|
图 20 对称波浪作用下方形波浪和单向规则波中运动幅值对比(H/λ=0.01) Fig. 20 The comparison of motion amplitudes with cross wave and regular wave by symmetric wave force (H/λ=0.01) |
本文以国际标模ONR内倾船为研究对象,结合RANS方法,建立方形波下船舶横摇-纵摇-垂荡的三自由度运动数值模拟方法,分析ONR内倾船在方形波浪作用下非线性运动特性,并与规则波下的运动进行了对比分析,得到了以下结论:
1)零航速时,在方形波浪中对称波浪条件下(SWb,SWd),除了横摇运动(对称波浪作用下横摇幅值很小),纵摇和升沉都大于非对称波浪条件作用的方形波和单向规则波下的运动幅值。
2)随着航速和波陡的增加,船舶在方形波浪中的运动幅值也随之增加。方形波浪下的垂荡幅值要大于单向规则波下的运动幅值。在非对称波浪作用下,方形波浪中横摇幅值要明显大于单向规则波中的运动幅值。
3)为了减小方形波浪中的航行危险,可以采用减小航速的方法。同时,在对称波浪作用下,通过改变航向合理地选择波浪中的航行线路,也可以有效地提高方形波浪下的航行安全。
| [1] |
TOFFOLIA A, LEFEVRE J. M., BITNER-GREGERSEN E., et al.. Towards the identification of warning criteria: Analysis of a ship accident database[J]. Applied Ocean Research, 27, 2005, 281-291. |
| [2] |
ONORATO M, PROMENT D., TOFFOLI A... Freak waves in crossing seas[J]. The European Physical Journal Special Topics, 2010(185): 45-55. DOI:10.1140/epjst/e2010-01237-8 |
| [3] |
MCALLISTER M. L., DRAYCOTT S., ADCOCK T. A. A... Laboratory recreation of the Draupner wave and the role of breaking in crossing seas[J]. J. Fluid Mech, 2019(860): 767-786. |
| [4] |
BRENNAN J., FRED ´ERIC DIAS. [C]//Proceedings of the ASME 34th International Conference on Ocean, Offshore and Arctic Engineering, 2015, Newfoundland, Canada.
|
| [5] |
LI Xiaoming, THOMAS K, JOHANNES S-S, et al. Validation and intercomparison of ocean wave spectra inversion schemes using ASAR wave mode data[J]. International Journal of Remote Sensing, 2010(31): 4969-4993. |
| [6] |
RENAUD M, REZENDE F, WAALS O. Second−order wave loads on a LNG carrier in multi−directional waves[C]//Proceedings of the ASME 27th International Conference on Ocean, Offshore and Arctic Engineering, June 15−20, 2008, Estoril, Portugal.
|
| [7] |
KIM J, O’SULLIVAN J, READ A. Ringing analysis on a vertical cylinder by Euler overlay method[C]//Proceedings of the ASME 31st International Conference on Ocean, Offshore and Arctic Engineering, 2012, Rio de Janeiro, Brazil.
|
 2021, Vol. 43
2021, Vol. 43
