潜艇作为一种典型的水下结构物,以其良好的水下探测、隐蔽航渡、隐蔽攻击、战略威慑等功能,成为各海军强国作战平台体系的重要组成部分。但随着现代反潜手段能力的不断完善,战时潜艇遂行使命任务能力及生存能力都受到极大威胁,其中最大的威胁来自鱼雷、水雷、深水炸弹等产生的水下爆炸。水下爆炸对潜艇的综合毁伤评估是一项复杂的系统工程,其毁伤效果不仅表现为壳体破裂、结构大变形等物理毁伤,还表现为对艇内人员、设备、管系、电缆、阀门等冲击毁伤,以及由此产生的动力性能降低、电力系统受损、攻击能力丧失等系统功能毁伤,而且潜艇受损后艇员的损管、抗沉、消防等行为也对潜艇的生命力存在重要影响。研究构建水下爆炸潜艇综合毁伤评估体系,对于统一衡量不同毁伤机理和毁伤模式下潜艇的抗毁伤效能、切实摸清各类实战条件下装备性能底数,具有重要军事意义和学术价值,也可为装备改进设计、战法设计以及仿真分析和试验研究的开展提供参考和依据。以往文献对潜艇结构在水下爆炸冲击下的动力响应开展了大量研究[1-6],形成了声固耦合、液固耦合、双渐进耦合、无网格法等仿真计算方法,并开发了多种商用有限元仿真分析软件[7],如Abaqus,Ls-dyna,Auto-dytran等。张阿漫等[8]就水下爆炸载荷对水中结构毁伤的研究现状进行了较为全面的综述。纵观已有文献,对潜艇结构毁伤引起的功能系统等毁伤研究较少,潜艇综合毁伤评估体系研究不够全面科学且定量方法缺失。
本文对水下爆炸潜艇综合毁伤评估体系开展研究,建立了包括前处理模块、一次毁伤分析模块、二次毁伤分析模块和后处理模块的综合毁伤评估体系结构,并在系统分析建模基本原则、关键影响因素和评价指标及其内在逻辑的基础上建立潜艇综合毁伤评估模型的构建流程与方法,研究结果可为水下爆炸潜艇毁伤效果精准定量评估及水中兵器反潜战术运用提供重要参考。
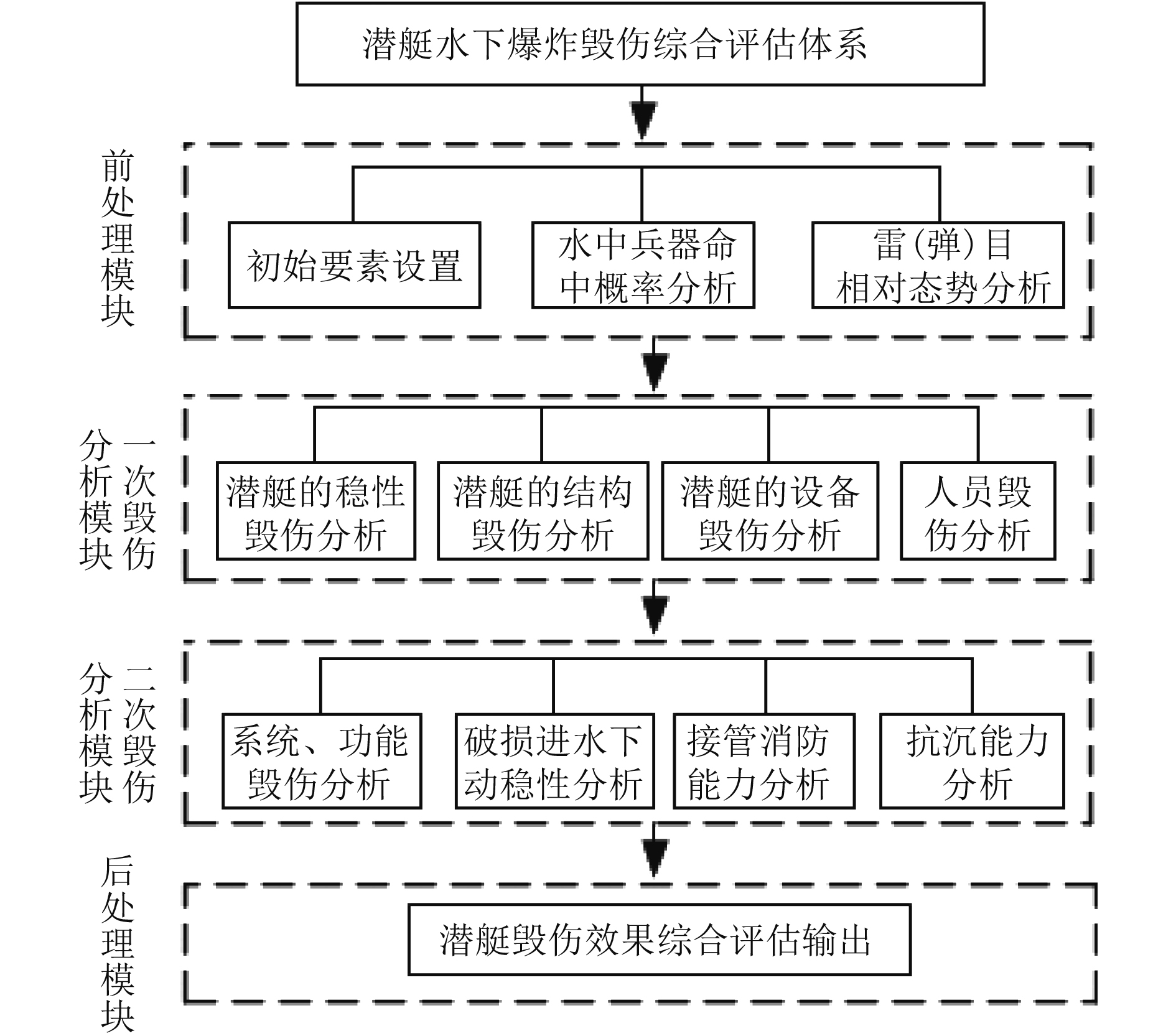
1 潜艇综合毁伤评估体系结构按照从攻击到毁伤全链路的时间先后顺序,可将毁伤评估体系划分为前处理模块、一次毁伤分析模块、二次毁伤分析模块和后处理模块,毁伤评估体系结构如图1所示。
|
图 1 毁伤评估体系结构 Fig. 1 Architecture of the damage assessment system |
结合鱼水雷引信动作机理、深水炸弹散布点、鱼雷和潜艇三维运动模型以及占位机动等典型战术运用,依托交战条件下鱼雷攻击命中潜艇全过程的仿真推演模型,分析鱼雷、水雷或深水炸弹爆炸瞬间的雷(弹)目相对态势,完成各型潜艇结构、材料、炸药模型参数设置,为基于潜艇变毁伤特性的抗爆抗冲击评估提供初始输入。
1.2 一次毁伤分析模块利用有限元仿真软件对不同雷(弹)目相对态势下潜艇的动态响应进行分析,主要分析潜艇破损、局部大变形、动力失稳等情况,以及艇内各人员战位、设备基座处的加速度、位移响应,与设计指标阈值比对,分析水下爆炸冲击对艇体、人员、设备等造成的直接损伤。
1.3 二次毁伤分析模块分析设备、人员损伤对潜艇综合毁伤效能的贡献率,建立潜艇水下抗爆抗冲击毁伤谱系。依据一次毁伤分析模块结果和毁伤链路谱系,重点分析潜艇破损进水、火灾、失电等极端情况下潜艇各设备、系统的功能毁伤,以及对潜艇生命力和作战能力的影响。
1.4 后处理模块结合二次毁伤分析模块结果,给出水下爆炸冲击下潜艇生命力、作战能力等综合效能评估结论。
2 综合毁伤评估模型构建方法潜艇作为一种典型的水下功能结构物,系统、功能、设备仪器、舱室划分方式等纷繁复杂,人员训练水平与指挥操纵策略各异,水下操纵相比于水面舰船难度更大,其生命力、战斗力受各类指标参数影响的敏感度更强,在综合毁伤评估建模中不可能面面俱到。本文以影响潜艇生命力和战斗力的基本原则为评价依据,分析关键因素并建立评价指标,综合毁伤评估按照毁伤程度由重到轻的判别顺序,先分析对潜艇生命力造成直接重大威胁的判别指标,再分析对生命力和作战能力造成间接重大影响的关键指标。
2.1 建模基本原则分析 2.1.1 相邻N舱破损不沉制原则水面舰船和潜艇设计时,通常会考虑相邻破舱不沉制指标,可描述为相邻N舱破损时可保证平台不沉性。潜艇舱室破损是最严重的毁伤情形且易于判断,是否满足相邻破舱不沉制原则可作为毁伤评估判别的第一步。如果相邻破舱个数小于N时,进行下一步评估;否则,认为潜艇生命力丧失,毁伤程度标定为1。
2.1.2 损管抗沉有效性原则潜艇水下操纵复杂,水下爆炸受损后操纵难度更大,即使受损潜艇满足相邻破舱不沉制原则,也并不能意味着潜艇生命力未丧失,还跟下一步的损管抗沉行为息息相关。损管抗沉有效性可表述为,受损潜艇通过各种静、动力抗沉措施,能否避免潜艇因强度、稳性丧失或其他原因导致沉没。抗沉有效性原则是评估潜艇生命力的重要依据,可作为毁伤评估判别的第二步,因静力抗沉中的压载水舱吹除系统以及动力抗沉能力等与功能系统毁伤情况相关,抗沉有效性评估依赖功能系统毁伤分析反馈结果,需并行开展。如果损管抗沉行为有效,进行下一步作战能力毁伤评估;否则,认为潜艇生命力丧失,毁伤程度标定为1。
2.1.3 毁伤关联度分级原则在潜艇生命力未完全丧失,即满足相邻破舱不沉制原则的情况下,与损管抗沉有效性评估并行开展功能系统毁伤评估,对潜艇作战能力的损失情况进行分析。将功能系统毁伤评估按功能、系统、设备划分为3层,下层节点通过边与上层节点建立关联,节点的现实意义可理解为各功能、系统、设备,边的现实意义可理解为各电缆、光缆、信号传输线、水管、油管、气管等。定义毁伤链路为若干下层节点为保证上一层节点正常运行所需的最小串行组合,每个节点的毁伤程度跟与之相联的各条毁伤链路相关联,每条毁伤链路中每个节点对上一节点的毁伤关联度取值范围为0~1,每条边对上一节点的毁伤关联度取值为0或1。与上层节点直接相联的下层节点定义为一级节点,与一级节点相联的节点定义为二级节点,以此类推,并依此建立相邻两层之间的毁伤链路谱。某系统的毁伤链路谱如图2所示,根据上述定义,该系统共有10条毁伤链路。

|
图 2 某系统的毁伤链路谱 Fig. 2 The relevant damage spectrum of X system |
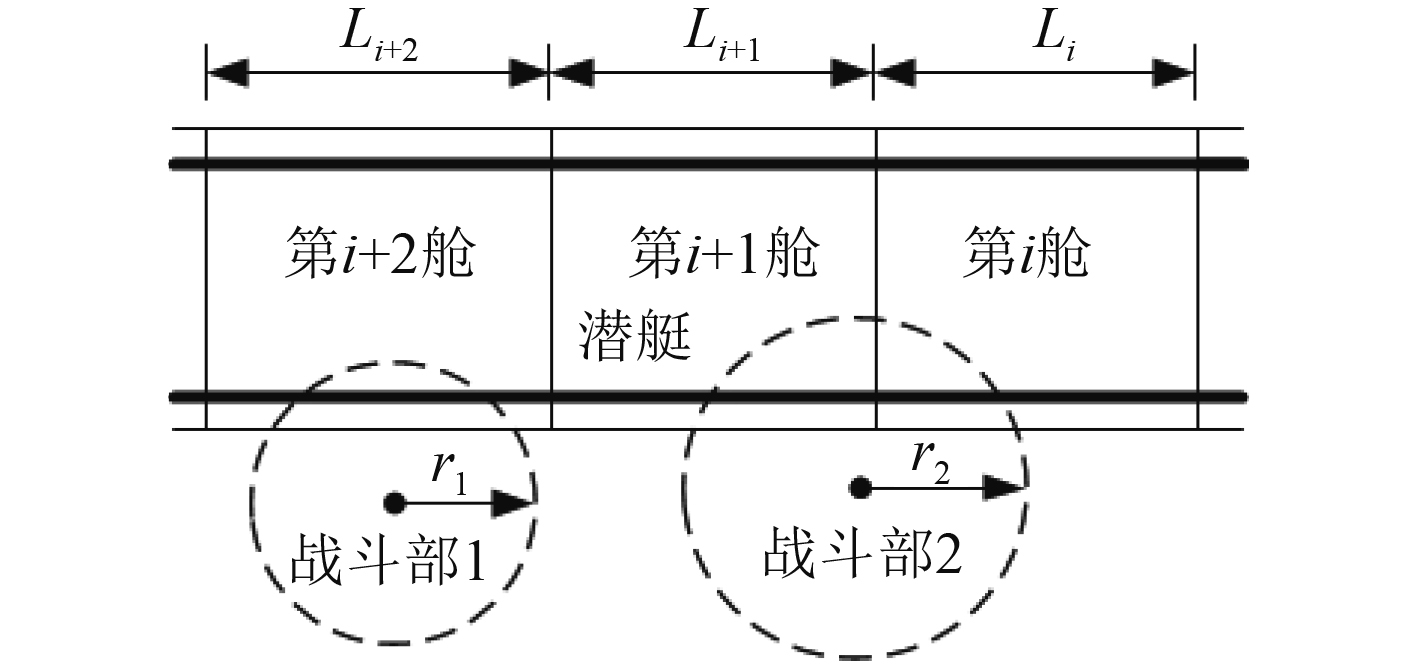
潜艇遭受鱼雷或深水炸弹近距离或接触命中时,往往会造成耐压壳体的破损,相邻破舱数量n是影响潜艇不沉性的直接关键因素。评价指标可集成为战斗部破坏半径r、潜艇各舱室长度Li及雷(弹)目交会态势。如图3所示,战斗部1对潜艇的破舱数量为1,战斗部2对潜艇的破舱数量为2。其中,战斗部破坏半径与战斗部装药种类、当量、距艇体的距离、角度、耐压壳体及肋骨材料、尺寸等多个因素有关,可通过理论或经验公式及仿真计算得到;雷(弹)目交会态势跟潜艇及鱼雷的初始态势、鱼雷导引方式、引信动作机理及潜艇机动行为等因素有关,可通过仿真分析得到[9]。
|
图 3 破舱数量评价示意图 Fig. 3 The quantitative assessment of broken cabins |
潜艇受水下爆炸破损变形后,艇体结构总纵强度及局部耐压强度均有所降低,评价指标可取剩余弹性极限弯矩
潜艇受水下爆炸破损进水后,由于浮力的损失,会产生向下的运动趋势,能否通过综合运用静力抗沉、动力抗沉措施,及时使潜艇到达安全深度,是评判损管抗沉有效与否的关键,评价指标可取为潜艇到达危险深度的临界时间
潜艇遭受深水炸弹或水雷水下中远场爆炸时,即使不会对潜艇壳体造成大破口而沉没,但也可能导致壳体产生大变形,并在艇载设施设备处产生巨大的冲击加速度,由此引发的功能、系统及设备的毁伤是综合毁伤评估的关键。依据毁伤链路谱,可将评价指标取为各节点和边的抗冲击阈值和最大容许变形量。提取某节点或边处的冲击加速度输入和变形量,与其设计阈值和最大容许量进行比较,若冲击加速度输入超出设计阈值或实际变形量超出容许值,认为该节点或边的毁伤程度为1;若冲击加速度输入未超出设计阈值且实际变形量未超出容许值,毁伤程度为0。
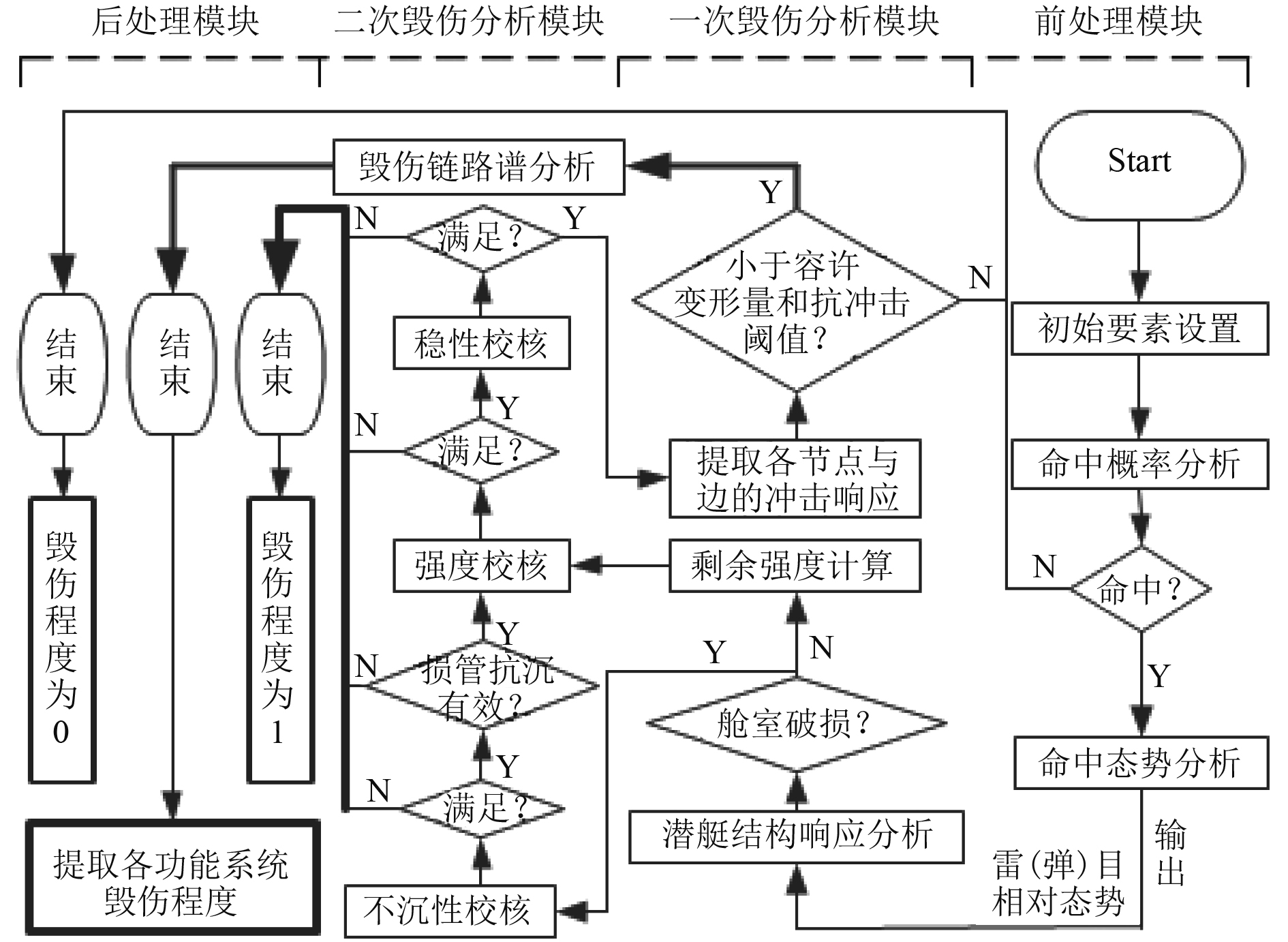
2.3 建模分析方法流程生命力是战斗力的基础和保障,建模分析分步实施:第1步,分析评估潜艇是否生命力完全丧失;第2步,在生命力未完全丧失的条件下,分析评估作战能力受损情况。建模分析流程如图4所示。
|
图 4 建模分析流程图 Fig. 4 The modeling and analysis flowchart |
本文对水下爆炸下潜艇综合毁伤评估体系开展研究,构建了包括前处理模块、一次毁伤分析模块、二次毁伤分析模块和后处理模块的综合毁伤评估体系结构;通过分析建模基本原则、关键影响因素和评价指标,建立了潜艇综合毁伤评估模型的构建流程与方法;通过对综合毁伤评估体系的研究,可以得出以下结论:
1)该毁伤评估体系覆盖了从水中兵器攻击到潜艇毁伤的全链路,任意单一因素的改变都可能对毁伤评估结果产生大的影响,必须对各毁伤要素及其内在逻辑进行系统分析,才能得到科学合理的评估结论。
2)命中态势是潜艇综合毁伤的外因,在潜艇综合毁伤的精准定量评估中,必须依托精确的外部输入;同时,遭受鱼雷等水中兵器攻击时,潜艇一方面可通过优化机动决策改变命中态势来降低水下爆炸对本艇的初始毁伤,另一方面可以通过有效的损管抗沉行动来降低本艇的后效毁伤。
3)潜艇各功能系统的毁伤链路是潜艇毁伤的内因,毁伤链路上各节点的毁伤程度及其毁伤体系贡献度对潜艇的综合毁伤效能有重要影响,在潜艇的抗水下爆炸性能体系优化设计上必须综合考量各毁伤链路的鲁棒性。
潜艇系统设备复杂多样,各系统设备的冲击可靠性和战损后的损管行动对潜艇生命力和作战能力具有重要影响,仅仅对潜艇结构开展毁伤分析已不能满足毁伤评估需求,建立潜艇综合毁伤要素数据库,并深化结构毁伤到功能毁伤的精准定量映射关系以及损管行动优化决策研究,是后续潜艇毁伤效能评估体系研究的重点问题。
| [1] |
KIRKPATRICK S W, HOLMES B S. Structural response of thin cylindrical shells subjected to impulsive external loads[J]. AIAA Journal, 1988, 26(1): 96-103. DOI:10.2514/3.9856 |
| [2] |
WIERZBICKI T, HOO FATT M S. Damage assessment of cylinders due to impact and explosive loading[J]. International Journal of Impact Engineering, 1993, 13(2): 215-241. DOI:10.1016/0734-743X(93)90094-N |
| [3] |
胡俊波, 张志华, 李庆民. 水下爆炸对水下目标的毁伤评估研究[J]. 振动与冲击, 2010, 29(10): 206-210. HU Jun-bo, ZHANG Zhi-hua, LI Qing-min. Damage evaluation for an underwater target under underwater explosion[J]. Journal of Vibration and Shock, 2010, 29(10): 206-210. DOI:10.3969/j.issn.1000-3835.2010.10.043 |
| [4] |
姚熊亮, 张阿漫, 许维军. 声固耦合方法在舰船水下爆炸中的应用[J]. 哈尔滨工程大学学报, 2005, 26(6): 707-712. YAO Xiong-liang, ZHANG A-man, XU Wei-jun. Application of coupled acoustic-structural analysis to warship underwater explosion[J]. Journal of Harbin Engineering University, 2005, 26(6): 707-712. DOI:10.3969/j.issn.1006-7043.2005.06.003 |
| [5] |
程素秋, 宁永成, 张臣, 等. 相似理论在水下爆炸模型试验中的应用[J]. 舰船科学技术, 2008, 30(3): 95-100. Cheng Su-qiu, Ning Yong-cheng, Zhang Chen, et al. The applicability of scaling laws to underwater explosion models tests[J]. Ship Science and Technology, 2008, 30(3): 95-100. DOI:10.3404/j.issn.1672-7649,2008.03.018 |
| [6] |
纪冲, 徐全军, 万文乾, 等. 钢质圆柱壳在侧向爆炸载荷下的动力响应[J]. 爆炸与冲击, 2012, 32(6): 585-591. JI Chong, XU Quan-jun, WAN Wen-qian, et al. Dynamic response of steel cylindrical shells under lateral explosion loading[J]. Explosion and Shock Waves, 2012, 32(6): 585-591. DOI:10.3969/j.issn.1001-1455.2012.06.005 |
| [7] |
宗智, 赵延杰, 邹丽. 水下爆炸结构毁伤的数值计算[M]. 北京: 科学出版社, 2014.
|
| [8] |
张阿漫, 王诗平, 彭玉祥, 等. 水下爆炸与舰船毁伤研究进展[J]. 中国舰船研究, 2019, 14(3): 1-13. Zhang A-man, Wang Shi-ping, Peng Yu-xiang, et al. Research progress in underwater explosion and its damage to ship structures[J]. Chinese Journal of Ship Research, 2019, 14(3): 1-13. |
| [9] |
韩大伟, 王天忠, 李宏明. 鱼雷现在方位攻击潜艇雷目交会态势分析[J]. 海军大连舰艇学院学报, 2020, 43(1): 11-15. Han Da-wei, Wang Tian-zhong, Li Hong-ming. Analysis on torpedo-target’s encountering situation for torpedo attacking submarine in guidance of present bearing[J]. Journal of Dalian Naval Academy, 2020, 43(1): 11-15. |
| [10] |
朱锡, 张振华, 梅志远, 等. 舰船结构毁伤力学[M]. 北京: 国防工业出版社, 2013.
|
| [11] |
韩大伟, 张东俊, 王天忠, 等. 潜艇单舱大深度破损进水模型数值分析[J]. 应用数学进展, 2019, 8(5): 876-882. Han Da-wei, Zhang Dong-jun, Wang Tian-zhong, et al. Numerical analysis to inflow changes model of single-cabin-broken submarine in large depths[J]. Advances in Applied Mathematics, 2019, 8(5): 876-882. DOI:10.12677/AAM.2019.85098 |
 2021, Vol. 43
2021, Vol. 43
