2. 海军研究院,北京 100161
2. Naval Research Institute, Beijing 100161, China
随着未来作战系统的信息化程度不断提高,水面无人艇(USV)因具有机动灵活、可替代人开展危险作业等特点,被广泛用于执行战场侦察、情报收集、反水雷等高危险任务作业[1-2]。为了更好实现水面无人艇的作业,精确的导航定位也至关重要。目前,常用的导航方法有惯导、卫导、长基线水声定位、多普勒计程仪等,其中惯导误差随时间呈发散趋势,卫导信号脆弱,易受攻击和压制,信标导航由于无需卫星信号即可实现精确定位而成为导航领域新的研究热点。如文献[3]采用单信标布置在水面船上,并利用卫导数据对信标进行定位,水下无人航行器借助装备的长基线系统测量相对于信标的距离,根据DVL和角度传感器进行航位推算,分别研究了EKF和粒子滤波算法的导航定位性能,验证了粒子滤波具有更高的定位精度;文献[4]研究了如何在给定机器人运动轨迹时最优布置信标位置,提高导航定位精度。基于已知信标位置的导航算法简单,导航误差小,具有良好的收敛性,但需要提前标定信标位置,花费大量时间和人力物力,特别是在战时或执行紧急任务时,无法满足对及时性的要求,限制了信标导航的应用范围。为减少系统启动时间,有专家学者提出基于随机信标的导航定位算法,为在一定区域内执行任务的无人艇通过飞机或母船布放一些信标,而不需要标定信标位置,实现导航定位和环境构图[5]。
目前,关于采用因子图算法进行同时定位构图的研究很多。如文献[6]采用滑动窗因子图基于地图上潜在路标位置进行三维路标地图和全部导航状态的非线性优化估计,提高卫星拒止环境下定位和路标位置估计精度;针对无人作战平台在室内等复杂环境下的高精度定位问题,蒋小强等[7]采用因子图模型对WLAN和单目视觉进行数据融合,从而获得精确的定位和地图信息;文献[8]研究了VO和IMU融合因子图模型,实现自动驾驶系统的即时定位和地图构建;Vadim Indelman等[9]把因子图应用于多源导航信息融合系统,将惯导、GPS和视觉传感器进行组合,实现导航定位和环境地图的构建;文献[10]将因子图模型应用于超宽带/INS组合导航中,实现无人飞行器的室内定位,相比于传统滤波算法提高了定位精度。但如何采用水声信息同时进行导航定位和信标位置估计的研究还较少。
本文提出一种基于随机信标的因子图同时定位构图算法,利用无人艇上装备的DVL和罗经测量无人艇移动速度和航向,通过测量无人艇相对于信标的距离,在无需标定信标位置的前提下,实现无人艇和信标的位置估计。
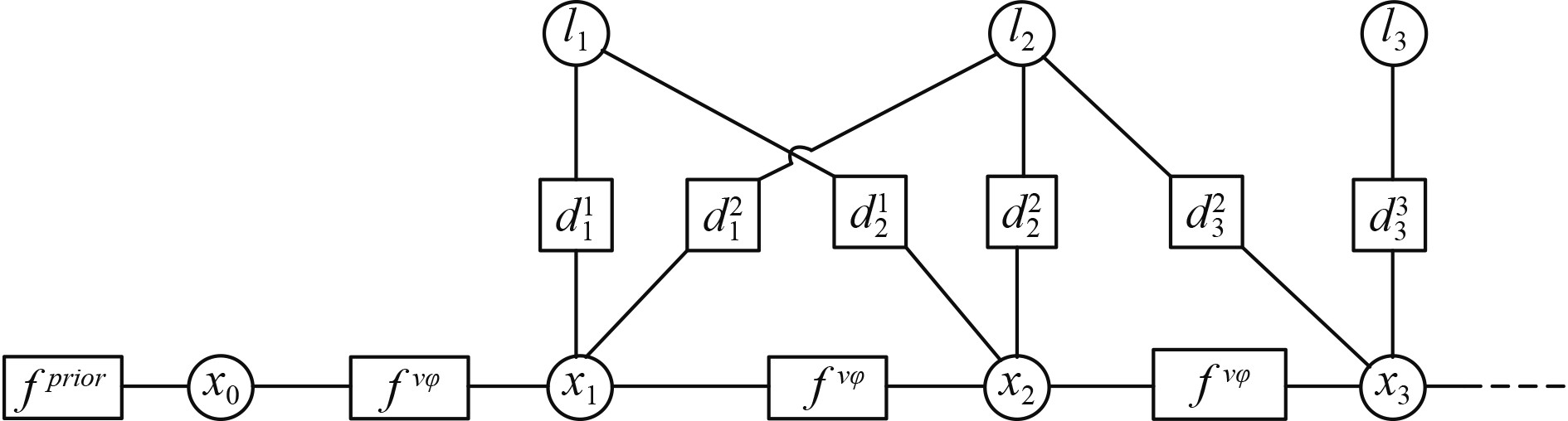
1 因子图模型架构设计 1.1 融合架构为简化模型,减小计算量,将水深视为固定值,在母船布放无人艇时测定。在构建基于随机信标的因子图同时定位构图模型中,变量节点包括无人艇的位置和航向、随机信标的位置,量测因子节点包括DVL测量的速度信息、罗经测量的航向信息和无人艇相对于信标的距离信息。设计如图1所示因子图模型架构。
|
图 1 基于随机信标的因子图同时定位构图模型架构 Fig. 1 Simultaneous localization and mapping model architecture of factor graph based on random beacon |
图中,USV离开母船时的初始位置和航向为
不同时刻之间的无人艇状态变量节点由DVL和罗经量测信息组合成的因子节点
根据图1描述的各个变量间的概率密度函数关系,可知USV和信标位置变量的后验概率密度函数如下:
| $ P\left( {{x_{0:k}},{l_{1:m}}|d_{1:k}^{1:m}} \right) \propto P\left( {{x_0}} \right)\prod\limits_{i = 1}^k {P\left( {{x_i}|{x_{i - 1}}} \right)\prod\limits_{j = 1,s = 1}^{j = k,s = m} {P\left( {d_j^s|{x_j},{l_s}} \right)} } ,$ | (1) |
基于最大后验概率估计,可得无人艇和信标位置估计的表达式如下:
| $ \begin{split} & X_k^ * = \mathop {\arg \max }\limits_{X_k^ * } P\left( {{x_{0:k}},{l_{1:m}}|d_{1:k}^{1:m}} \right) = \mathop {\arg \min }\limits_{X_k^ * } \times \\ &\left\{ \begin{gathered} {\left\| {{x_0} - {{\hat x}_0}} \right\|_{{P_0}}} + \sum\limits_{i = 1}^k {{{\left\| {{x_k} - {h^{v\varphi }}\left( {{x_{k - 1}},{{\hat v}_{k - 1}},{{\hat \varphi }_{k - 1}}} \right)} \right\|}_{{P_{k - 1}}}}} + \\ \sum\limits_{j = 1,s = 1}^{j = k,s = m} {{{\left\| {d_k^i - {h^d}\left( {{x_k},{l_k}} \right)} \right\|}_{{R_{ki}}}}} \\ \end{gathered} \right\} \text{。} \end{split} $ | (2) |
USV运动学模型为:
| $ \dot x = \left[ \begin{gathered} {{\dot p}_x} \hfill \\ {{\dot p}_y} \hfill \\ {\dot \varphi } \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} {v_x} \hfill \\ {v_y} \hfill \\ \omega \hfill \\ \end{gathered} \right]\text{。} $ | (3) |
式中:
| $ \begin{split} {x_k} =& {h^{v\varphi }}\left( {{x_{k - 1}},{{\hat v}_{k - 1}},{{\hat \varphi }_{k - 1}}} \right) = \left[ \begin{gathered} p_k^x \\ p_k^y \\ {\varphi _k} \\ \end{gathered} \right] =\\ &\left[ \begin{gathered} p_{k - 1}^x + {v_{k - 1}}\cos {\varphi _{k - 1}}T \\ p_{k - 1}^y + {v_{k - 1}}\sin {\varphi _{k - 1}}T \\ {\varphi _{k - 1}} + {\omega _{k - 1}}T \\ \end{gathered} \right] = {x_{k - 1}} + T\left[ \begin{gathered} {v_{k - 1}}\cos {\varphi _{k - 1}} \\ {v_{k - 1}}\sin {\varphi _{k - 1}} \\ {\omega _{k - 1}} \\ \end{gathered} \right] \text{。} \end{split} $ | (4) |
式中:
考虑DVL和罗经存在测量误差,记
| $ \begin{split} &{f^{v\varphi }}\left( {{x_k},{x_{k - 1}}} \right) = P\left( {{x_k}|{x_{k - 1}}} \right) = \\ & k_k^{v\varphi }\exp \left( - \frac{1}{2}{{\left\| {x_k} - {h^{v\varphi }}\left( {x_{k - 1}},{{\hat v}_{k - 1}},{{\hat \varphi }_{k - 1}} \right) \right\|}_{{P_{k - 1}}}} \right)\text{。} \end{split} $ | (5) |
式中,
将式(5)在估计位置处作泰勒展开,忽略二次及以上项,可得:
| $ \begin{split} {{\hat x}_k} - \delta {x_k} =& {{\hat x}_{k - 1}} - \delta {x_{k - 1}} + \left[ \begin{gathered} {{\hat v}_{k - 1}}\cos {{\hat \varphi }_{k - 1}}T \\ {{\hat v}_{k - 1}}\sin {{\hat \varphi }_{k - 1}}T \\ {{\hat \omega }_{k - 1}}T \\ \end{gathered} \right] + \\ & F\delta {x_{k - 1}} + \left[ \begin{gathered} - \cos {{\hat \varphi }_{k - 1}}{w_{vk - 1}}T \\ - \sin {{\hat \varphi }_{k - 1}}{w_{vk - 1}}T \\ - {w_{\omega k - 1}}T \\ \end{gathered} \right] \text{。} \\ \end{split} $ | (6) |
式中,
| $ \delta {b_k} = {\hat x_k} - {\hat x_{k - 1}} - \left[ \begin{gathered} {{\hat v}_{k - 1}}\cos {{\hat \varphi }_{k - 1}}T \hfill \\ {{\hat v}_{k - 1}}\sin {{\hat \varphi }_{k - 1}}T \hfill \\ {{\hat \omega }_{k - 1}}T \hfill \\ \end{gathered} \right], $ |
| $ {\Phi _{k - 1}} = I - F = \left[ \begin{gathered} \begin{array}{*{20}{c}} 1&0&{\begin{array}{*{20}{c}} {} \end{array}{{\hat v}_{k - 1}}\sin {{\hat \varphi }_{k - 1}}T} \end{array} \hfill \\ \begin{array}{*{20}{c}} 0&1&{ - {{\hat v}_{k - 1}}\cos {{\hat \varphi }_{k - 1}}T} \end{array} \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 0&0 \end{array}}&{}&{}&1 \end{array} \hfill \\ \end{gathered} \right], $ |
| $ {\Gamma _{k - 1}} = \left[ \begin{gathered} \begin{array}{*{20}{c}} {T\cos {{\hat \varphi }_{k - 1}}}&0 \end{array} \hfill \\ \begin{array}{*{20}{c}} {T\sin {{\hat \varphi }_{k - 1}}}&0 \end{array} \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&0 \end{array}}&{}&T \end{array} \hfill \\ \end{gathered} \right] ,$ |
| $ {w_{k - 1}} = {\left[ {\begin{array}{*{20}{c}} {{w_{vk - 1}}}&{{w_{\omega k - 1}}} \end{array}} \right]^{\rm{T}}}, $ |
DVL和罗经的噪声协方差矩阵为:
| $ {Q_{k - 1}} = E\left[ {{w_{k - 1}}w_{k - 1}^{\rm{T}}} \right] = \left[ \begin{gathered} \begin{array}{*{20}{c}} {{\sigma _{vk - 1}}}&0 \end{array} \hfill \\ \begin{array}{*{20}{c}} 0&{\begin{array}{*{20}{c}} {} \end{array}{\sigma _{\omega k - 1}}} \end{array} \hfill \\ \end{gathered} \right] ,$ |
则式(6)可整理如下:
| $ \delta {x_k} = {\varPhi _{k - 1}}\delta {x_{k - 1}} + \delta {b_k} + {\varGamma _{k - 1}}{w_{k - 1}}\text{。} $ | (7) |
由上述分析可知,
| $ {P_{k - 1}} = E\left[ {\left( {{\varGamma _{k - 1}}{w_{k - 1}}} \right){{\left( {{\varGamma _{k - 1}}{w_{k - 1}}} \right)}^{\rm{T}}}} \right] = {\varGamma _{k - 1}}{Q_{k - 1}}\varGamma _{k - 1}^{\rm{T}}, $ | (8) |
| $ d_k^i = {h^d}\left( {{x_k},{l_k}} \right) + {w_d} = \sqrt {{{\left( {p_k^x - l_i^x} \right)}^2} + {{\left( {p_k^y - l_i^y} \right)}^2}} + {w_d} ,$ | (9) |
式中,
| $ {R_{ki}} = E\left[ {{w_d} w_d^{\rm{T}}} \right] = {\sigma _d}, $ | (10) |
定义信标量测因子节点模型为:
| $ {f^d}\left( {{x_k},{l_k}} \right) = P\left( {d_k^i|{x_k},{l_k}} \right) = k_{ki}^d\exp \left( { - \frac{1}{2}{{\left\| {d_k^i - {h^d}\left( {{x_k},{l_k}} \right)} \right\|}_{{R_{ki}}}}} \right), $ | (11) |
式中,
记初始时刻导航状态估计为
| $ f_x^{prior}\left( {{x_0}} \right) = P\left( {{x_0}} \right) = k_x^{prior}\exp \left( { - \frac{1}{2}{{\left\| {{{\hat x}_0} - {x_0}} \right\|}_{{P_0}}}} \right), $ | (12) |
式中,
将式(9)在估计位置处作泰勒展开,忽略二次及以上项,记第
| $ \begin{split} & \sqrt {{{\left( {p_k^x - l_i^x} \right)}^2} + {{\left( {p_k^y - l_i^y} \right)}^2}} = \sqrt {{{\left( {\hat p_k^x - \hat l_i^x} \right)}^2} + {{\left( {\hat p_k^y - \hat l_i^y} \right)}^2}} - \\ & \qquad \frac{{\left( {\hat p_k^x - \hat l_i^x} \right)}}{{\sqrt {{{\left( {\hat p_k^x - \hat l_i^x} \right)}^2} + {{\left( {\hat p_k^y - \hat l_i^y} \right)}^2}} }}\left( {\delta p_k^x - \delta l_i^x} \right) -\\ &\qquad\frac{{\hat p_k^y - \hat l_i^y}}{{\sqrt {{{\left( {\hat p_k^x - \hat l_i^x} \right)}^2} + {{\left( {\hat p_k^y - \hat l_i^y} \right)}^2}} }}\left( {\delta p_k^y - \delta l_i^y} \right) , \end{split} $ |
记
| $ \delta d_k^i = - u_{ki}^x\left( {\delta p_k^x - \delta l_i^x} \right) - u_{ki}^y\left( {\delta p_k^y - \delta l_i^y} \right) + {w_d}, $ | (13) |
式中,
根据上述分析,将式(2)在状态变量和信标位置估计值处作泰勒展开并保留一次项,记变量节点估计误差集合为
| $ J\delta X = b ,$ | (14) |
式中,各符号定义如下:
| $ J = \left[ \begin{gathered} \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{}&{}&{} \end{array}}&{}&{}&{\begin{array}{*{20}{c}} {\sqrt {{\Sigma _0}} \delta {x_0}}&{\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array}}&{} \end{array}}&{} \end{array}} \end{array} \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{}&{}&{} \end{array}}&{}&{}&{\begin{array}{*{20}{c}} { - \sqrt {{\Sigma _1}} {\Phi _0}\delta {x_0}}&{\sqrt {{\Sigma _1}} \delta {x_1}}&{} \end{array}} \end{array} \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{}&{}&{} \end{array}}&{}& \vdots &{} \end{array} \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\sqrt {{R_{11}}} {u_{11}}}&{}&{}&{\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array}} \end{array}}&{\begin{array}{*{20}{c}} {}&{} \end{array}}&{ - \sqrt {{R_{11}}} {u_{11}}H}&{} \end{array} \hfill \\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} \begin{gathered} \hfill \\ \hfill \\ \end{gathered} &\begin{gathered} \hfill \\ \hfill \\ \end{gathered} &\begin{gathered} \sqrt {{R_{12}}} {u_{12}} \hfill \\ \hfill \\ \end{gathered} &\begin{gathered} \hfill \\ \vdots \hfill \\ \end{gathered} \end{array}}&\begin{gathered} \hfill \\ \hfill \\ \end{gathered} &\begin{gathered} \hfill \\ \hfill \\ \end{gathered} &\begin{gathered} \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{ - \sqrt {{R_{12}}} {u_{12}}H} \end{array} \hfill \\ \hfill \\ \end{gathered} \end{array} \hfill \\ \end{gathered} \right], $ | (15) |
| $ b = \left[ \sqrt {{\Sigma _0}} \delta {{\hat x}_0}\quad {\sqrt {{\Sigma _1}} \delta {b_1}} \quad \cdots \quad {\sqrt {{R_{11}}} \delta d_1^1}\quad {\sqrt {{R_{12}}} \delta d_1^2}\quad \cdots \quad \right]^{\rm{T}}. $ | (16) |
式中:
因子图同时定位构图算法:
1) 构建因子图
2) 当接收到DVL和罗经测量信息时,创建因子节点
3) 提取受新插入因子节点影响的子图
4) 根据量测因子节点计算变量节点的初始估计值
5) 在变量节点估计值处线性化各因子节点建立雅克比矩阵和残差向量;
6) 计算变量节点估计误差并进行修正;
7) 计算残差向量,若大于设定阈值,则转步骤5)进行迭代,否则,完成当前导航状态估计,转步骤2),等待新量测因子的插入。
3 数值仿真验证与分析设定仿真区域1 000 m×1 000 m,随机布放12个信标,采用DVL和罗经测量速度和航向,测速误差为0.2 m/s,刻度系数误差3%,航向测量误差10°/h,距离测量误差5 m,位置初始误差1 m,初始航向误差1°。
设置圆形和蛇形2种运动轨迹进行数值仿真验证,将因子图算法与EKF滤波算法进行比较,仿真结果如图2~图7所示。
|
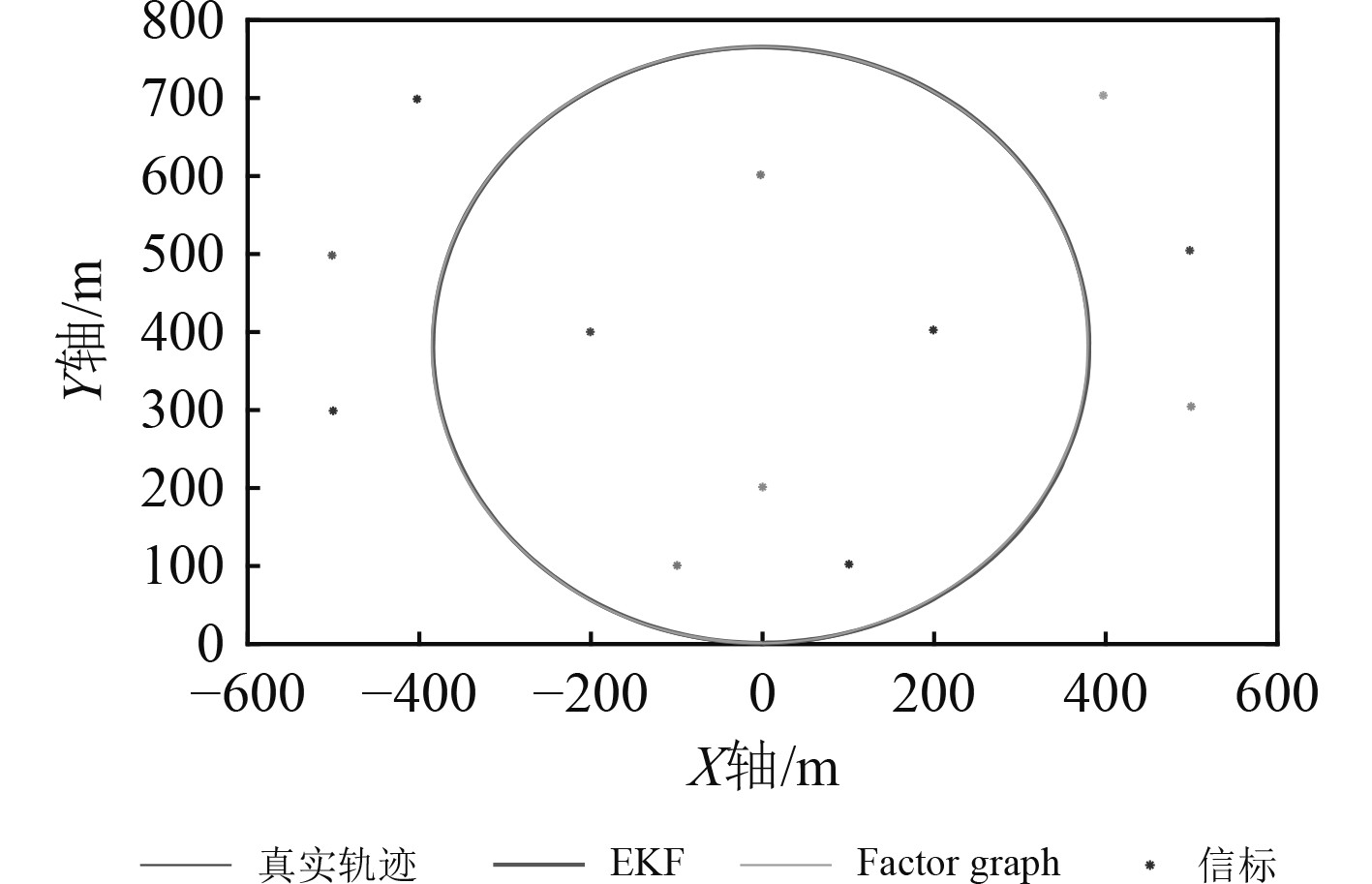
图 2 圆形运动轨迹对比图 Fig. 2 Comparison chart of circular trajectory |
|
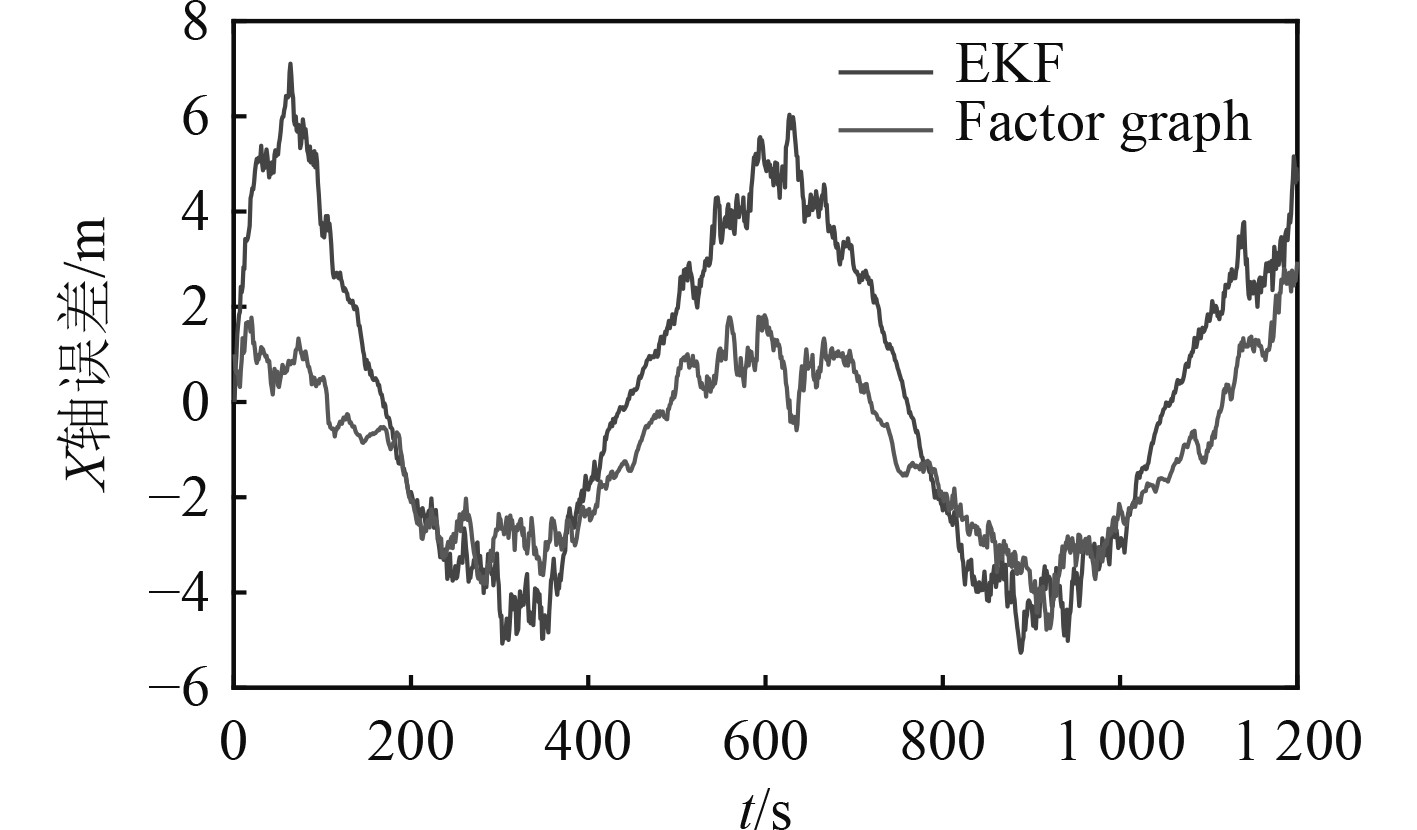
图 3 圆形运动轨迹下X轴方向估计误差 Fig. 3 Estimation error of x-axis direction in circular trajectory |
|
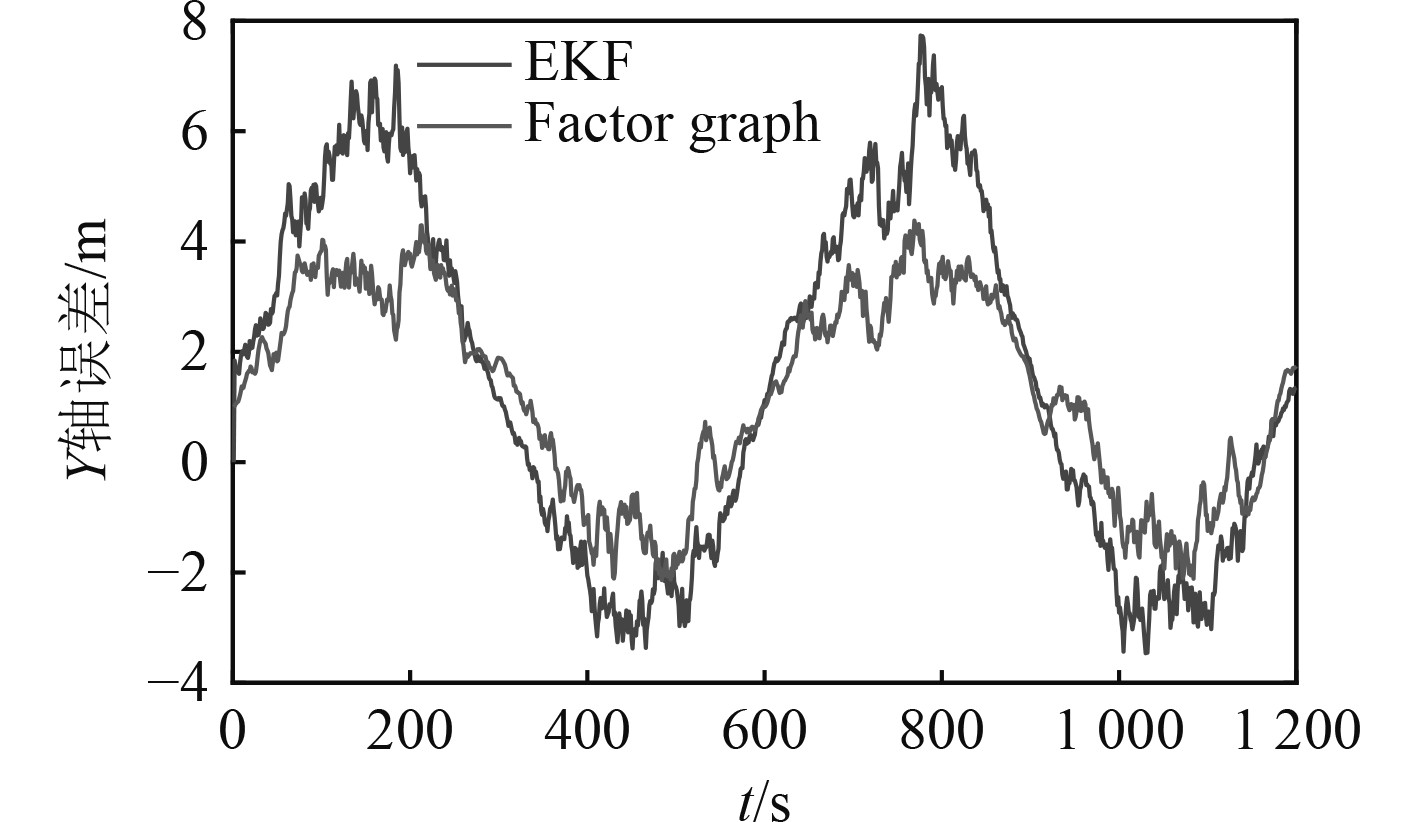
图 4 圆形运动轨迹下Y轴方向估计误差 Fig. 4 Estimation error of y-axis direction in circular trajectory |
|
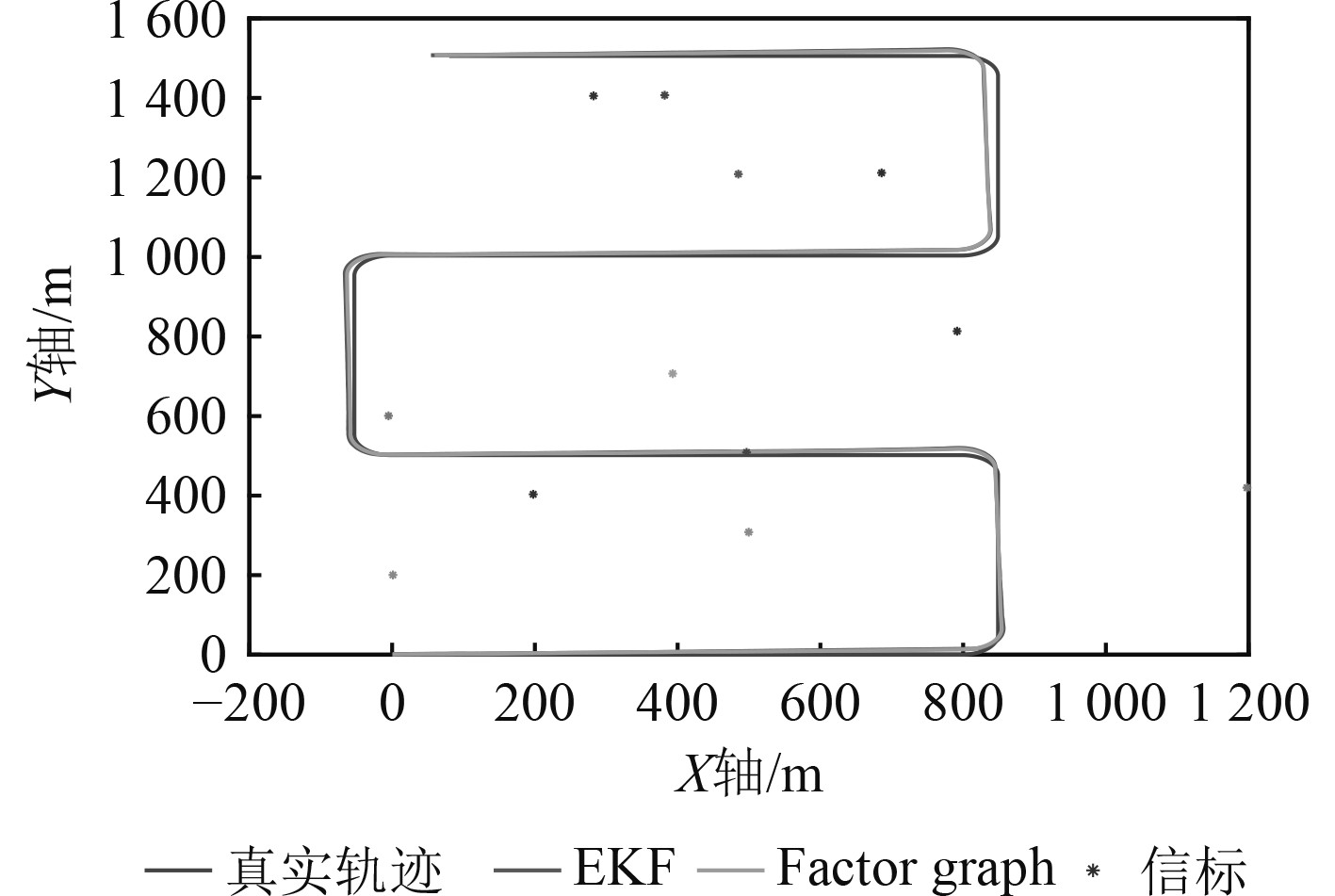
图 5 蛇形运动轨迹对比图 Fig. 5 Comparison chart of serpentine trajectory |
|
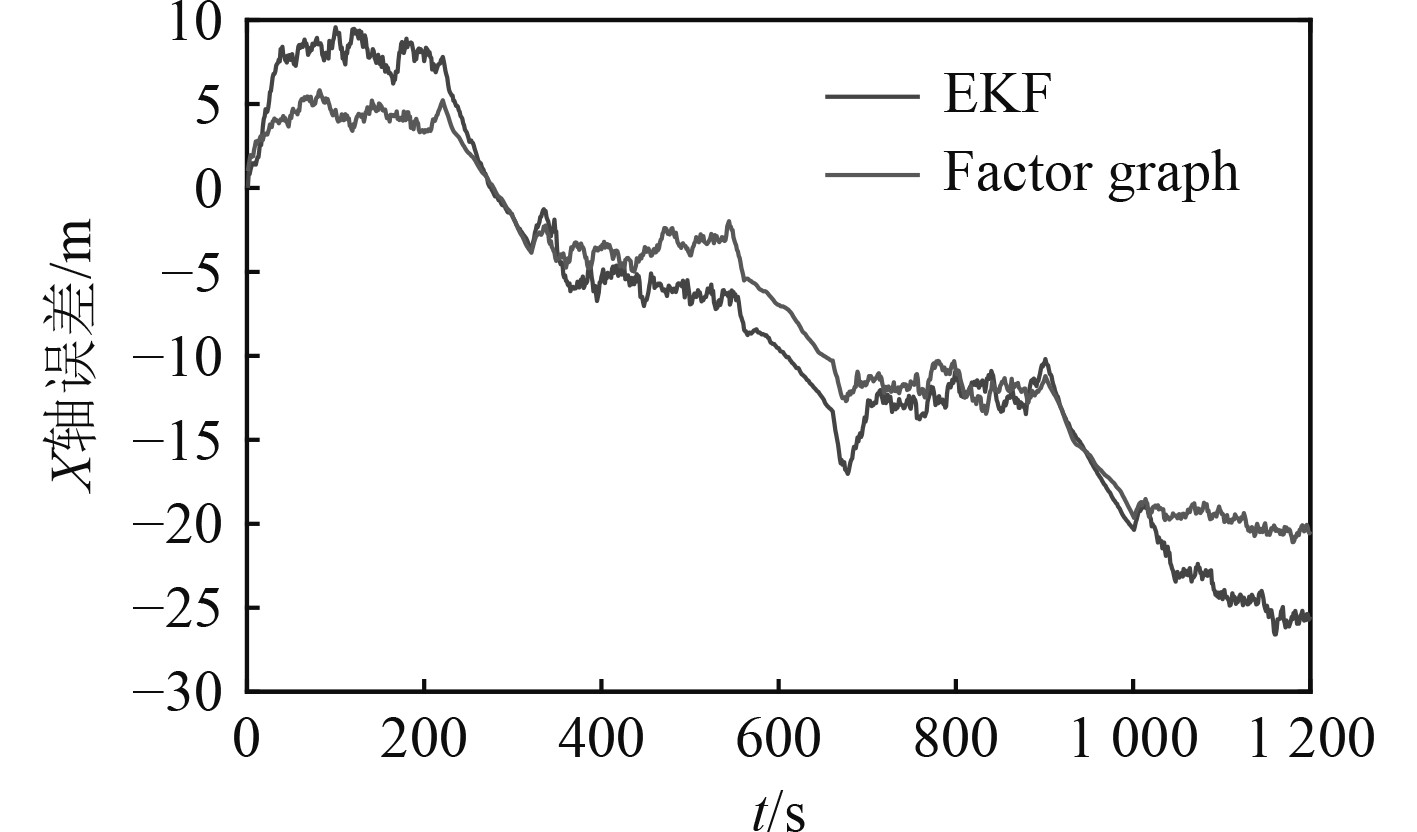
图 6 蛇形运动轨迹下X轴方向估计误差 Fig. 6 Estimation error of x-axis direction in serpentine trajectory |
|
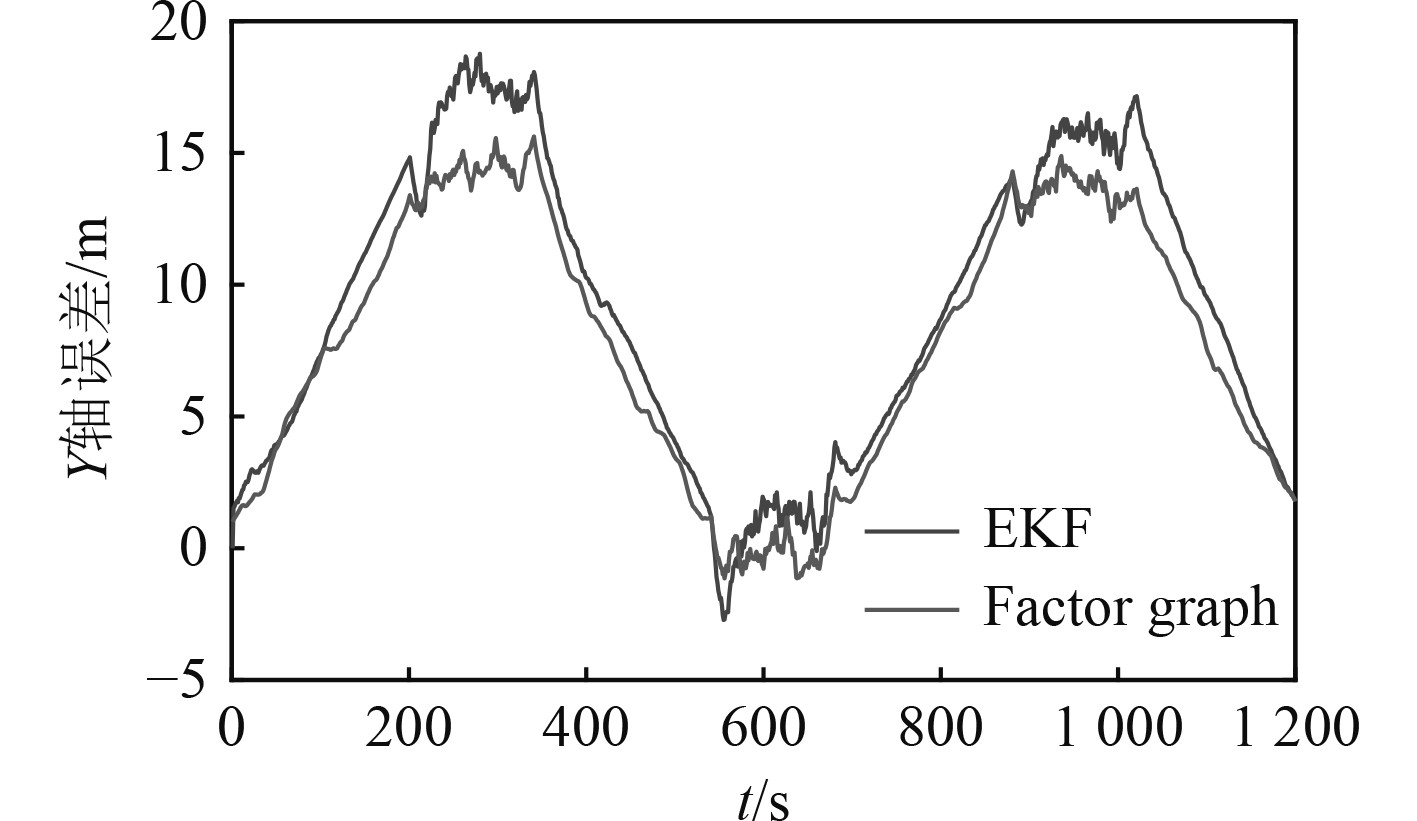
图 7 蛇形运动轨迹下Y轴方向估计误差 Fig. 7 Estimation error of y-axis direction in serpentine trajectory |
因子图算法、EKF算法导航定位误差和信标位置估计误差如表1和表2所示。
|
|
表 1 因子图算法、EKF算法定位误差 Tab.1 Location error of factor graph and EKF |
|
|
表 2 因子图算法、EKF算法信标位置误差 Tab.2 Beacon location error of factor graph and EKF |
从图2~图7及表1和表2可以看出,基于随机信标,在圆形轨迹和蛇形轨迹2种情况下因子图定位精度和信标位置估计精度均优于传统EKF滤波算法;圆形轨迹和蛇形轨迹仿真验证中,因子图算法相比EKF滤波算法定位精度分别提高37.6%和14.6%,平均信标位置估计误差分别提高14.1%和13.1%。由理论分析可知,因子图算法通过利用所有时刻量测信息,采用非线性最小二乘优化算法进行导航状态估计,EKF滤波算法只考虑当前时刻量测信息,采用非线性滤波算法进行导航状态和信标位置估计,利用量测信息不充分且具有系统线性化误差,因此,因子图算法估计精度应优于EKF滤波算法,与数值仿真验证结果一致。
4 结 语本文针对战时或执行紧急任务时的导航定位问题,研究了一种基于随机信标的因子图同时定位构图算法,建立了DVL和罗经因子节点、信标因子节点数学模型,构建了因子图架构,同时对水面无人艇和信标的位置进行估计,并对该算法开展了数值仿真试验验证。仿真结果表明:因子图算法克服传统水声定位必须提前标定信标位置的缺点,且比EKF滤波算法具有更好的定位精度和信标位置估计精度,为快速实现信标导航提供了一种导航方法。但是,由于本文只进行了理论分析与数值仿真,还有待进一步开展实船试验进行验证和完善。
| [1] |
胡常青 朱玮, 何远清等. 无人水面艇自主导航技术[J]. 导航与控制, 2019, 18(1): 24-31+95. |
| [2] |
林龙信, 张比升. 水面无人作战系统技术发展与作战应用[J]. 水下无人系统学报, 2018.
|
| [3] |
DUBROVIN F S, SCHERBATYUK A F. Studying some algorithms for AUV navigation using a single beacon: The results of simulation and sea trials[J]. Gyroscopy and Navigation, 2016, 7(2): 189-196. DOI:10.1134/S2075108716020024 |
| [4] |
ALLEN R., MACMILLAN N., MARINAKIS D., et al. Whitesides, The Range Beacon Placement Problem for Robot Navigation, 2014 Canadian Conference on Computer and Robot Vision, Montreal, QC, 2014, pp. 151−158, doi: 10.1109/CRV.2014.28.
|
| [5] |
刘明雍, 董婷婷, 张立川. 基于随机信标的水下SLAM导航方法[J]. 系统工程与电子技术, 2015.
|
| [6] |
CHIU H P, WILLIAMS S, DELLAERT F, et al. Robust vision-aided navigation using Sliding-Window Factor graphs[C]// Robotics and Automation(ICRA), 2013 IEEE International Conference on. IEEE, 2013.
|
| [7] |
蒋小强, 卢虎, 贺磊南. 面向无人平台的室内精密定位与构图技术[J]. 空军工程大学学报. 自然科学版, 2019, 20(1): 107-114. |
| [8] |
袁子叶, 尹慧琳, 伍淑莉. 基于因子图的自动驾驶融合定位研究[J]. 汽车工程学报, 2019, 9(4): 243-251. |
| [9] |
VADIM I., STEPHEN W., MICHAEL K., et al. Factor graph based incremental smoothing in inertial navigation systems[C]// International Conference on Information Fusion. IEEE, 2012.
|
| [10] |
Yang S, HSU L T. Tightly coupled integrated navigation system via factor graph for UAV indoor localization[J]. Aerospace Science and Technology, 2020, 108: 106370. |
 2021, Vol. 43
2021, Vol. 43
