2. 中国舰船研究院,北京 100101
2. China Ship Research and Development Academy, Beijing 100101, China
传动系统是各种机械装置最为关键的运动部件之一,特别是传动系统中的斜齿轮副,其安全、可靠、平稳地运转对整个传动系统有着极其重要的意义。齿轮工作时在啮合处会产生接触应力,接触应力反复作用在齿面上导致齿面发生点蚀。发生点蚀容易导致齿面传动性能下降,产生噪声等。所以,轮齿传动时齿面的接触应力对其齿轮的承载能力和可靠性具有重要影响。但在齿轮的制造、加工、使用过程中,由于各类随机因素的存在,例如结构尺寸公差、外界载荷波动、材料特性的分散性等,都会对接触应力产生影响。因此,在进行齿轮结构设计时,就需要对结构在不同设计参数下的接触强度进行可靠性分析,甚至要通过各个方案对比分析,以筛选出最合理的方案,并达到优化设计的目的。因此开展齿轮接触强度可靠性分析对于传动装置安全可靠运行具有非常重要的意义。
目前在齿轮接触强度可靠性评估时,齿面的接触应力分析多采用经验公式和有限元法[1-6],采用KISSsoft 软件进行齿轮接触应力分析的文献还相对较少。KISSsoft作为一款专业的传动系统设计软件, 在传动系开发过程中,能很好地避免需要开发人员翻阅各种设计手册和相关标准来对参数进行繁琐计算的问题。可以根据一系列计算标准和用户特殊需要产生一系列可选参数,通过对这些参数的选择对齿轮等进行自动建模,是传动装置齿轮参数优化设计的良好工具平台。其在齿轮、轴、轴承等元件的强度和寿命计算校核方面的使用越来越广泛 。唐进元等[7]基于KISSsoft 对某五级行星减速机齿轮参数进行分析计算,并对齿轮设计参数进行优化,改善了齿轮传动的强度、振动等传动性能指标。王红霞等[8]针对某减速器中的斜齿轮副齿面中出现的沿齿宽方向的应力集中以及传递误差波动现象, 使用KISSsoft中不同的修形方式对斜齿轮副轮齿进行修形设计,提高了斜齿轮的强度,改善了斜齿轮的传动性能,提高了啮合质量。姜雪燕等[9]对于斜齿轮高速重载复杂工况、疲劳寿命要求高等问题,运用KISSsoft软件对斜齿轮等效应力、接触应力、接触刚度、瞬时温度等动态啮合接触特性参数进行仿真分析,为斜齿轮动态啮合接触特性的改善、疲劳寿命的增加提供了理论依据。但上述文献都是在确定性的设计参数下进行的分析,没有考虑设计参数的随机不确定性,也没有进一步开展齿轮的可靠性评估工作。
本文通过Visual Basic语言调用KISSsoft软件建立齿轮的参数化仿真模型,并用外部命令实现了齿轮接触应力分析的参数化和自动化,并在ISIGHT软件平台上,以蒙特卡罗法为例实现了齿轮接触强度的可靠性分析和参数灵敏度分析。本文所提方法具有非常好的工程适用性,能够充分考虑输入变量的随机不确定性,准确分析出在输入参数分散性存在下齿轮接触应力强度可靠性结果,并能给出各随机参数对接触应力的影响规律,可为齿轮接触强度可靠性分析提供技术参考。
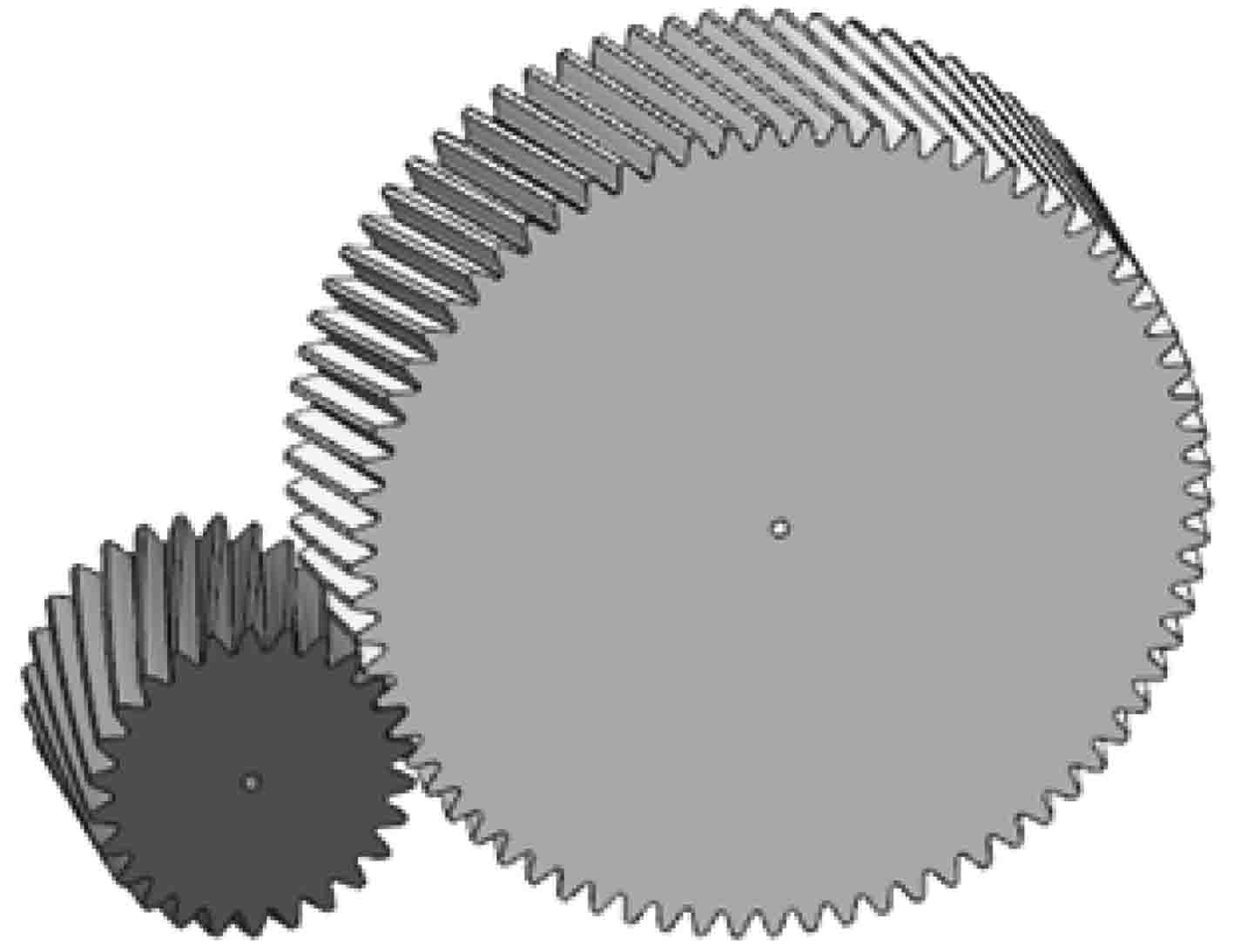
1 齿轮副接触应力的参数化仿真分析 1.1 KISSsoft确定性分析模型的建立在进行可靠性分析之前要完成对齿轮副模型的建立,对齿轮副模型进行接触强度的确定性分析。因此在KISSsoft 软件中,根据表1中齿轮基本参数生成一对齿轮的模型,如图1所示。
|
|
表 1 斜齿轮副参数表 Tab.1 Parameters of helical gear pair |
|
图 1 KISSsoft 软件生成的齿轮副分析模型 Fig. 1 Gear pair analysis model generated by KISSsoft |
在功率P=660 kW、转速N=1400r/min工况下,KISSsoft计算出最大接触应力σmax = 1 575.5 MPa,而其齿面许用接触应力σHS = 2 400 MPa,则其接触强度安全系数SH =1.53。根据GB6336-93或者ISO6336-93标准, 当SH ≥ 1.25时,齿轮设计满足较高安全可靠性要求[10]。从静力学角度分析来看,结构满足强度设计要求。
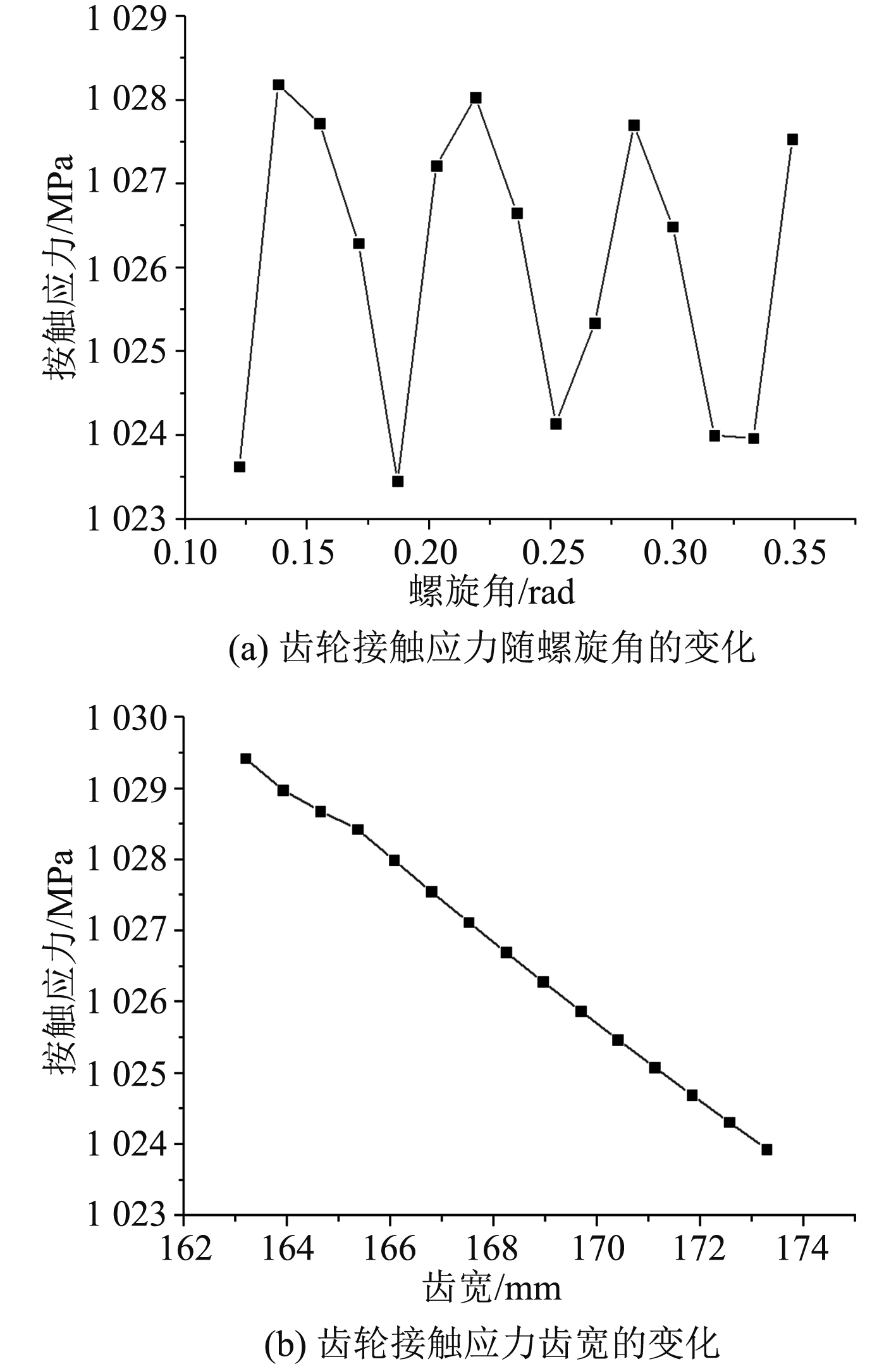
齿轮一些参数的变化势必对接触应力的大小造成影响。如图2所示,以螺旋角、齿宽2个结构参数为例,在保持其他参数不变的情况下,得到参数在不同设计水平下的接触应力变化规律曲线。
|
图 2 齿轮接触应力随参数的变化 Fig. 2 Variation of gear contact stress with parameters |
从图2(a)可以发现,螺旋角对接触应力的影响呈现高度非线姓,因此在设计时应该重点关注。从图2(b)可以看到,随着齿宽的增加,接触应力呈现下降趋势,这也和工程实际相吻合,验证了分析的有效性。
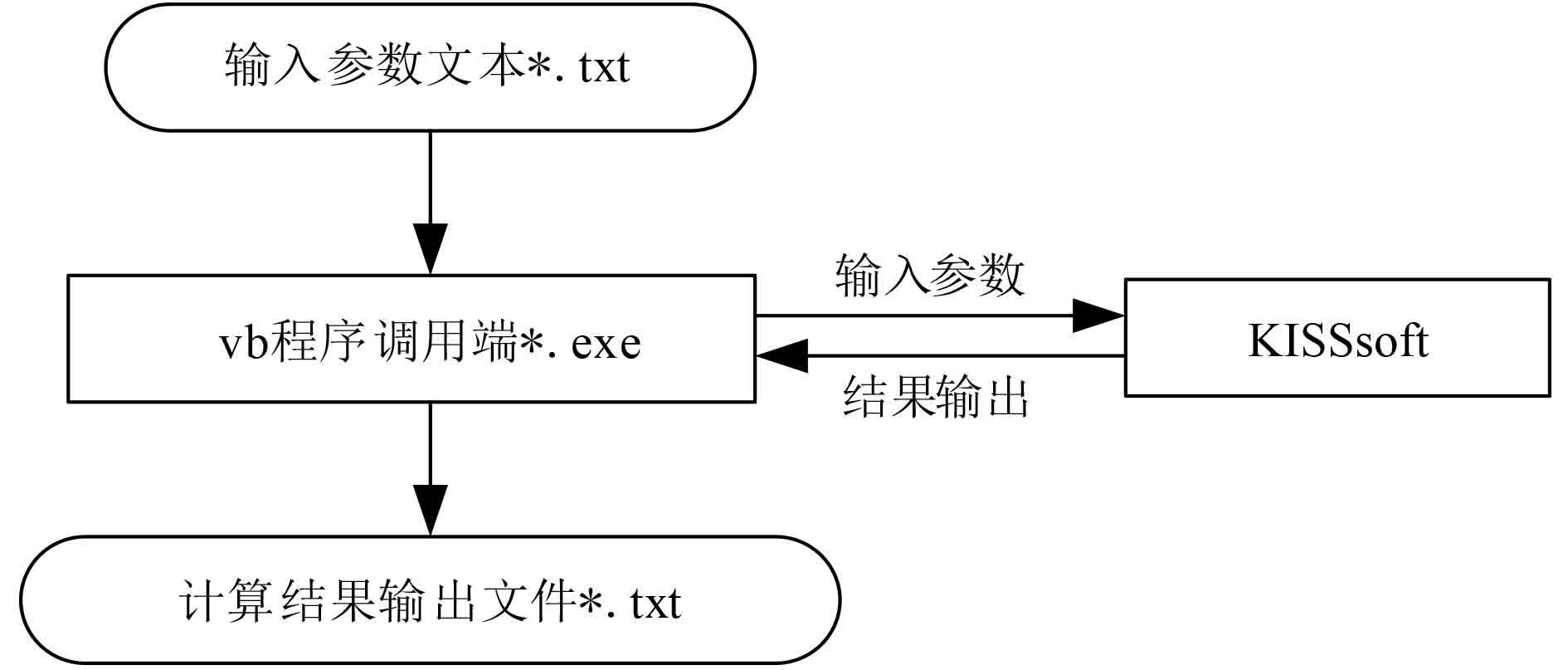
1.3 齿轮接触应力分析的参数化实现过程KISSsoft 软件提供了可以用于外部调用的 COM服务器,这就为外部软件对其进行数据交互和传输提供了可能。实际上,基于该 COM 接口,使用者无需打开软件界面,而利用Visual Basic,MS Office,JAVA,Matlab等开发自己需要的计算模块。本文利用VB 对KISSsoft “接触分析”模块进行开发,通过封装小程序*.exe文件完成参数输入、软件调用、模型建立和结果的输出。参数化建模基本原理如图3所示。
|
图 3 KISSsoft参数化建模基本原理图 Fig. 3 Schematic diagram of KISSsoft parametric modeling |
其中,VB程序调用端*.exe文件用于提取指定路径下参数文本中对应的参数,并通过调用COM服务器传递给KISSsoft 软件进行建模和相关计算,并把计算结果以文本的形式输出到指定路径下的文件夹中。
完成以上关于KISSsoft模块的开发后,只需在输入“参数文本”中直接修改齿轮副的相关参数就能完成参数化模型的建立,这为下一步利用ISIGHT进行可靠性分析做好铺垫工作。
2 基于ISIGHT平台的可靠性分析ISIGHT 是一款计算可靠性与目标优化的计算机辅助软件,其自带的各种可靠性和目标优化算法可以集成各种软件工具。ISIGHT利用数据文件的传递实现软件的集成、运行与结果提取的自动化。用户可以通过拖拉的方式搭载建立所需的各种分析流程,并且可以修改和设计参数,自动进行分析循环[12]。
2.1 基于蒙特卡罗法的可靠性建模蒙特卡罗模拟法又称随机抽样法,概率模拟法或统计试验法,该方法是以概率论和数理统计理论为基础,通过随机模拟或统计试验进行结构可靠性分析的近似数字模拟法。由于该方法对变量个数、变量概率分布、极限状态均无限制而深受重视,并作为验证其他可靠性分析方法结果的参考方法[13-14]。因此本文以蒙特卡罗模拟法为例,构建齿轮接触强度的可靠性分析模型。
在可靠性模型的建立过程中,对随机变量的选取以及对这些随机变量分布特征的确定是其中一个非常重要的环节。影响齿轮接触强度的不确定因素主要有结构尺寸、外界载荷、材料特性等,本文可靠性建模主要考虑齿轮结构尺寸和外部载荷对可靠性的影响。选择齿轮的螺旋角、齿宽、模数、功率、转速为研究变量,选取的随机变量及其分布特征如表2所示。
|
|
表 2 随机变量及其分布特性 Tab.2 Random variables and their distribution characteristics |
通过KISSsoft确定性分析许用接触应力 ,以齿轮最大接触应力大于许用接触应力作为其失效判据,其接触强度功能函数为:
| $ g={\sigma }_{HS}-\text{ }{\sigma }_{\mathrm{max}}(\beta ,m,B,P,N){\text{,}} $ | (1) |
式中,
| $ \left\{ \begin{aligned} g = {\sigma _{HS}} - {\sigma _{\max }} > 0\text{,}{\text{安全区域}}{\text{,}}\\ g = {\sigma _{HS}} - {\sigma _{\max }} = 0\text{,}{\text{临界区域}}{\text{,}}\\ g = {\sigma _{HS}} - {\sigma _{\max }} < 0\text{,}{\text{失效区域}}{\text{。}} \end{aligned} \right. $ | (2) |
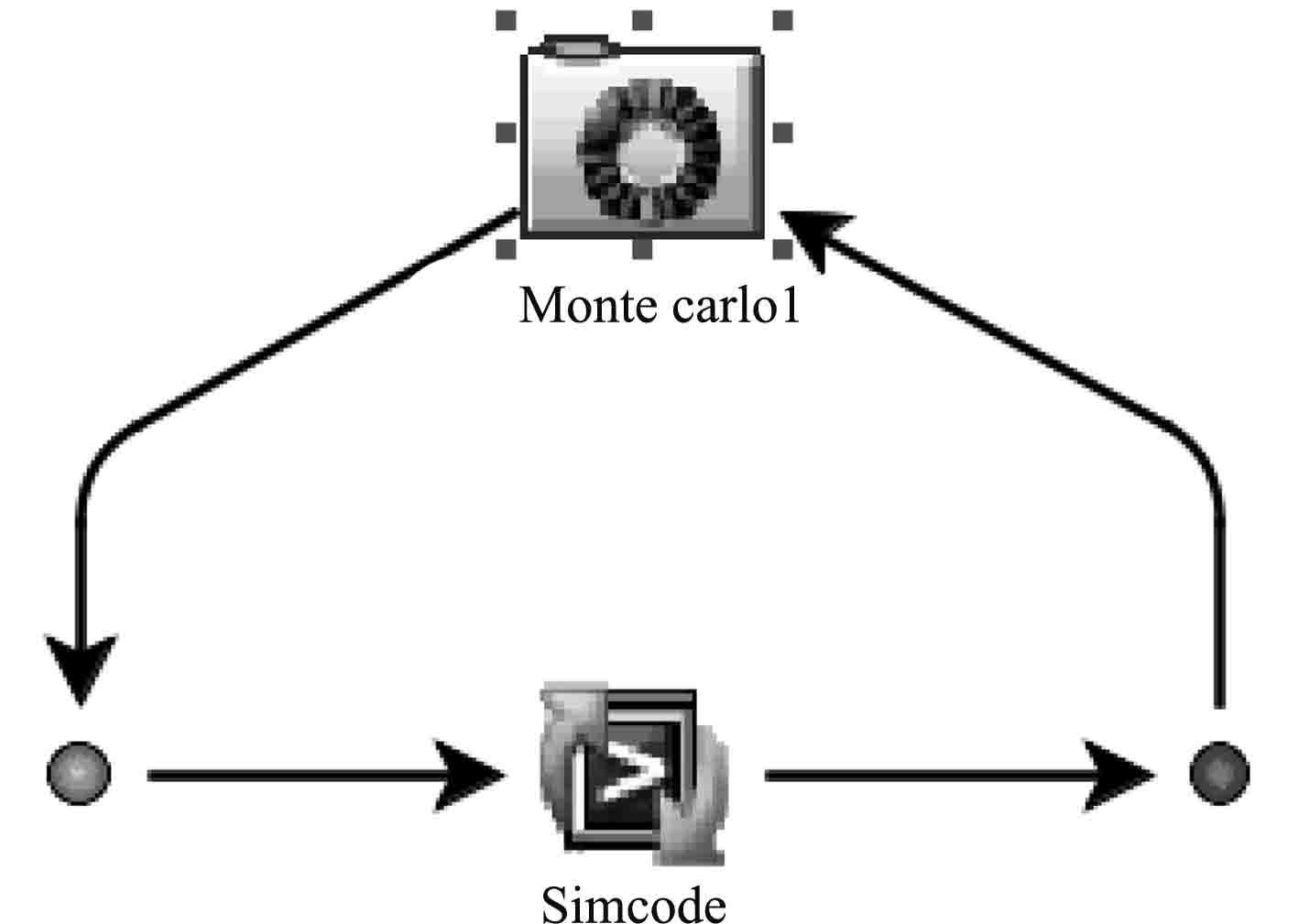
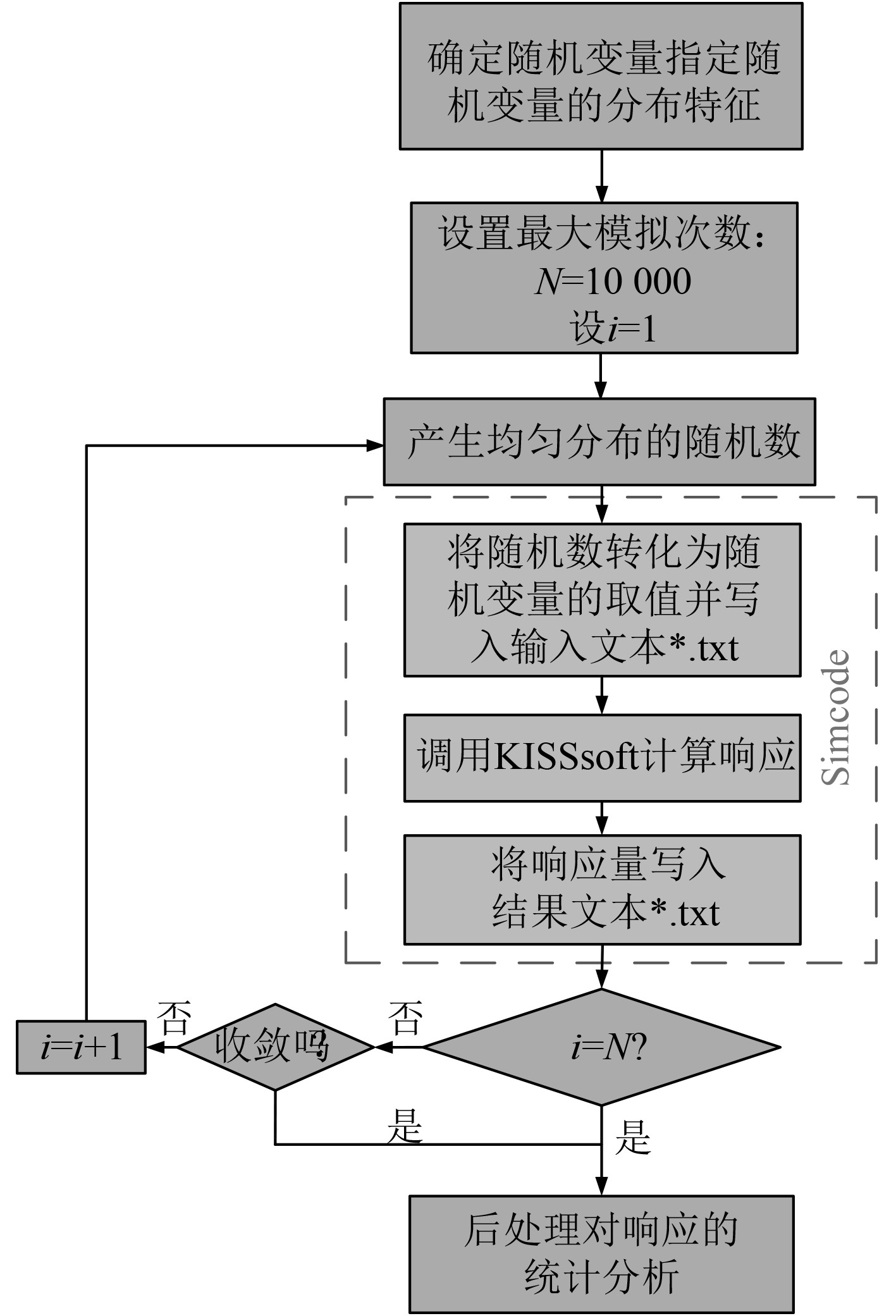
以 ISIGHT 为集成平台,集成结果如图4所示。首先拖入一个程序集成组件Simcode,它能自动完成参数的修改输入、程序的执行、结果的输出。在其中设置好输入、输出参数的映射关系以及对*.exe文件的调用。在Monte Carlo1组件中进行随机变量及其分布特征、响应量、抽样方法和抽样次数的设置。计算搭载流程如图5所示。
|
图 4 可靠性集成平台 Fig. 4 Reliability integration platform |
|
图 5 集成计算流程图 Fig. 5 Integrated calculation flow chart |
对随机变量简单随机抽样10000次,得到接触应力概率分布图如图6所示。

|
图 6 实际接触应力概率分布图 Fig. 6 Probability distribution of actual contact stress |
从频率分布上可以看到,接触应力的大小主要集中在1 575 MPa左右。在许用接触应力为σHS = 2400 MPa的情况下,得到齿轮发生接触强度失效的概率为
在可靠性分析的基础上,同时基于秩相关系数进行结构参数对齿轮接触应力的灵敏度分析,分析各设计参数对对齿面接触应力影响规律。
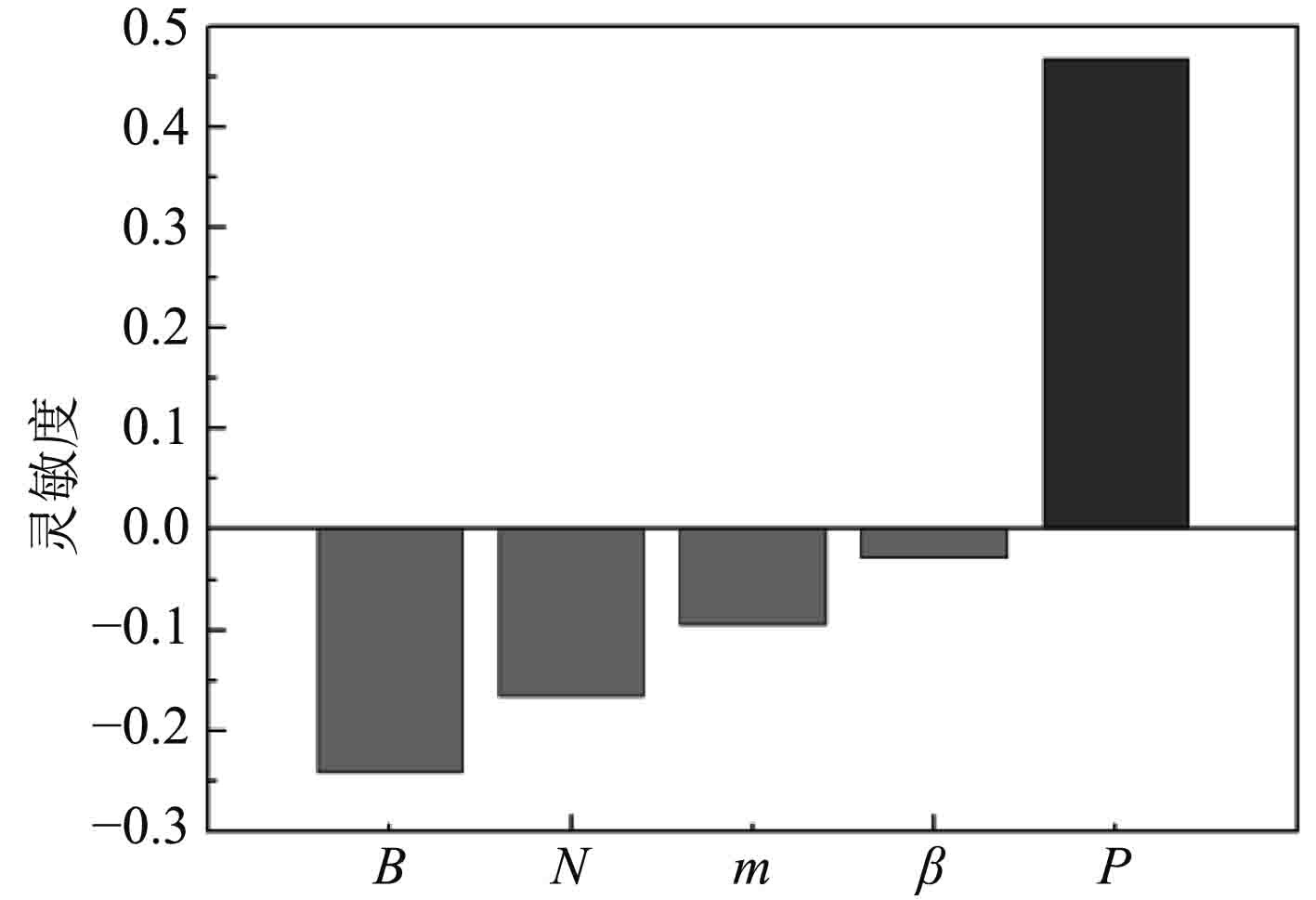
随机因素的灵敏度分析结果分布图如图7所示。
|
图 7 随机因素的灵敏度分析结果分布图 Fig. 7 Distribution of sensitivity analysis results of random factors |
图7中正的灵敏度值表示该参数的增大会增加输出响应量,负的灵敏度表示该参数的增大会降低输出响应量。由图7可知,影响齿轮接触强度最主要的几何尺寸参数为齿宽B、模数m,影响齿轮接触强度最主要的外部载荷主要是功率,因此在进行结构优化时应重点优化齿宽B、模数m来提高齿轮的接触强度性能。
3 结 论本文以斜齿轮副接触应力的可靠性分析为研究对象,基于KISSsoft技术,在ISIGHT平台下实现了齿轮接触强度的可靠性分析。可靠性分析的研究结果表明,齿宽B、模数m对齿轮的接触应力影响非常大,是齿轮结构设计过程中需要重点关注的设计参数。本文采用的方法具有非常高的计算效率和广泛的适用性,不仅可以用于齿轮的接触强度可靠性分析,还可以为齿轮其他失效模式的可靠性分析提供技术参考。
| [1] |
杨生华. 齿轮接触有限元分析[J]. 计算力学学报, 2003(2): 189−194. YANG Shenghua. Finite element analysis of gear con-tact [J]. Chinese Journal of Computational Mechanics. 2-003(2): 189−194. |
| [2] |
凡增辉, 赵熙雍, 晏红文. 基于ANSYS的斜齿轮接触有限元分析[J]. 机械传动, 2010, 34(4): 68−70. FAN Enhui, ZHAO Xiyong, YAN Hongwen. ANSYS based finite element analysis of oblique gear contact [J]. Journal of Mechanical Transmission. 2010, 34 (4): 68−70 |
| [3] |
高勇, 王勇, 淡勇, 等. 齿轮泵静力结构及接触应力的数值模拟[J].当代化工, 2018, 47(7): 1416−1419. GAO Yong, Wang Yong, DAN Yong, et al. Numerical simulation of the static structure and contact stress of gear pump [J]. Contemporary Chemical Industry. 2018, 47 (7): 1416−1419. |
| [4] |
李嘉, 李华聪, 王万成, 等. 高压航空燃油齿轮泵的齿轮强度校核及应力仿真分析[J]. 液压与气动, 2021(2): 105−113. LI jia, LI Huachong, WAMG Wancheng, et al. Strength check and stress simulation for the gear of a high - pressure aero - fuel Gear [J]. Pump Chinese Hydraulics & Pneumatics. 2021(2): 105−113. |
| [5] |
李瑞. 基于Kriging的齿轮可靠性分析[D].沈阳:东北大学, 2017. LI Run. Research on reliability of gears based on Kriging model[D]. Shenyang:Northeastern University, 2017. |
| [6] |
胡明用, 胡云波, 李金库, 等. 基于蒙特卡罗法的斜齿轮随机啮合效率可靠性分析[J]. 机械传动, 2021, 45(6): 127−131. HU Mingyong, HU Yunbo, Li Jinku, et al. Reliability analysis on random meshing efficiency of helical gear based on Monte Carlo method[J]. Journal of Mechanical Transmission. 2021, 45(6): 127−131. |
| [7] |
唐进元, 雷敦财. 基于Kisssoft软件的行星传动装置齿轮参数优化设计[J]. 机械传动, 2010, 34(12): 15−19. TANG Jinyuan, LEI Duncai. The parameter optimization design of planetary reducer based on Kisssoft software[J]. Journal of Mechanical Transmission. 2010, 34(12): 15−19. |
| [8] |
王红霞, 孙胜苗, 谯艳娟. 基于Kisssoft的斜齿轮副齿形优化设计[J]. 湖北汽车工业学院学报, 2015, 29(3): 66−69+73. WANG Hongyan, SUN Shengmiao, JIAO Yanjuan. O-ptimization design of tooth profile for helical gear pairs based on Kisssoft[J]. Journal of Hubei Universi-ty of Automotive Technology. 2015, 29(3): 66−69+73. |
| [9] |
姜雪燕, 王丽卿, 陈娟. 基于KISSsoft的斜齿轮接触特性仿真分析[J]. 煤矿机械, 2020, 41(2): 200−202. JANG Xueyan, WANG LiQing, CHEN Juan. Simulation analysis of contact characteristics for helical Gear based on KISSsoft[J]. Coal Mine Machinery. 2020, 41(2): 200−202. |
| [10] |
唐定国, 袁和相. 齿轮设计中的强度安全系数[J]. 机械传动, 1994(3): 18−20+56-57. TANG Dingguo, YUAN Hexiang. Strength safety factor in gear design. Journal of Mechanical Transmission. 1994(3): 18−20+56-57. |
| [11] |
郑站强, 刘世谦. 基于VB的KISSsoft软件二次开发及其在齿轮强度计算中的应用[J]. 拖拉机与农用运输车, 2020, 47(1): 29−31+35. ZHANG Zhanqiang, LIU Shiqian. Secondary development of KISSsoft software based on VB and its application in gear strength calculation [J]. Tractor &FarmTransporter. 2020, 47(1): 29−31+35. |
| [12] |
赖宇阳, 姜欣. Isight参数优化理论与实例详解[M]. 北京:北京航空航天大学出版社, 2012.
|
| [13] |
Melchers R E, Ahammed M. A fast approximate method for parameter sensitivity estimation in Monte-Carlo strucrural reliability[J]. Computers and Structures, 2004, 82(1): 55-61. DOI:10.1016/j.compstruc.2003.08.003 |
| [14] |
Roger M, Jan CM, Noortwijk V. Loacal probabilistic sensitivity measures for comparing FORM and MonteCarlo calculations illustrated with dike ring reliability calculations[J]. Computer Physics Communications, 1999, 117(1-2): 86-98. DOI:10.1016/S0010-4655(98)00166-0 |
 2021, Vol. 43
2021, Vol. 43
