轴系是动力装置的重要组成部分,在轴系运行过程中可能会产生轴承负荷不均或者轴系弯矩剪力过大的情形而导致轴系损坏,导致安全问题发生[1]。为了提高整个动力系统传递的效率、寿命及性能,国内外的专家、学者做了大量轴系校中的研究工作[2-4]。
轴系校中过程中实际需要考虑许多因素,除了温度、装载等“环境因素”之外,还需要考虑轴系振动等“动力因素”。将轴系支撑在筏架上的方法虽然有效地衰减了横向、轴向低频振动,却对轴系校中带来了很大的影响。筏架如果很长,则在推力、摇摆倾斜等工况下会出现较大的弹性变形,支撑系统的状态就会变化,轴承脱空的现象亦会产生。赵兴乾等[7]利用径向轴承载荷增量的评价方法讨论了筏架上的支撑设备的静态安全性,得出隔振器分布于筏架首部方向时更有利于轴承载荷增量的降低。何江洋等[8]分析得出推力轴承径向位移在筏架上会改变支撑系统的负荷状态,因此,在筏架上推力轴承基座的安装位置应靠近筏架的转动中心。Zhang Y.等[9]设计了一种智能浮筏系统,通过浮筏的变形监测来提升校中质量。总体来说,国内外对筏体的研究较为深入,但将阀体和轴系相结合的研究较少。本文以某筏架轴系为研究对象,对筏架和轴系分别建立有限元模型,基于有限元校中方法,分析考虑筏架对轴系校中的影响规律。
1 轴系有限元校中方法轴系校中计算模型采用的是离散型的轴承模型,计算方法有:迁移矩阵法、传递矩阵法,三弯矩法以及有限元法,其中迁移矩阵法因为计算繁琐且精度低而很少使用被淘汰,而有限元法是从20世纪50年代以来随着计算机应用日益广泛而迅速发展起来的一种极其有效的偏微分方程数值算法,是目前世界范围内计算机辅助工程分析(CAE)过程中普遍采用的方法。
有限元法的基本思想是将连续的实体模型离散化为有限个模式单元,这些单元通过节点相互连接起来构成一个有限元模型。模型中,每个单元都有形函数表征的有限元方程,所有单元的有限元方程按照设定的组合方法,即可形成整体模型的有限元方程。实体模型受限于工作环境,通过规则约束拟化为合适的边界条件,代入至有限元总方程中,按照数值求解的方法即可得到整个模型的相关物理状态参数。魏海军[10]在其开发的轴系校中软件中证明了有限元法的优越之处,通过实例计算对轴系校中过程中需要考虑的刚度、支撑位置和负荷影响系数等问题进行了深入讨论。本文选用有限元法进行轴系校中计算对比分析。
2 建模与分析 2.1 模型建立以某长轴系为研究对象,分别建立轴系和筏架的三维模型,如图1所示。长轴系包含尾轴1根,中间轴2根(可去掉1根)和推力轴1根,尾轴与中间轴采用套合连接,中间轴之间采用整锻法兰连接。推力轴由2个径向油润滑轴承支撑。筏架为平板式的镂空腹板浮筏。
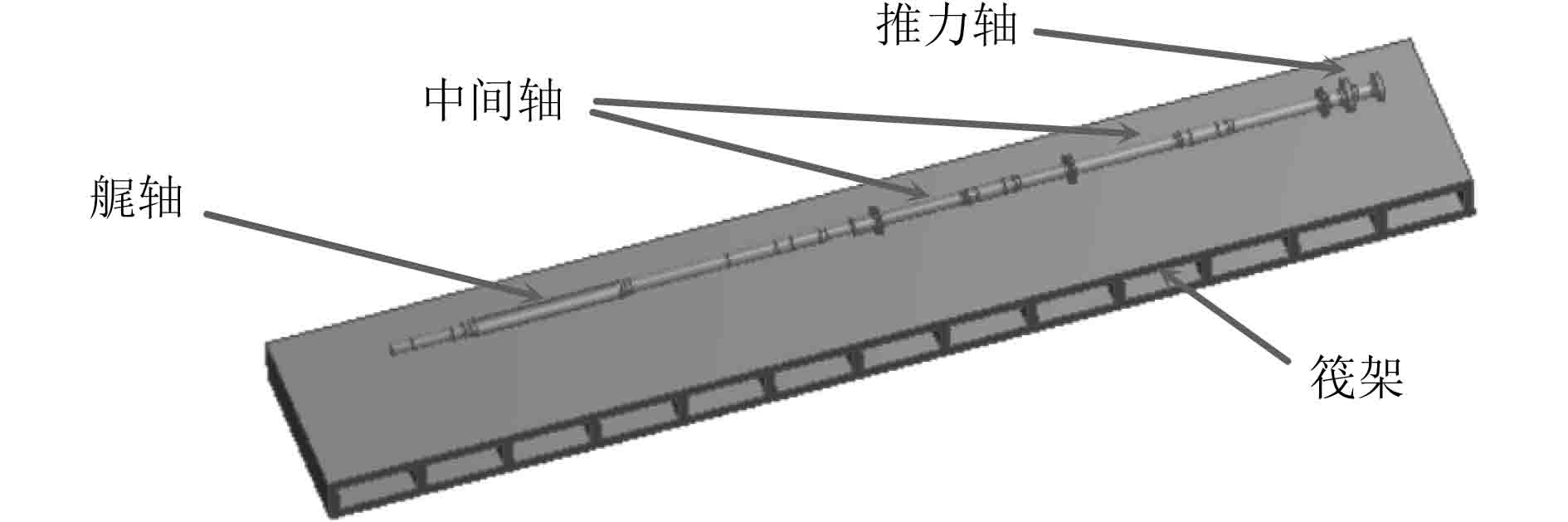
|
图 1 筏架轴系三维模型 Fig. 1 3D model of raft frame shafting |
1)不考虑浮筏的轴系校中
对于未安装在浮筏上的轴系,各轴承支座固定在结构上,在不考虑结构变形的条件下,可在轴系的各支点位置与结构对应安装位置施加线弹簧,弹簧的一端连接轴系,另一端设定为固定约束,如图2所示。
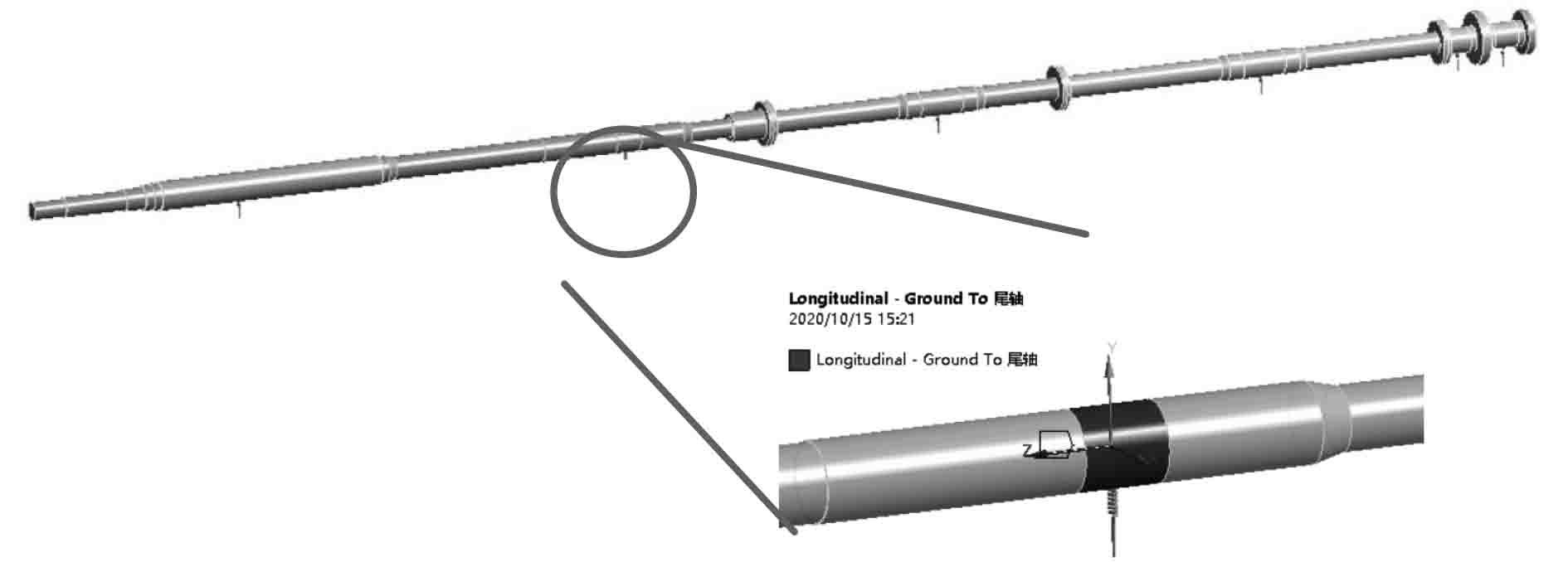
|
图 2 无筏架轴系校中支撑设置 Fig. 2 Shaft alignment support setting without raft frame |
各支撑轴承的刚度在线弹簧的Longitudinal Stiffness中进行输入,参考文献[11],具体的刚度数据如表1所示。由于校中分析属于静态分析,所以忽略线弹簧的阻尼输入。支座的刚性大,变形很小,因此各线弹簧的行为模式设置为Rigid。
|
|
表 1 支撑参数表 Tab.1 Support parameters |
关于轴承支点位置,为了简化模型,假设各轴承与轴颈接触状态正常,按照规范,设定后轴承支点位置为轴承的1/3处,其余前轴承、中间轴承和推力径向轴承均将轴承中点作为支承点近似位置。另外,除了考虑全轴系的自重,还需要在负载安装位置施加远端力的方式模拟其集中质量,假设为1000 kg。由于推力轴承末端与动力系统输出端固接,因此,设置推力轴末端法兰面为Fix Support约束,如图3所示。
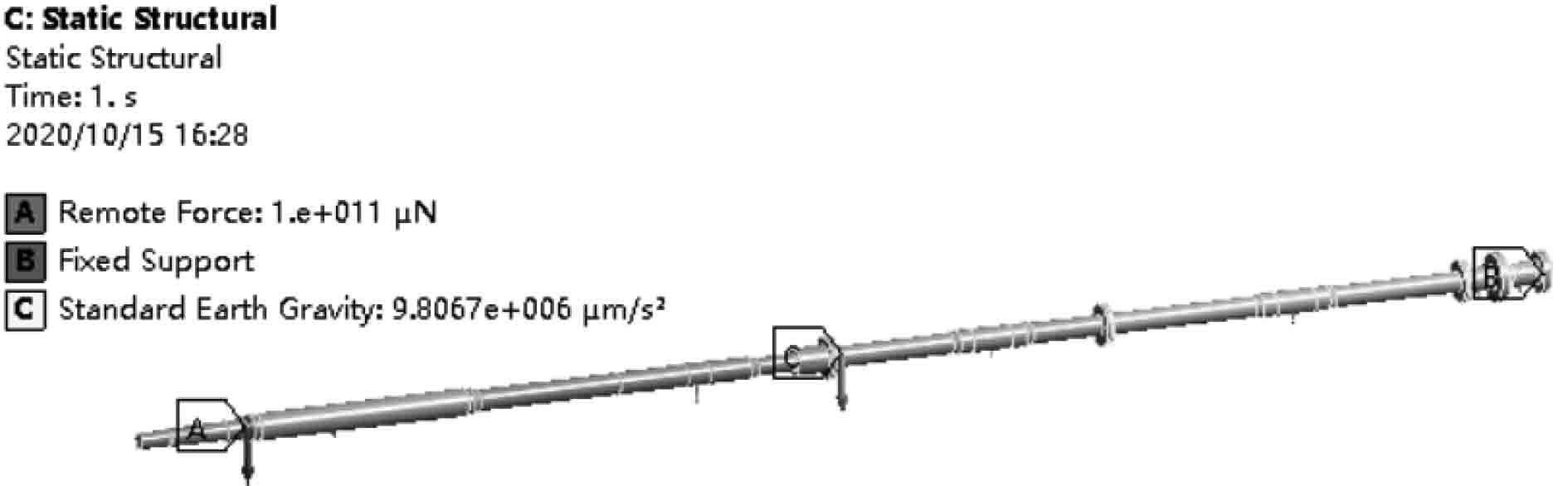
|
图 3 无筏架轴系校中约束设置 Fig. 3 Shaft alignment constraints setting without raft frame |
2)考虑浮筏的轴系校中
安装在浮筏上的轴系,各轴承支座通过上隔振器连接到筏架上,筏架再通过下隔振器安装在结构上,在不考虑结构变形的条件下,可在轴系的各支点位置与筏架对应安装位置施加线弹簧,弹簧的一端连接轴系,另一端连接筏架;另外,在筏架模型的4个角也设置线弹簧,线弹簧的一端连接筏架,另一端固定。如图4所示。

|
图 4 筏架轴系校中支撑设置 Fig. 4 Shaft alignment support setting with raft frame |
连接轴系与筏架的线弹簧的刚度设定与无筏架的轴系设置取一样的值,区别在于计入了隔振器,但上隔振器刚度远小于支撑系统刚度。另外,参考文献[12],设定下隔振器所简化的线弹簧其刚度为3.9E6 N/m,各轴承支点位置与无筏架条件下一致。除了推力轴承末端法兰设置为固定外,由于筏架在水平方向上有限位装置,故将筏架左右侧面和前后侧面都设定为固定约束,其他重力及载荷条件亦如无筏架条件下的轴系设定。
2种情况的轴系均采用全局尺寸控制的网格划分方法,轴系网格尺寸设定为10 mm,筏架属于规则结构,尺寸放大到200 mm,如图5所示。在建模过程中,对于联轴器等非关键性部件进行了适当简化。因此,在尺度上建模之后的数据与实际台架的数据存在小数级差异,这在整个轴系的尺度上可以忽略该误差带来的影响。

|
图 5 网格划分 Fig. 5 Meshing |
隔振器在安装时一般限制了变形,故弹簧的行为模式可设置为Rigid,而限位器释放后,则隔振器存在不能忽视的变形。因此,为了探讨筏架对轴系校中的影响,将线弹簧的行为模式分别设置为Rigid和Deformable进行仿真计算。轴系载荷分布、轴系扰度曲线是轴系校中后的2个关键结论。将后轴承、前轴承、1#中间轴承、2#中间轴承、1#径向轴承和2#径向轴承按顺序1~6进行编号,2种行为模式下的轴系校中计算结果如图6所示。
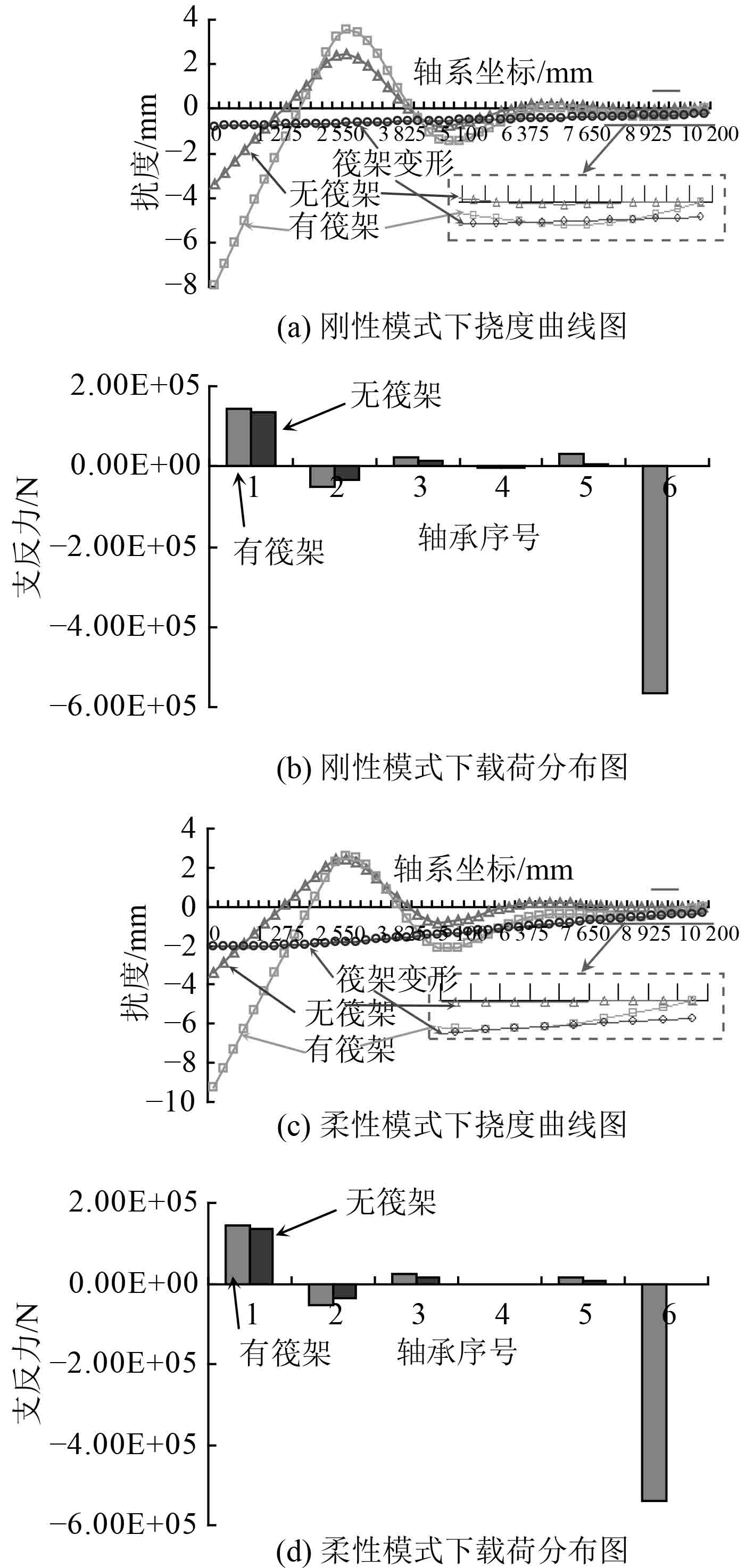
|
图 6 轴系校中计算结果 Fig. 6 Results of shaft alignment |
由图6(a)和图6(c)可知,柔性模型下的筏架变形比刚性模型大,但形态与刚性模式一样,都向轴系的重心侧倾斜。筏架变形对轴系扰度曲线的影响主要体现在数值上,曲线形状变化不大。相比无筏架下的轴系扰度曲线,有筏架的轴系在尾轴段的扰度峭度更大,靠近固定端的中间轴和推力轴则变化较小。另外,该模式下较大的筏架变形将轴系扰度曲线以轴系固定端为参考点整体拉低,对扰度曲线的数值和形态影响很小。从图6(b)和图6(d)可以看出,筏架的变形对后轴承、前轴承、1#中间轴承、2#中间轴承和1#径向轴承的负荷改变较小,对2#径向轴承的负荷改变非常大,超过了主要承担载荷的后轴承,且为负值。这是因为筏架在2#径向轴承处,筏架的变形量比该处的扰度还大,说明推力轴已经腾空,向上顶住了2#径向轴承,且由于靠近固定端,所以产生了较大的负荷。
综合以上分析结果可知,筏架的变形对轴系自由端的扰度影响较大,负荷影响较小,而对轴系固定端的扰度影响较小,负荷影响较大。而轴系校中计算规范重在各支点的负荷不能超过轴承的允许比压。因此,从降低对载荷分布的影响考虑,带有筏架的轴系与动力系统进行连接时,必须采用允许一定垂向位移的弹性联轴节,以便轴系校中时对首端能采用自由端处理。
4 结 语1)筏架在刚性与柔性模型下对轴系校中的影响规律是一致的,这也就说明在安装阶段使轴系各支点负荷满足规范要求后,在运行阶段也会满足要求。
2)在轴系自由端筏架的变形对扰度影响较大,负荷影响较小,而在轴系固定端则对扰度影响较小,负荷影响较大。
3)从满足轴系校中规范的角度来设计,带有筏架的轴系与动力系统进行连接时,须采用允许一定垂向位移的弹性联轴节,以便轴系校中时对前端能采用自由端处理。
| [1] |
杨勇. 船舶轴系校中技术研究[D]. 大连: 大连理工大学. 2005. YANG Yong, The study of shipping shaft system alignment[D]. DaLian: Dalian University of Technology, 2005. |
| [2] |
王琴, 卢善兵. 基于三弯矩法的小型船舶轴系校中研究[J]. 机械工程师, 2019(6): 95-97. WANG Qing, LU Shanbing. Research on centering of small ship shafting based on three-moment method[J]. Mechanical Engineering, 2019(6): 95-97. DOI:10.3969/j.issn.1002-2333.2019.05.033 |
| [3] |
刘义军, 刘伟, 俞强, 等. 船舶轴系直线校中有限元计算与试验分析[J]. 中国水运, 2014(9): 170-171. LIU Yijun, LIU Wei, YU Qiang, et al. Finite element calculation and test analysis of ship shafting alignment[J]. China Water Transport, 2014(9): 170-171. |
| [4] |
常宁, 刘正林, 魏颖春. 基于有限元法轴段偏中时轴系校中状态的研究[J]. 机械设计与制造, 2011(6): 52-54. CHANG Ning, LIU Zhenglin, WEI Yingchun. Research on shafting alignment as shaft segment is misalignment based on finite element method[J]. Machinary Design and Manufacture, 2011(6): 52-54. DOI:10.3969/j.issn.1001-3997.2011.08.020 |
| [5] |
HE L, XU W, BU W J. Dynamic analysis and design of air spring mounting system for marine propulsion system[J]. Journal of Sound and Vibration, 2014, 333(20): 4912-4929. DOI:10.1016/j.jsv.2014.05.045 |
| [6] |
DYLEJKO P G, KESSISSOGLOU N J, TSO Y K, et al. Optimisation of a resonance changer to minimise the vibration transmission in marine vessels[J]. Journal of Sound And Vibration, 2007, 300(1/2): 101-116. |
| [7] |
赵兴乾, 帅长庚, 徐伟, 等. 船舶艉部整体隔振系统中轴承载荷增量研究[J]. 工程力学, 2019, 36(6): 311-315. ZHAO Xingqian, SHUAI Changgen, XU Wei, et all. Research on bearings load-increment in integrated vibration isolation system of ship stern[J]. Engineering Mechanics, 2019, 36(6): 311-315. |
| [8] |
何江洋, 何琳, 徐伟. 船舶推力轴承集成减振系统的轴系校中影响分析[J]. 海军工程大学学报, 2017, 29(3): 32-36. HE Jiangyang, HE Lin, XU Wei. Impact analysis of shafting alignment of integrated vibration isolation system of thrust bearing in ships[J]. Journal of Naval University of Engineering, 2017, 29(3): 32-36. DOI:10.7495/j.issn.1009-3486.2017.03.007 |
| [9] |
ZHANG, Y., XU, W., LI, Z. et al. Alignment and safety analysis of marine propulsion shafting using intelligent floating raft system[J]. J Mar Sci Technol, 2020. |
| [10] |
WEI Haijun, TONG Chentao, YIN Feng. Finite-element method of shipping shaft alignment[J]. Journal of Dalian Maritime University, 2003(S1): 61-64. |
| [11] |
陈锡恩, 高景. 船舶轴系回旋振动计算及其参数研究[J]. 船海工程, 2001(5): 8-11. CHEN Xien, GAO Jing. Calculation and parameter study of ship shafting cyclotron vibration[J]. Ship and Ocean Engineering, 2001(5): 8-11. DOI:10.3963/j.issn.1671-7953.2001.05.003 |
| [12] |
金鼎. 基于有限元法的浮筏隔振系统性能分析及结构优化[D]. 武汉: 华中科技大学. 2019. JIN Ding. Performance analysis and structure optimization of floating raft system based on finite element method[D]. Wuhan: Huazhong University of Science and Technology. 2019. |
 2021, Vol. 43
2021, Vol. 43
