2. 船舶与海洋工程动力系统国家工程实验室,上海 201108;
3. 江苏科技大学 能源与动力学院,江苏 镇江 212003;
4. 江苏海事职业技术学院 船舶与海洋工程学院,江苏 南京 211170
2. National Engineering Laboratory for Marine and Ocean Engineering Power System, Shanghai 201108, China;
3. School of Energy and Power, Jiangsu University of Science and Technology, Zhenjiang 212003, China;
4. School of Ship and Ocean Engineering, Jiangsu Maritime Institute, Nanjing 211170, China
声子晶体通常是指由2种或2种以上材料周期性组合而成的材料或结构,其最显著的特征是具有带隙(禁带)特性[1-3]。由于声子晶体是一种新的功能性材料,因此声子晶体的概念从提出开始就备受国内外广大学者的关注[4-5]。由于弹性波和周期结构的相互作用,使得只有一部分频率范围内的弹性波可以顺利通过周期结构,这个频率带称为通带[6-8],其他范围内的频率将无法通过周期结构继续传播,起到了隔振降噪的效果[9],此频率范围称为弹性波带隙[10-11]。基于声子晶体的特殊性质,声子晶体在振动控制、航空航天、军工武器等领域,以及导管减振和隔声减振降噪等方面具有广阔的应用前景[12]。
近年来众多学者对周期管路结构进行了深入研究,目前关于声子晶体的研究方法有平面波展开法[13]、传递矩阵法[14]、集中质量法[13]、有限元法[15]等。声子晶体带隙产生的机理有布拉格散射型和局域共振型2种。布拉格散射型机理认为带隙产生的主要原因是由于各个原胞之间相互作用,局域共振的机理是在特定频率弹性波的激励下,散射体发生局域同时和弹性波之间发生共同作用导致弹性波不能继续传播。
本文将声子晶体的周期结构思想引入到海洋平台导管设计中,然后对周期导管结构施加纵向激励,通过平面波展开法研究周期导管结构的材料参数和几何结构参数对振动的第一带隙的起始频率、终止频率、带隙宽度和中心频率的影响。其中,材料参数包括材料的密度和弹性模量;几何结构参数包括晶格常数、厚度和组分比。
1 周期导管结构和弹性波波动方程在Ansys有限元软件中,建立聚氨酯-钢周期导管一维声子晶体导管如图1所示。晶体导管的截面内径为1 m,外径为1.3 m,晶格常数为12 m,周期导管共5个周期,总长60 m。图中A为聚氨酯材料,B为金属钢材料,如图1所示排列。A杆的长度为l1,B杆的长度为l2,晶格常数a的长度为l1+l2,A和B材料参数如表1所示。

|
图 1 周期导管一维声子晶体结构示意图 Fig. 1 Schematic diagram of one-dimensional phononic crystal structure of periodic catheter |
|
|
表 1 材料参数 Tab.1 Material parameters |
根据弹性动力学理论,在材料连续性、均匀和各向同性、完全线弹性以及小变形和无初始应力假设条件下,对弹性介质中任意一个小的体积微元(质点),质点力、位移以及应力应变之间的关系为:
运动微分方程
| $ \sigma _{ij,i}+\rho {f}_{j}=\rho {ü}_{j}\text{,} $ | (1) |
几何方程
| $ \varepsilon _{ij}=\frac{1}{2}({u}_{i,j}+{u}_{j,i})\text{,} $ | (2) |
物理方程
| $ \sigma_{ij}=\lambda \varepsilon_{kk}\delta _{ij}+2\mu \varepsilon_{ij}\text{。} $ | (3) |
式中:
在考虑无外力激励条件下,可以得到弹性波波动方程:
| $ \rho {\ddot u_i} = \rho {f_i} + \displaystyle\mathop \sum \limits_{j = 1}^3 \left\{ {\frac{\partial }{{\partial {x_i}}}} \right.\left( {\lambda \frac{{\partial {u_j}}}{{\partial {x_j}}}} \right)\left. { + \frac{\partial }{{\partial {x_j}}}\left[ {\mu \left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right)} \right]} \right\} \text{。}$ | (4) |
式中:
纵波波速
| $ {c_l} = \sqrt {\frac{{\lambda + 2\mu }}{\rho }}\text{,} $ | (5) |
横波波速
| $ {{\text{c}}_t} = \sqrt {\frac{\mu }{\rho }}\text{。} $ | (6) |
用位移表示的弹性波方程式(4)可以表示为:
| $ \rho \ddot u = \rho f + (\lambda + \mu )\nabla (\nabla \cdot u) + \mu {\nabla ^2}u \text{。}$ | (7) |
声子晶体导管的纵向振动方程为:
| $ \rho \frac{{{\partial ^2}{\text{u}}}}{{{\partial ^2}t}} = \frac{\partial }{{\partial x}}\left(E\frac{{\partial {\text{u}}}}{{\partial x}}\right)\text{。} $ | (8) |
式中:
第
| $ {U_{n1}}({x'}) = {P^ + }_{n1}{e^{i{a_1}{x'}}} + {P^ - }_{n1}{e^{ - i{a_1}{x'}}}\text{。} $ | (9) |
第
| $ {U}_{n2}({x}^{\text{'}})={P}^+{}_{n2}{e}^{i{a}_{2}x"}+{P}^-{}_{n2}{e}^{-i{a}_{2}{x}^{"}} \text{。}$ | (10) |
式中:
第
| $ {\psi _{n2}} = T{\psi _{(n - 1)2}} \text{。}$ | (11) |
其中:
周期导管在
| $ {\psi _{n2}} = {e^{ika}}{\psi _{(n - 1)2}} \text{,}$ | (12) |
由式(11)和式(12)得标准矩阵特征值为:
| $ \left| {\boldsymbol{T} - {e^{ika}}\boldsymbol{I}} \right| = 0 \text{。}$ |
其中:
通过求解矩阵
| $ \begin{split}\cos \left( {ka} \right) =\,& \cosh ({\alpha _1}{a_1})\cosh \left( {{\alpha _2}{a_2}} \right) + \\ &\frac{{{F^2}{\text{ + }}1}}{{2F}}\sinh \left( {{\alpha _1}{a_1}} \right)\sinh \left( {{\alpha _2}{a_2}} \right)\end{split}\text{。}$ | (13) |
将建立的周期导管结构的晶格常数和材料参数代入式(13),通过软件Matlab进行求解,得到的能带结构曲线如图2所示。从能带结构曲线图中可以看出:在0~400 Hz的频率范围内,周期导管结构有3个频率范围完全存在着不可传播的波(灰色),该形状称为完全带隙。3条带隙的频率范围分别是28.0~121.0 Hz,128.5~241.7 Hz,246.8~358.7 Hz。弹性波在这些区域内将被抑制而无法传播,因此,本文建立的周期管结构将在上述3个带隙具有好的减振性能。
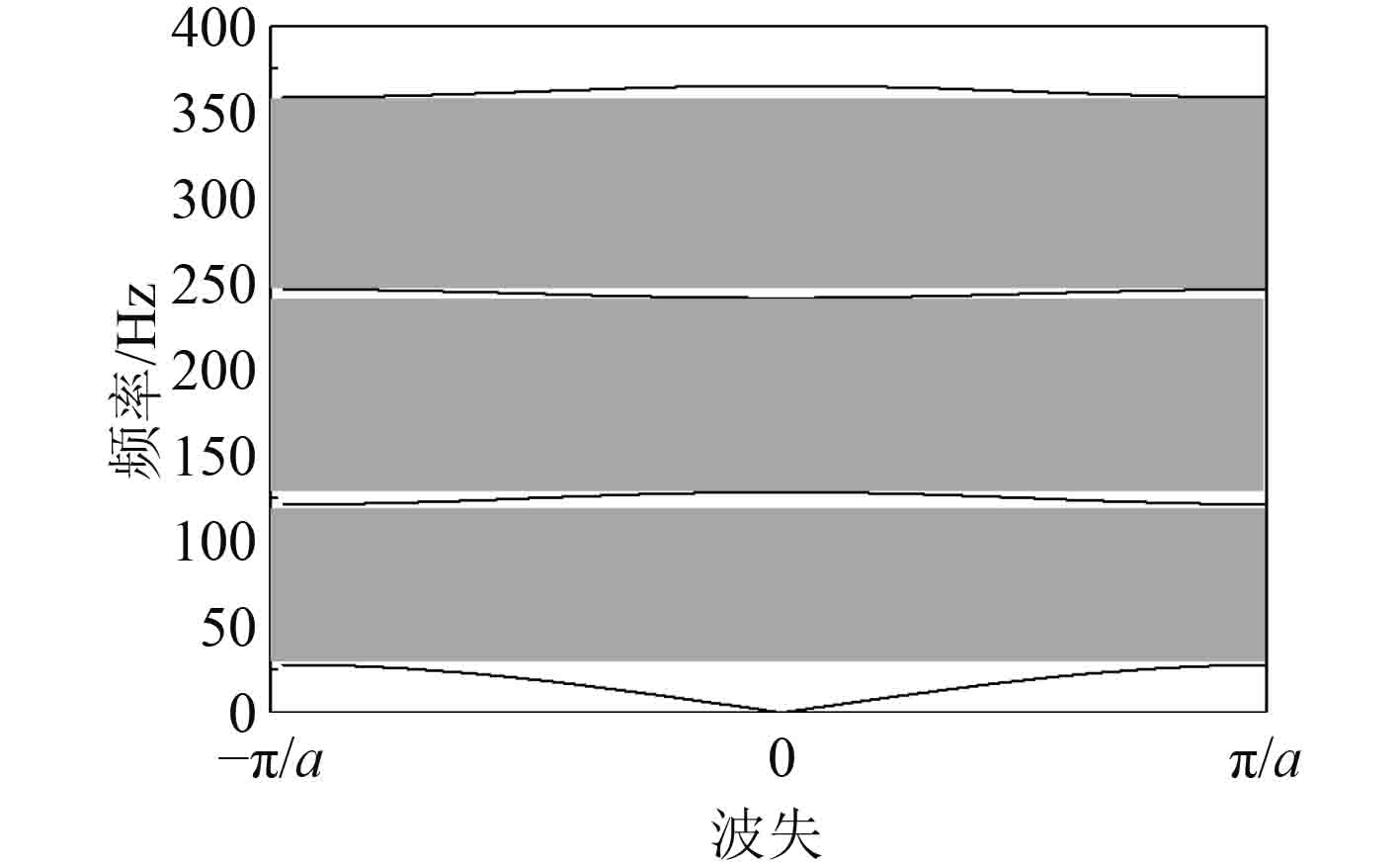
|
图 2 一维声子晶体导管结构带隙图 Fig. 2 Band gap diagram of one-dimensional phononic crystal tube structure |
如果需要周期导管结构在其他频段具有带隙特性,可以通过重新设计周期导管的晶格常数和材料参数实现。
3 周期导管带隙特性分析研究周期导管结构几何结构参数和材料参数对带隙特性的影响以及晶格常数、组分比、壁厚、弹性模量和密度等参数对周期导管结构能带图的影响规律,分析材料参数和几何参数对周期导管结构第一带隙特性的影响规律。带隙的起止频率和带隙宽度由共振峰的峰值所对应的频率决定,共振峰峰值的固有频率公式如下:
| $ f = \frac{1}{{2\text{π} }}\sqrt[{}]{{\frac{k}{m}}}\text{。} $ | (14) |
式中:
基于周期导管结构模型,保持其他参数不变,研究单胞的晶格常数对带隙特性的影响规律。晶格常数分别取6 m,8 m,10 m,12 m,14 m和16 m 时,计算周期导管结构的能带,结果如图3所示。由图3可知,当晶格常数从6 m增加到16 m时,带隙的起始频率和截止频率逐渐降低,其中截止频率下降的梯度更大,带宽也随着晶格常数的增大而减小。所以,增加晶格常数可以有效降低周期导管结构振动带隙的中心频率。
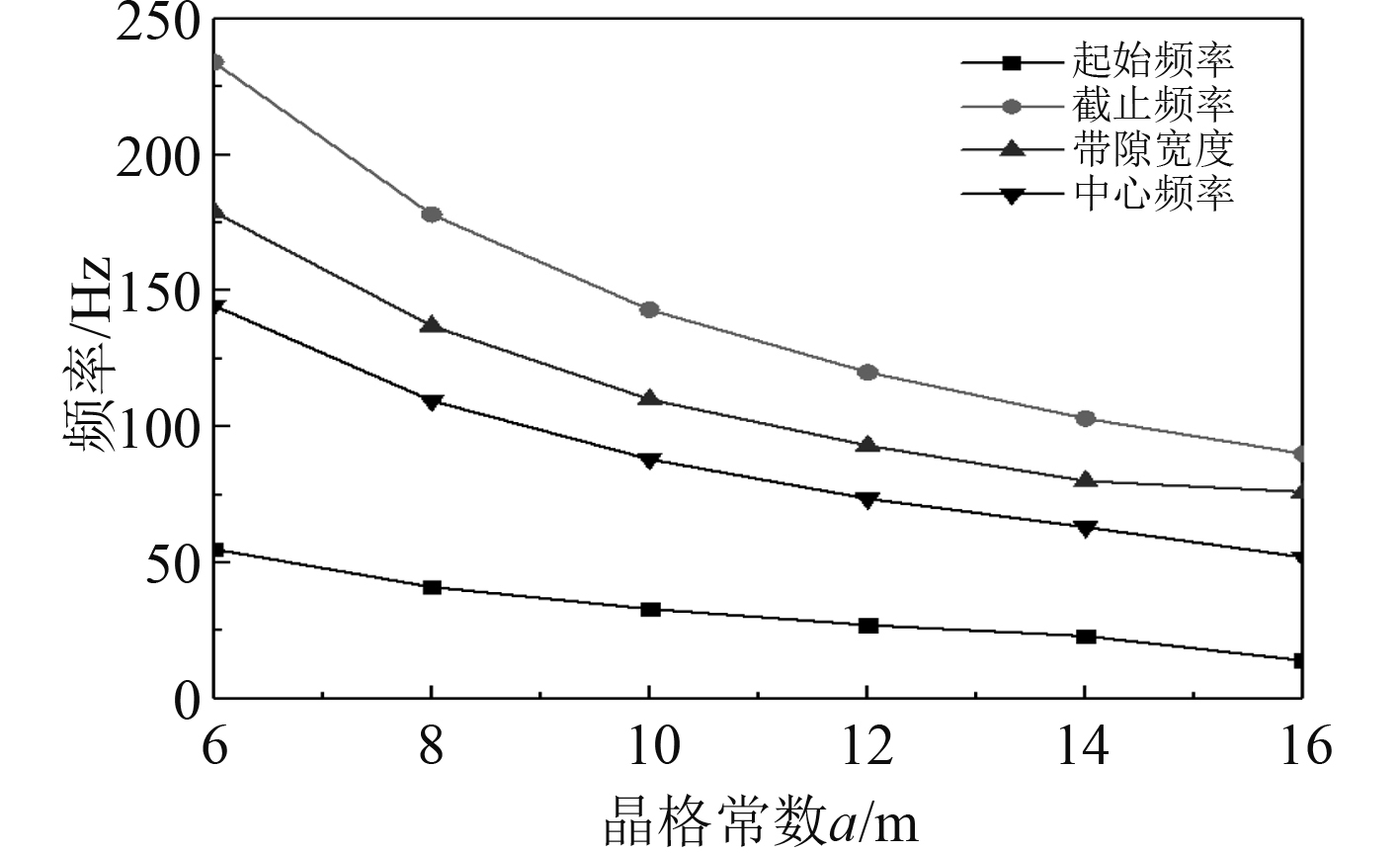
|
图 3 晶格常数对带隙的影响 Fig. 3 Effect of lattice constant on band gap |
首先,建立周期导管的一维聚氨酯-钢周期导管模型,如图1所示。组分比是指聚氨酯材料和钢材料在周期导管一维聚氨酯-钢声子晶体中的长度比。组分比分别取0.20,0.33,0.50,0.71,1.00,1.40,2.00,3.00和5.00时,周期导管聚氨酯-钢声子晶体结构的带隙特性如图4所示。
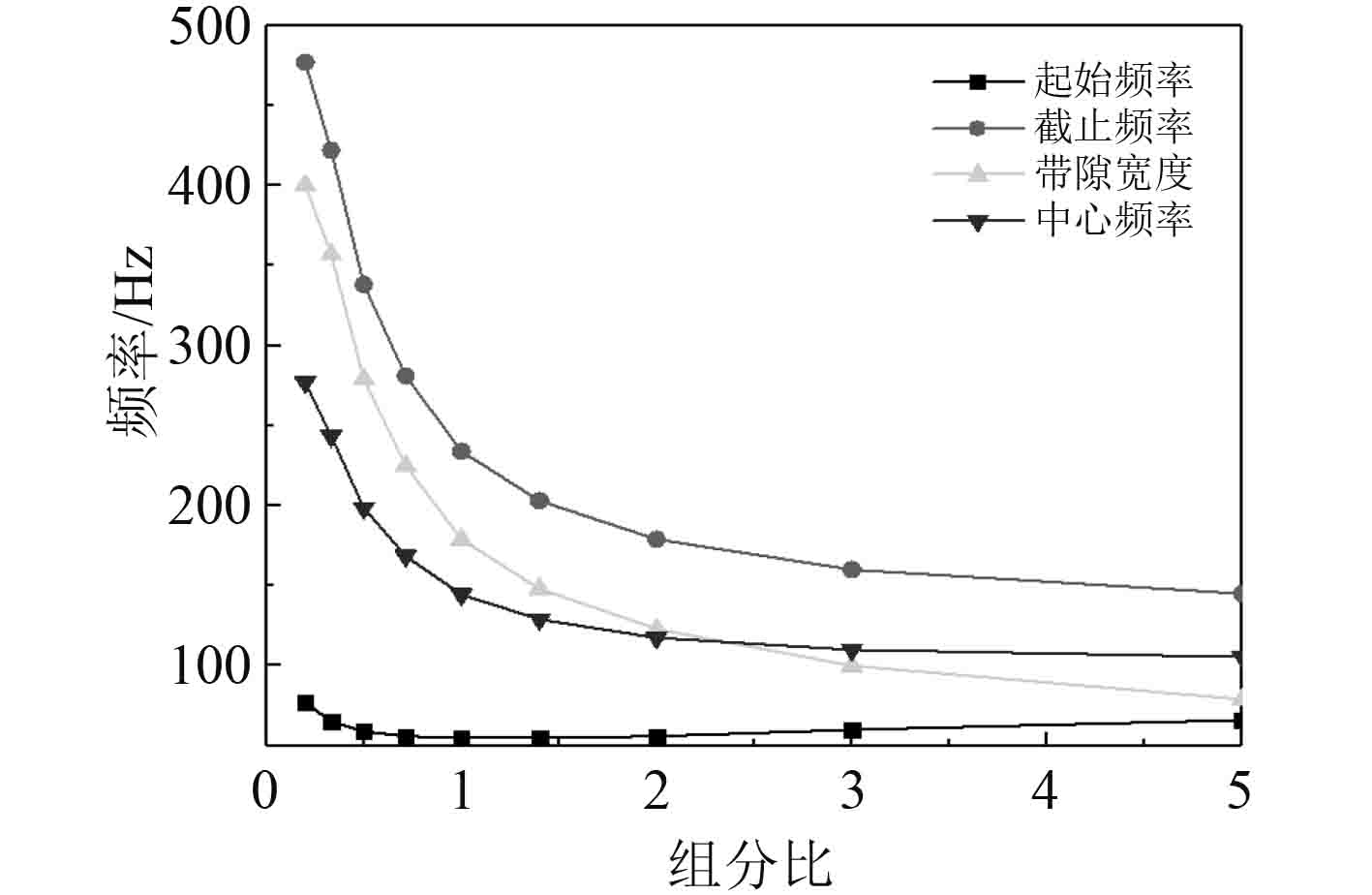
|
图 4 组分比对带隙的影响 Fig. 4 Effect of composition ratio on band gap |
由图4可以看出:当组分比小于1时,周期导管结构的带隙起始频率慢慢减小;当大于1时,周期导管结构的起始频率慢慢递增且递增的梯度较为平稳。随着组分比的增大,周期导管结构的带隙的截止频率、中心频率以及带隙宽度均下降。
3.1.3 壁厚对带隙范围的影响在周期导管聚氨酯-钢声子晶体模型中,保持其他材料参数不变,研究导管壁厚对其带隙特性的影响规律。导管壁厚分别取10 mm,15 mm,20 mm,25 mm,30 mm,35 mm和40 mm时,周期导管的带隙如图5所示。可以看出,周期导管结构的壁厚对其带隙的起始频率、截止频率和中心频率影响很小,因此对其带隙宽度影响也很小。
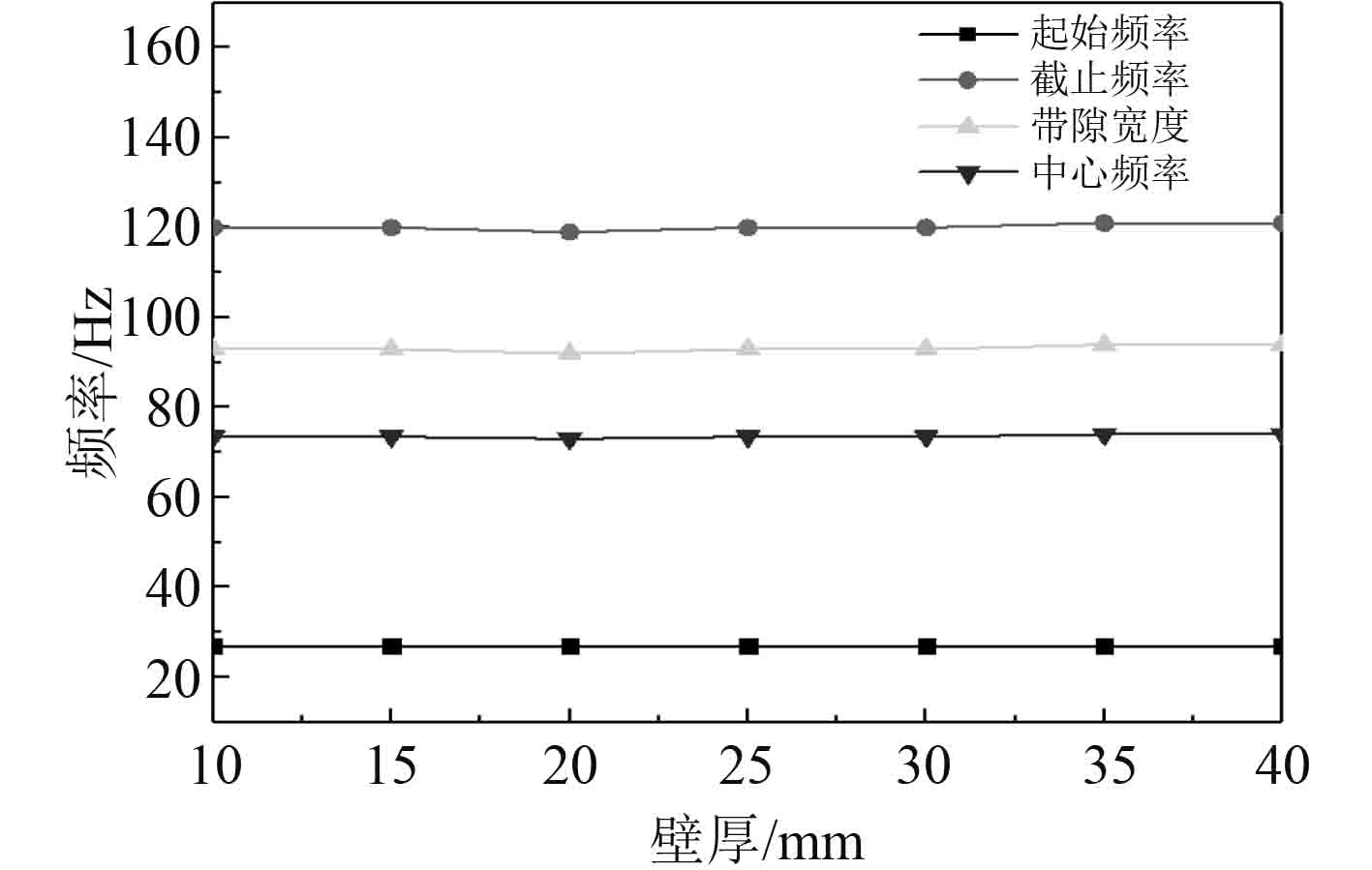
|
图 5 壁厚对带隙的影响 Fig. 5 Effect of wall thickness on band gap |
保持材料参数和材料几何尺寸不变,聚氨酯材料A的密度分别取1140 kg/m3,1200 kg/m3,1300 kg/m3,1400 kg/m3,1500 kg/m3和1600 kg/m3,研究聚氨酯材料的密度对带隙特性的影响规律,结果如图6所示。可以看出,随着聚氨酯材料密度的增加,周期导管结构的带隙起始频率基本保持不变,而带隙的截止频率、中心频率、带隙宽度均缓慢下降。因此,增加聚氨酯密度不能改变带隙的起始频率,而且会导致周期导管结构带隙的宽度变小。
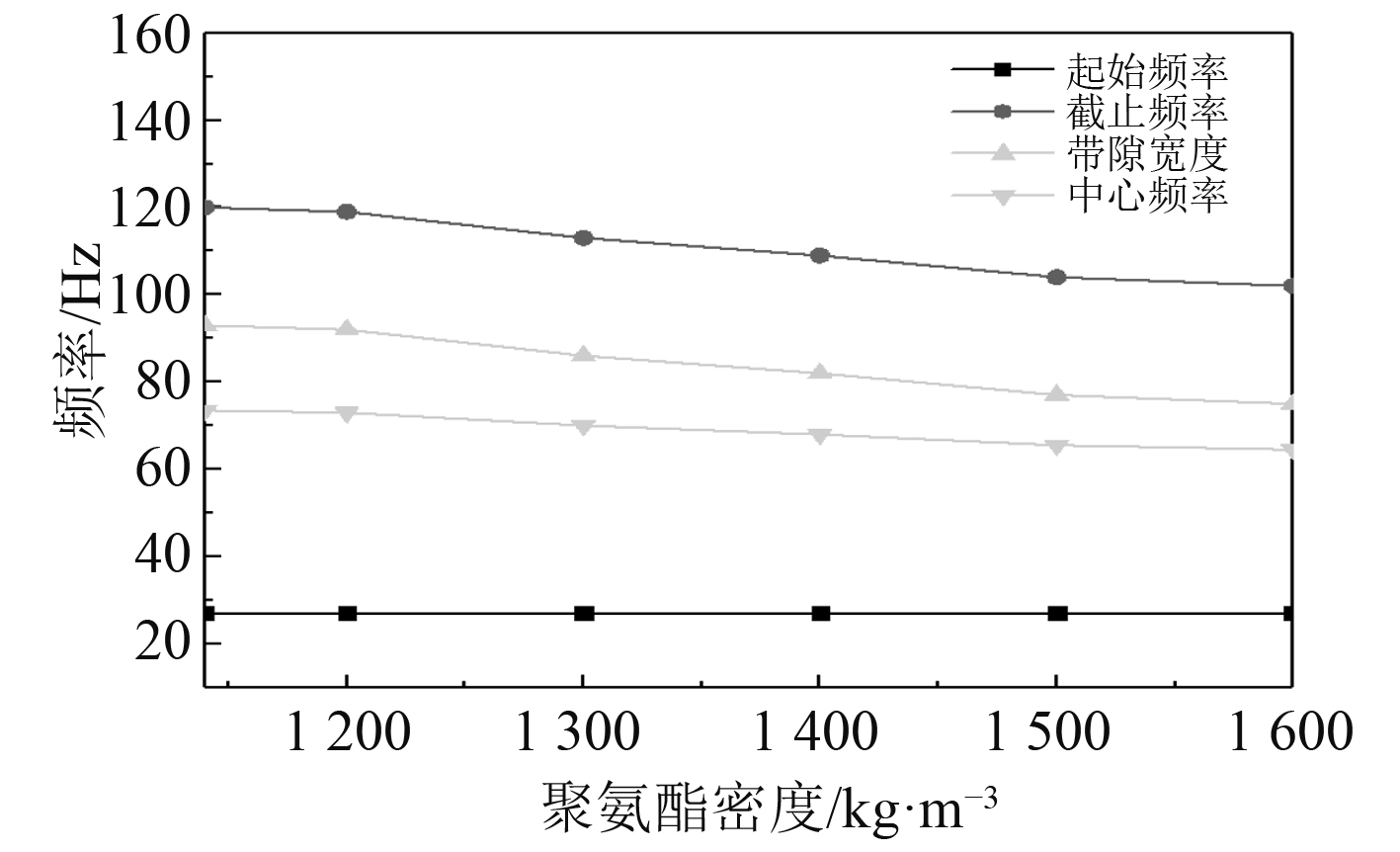
|
图 6 聚氨酯密度对带隙的影响 Fig. 6 Effect of polyurethane density on band gap |
金属钢密度分别取7750 kg/m3,7850 kg/m3,7950 kg/m3,8050 kg/m3和8150 kg/m3时,聚氨酯-钢周期导管结构的带隙特性曲线如图7所示。可以看出,金属密度的变化,对周期导管结构带隙的起始频率、截止频率、带隙宽度和中心频率影响很小,因此,改变金属钢的密度对带隙的影响不大。
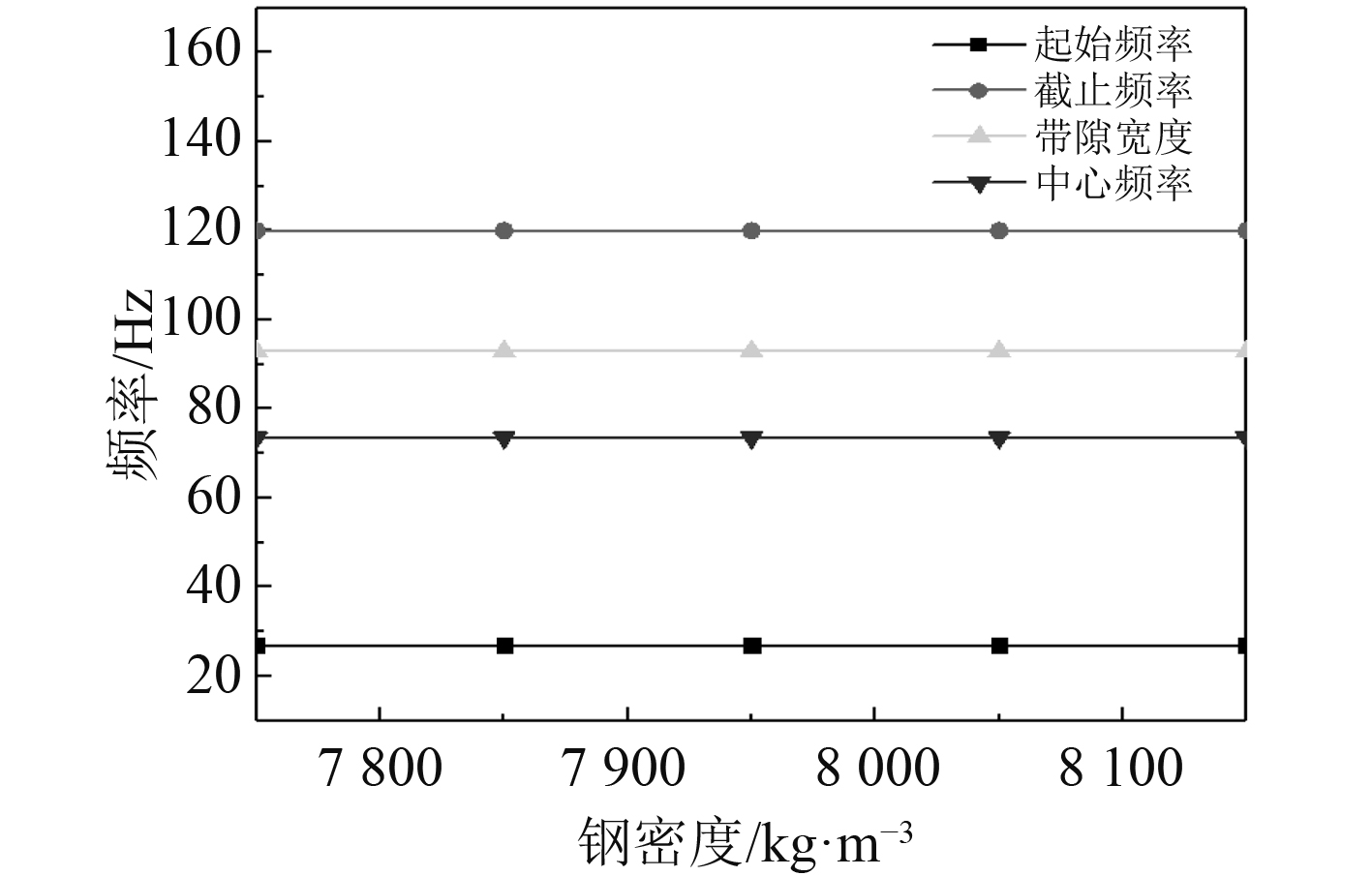
|
图 7 金属钢密度对带隙的影响 Fig. 7 The influence of metal steel density on the band gap |
聚氨酯弹性模量对周期导管带隙特性的影响规律如图8所示。可以看出,随着聚氨酯弹性模量的增加,周期导管结构的带隙起始频率、截止频率、带隙宽度和中心频率都呈增大的趋势,且带隙的截止频率增幅较更大,导致其带隙宽带变宽。
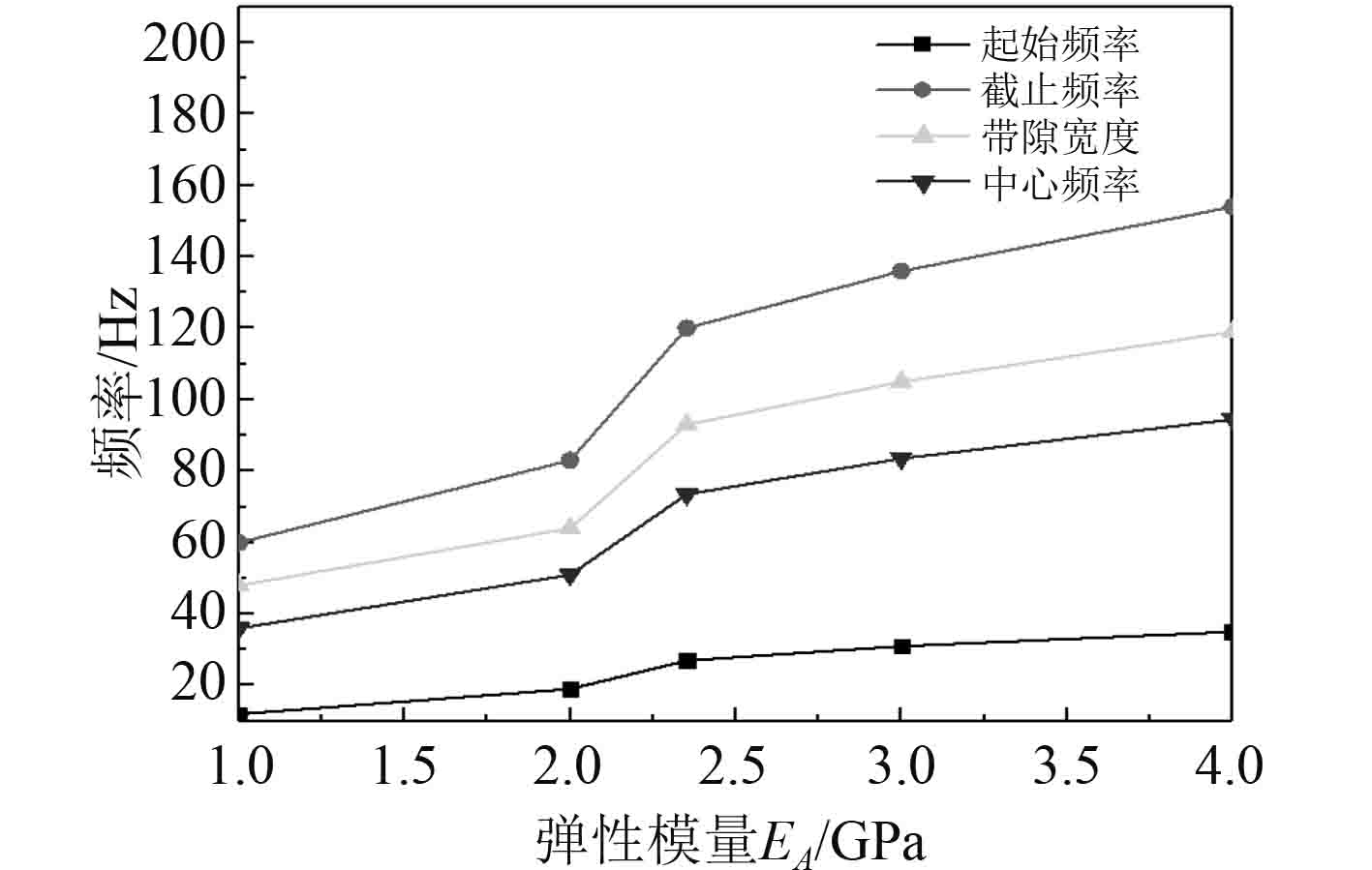
|
图 8 聚氨酯弹性模量对带隙的影响 Fig. 8 Effect of polyurethane elastic modulus on band gap |
在周期导管聚氨酯-钢声子晶体中模型中,其他参数保持不变,研究聚氨酯材料的弹性模量对其带隙特性的影响规律。聚氨酯弹性模量分别取100 GPa,150 GPa,200 GPa,250 GPa和300 GPa时,周期导管结构的带隙特性如图9所示。可以看出,金属钢的弹性模量对周期导管结构的带隙起始频率、截止频率、带隙宽度和中心频率影响都很小。
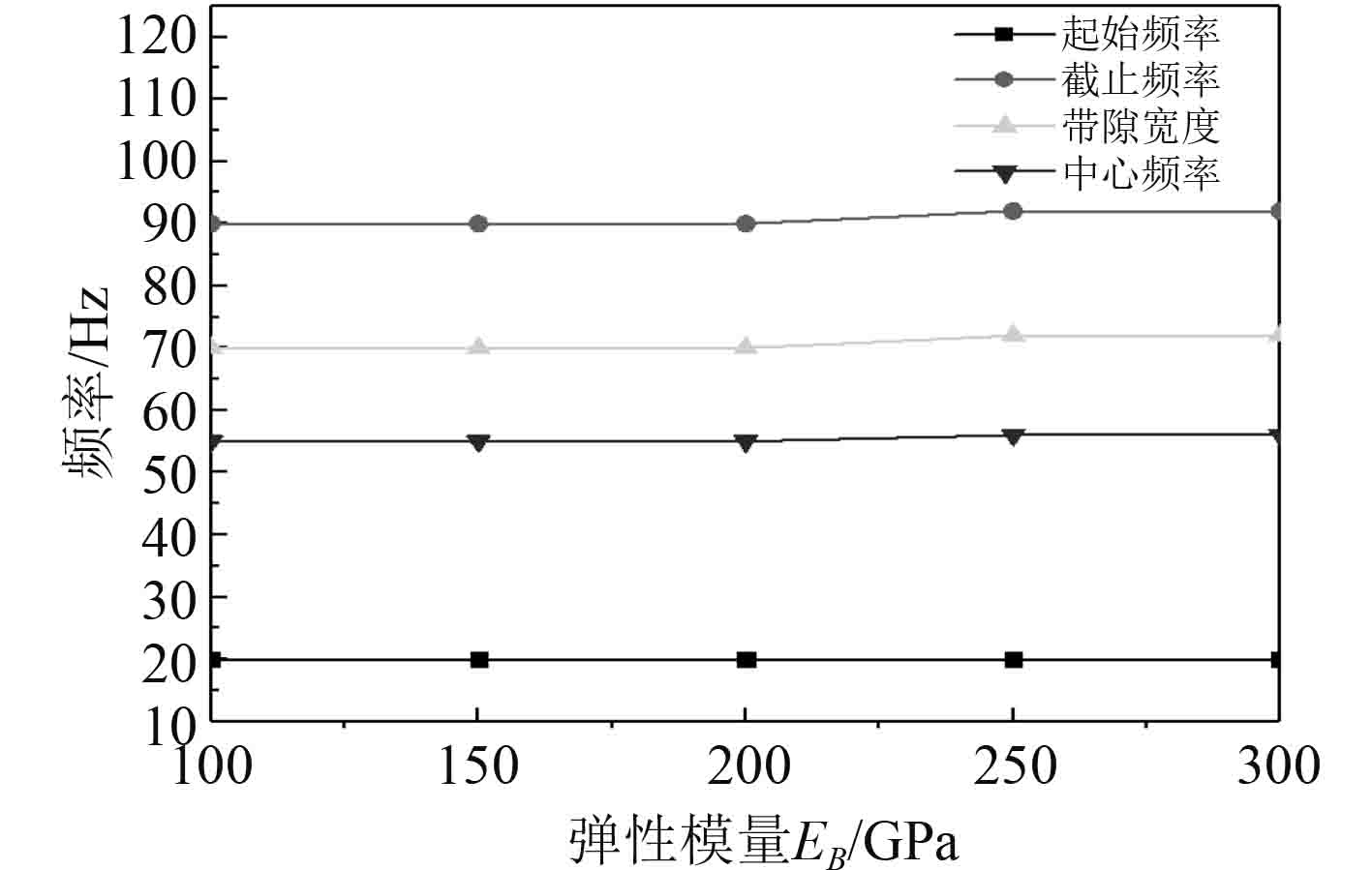
|
图 9 金属钢弹性模量对带隙的影响 Fig. 9 Effect of elastic modulus of metal steel on band gap |
本文通过研究材料参数和几何参数对周期导管聚氨酯-钢结构的带隙特性影响规律,得出主要结论如下:
1)晶格常数的增大可以有效降低带隙的起始频率和截止频率,带隙的宽度和带隙的中心频率随着晶格常数的增加而逐渐减小。
2)周期导管的带隙起始频率随着材料的组分比增大先减小后增大,而带隙的截止频率、带隙宽度和中心频率随着组分比的增大先急剧下降后来慢慢趋于稳定。
3)壁厚、金属钢的密度和弹性模量的变化对带隙特性的起始频率、截止频率、带隙宽度和中心频率的影响很小。
4)增加聚氨酯材料的密度可以有效降低带隙的截止频率,但对其起始频率影响很小。因此,增加聚氨酯材料的密度可以降低周期导管结构的带隙宽度和中心频率。
5)增加聚氨酯材料的弹性模量,周期导管的带隙起始频率和截止频率都会增加,其中截止频率相比起始频率增加的梯度较大,导致其带隙宽度和中心频率都增大。
| [1] |
温激鸿, 王刚, 郁殿龙, 等. 声子晶体振动带隙及减振特性研究[J]. 中国科学:技术科学, 2007, 37(9): 1126. |
| [2] |
YANG S, PAGE J H, LIU Z, et al. Focusing of sound in a 3D phononic crystal[J]. Physical Review Letters, 2004, 93(2): 024301. DOI:10.1103/PhysRevLett.93.024301 |
| [3] |
梁孝东, 缪林昌, 尤佺, 等. 局域共振二维声子晶体的低频带隙特性研究[J]. 人工晶体学报, 2019(7). DOI:10.3969/j.issn.1000-985X.2019.07.016 |
| [4] |
MARTINEZ-SALA R., SANCHEZ J., SANCHEZ J. V. et al.. Sound attenuation by sculpture[J]. Nature, 1995, 378: 241. |
| [5] |
张研, 韩林, 蒋林华. 声子晶体的计算方法与带隙特性[M]. 北京: 科学出版社, 2014.
|
| [6] |
陈荣, 吴天行. 周期结构空腹梁的动态特性研究[J]. 振动与冲击, 2013(14): 127-131. DOI:10.3969/j.issn.1000-3835.2013.14.022 |
| [7] |
徐冰茹, 徐少辉, 王连卫. 一维多孔硅声子晶体的带隙研究[J]. 人工晶体学报, 2012(5): 296-301. |
| [8] |
LIU Z Y, ZHANG X X. Locally resonant sonic materials[J]. Science, 2000, 289: 1734-1736. DOI:10.1126/science.289.5485.1734 |
| [9] |
沈礼, 吴九汇, 陈花玲. 声子晶体结构在汽车制动降噪中的理论研究及应用[J]. 应用力学学报, 2010, 27(2): 293-297. |
| [10] |
MOHAMMAD H. A, KHORASANI S.. Optical wave evolution due to interaction with elastic wave in a phoxonic crystal slab waveguide[J]. Applied Physics B, 2017, 123(8): 218. DOI:10.1007/s00340-017-6792-x |
| [11] |
CERJAN C, KOSLOFF D, KOSLOFF R, et al. A nonreflecting boundary condition for discrete acoustic and elastic wave equations[J]. Geophysics, 1985, 50(4): 705-708. DOI:10.1190/1.1441945 |
| [12] |
王连坤. 用于声子晶体检测的光外差测量技术研究[D]. 长春: 中国科学院研究生院(长春光学精密机械与物理研究所), 2010
|
| [13] |
温激鸿, 王刚, 刘耀宗, 等. 基于集中质量法的一维声子晶体弹性波带隙计算[J]. 物理学报, 2004(10): 140-144. |
| [14] |
刘江伟, 郁殿龙, 温激鸿, 等. 周期附加质量充液管路减振特性研究[J]. 振动与冲击, 2016, 35(6): 141-145. |
| [15] |
郁殿龙, 刘耀宗, 王刚, 等. 一维杆状结构声子晶体扭转振动带隙研究[J]. 振动与冲击, 2006(1): 107-109+172-173. DOI:10.3969/j.issn.1000-3835.2006.01.028 |
 2021, Vol. 43
2021, Vol. 43
