2. 江苏自动化研究所,江苏 连云港 222061;
3. 海军指挥学院,江苏 南京 210016
2. Jiangsu Automation Research Institute, Lianyungang 222061, China;
3. Naval Command College, Nanjing 210016, China
水下无人航行器作为一种发展迅速的新型作战力量,将推动未来战争形态由信息化战争向智能化战争转变,成为海军作战力量体系中的重要组成部分。依据被动声呐方程,开展潜艇与UUV的探测能力建模估算,并对UUV规避潜艇开展运动建模和仿真分析,探索水下无人航行器在未来作战中的使用方式和方法。
1 UUV探测潜艇能力分析相比于潜艇装备,UUV具有体积小、隐身性好、机动灵活、成本低、可组网使用等优势,在未来反潜作战中具有很大的应用潜力[1 - 2]。但随着现代潜艇隐身性能和探测能力逐渐提升,对UUV反潜提出了更高的要求。由于负载能力有限,单平台UUV水下探测能力相对潜艇较弱,在UUV探测潜艇的过程中能否先敌发现是核心关键,需要综合两者的隐身与探测能力进行综合评估[3],本文选取UUV和潜艇的被动声呐为研究对象,在对各自辐射噪声仿真的基础上,分析对比了UUV和潜艇的相互发现距离。
1.1 潜艇辐射噪声的特征潜艇辐射主要包括宽带噪声和特征线谱噪声,噪声源分为3类:机械噪声、水动力噪声和推进器噪声[4]。低航速工况下(约10 kn以下),辐射噪声以机械噪声为主,在此阶段随着航速的增加,主要设备功率逐渐增大,设备及轴系激励不断变大,辐射噪声也随之增加;中高航速(超过10~12 kn)下水动力噪声和螺旋桨噪声逐渐占主导,其中水动力噪声辐射声功率随航速的5~6次方关系增长;当航速超过推进器空泡临界航速时,高频噪声显著增强,空泡出现初始阶段高频段噪声跃升量约5~10 dB,随着航速进一步提高,空泡噪声将成为辐射噪声主导成分,随航速的7~10次方关系增长[5]。
1.2 潜艇辐射噪声估算考虑到各类潜艇声学设计和性能特点具有较大差异,辐射噪声随航速的增长关系较为复杂,目前尚无可用于工程应用的辐射噪声与航速关系的计算方法。为满足UUV探潜建模仿真中声呐方程解算需求,本文参考文献[6],利用辐射噪声与航速的经验公式,通过合理选择参数表征典型潜艇声学特性,满足一般规律性要求。
| $ SL = \left\{ {\begin{array}{*{20}{l}} {25{\rm{log}}{V_m} + 77 + 20a},&{{V_m} < {V_T}},\\ {104 + 20a + \Delta },& {{V_m} = {V_T}},\\ {104 + 20a + \Delta + b({V_m} - {V_T})},&{Vm > {V_T}}\text{。} \end{array}} \right. $ | (1) |
其中:
假设潜艇临界速度
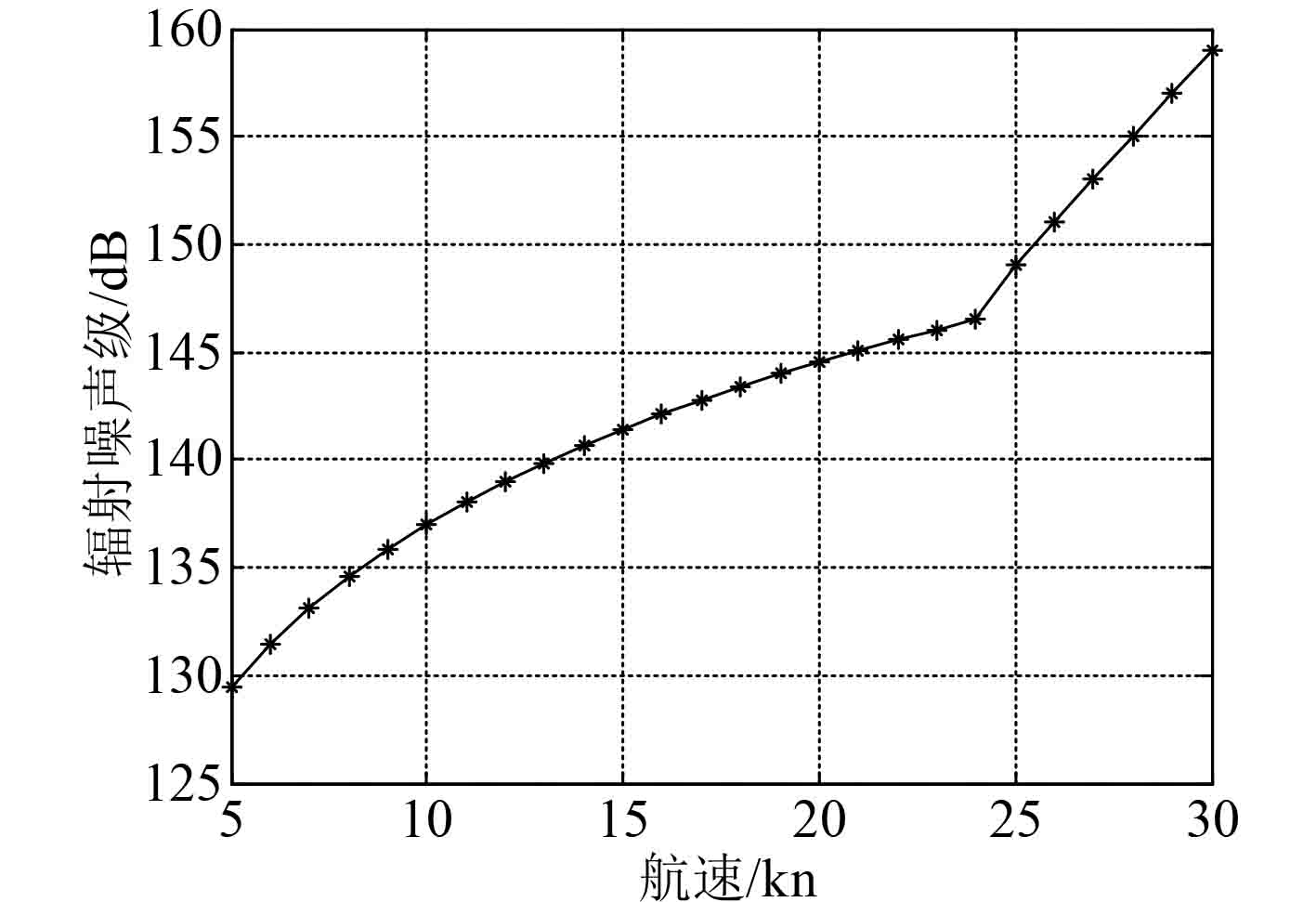
|
图 1 潜艇辐射噪声级随航速变化曲线 Fig. 1 Variation of submarine radiation noise level with different velocity |
因为缺少UUV装备辐射噪声数据,假设UUV水下排水量为10 t,常规潜艇和核潜艇的水下排水量分别按3000 t,7000 t计,根据文献[1]模型计算可知,在相同航速下UUV辐射噪声级分别比常规潜艇、核潜艇的低约20 dB,25 dB。考虑到UUV辐射噪声机械噪声、水动力噪声、推进器噪声等三大噪声源产生,同样存在推进空化噪声问题,因此本文在潜艇辐射噪声预报模型的基础上通过修正进行UUV辐射噪声评估。将式(2)中的每一项减去一固定值(20 dB),并参考安静潜艇的噪声量级进行估算,得到UUV的辐射噪声估算模型:
| $SL = \left\{ {\begin{array}{*{20}{l}} {25{\rm{log}}{V_m} + 57},&{{V_m} < {V_T}},\\ {84 + {\Delta _1}},&{{V_m} = {V_T}},\\ {84 + {\Delta _1} + {b_1}({V_m} - {V_T})},&{{V_m} > {V_T}}\text{。} \end{array}} \right.$ | (2) |
其中:
在临界航速下,计算UUV的辐射噪声级为84 dB,这与文献[7]中设定的UUV辐射噪声级为75~90 dB比较接近。假设UUV航速为1~8 kn,临界航速为5 kn,
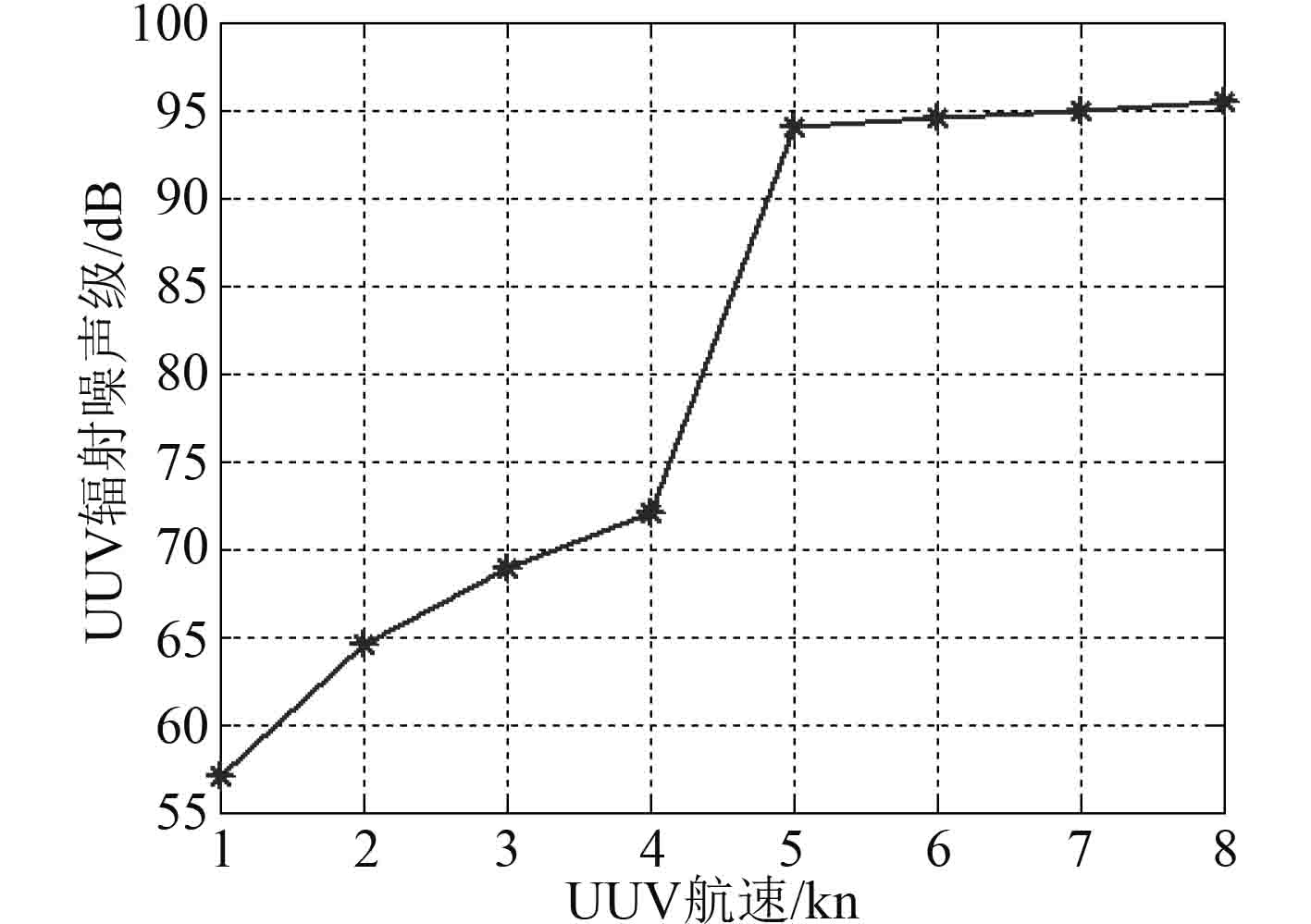
|
图 2 UUV在不同航速时的辐射噪声级 Fig. 2 Variation of UUV radiation noise level with different velocity |
1)潜艇发现UUV的距离估计
根据被动声呐方程:
| $SL - TL - (NL - DI) = DT,$ | (3) |
定义被动声呐优质因素FOM为[8]:
| $FOM = SL - (NL - DI + DT)\text{。}$ | (4) |
FOM在被动声呐中,等于允许有最大单程传播损失,且在该距离上声呐的发现概率为50%。其中,
1)潜艇被动声呐的检测阈
假设潜艇被动声呐利用宽带平方律检波器对接收到的噪声信号进行检波[9],因此检测阈
| $DT = 5\lg d - 5\lg B{T_e} - 5\lg n\text{。}$ | (5) |
式中:
在不同类型潜艇对UUV目标进行检测时的DT存有差别,根据文献[9]中5lgd的值及建议的适用范围,选取为5,6,7,8。文献[9]中将对鱼雷和潜艇的积分时间
假定声呐处理信号带宽B=2000 Hz,通过求解声呐方程,可以得到不同类型潜艇的检测阈如表1所示。
|
|
表 1 不同类型潜艇的检测阈 Tab.1 Detection index of different submarine type |
2)潜艇被动声呐的指向性指数
文献[4]中潜艇被动声呐利用长8 m、高4 m的舷侧基阵接收信号,该基阵的设计频率为2000 Hz,则
| $DI = 3 + 10\lg 200 + 20\lg 1.5 = 29(\rm{dB}),$ | (6) |
同时在低频段,由于舷侧基阵被壳体隔离起来,所以
3)潜艇发现UUV的距离
在FOM公式中,UUV的辐射噪声级
| $r = \frac{{20}}{{K*\ln (10)}}{\rm{lambertw}}\left(\frac{K}{{20}}*\ln (10)*{10^{\frac{{FOM}}{{20}}}}\right)\text{。}$ | (7) |
式中:
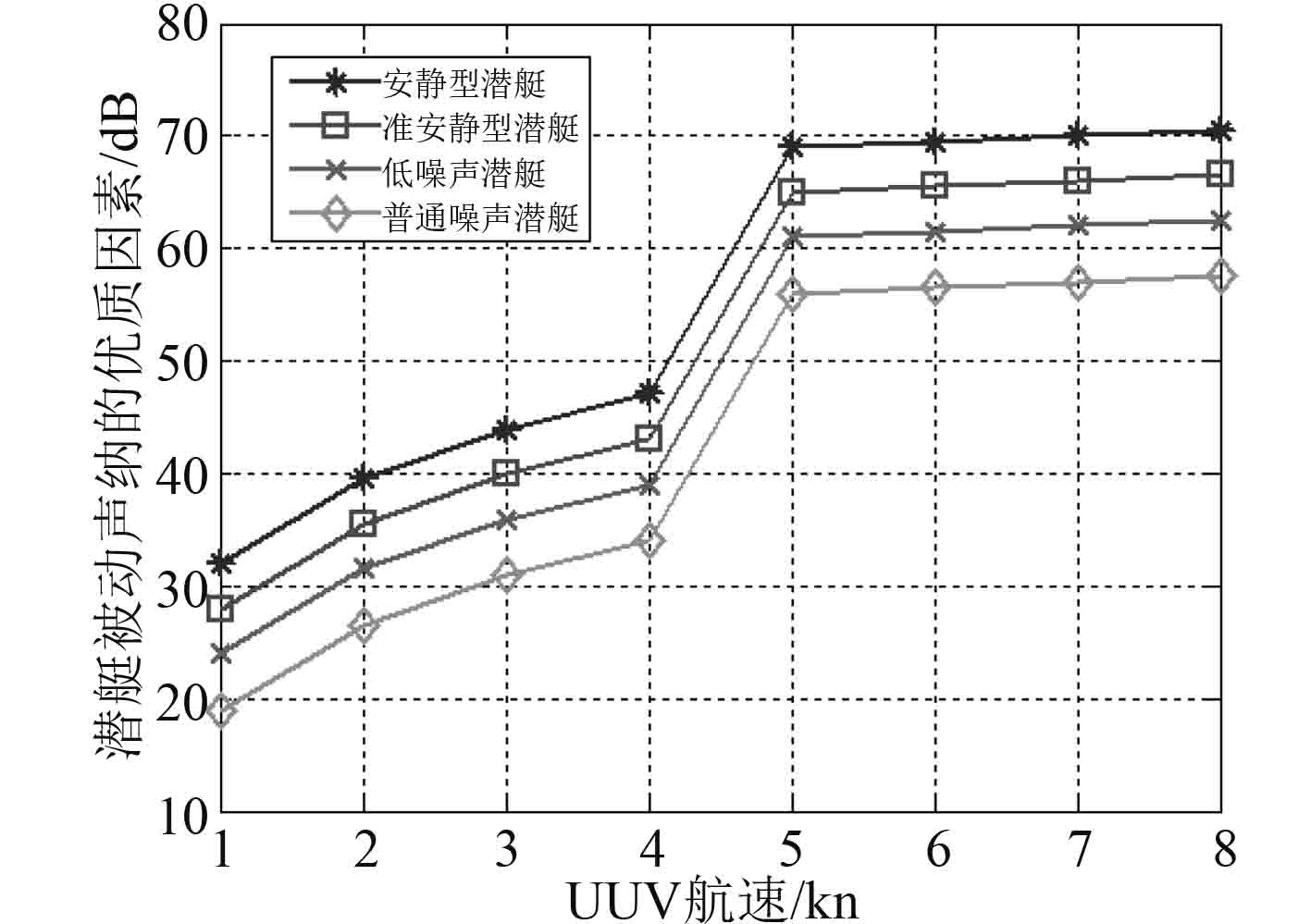
|
图 3 UUV不同航速下潜艇被动声呐的优质因素 Fig. 3 Submarine passive sonar FOMwith different UUV velocity |
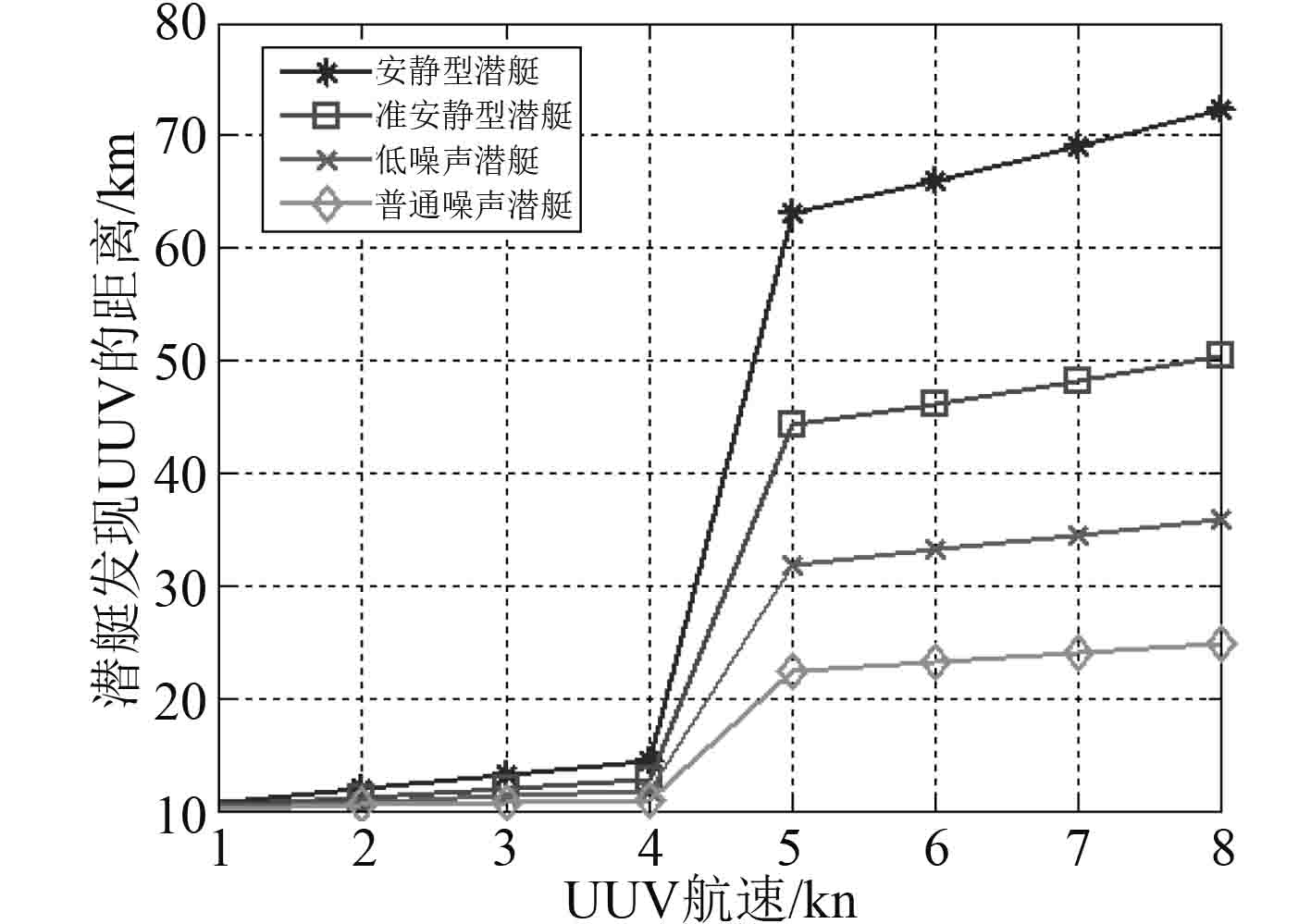
|
图 4 UUV不同航速下潜艇发现UUV的距离 Fig. 4 UUV detection range of submarine passive sonar with different UUV velocity |
2)UUV发现潜艇的距离估计
UUV利用宽带平方律检波器进行信号检测时,假设其检测阈与普通噪声潜艇的接近,并设为
与估计潜艇的被动声呐的指向指数相似,假设UUV被动声呐,利用长1 m、高0.5 m的舷侧基阵接收信号,该基阵的设计频率为2000 Hz,则
| $DI = 10\lg 10 = 10(\rm{dB})\text{。}$ | (8) |
假设潜艇的临界航速均为6 kn,根据实际情况分析,潜艇航速一般在低于临界航速下工作,因此下面仅分析UUV对低于6 kn航速潜艇的发现距离。
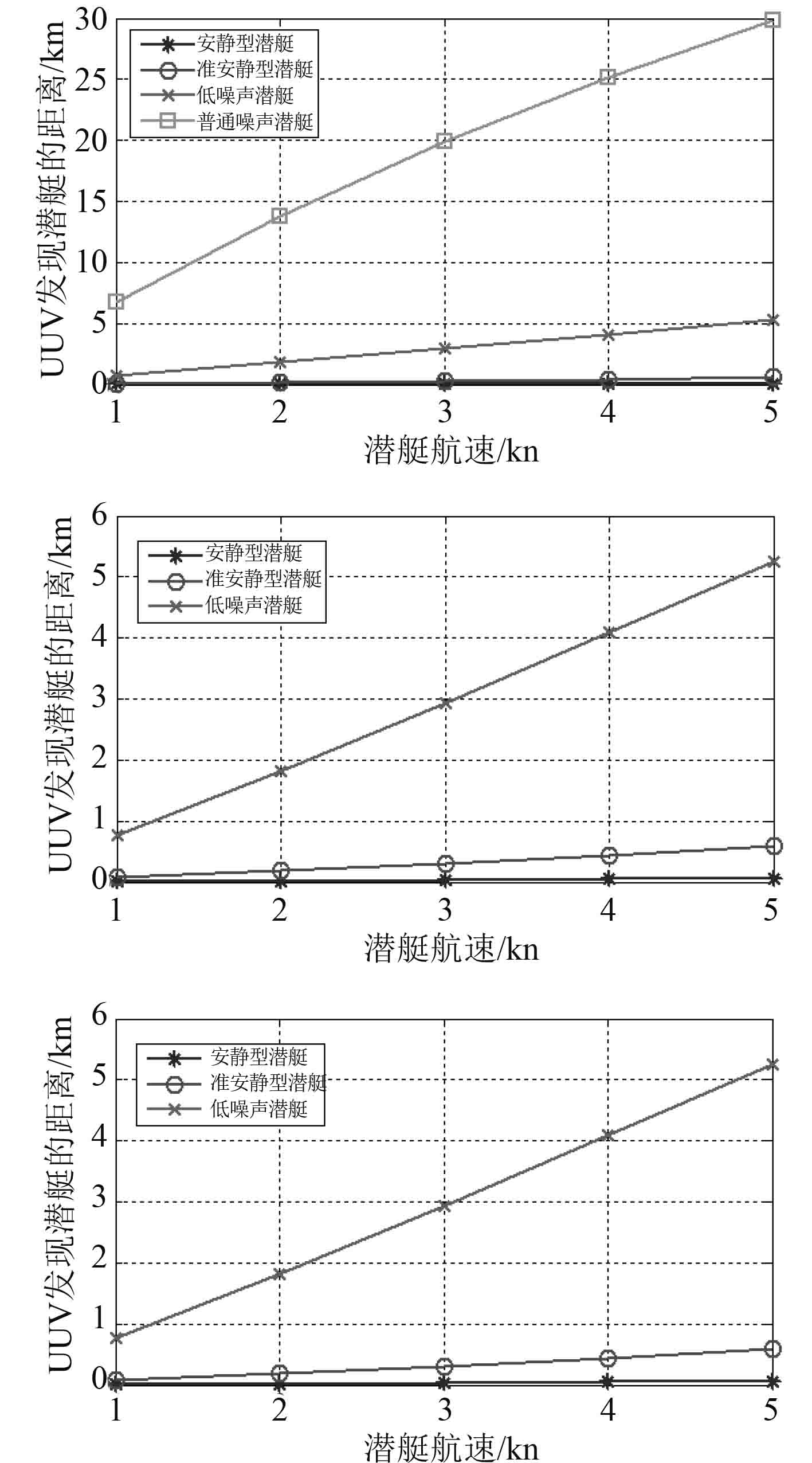
根据潜艇辐射噪声级模型,计算潜艇的辐射噪声级,再计算优质因素,然后利用式(7),求出UUV对潜艇的发现距离。利用Matlab软件计算得到在潜艇不同航速时,UUV对潜艇的发现距离,如图5所示。
|
图 5 潜艇不同航速下UUV发现潜艇的距离 Fig. 5 Submarine detection range of UUV passive sonar with different submarine velocity |
在UUV指向性指数为10 dB,环境噪声90 dB,检测阈为-21 dB时,从图5可以看出,UUV在5 km外就可以发现普通噪声潜艇,对低噪声潜艇发现距离也大于0.8 km,对于航速5 kn准安静型潜艇的发现距离不大于0.6 km,对于航速5 kn安静型潜艇的发现距离不大于60 m。
假设UUV在反潜中采用4 kn的速度搜索,潜艇以5 kn的速度航行,其余参数与上述2个仿真情形相同,那么各自对对方的发现距离如表2所示。因此,UUV在与潜艇的对抗过程中,除了不能先发现安静型潜艇外,对其余类型潜艇均可以先敌发现。
|
|
表 2 UUV与潜艇各自发现对方的距离表 Tab.2 Detection range of submarine and UUV |
UUV的运动模型对于作战模拟、装备论证有着重要的意义。针对UUV规避潜艇搜索进行分析、建模,针对不同的初始距离、转向时间对UUV采取不同的规避航向、航速进行计算机仿真,得到了UUV机动规避成功率较高的航向航速设置,并深入分析了初始距离和转向时间对敌潜艇搜索的影响。最后对UUV的机动能力和探测能力提出了要求。
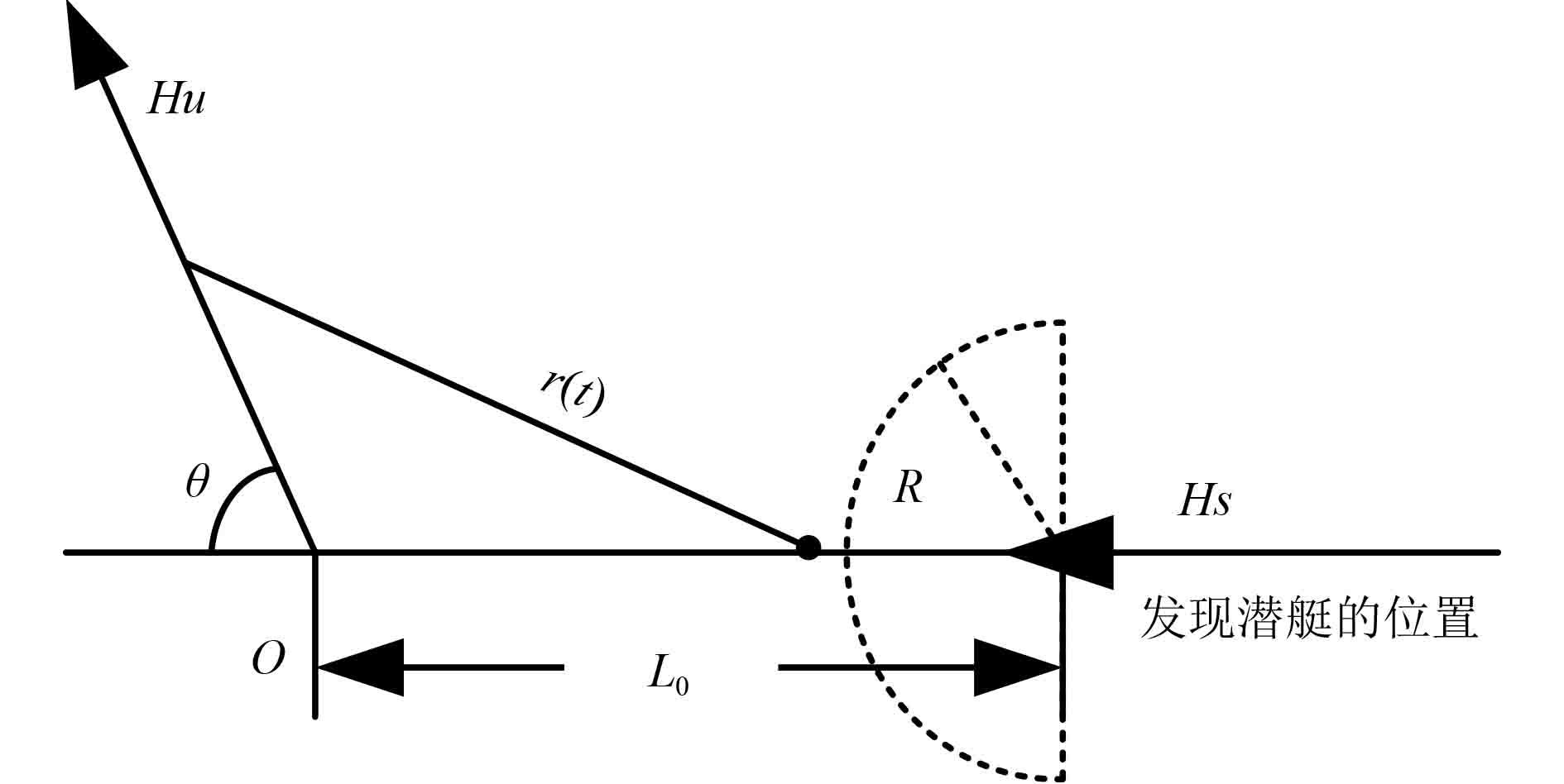
2.1 初始态势及相关参数计算由于UUV体积小、航速低,辐射噪声要远小于潜艇,但是UUV的巡航速度小于潜艇的巡航速度,且不能高速机动,因此,在UUV与敌潜艇遭遇过程中,必须要能先发现对方。UUV与敌潜艇遭遇可以有多种情况,为便于研究假设敌潜艇与UUV相向而行,而且在UUV发现潜艇后,潜艇仍按原方向航行。此时,潜艇与UUV的运动态势如图6所示。
|
图 6 潜艇与UUV的运动态势 Fig. 6 Motion potential of enemy submarine and UUV |
图6中,Hu为UUV规避航向;Vu为UUV规避航速;tz为UUV转向时间;
因此,根据余弦定理得:
| $\begin{split}&r(t) = \\ &\sqrt {{{\left[ {{L_0} - {V_s} \cdot \left( {t + {t_z}} \right)} \right]}^2} + {V_u}^2 \cdot {t^2} + 2\left[ {{L_0} - {V_s} \cdot \left( {t + {t_z}} \right)} \right] \cdot {V_u} \cdot t \cdot \cos \theta } \end{split}\text{。}$ | (9) |
且,
UUV能够成功规避敌潜艇的条件为:
| $\left\{ \begin{array}{*{20}{l}} {{L_0} > {V_s} \cdot {t_z}}, \\ {{L_0} > R}, \\ \min \left[ {r(t)} \right] > R\text{。} \end{array} \right.$ | (10) |
1)仿真参数设置
在良好水文条件下,UUV航速2~8 kn时,对航速3~12 kn的潜艇发现距离为10~25 cab;初始距离L0为10~25 Cab,UUV转向时间为2~8 min;敌我航向夹角
|
|
表 3 正交试验设计表 Tab.3 Design table of orthogonal experiment |
2)仿真结果分析
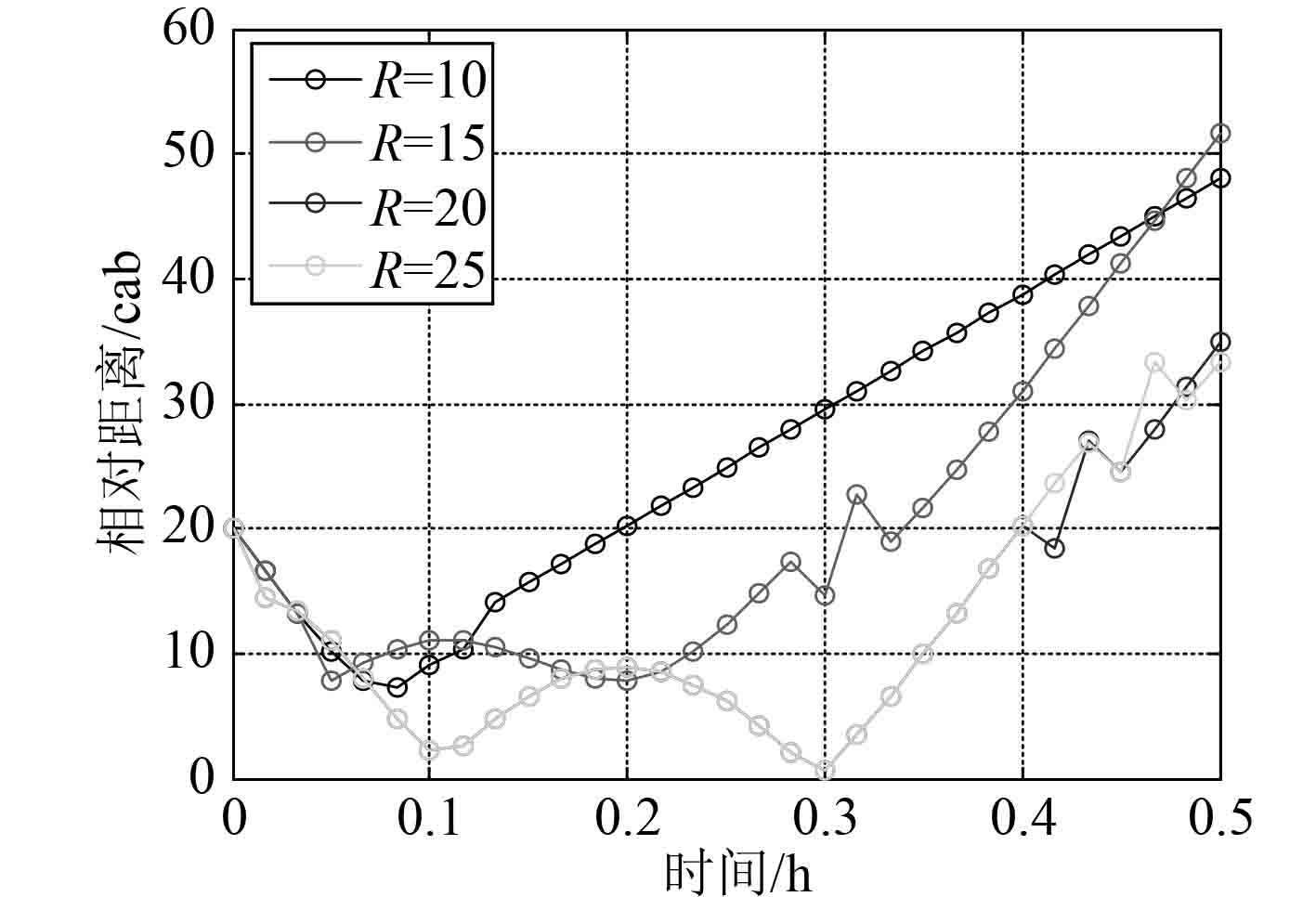
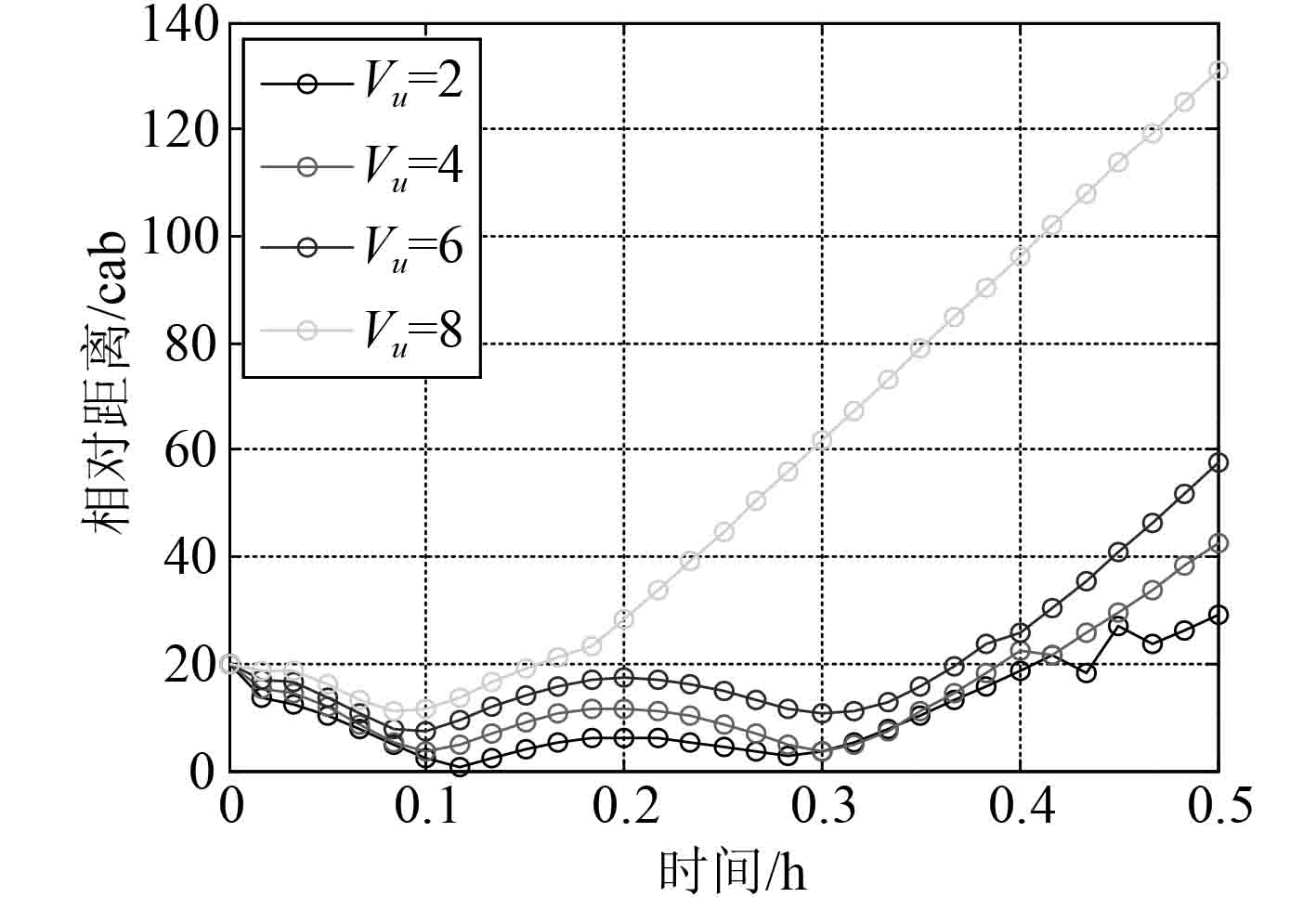
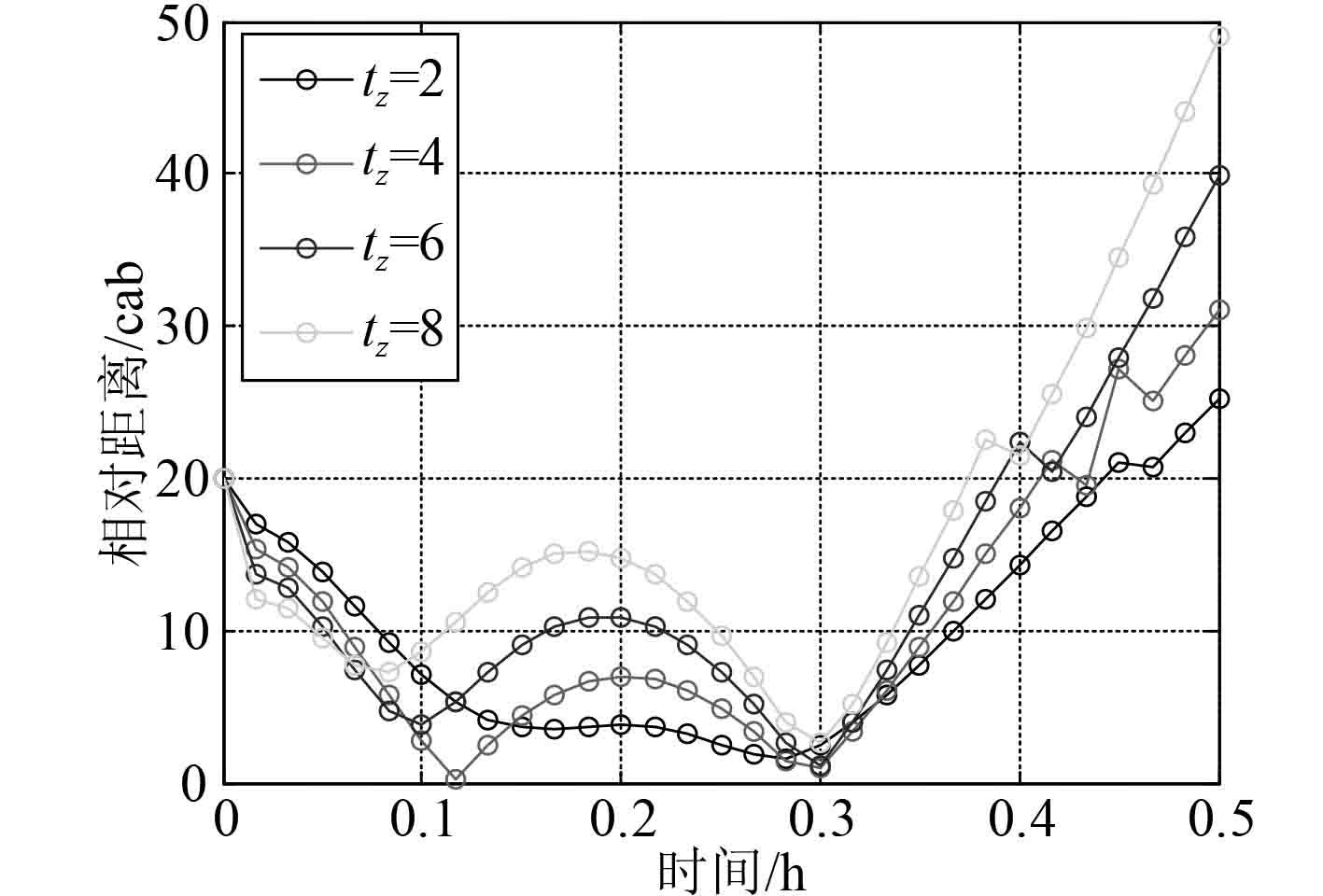
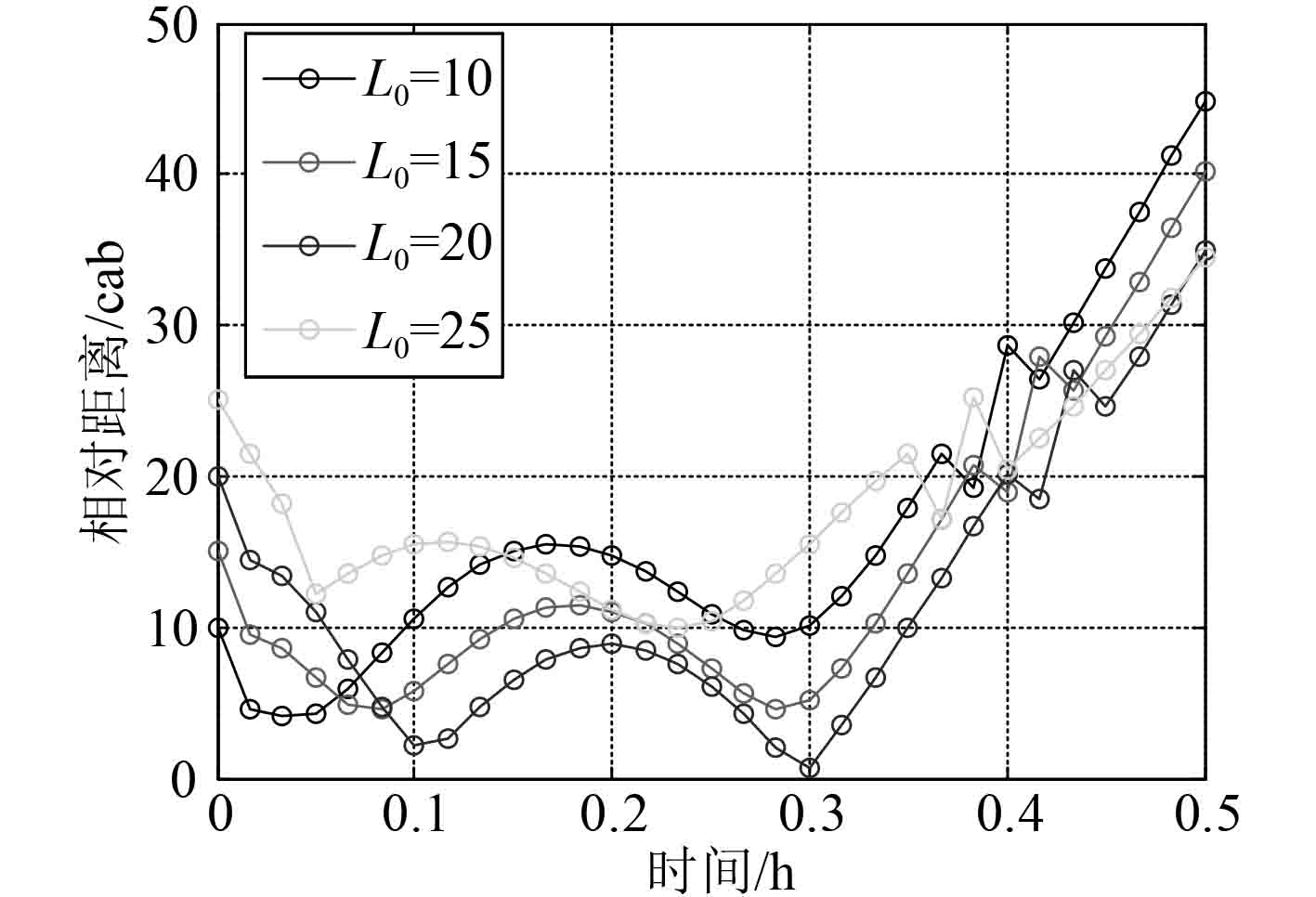
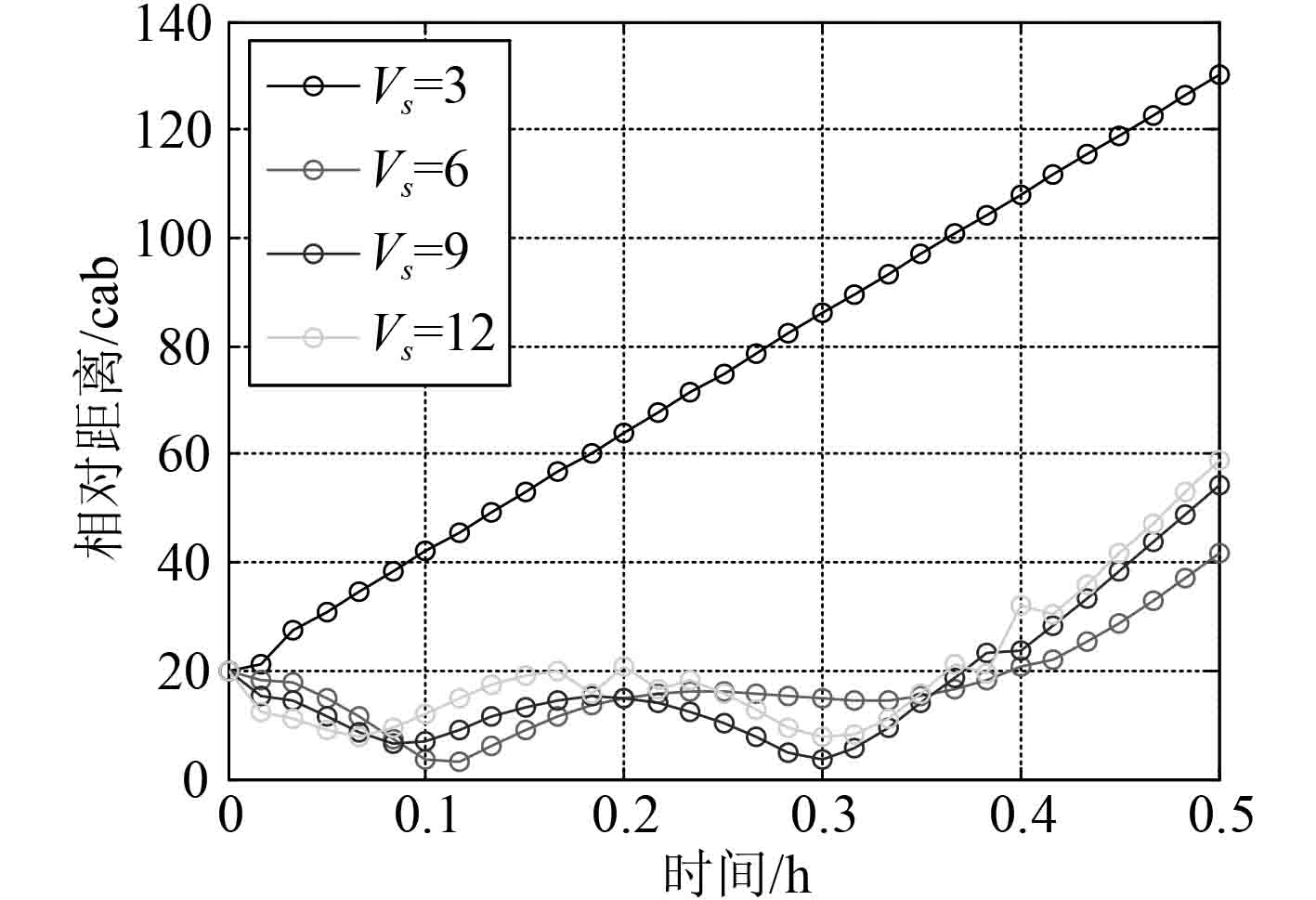
按照表3给出的影响因素正交设计表进行仿真,得到不同探测距离、不同UUV航速、不同转向时间、不同初始距离、不同潜艇航速和不同航行夹角下UUV与潜艇间相对距离随时间的变化情况,分别如图7~图12所示。可以看出除去潜艇航速3 kn的情况之外,在仿真开始的0.4 h时间范围内,均存在UUV与潜艇之间的相对距离小于UUV对潜艇发现距离的时间段。因此,UUV可在大部分情况下发现潜艇,并做出规避动作。
|
图 7 不同探测距离 Fig. 7 Different detection range |
|
图 8 不同UUV航速 Fig. 8 Different UUV velocity |
|
图 9 不同转向时间 Fig. 9 Different turning time |
|
图 10 不同初始距离 Fig. 10 Different original range |
|
图 11 不同潜艇航速 Fig. 11 Different submarine velocity |

|
图 12 不同航行夹角 Fig. 12 Different heading angle |
依据被动声呐方程,在分析潜艇与UUV被动声呐检测阈和指向性指数 基础上,结合辐射噪声与航速的经验公式,对潜艇和UUV之间的相互发现距离进行了仿真计算,得出UUV在与潜艇的对抗过程中,除了不能先敌发现安静型潜艇外,对其余类型潜艇均可以先敌发现。在UUV对潜探测能力分析的基础上,构建UUV规避潜艇运动模型,设计正交实验,对不同探测距离、不同UUV航速、不同转向时间、不同初始距离、不同潜艇航速和不同航行夹角下UUV与潜艇间相对距离随时间的变化情况进行了仿真计算,仿真结果表明UUV可在大部分情况下发现潜艇,并做出规避动作。
| [1] |
陈强, 张林根. 美国军用UUV现状及发展趋势分析[J]. 舰船科学技术, 2010, 32(7): 129-134. |
| [2] |
王光荣.无人潜航器任务构想[M]. 北京: 海潮出版社, 2010.11.
|
| [3] |
胡必文, 程彬彬. 浅析水下无人作战平台现状及未来作战使命[J]. 水雷战与舰船防护, 2013, 21(4): 67-71. |
| [4] |
邹建, 陈庆元, 张桂英. 水声对抗仿真系统中的被动声纳仿真[J]. 计算机仿真, 2010, 27(7): 309-312. DOI:10.3969/j.issn.1006-9348.2010.07.075 |
| [5] |
廖宏宇. 被动声纳目标/背景建模与仿真[J]. 计算机仿真, 2006, 23(4): 1-4. DOI:10.3969/j.issn.1006-9348.2006.04.001 |
| [6] |
陈强.水下无人航行器[M]. 北京: 国防工业出版社, 2014.01.
|
| [7] |
Department of The Navy. The Navy Unmanned undersea vehicle (UUV) master plan[EB/OL].(2004-11). http://www.Navy.Mil/navata/technology.
|
| [8] |
陈强, 袁思鸣. 水下无人航行器总体论证方法研究[J]. 论证与研究, 2013(4): 30-33. |
| [9] |
赵祚德, 刘保果. 水下无人作战平台与水下作战[J]. 舰艇论证参考, 2004(4): 61-65. |
 2021, Vol. 43
2021, Vol. 43
