2. 中国海洋大学信息科学与工程学院,山东 青岛 266100
2. School of Information Science and Engineering, Ocean University of China, Qingdao 266100, China
自主式水下航行器(Autonomous Underwater Vehicle,AUV)是人们探索开发海洋的主要工具。AUV的航程长短对AUV的应用至关重要[1]。提高航程长度,应最小化航行阻力和最大化电池容量[2]。与有缆水下航行器不同,AUV利用无线通信技术与岸上技术人员交互需要一个非金属的天线。在AUV水下航行时,无线电衰减很快,基本无法传播,普通AUV不会安装体积大,功率高的超低频天线[3]。暂时“多余”的附体势必成为AUV航行阻力,从而影响航行距离。
为了解决这一问题,王广耀等[4]设计了一种可升放式的天线装置,虽然能有效降低附体迎风面积从而降低阻力,但天线体积小、仍有附体阻力;申洪彬等[5]利用双摇杆机构实现折叠天线,方案有效可行,但存在双摇杆机构运动空间大的缺点,在不宽裕的AUV空间内占据较大的空间。本方案使用滑块连杆机构实现折叠天线功能,有占用体积小、能完全减去附体阻力的优点。
1 AUV阻力分析AUV在水下可以实现六自由度运动,但在日常使用或者水下实验过程中,AUV直航频率最高、时间最长,通过降低AUV水下直航阻力便可提高AUV航行时间和距离。
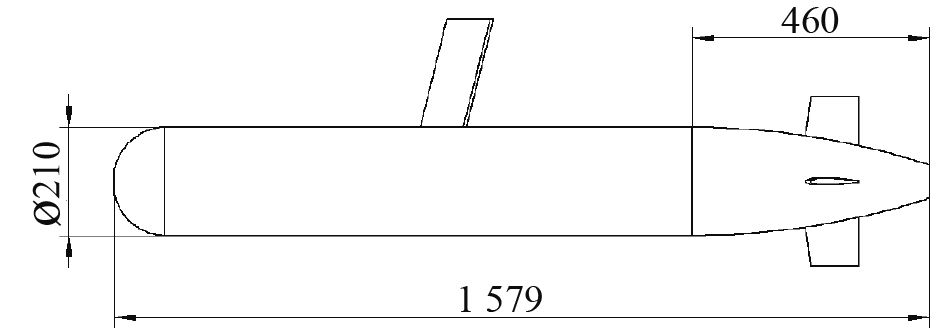
1.1 AUV三维模型为了获得较长的航程,AUV的外形选择上既要在水下航行阻力尽量小的同时,还要尽可能提高舱内可用体积用于储存锂电池,提供更多的能量。通过比较航行阻力与质量的比值来为AUV的外形设计提供参考,最终选取椭圆型头部曲线和MYRING型尾部曲线[6]和作为AUV的主体外形,如图1所示。
|
图 1 AUV主体外形图 Fig. 1 AUV main body drawing |
为计算天线附体对整体AUV直航阻力的影响,需要建立2个三维模型。模型1为舱体加4个尾舵,模型2为在模型1的基础上加入天线,拟定天线高度为210 mm,取天线形状为流线型的NACA0020,天线后掠角为85°。
1.2 仿真计算获得三维模型后使用ICEM CFD构建结构网格,结构网格具有网格质量高、仿真运算快、结果精确的优点。求解雷诺应力平均N-S方程,湍流模型选择自由剪切流动和壁面限制边界层流动优势明显的SST k-omega[7]。而使用这个模型就要考虑边界层的首层高度为:
| $y = \dfrac{{{y^ + } \cdot \upsilon }}{{{u^*}}} = \dfrac{{\sqrt 2 \cdot {y^ + } \cdot \upsilon }}{{u \cdot \sqrt {0.057{{{\rm{Re}} }^{ - 0.2}}} }}\text{。}$ | (1) |
其中:

|
图 2 模型1的结构网格图 Fig. 2 Structured grid diagram of model 1 |

|
图 3 模型2的结构网格图 Fig. 3 Structured grid diagram of model 2 |
导入Fluent软件中,湍流模型选用k-omega SST,如图4所示,入口边界条件设置为velocity inlet,出口边界条件设置为outflow,壁面设置为symmetry,求解方法选用SIMPLE。结果如表1所示。

|
图 4 边界条件设置图 Fig. 4 Boundary condition setting diagram |
|
|
表 1 模型1和模型2在不同速度下的阻力对比表 Tab.1 Comparison table of resistance of model 1 and model 2 at different speeds |
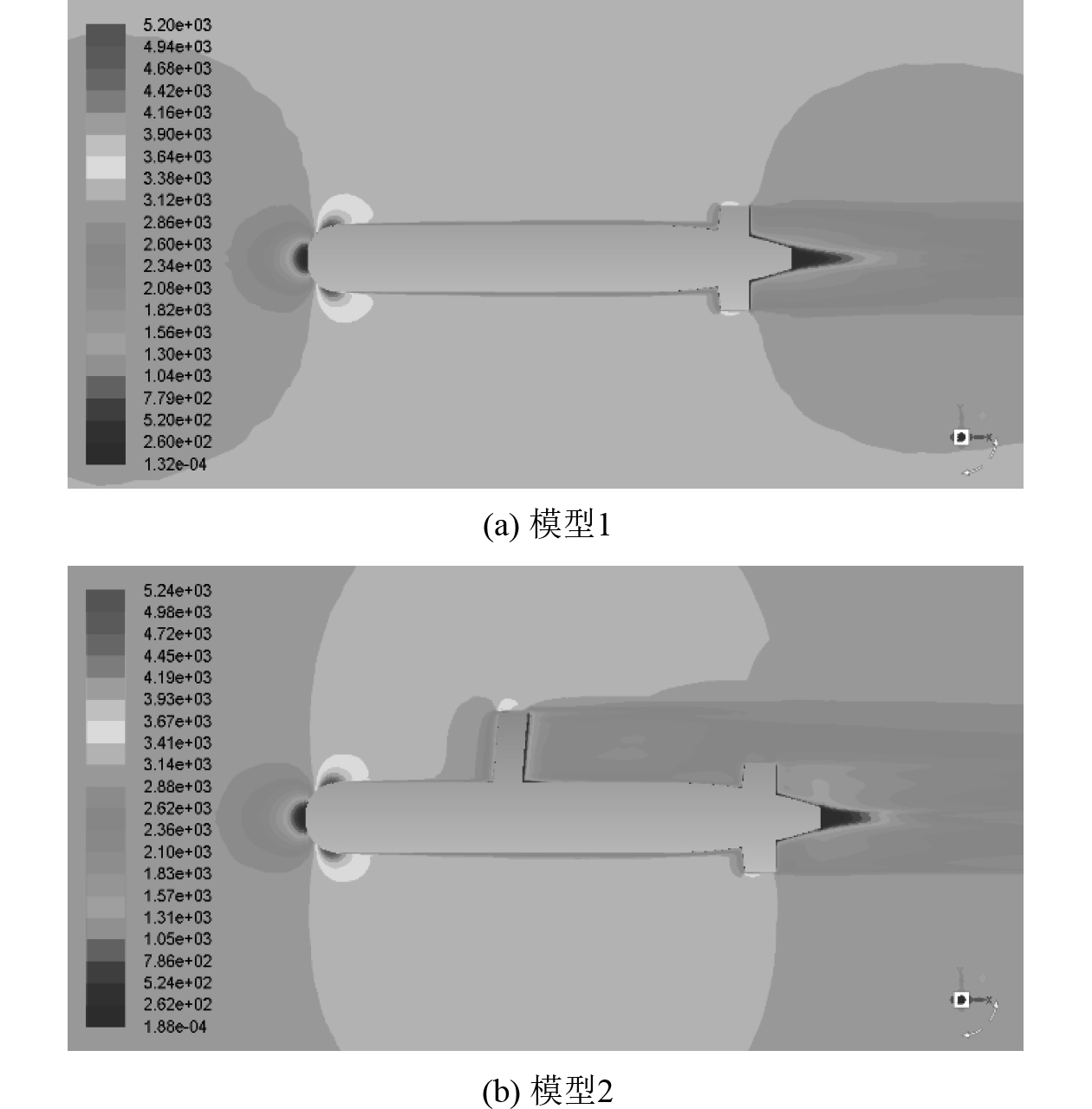
模型1与模型2的压力云图如图5所示。
|
图 5 模型在2.5 m/s下的压力云图 Fig. 5 Model contour of dynamic pressure at 2.5 m/s |
经过结果对比,航行器增加天线附体会比没有天线附体增加至少阻力19%,且航速越快,天线阻力占比越大,因此实现折叠天线能有效降低航行阻力从而增加航行距离。
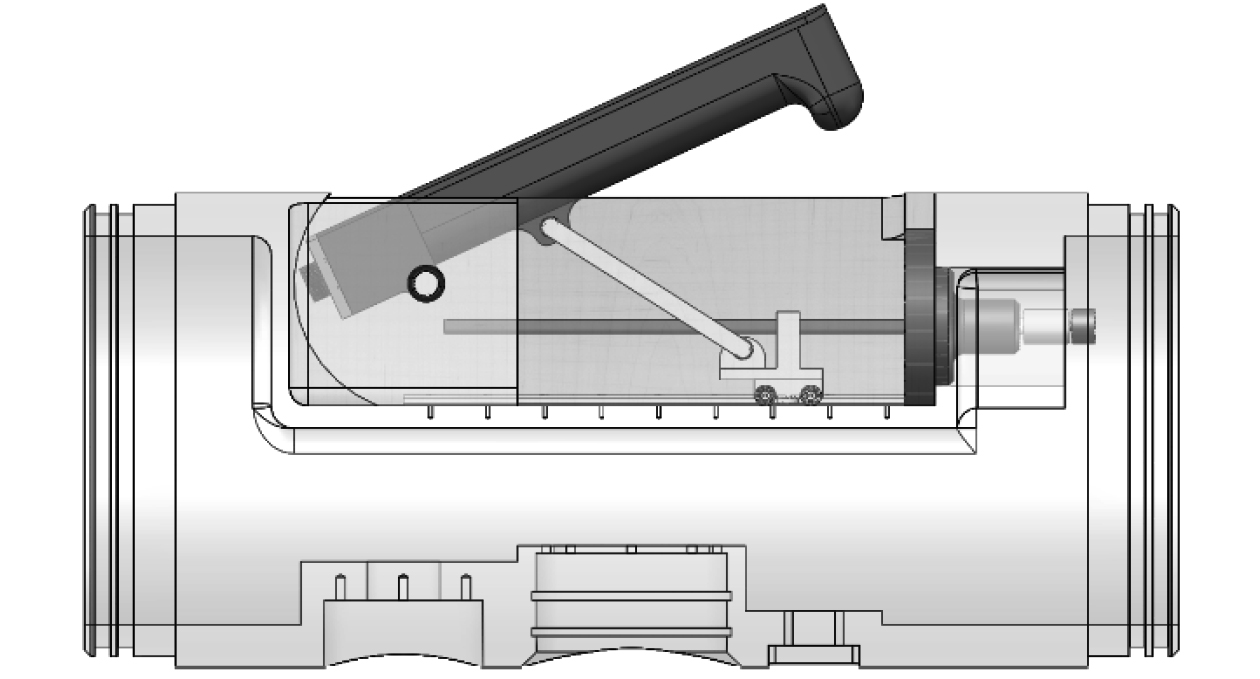
2 折叠天线的机械设计折叠天线装置包括驱动机构、传动机构、天线本体和舱体4个部分,整机的机构简图如图6所示。驱动机构是步进电机。传动机构包括滚珠丝杆,滑块滑轨,连杆和轴承,在水下实现滑块前进后退这种直线往复运动的装置有防水直线电机,因为价格昂贵,控制方法相对复杂,本文使用价格不高控制方便的“滚珠丝杆-滑块滑轨”机构将转动转化为直线运动。整体机构运动规律与雨伞的开合运动相似,舱内控制电机正转,电机输出轴通过联轴器带动丝杆转动,滑块向前推进,同时连杆1带动天线整体转动,实现天线的升起,同理舱内控制电机反转,滑块向后移动,天线折叠收起。
|
图 6 折叠天线模型图 Fig. 6 Folded antenna model diagram |
通过对整体机构平面自由度的分析,验证机构具有唯一确定的运动,并通过几何和力学分析,找到在现实条件下的最优结构参数。
3.1 运动学计算
|
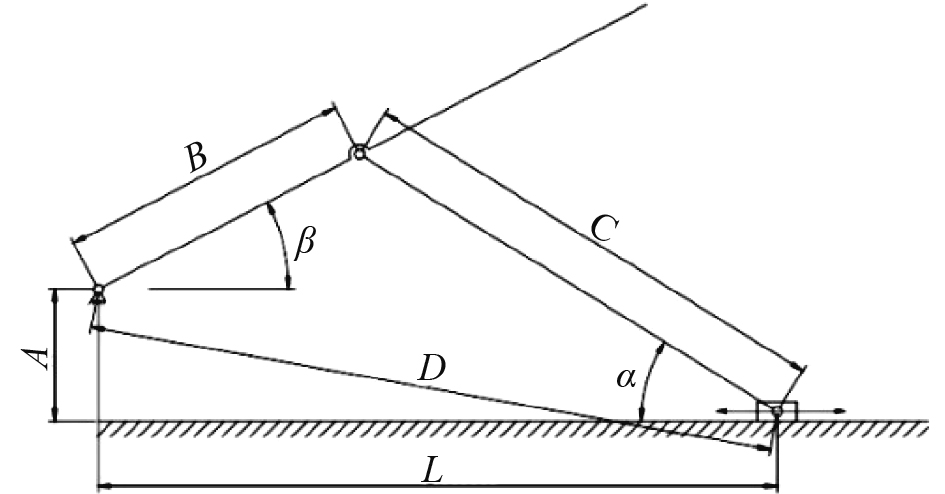
图 7 平面机构运动简图 Fig. 7 Plane mechanism movement diagram |
| $F = 3N - 2{P_L} - {P_H}\text{。}$ | (2) |
其中:
由几何关系可得如下关系式:
| ${L_{MAX}} = B + \sqrt {{C^2} - {A^2}} \text{,}$ | (3) |
| ${L_{MIN}} = \sqrt {{C^2} - \left( {{A^2} + {B^2}} \right)}\text{,} $ | (4) |
| ${V_0} = \left( {{L_{MAX}} - {L_{MIN}}} \right)/T\text{,}$ | (5) |
| $V = {V_0}\cos \alpha \sin \left( {\alpha + \beta } \right)\text{,}$ | (6) |
| $\omega = V/B\text{,}$ | (7) |
| $\Delta \beta = \omega \Delta t = \left[ {{V_0}\cos \alpha \sin \left( {\alpha + \beta } \right)\Delta t} \right]/B\text{,}$ | (8) |
| $\cos \left( {\pi - \alpha - \beta } \right) = \left[ {{B^2} + {C^2} - {D^2}} \right]/2BC\text{,}$ | (9) |
| ${D^2} = {A^2} + {\left( {{L_{MAX}} - {V_0}t} \right)^2}\text{,}$ | (10) |
| $\sin \alpha = \left( {B\sin \beta + A} \right)/C\text{,}$ | (11) |
| $0 \leqslant \beta \leqslant {\text{π}} /2\text{。}$ | (12) |
式中:
简化可得:
| $\left\{ \begin{array}{l} t = \dfrac{{{L_{MAX}} - \sqrt {{B^2} - C\sin \alpha - {A^2}} - C\cos \alpha }}{{{L_{MAX}} - {L_{MIN}}}} \cdot T \text{,}\\ \Delta t = \dfrac{{B \cdot \Delta \beta \cdot {{\left[ {1 - {{\left( {\dfrac{{A + B\sin \beta }}{C}} \right)}^2}} \right]}^{ - 0.5}} \cdot V_0^{ - 1}}}{{\left( {\dfrac{{A + B\sin \beta }}{C}\cos \beta + \sqrt {1 - {{\left( {\dfrac{{A + B\sin \beta }}{C}} \right)}^2}\sin \beta } } \right)}} \text{。} \end{array} \right.$ | (13) |
设
根据上述方程,利用Matlab软件可得
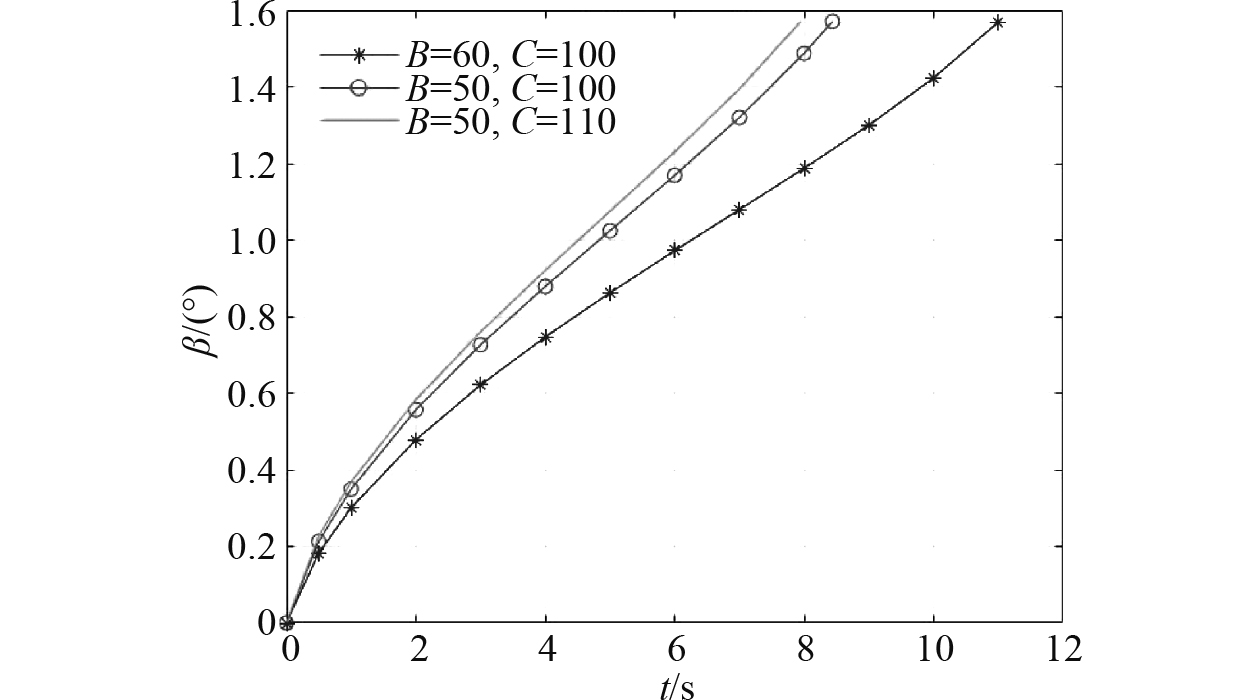
|
图 8 β-t的曲线图 Fig. 8 Graph of β with respect to t |
折叠天线涉及分体式天线的局部运动和滚珠丝杆的连续转动,需要对这两部分进行防水处理。
4.1 密封设计天线的密封如图9所示。本文采用2处静密封[8],分别是天线和天线压盖中间的一处和天线压盖与穿线螺母中间的一处,通过两道静密封[9]实现天线整体密封,静密封O型圈型号及密封槽尺寸均选用司达行的密封标准;同时天线出线端使用穿线螺丝和穿线螺母将天线内传感器模块的信号线和电源线引到天线外部,而后使用环氧树脂对穿线螺钉进行灌封。对于滚珠丝杆的转动,需要对舱体和丝杆转动处进行旋转动密封[10],如图10所示。为了方便加工和降低加工成本,将整个密封装置模块化分块,密封压盖A与舱体之间使用一道静密封,密封压盖A内端有一道O型密封圈,通过密封压盖B紧压轴承进而挤压轴承压盖保证该道密封圈的密封效果,为保险起见,在密封压盖中再加入一道动密封O型圈,同时在密封压盖A和密封压盖B中间加一道静密封从而保证2个零件水密。密封圈和密封槽尺寸同样选用司达行的密封标准。
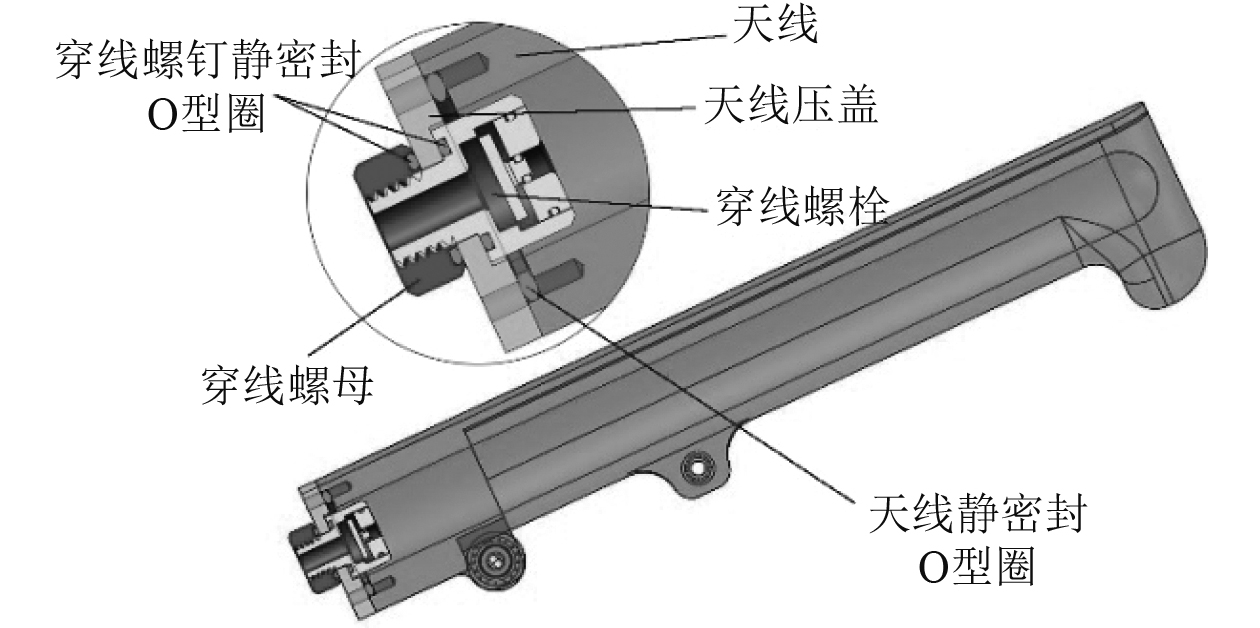
|
图 9 天线密封设计 Fig. 9 Antenna seal design |
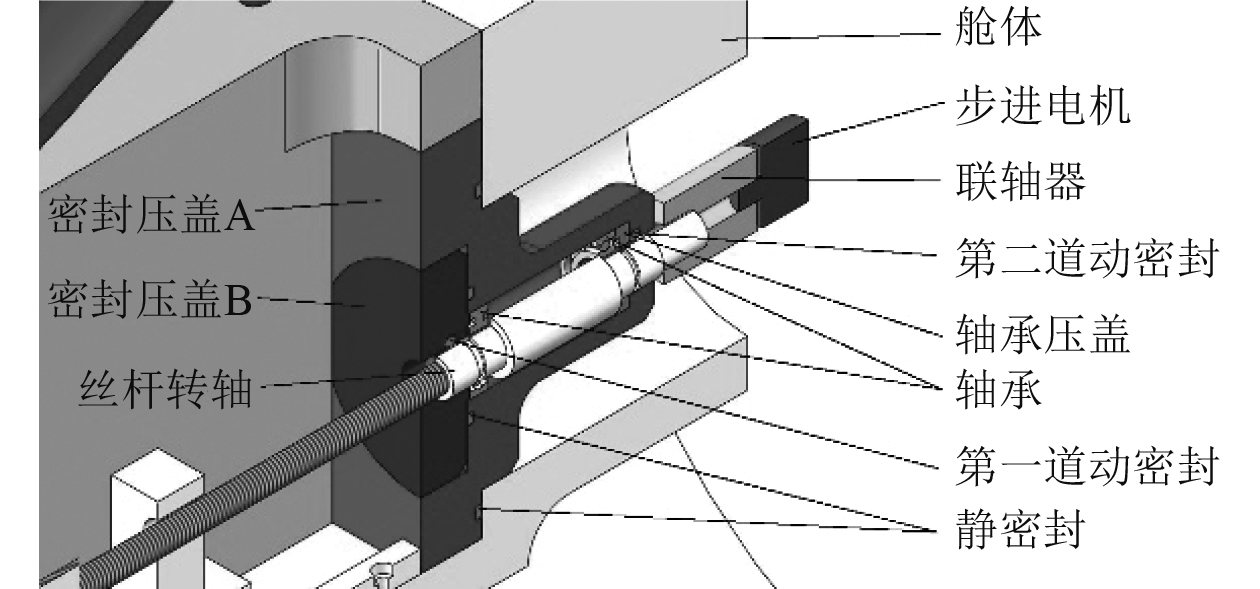
|
图 10 转轴密封设计 Fig. 10 Rotary shaft seal design |
为验证密封设计的可行性,本文通过转动轴不同角度并进行多次打压实验进行验证,验证整个装置的静态水密性和转动后的水密性。
4.2 可行性分析为了验证滚珠丝杆处的旋转动密封,将模型依次安装在水下密封舱中,进行模拟水下200 m的打压实验,在压力罐中加压2 MPa,并保压1 h,验证其水下密封性。结果表明,密封方案可行。
5 结 语本文通过CFD仿真对比,得出在直航的情况下,传统AUV直立天线比实现折叠天线后的新型长航程AUV阻力要增加至少19%。因此实现水下航行时天线收起,需要使用时再折叠伸出具有很强的使用需求。通过机械结构设计,利用滚珠丝杆将步进电机的转动转化为滑块的直线运动,通过滑块的直线运动带动滑块上的连杆运动,通过连杆间的约束,实现天线的折叠升降。确定折叠方案后绘制平面机构简图,通过计算机构自由度得出当滑块直线运动时,整体机构有确定、唯一的运动。通过几何关系和实际情况,设计各个构件的具体参数,推导出几何关系式,为后续的设计提供理论基础,并通过理论计算得出相对较优的参数。打压实验验证了天线密封和运动机构密封方案的可行性。
| [1] |
WYNN R B, HUVENNE V A I, LE BAS T P, et al. Autonomous Underwater Vehicles (AUVs): Their past, present and future contributions to the advancement of marine geoscience[J]. Marine Geology, 2014, 352: 451-468. DOI:10.1016/j.margeo.2014.03.012 |
| [2] |
GAFUROV, SALIMZHAN, V. KLOCHKOV, EVGENIY. Autonomous unmanned underwater vehicles development tendencies[J]. Procedia Engineering, 2015, 106: 141-148. DOI:10.1016/j.proeng.2015.06.017 |
| [3] |
罗建新, 冯扬. 潜艇通信天线技术现状及发展趋势[J]. 舰船科学技术, 2008(S1): 19-22. |
| [4] |
王广耀, 严天宏, 何波, 等. 一种可升放式水下航行器卫星天线装置: CN205488503U[P].
|
| [5] |
申洪彬, 严天宏, 赵梓奎. 一种自主水下航行器用可折叠天线装置: CN109904583A[P].
|
| [6] |
孟凡豪, 严天宏, 何波, 徐新胜. 水下滑翔器整体外形设计及水动力性能分析[J]. 海洋工程, 2014, 32(2): 61-71. |
| [7] |
庞永杰, 王亚兴, 杨卓懿, 等. Myring型回转体直航阻力计算及艇型优化[J]. 哈尔滨工程大学学报, 2014, 35(9): 1093-1098. |
| [8] |
成大先. 机械设计手册[M]. 北京: 化学工业出版社, 2016. CHENG-Daxian. Mechanical design manual[M]. Beijing: Chemical Industry Press, 2016 |
| [9] |
彭旭东, 王玉明, 黄兴, 等. 密封技术的现状与发展趋势[J]. 液压气动与密封, 2009, 29(4): 4-11. DOI:10.3969/j.issn.1008-0813.2009.04.002 |
| [10] |
袁夫彩, 陆念力, 王立权. 水下船体表面清刷机器人密封的设计[J]. 润滑与密封, 2007(5): 69-72. DOI:10.3969/j.issn.0254-0150.2007.05.020 |
| [11] |
李波, 冯凯, 傅晓晗, 等. 水下传感器承压密封结构设计[J]. 传感器与微系统, 2017, 36(8): 72-74. |
 2021, Vol. 43
2021, Vol. 43
