2. 中国科学院 机器人与智能制造创新研究院,辽宁 沈阳 110169
2. Institutes for Robotics and Intelligent Manufacturing, Chinese Academy of Sciences, Shenyang 110169, China
水面/水下自主航行器,作为搭载探测仪器与工程设备的自主航行载体,可有效地辅助人类进行海洋数据采集、资源探测和海洋工程实施,对海洋资源探索技术的发展具有重大意义[1-3]。良好的航行控制能力是实现不同需求任务的根本,而对典型航迹的跟踪精度是航行控制效果的良好体现。而目前在USV轨迹跟踪控制的研究中,主要存在以下难点:1)USV系统水动力系数随USV航行速度的变化而改变,因此该系统具有不确定性、时变性和非线性等特点;2)USV具有明显的欠驱动特性,因此很多非线性控制算法不能直接进行应用;3)目前所研究的轨迹跟踪方法多数为基于仿真或无人艇低速状态下的试验,却无法确保在复杂环境、无人艇高速状态下对轨迹的精确跟踪[4]。
无人艇对典型轨迹直线和环形的跟踪能力,是其执行任务应当具备的基本能力。环形轨迹对无人艇的航行控制方法具有较强的能力要求,本文针对环形轨迹跟踪方法进行研究及实现。由于系统模型的不确定性,选用基于拟合偏差的最小二乘航向辨识法建立模型集,实时计算选择最优模型参与控制计算,并以此搭建仿真平台对航向控制、控制策略及制导律等进行设计仿真。本文方法以USV航向控制为核心,结合控制策略的强抗干扰性,以“勇士”号无人水面艇为验证载体,对算法有效性和适用性进行实航验证。
1 基于拟合偏差的最小二乘航向辨识法“勇士”号USV航向和速度控制执行机构分别为尾部喷嘴和喷泵,通过尾部喷嘴的左右调节改变航向,喷泵向后喷水产生反作用力控制纵向速度。
USV系统航向控制模型采用一般的船舶首摇响应线性方程[5]:
| $ {T_1}{T_2}\ddot r + \left( {{T_1} + {T_2}} \right)\dot r + r = K\delta + K{T_3}\dot \delta {\text{。}} $ | (1) |
其中:
1957年野本谦使用自动调节原理方法分析式(1),在执行操作非频繁情况下,略去2阶以上的小量,并设
| $ T\dot r + r = K\delta {\text{。}} $ | (2) |
式中:
| $ \dot r = - \frac{1}{T}r + \frac{K}{T}\delta = ar + b\delta \text{,} $ | (3) |
式中,
| $ \left\{ \begin{split} \dot \psi &= r\text{,} \\ \dot r &= ar + b\delta \text{,}\\ \end{split} \right. $ | (4) |
基于S形开环试验法,获取辨识所需数据,根据最小二乘法辨识参数[8],构建USV SIMO(sigle input multiple output)模型。设辨识模型为:
| $ {y_1}\left( {k + 1} \right) = a{y_2}\left( k \right) + bU\left( k \right) + e\left( k \right)\text{,} $ | (5) |
式中:
| $ \left\{ \begin{split} \varphi \left( k \right) = {\left[ {\begin{array}{*{20}{c}} {{y_2}\left( k \right)}&{U\left( k \right)} \end{array}} \right]^{\rm{T}}} \text{,} \\ \theta = {\left[ {\begin{array}{*{20}{c}} a&b \end{array}} \right]^{\rm{T}}} \text{,}\qquad\qquad\;\; \\ \end{split} \right. $ | (6) |
辨识模型即为:
| $ y\left( {k + 1} \right) = \varphi {\left( k \right)^{\rm{T}}}\theta \left( k \right) + e\left( k \right){\text{。}} $ | (7) |
设采样数组数据量为
| $ J = \sum\limits_{i = 0}^{M - 1} {{{\left( {{y_1}\left( {k + 1 - i} \right) - {\varphi ^{\rm{T}}}\left( {k + i} \right)\tilde \theta } \right)}^2}} \text{,} $ | (8) |
根据极大值原理,则其取最小值时,应满足
| $ - \left( {\Phi _M^{\rm{T}}\left( {{Y_M} - {\Phi _M}\tilde \theta } \right) + \Phi _M^{\rm{T}}\left( {{Y_M} - \Phi _M^{\rm{T}}\tilde \theta } \right)} \right) = 0\text{,}$ | (9) |
式中,若矩阵
| $ {\tilde \theta _M} = {\left( {\varPhi _M^{\rm{T}}{\Phi _M}} \right)^{ - 1}}\varPhi _M^{\rm{T}}{Y_M}{\text{。}} $ | (10) |
输入用于参数验证的数据,由原值
| $ {\bar e_{jM}} = \frac{{\left( {{Y_{iM}} - \Phi _{iM}^{\rm{T}}{{\tilde \theta }_j}} \right)}}{M}\text{。} $ | (11) |
选择多组数据进行辨识,所得结果在取得拟合偏差后,计算多组结果偏差均值得到阈值
根据以上原理,通过对“勇士”号USV实航数据进行模型辨识,得到多组模型后选择低于阈值
|
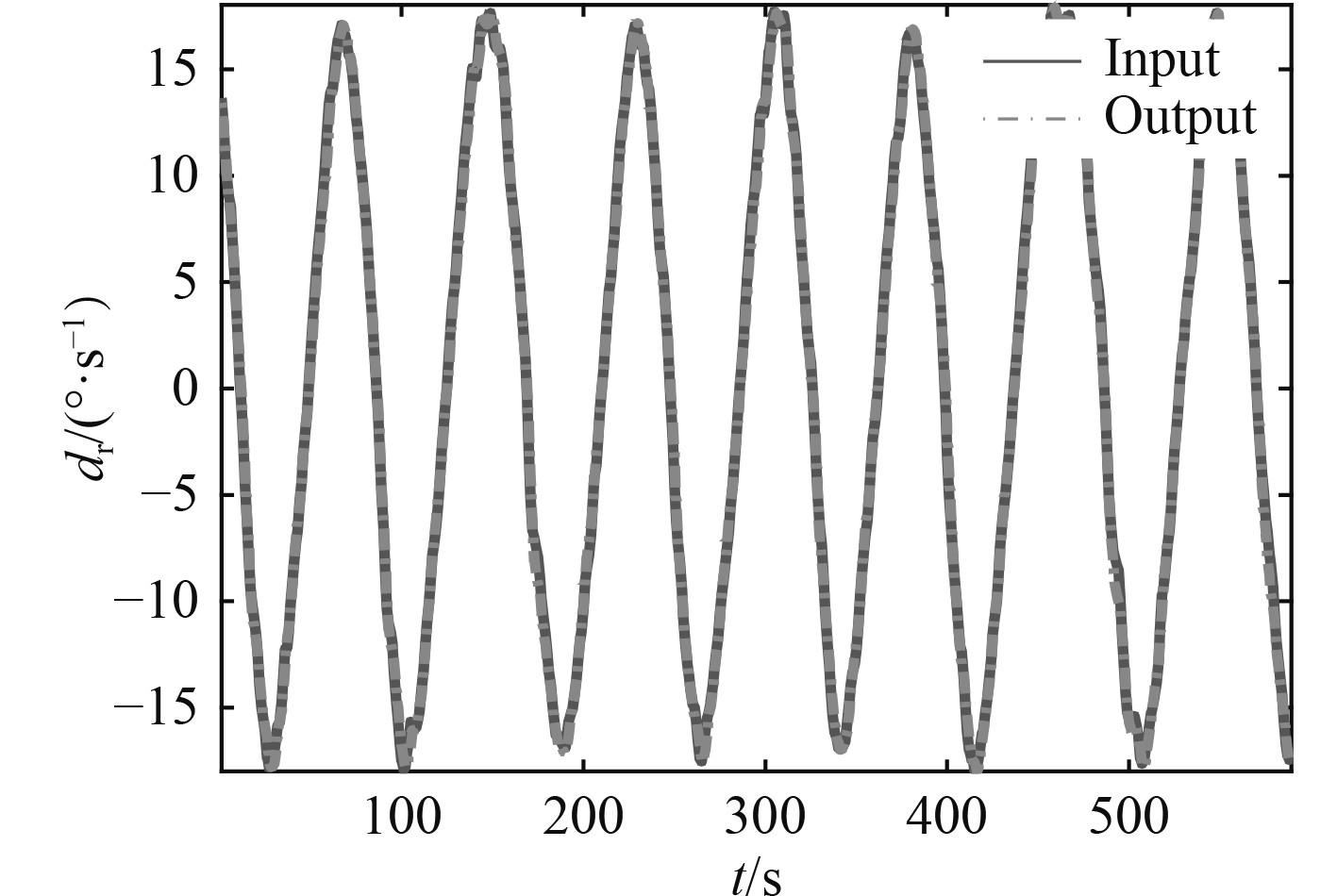
图 1 实际曲线与拟合曲线对比 Fig. 1 Comparison between the fitting curve and practical curve |
经过多组数据验证,算法拟合输出与实际输入基本吻合,且其平均拟合偏差较小,符合构建模型条件。
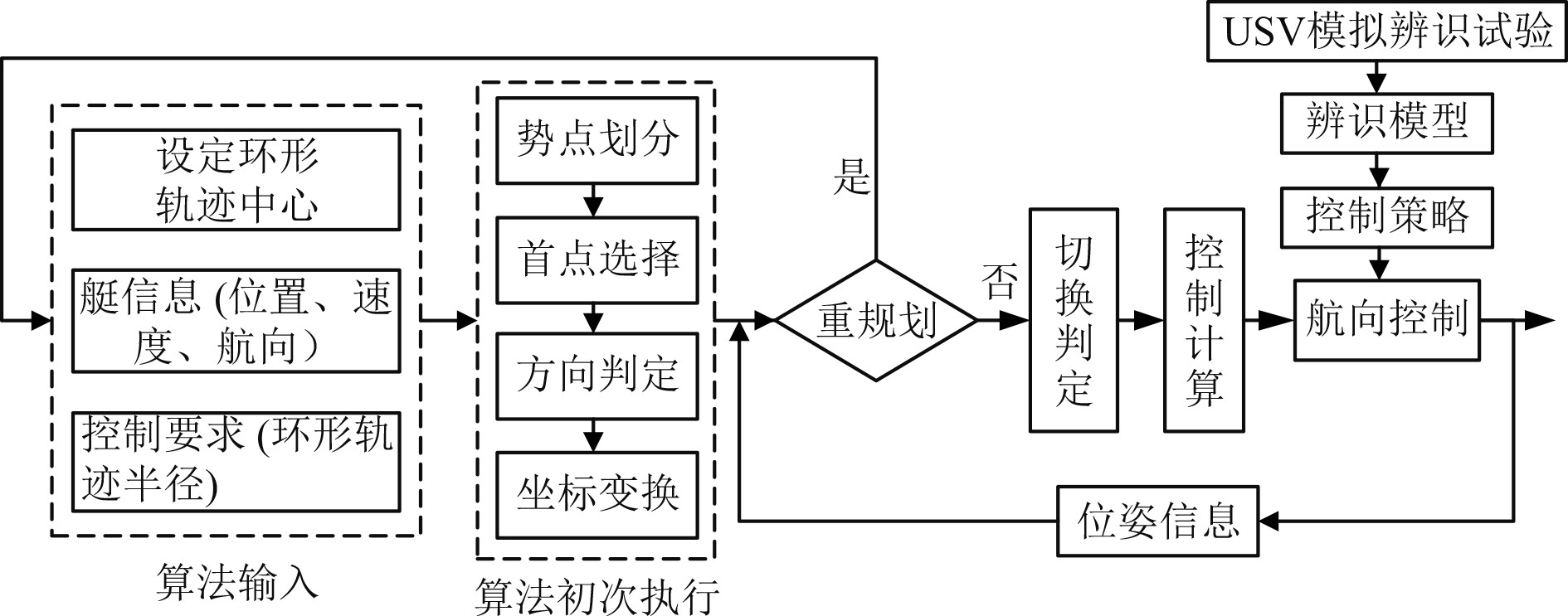
2 势点跟踪算法原理设定环形轨迹中心和半径,输入当前USV的位置、速度、航向信息,完成势点的划分、首势点选择及环绕方向判定,实时将有序势点进行坐标转换,以获得USV在所跟踪势点的运动坐标系下坐标,通过势点切换判据更新所跟踪的势点,并实时计算期望航向角。根据USV辨识模型所设计的控制策略对航向进行控制,实现对势点的稳定跟踪[9-11]。算法实现流程如图2所示。
|
图 2 势点跟踪算法实现流程 Fig. 2 Implementation process of potential point tracking algorithm |
根据水面无人艇动力学模型及运动学模型,将系统航向控制模型式(4)转换为状态空间表达式[12]:
| $ \left[ \begin{array}{l} {\dot \psi } \\ {\dot r} \\ \end{array} \right] = \left[ {\begin{array}{*{20}{c}} 0&1 \\ 0&a \end{array}} \right]\left[ \begin{array}{l} \psi \\ r \\ \end{array} \right] + \left[ \begin{array}{l} 0 \\ b \\ \end{array} \right]{\delta _{\rm{r}}}\text{,} $ | (12) |
首先,预设闭环系统矩阵极点为
| $ {\delta _{\rm{r}}}\left( t \right) = \frac{{{\lambda _1} + {\lambda _2} + a}}{b}r - \frac{{{\lambda _1}{\lambda _2}}}{b}\psi \text{。} $ | (13) |
其中,
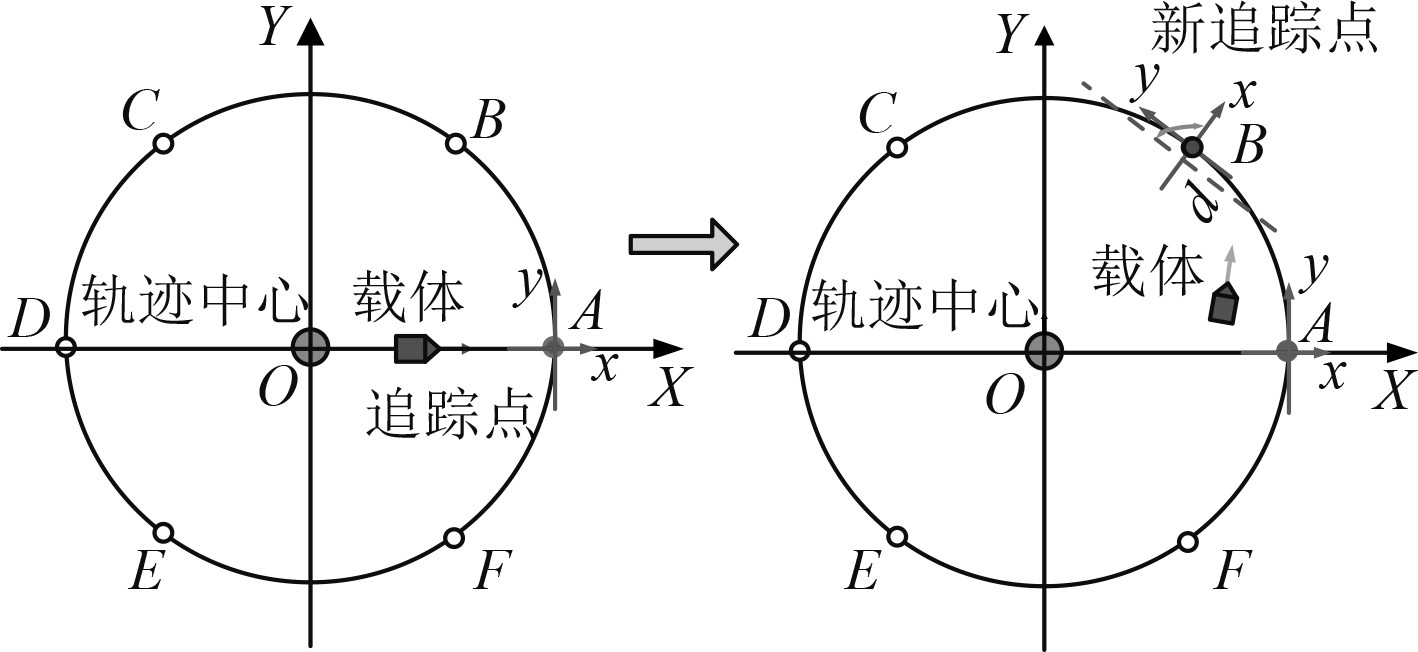
依托于水平面航向控制器[14-16],采用势点跟踪算法实现环形轨迹跟踪,如图3所示。首先设定环形轨迹中心位置以及环形半径,根据中心位置建立运动坐标系,并预置有序势点集合。对航行器位置进行坐标变换,转至运动坐标系下,依次跟踪每一个势点,进而形成环形轨迹。
|
图 3 势点跟踪算法基本原理图 Fig. 3 Basic schematic diagram of potential point tracking algorithm |
根据轨迹半径、航行速度,计算势点数量,并将所得到的势点存入
| $\beta = \alpha {\text{π}} \cdot {\left( {floor\left( {2{\text{π}} R \cdot {{\left( {20v{d_{\rm{f}}}} \right)}^{ - 1}}} \right) + 100} \right)^{ - 1}}{\text{,}}$ | (14) |
| $ n = floor\left( {\frac{{2 \cdot {\text{π}} }}{\varsigma }} \right){\text{。}} $ | (15) |
式中:
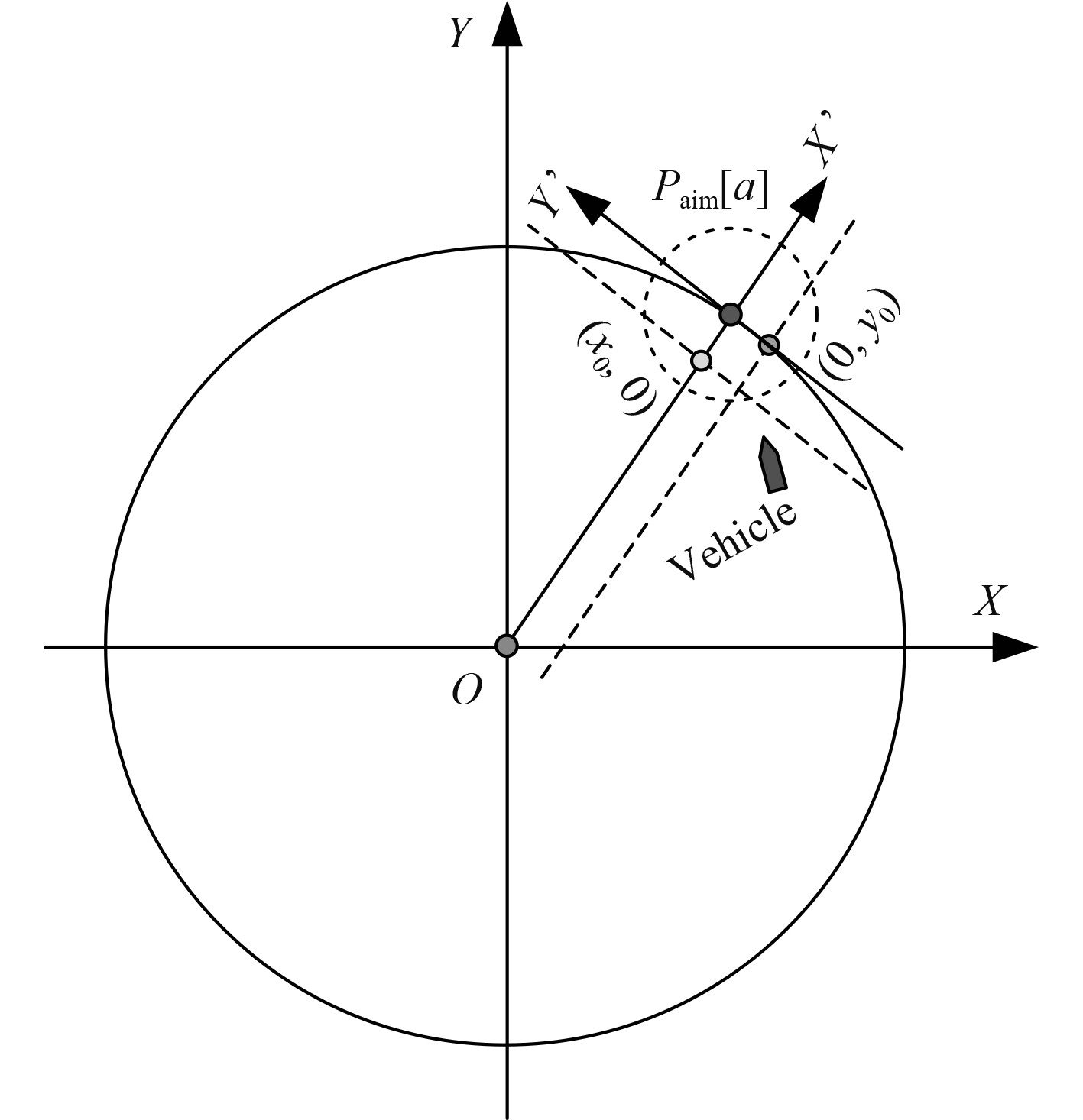
在大地坐标系下,根据当前跟踪势点
|
图 4 势点切换判据原理图 Fig. 4 Principle diagram of potential point switching criterion |
当满足如下切换条件,切换至下一势点继续跟踪。
| $\left( {{X_{n}} > {x_0}} \right) \cap \left( {{Y_{n}} > {y_0}} \right) \cup \left( {d > {d_{m}}} \right)\text{。} $ | (16) |
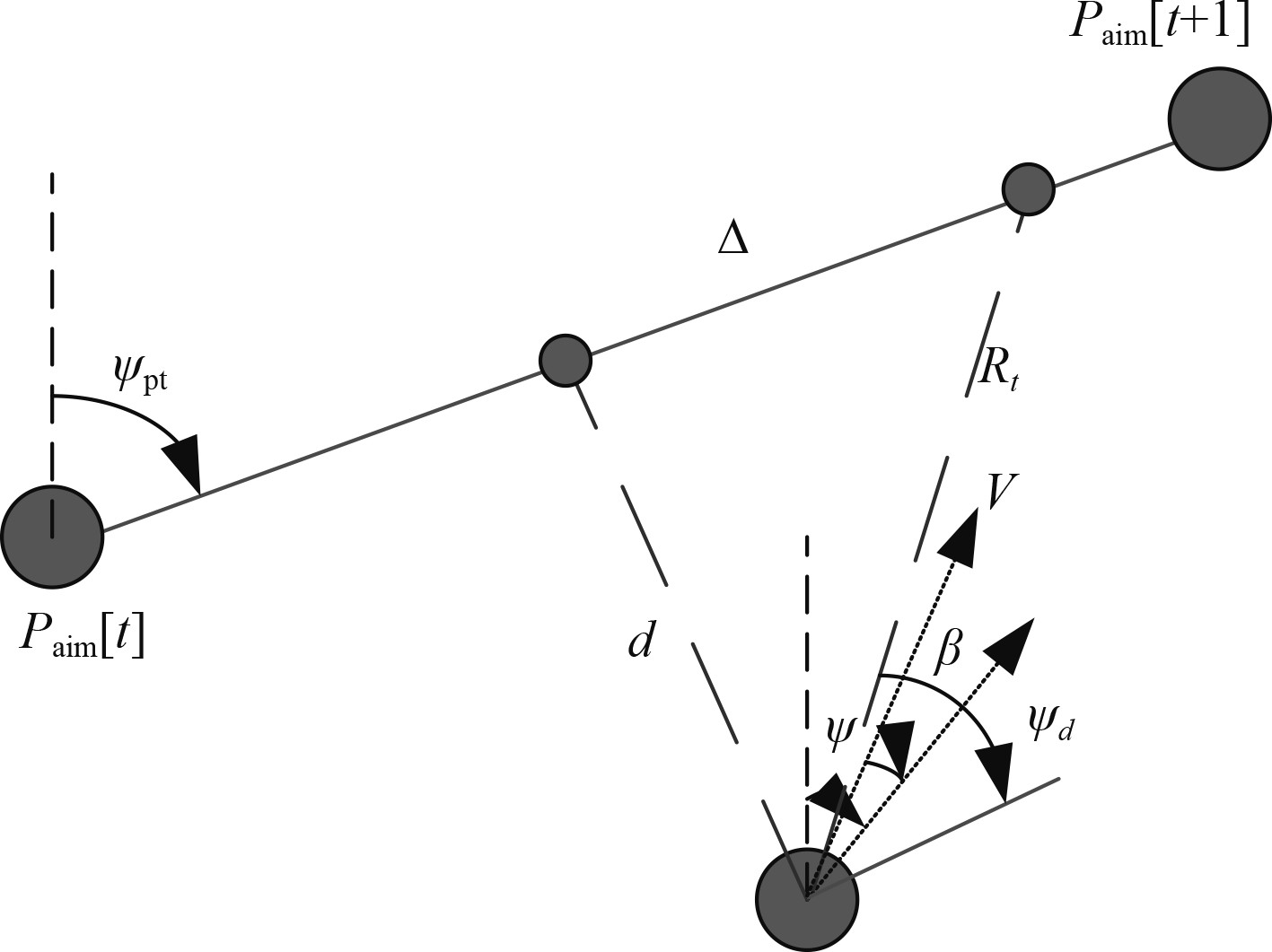
基于视线导引方法设计路径跟随制导系统,期望路径由一系列点
|
图 5 航向控制计算原理图 Fig. 5 Course control calculation schematic digram |
其中:
| $ {\psi _{{\rm{pt}}}} = a\tan 2\left( {{y_{{\rm{nt}} + 1}} - {y_{{\rm{nt}}}},{x_{{\rm{nt}} + 1}} - {x_{{\rm{nt}}}}} \right)\text{,} $ | (17) |
则可求横向距离
| $d = \left( {{y_{\rm{t}}} - {y_{{\rm{nt}}}}} \right)\cos \left( {{\psi _{{\rm{pt}}}}} \right) - \left( {{x_{\rm{t}}} - {x_{{\rm{nt}}}}} \right)\sin \left( {{\psi _{{\rm{pt}}}}} \right)\text{,}$ | (18) |
| $ \Delta = \sqrt {{R_{\rm{t}}}^2 - {d^2}} \text{,} $ | (19) |
| $ {\psi _{\rm{d}}} = \arctan \left( { - \frac{d}{\Delta }} \right){\text{。}} $ | (20) |
由此可得USV航向期望角度为:
| $ {\psi _{{\rm{ex}}}} = {\psi _{\rm{d}}} + {\psi _{{\rm{pt}}}} - \beta \text{,} $ | (21) |
当横向误差
| $ {R_{\rm{t}}} = \frac{\mu }{{\left| d \right| + 1}} + \zeta \left| d \right|,\left( {0 < \zeta < 1} \right){\text{。}} $ | (22) |
通过调节参正数
为减小因水流干扰产生的稳态误差,计算视线角时将横向误差进行积分,其方式为:
| $ {\psi _{\rm{d}}} = \arctan \left( { - \frac{1}{\Delta }(d + {k_{\rm{i}}}\int {d{\rm{dt}}} )} \right)\text{,} $ | (23) |
其中,
| ${\psi _{{\rm{ex}}}} = \arctan \left( { - \frac{1}{\Delta }(d + {k_{\rm{i}}}\int {d{\rm{dt}}} )} \right) + {\psi _{{\rm{pt}}}} - \beta \text{。}$ | (24) |
该无人艇制导律可通过航向调节快速有效的收敛到环形轨迹上,同时,消除外界干扰导致的稳态误差,增强系统的鲁棒性[20]。
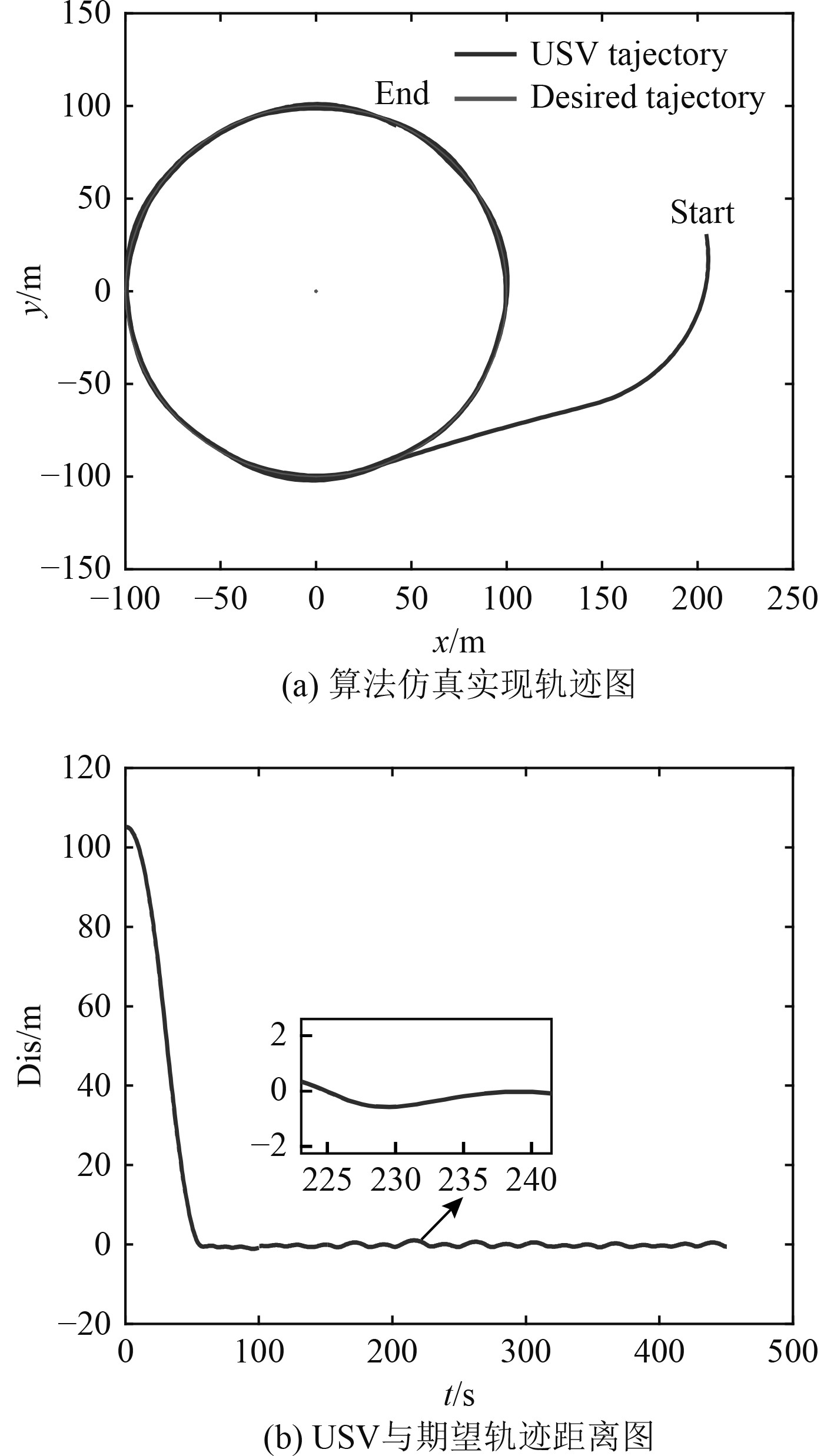
3 实验仿真及外场试验经由辨识方法得到的USV数学模型,搭建仿真平台,在此平台下进行多工况环形轨迹跟踪方法验证。设定环形轨迹半径100 m,USV速度9 m/s,进行环形轨迹跟踪。仿真结果如图6所示:
|
图 6 仿真平台下的环形轨迹跟踪 Fig. 6 Circular trajectory tracking in simulation platform |
由图6(b)中间距稳定状态可知,USV对环形轨迹的跟踪效果良好。经过计算,在该仿真状态下其实航轨迹RMS为0.8 m,具备良好的轨迹跟踪能力。
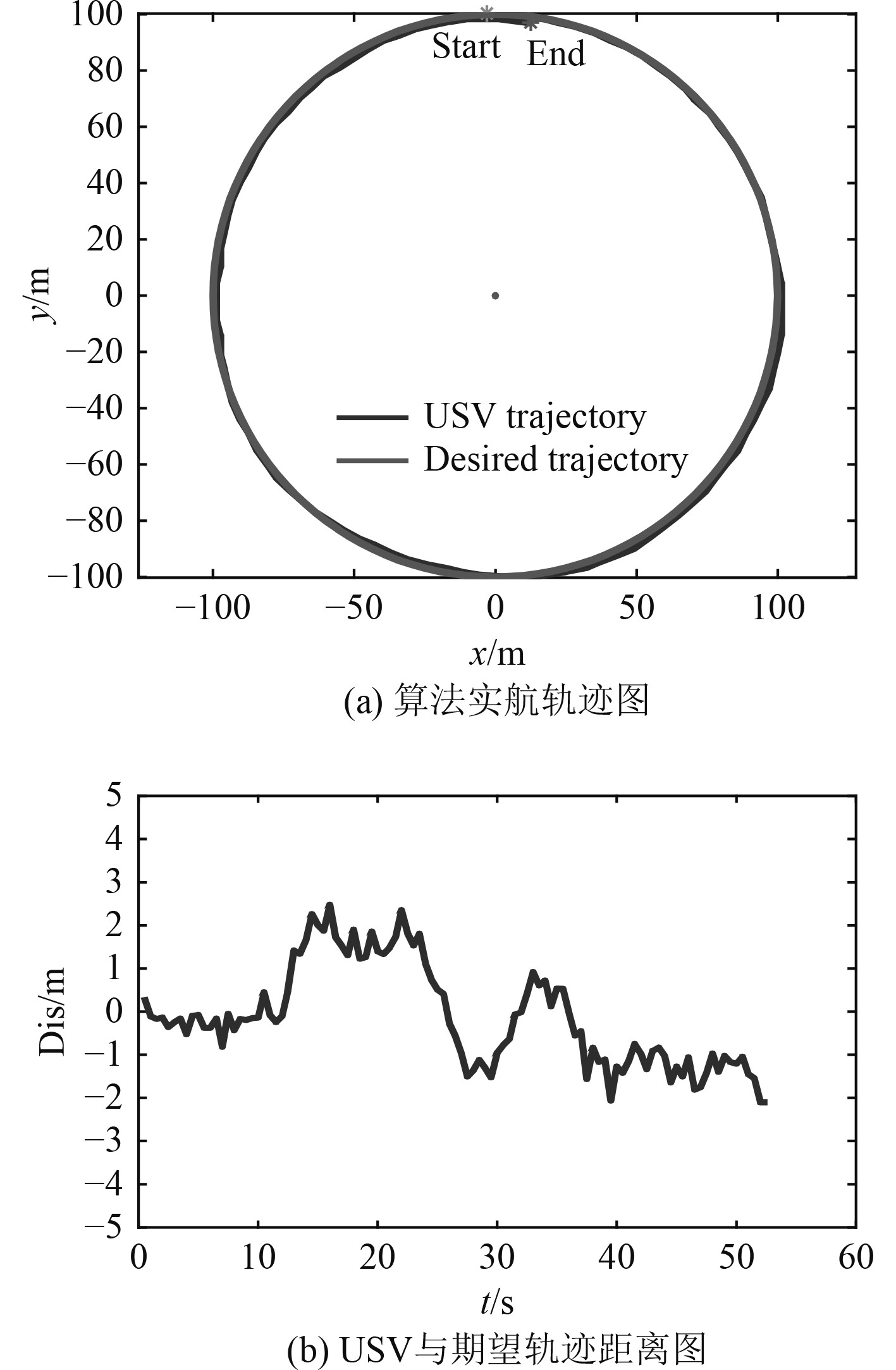
为提高算法的实用性,以“勇士”号USV为验证平台,进行典型海况下(3级海况)海上环形轨迹跟踪多条次试验。设定环形轨迹半径为100,航行速度为11 m/s,USV对所设定的环形轨迹进行跟踪,经对数据整合处理,其实航轨迹效果如图7所示。
|
图 7 海试中环形轨迹跟踪 Fig. 7 Circular trajectory tracking in sea trial |
在海上环境中,由于风浪流等环境干扰,将对环形轨迹跟踪方法的抗干扰能力进行检验。由图7(b)可知,USV按照所设计的势点跟踪算法及制导律进行运行,其能够按照预定航向、航迹航行,且通过对实航数据的计算得出实航轨迹RMS为1.2 m,表明环形轨迹跟踪方法具有较强的抗干扰能力,即在较强环境干扰、高速状态下亦可实现对环形轨迹的稳定跟踪。
4 结 语本文针对USV在实航中模型参数不确定、高速状态下对环形轨迹的准确跟踪能力方面研究薄弱问题,提出了基于势点跟踪算法的环形轨迹跟踪方法。算法以“勇士”号USV作为验证平台,经过模型参数辨识得到系统数学模型集,进而建立USV仿真平台,基于系统模型辨识构建跟踪策略以及制导律,对环形轨迹跟踪方法进行仿真验证,并在典型海况下多条次环形轨迹跟踪试验进行验证。实航数据中轨迹的RMS较小,可良好的在环境干扰、高速状态下实现对环形轨迹的精确跟踪,表明在USV平台下该方法对环形轨迹稳定跟踪的有效性、适用性以及鲁棒性。
| [1] |
张慧琳, 李醒飞, 杨少波, 等. 深海自持式智能浮标双闭环模糊PID定深控制[J]. 信息与控制, 2019, 48(2): 202-208. |
| [2] |
XU T, SUTTON R, SHARMA S. A multi-sensor data fustion navigation system for an unmanned surface vehicle[J]. Journal of Engineering for the Maritime Environment, 2007, 221(4): 167-182. |
| [3] |
黄琰, 李岩, 余建成, 等. AUV智能化现状与发展趋势[J]. 机器人, 2020, 42(2): 215-231. |
| [4] |
王常顺, 肖海荣. 基于自抗扰控制的水面无人艇路径跟踪控制器[J]. 山东大学学报, 2016, 46(4): 55-59. |
| [5] |
周焕银, 封锡盛, 胡志强, 等. 基于多辨识模型优化切换的USV航向动态反馈控制[J]. 机器人, 2013, 35(5): 553-557. |
| [6] |
谭西都. 搜救无人艇航速及航向控制[D]. 浙江: 浙江大学, 2019.
|
| [7] |
陈霄, 刘忠, 姜晓政. 无人艇非线性K-T模型参数辨识算法[J]. 电光与控制, 2018, 25(8): 29-31. |
| [8] |
王舜. 无人艇直线路径跟踪控制的研究与实现[D]. 大连: 大连海事大学, 2017.
|
| [9] |
FAN Y S, SUN Y T, WANG G F. On Model Parameter Identification and Trajectory Tracking Control for USV Based on Backstepping[C]//Proceedings of the 36th Chinese Control Conference. Dalian, China: Chinese Control Conference, 2017: 4757−4761.
|
| [10] |
DONG Z P, WAN L, LI Y M, et al. Trajectory tracking control of underactuated USV based on modified backstepping approach[J]. Ocean Engineering, 2015, 7: 817-832. |
| [11] |
廖煜雷. 无人艇的非线性运动控制方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2012.
|
| [12] |
张操. 无人水面船运动控制体系结构及航迹跟踪控制方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2013.
|
| [13] |
付悦文. 小型无人艇的无模型自适应跟踪方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2017.
|
| [14] |
WU G X, ZOU J, WAN L, et al. Design of the motion control system for water-jet-propelled unmanned surface vehicle[J]. Control Theory & Applications, 2010, 27(2): 257-262. |
| [15] |
田勇. 水面无人艇运动控制系统设计与实现[D]. 大连: 大连海事大学, 2016.
|
| [16] |
朱齐丹, 马俊达, 刘可. 基于扰动观测器的无人水面船鲁棒轨迹跟踪[J]. 电机与控制学报, 2016, 20(12): 66-73. ZHU Qi-dan, MA Jun-da, LIU Ke. A nonlinear disturbance observer based on robust approach to the trajectory tracking of an unmanned surface vehicle[J]. Electric Machines and Control, 2016, 20(12): 66-73. |
| [17] |
BRHAUGE, PAVLOV A, PANTELEY E, et al. Straight line path following for formations of underactuated marine surface vessels[J]. IEEE Transaction Control Systems Technology, 2011, 19(3): 493-506. DOI:10.1109/TCST.2010.2050889 |
| [18] |
陈霄, 刘忠, 张健强, 等. 基于改进积分视线导引策略的欠驱动无人水面艇路径跟踪[J]. 北京航空航天大学学报, 2018, 44(3): 489-499. CHEN Xiao, LIU Zhong, ZHANG Jian-qiang, et al. Path following of underactuated USV based on modified integral line-of-sight guidance strategies[J]. Journal of Naval University of Engineering, 2018, 44(3): 489-499. |
| [19] |
陈霄, 刘忠, 董蛟, 等. 欠驱动无人艇路径跟踪控制算法[J]. 海军工程大学学报, 2018, 30(3): 108-112. |
| [20] |
董早鹏, 万磊, 廖煜雷, 等. 基于非对称模型的欠驱动USV路径跟踪控制[J]. 中国造船, 2017, 57(1): 117-126. DONG Zao-peng, WAN Lei, LIAO Yu-lei, et al. Path following control of underactuated USV based on asymmetric model[J]. Shipbuilding of China, 2017, 57(1): 117-126. |
 2021, Vol. 43
2021, Vol. 43
