2017年5月,CCS制定了无人船检验指南的相关计划,并于2017年底发布了指南。该指南大力提倡降低无人船艇对远程操控人员的依赖,同时扩展多无人船艇协同配合,提高无人船艇自主决策和智能避障能力。随着对无人船任务的要求越来越高,其运行环境被推向了更加恶劣的层次,CCS的技术规范也对无人船的抗冲击问题极为重视。无人船体型较小,冲击损伤常常不是直接破坏船舶结构,但会引起船体的剧烈震动甚至推进轴系的断裂,也足以使船舶丧失航行能力。研究无人船推进轴系的抗冲击性能,是综合研究船舶可靠性及生命力的关键环节,更是发展无人船舶必不可少的技术准备[1-3]。
国内外很多文献均对推进轴系的抗冲击响应进行了大量介绍。文献[4]以傅里叶函数为工具,通过建立模型分析了轴系回转振动特性;文献[5]为了控制轴系振动响应频率,在前有的基础上提出了一种新的计算方法;文献[6]通过数值模拟,推导出电动机负载动力学方程,分析电机电磁激励力对轴系扭转振动的影响;文献[7]根据船舶在海洋上所面临的各种波浪荷载,建立了具有非线性油膜力作用的尾轴—油膜—尾部结构耦合系统动力学模型,分析了不同转速下尾轴的非线性动力学特征,总结了尾部结构参数对尾轴振动特性的影响。
当前国内对动力轴系冲击的相关研究主要集中在传统推进轴系上,因此,本文在模型简化的基础上,建立电机-负载动力学模型并分析冲击加速度激励对轴系的影响,提出了基于冲击响应的转速设计,有助于提升无人船可靠性设计中的工程适应性。
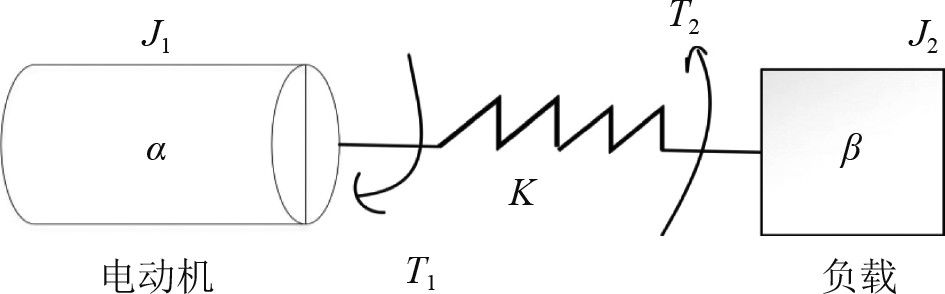
1 电机-负载耦合特性分析无人船多采用电力推进系统,其中电动机为电力推进的核心动力装置。根据电机动力学原理,建立电动机-负载动力学模型如图1所示。
|
图 1 电机-负载动力学模型 Fig. 1 Motor - load dynamics model |
由图1可知:
系统动能
| $ E_v = \frac{1}{2} J_1 {\dot \alpha ^2} + \frac{1}{2} J_2 {\dot \beta ^2}\text{,} $ | (1) |
系统势能
| $ E_u = \frac{1}{2}K{\left( {\alpha - \beta } \right)}2 \text{。} $ | (2) |
式中:
考虑到电磁能通过场对运动电荷做功转化为机械能,因此引入电机电磁能。电机气隙磁场能为:
| $\begin{split} W = &\dfrac{1}{2}x_s i_D^2 + \dfrac{1}{2}x_s i_Q^2 + \dfrac{1}{2}x_r i_d^2 + \dfrac{1}{2}x_r i_q^2 +\\ & x_m i_D i_d \cos (p\alpha ) - x_m i_D i_d \sin (p\alpha )+ \\ & x_m i_Q i_q \sin (p\alpha ) + x_m i_Q i_q \cos (p\alpha ) \text{。} \end{split} $ | (3) |
式中:
由拉格朗日函数定义,可知该系统的拉格朗日函数为:
| $L{\rm{ = }}\frac{1}{2} J_1 {\dot \alpha ^2} + \frac{1}{2} J_2 {\dot \beta ^2} - \frac{1}{2}K{(\alpha - \beta )}^2\text{,} $ | (4) |
由于该系统为力电混合系统,考虑到电机气隙磁场能,故上式拉格朗日函数进一步变为,
| $L{\rm{ = W + }}\frac{1}{2} J_1 {\dot \alpha ^2} + \frac{1}{2} J_2 {\dot \beta ^2} - \frac{1}{2}K{(\alpha - \beta )}^2\text{。} $ | (5) |
电阻上产生焦耳热,它是一种耗散性元件,所以,所构造的耗散函数中应与焦耳热有关,故该系统的耗散函数为:
| $D = \frac{1}{2}R_s i_D^2 + \frac{1}{2}R_s i_Q^2 + \frac{1}{2}R_r i_d^2 + \frac{1}{2}R_r i_q^2 + \frac{1}{2}C\mathop {(\dot \alpha - \dot\beta )}\nolimits^2 \text{。}$ | (6) |
式中:
将式(5)和式(6)代入拉格朗日耗散方程,对微分方程组进行化简得到电动机-负载机电耦合动力学方程。
| $\begin{split} \mathop {i_D }\limits^. =& \mathop g\nolimits_1 - \mathop g\nolimits_2 i_D + \mathop g\nolimits_3 i_d + \mathop g\nolimits_4 i_Q + \mathop g\nolimits_5 i_q-\\ & (1 - \omega - J_0 \mathop \varphi \nolimits_1 )(\mathop g\nolimits_5 i_q + \mathop g\nolimits_6 i_Q )\text{,} \\ \mathop {i_d }\limits^. = &- \mathop g\nolimits_7 + \mathop g\nolimits_8 i_D {\rm{ - }}\mathop g\nolimits_9 i_d - \mathop g\nolimits_2 i_Q - \mathop g\nolimits_6 i_q+\\ & (1 - \omega - J_0 \mathop \varphi \nolimits_1 )(\mathop g\nolimits_4 i_q + \mathop g\nolimits_2 i_Q )\text{,} \\ \mathop {i_q }\limits^. =& \mathop g\nolimits_8 i_Q - \mathop g\nolimits_9 i_q + \mathop g\nolimits_2 i_D + \mathop g\nolimits_6 i_d-\\ & (1 - \omega - J_0 \mathop \omega \nolimits_1 )(\mathop g\nolimits_1 \mathop I\nolimits_d + \mathop g\nolimits_2 i_D )\text{,} \\ \mathop {i_Q }\limits^. =& - \mathop g\nolimits_2 i_Q + \mathop g\nolimits_3 i_q - \mathop g\nolimits_4 i_D - \mathop g\nolimits_5 i_d+\\ & (1 - \omega - J_0 \mathop \varphi \nolimits_1 )(\mathop g\nolimits_5 i_d + \mathop g\nolimits_6 i_D ) \text{,}\\ \mathop \varphi \limits^. =& \mathop \varphi \nolimits_1\text{,} \\ \mathop {\mathop \varphi \nolimits_1 }\limits^. =& - \varphi - \mathop k\nolimits^2 \varphi + T/ J_1 \text{,}\\ \mathop \omega \limits^. =& (T - C\omega )/( J_1 + J_2 )\text{,} \\ T{\rm{ =}}&{{1.5}}px_m (i_D i_q {\rm{ - }}i_Q i_d ) \text{。} \end{split} $ | (7) |
式中:
利用Matlab对上述方程进行求解,不仅可以看到定转子电流变化情况,还可以得到电动机质量点的扭转振动时域曲线,如图2所示。

|
图 2 电机质量点的扭转振动幅值 Fig. 2 Amplitude of torsional vibration of motor mass point |
由图2可知,在电机启动过程中,初始时间内电动机质量点有着明显的振幅波动,说明电机电磁激励力矩对扭转振动有着较大的影响。随着时间变化,当电机达到某转速时,电磁激励力矩对扭转振动的影响较小。
2 电力推进轴系的冲击响应分析通常电力推进轴系受到的冲击可按国际标准近似为随简单的几何图形,如半正弦、三角波等。令半正弦加速度脉冲波的持续时间为
| $\ddot a = \mathop A\nolimits_m \sin \Bigg(\pi \frac{t}{{\mathop t\nolimits_m }}\Bigg),0 < t < \mathop t\nolimits_m \text{。}$ | (8) |
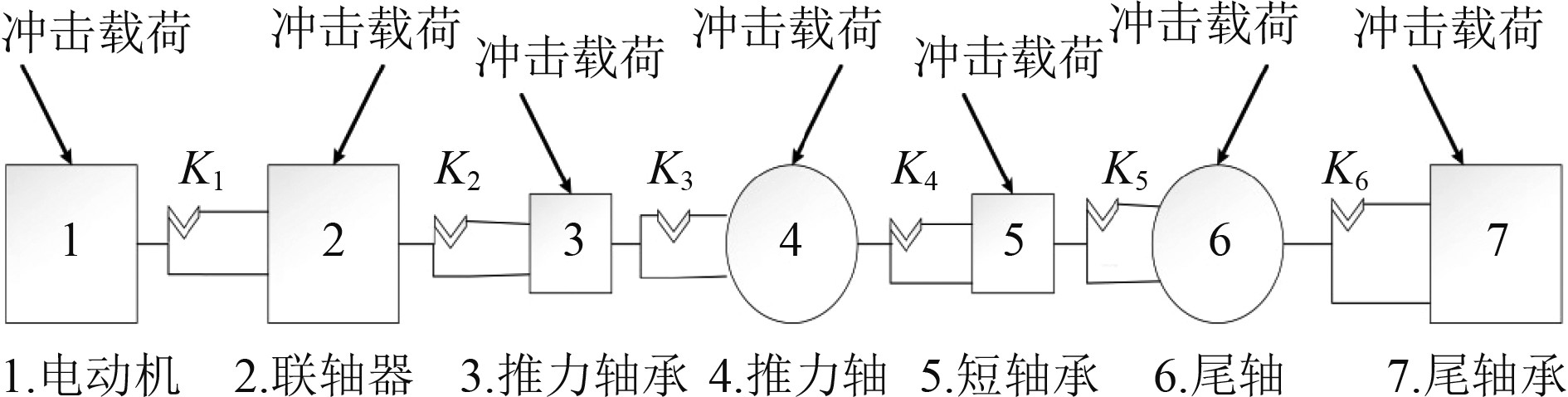
冲击加速度激励作用在推进轴系上,将会使轴系产生较大的振动位移。以某科考船电力推进轴系为研究对象,利用集总参数模型的方法将电动机、联轴器、轴系分别简化为集中质量的元件,相互之间用无质量的弹性轴节进行连接,耦合的系统模型如图3所示。
|
图 3 电力推进轴系结构耦合模型 Fig. 3 coupling model of electric propulsion shafting structure |
以半正弦冲击波作用在动力轴系上为例,列出该系统的微分振动方程:
| $\mathop M\nolimits_k \mathop {\ddot x}\nolimits_k + \mathop k\nolimits_{k - 1,k} (\mathop x\nolimits_k - \mathop x\nolimits_{k - 1} ) + \mathop k\nolimits_{k,k + 1} (\mathop x\nolimits_k - \mathop x\nolimits_{k + 1} ) = - \mathop M\nolimits_k \ddot a\text{。}$ | (9) |
式中:
设置系统的初始参数为:
|
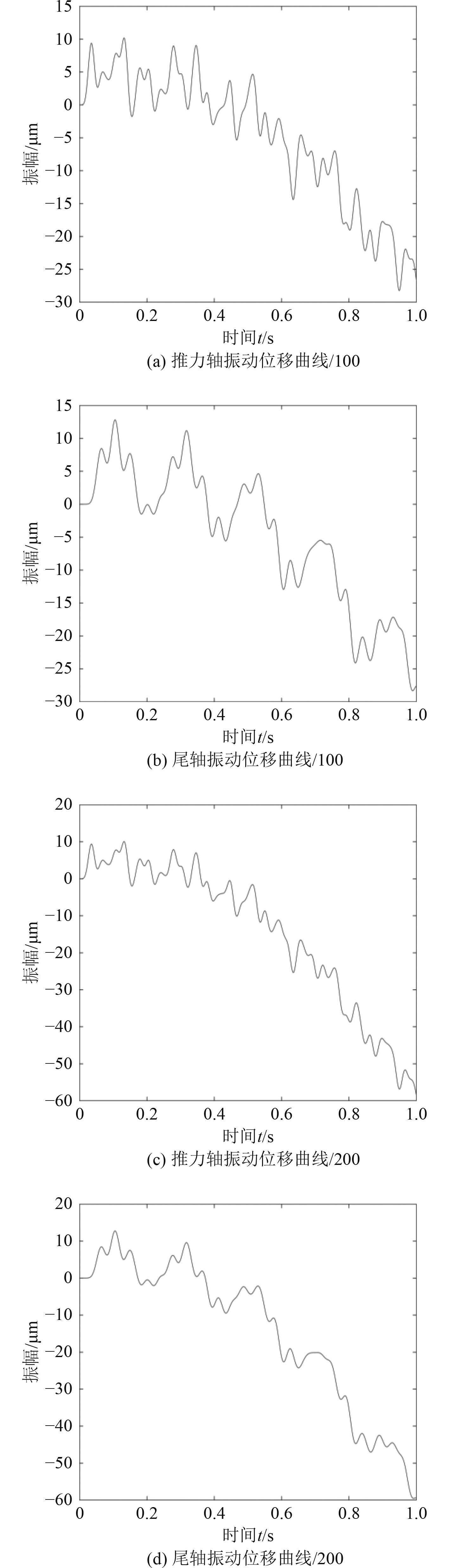
图 4 推力轴、尾轴振动位移曲线 Fig. 4 Vibration displacement curves of thrust shaft and stern shaft |
观察图4(a)和图4(b)可以发现,在冲击加速度激励下,推力轴与尾轴的振动位移迅速增加,初始时间内出现几个正向周期,随着冲击时间增加,周期性逐渐消失,出现了负向位移,且峰值远大于正向位移,说明冲击时间越长,振动位移越大。
图4(c)和图4(d)说明,在一定的冲击时间内,由于电力推进轴系模型为线性系统,冲击加速度激励的曲线峰值越大,推进轴系的振动位移峰值越大,二者之间呈线性关系。2种工况下的推力轴、尾轴曲线走势大致相同,区别在于随着冲击加速度最大值的增加,振动位移正向曲线的周期性越来越不明显,说明剧烈的冲击造成更加复杂的振动。
3 基于冲击响应分析的转速设计方法为了综合计算多工况下的轴系冲击振幅大小,为无人船在应用领域中运动控制、应急操纵以及减损降灾中选择转速提供参考依据,需要大量进行转速下的冲击响应计算。因此,继续选取多组轴系的转速,并按照冲击载荷分别为20 kg,30 kg,40 kg,50 kg,60 kg,70 kg,80 kg,90 kg设置了8种工况进行冲击载荷响应计算,计算结果的部分数据如表1所示。
|
|
表 1 不同转速、冲击载荷下的冲击振幅 Tab.1 Shock amplitude under different rotating speeds and impact loads |
由表1的计算结果可以看出,随着冲击载荷的增大,其激起的冲击幅值随之增加,但不同的轴系转速下振幅增速不同,转速越低,振幅增速越小。为了揭示在不同工况下,碰撞载荷与尾轴冲击振幅的变化趋势,可将表1的参数变化规律作进行曲线拟合。根据数据分布特点,用含有指数项的函数表示为:
| $y = c{e^{fx}},{\rm{ }}f > 0\text{。}$ | (10) |
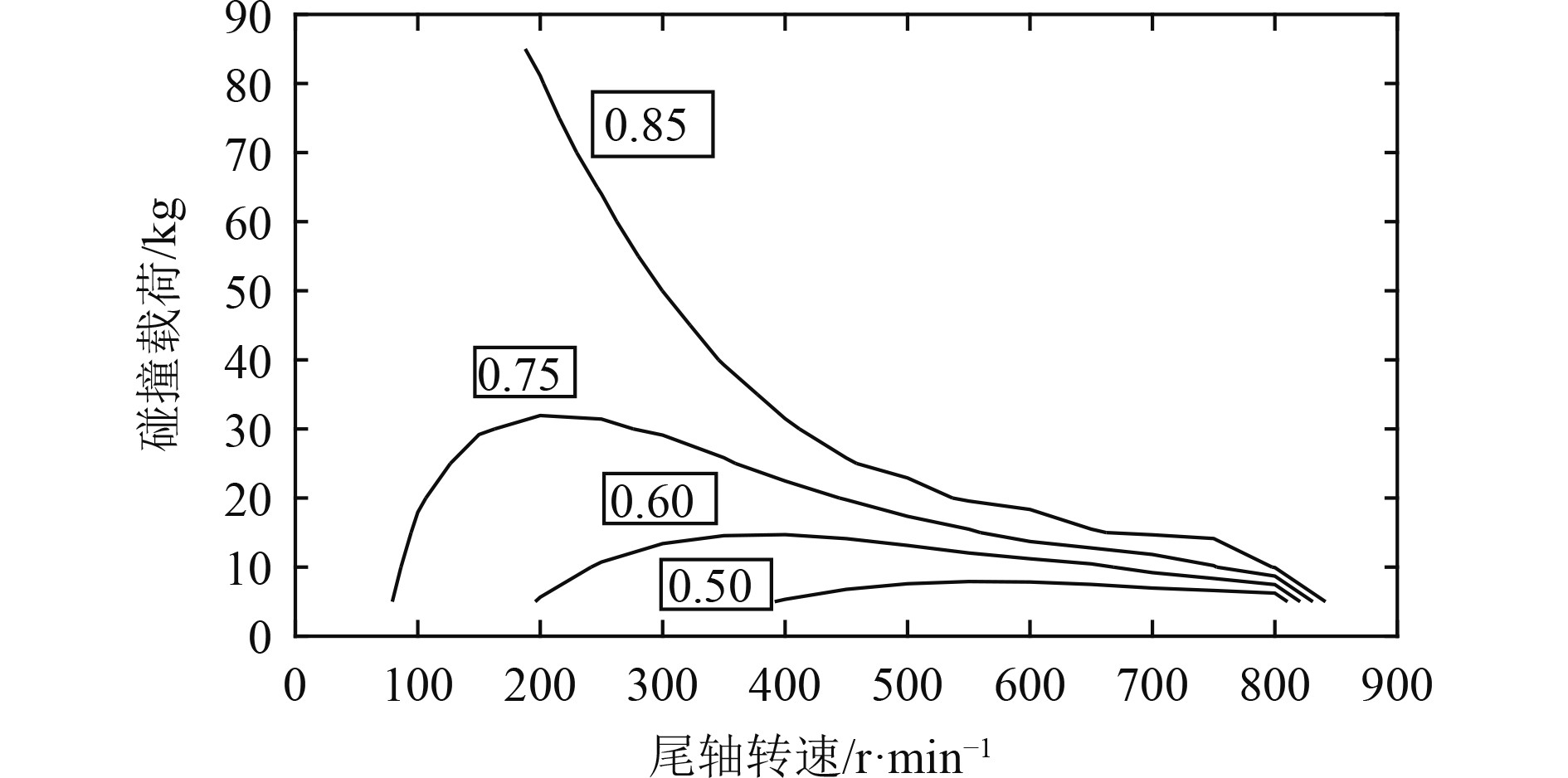
根据得到的拟合函数,按照轴系安全使用范围冲击振幅分别为0.85,0.75,0.60,0.50时,得到转速和碰撞载荷二者之间的相关曲线如图5所示。
|
图 5 以冲击振幅为指标的评价图谱 Fig. 5 Evaluation map with shock amplitude as index |
图5所呈现的曲线规律与常规船舶的抗冲击图谱完全相似[8],同时由于电机与负载动力学特性的影响,具有如下特征:
1)推进轴系发生冲击时,若冲击载荷一定,由于平均冲击力随转速增大而增加,轴系振动响应受转速影响很大;当冲击载荷较大时,转速越高则冲击响应越大,因此应该降低无人船的航速,航速在3.5~4 m/s时,无人船舶推进轴系受到冲击造成的损伤较小,同时保持轴系的转速在500~600 r/min之间,船舶推进轴系受到冲击造成的损伤最小。
2)当无人船的航速难以快速降低时,在6 m/s以上,应该降低轴系的转速在200~400 r/min之间,这样轴系的损伤最小;在船速超过10 m/s发生冲击时,已经使轴系冲击振幅严重超过许用值,可能发生轴系卡死或碰摩等现象,其对应关系如表2所示。
|
|
表 2 轴系受损情况和船速及轴速对应关系 Tab.2 Relationship between damage of shafting and ship speed and axle speed |
由于无人船常常工作在恶劣的环境中,会受到外部撞击载荷作用,冲击力会引起船体的剧烈振动甚至导致推进轴系的卡死,从而影响无人船的生命力。因此,本文针对无人船推进系统的特点,选取电机-负载动力学模型进行分析,研究冲击加速度激励对轴系产生的影响,最后利用Matlab软件计算了不同碰撞载荷与轴系转速下的轴系冲击振幅,数值模拟得到的结论如下:
1)电动机启动过程中电磁激励力在轴系上产生不可忽略的影响,基于电机-负载动力学的简化模型较好地描述了轴系的抗冲击特性。
2)对于一个线性的系统模型,在冲击时间一定的情况下,冲击加速度最大值越大,推进轴系的振动位移峰值越大。冲击加速度一定的情况下,冲击时间越长,振动位移越大。
3)无人船发生冲击时,冲击载荷的大小以及转速的高低对轴系的影响各不相同,为了减少对轴系的损伤,应该制定好船轴系安全转速图谱,作为无人船的应急操纵方案。
| [1] |
杨翼, 王旭荣, 王明坤, 等. 船舶推进轴系的扭转-纵向冲击响应[J]. 振动与冲击, 2017, 36(13): 96-102. |
| [2] |
纪昌禄, 蒋丰. 考虑转速的船舶推进轴系建模和冲击响应分析[J]. 船舶力学, 2013, 17(12): 1473-1480. DOI:10.3969/j.issn.1007-7294.2013.12.011 |
| [3] |
汪玉, 计晨, 杜俭业, 等. 舰船动力轴系冲击响应性能分析[J]. 振动与冲击, 2011, 30(5): 164-168. DOI:10.3969/j.issn.1000-3835.2011.05.034 |
| [4] |
卢志珍. 船舶推进轴系的回旋振动特性分析[J]. 舰船科学技术, 2020, 42(2): 91-93. |
| [5] |
李琦, 苏颖. 船用尾轴架轴系振动响应的频率控制方法[J]. 舰船科学技术, 2020, 42(10): 10-12. |
| [6] |
肖能齐, 周瑞平, 徐翔, 等. 冰载荷电力推进轴系扭转振动研究[J]. 船舶力学, 2018, 22(5): 603-614. DOI:10.3969/j.issn.1007-7294.2018.05.009 |
| [7] |
董良雄, 张涛, 温小飞, 等. 船舶尾部结构对尾轴振动特性影响研究[J]. 船舶工程, 2016, 38(10): 72-75. |
| [8] |
董良雄, 杨意, 高军凯, 等. 基于船舶尾轴-油膜-尾部结构系统的碰撞载荷响应研究[J]. 中国舰船研究, 2017, 12(1): 122-127. DOI:10.3969/j.issn.1673-3185.2017.01.018 |
 2021, Vol. 43
2021, Vol. 43
