0 引　言

近年来，船舶换热设备板状元件、大功率电子芯片以及微电子晶体管等技术发展迅猛，在高功率密度条件下，其内部冷却介质会形成汽−液两相流，汽−液两相流阻力特性影响换热性能。因此，竖直窄通道汽−液两相流多变性和复杂性流动机理越来越受到重视，对其阻力压降特性的研究已经成为汽−液两相流研究方面的一个重点。国内外很多学者对其进行了大量的实验研究^[1]，孙斌等^[2]以空气—水为介质，模拟气液两相流，运用小波包变换系数等方法，对水平管内两相流型和阻力特性进行了实验研究，根据实验结果绘制了流型图，并与传统的实验结果进行了比较。周云龙等^[3]运用高速图像采集等方法，对正方形小通道内向上流动汽−液两相流可视化进行了相关研究。峦峰等^[1]对摇摆条件下竖直管内汽−液两相流流型的的影响进行了分析。但是，大部分研究主要是在非摇摆条件下进行。因此，需要对摇摆条件下竖直窄矩形通道内汽−液两相流阻力压降特性进行研究，为船舶高功率换热设备实际运行条件提供研究依据。

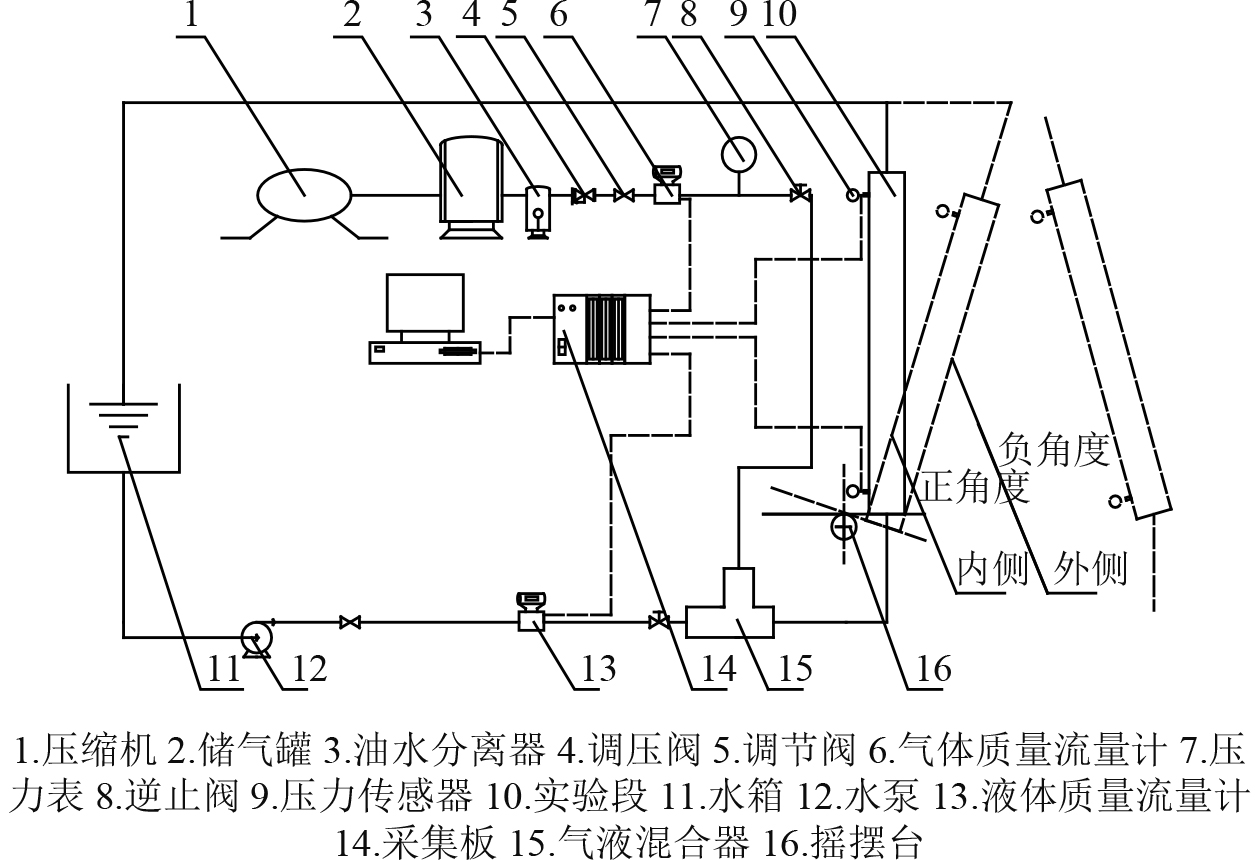
1 试验研究 1.1 试验装置

试验在常温常压下进行，试验流程图如图1所示。试验通过压缩空气代替水蒸汽，模拟汽液两相流。试验系统为强制循环回路，由信息采集/测量系统、气回路（代替水蒸汽）、水回路以及摇摆装置4部分组成。水从水箱中用水泵抽取后，通过质量流量计和气液混合器进入实验段；空气由压缩机压缩后储存在储气罐中，经过减压阀、气相质量流量计、气液混合器后，与水充分混合进入实验段。摇摆装置在液压动力的驱动下，围绕摇摆中心轴以定角度、变周期做摇摆运动，摇摆运动规律如下式：

$\theta {\rm{ = }}{\theta _m}\sin \left(\frac{{2{\text{π}} }}{T}t + 2k{\text{π}} \right)\text{，}$

(1)

$\omega = \frac{{\partial \theta }}{{\partial t}} = {\theta _m}\frac{{2{\text{π}} }}{T}\cos \left(\frac{{2{\text{π}} }}{T}t + 2k{\text{π}} \right)\text{，}$

(2)

$\begin{split} \beta =& \dfrac{{{\partial ^2}\theta }}{{\partial {t^2}}} = - {\theta _m}{\left(\dfrac{{2{\text{π}} }}{T}\right)^2}\sin \left( {\dfrac{{2{\text{π}} }}{T}t + 2k{\text{π}} } \right)\text{，} \\ k =& 0,1,2,3 \cdots \cdots \text{。} \end{split}$

(3)

式中： $\theta $ 为 $t$ 时刻的摇摆角度，rad； ${\theta _m}$ 为最大摇摆角度，rad； $\omega $ 为摇摆角速度，rad/s； $\ \beta $ 为摇摆角加速度，rad/s²； $T$ 为摇摆周期，s； $ {t}$ 为时间，s。

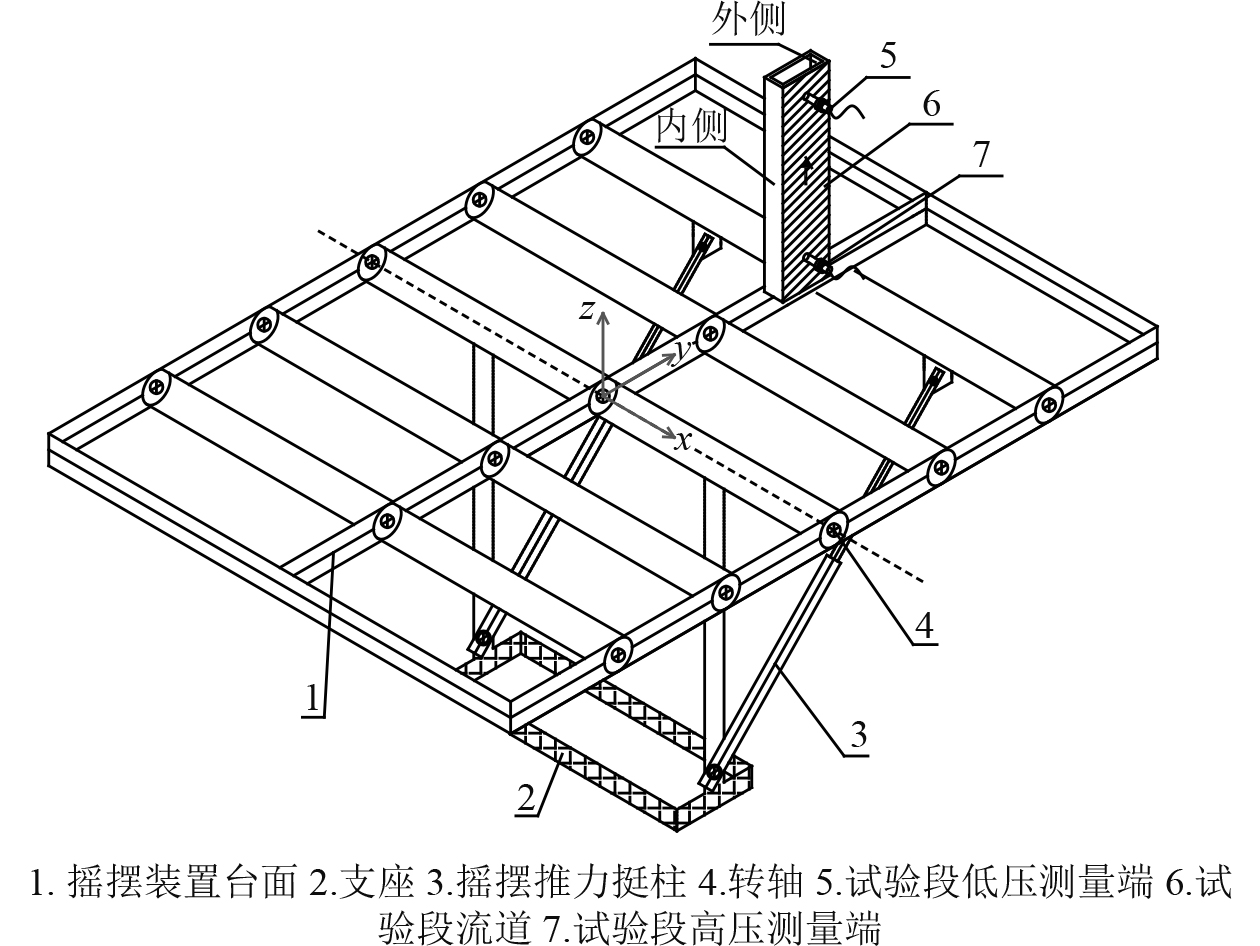
试验摇摆装置如图2所示，在其运动过程中，设置最大摇摆角度为10°，摇摆周期依次为8 s，12 s，16 s。

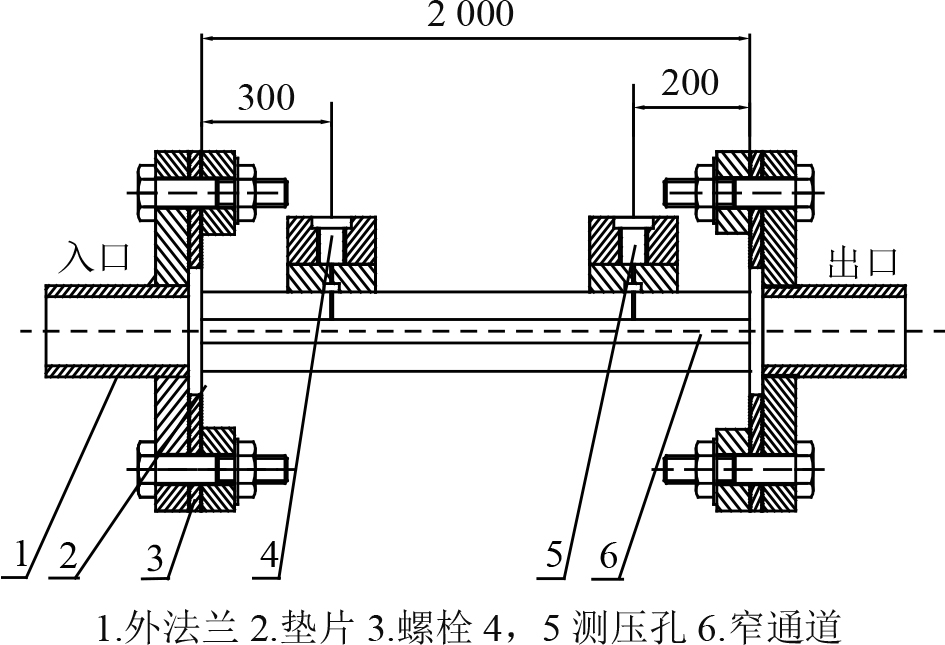
窄矩形通道试验段如图3所示，将其竖直安装于摇摆装置台面转轴一侧（见图2）。流体介质由下向上流动，在试验段的上部和下部分别设置压降采集点，采集压力信号。

1.2 试验结果

通过对窄矩形通道试验段压降数据进行分析，在摇摆角度为10°，摇摆周期从8 s，12 s，16 s阶段增加过程中，上下测压孔的压降信号逐渐减小，变化频率逐渐较小，周期性越来越明显，如图4所示。

2 理论分析 2.1 摇摆条件下总压降理论分析

本实验介质采用强制循环的条件下流动，模拟船舶设备实际运行装置，因此，理论分析过程中，假设通道内流体介质为均匀流体，流量不随时间产生周期波动。摇摆条件下，竖直窄矩形通道内汽−液两相流两点之间的总压降如下式：

$\Delta p = \Delta {p_g} + \Delta {p_a} + \Delta {p_f} + \Delta {p_s}\text{。}$

(4)

式中， $ \Delta p$ 为总压降，kPa； $\Delta {p_g}$ 为重位压降，kPa； $\Delta {p_a}$ 为加速压降，kPa； $\Delta {p_f}$ 为摩擦压降，kPa； $\Delta {p_s}$ 为附加压降，kPa。

2.2 摇摆条件下窄矩形通道重位压降 $\Delta {P_g}$ 分析

经过对不同试验工况数据的分析和对比，试验段当量直径De<80 mm，质量流速G>200 kg/（m²·s）⁻¹，可以考虑采用均相流模型^[4]，但是当液相粘度大于0.01 N.s/m²时，不宜采用均相流模型^[5]。计算竖直窄矩形通道内重位压降，必须通过空泡份额进行模型计算。空泡份额分相流模型中，通常用到滑速比模型，变密度模型，漂移流模型，动量交换模型等，在窄矩形通道计算中，应用漂移流模型可以很好的计算其折算流速和空泡份额^[6]。Mishima K等^[7]在近些年对窄通道的研究中，同样应用漂移流模型来预测矩形通道内的折算流速和空泡份额。

1）气相折算流速 ${j_{\rm{g}}}$ 计算

气相折算流速 ${j_{\rm{g}}}$ 可根据储气罐内压力变化、温度变化、时间间隔及窄矩形通道流通面积进行计算，如下式：

$\begin{split} {j_{\rm{g}}}{\rm{ = }}\dfrac{{N''}}{A} = \dfrac{{\Delta V''}}{{{t_{1\sim 2}}A}} = &\dfrac{{\dfrac{{{P_1}V''}}{{{T_1} + 273.15}} \cdot \dfrac{{{T_0} + 273.15}}{{{P_0}}}}}{{{t_{1\sim 2}}\left( {ab} \right)}} -\\ & \dfrac{{\dfrac{{{P_2}V''}}{{{T_2} + 273.15}} \cdot \dfrac{{{T_0} + 273.15}}{{{P_0}}}}}{{{t_{1\sim 2}}\left( {ab} \right)}} \text{。}\end{split} $

(5)

其中： $N''$ 为气相体积流量， ${{\rm{m}}^3}/{\rm{s}}$ ； $A$ 为通道流通面积， ${{\rm{m}}^2}$ ； $a,b$ 为通道流通边长， ${\rm{m}}$ ； $\Delta V''$ 为气相流通容积差， ${{\rm{m}}^3}$ ； ${t_{1\sim 2}}$ 为储气罐 ${P_1}$ 压力降至 ${P_2}$ 压力所用时间， ${\rm{s}}$ ； ${P_0}$ 为环境压力，MPa，取0.101325 MPa； ${T_0}$ 为环境温度，℃； ${P_1}$ 为储气罐初始压力，MPa； ${T_1}$ 为 ${P_1}$ 压力下储气罐内气体温度，℃； ${P_2}$ 为储气罐终止压力，MPa； ${T_2}$ 为 ${P_2}$ 压力下储气罐内气体温度，℃。

2）气−液两相流折算流速 $j$ 计算

以漂移流模型为基础，窄矩形通道气液两相流折算流速 $j$ 如下式：

$\begin{split} j{\rm{ = }}\dfrac{{N'' + N'}}{A} = &\dfrac{{\dfrac{{\Delta V''}}{{{t_{1\sim 2}}}} + N'}}{A} = \dfrac{\dfrac{{{P_1}V''}}{{{T_1} + 273.15}} \cdot \dfrac{{{T_0} + 273.15}}{{{P_0}}} }{{{t_{1\sim 2}}}(ab)}-\\ & \dfrac{ \dfrac{{{P_2}V''}}{{{T_2} + 273.15}} \cdot \dfrac{{{T_0} + 273.15}}{{{P_0}}}} {{{t_{1\sim 2}}}(ab)} + N'\text{。}\\[-15pt]\end{split} $

(6)

其中： $N'$ 为气−液两相流液相体积流量， ${{\rm{m}}^3}/{\rm{s}}$ 。

3）分布修正参数 ${C_0}$ 计算

根据Jones O.C.和Zuber N^[6]研究成果，分布修正参数计算方法如下式：

${C_0} = 1.35 - 0.35{(\nu {\rm{'}}/\nu '{\rm{'}})^{0.5}}\text{。}$

(7)

其中： $\nu '$ 为 ${P_0}$ 条件下气−液两相流液相比容， ${{\rm{m}}^3}/{\rm{kg}}$ ； $\nu ''$ 为 ${P_0}$ 条件下气−液两相流气相比容， ${{\rm{m}}^3}/{\rm{kg}}$ 。

4）空泡份额 $\alpha $ 计算

Jones and Zuber（1979）^[6]通过对窄矩形通道内空泡份额研究得出关系式，如下式：

$\alpha = \dfrac{{{j_{\rm{g}}}}}{{{C_0}j + (0.23 + 0.13a/b)\sqrt {\left(\dfrac{1}{{\nu '}} - \dfrac{1}{{\nu ''}}\right)gb\nu '} }}\text{。}$

(8)

其中： $\alpha $ 为窄矩形通道空泡份额； $g$ 为重力加速度，取9.8 ${\rm{m}}/{{\rm{s}}^2}$ 。

5）重位压降 $\Delta {P_g}$ 计算

在试验过程中，外部温度和流体介质温度相差很小，而且流体在管道内快速通过，流体边界与外界热交换十分微小，可忽略不计，因此认为 $\alpha $ 沿通道长度不变^[5]，则重位压降如下式：

$\Delta {P_g} = \left(\frac{\alpha }{{\nu ''}} + \frac{{1 - \alpha }}{{\nu '}}\right)gl\cos \theta \text{。}$

(9)

其中： $l$ 为高、低压力测量端间距，m。

综合式(1)和式(9)，可知摇摆条件下的重位压降，如下式：

$\begin{split} \Delta {P_g} = &\left( {\dfrac{\alpha }{{\nu ''}} + \dfrac{{1 - \alpha }}{{\nu '}}} \right)gl\cos \left[{\theta _m}\sin \left(\dfrac{{2{\text{π}} }}{T}t+ 2k\pi \right)\right]\text{。}\\ &k = 1,2,3 \cdots \cdots \text{。} \end{split}$

(10)

由式(3)、式(6)～式(8)、式(10)可知，气、液流量、最大摇摆角度 ${\theta _m}$ 保持不变的情况下，摇摆周期的改变只会影响重位压降变化的频率，不会引起重位压降幅值的改变。

2.3 摇摆条件下窄矩形通道加速压降 $\Delta {p_a}$ 分析

竖直窄矩形通道内加速压降主要由于通道壁面换热产生，本试验中，外部温度和流体介质温度相差很小，而且流体在管道内快速通过，流体边界与外界热交换十分微小，可忽略不计，因此， $\Delta {p_a}{\rm{ = }}0$ kPa。

2.4 摇摆条件下窄矩形通道摩擦压降 $\Delta {P_f}$ 分析

1）液相质量流量计算

$M' = \frac{{N'}}{{3\;600\nu '}}\text{。}$

(11)

其中： $M'$ 为气−液两相流液相质量流量， ${\rm{kg}}/{\rm{s}}$ 。

2）气−液两相流气相质量流量计算

$\begin{split} M'' = &\dfrac{{V''\left( {\dfrac{1}{{\nu _1^{''}}} - \dfrac{1}{{\nu _2^{''}}}} \right)}}{{{t_{1\sim 2}}}} \text{，} \dfrac{1}{{\nu _1^{''}}} = 1.293 \times \dfrac{{{P_1} + {P_0}}}{{{P_0}}} \times \dfrac{{273.15}}{{{T_1} + 273.15}} \text{，}\\ \\ \dfrac{1}{{\nu _2^{''}}} = &1.293 \times \dfrac{{{P_2} + {P_0}}}{{{P_0}}} \times \dfrac{{273.15}}{{{T_2} + 273.15}}\text{。} \\[-15pt]\end{split} $

(12)

其中： $M''$ 为气−液两相流气相质量流量， ${\rm{kg}}/{\rm{s}}$ ； $V''$ 为实验气相储存容积， ${{\rm{m}}^3}$ ； $\nu _1^{''}$ 为 ${P_1}$ 压力下气相比容， ${{\rm{m}}^3}/{\rm{kg}}$ ； $\nu _2^{''}$ 为 ${P_2}$ 压力下气相比容， ${{\rm{m}}^3}/{\rm{kg}}$ 。

3）气−液两相流质量流速计算

$\begin{split} G = &\dfrac{{M' + M''}}{A} = \dfrac{{M' + M''}}{{ab}} =\\ &\dfrac{{ \dfrac{{N'}}{{3600\nu '}} + \dfrac{{353.183 \times V''}}{{{t_{1\sim 2}} \cdot {P_0}}}\left( {\dfrac{{{P_1} - {P_2}}}{{{T_{12}} + 273.15}}} \right)}}{{ab}} \text{。}\end{split} $

(13)

其中： $G$ 为气−液两相流质量流速， ${\rm{kg}}/({{\rm{m}}^2}\cdot{\rm{s}})^{-1}$ 。

4）气−液两相流质量含气率计算

$x{\rm{ = }}\frac{{M''}}{{M' + M''}}\text{。}$

(14)

其中： $x$ 为气−液两相流质量含气率。

将式(11)和式(12)代入式(14)，气−液两相流质量含气率如下式：

$x{\rm{ = }}\dfrac{{\dfrac{{353.183 \times V''}}{{{t_{1\sim 2}} \cdot {P_0}}}\left( {\dfrac{{{P_1} - {P_2}}}{{{T_{12}} + 273.15}}} \right)}}{{\dfrac{{N'}}{{3\;600\nu '}} + \dfrac{{353.183 \times V''}}{{{t_{1\sim 2}} \cdot {P_0}}}\left( {\dfrac{{{P_1} - {P_2}}}{{{T_{12}} + 273.15}}} \right)}}\text{。}$

(15)

5）分液相流摩阻压降梯度计算

${\left( {\frac{{{{ d}_{pf}}}}{{{{d}_Z}}}} \right)_l}{\rm{ = }}\frac{{{\lambda _l}}}{D} \times \frac{{{G^2}{{(1 - x)}^2}\nu '}}{2}\text{。}$

(16)

其中： ${\left( {\dfrac{{{{d}_{pf}}}}{{{{d}_Z}}}} \right)_l}$ 为分液相流摩阻压降梯度； $D$ 为通道当量直径， $m$ ； ${\lambda _l}$ 为液两相分液相流摩阻系数； ${\lambda _l} $ 为液两相分液相流摩阻系数。

6）气−液两相流分布修正参数计算

$X{\rm{ = }}{\left[ {{{\left( {\frac{{1 - x}}{x}} \right)}^2} \times \frac{{\nu '}}{{\nu ''}}} \right]^{\frac{1}{2}}}\text{。}$

(17)

其中： $X$ 为分布修正参数。

7）气−液两相流分液相流折算系数计算

$\varPhi _l^2 = 1 + \frac{c}{X} + \frac{1}{{{X^2}}}\text{。}$

(18)

其中： $\varPhi _l^2$ 为气−液两相流分液相流折算系数； $c$ 为Chisholm推荐系数^[5]。

8）气−液两相流摩擦压降梯度计算

分相流模型具有广泛的适用性^[5]，在对于窄矩形通道内是气−液两相流研究中，大多数学者采用此模型进行分析研究。但是采用分相流模型，必须对管道内气−液两相流进行如下假设：

假设1　气−液两相之间无相互作用，气相压降和液相压降相等，且沿管子径向不存在静压降；

假设2　液相所占管道体积与气相所占管道体积之和等于管道总体积^[5]；

假设3　汽液两相流在该通道内流通的摩阻系数等于分液相流在通道内流通的摩阻系数等于分气相流流在通道内流通的摩阻系数^[5]。

即

$\begin{split} \dfrac{{{d_{pf}}}}{{{d_Z}}} =& \dfrac{{{d_{pfl}}}}{{{d_Z}}} = \dfrac{{{d_{pfg}}}}{{{d_Z}}} \text{，}\\ \lambda = &{\lambda _l} = {\lambda _g} \text{。}\end{split} $

(19)

其中： $\dfrac{{{d_{pf}}}}{{{d_Z}}}$ 为气−液两相流压降梯度； $\dfrac{{{d_{pfl}}}}{{{d_Z}}}$ 为气−液两相流液相部分压降梯度； $\dfrac{{{d_{pfg}}}}{{{d_Z}}}$ 为气−液两相流气相部分压降梯度； $\lambda $ 为气−液两相流摩阻系数； ${\lambda _l}$ 为气−液两相分液相流摩阻系数； ${\lambda _{\rm{g}}}$ 为气−液两相分气相流流摩阻系数。

根据奇斯霍姆（Chisholm）模型^[5]，气−液两相流摩擦压降梯度如下式：

$\dfrac{{{d_{pf}}}}{{{d_Z}}}{\rm{ = }}\Phi _l^2{\left( {\dfrac{{{d_{pf}}}}{{{d_Z}}}} \right)_l}\text{。}$

(20)

将式(16)和式(18)代入式(20)，气−液两相流摩擦压降梯度如下式：

$ \dfrac{{{d_{pf}}}}{{{d_Z}}}{\rm{ = }}\Phi _l^2{\left( {\dfrac{{{d_{pf}}}}{{{d_Z}}}} \right)_l} {\rm{ = }}\left( {1 + \dfrac{c}{X} + \dfrac{1}{{{X^2}}}} \right)\left( {\dfrac{{{\lambda _l}}}{D}\dfrac{{{G^2}{{(1 - x)}^2}\nu '}}{2}} \right) \text{。} $

(21)

8）摩擦阻力压降计算

$\Delta {P_f} = l\frac{{{d_{pf}}}}{{{d_Z}}}\text{。}$

由摩擦阻力压降计算公式，将摩擦压降梯度式(21)代入，如下式：

$\Delta {P_f} = l\left( {1 + \frac{c}{X} + \frac{1}{{{X^2}}}} \right)\left( {\frac{{{\lambda _l}}}{D}\frac{{{G^2}{{(1 - x)}^2}\nu '}}{2}} \right)\text{。}$

(22)

通过以上分析可知，摇摆条件下，竖直窄矩形通道内气−液两相摩阻压降不受摆影响。

2.5 摇摆条件下窄矩形通道附加压降分析

对于摇摆条件下竖直窄矩形通道内介质惯性附加压降，受力分析如图5所示。

1）法向加速度 ${{\mathop a\limits^ \rightharpoonup} _n}$ 计算

$\begin{split} {{\mathop a\limits^ \rightharpoonup}_n} =\,& {\mathop \omega\limits^ \rightharpoonup} \times \left( {{\mathop \omega\limits^ \rightharpoonup} \times \overrightarrow {r'} } \right) = \omega \overrightarrow i \times \left[\omega \overrightarrow i \times (x\overrightarrow i + y\overrightarrow j + z\overrightarrow k )\right]=\\ &- {\omega ^2}y\overrightarrow j - {\omega ^2}z\overrightarrow k = - {\omega ^2}\left(y\overrightarrow j + z\overrightarrow k \right) \text{。}\end{split}$

(23)

其中： ${{\mathop a\limits^ \rightharpoonup} _n}$ 为摇摆条件下法向加速度；

2）切向加速度 ${\overrightarrow a _t}$ 计算

$\begin{split} {\overrightarrow a _t} \!=\! {\mathop \beta\limits^ \rightharpoonup} \!\times\! \overrightarrow {r'} \!=\! \beta \overrightarrow i \!\times\! \left(x\overrightarrow i \!+\! y\overrightarrow j \!+\! z\overrightarrow k \right) \!=\! \beta \left( - \!z\overrightarrow j \!+\! y\overrightarrow k \right) \text{。}\end{split} $

(24)

其中： ${\overrightarrow a _t}$ 为摇摆条件下切向加速度。

3）科氏加速度 ${\overrightarrow a _{{}_k}}$ 计算

${\overrightarrow a _{{}_k}} = 2{\mathop \omega\limits^ \rightharpoonup} \times \overrightarrow v '\text{。}$

(25)

${\overrightarrow a _{{}_k}}$ 为摇摆条件下科氏加速度。

4）摆状态下附加惯性力 $d\overrightarrow F $ 计算

$\begin{split} d\overrightarrow F =& - \left(\dfrac{\alpha }{{\nu ''}} + \dfrac{{1 - \alpha }}{{\nu '}}\right)Adl\;\overrightarrow a =\\ & - \left(\dfrac{\alpha }{{\nu ''}} + \dfrac{{1 - \alpha }}{{\nu '}}\right)Adl\left(\overrightarrow {{a_n}} + \overrightarrow {{a_t}} + \overrightarrow {{a_k}} \right)\text{。} \end{split} $

(26)

其中： $d\overrightarrow F $ 为附加惯性力。

5）摆状态下附加压降 $\Delta {p_{s12}}$ 计算

$\begin{split}& \Delta {p_{s12}} =\\ & \dfrac{{\rm{1}}}{{\rm{A}}}\displaystyle \int_1^2 {\dfrac{{{\rm d}\overrightarrow {F} \cdot {\rm d}\overrightarrow {l} }}{{{\rm d}l}}} {\rm{ = }} - \left(\dfrac{\alpha }{{\nu ''}} + \dfrac{{1 - \alpha }}{{\nu '}}\right)\displaystyle\int_1^2 {\left(\overrightarrow {{a_n}} + \overrightarrow {{a_t}} + \overrightarrow {{a_k}} \right)} \cdot {\rm d}\overrightarrow {l} = \\ &- \left(\dfrac{\alpha }{{\nu ''}} + \dfrac{{1 - \alpha }}{{\nu '}}\right)\displaystyle\int_1^2 {\left(\overrightarrow \omega \times \left(\overrightarrow \omega \times \overrightarrow {r'} \right)+ \overrightarrow \beta \times \overrightarrow {r'} + 2\overrightarrow \omega \times \overrightarrow v ' \right)} \cdot {\rm d}\overrightarrow {l} =\\ & - \left(\dfrac{\alpha }{{\nu ''}} + \dfrac{{1 - \alpha }}{{\nu '}}\right)\displaystyle\int_1^2 \left\{ \omega \overrightarrow i \times \left[ {\omega \overrightarrow i \times \left(x\overrightarrow i + y\overrightarrow j + z\overrightarrow k \right)} \right] +\right.\\ & \left.\left[ {\beta \overrightarrow i \!\times\! \left(x\overrightarrow i \!+\! y\overrightarrow j \!+\! z\overrightarrow k \right)} \right] \!+\! 2\omega \overrightarrow i \!\times\! {v^{'}}\overrightarrow k \right\} \!\cdot\! \left( {{\rm d}x\overrightarrow i \!+\! {\rm d}y\overrightarrow j \!+\! {\rm d}z\overrightarrow k } \right)= \\ & - \left(\dfrac{\alpha }{{\nu ''}} + \dfrac{{1 - \alpha }}{{\nu '}}\right)\displaystyle\int_1^2 {\left[ { - {\omega ^2}\left(y\overrightarrow j + z\overrightarrow k \right) + \beta \left(y\overrightarrow k - z\overrightarrow j \right)} \right]} \times\\ & \left( {{\rm d}x\overrightarrow i + {\rm d}y\overrightarrow j + {\rm d}z\overrightarrow k } \right) = \left(\dfrac{\alpha }{{\nu ''}} + \dfrac{{1 - \alpha }}{{\nu '}}\right)\left[ \displaystyle\int_1^2 {{\omega ^2}\left( {y{\rm d}y + z{\rm d}z} \right)} - \right.\\ &\left.\displaystyle\int_1^2 {\beta \left( {ydz - zdy} \right)} \right] = \dfrac{{{\omega ^2}\left(\dfrac{\alpha }{{\nu ''}} + \dfrac{{1 - \alpha }}{{\nu '}}\right)}}{2}\left[ \left( {y_2^2 - y_1^2} \right) + \right.\\ & \left.\left( {z_2^2 - z_1^2} \right) \right] -{\rho _m}\displaystyle\int_1^2 {\beta \left( {ydz - zdy} \right)}\text{。}\\[-10pt] \end{split} $

(27)

由于 ${y_2} - {y_1}$ 在摇摆过程中变化很小接近于0，即

$ {\left( {{y_2} - {y_1}} \right)_{{\rm{max}}}}{\rm{ = }}L{\rm{r}}(1 - \cos {\theta _m}) = 4.635 \times {10^{ - 6}}L{\rm{r}} \approx {\rm{0}}\text{，} $

(28)

因此：

$\Delta {p_{s12}} = \dfrac{{\left(\dfrac{\alpha }{{\nu ''}} + \dfrac{{1 - \alpha }}{{\nu '}}\right){\omega ^2}}}{2}\left( {z_2^2 - z_1^2} \right) - \rho \beta y\left( {{z_2} - {z_1}} \right)\text{，}$

(29)

综合式(2)、式(3)和式(29)得出摇摆条件下附加压降如下式：

$\begin{split} \Delta {p_{s12}} =& \dfrac{{\left(\dfrac{\alpha }{{\nu ''}} + \dfrac{{1 - \alpha }}{{\nu '}}\right){{\left[{\theta _m}\dfrac{{2{\text{π}} }}{T}\cos \left(\dfrac{{2{\text{π}} }}{T}t + 2k{\text{π}} \right)\right]}^2}}}{2}\left( {z_2^2 - z_1^2} \right) +\\ &\left(\dfrac{\alpha }{{\nu ''}} + \dfrac{{1 - \alpha }}{{\nu '}}\right)y\left[{\theta _m}{\left(\dfrac{{2{\text{π}} }}{T}\right)^2}\sin \left(\dfrac{{2{\text{π}} }}{T}t + 2k{\text{π}} \right)\right]\left( {{z_2} - {z_1}} \right) \text{。}\end{split} $

(30)

对于式(28)，右侧第1项即法向惯性力引起的附加压降；右侧第2项即切向惯性力引起的附加压降，气、液流量、最大摇摆角度 ${\theta _m}$ 保持不变的情况下，摇摆周期的改变会影响附加压降变化的频率和最大幅值，摇摆周期增加，附加惯性压降最大幅值减小，频率减小。

3　结　语

1）通过试验数据表明，随着摇摆周期的增加，试验段的总压降幅值逐渐减小，变化频率逐渐较小，周期性越来越明显；

2）通过理论分析，试验结论是由于竖直窄矩形通道内部汽−液两相流重位压降和附加压降贡献。介质流量、最大摇摆角度 ${\theta _m}$ 等参数保持不变的情况下，摇摆周期的增加，摩擦压降频率和幅值不变；重位压降变化频率减小，幅值不变；附加压降变化频率减小，幅值减小。以上因素造成总压降幅值逐渐减小，变化频率逐渐较小，周期性越来越明显。