2. 英国格拉斯哥斯凯莱德大学,英国;
3. 招商局海洋装备研究院,广东 深圳 518000;
4. 南方海洋科学与工程广东省实验室(珠海),广东 珠海 519000;
5. 哈尔滨工程大学 船舶工程学院,黑龙江 哈尔滨 150001
2. Ocean and Marine Engineering, University of Strathclyde, Glasgow, UK;
3. China Merchants Marine and Offshore Research Institute, Shenzhen 518000, China;
4. Southern Marine Science and Engineering Guangdong Laboratory (Zhuhai), Zhuhai 519000, China;
5. College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China
随着船舶减振降噪技术的发展,现代船舶设计对舱室噪声控制提出了更高的要求,通过敷设舾装声学材料,是有效改进船舶舱室噪声水平的措施之一[1-2]。通常,在船舶实际舾装中,声学材料表面将设置铺层以达到防潮、阻燃、美观等目的。然而表面铺层的存在将改表原本声学材料的吸隔声性能,进而影响舱室空气噪声预报的准确性。因此,开展声学材料表面铺层对船舶舱室噪声影响研究,对准确评估实际船舶舱室噪声水平并指导开展船舶舱室噪声控制具有重要意义。
窦玲玲等[3]针对直升机舱室低频噪声控制问题,研究了局域振子质量、层间结构对舱室壁板双层结构隔声性能的调控规律。汪婕等[4]将薄层材料看作3层复合材料的中间层,应用传递矩阵法推导了薄层材料的声学特性。Felhi等[5]通过数值模拟方法,分析了粘弹性和多孔材料对多层系统传声的影响。Yablonik[6]改进了Biot计算模型,利用提出一种计算多层多孔纤维材料隔声的简化方法。韩峰等[7]利用阻抗管小样试验结果,基于声学有限元法对应用多孔纤维材料的壁板结构进行隔声性能影响分析。李维鑫等[8]利用驻波管测得吸声材料刚性背衬及空腔下声阻抗率,计算得到材料的复波数与复特性阻抗。冯博等[9]应用统计能量分析方法对不同类型船舶舱室进行了噪声预报,并针对不满足舱室噪声限值的舱室给出了降噪措施建议。
现有文献大多聚焦于单一声学材料或多层声学材料声学特性分析,忽视了在工程应用中,实际舾装措施对材料声学特性产生的影响。为此,本文在已有研究成果的基础上,考虑船舶舱室实际舾装中表面铺层对材料声学性能的影响,提出船舶舾装声学材料噪声特性分析方法,旨在为船舶舱室空气噪声准确预报提供有效输入参数。
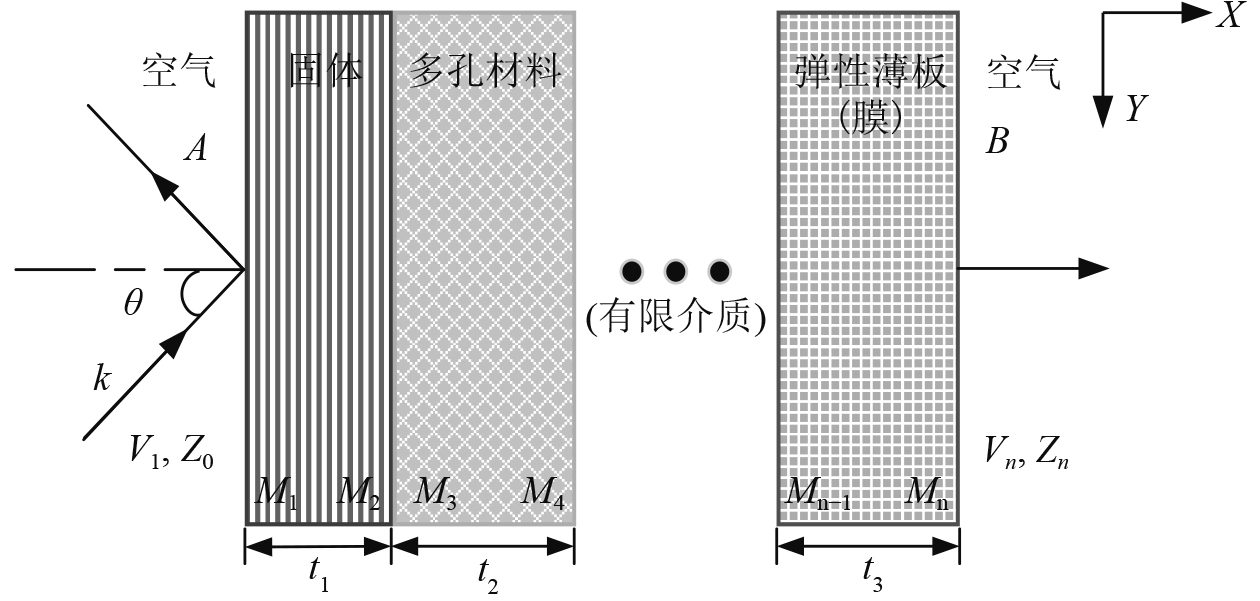
1 舾装声学材料吸隔声特性分析方法 1.1 多层复合材料声学特性分析模型通常,舾装声学材料为多种材料分层复合而成,使其兼有隔声、吸声、阻燃等特点[10]。为获取多层复合材料声学特性参数,基于传递矩阵法,建立多层复合材料声学特性分析模型,如图1所示。
|
图 1 多层复合材料分析模型 Fig. 1 Analysis model of multilayer composites |
将多层复合材料假设为若干离散薄层的组合并进行声传播理论分析。波数为
| $ {V_1} = [{T_{1n}}]{V_n}\text{。} $ | (1) |
式中:
在多层复合声学材料中,其离散层可归纳为流体层、固体层、多孔材料层以及粘弹性层四类。各介质间其状态矢量分别表示为:
| $ {V^f}(M) = {\left[P(M),v_x^f(M)\right]^{\rm{T}}}\text{,} $ | (2) |
| $ {V^s}(M) = {\left[v_x^s(M),v_y^s(M),\sigma _{xx}^s(M),\sigma _{xy}^s(M)\right]^{\rm{T}}} \text{,}$ | (3) |
| $ \begin{split} {V^p}(M) = \Bigg[v_x^f(M),v_x^s(M),v_y^s(M),\sigma _{xx}^f(M), {\rm{ }}\sigma _{xx}^s(M),\sigma _{xy}^s(M){\Bigg]^{\rm{T}}}{\rm{ }} \text{。}\\ \end{split} $ | (4) |
式中:上标
声波在流体介质中传播时,其传递矩阵形式为:
| $ \begin{split} \left[ {\begin{array}{*{20}{c}} {p({M_1})} \\ {v({M_1})} \end{array}} \right] = &\left[ {\begin{array}{*{20}{c}} {\cos (kd\cos \theta )}&{j\dfrac{{\rho c\sin (kd\cos \theta )}}{{\rho c}}} \\ {j\dfrac{{\sin (kd\cos \theta )}}{{\rho c}}\cos \theta }&{\cos (kd\cos \theta )} \end{array}} \right]\times \\ &\left[ {\begin{array}{*{20}{c}} {p({M_2})} \\ {v({M_2})} \end{array}} \right]\text{。}\\[-15pt]\end{split}$ | (5) |
式中:
当声波入射固体介质时,会产生折射的纵波和横波以及反射的纵波和横波,对应的位移势函数可写成:
| $ \varphi = {C_1}{e^{j(\omega t - {k_y}y - {k_{yx}}x)}} + {C_2}{e^{j(\omega t - {k_y}y + {k_{yx}}x)}}\text{,} $ | (6) |
| $ \psi = {C_3}{e^{j(\omega t - {k_y}y - {k_{xx}}x)}} + {C_4}{e^{j(\omega t - {k_y}y + {k_{xx}}x)}}\text{。} $ | (7) |
式中,
由固体的基本弹性性质,假设:
| $ {C^s} = {\left[ {({C_1} + {C_2}),({C_1} - {C_2}),({C_3} + {C_4}),({C_3} - {C_4})} \right]^{\rm{T}}}\text{,} $ | (8) |
则固体层状态变量
| $ {V^s}({M_n}) = \varGamma ({M_{n - 1}}){C^s}\text{,} $ | (9) |
式中:
| $\begin{split} \varGamma (x) =\,& \left( {\begin{array}{*{20}{c}} {\omega {k_y}\cos ({k_{yx}}x)}&{ - j\omega {k_y}\sin ({k_{yx}}x)}\\ { - j\omega {k_{yx}}\sin ({k_{yx}}x)}&{\omega {k_{yx}}\cos ({k_{yx}}x)}\\ { - {D_1}\cos ({k_{yx}}x)}&{j{D_1}\sin ({k_{yx}}x)}\\ {j{D_2}{k_{yx}}\sin ({k_{yx}}x)}&{ - {D_2}{k_{yx}}\cos ({k_{yx}}x)}\\ \end{array}}\right.\\ & \left. \begin{array}{*{20}{c}} {j\omega {k_{xx}}\sin ({k_{xx}}x)}&{ - \omega {k_{xx}}\cos ({k_{xx}}x)} \\ {\omega {k_y}\cos ({k_{xx}}x)}&{ - j\omega {k_y}\sin ({k_{xx}}x)} \\ {j{D_2}{k_{xx}}\sin ({k_{xx}}x)}&{ - {D_2}{k_{xx}}\cos ({k_{xx}}x)} \\ {{D_1}\cos ({k_{xx}}x)}&{ - j{D_1}\sin ({k_{xx}}x)} \end{array}\right)\text{。}\end{split} $ | (10) |
式中:
| $ {D_1} = \lambda \left({k_y}^2 + {k_{yx}}^2\right) + 2\mu {k_{yx}}^2\text{,} $ | (11) |
| $ {D_2} = 2\mu {k_y}^2\text{。} $ | (12) |
令式(10)中x分别取0和t,可得声波在固体层中传递矩阵:
| $ {T^s} = \varGamma (0){\varGamma ^{ - 1}}(t)\text{,} $ | (13) |
对于多孔材料层,其综合了流体层合固体层的特点,依据Biot多孔介质声传播理论[12],其位移势函数包括:
| $ \varphi _1^s = {C_1}{e^{j(\omega t - {k_y}y - {k_{yx}}x)}} + {C_2}{e^{j(\omega t - {k_y}y + {k_{yx}}x)}}\text{,} $ | (14) |
| $ \varphi _2^s = {C_3}{e^{j(\omega t - {k_y}y - {k_{zx}}x)}} + {C_4}{e^{j(\omega t - {k_y}y + {k_{zx}}x)}}\text{,} $ | (15) |
| $ \psi _2^s = {C_5}{e^{j(\omega t - {k_y}y - {k_{xx}}x)}} + {C_6}{e^{j(\omega t - {k_y}y + {k_{xx}}x)}}\text{,} $ | (16) |
| $ \varphi _i^f = {\mu _i}\varphi _i^s{\rm{ }}(i = 1,2)\text{,} $ | (17) |
| $ \psi _1^f = {\mu _3}\varphi _2^s\text{。} $ | (18) |
式中,
同理,由多孔材料的应力应变关系,令
| $ {C^p} = {\left[ \begin{array}{l} ({C_1} + {C_2}),({C_1} - {C_2}),({C_3} + {C_4}), \\ ({C_3} - {C_4}),({C_5} + {C_6}),({C_5} - {C_6}) \\ \end{array} \right]^{\rm{T}}}\text{,} $ | (19) |
则多孔材料层状态变量
| $ {V^p}({M_n}) = \varGamma ({M_{n - 1}}){C^p}\text{,} $ | (20) |
经化简,得到声波在厚度为t的多孔材料层中传递矩阵:
| $ {T^p} = \varGamma (0){\varGamma ^{ - 1}}(t)\text{。} $ | (21) |
根据各离散层间的连续性条件,对各介质传递矩阵进行组装,得到多层复合材料间传递矩阵:
| $ \left[{I_{f,1}}\right]V_1^f + \left[{J_{f,1}}\right]V_{M2}^f = 0\text{,} $ | (22) |
| $ \begin{split} &\left[{I_{k,k + 1}}\right]V_{{M_{2k}}}^k + \left[{J_{k,k + 1}}\right]V_{{M_{2(k + 1)}}}^f = 0 \text{,}\\ &{{ (k = 1,2,}}\cdots{{,n - 1)}} \end{split} $ | (23) |
整理得:
| $ {{\boldsymbol{D}}_m}{V_0} = 0\text{。} $ | (24) |
式中:
| $ {{\boldsymbol{D}}_m}{\rm{ = }}\left[ {\begin{array}{*{20}{c}} {{I_{f,1}}}&{{J_{f,1}}{T^1}}&0&0&0 \\ 0&{{I_{1,2}}}&{{J_{1,2}}{T^2}}&0&0 \\ \ldots & \ldots & \ldots & \ldots & \ldots \\ 0&0&{{I_{(n - 2)(n - 1)}}}&{{J_{(n - 2)}}{T^{n - 1}}}&0 \\ 0&0&0&{{I_{(n - 1)n}}}&{{J_{(n - 1)(n)}}} \end{array}} \right]\text{,} $ | (25) |
结合复合材料入射端与透射端的边界条件或声压与速度的阻抗方程,即可求得总传递矩阵
根据介质的表面阻抗定义,复合材料两端表面阻抗可表示为:
| $ {Z_0} = p({M_1})/v_0^f({M_1})\text{,} $ | (26) |
| $ {Z_s} = \frac{{D'}}{{D{''}}}\text{。} $ | (27) |
式中:
当多层材料末端为刚性背衬时,多层复合材料反射系数及吸声系数可表示为:
| $ R = \frac{{{Z_s}\cos \theta - {Z_0}}}{{{Z_s}\cos \theta + {Z_0}}}\text{,} $ | (28) |
| $ \alpha = 1 - {\left| R \right|^2}\text{。} $ | (29) |
当多层材料末端为半无限流体域时,透射系数
| $ \frac{{p(A)}}{{1 + R}} = \frac{{p(B)}}{T}\text{,} $ | (30) |
将式(30)代入总传递矩阵,同理可求得传递损失:
| $ TL = - 10\lg \left(\left| {T{{(\theta )}^2}} \right|\right)\text{。} $ | (31) |
对船舶实际舾装中,几种典型复合声学材料,基于传递矩阵法,建立其声学性能评估数值模型,所选复合材料如表1所示。
|
|
表 1 计算舾装材料组成表 Tab.1 The calculated material composition |
对上述涉及组成材料进行材料性能试验,并结合材料购置规格文件,得到材料主要参数如表2所示。
|
|
表 2 材料参数表 Tab.2 The calculated material parameters |
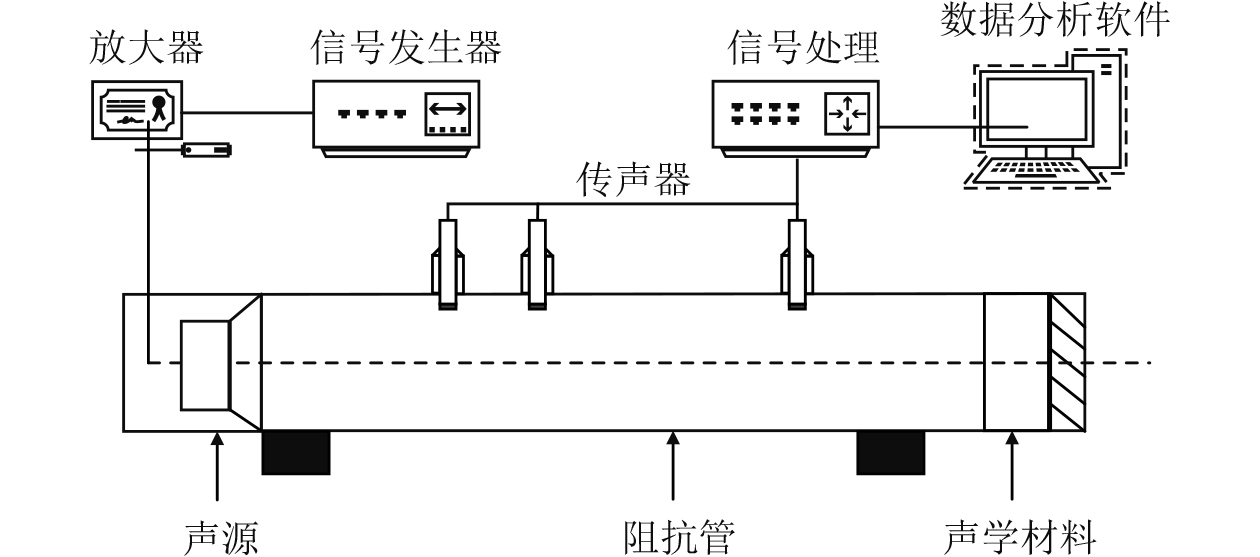
选取典型舾装材料中玻璃棉材料(材料1)为研究对象,对结构吸声系数和隔声量数值计算,并基于阻抗管法开展典型舾装复合结构吸声系数测试试验,试验示意图如图2所示。
|
图 2 阻抗管声学性能试验图 Fig. 2 Impedance tube acoustic performance test |
其中,材料隔声性能测试在
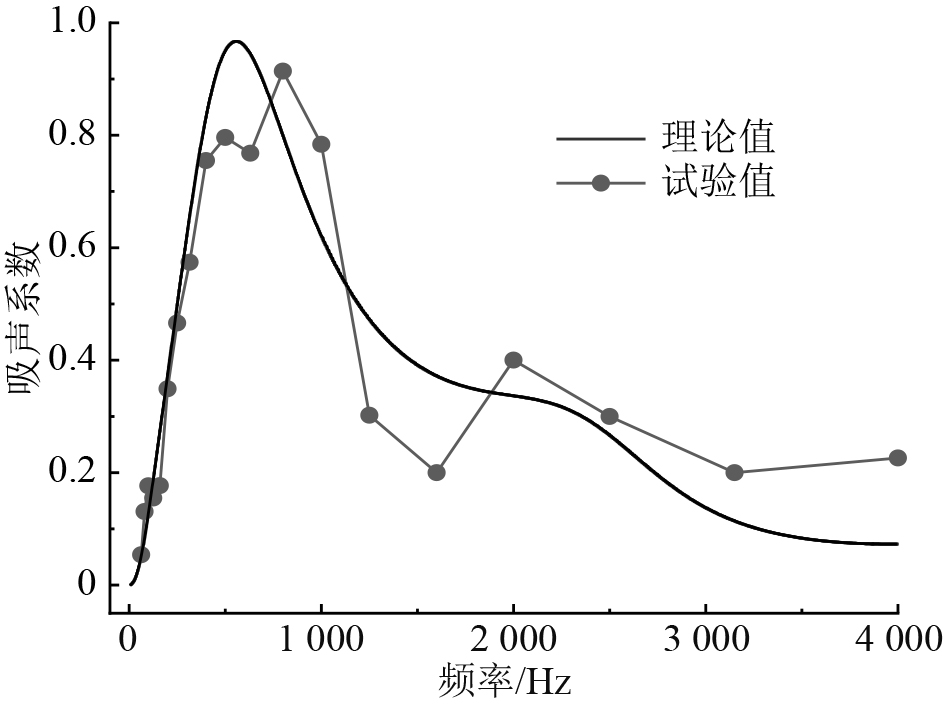
|
图 3 隔音棉吸声系数对比图 Fig. 3 Comparison of sound absorption coefficient of sound insulation cotton |

|
图 4 隔音棉传递损失对比图 Fig. 4 Comparison of transmission loss of sound insulation cotton |
由图3和图4对比结果可知,基于传递矩阵法的船舶舾装隔音棉材料吸声系数、传递损失计算曲线和测量曲线在频点处虽存在数值差异,但是2种曲线整体趋势基本一致,曲线总体吻合较为良好。由此可见,本文提出基于传递矩阵法的船舶舾装材料声学特性分析方法有效,可用于多层复合材料的吸隔声性能参数计算。
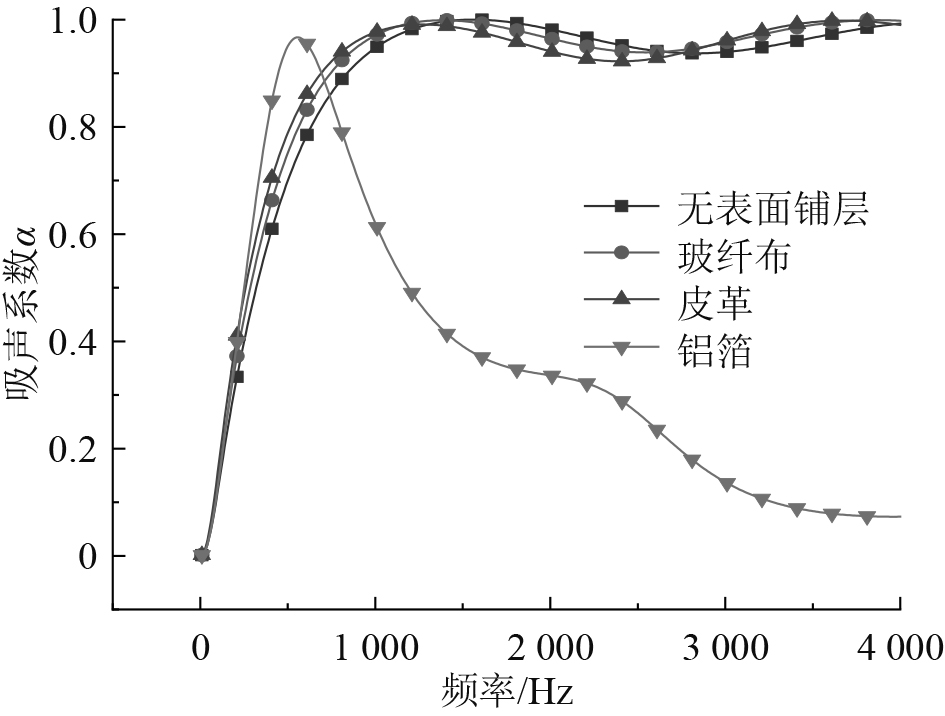
2.3 不同表面铺层对材料声学特性影响应用前文提及方法,对6种舾装材料模型进行声学性能计算,并对计算结果进行归类。选取常见的材料表面铺层材料,分别计算舾装材料表面包裹铝箔(材料1)、玻纤布(材料2)、皮革(材料3)时,舾装声学材料吸声性能,并与单一声学材料无敷设表面铺层的玻璃棉吸声系数对比,计算结果如图5所示。
|
图 5 不同表面铺层吸声系数对比图 Fig. 5 Comparison of sound absorption coefficient of different surface layers |
可见在实际舾装过程中,表面铺层将对材料吸声特性分析有一定影响,其中表面包裹铝箔相比无表面铺层影响最为明显,当频率达到1000 Hz后,其吸声系数呈明显下降趋势,材料表面包裹皮革、玻纤布对材料吸声特性影响依次减弱。
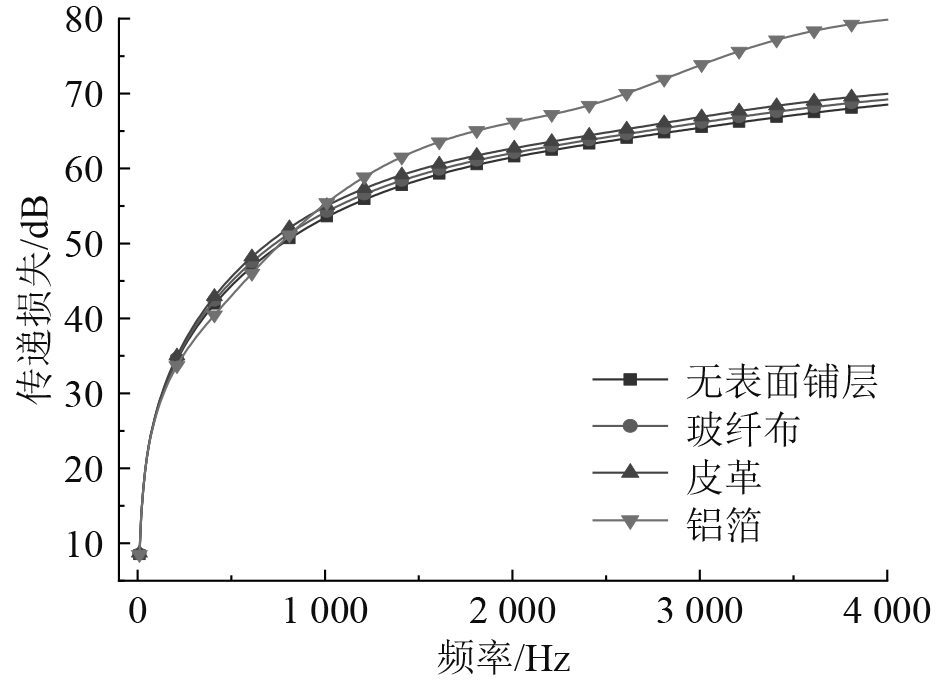
当材料含刚性背衬时,分析各表面铺层对声学材料隔声性能影响规律,各铺层情况下复合材料传递损失计算结果如图6所示。
|
图 6 不同表面铺层复合结构传递损失对比图 Fig. 6 Comparison of transfer loss of composite structures with different surface layers |
由计算结果表明,在刚性背衬下,声学材料不同的表面包裹会对材料的隔声性能造成影响。故在实际舱室舱壁敷设声学材料时噪声评估中,应综合考虑“表面铺层+材料”形式下其声学性能。
3 基于统计能量法的船舶典型舱室噪声预报 3.1 模拟舱室敷设舾装声学材料仿真计算选取船舶典型舱室为研究对象,开展模拟舱室敷设舾装材料噪声仿真计算及模型试验,验证声学材料表面铺层对舱室噪声控制效果的影响,并对比了应用本文方法时模拟舱室空气噪声预报水平,模拟舱室结构相关参数如表3所示。
|
|
表 3 模拟舱室主尺度表 Tab.3 Main dimensions of simulated cabin |
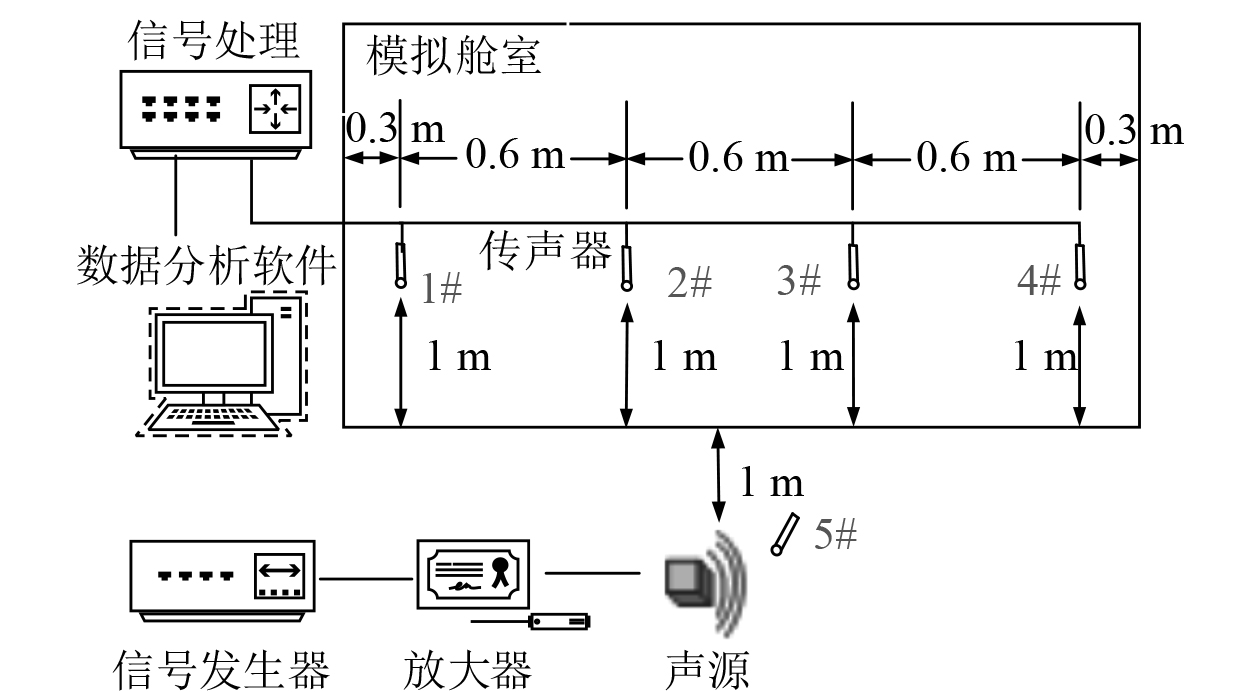
模拟舱室试验模型内敷设玻璃棉材料(铝箔+40 mm超细玻璃棉),无指向性声源发出10~20 k白噪声激励,测量模拟舱室内1.5 m高度处平均声压级及当前敷设情况下舱室内外隔声量。试验示意图如图7所示。
|
图 7 模拟舱室声学试验示意图 Fig. 7 Simulated cabin acoustic test |
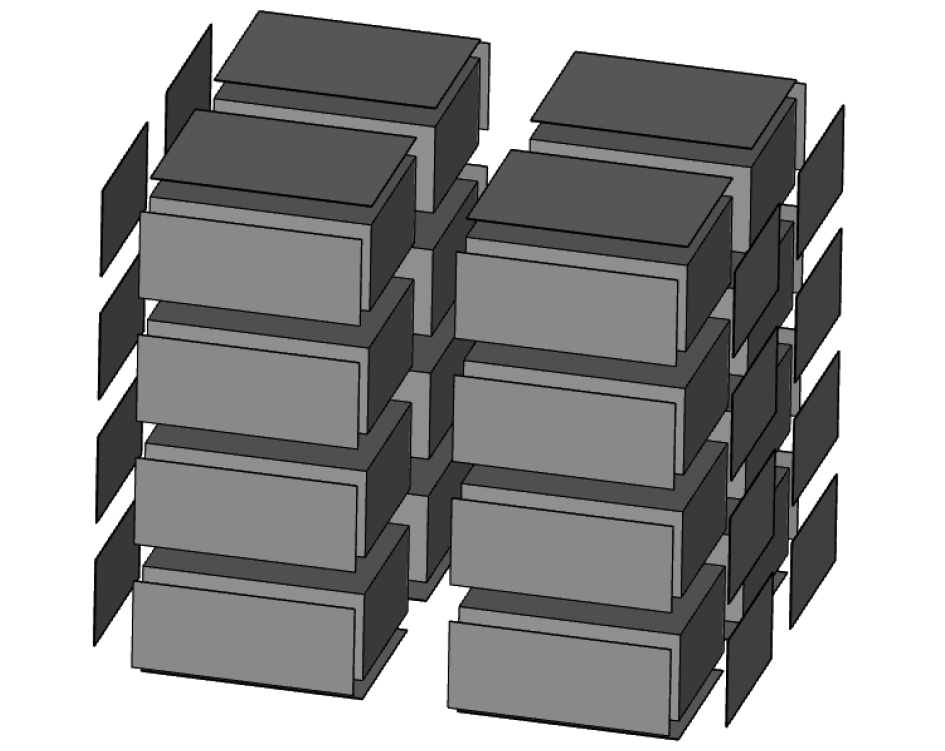
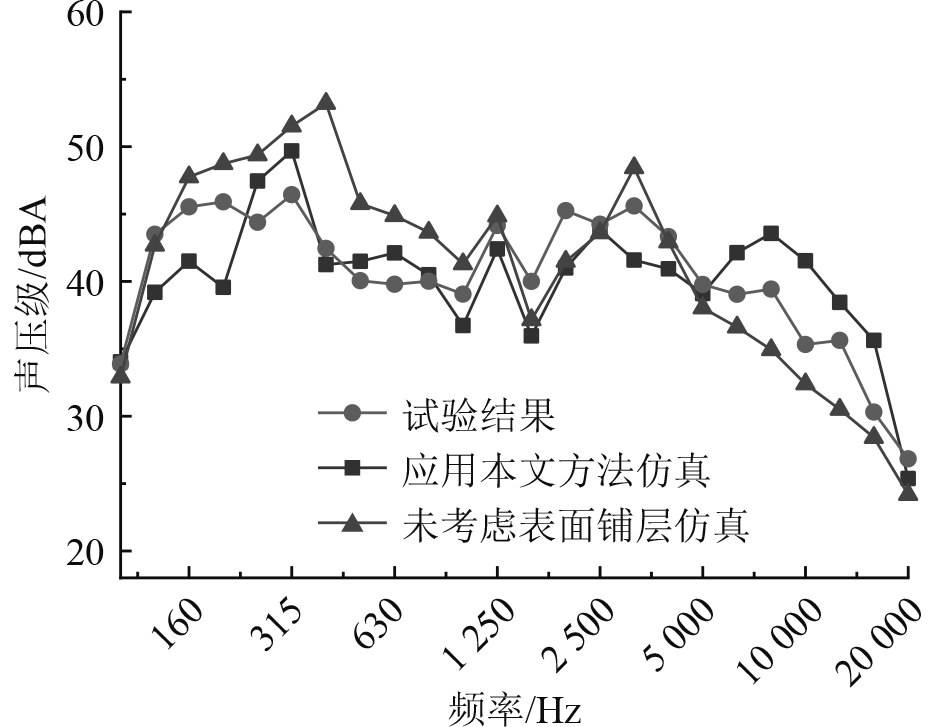
应用本文分析方法,计算当前舾装材料的吸声系数及传递损失,并作为舱室空气噪声评估模型的输入参数,进而基于统计能量法对评估模型进行噪声预报,声压考核点选取距舱壁1 m,高度1.5 m处,计算当前工况下舱室内噪声水平,板壳子系统模型如图8所示,舱室内考核点声压级及舱室内外隔声量计算结果如图9和图10所示。
|
图 8 模拟舱室统计能量模型 Fig. 8 SEA model of simulated cabin |
|
图 9 舱室内考核点声压对比图 Fig. 9 Comparison of sound pressure in the cabin |
|
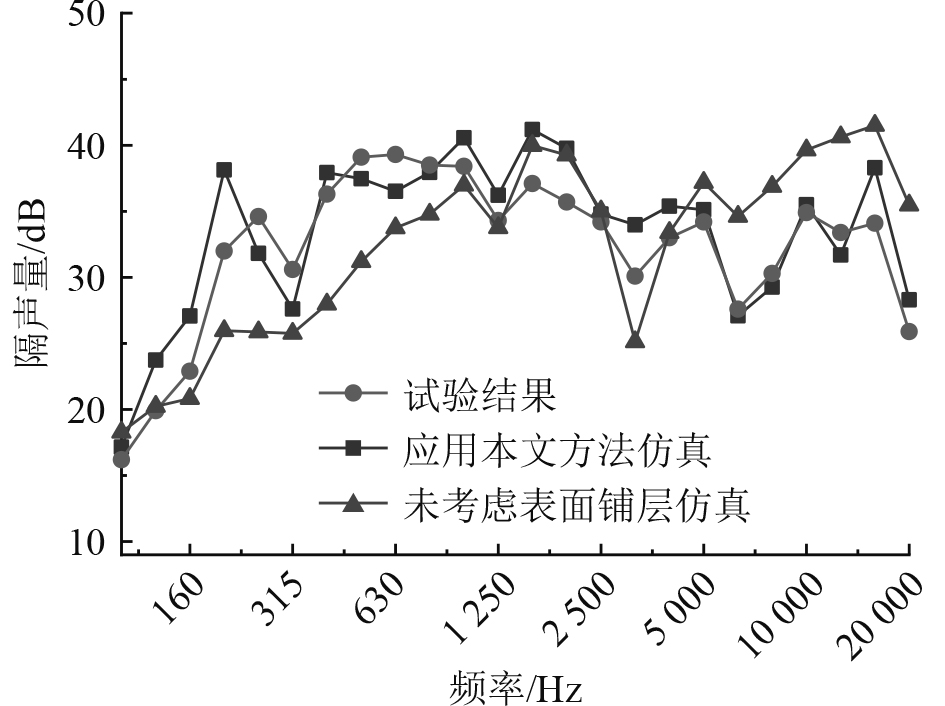
图 10 舱室内外隔声量对比图 Fig. 10 Comparison of sound insulation |
由计算结果表明,应用本文方法考虑声学材料表面铺层后的模拟舱室空气噪声预报结果相较于仅考虑声学材料层计算结果更接近试验值,且与试验结果曲线趋势基本一致,在考核频段内,应用本文分析方法隔声量总级计算结果和未考虑表面铺层结果与试验测试所得隔声量总级分别相差2.5 dB和3.4 dB。故针对在敷设舾装材料的船舶舱室空气噪声预报中,应用船舶舾装材料声学特性分析方法,将考虑表面铺层的声学材料吸隔声参数作为有效输入,可使舱室预报结果更为有效。
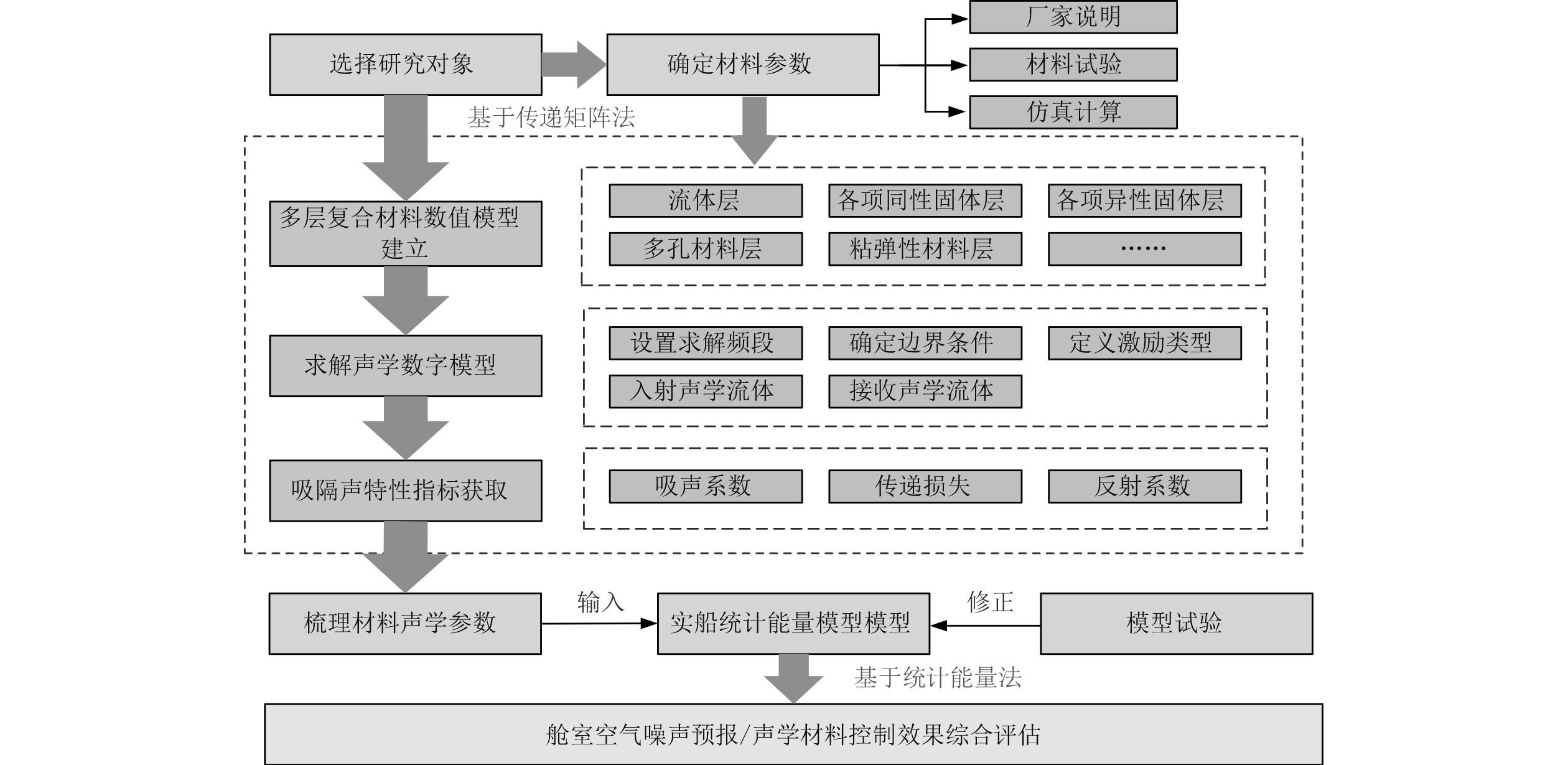
3.2 船舶舾装材料声学特性分析方法应用流程对船舶舾装声学材料噪声控制效果分析方法进行梳理,针对船舶舱室空气噪声控制问题,形成船舶舾装声学材料噪声控制方法应用流程,如图11所示。
|
图 11 船舶舾装声学材料噪声控制方法应用流程图 Fig. 11 Frequency spectrum of vibration speed response |
本文针对船舶舱室空气噪声控制等问题,基于传递矩阵法,开展不同声学材料表面铺层对船舶舱室噪声影响研究,应用该方法探究了考虑声学材料表面铺层与否对船舶舱室噪声控制效果的影响。主要得出如下结论:
1)经过与阻抗管试验结果对比,基于声传递矩阵的船舶舾装材料声学特性分析方法应用在多层复合材料声学特性求解是可行的。
2)实际船舶舾装中声学材料表面包裹铺层将对材料声学性能噪声产生影响。其中,声学材料表面包裹铝箔时材料吸隔声性能影响最为明显,故在船舶舱室空气噪声预报中,应综合考虑 “表面铺层+材料”形式下的声学性能。
3)声学材料表面铺层将影响船舶舱室噪声水平,在舱室噪声预报中,综合考虑材料复合结构相较仅考虑声学材料层特性的结果更接近试验值,隔声量总级与试验结果分别相差2.5 dB和3.4 dB,故应用本文方法可有效提升船舶舱室噪声预报准确性。
| [1] |
夏兆旺, 王宗耀, 温华兵, 等. 复合隔声结构声学性能研究综述[J]. 船舶工程, 2020, 42(7): 14-21. |
| [2] |
曲雪, 董博文, 罗凯, 等. 船舶舾装复合结构声学性能分析方法及应用[J]. 舰船科学技术, 2019, 41(19): 50-54. |
| [3] |
窦玲玲, 米永振, 黄斌根, 等. 直升机舱室声学超材料壁板的低频隔声性能分析[J]. 噪声与振动控制, 2021, 41(1): 12-15, 20. DOI:10.3969/j.issn.1006-1355.2021.01.003 |
| [4] |
汪婕, 冯涛, 杨梦露, 等. 应用传递矩阵测量中间薄层材料声特性[J]. 声学技术, 2019, 38(3): 334-339. |
| [5] |
Felhi H, Trabelsi H, Taktak M, et al. Effects of viscoelastic and porous materials on sound transmission of multilayer systems[J]. Journal of Theoretical and Applied Mechanics, 2018, 56(4): 961-976. |
| [6] |
Yablonik L R. A Simplified Method for Calculating Multilayer Sound Insulation with Layers of Fibrous Porous Material[J]. Acoustical Physics, 2018, 64(5): 643-650. DOI:10.1134/S106377101805010X |
| [7] |
韩峰, 何立燕, 李晨曦. 多孔纤维材料对飞机壁板结构隔声性能的影响分析[J]. 噪声与振动控制, 2020, 40(4): 167-172. DOI:10.3969/j.issn.1006-1355.2020.04.030 |
| [8] |
李维鑫, 郭锐, 王新, 等. 用阻抗法测量材料固有参数研究多层吸声特性[J]. 噪声与振动控制, 2020, 40(3): 265-269. DOI:10.3969/j.issn.1006-1355.2020.03.047 |
| [9] |
冯博, 桂洪斌, 杨群. 船舶尾部舱室噪声预报及控制分析[J]. 舰船科学技术, 2017, 39(15): 22-27. |
| [10] |
田宏业. 基于SEA的船舶舱室噪声预报系统化方法研究[D]. 哈尔滨工程大学, 2019.
|
| [11] |
Yablonik L R. A Simplified Method for Calculating Multilayer Sound Insulation with Layers of Fibrous Porous Material[J]. Acoustical Physics, 2018, 64(5): 643-650. DOI:10.1134/S106377101805010X |
| [12] |
詹沛, 白国锋, 牛军川, 等. 含空气层与多孔材料的复合结构隔声特性研究[J]. 应用声学, 2014, 33(5): 426-432. DOI:10.11684/j.issn.1000-310X.2014.05.008 |
 2021, Vol. 43
2021, Vol. 43
