2. 陆军军事交通学院镇江校区,江苏 镇江 212003
2. Zhenjiang Watercraft College, Zhenjiang 212003, China
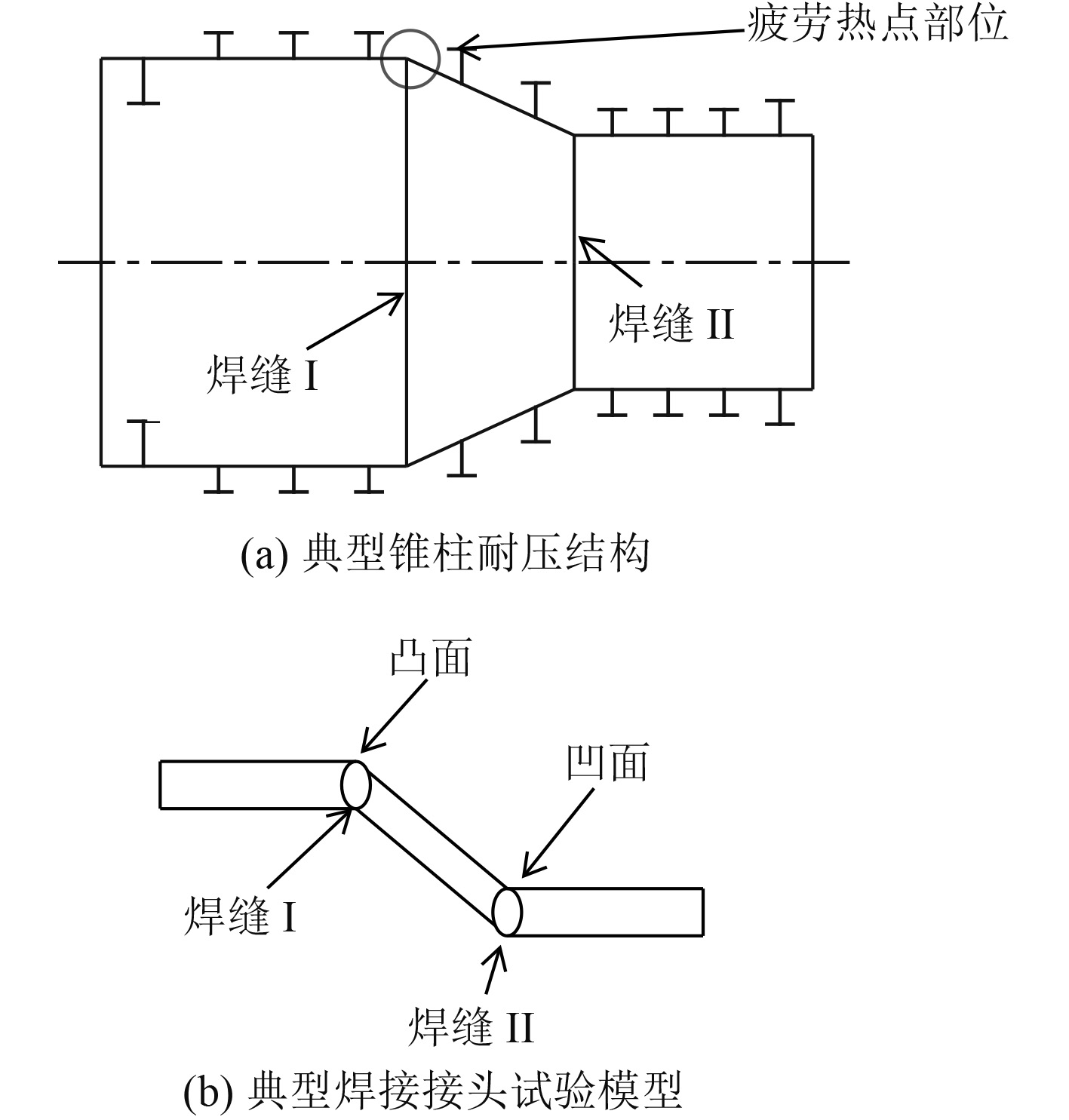
锥柱耐压壳是潜器最为重要的焊接结构之一,而高强度钢为潜器耐压壳常用材料之一。由于潜器下潜和上浮的循环往复而产生了交变载荷,使得锥柱耐压壳部位成为了疲劳热点区域[1] ,如图1所示。残余应力和潜器外载荷相叠加,易使该部位提早发生疲劳损伤。
|
图 1 耐压结构典型焊接接头 Fig. 1 Typical welded joints for compression structures |
文献[2-3]采用试验方法对耐压壳焊缝附近的残余应力进行测试,结果发现焊缝处存在着较大的焊接残余应力;文献[4-5]分析得到当潜器下潜时锥柱耐压壳附近会产生较大的拉压应力。为了降低成本,可采用带一定角度的平板焊接接头模型来模拟锥柱焊接接头,如图1(b)所示。总体来说,对锥柱耐压壳典型焊接接头残余应力数值模拟和试验研究较少。
本文以高强度钢耐压壳典型焊接接头模型为研究对象,采用数值模拟和试验相结合的方法对锥柱耐压壳典型焊接残余应力分布规律进行研究,并分析典型焊接接头几何参数和焊接工艺参数等对残余应力的影响。研究结果可为高强度钢水下耐压结构的安全性研究提供相关理论基础。
1 焊接残余应力有限元分析方法利用有限元法分析焊接温度场时,假设单个单元内的节点温度在空间域上呈线性分布,节点温度的一阶常系数微分方程组利用变分公式推导。时间域上,使用有限差分法将其转化为节点温度线性代数方程组的递推公式,叠加每个单元矩阵,从而形成节点温度的线性方程组,进而可以求得节点的温度,其方法如下:
将空间域离散,形函数记为
| $ T = N {T^e}\text{,} $ | (1) |
焊接残余应力的本质在于焊接过程中产生了不可恢复的塑性变形,材料处于弹塑性状态的应力应变关系[6]为
| $ {\rm{d}}\sigma=D {\rm{d}}\varepsilon-C{\rm{d}}T \text{。} $ | (2) |
式中:
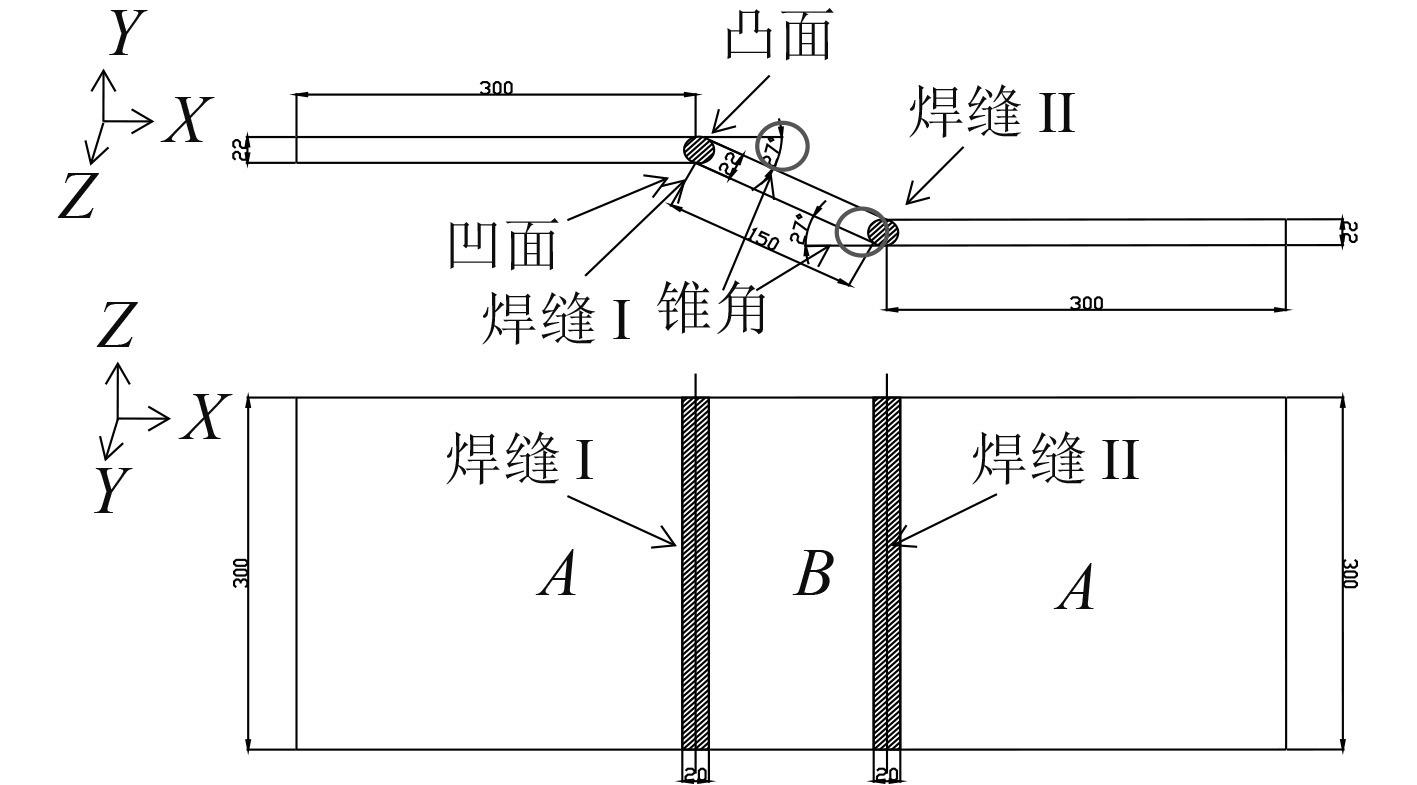
耐压壳典型焊接接头模型由2块尺寸为300 mm×300 mm×22 mm的高强度钢平板(A板)和1块尺寸为150 mm×300 mm×22 mm的高强度钢平板(B板)分别呈27°锥角焊接而成,形成两道焊缝,分别为焊缝I和焊缝II,焊缝尺寸为20 mm×300 mm×22 mm,焊接接头有凹凸面之分,如图2所示。
|
图 2 焊接接头模型几何尺寸 Fig. 2 Geometry size model of welding joint |
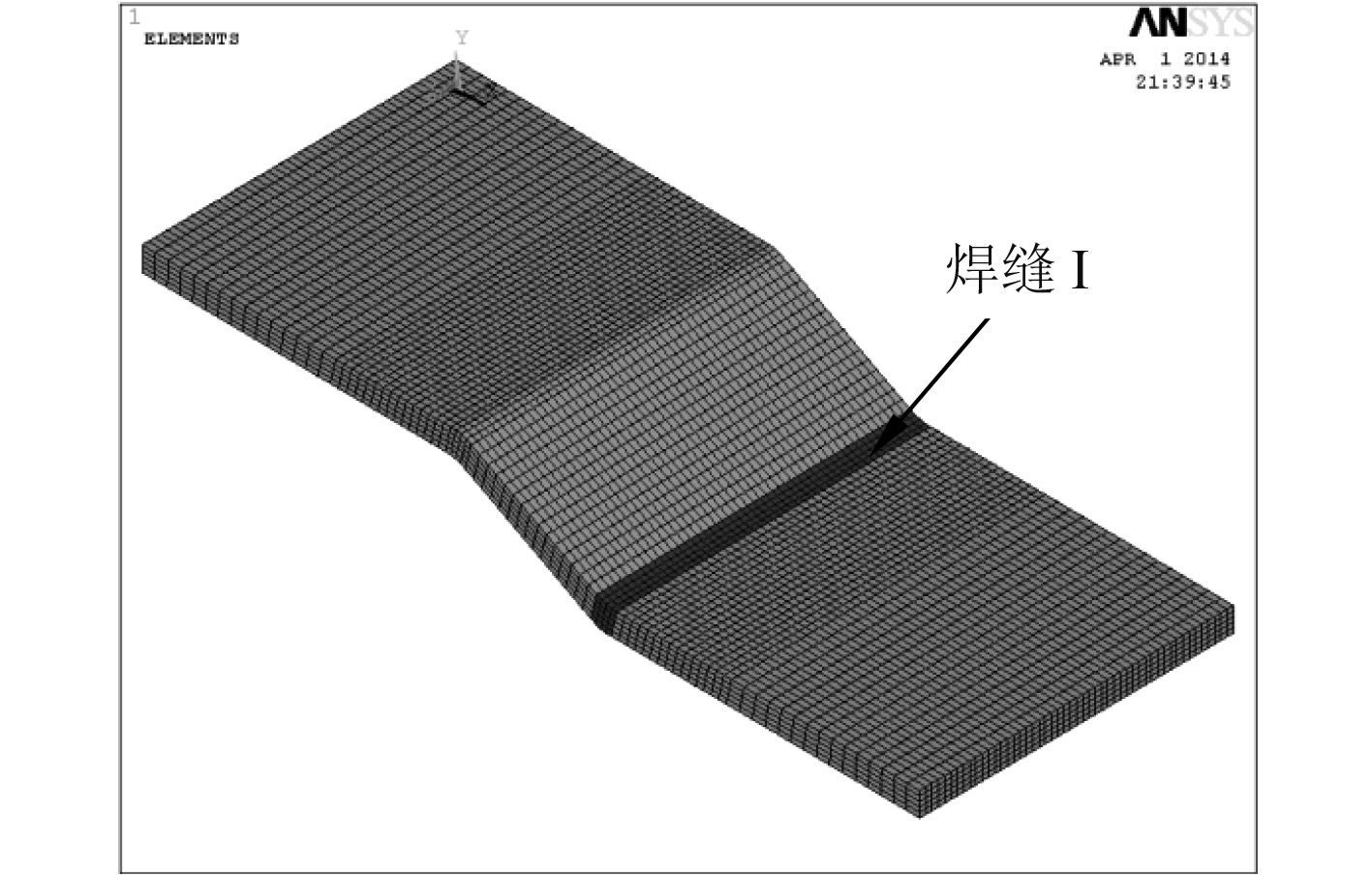
参考实际焊接工艺流程等相关参数,基于有限元分析软件Ansys的APDL语言二次开发了典型锥柱耐压壳焊接接头的焊接数值模拟程序。网格划分在焊缝区域处较密集,而随远离焊缝距离的增加网格逐渐变疏,如图3所示。
|
图 3 焊接接头有限元模型 Fig. 3 Finite element model of welded joint |
高强度钢耐压壳典型焊接接头模型材料的热物理性能和应力应变特性参数如表1及表2所示。
|
|
表 1 某高强度钢材料的热物理性能参数 Tab.1 Thermophysical properties of a high strength steel material |
|
|
表 2 某高强度钢材料的应力应变特性(MPa) Tab.2 Stress and strain characteristics of a high strength steel material (MPa) |
焊接过程采用手工电弧焊焊接,焊接电流为23 A,焊接电压为112 V,焊接速度为125 mm/min,焊接热效率为0.7,焊喉初始温度为1300℃。在模拟焊接过程时在焊缝厚度方向上简化成若干道焊缝,采用沿厚度方向交替焊的焊接工艺。
采用生死单元方法模拟焊缝的填充,净焊接热输入的方程如下式:
| ${Q_{net}} = \frac{{\eta UI}}{v}\text{。}$ | (3) |
式中:v为焊接速度;
初始温度设定为25 ℃,对流换热系数为62.5 W/m2·℃。将模型的4个角边刚性固定以防止其在计算过程中产生刚体位移。
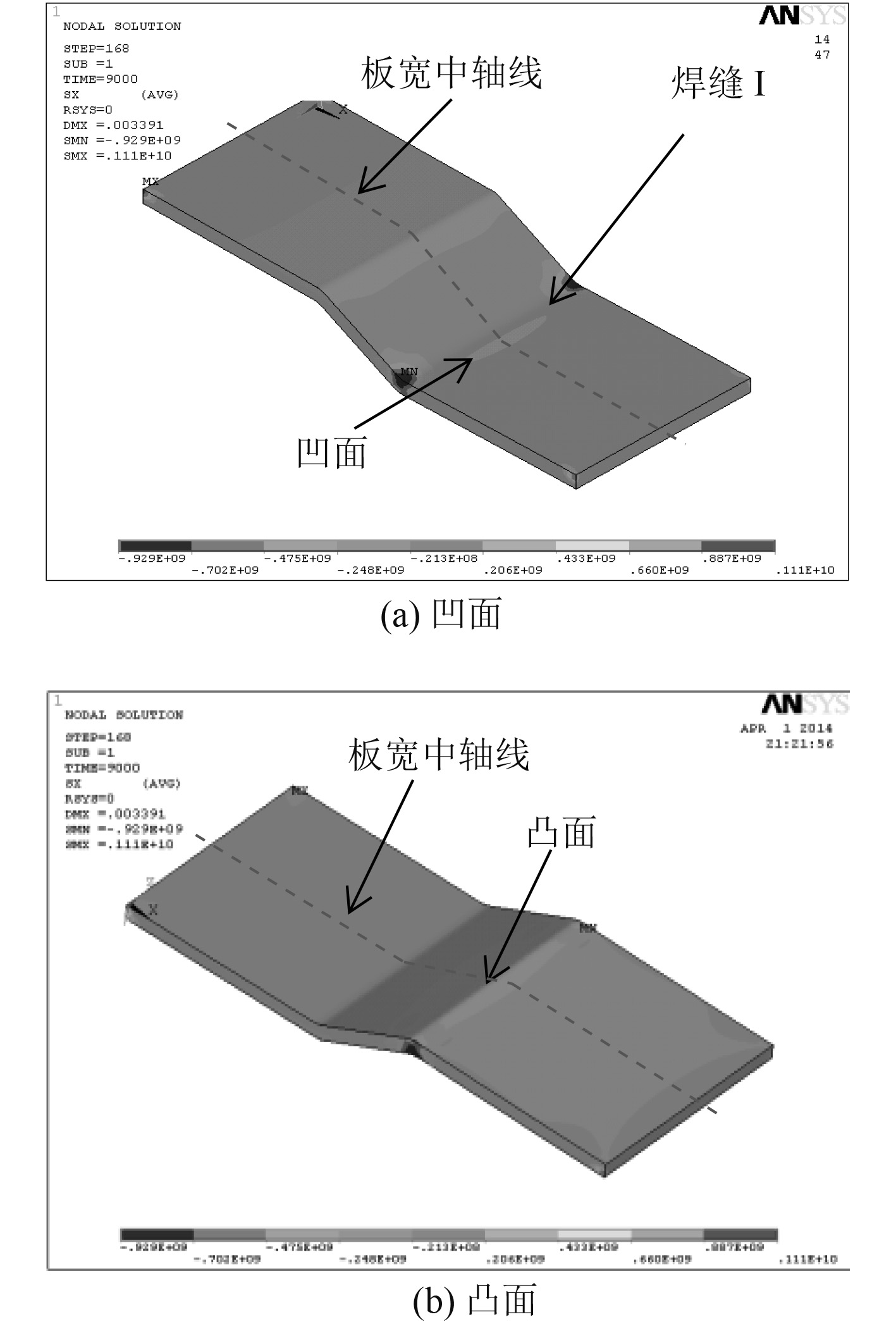
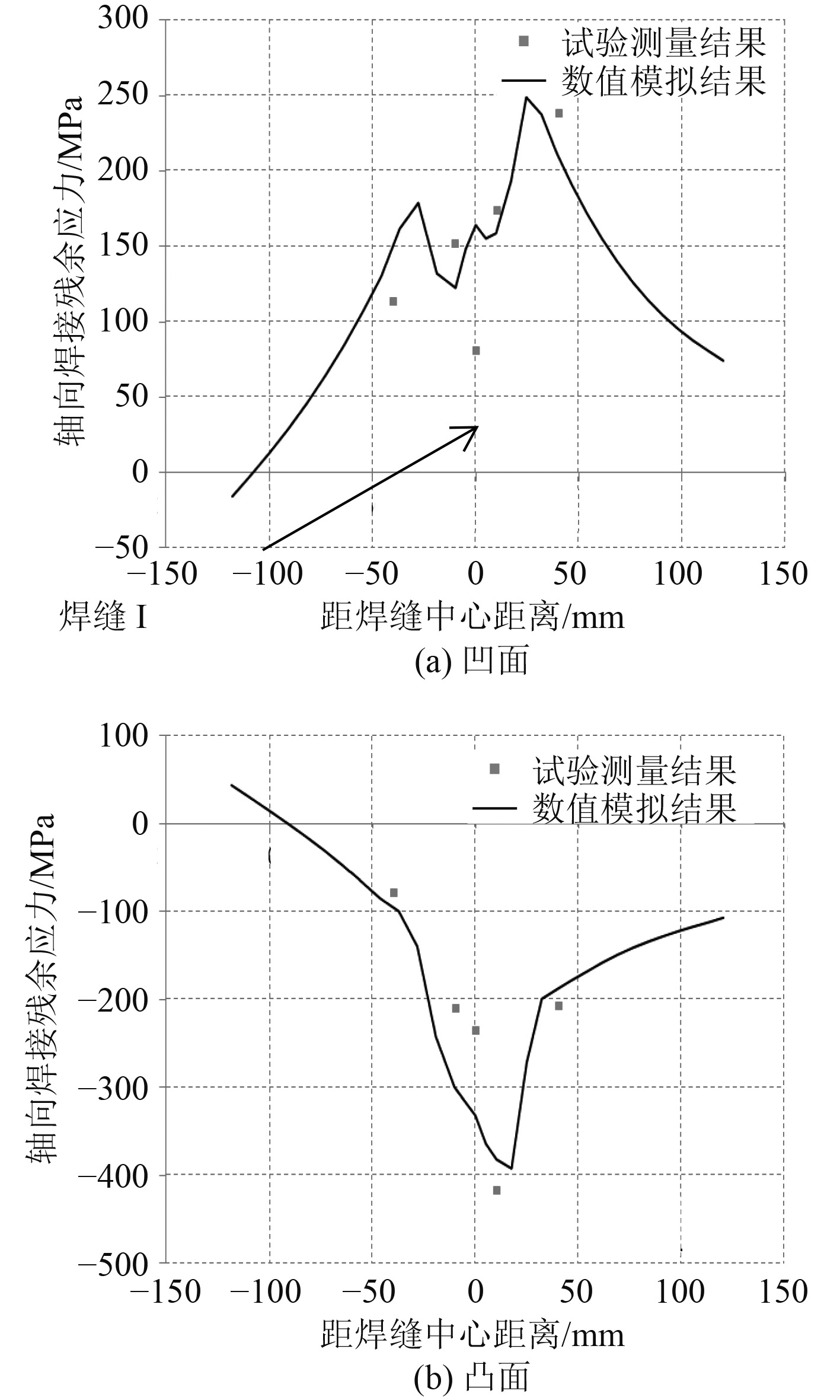
2.4 数值模拟结果及分析由于模拟和试验中发现轴向焊接残余应力对裂纹以及模型的疲劳有重要影响,所以本文着重对轴向焊接残余应力研究,且在模拟中焊缝II(图1和图2)轴向焊接残余应力在距焊缝100~150 mm左右基本已经降到很低,因此,耐压壳典型焊接接头中焊缝II对焊缝I热影响区的影响可以忽略,所以本文只对焊缝I(图1和图2)进行残余应力研究。图4和图5分别为模型焊缝I凹面及凸面表面轴向焊接残余应力(垂直于焊缝方向的残余应力)分布和残余应力分别在凹、凸表面板宽中轴线的分布曲线,工艺参数参照实际的焊接参数。
|
图 4 轴向焊接残余应力的分布(焊缝I) Fig. 4 Distribution of axial welding residual stress (weld seam I) |
|
图 5 轴向焊接残余应力在板宽中轴线分布(焊缝I) Fig. 5 Distribution axial welding residual stress along width centerline (weld seam I) |
从图4和图5可以看出:焊缝I凹面的轴向焊接残余应力呈双峰形状分布,且为拉应力,最大值有249 MPa左右;焊缝I凸面轴向焊接残余压应力呈单峰形状分布,最大值有390 MPa左右;且均在焊缝区域较大。
3 耐压壳典型焊接接头残余应力试验研究采用X射线法对耐压壳典型焊接接头模型表面焊缝附近区域的轴向焊接残余应力进行测量。
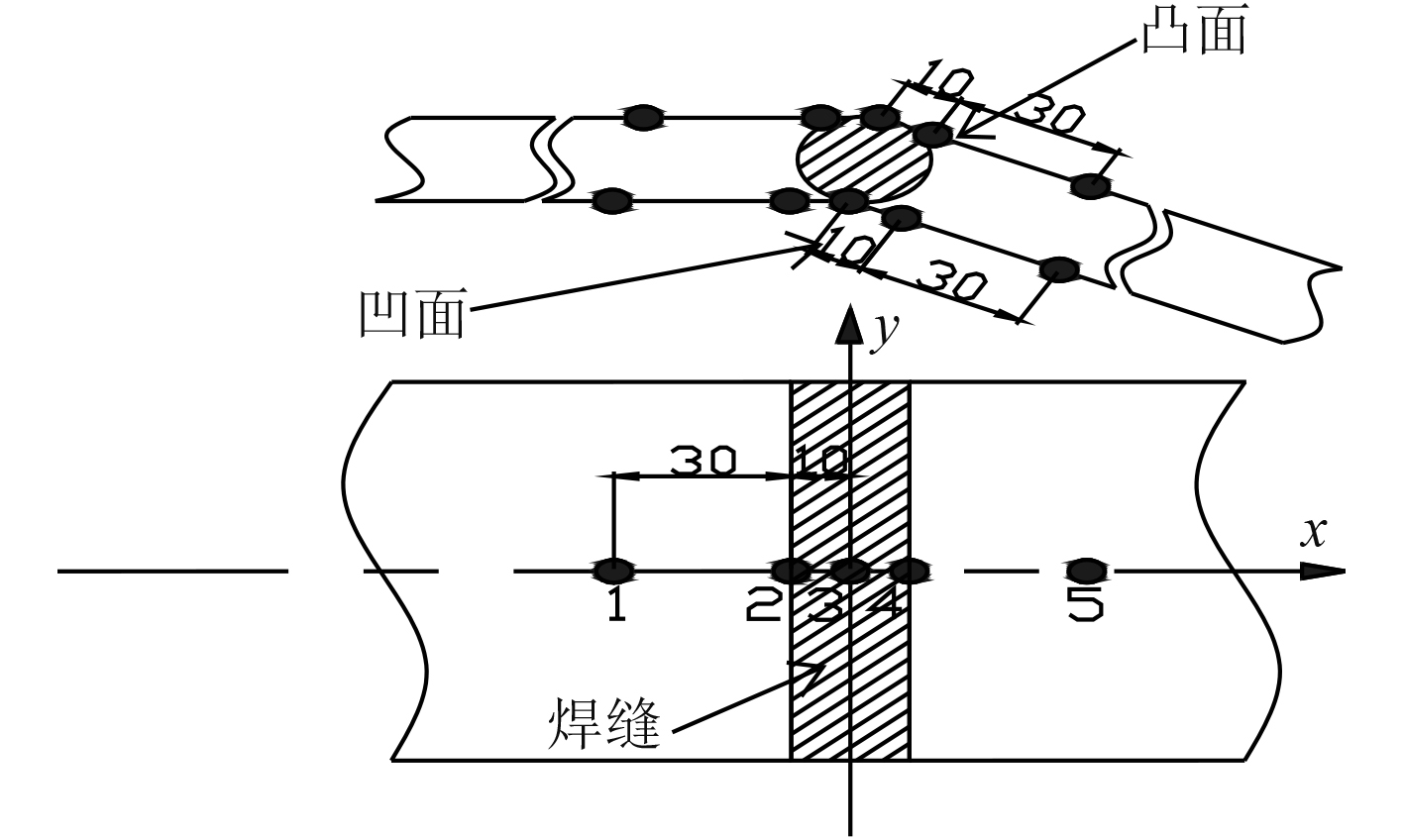
3.1 试验测量步骤1)在测试表面划线定点、标示坐标系、确定测量位置及编号,如图6所示。X轴为板宽的中心线,Y轴为焊缝I中心线。
|
图 6 试验测点布置图 Fig. 6 Layout of test point |
2)实验之前先用电动打磨机,去除各测点处表面的氧化膜和锈斑,之后再用细砂纸,打磨整个试件表面直至平整。
3)对模型试件表面进行电解抛光处理,消除因打磨产生的加工应力,抛光深度约为100 µm。电解抛光处理后立即将试件表面擦净,用纸和布将其遮护,确保模型试件表面干燥,防止生锈。
4)用X射线残余应力仪进行测试时,对每个测点依次完成仪器的定位和标定、测点对中和测量4个步骤。
3.2 测量结果通过试验测量并得到耐压壳典型焊接接头模型焊缝I附近表面处的轴向焊接残余应力,测量结果如表3所示。
|
|
表 3 轴向焊接残余应力测量结果(MPa) Tab.3 Measurement result of axial welding residual stress (MPa) |
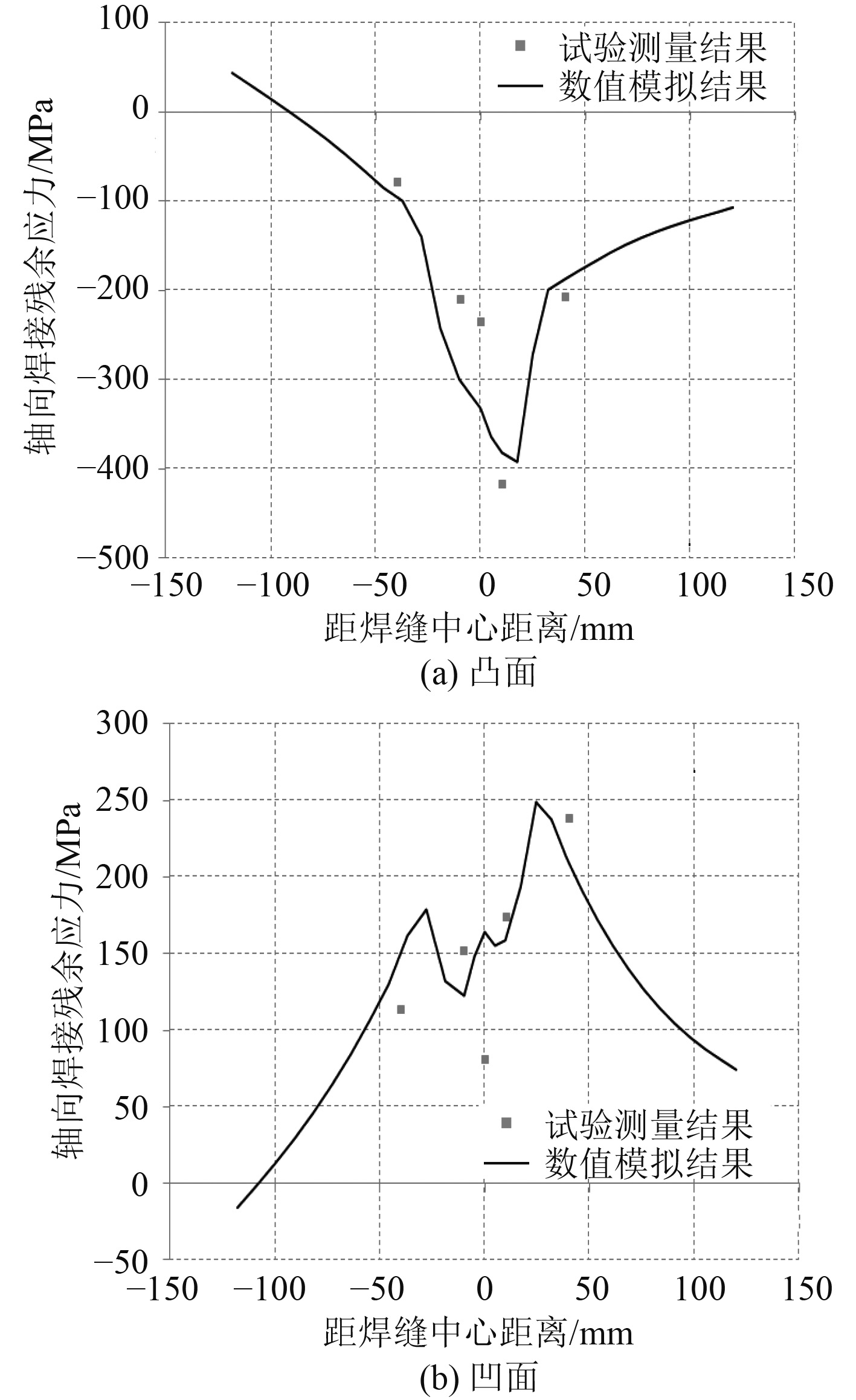
将有限元计算得到的模型轴向焊接残余应力与试验测量值进行比较,如图7所示。
|
图 7 残余应力模拟值与试验值比较 Fig. 7 Comparison between simulation and test of residual stresses |
从图7可以看出数值模拟结果与试验测量结果趋势基本一致,所以本文采用的有限元数值模拟方法对耐压壳典型焊接接头模型焊接残余应力进行计算分析是合理的。
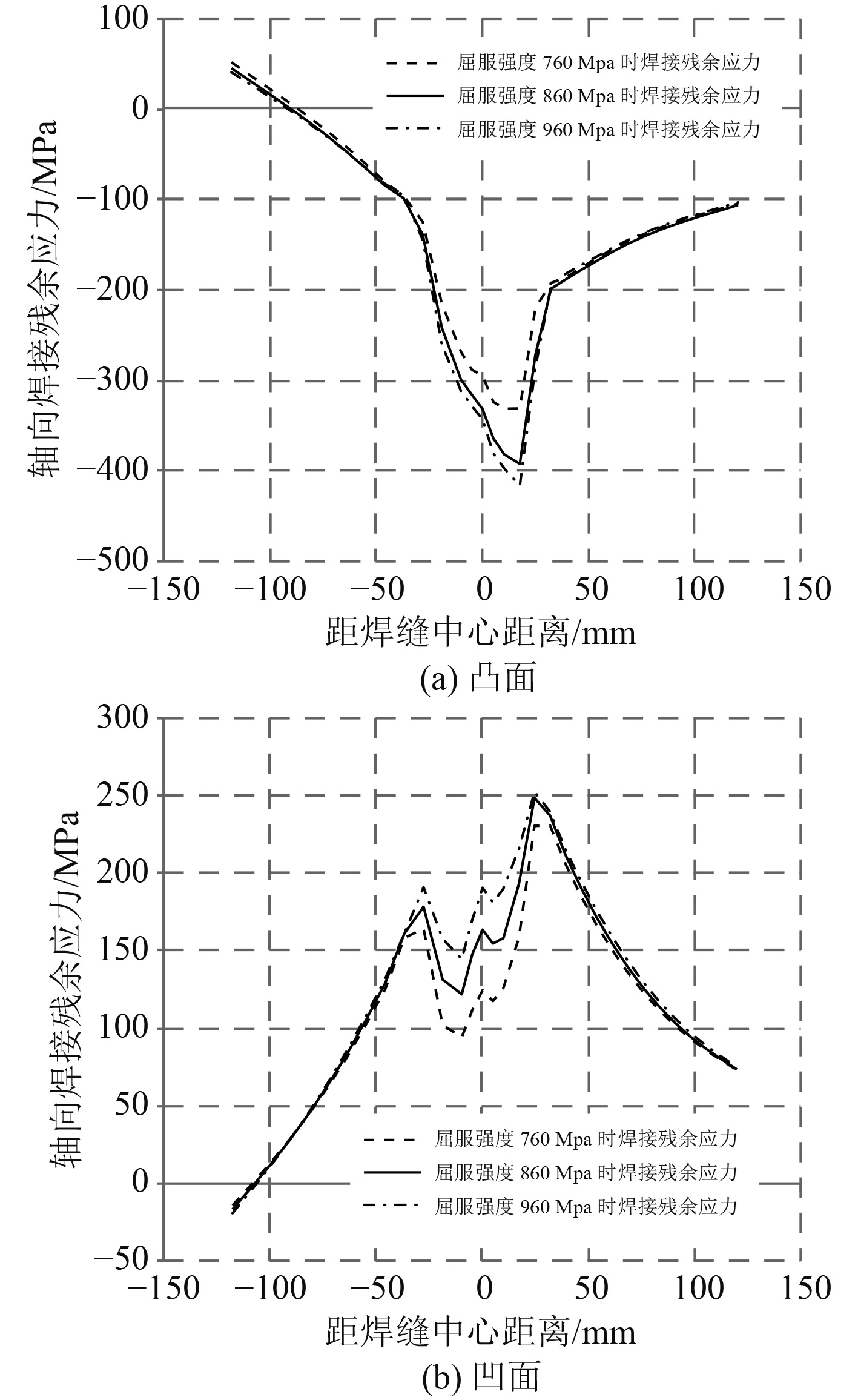
5 材料参数对耐压壳模型焊接残余应力的影响 5.1 材料屈服强度在假定其他参数相同的情况下,分别设屈服强度为760 MPa,860 MPa和960 MPa,对典型耐压壳焊接接头模型进行焊接残余应力的数值模拟计算,结果如图8及表4所示。
|
图 8 材料屈服强度对模型轴向焊接残余应力的影响 Fig. 8 Effect of material yield strength on axial welding residual stress |
|
|
表 4 不同屈服强度材料的模型轴向焊接残余应力最大值(MPa) Tab.4 Maximum axial welding residual stress of different yield strength materials(MPa) |
可以看出,当材料屈服强度不同时:
1)轴向焊接残余应力的分布趋势基本一致;
2)当材料屈服强度增大时,模型凸面的轴向焊接残余压应力以及凹面的轴向焊接残余拉应力都会随着增大,在焊缝区表现的最为明显;
3)相对模型凸面轴向焊接残余压应力的增加,模型凹面轴向焊接残余拉应力的增加不大。
5.2 材料热膨胀系数在假定其他参数相同的情况下,分别设热膨胀系数为1.06E-5,1.56E-5和2.06E-5,对典型耐压壳焊接接头模型进行焊接残余应力的数值模拟计算,结果如图9及表5所示。
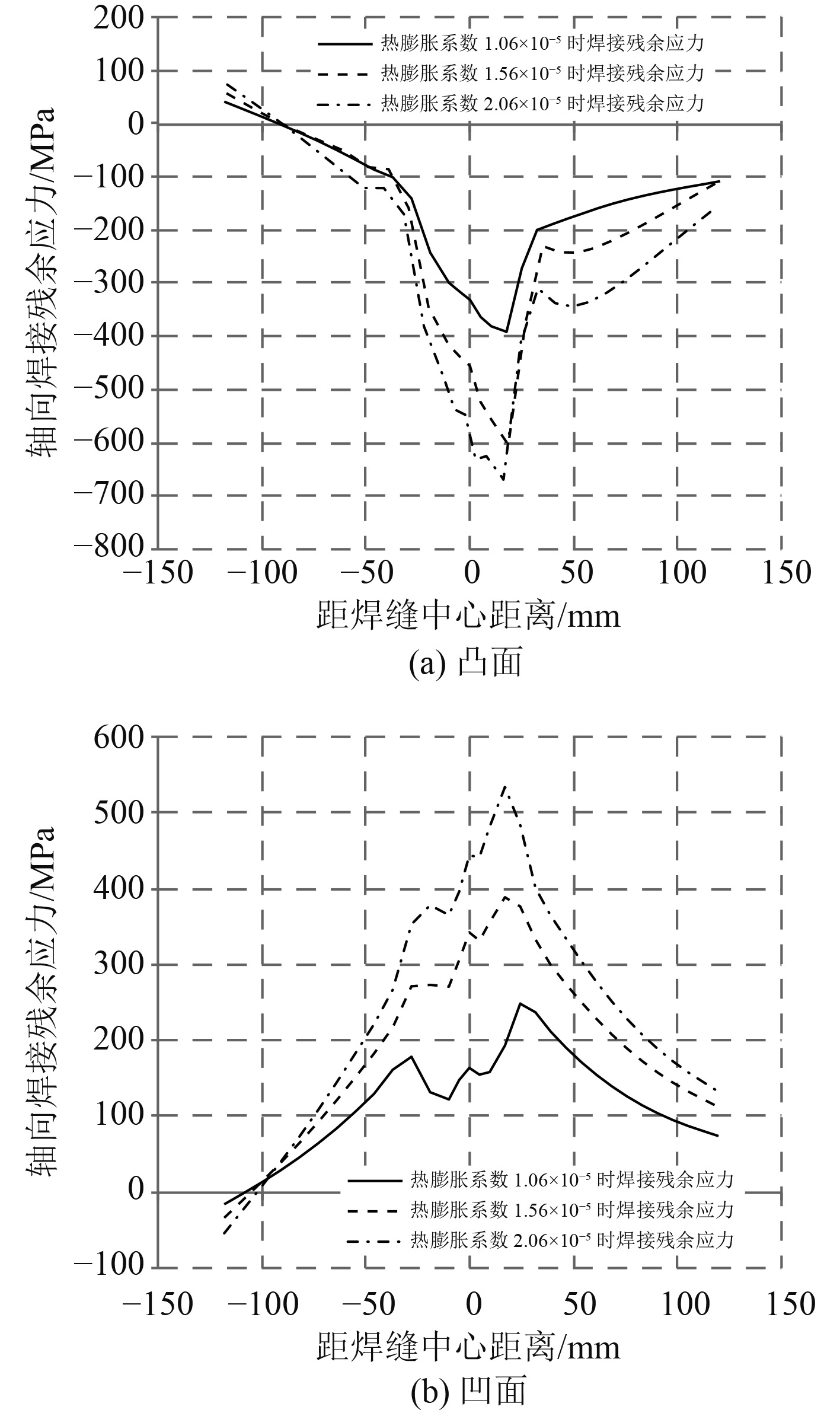
|
图 9 热膨胀系数对模型轴向焊接残余应力的影响 Fig. 9 Effect of thermal expansion coefficient on axial welding residual stress |
|
|
表 5 不同热膨胀系数模型的轴向焊接残余应力最大值(MPa) Tab.5 Maximum axial welding residual stress of different thermal expansion coefficients (MPa) |
可以看出,模型凸面的轴向焊接残余压应力以及凹面的轴向焊接残余拉应力都随着材料热膨胀系数的增大而增大,且在焊缝附近区域的增幅比较明显。
5.3 材料热传导率在假定其他参数相同的情况下,分别设热传导率为16.3,26.3和36.3,对典型耐压壳焊接接头模型进行焊接残余应力的数值模拟计算,结果如图10及表6所示。
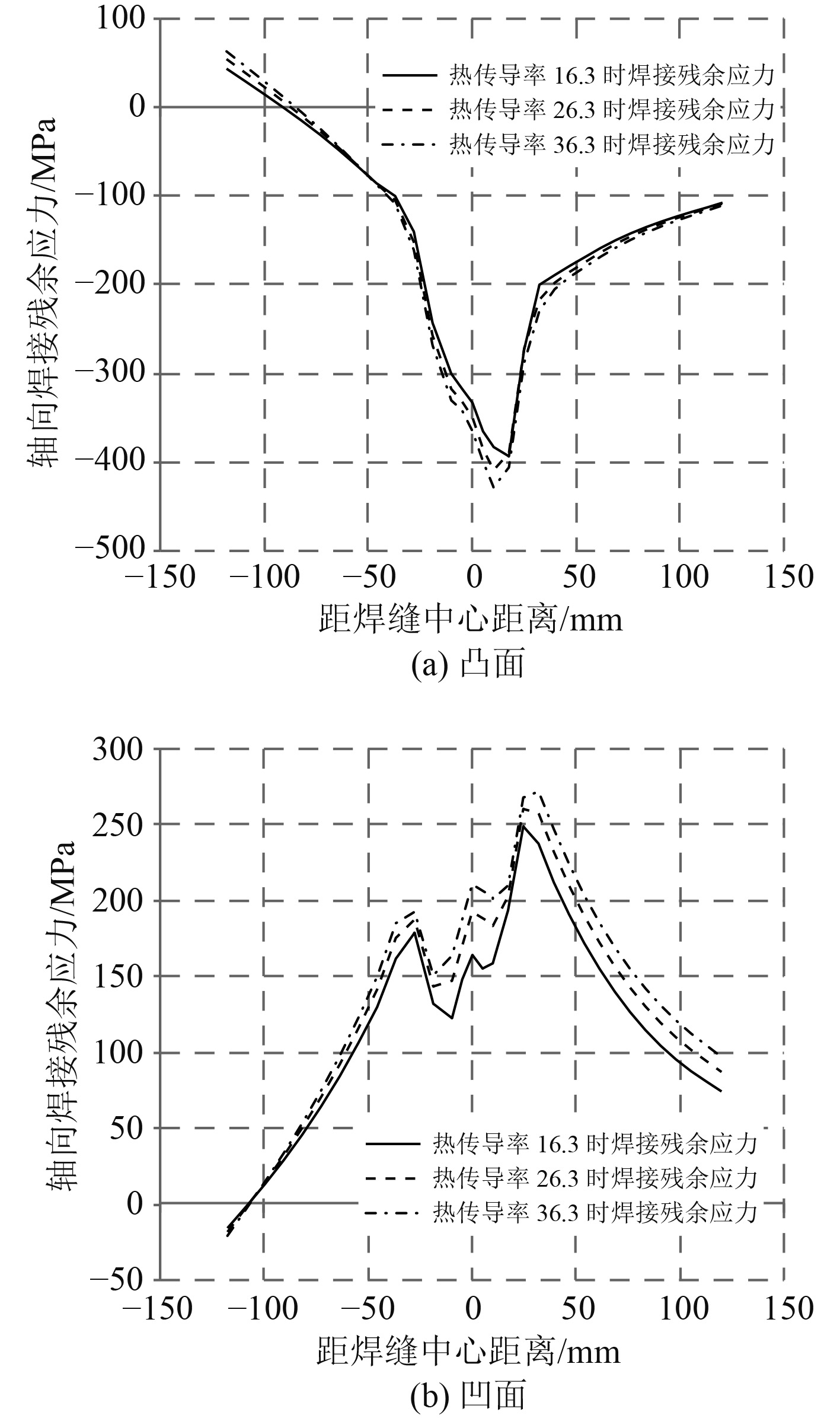
|
图 10 热传导率对模型轴向焊接残余应力的影响 Fig. 10 Effect of thermal conductivity on axial welding residual stress |
|
|
表 6 不同热传导率的模型轴向焊接残余应力最大值(MPa) Tab.6 Maximum axial welding residual stress with the different thermal conductivity (MPa) |
可以看出,当材料热传导率增大时,模型凸面的轴向焊接拉应力和凹面的轴向焊接残余压应力都不断加大。
6 边界条件对耐压壳模型焊接残余应力的影响在假定其他参数相同的情况下,分别设边界条件两边端面8个点约束、4条边约束及8条边约束(约束由弱到强),对典型耐压壳焊接接头模型进行焊接残余应力的数值模拟计算,结果如图11及表7所示。
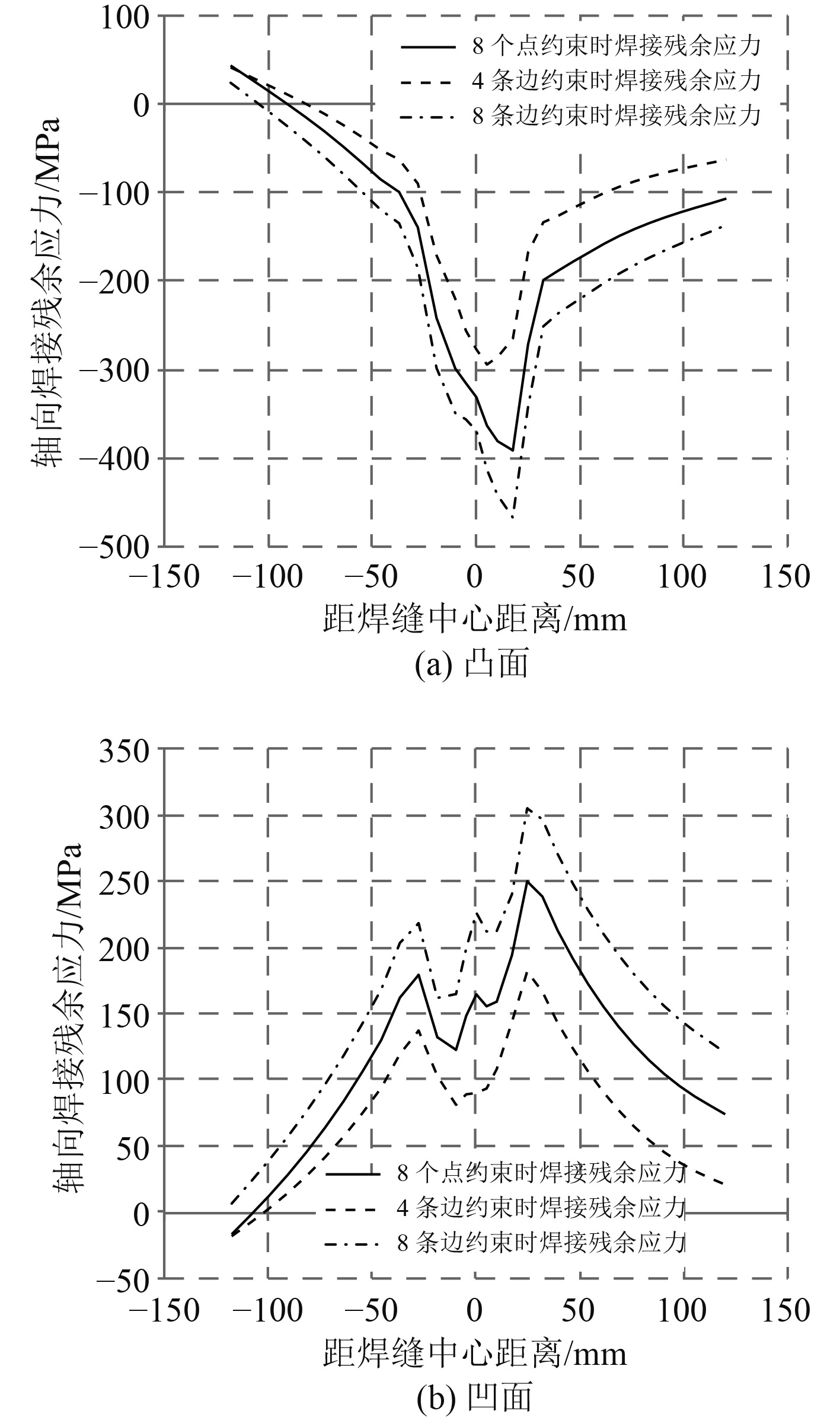
|
图 11 边界条件对模型轴向焊接残余应力的影响 Fig. 11 Influence of boundary condition on axial welding residual stress |
|
|
表 7 不同边界条件的模型轴向焊接残余应力最大值(MPa) Tab.7 Maximum axial welding residual stress with the different boundary conditions (MPa) |
可以看出,当边界条件不同时:
1)轴向焊接残余应力的分布趋势基本保持一致;当约束减弱时,模型凹面的轴向焊接残余拉应力的双峰分布更为明显;
2)随着约束的增强,模型凸面轴向焊接残余压应力及凹面轴向焊接残余拉应力的应力水平都会有不同程度的增加。
7 结 语通过对高强度钢典型焊接接头残余应力及相关参数对残余应力影响的研究,可以得到以下结论:
1)材料属性和边界条件和对耐压壳典型焊接接头模型残余应力有影响;改变材料属性和边界条件后,耐压壳典型焊接接头模型残余应力分布趋势不发生明显改变,只是应力值发生了变化,并在焊缝附近区域表现更为明显。
2)在边界条件相同的情况下,当材料屈服强度、材料膨胀系数以及热传导率增大时,模型凸面的轴向焊接残余压应力以及凹面的轴向焊接残余拉应力都随之增大;当材料屈服强度增加时,相对模型凸面轴向焊接残余压应力的增加,模型凹面轴向焊接残余拉应力的增加不大。
3)在材料属性相同的情况下,当边界约束增强时,模型凸面轴向焊接残余压应力和凹面轴向焊接残余应力拉应力都会有不同程度的增加;随着边界约束的减弱,模型凹面的轴向焊接残余拉应力的双峰分布更为明显。
| [1] |
张可成, 罗广恩, 李良碧. 潜艇锥柱典型节点表面裂纹扩展数值模拟[J]. 舰船科学技术, 2012, 34(3): 9-14. DOI:10.3404/j.issn.1672-7649.2012.03.002 |
| [2] |
候海量, 洪江波, 刘润泉, 等. 潜艇耐压环焊缝焊接残余应力模拟试验研究[C]. 2005年船舶结构力学学术会议, 2005.
|
| [3] |
McGregor R, Rogge R. Residual stress characterization of a fabrication weld from the VICTORIA-Class submarine pressure hull: Revealing the unseen[J]. Canadian Journal of Physics, 2010, 88(10): 759-770. DOI:10.1139/P10-076 |
| [4] |
董师润, 顾晓波, 徐秉汉, 等. 提高潜艇重要构件疲劳寿命的工艺措施——超声冲击技术[J]. 2004, 45(3), 38−42.
|
| [5] |
石德新, 耿峰, 黄小平, 等. 潜艇结构疲劳裂纹形成寿命的分析[J]. 哈尔滨工程大学学报. 2000, 21(3), 70−74.
|
| [6] |
拉达伊. 焊接热效应: 温度场﹑残余应力﹑变形[M]. 北京: 机械工业出版社, 1997.
|
 2021, Vol. 43
2021, Vol. 43

