0 引　言

裂纹是船体局部结构一种重要的损伤形式，对船体结构安全影响非常大。损伤模式分类是把样本数据分为若干类，对于待分析的新数据，基于某种分类方法对该数据所属类别进行判定^[1]。船体结构在不同的损伤状态下会表现出不同的响应模式，提取出对应状态下的特征参数，以此作为分类依据，可以实现损伤模式分类。首先需要确定结构的各种基准模式状态，然后再将待分析模式状态与基准模式状态比较，最后确定待分析模式状态所属的类别。利用支持向量机的方法进行故障诊断和模式分类已经取得了一定的效果。高伟等^[2]通过SVD方法得到有效奇异值并作为特征量，输入到多级SVM进行训练和分类识别，对配电网10种故障模式具有较高的识别正确率。李辉等^[3]以水电机组振动信号作为分析对象，采用经验模态分解和SVM相结合的方法，确定故障类型并为机组维修人员提供参考依据。陈勇旗等^[4]通过ITD方法处理滚动轴承振动信号，将特征值输入到支持向量机，实现了滚动轴承的故障诊断。可见，SVM方法在故障诊断方面具有一定的可行性和有效性，但是SVM在船体结构裂纹识别方向的研究成果并不多见。

本文以十字加筋板作为分析对象，裂纹所在不同位置代表不同的损伤模式，通过试验获得振动信号，采用ITD-SVD和SVM相结合的方法，实现裂纹损伤模式分类识别。

1 基于ITD-SVD的特征向量提取方法

固有时间尺度分解（ITD）以线性变换为基础，可以将振动信号分解为固有旋转分量（PRC）和一个余项之和，进而得到原始信号不同频率点上信号幅值累计分布情况。对于一个给定的振动信号 ${X_t}$ ，ITD算法对信号分解过程如下^[5]：

定义基线提取因子 $L$ ，利用 $L$ 从振动信号 ${X_t}$ 中提取和分离基线信号，剩余项我们称其为旋转分量（PRC）。该过程可以描述为：

${X_t} = L{X_t} + \left( {1 - L} \right){X_t} = {L_t} + {H_t}{\text{。}}$

(1)

式中： ${L_t}$ 为基线信号（低频信号部分）； ${H_t}$ 为PRC（高频信号部分）。

对式（1）中的基线信号 ${L_t}$ 再做如上的分解过程，直至基线信号变为单调函数或信号中少于3个极值点时，分解结束。振动信号 ${X_t}$ 的整个分解过程可表示为：

$\begin{split} {X_t} = &H{X_t} + L{X_t} = H{X_t} + (H + L)L{X_t} = \\ &[H(1 + L) + {L^2}]{X_t} = \left(H \displaystyle \sum\limits_{k = 0}^{p - 1} {{L^k}{\rm{ + }}{L^p} )} \right){X_t}\text{。}\end{split} $

(2)

式中： $H{L^k}{X_t}$ 是第 $k + 1$ 层PRC分量； ${L^p}{X_t}$ 为振动信号单调趋势分量，即最后获得的余项。

PRC分量和余项包含振动信号的特征信息，对PRC分量和余项构成的特征矩阵进行奇异值分解（SVD），得到2个正交矩阵和1个对角阵，对角阵中的元素是由大到小排列的奇异值，选取前2阶奇异值构成二维特征向量，实现了振动信号特征向量的提取。

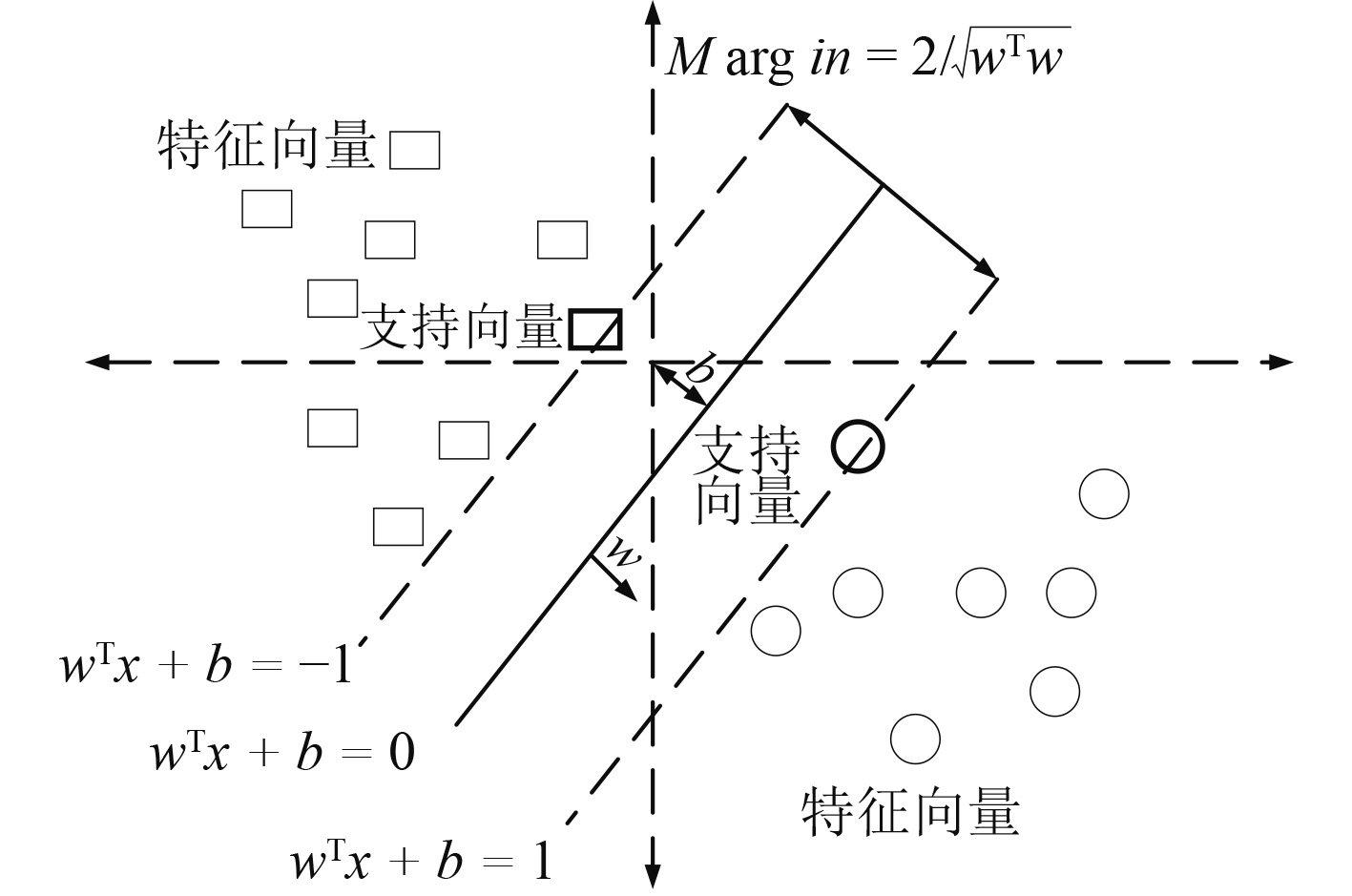
2 基于SVM的分类方法

对不同的振动信号进行ITD-SVD处理，可以提取到不同的特征向量，作为SVM二分类算法的样本数据。不同的特征向量在二维平面上表示为不同的点，SVM分类就是在两类特征向量点之间确定最优超平面，使其间隔最大，实现分类功能，其示意图如图1所示。

图中， $w$ 为法向量，决定了超平面的方向， $b$ 为位移量，决定了超平面与原点的距离。准确的分类需要特征差异显著的输入数据，即特征向量差异越显著，分类效果越好，分类准确率越高。

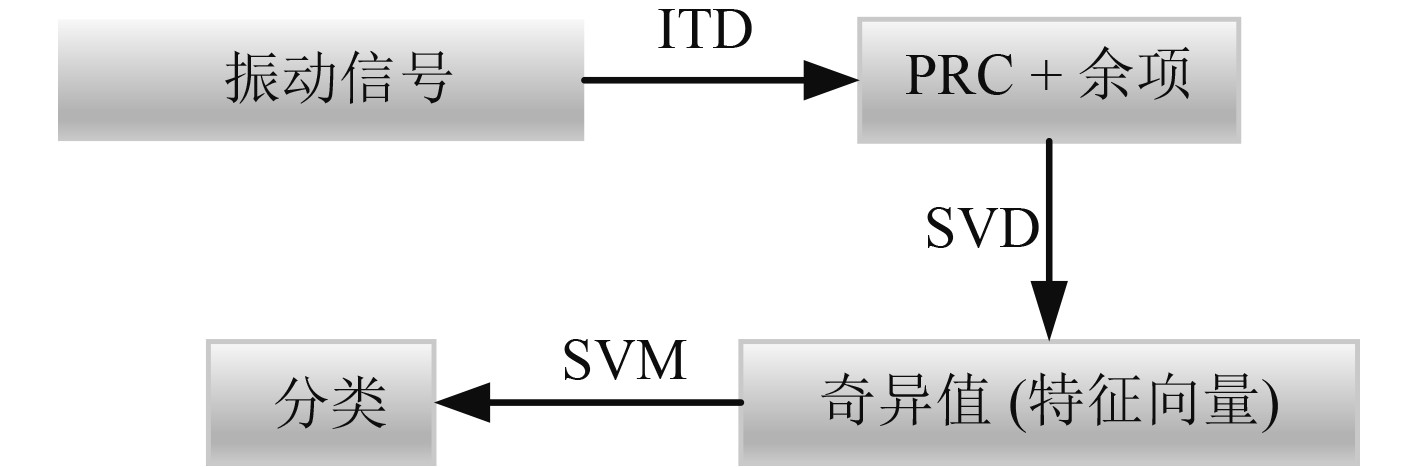
提出的基于SVM分类方法流程图如图2所示。

3 十字加筋板损伤模式分类识别

为了实现SVM算法在典型船体结构损伤模式识别中的应用，选取含裂纹损伤的十字加筋板作为分析对象，进行损伤模式分类方法研究。

3.1 十字加筋板固有模态试验

依据《船体结构疲劳强度指南》^[7]，焊接节点处由于应力集中或焊接工艺不达标产生的缺陷和咬边，容易造成疲劳裂纹从焊趾处延伸到母材。船体板结构尤其是船体外板、甲板板，接触海水，在腐蚀情况严重时甚至会产生穿透型裂纹。本文以十字加筋板作为典型船体局部结构，试验板如图3所示。

其中，a类板是穿透型裂纹位置在面板上（模式1），b类是穿透型裂纹在骨材上（模式2），以上述2种模式作为损伤模式进行分类识别研究。对其进行固有模态试验，试验装置如图4所示。

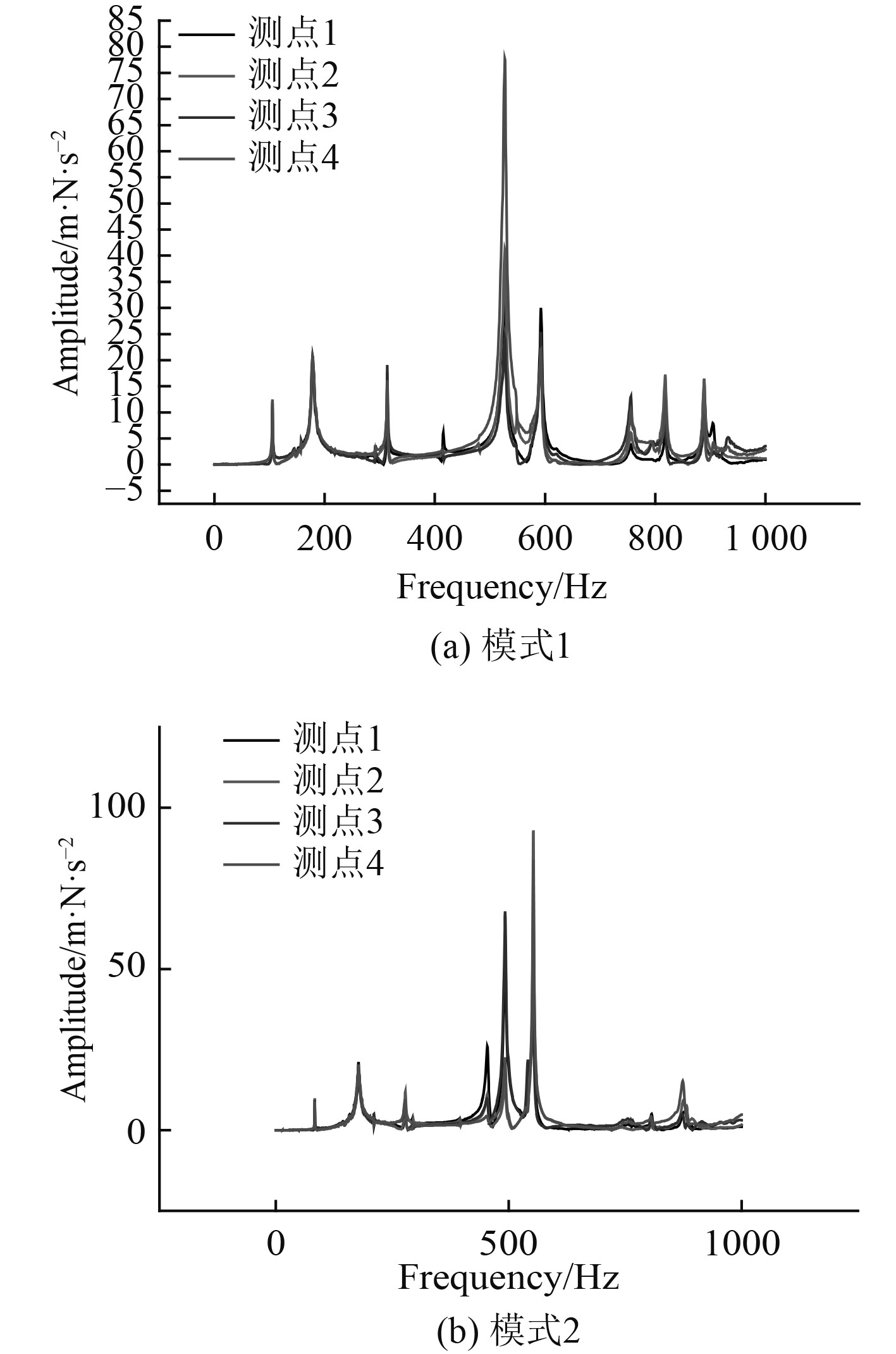
每种损伤模式有3块试验板，板的中央位置加载锤击激励载荷，每次试验进行3次敲击，通过板上4个测点处的加速度传感器，将振动信号传递至计算主机，振动信号谱图如图5所示。

3.2 损伤特征向量的提取

分别对两类模式中的谱线进行ITD处理，获得分解图如图6所示。

前2个PRC分量组成特征矩阵，应用SVD方法得到2个奇异值，如表1所示。

表1中的结果是对2条谱线进行SVD分析后得到的，2种模式各选取15条谱线进行SVD分析，得到30组损伤特征向量，为基于SVM算法的分类识别提供了样本数据。

3.3 SVM算法在损伤模式分类识别中的应用

以Matlab软件为平台，选取上述30组损伤特征向量作为输入向量，其中20组数据是带有类别标签的训练样本数据，另外10组数据是验证样本数据，需要对其进行类别预测。利用SVM工具箱中的函数对十字加筋板2种典型损伤模式进行分类识别研究。由于线性分类器分类效果更为直观，分类速度快，所以选用线性核函数linear参数，得到20组样本分类图如图7所示。

由于训练样本数据类别已知，通过有监督的学习方法，SVM对20组训练样本数据进行了正确分类。

为了评估SVM算法对验证样本进行分类预测的准确性，引入BP神经网络算法进行对比分析。BP神经网络是应用最为广泛的机器学习算法，在损伤识别领域具有一定的识别准确率。上述20组损伤特征向量作为训练样本，通过有监督的学习方法，BP神经网络进行学习，形成损伤特征向量到所属类别的映射关系。2种算法对10组验证样本数据进行类别预测，类别预测结果如表2所示。

从表2可以看出，以实际输出向量的正负号评价分类结果，SVM模式分类识别准确率达到90%，而BP算法对其中的2个标签为1的样本识别成了标签0，识别准确率为80%，SVM算法识别准确率更高，选用二分类SVM算法可以对2种损伤模式进行准确的分类和识别。由于工程实际中大多是获得数量有限的小样本试验数据，相比于BP神经网络算法，SVM分类算法对于小样本试验数据具有更好的工程应用价值。

4 结　语

为识别典型船体结构的裂纹损伤，本文提出提取振动信号特征向量，通过SVM对其特征向量进行分类的方法，并进行十字加筋板固有模态频率响应试验验证方法的可行性和有效性。对振动信号谱图运用上述ITD-SVD方法得到特征向量，作为SVM的样本数据，以实际输出向量的正负号评价分类结果，模式分类识别准确率达到90%，BP算法识别准确率为80%，表明SVM算法对于十字加筋板损伤模式分类具有一定的正确性和可行性。由于工程实际中多是获得有限样本数据，与BP算法进行比较后，证明了SVM算法可以对小样本数据进行更为准确的分类，具有较大的工程应用价值，可以为结构的维修保养和管理决策提供有效指导。