船舶螺旋桨安装在船体尾部,由于船体和附体的影响,导致螺旋桨的进流在空间分布非均匀,螺旋桨在旋转过程中会产生不定常桨叶载荷,一方面,螺旋桨不定常的载荷可以通过轴系传递到船体上,这种通过轴系传递到船体上的螺旋桨非定常力称为轴承力;另一方面,桨叶表面的非定常压力还会引起周围流体压力的变化,从而引起船体表面的压力产生周期性的脉动,这种螺旋桨非定常载荷通过流体引起船体表面的压力脉动称之为螺旋桨诱导的船体脉动压力,螺旋桨轴承力和螺旋桨诱导的脉动压力统称螺旋桨激振力,螺旋桨激振力是船体尾部振动和噪声的主要来源。
国内某五叶双桨水面船由于发生意外,其左侧螺旋桨发生了变形,继而发生了异常振动现象,无论在中速还是高速工况,船体尾部振动和噪声比变形前明显增大,船体尾部的振动超出了规定范围,在双轴工况时,左舷中间轴承比右舷中间轴承的总振级大13%,左轴功率比右轴功率明显增大,而且左轴较右轴有较为明显的其他倍轴频特性,这严重影响了船舶的航行性能。经过检测,发现有4片叶片发生了变形,其中2片叶片变形较大。将受损变形的左桨更换为新的备用桨后,振动异常的情况就消失了。因此,可以判断出是螺旋桨发生的变形导致了船体异常振动现象。
本文将针对该实际问题中的原桨以及变形桨,在船体非均匀伴流的条件下进行CFD计算,研究螺旋桨变形对螺旋桨动惯性矩、轴承力和脉动压力的影响进行分析,形成一套非均匀伴流场下螺旋桨变形对其激振力影响的数值计算方法,该方法既可以对变形螺旋桨的振动性能进行评估,也可以为确定加工容许误差或变形容许范围提供理论基础,具有重要的理论意义和工程应用价值。
1 数值计算方法研究为了分析螺旋桨在非均匀伴流场工作时的激振力,以标准桨 DTMB P4119为研究对象,对计算的区域大小设置、网格划分形式进行研究,初步形成一套非均匀伴流场中螺旋桨激振力数值计算方法,以达到所需要的预报精度。
1.1 控制方程与湍流模型在不可压缩流体的条件下,流场的连续方程和动量方程分别为:
| $ \begin{aligned} \displaystyle\frac{{\partial {u_i}}}{{\partial {x_i}}} =0\text{,}\qquad\qquad\qquad\qquad\\ \rho\dfrac{\partial(u_iu_j)}{\partial x_j}= \displaystyle\frac{{\partial p}}{{\partial {x_i}}} + {\rm{\rho}} {g_i} + {\rm{\rho}} \displaystyle\frac{\partial }{{\partial {x_j}}}\left[ {\mu \left( {\frac{{\partial {u_i}}}{{\partial {u_j}}} + \frac{{\partial {u_j}}}{{\partial {u_i}}}} \right) - \overline {u_i^\prime u_j^\prime } } \right]{\text{。}} \end{aligned} $ |
式中:
方程中出现了新的未知量雷诺应力,所以要使方程封闭就要对雷诺应力项进行某种假定,即建立应力的表达式或者引入新的湍流模型,将其中的脉动值和时均值联系起来。
为了实现控制方程组的封闭,引入新的湍流模型。根据文献[3],本文采用可实现的k−ε两层模型。
1.2 研究对象以标准桨DTMB P4119为研究对象,采用滑移网格对其进行数值计算。该桨的主尺度与几何示意图分别如表1和图1所示。
|
|
表 1 DTMB P4119螺旋桨主要参数 Tab.1 Main parameters of DTMB P4119 |

|
图 1 DTMB P4119螺旋桨 Fig. 1 The propeller DTMB P4119 |
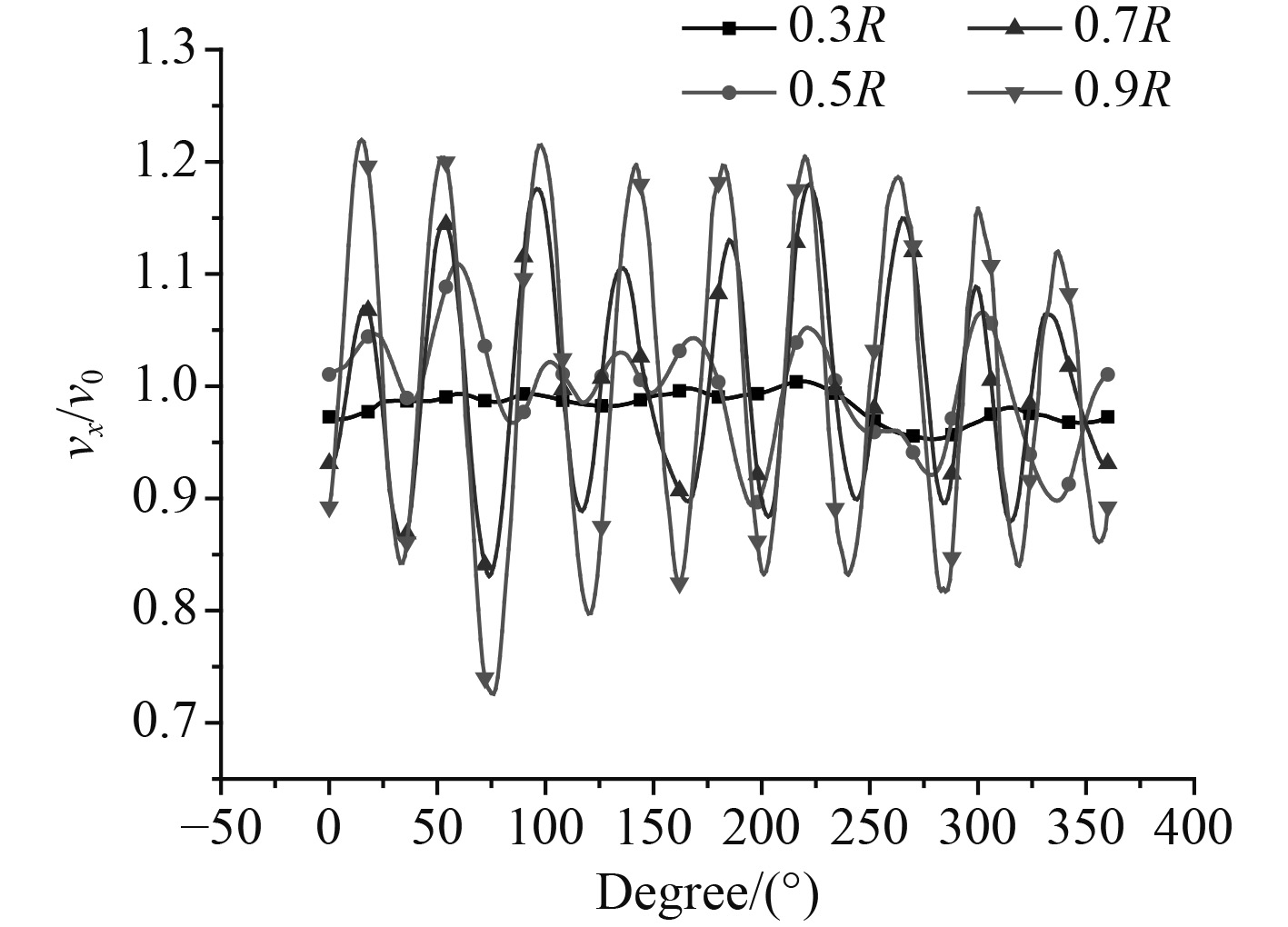
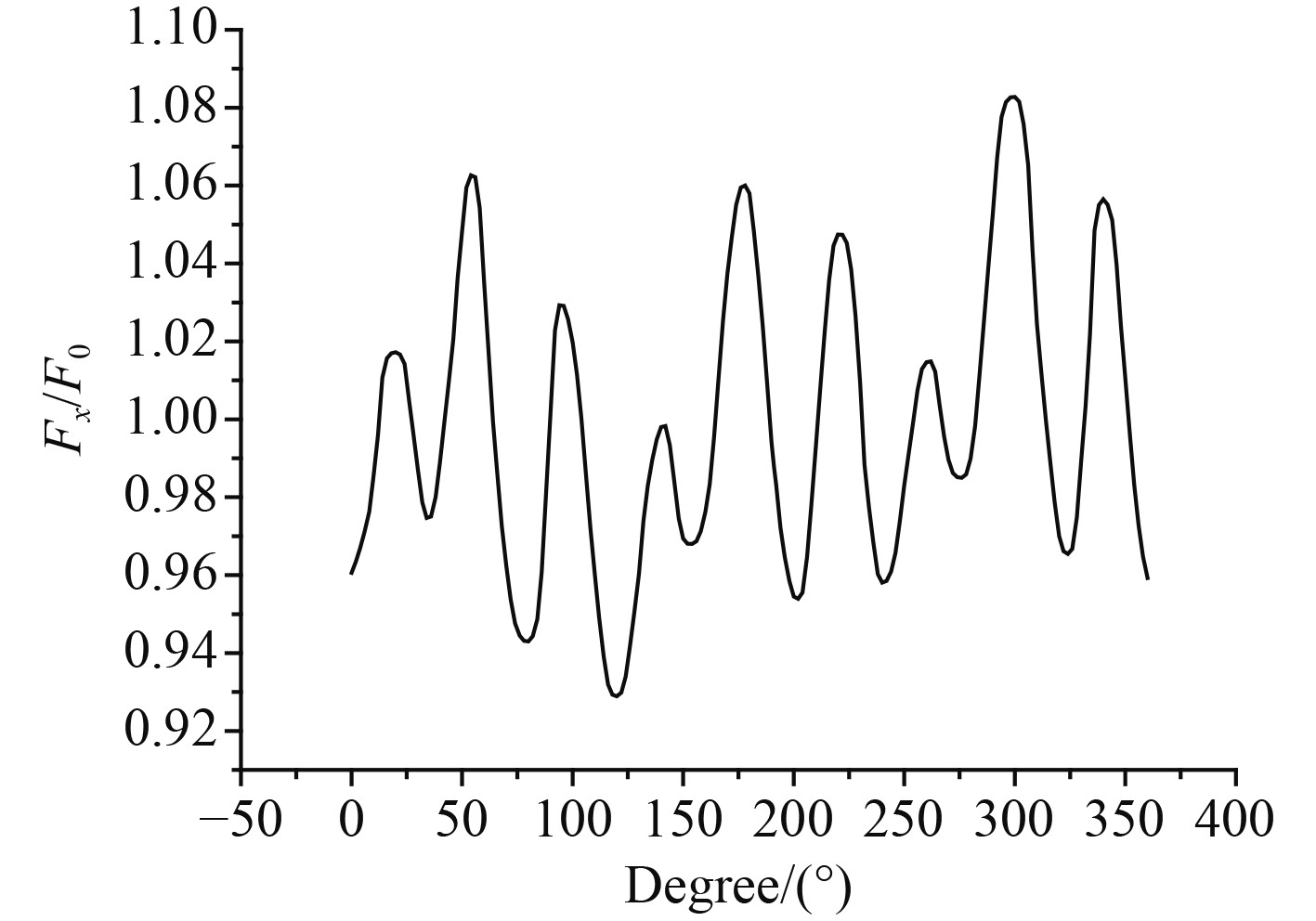
螺旋桨转速取为30 r/min,桨盘面处的轴向平均速度V0为9.996 m/s,周向伴流和径向伴流很小,可忽略不计,桨盘面各半径处的轴向速度分布如图2所示。图中R为螺旋桨半径,从桨后方沿着桨轴方向观察,12点钟方向为0o角度位置,3点钟方向为90o角度位置。在该条件下,测量得到的螺旋桨非定常力如图3所示。
|
图 2 伴流场速度分布曲线 Fig. 2 Velocity distribution curves of wake field |
|
图 3 非定常力实验结果 Fig. 3 Experimental results of unsteady forces |
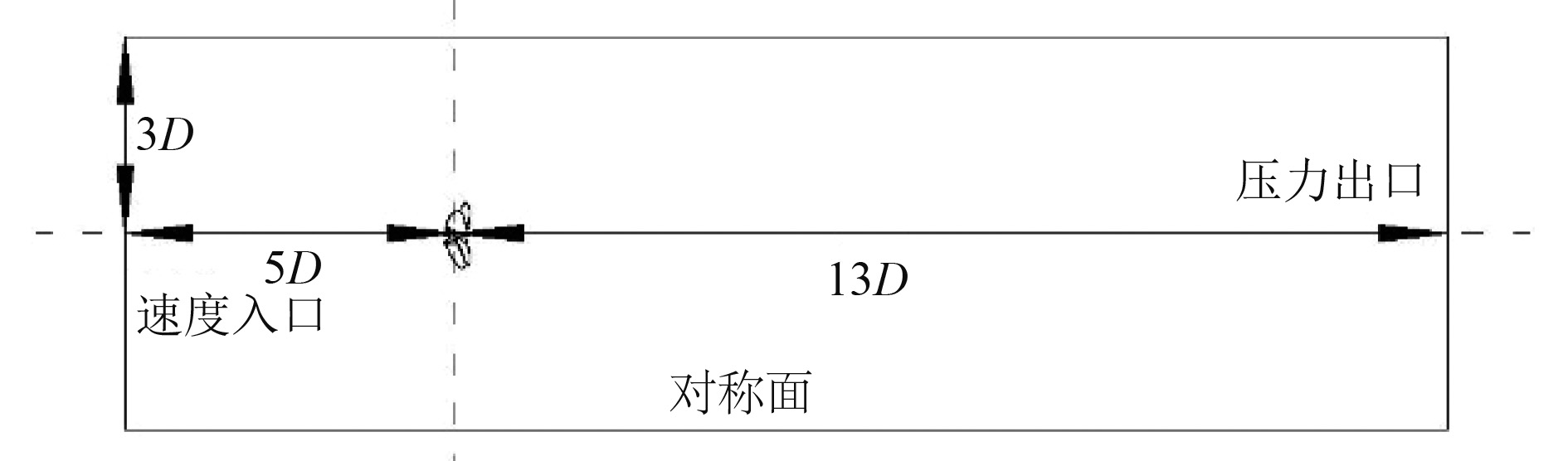
模型试验中螺旋桨的伴流场是在桨盘面处测量得到的,但在CFD数值计算中,无法直接在桨盘面处设置非均匀伴流分布,一般是在速度入口处设置非均匀伴流分布。速度入口处的非均匀伴流传递到桨盘面处存在着速度耗散,伴流分布形式会发生变化,影响速度耗散的主要因素是速度入口的位置,速度入口距桨盘面越远,耗散越大,因此入口处距桨盘面的距离不能太大。但如果入口处距桨盘面的距离太近,由于边界条件形式与实际情况的差异,会无法正确反映螺旋桨诱导速度对周围流场的影响,通过计算,速度进口位置距桨盘面的距离在6倍直径以内,速度耗散对非定常力的影响可以忽略,速度进口位置距桨盘面的距离在3倍直径以上时,引起的螺旋桨诱导速度的误差可以忽略。综合考虑上述影响,将速度进口的位置设置在距桨盘面5D处。区域尺寸设置如图4所示。旋转域直径只需稍大于螺旋桨直径,取为0.42 m。
|
图 4 计算区域划分 Fig. 4 The division of calculation area |
在进行网格划分时,考虑到存在非均匀伴流场的输入,当速度入口处的网格尺寸太大时,可能无法对伴流场的速度进行精确捕捉以及传递。在实际计算时因没对入口处进行加密导致非定常力的部分波峰和波谷的缺失,所以要对速度入口以及速度入口到桨盘面处的传递路径进行加密。
根据图2可知,已知3个半径处的伴流场的数据,入口其他半径处的速度值可通过插值得到,并且入口大半径处的伴流场对结果影响较小。所以为了节省网格数量,提高计算效率,并综合考虑螺旋桨对流体的扰动,在速度入口以及速度入口到桨盘面处的传递路径设置一个半径为2R的圆柱加密体,计算区域网格划分如图5所示。

|
图 5 计算区域网格划分 Fig. 5 The mesh of calculation area |
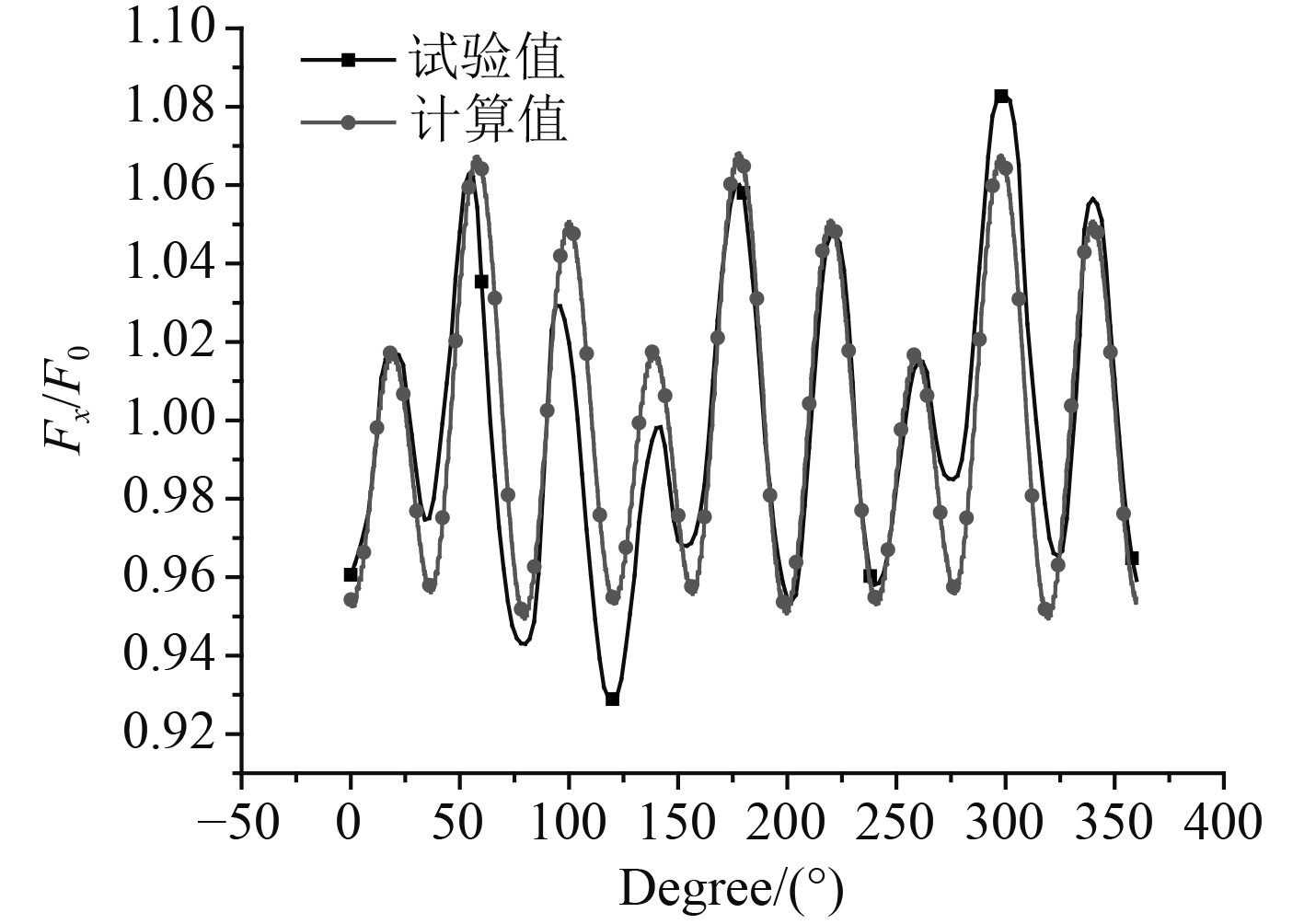
其余网格以及求解设置参考文献[7-9],以该方法对非均匀伴流场下的螺旋桨激振力进行计算,计算值与试验值对比结果如图6所示。可以发现该结果从变化规律上与试验结果一致,并且拟合程度较好,说明该方法能够对非均匀伴流场下的螺旋桨激振力进行较为准确的预报。
|
图 6 轴向力对比曲线 Fig. 6 Contrast curves of axial force |
本文所计算的螺旋桨原桨几何模型如图7所示,主尺度如表2所示。

|
图 7 螺旋桨原桨几何模型 Fig. 7 Geometric model of the propeller |
|
|
表 2 螺旋桨主要参数 Tab.2 Main parameters of the propeller |
螺旋桨受损变形后,通过三维扫描方式对其几何形状进行测量。结果显示,变形桨与原桨相比,变形桨的4片桨叶存在变形,其中2片变形较大,并且变形大多存在于0.7,0.8,0.9等半径处,且最大变形发生在随边处。其中1号,5号桨叶在0.8,0.9,0.95,0.975倍半径处螺距与标准值偏差约5%~15%,2号、4号桨叶在上述半径处的螺距与标准值偏差约1%~4%,均超出了规范的允许范围,3号叶片数据符合要求,其中1号桨叶变形对比如图8所示。

|
图 8 桨叶变形对比 Fig. 8 Comparison of pre and post deformed propeller |
原桨和受损变形桨采用缩比模型进行计算,螺旋桨缩比模型的直径为0.2 m,计算域与网格划分方法与1.3节中的方法一致。
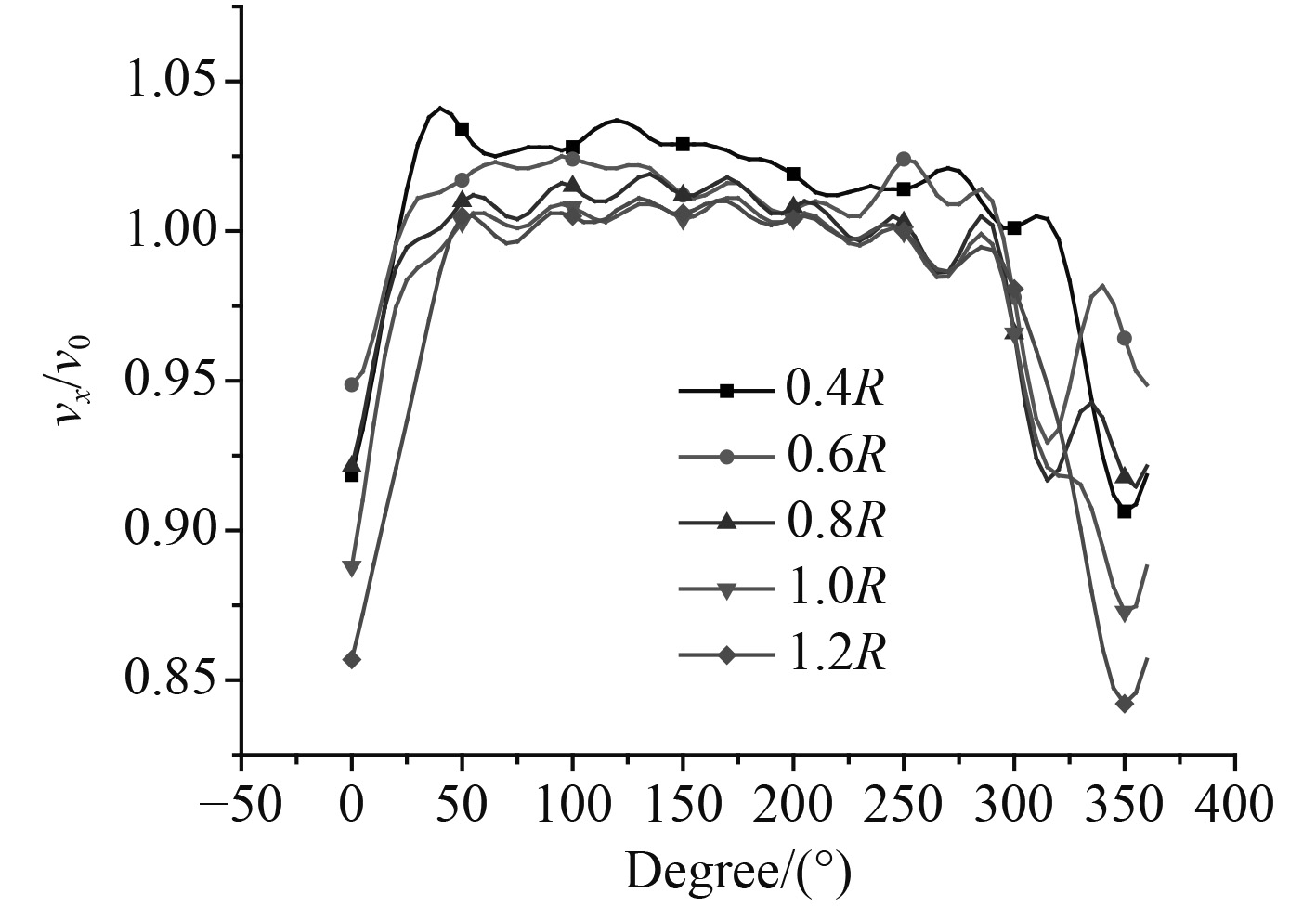
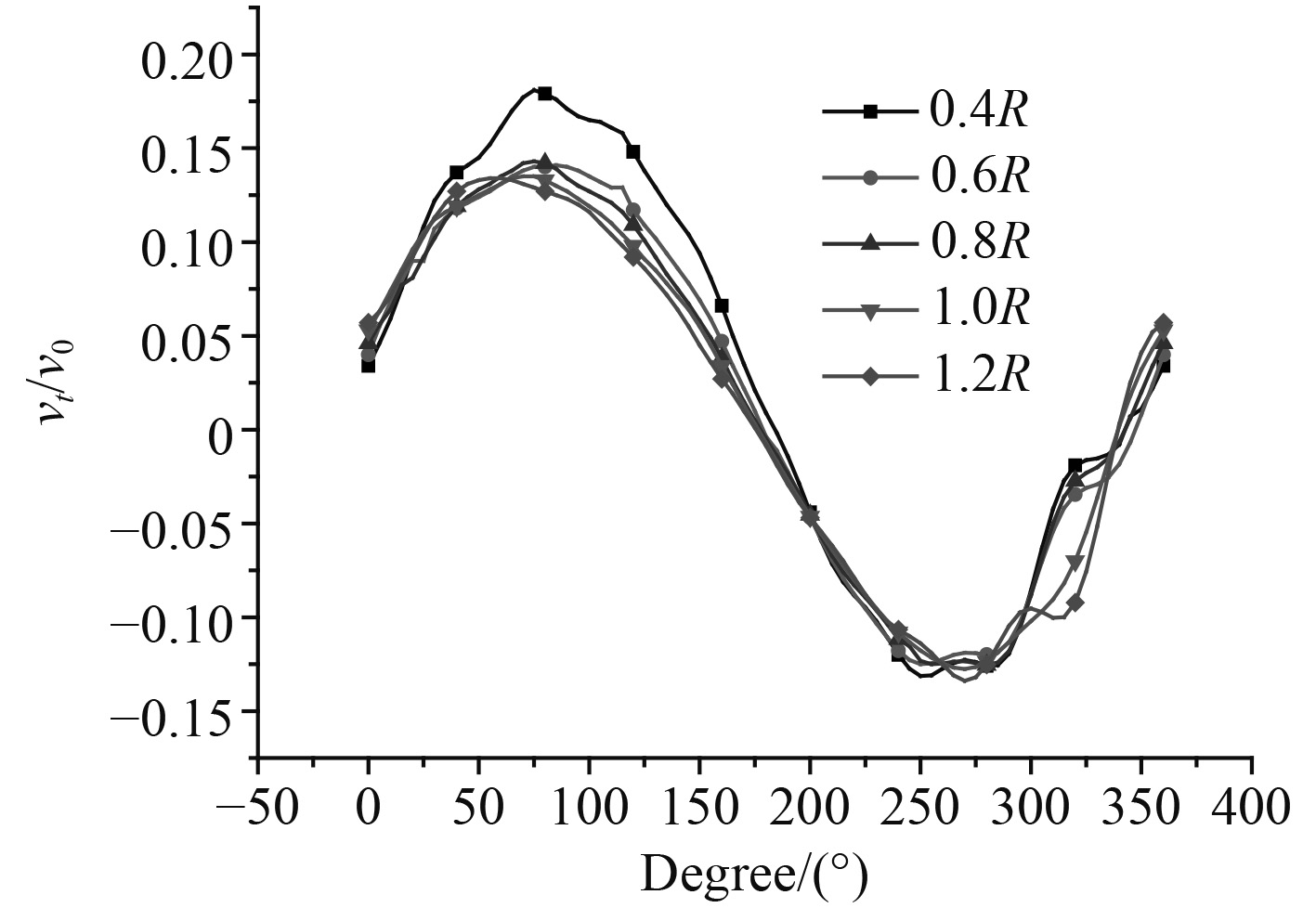
进速Vs设定为4 m/s,转速为1200 r/min。将实船下螺旋桨处的无因次伴流场进行换算后作为速度入口的输入量,该无因次伴流场轴向速度分布如图9所示,周向速度分布如图10所示。
|
图 9 伴流场轴向速度分布 Fig. 9 Axial velocity distribution of wake field |
|
图 10 伴流场周向速度分布 Fig. 10 Circumferential velocity distribution of wake field |
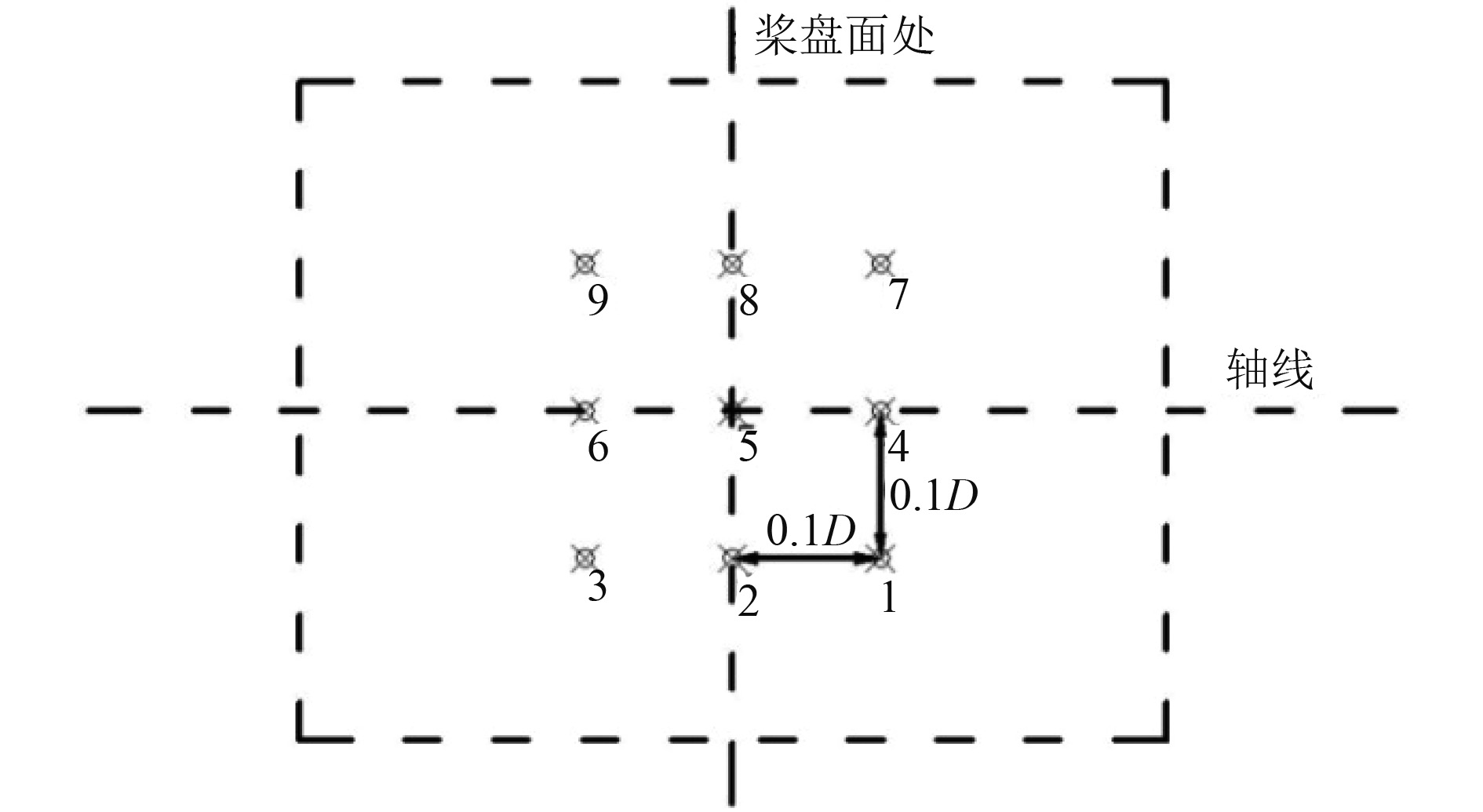
为了分析桨叶受损变形对螺旋桨诱导脉动压力的影响,在距桨叶梢以上0.1D水平平面取9个点作为脉动压力的监测点,该平面处点的分布形式如图11所示。
|
图 11 0.1D平面处监测点分布 Fig. 11 Distribution of monitoring points at the 0.1D plane |
在所建立的三维坐标系中,x方向沿着桨轴方向,正方向指向下游;z轴正方向竖直向上;y轴正方向指向船体右舷。在此坐标系下,螺旋桨在3个方向上随时间变化的力和力矩分别记为
| $ \begin{array}{*{20}{c}} {F_i^\prime \left( t \right) = \displaystyle\frac{{{F_i}\left( t \right)}}{{{\rm{\rho}} {n^2}{D^4}}}}\text{,}\\ {M_i^\prime \left( t \right) = \displaystyle\frac{{{M_i}\left( t \right)}}{{{\rm{\rho}} {n^2}{D^5}}}}\text{。} \end{array} $ |
式中:
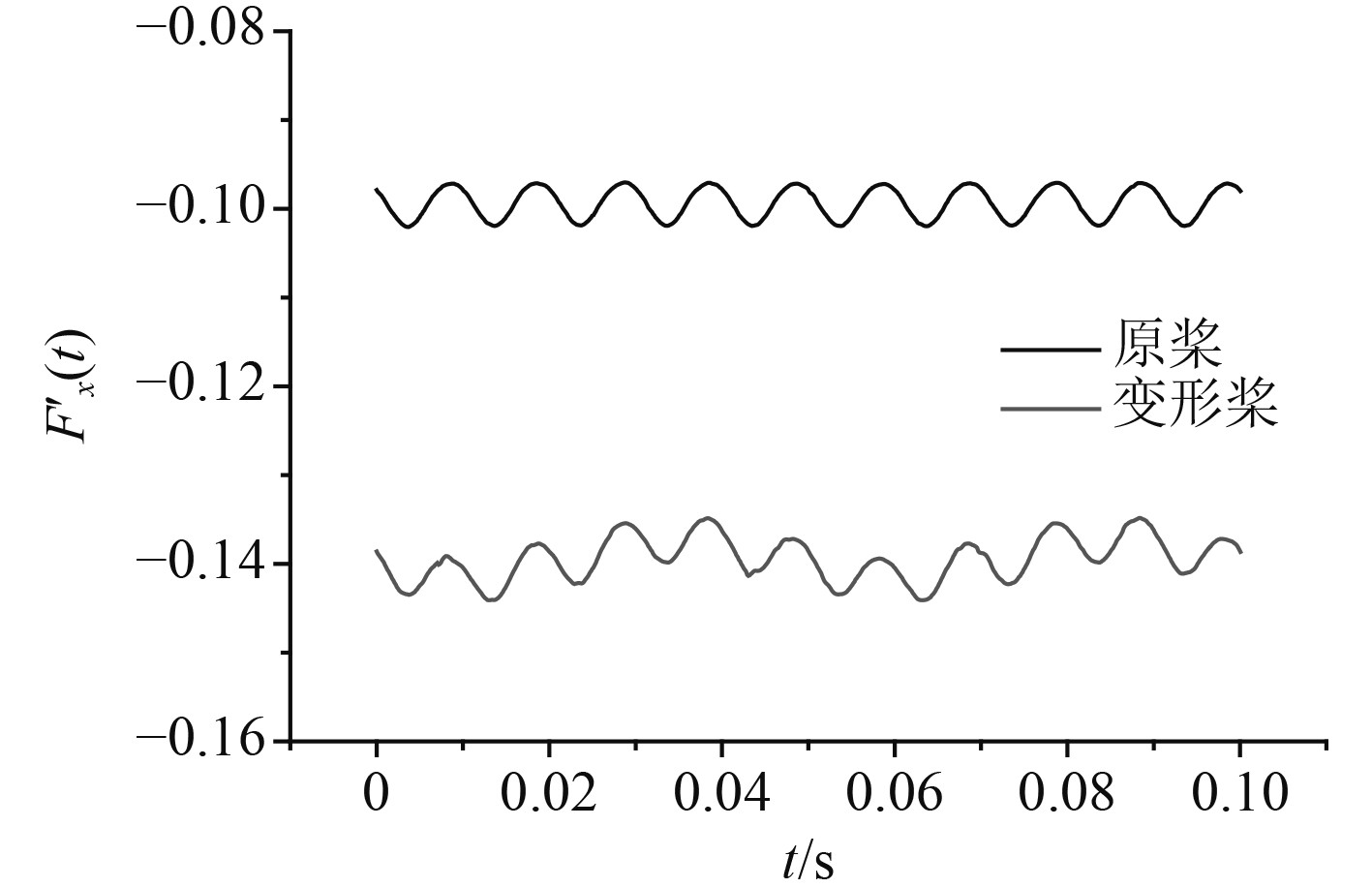
原桨和受损变形桨在轴向、垂向以及横向上的非定常力和力矩的时历曲线计算结果如图12~图17所示,对该结果进行Fourier分析,可以得到频域分析结果,如表3~表4所示。
|
图 12 螺旋桨变形前后轴向非定常力对比 Fig. 12 Comparison of unsteady axial forces before and after propeller deformation |
|
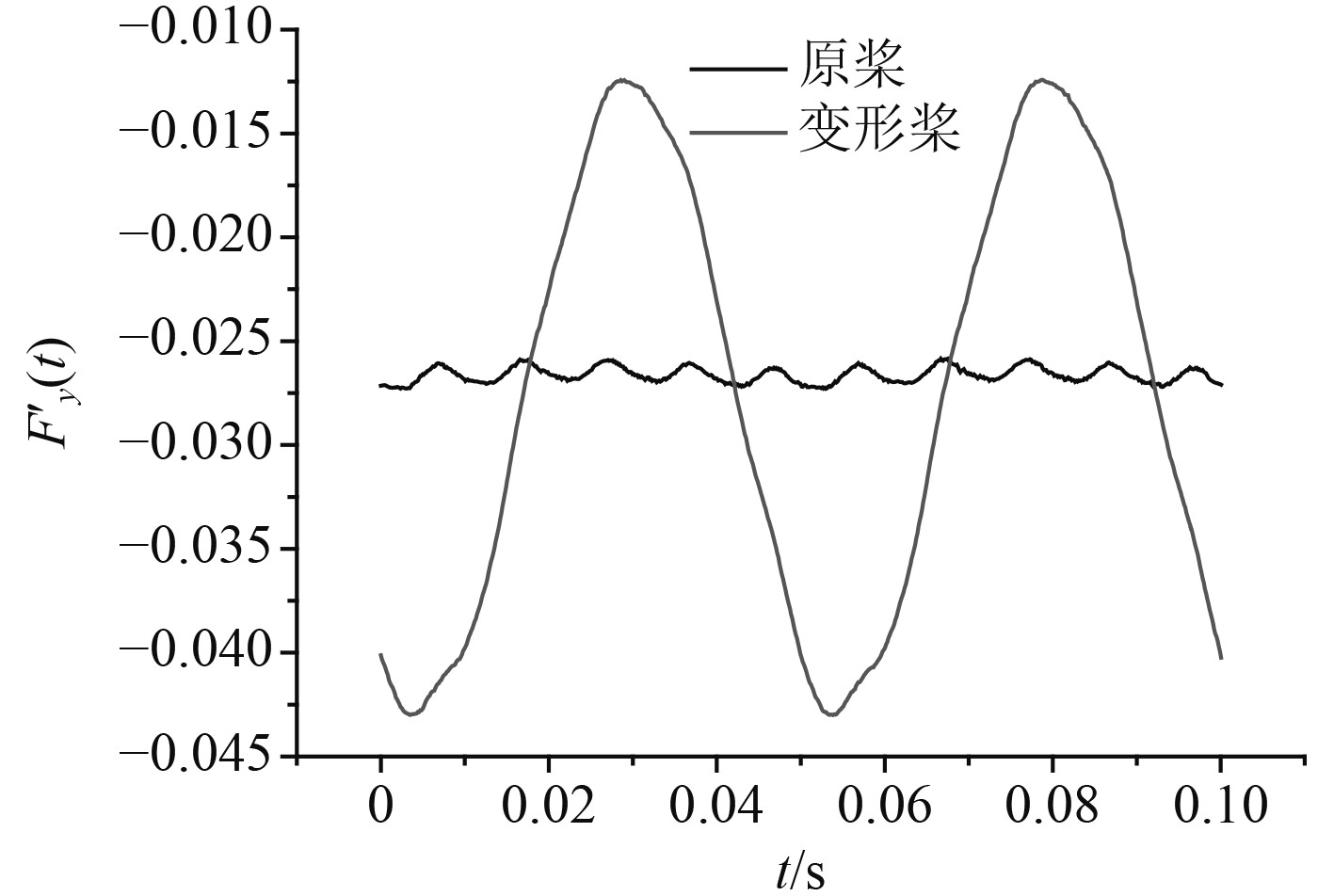
图 13 螺旋桨变形前后横向非定常力对比 Fig. 13 Comparison of unsteady transverse forces before and after propeller deformation |
|
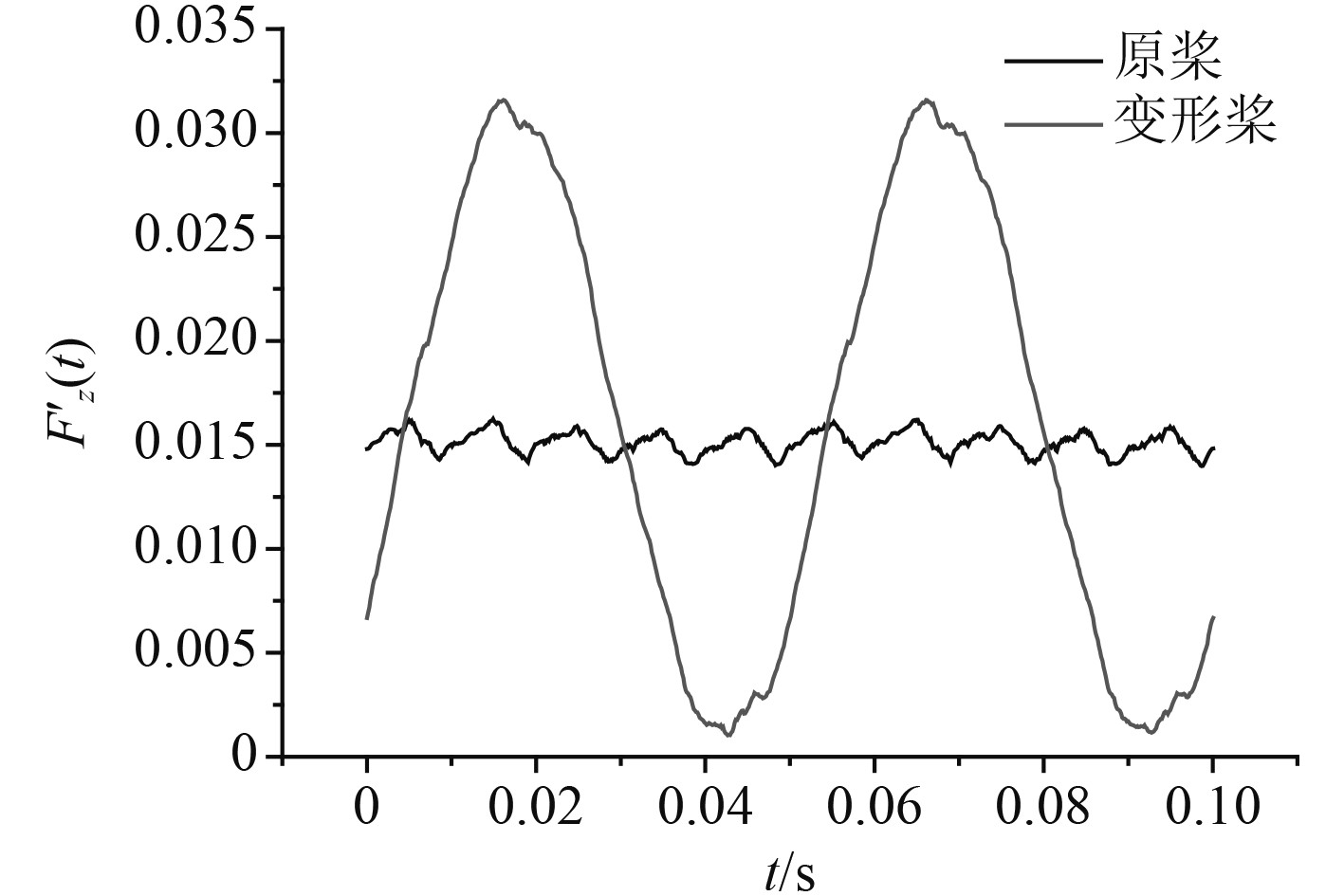
图 14 螺旋桨变形前后垂向非定常力对比 Fig. 14 Comparison of vertical unsteady forces of pre and post deformed propeller |
|
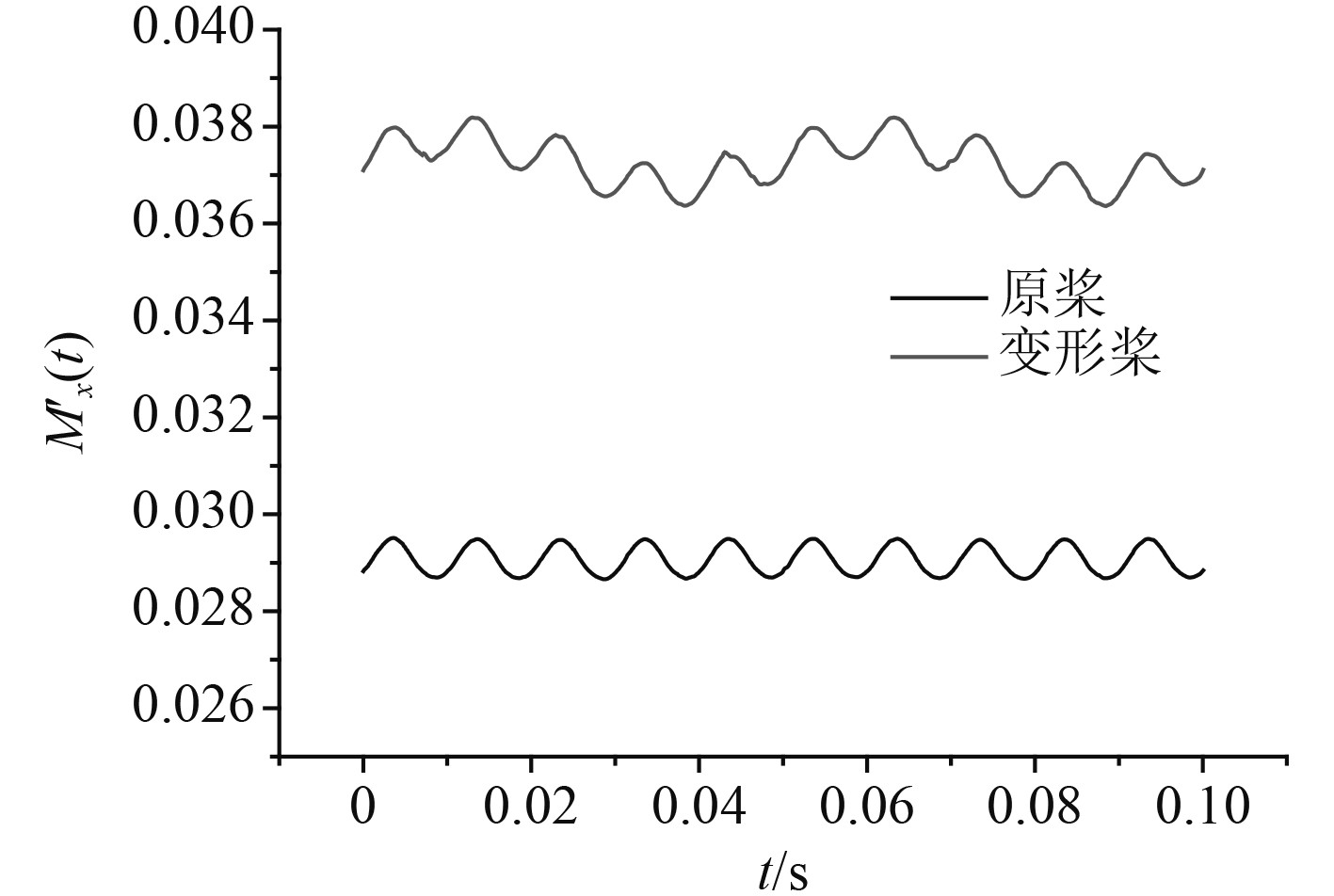
图 15 螺旋桨变形前后轴向非定常力矩对比 Fig. 15 Comparison of unsteady axial moment of pre and post deformed propeller |
|
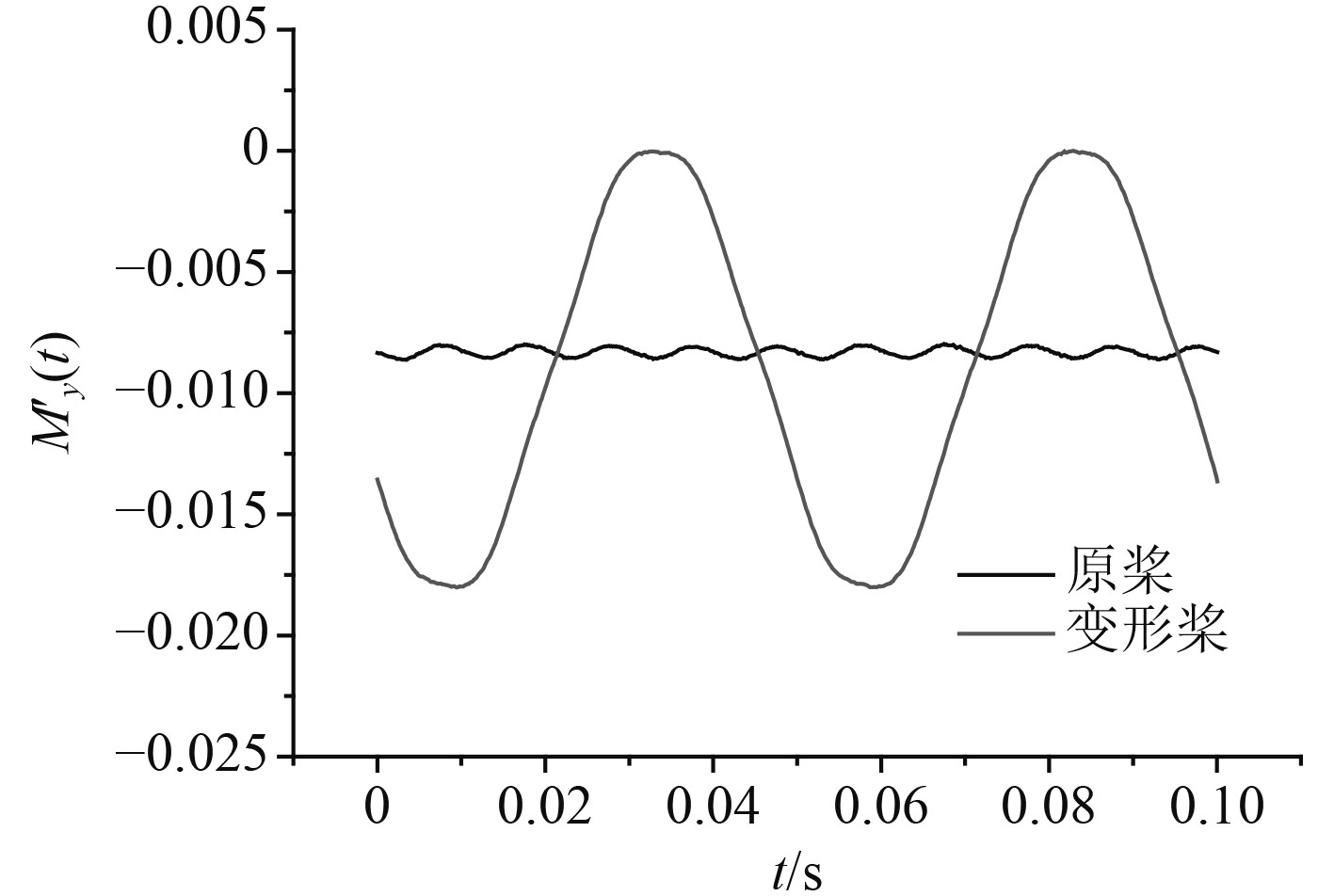
图 16 螺旋桨变形前后横向非定常力矩对比 Fig. 16 Comparison of the unsteady transverse moment of pre and post deformed propeller |
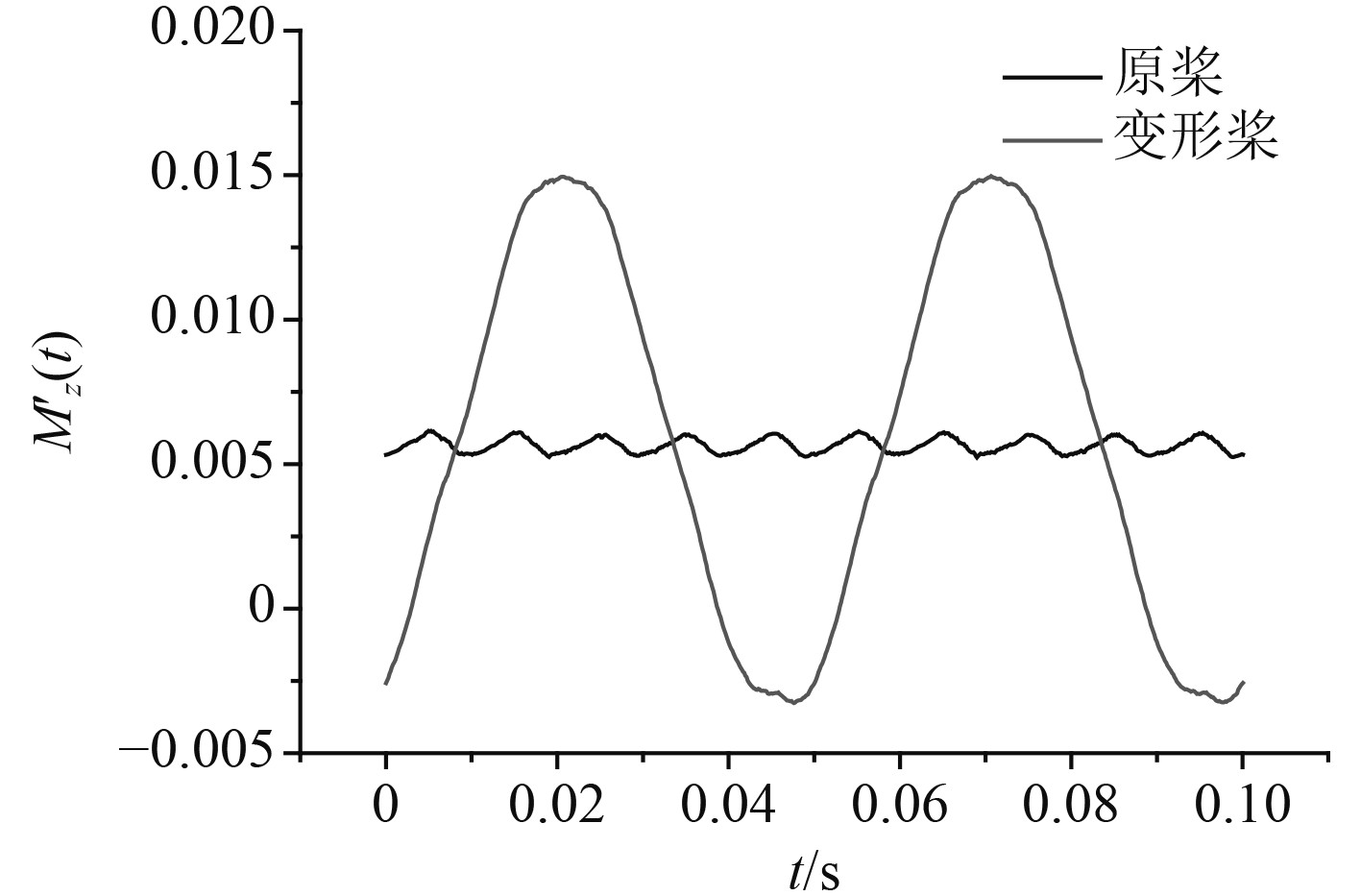
|
图 17 螺旋桨变形前后垂向非定常力矩对比 Fig. 17 Comparison of vertical unsteady moments pre and post deformed propeller |
|
|
表 3 非定常力对比 Tab.3 Comparison of unsteady forces |
|
|
表 4 非定常力矩对比 Tab.4 Comparison of unsteady moments |
从图12~图17和表3~表4可以看出,螺旋桨受损变形前,各方向的非定常力(力矩)均体现出了明显的叶频特性,非定常力幅值主要集中在1阶叶频处,轴频幅值基本可以忽略不计;在3个方向的非定常力(力矩)中,轴向非定常力的变化幅值最大,横向和垂向非定常力(力矩)的变化幅值是小量。
螺旋桨受损变形后,轴向推力和转矩(轴向非定常力和力矩平均值)比原桨明显增加,增加约40%左右,反映出变形桨的负荷明显增大,这与螺旋桨受损变形后实船轴功率测量结果一致。
螺旋桨受损变形后,3个方向的非定常力(力矩)变化幅值与原桨相比明显增大,从频域分析结果可以看出,变形后各方向非定常力(力矩)在叶频处的幅值与原桨基本相当,而轴频处的幅值增量很大。
轴向非定常力(力矩)的变化幅值比原桨增大1倍左右,通过频域分析结果可以看出,变形桨1阶轴频轴向轴承力幅值与原桨1阶叶频轴向轴承力幅值相当,导致变形桨轴向轴承力总的变化幅值增大1倍左右。
受损变形后横向和垂向非定常力(力矩)脉动幅值比原桨高很多,主要是因为轴频轴承力幅值大幅增加,横向和垂向非定常力轴频幅值比损坏前增加70倍左右,横向和垂向非定常力矩轴频幅值比损坏前的增加了300倍左右。受损变形后,横向和垂向轴承力脉动幅值甚至远大于原桨轴向轴承力脉动幅值,横向和垂向非定常力脉动幅值达到了原桨轴向非定常力脉动幅值的6倍左右,横向和垂向非定常力矩脉动幅值达到了原桨轴向力矩脉动幅值的20多倍。受损变形后,螺旋桨横向和垂向轴承力幅值也明显大于轴向轴承力幅值,说明变形前后,引起螺旋桨振动的主要因素和横向和垂向轴频轴承力。
该桨变形后,螺旋桨轴承力大幅增加,必然会引起船体振动加剧,实船振动测量结果也证实了这一点。
3.2 脉动压力为了便于表示将所得到的结果进行无因次化,即
| $P_i^\prime \left( t \right) = \frac{{{P_i}}}{{{\rm{\rho}} {n^2}{D^2}}}\text{。}$ |
式中:
将各监测点压力时域变化值进行Fourier分析,得到各监测点脉动压力在各频率处的幅值。原桨脉动压力体现出明显叶频特性,能量主要集中在1阶叶频,脉动压力轴频幅值可以忽略,受损变形后,螺旋桨脉动压力不仅有叶频成分,还有轴频成分,表5为原桨和变形桨在各测点1阶叶频脉动压力幅值的比较结果。通过比较可以看出,变形后叶频脉动压力幅值与原桨基本相当。
|
|
表 5 距桨叶梢0.1D平面处叶频脉动压力 Tab.5 Fluctuating pressure of blade frequency at 0.1D plane from blade tip |
受损变形桨在各监测点的轴频和2阶轴频脉动压力幅值如表6所示。结果显示,变形桨轴频和2阶轴频脉动压力幅值与原桨叶频脉动压力幅值相比是小量。因此在不考虑空化影响的条件下,该桨的受损变形对脉动压力的影响不如对轴承力的影响明显。
|
|
表 6 变形桨各测点轴频脉动压力 Tab.6 Axial frequency fluctuating pressure of each measuring point of deformed propeller |
从变形前后螺旋桨轴承力和脉动压力的变化情况来看,轴承力大幅增加,而且能量集中在横向和垂向轴频轴承力上,脉动压力增幅较小,因此该桨变形后,船体振动加剧主要是螺旋桨轴承力剧烈增加所导致的。
4 结 语在对螺旋桨变形前后进行伴流场下非定常力计算之后发现:
1)螺旋桨在梢部发生变形后,螺距变大,所产生的推力增大,且变化幅度较大,因为螺旋桨的推力主要依靠桨叶0.7R以上部分来提供。
2)在此变形量基础上引起轴承力脉动幅值增大,且轴频特性明显,轴频处幅值增大,从而引起的振动较之前增加较大。
3)在此变形量基础上引起的脉动压力在时域上的大小以及波动幅度与原桨相差不大。
4)螺旋桨实际加工中也存在着误差,根据本文研究,工程中一定要避免梢部变形引起的螺距变化,其相关数据要符合规范要求,而且在螺旋桨的维修中要小心注意,避免类似事故发生。
| [1] |
孙自力. 船舶用螺旋桨原理及修理[M]. 哈尔滨: 哈尔滨工程大学出版社, 2009.
|
| [2] |
何友声, 王国强. 螺旋桨激振力[M]. 上海: 上海交通大学出版社, 1987.
|
| [3] |
黄胜, 王超, 王诗洋, 等. 不同湍流模型在螺旋桨水动力性能计算中的应用与比较[J]. 哈尔滨工程大学学报, 2009, 30(5): 55-58. HUANG Sheng, WANG Chao, WANG Shiyang, et al. Application and comparison of different turbulence models in propeller hydrodynamic performance calculation[J]. Journal of Harbin Engineering University, 2009, 30(5): 55-58. |
| [4] |
刘登成. 伴流中螺旋桨非定常力黏性数值方法研究[C]// 第二十三届全国水动力学研讨会暨第十届全国水动力学学术会议, 2011. LIU Dengcheng. Numerical method research on unsteady force viscosity of propeller in wake flow[C]// 23rd National Symposium on Hydrodynamics and 10th National Symposium on Hydrodynamics, 2011. |
| [5] |
丁举. 桨模加工误差影响分析[C]// 船舶力学学术会议, 2007. DING Ju. Analysis of the influence of the machining error of the propeller mould[C]// Academic Conference on ship mechanics, 2007. |
| [6] |
王福军. 计算流体动力学分析-CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004.
|
| [7] |
李明, 李季高. STAR-CCM+与流场计算[M]. 北京: 机械工业出版社, 2001.
|
| [8] |
盛振邦, 刘应中. 船舶原理[M]. 上海: 上海交通大学出版社, 2004.
|
| [9] |
张凯奇, 叶金铭, 于安斌. 不均匀进流场下螺旋桨非定常力的数值模拟[J]. 舰船科学技术, 2018, 40(3): 33-38. ZHANG Kaiqi, YE Jinming, YU Anbin. Numerical simulation of propeller unsteady force under nonuniform inflow field[J]. Ship Science and Technology, 2018, 40(3): 33-38. |
 2021, Vol. 43
2021, Vol. 43
