舰船科学技术  2021, Vol. 43 Issue (9): 37-43    DOI: 10.3404/j.issn.1672-7649.2021.09.007   PDF    
引用本文
马清勇, 田阿利, 赵元帅, 傅梓轩, 姚鹏. 基于Box-Behnken响应面法的SPS烟囱结构设计优化. 舰船科学技术, 2021, 43(9): 37-43  
MA Qing-yong, TIAN A-li,  ZHAO Yuan-shuai, FU Zi-xuan, YAO Peng. Structural design of SPS chimney and optimization of Box-Behnken response surface method. Ship Science and Technology, 2021, 43(9): 37-43  
基于Box-Behnken响应面法的SPS烟囱结构设计优化
马清勇, 田阿利, 赵元帅, 傅梓轩, 姚鹏     
江苏科技大学 船舶与海洋工程学院，江苏 镇江 212000
收稿日期: 2020-05-13.
基金项目: 国家自然科学基金资助项目(51109101，51509115)；高技术船舶科研项目(K24367)
作者简介: 马清勇(1992-)，男，硕士研究生，主要从事船舶结构力学性能研究
摘要: 为实现舰船轻量化设计，且具备更优良的力学性能，采用钢聚氨酯夹层板（Steel-Polyurethane Sandwich plate，SPS）结构替代传统钢制加筋板，形成新型烟囱结构设计方案，并基于Box-Behnken响应面法开展SPS烟囱结构的优化。以烟囱结构位移和等效应力作为优化目标，结构尺寸和总重量为约束条件，建立优化模型，得到优化后的SPS烟囱结构设计方案，并采用有限元法，对优化前后的方案进行仿真计算；对优化目标进行分析对比，验证了优化结果的有效性和准确性。结果表明，优化后适用的SPS烟囱结构，在减重13.16%的情况下，位移减小19.50%，应力降低31.96%，说明采用响应面法对SPS烟囱实现多目标优化可行，且优化效果明显。
关键词: SPS烟囱     替代设计     结构参数优化     响应面法    
Structural design of SPS chimney and optimization of Box-Behnken response surface method
MA Qing-yong, TIAN A-li,  ZHAO Yuan-shuai, FU Zi-xuan, YAO Peng     
School of Naval Architecture and Ocean Engineering, Jiangsu University of Science and Technology, Zhenjiang 212000, China
Abstract: In order to realize the lightweight design of the ship and have better mechanical properties, a steel-polyurethane sandwich plate (SPS) structure are used instead of the traditional steel stiffened plate to form a new chimney structure design scheme, and based on Box -Behnken response surface method for optimization of SPS chimney structure. Taking the displacement and equivalent stress of the chimney structure as the optimization target, the structure size and the total weight as the constraint conditions, an optimization model was established, and the optimized SPS chimney structure design plan was obtained; and the finite element method are used to simulate the calculation before and after the optimization. The comparison and analysis of the optimization goals verify the validity and accuracy of the optimization results. The results show that the optimized SPS chimney structure has a displacement reduction of 19.50 % and a stress reduction of 31.96% with a weight reduction of 13.16%, which indicates that it is feasible to achieve multi-objective optimization of the SPS chimney by response surface method, and the optimization effect is obvious.
Key words: SPS chimney     structural parameter optimization     response surface method     alternative design    
0 引　言

轻量化船舶结构设计已成为目前船舶设计建造追求的目标。钢聚氨酯夹层板结构因其具有重量轻、比强度高、比刚度大、耐疲劳性和可减少焊接施工等优点，广泛应用于当代军事、航空航天、桥梁工程、能源工程、船舶与海洋工程等领域[1]。由于夹层板结构设计变量，相关约束较多，选取合理、高效的优化设计方法，对提高复合材料夹层板结构的设计能效有重要意义。

响应面法是一种采用数学建模和试验设计相结合的优化方法，具有高效率、高精度、较少试验次数、显性表述设计变量和响应值之间影响等优点，得到了广泛的应用[2-5]。鲍诺[2]将响应面和优化方法相结合，以飞机基准模型作为算例，验证了响应面和优化方法相结合在结构分析中的有效性。郑彬[3]将工作台作为结构优化研究对象，对主要结构参数进行Box-Behnken试验设计，采用优化算法对响应面模型进行优化，确定了最佳优化方案。王萌[4]采用响应面法建立了目标函数与设计变量之间的非线性关系，将整车的操纵性、内部空间、车身质量进行优化，实现了减重的同时操纵性的改善。

本文为实现烟囱结构轻量化的同时具有更优良力学性能的目标，基于重量相当的原则，对传统钢加筋板烟囱结构进行钢聚氨酯夹层板结构初步替代设计，采用精度高、设计试验次数较少的Box-Behnken响应面法开展SPS烟囱结构的优化，以结构位移和等效应力为优化目标，结构上下面板、芯层、支撑高度和厚度，总重量为约束条件，建立关于结构优化目标的2阶响应面优化模型，得到优化后的SPS烟囱结构设计方案，并利用有限元方法，对原钢质烟囱结构，替代设计结构和优化后的结构进行仿真计算，对优化目标进行详细对比，验证了优化结果的有效性。优化结果可为烟囱及船体结构轻量化设计，提升结构力学性能提供参考。

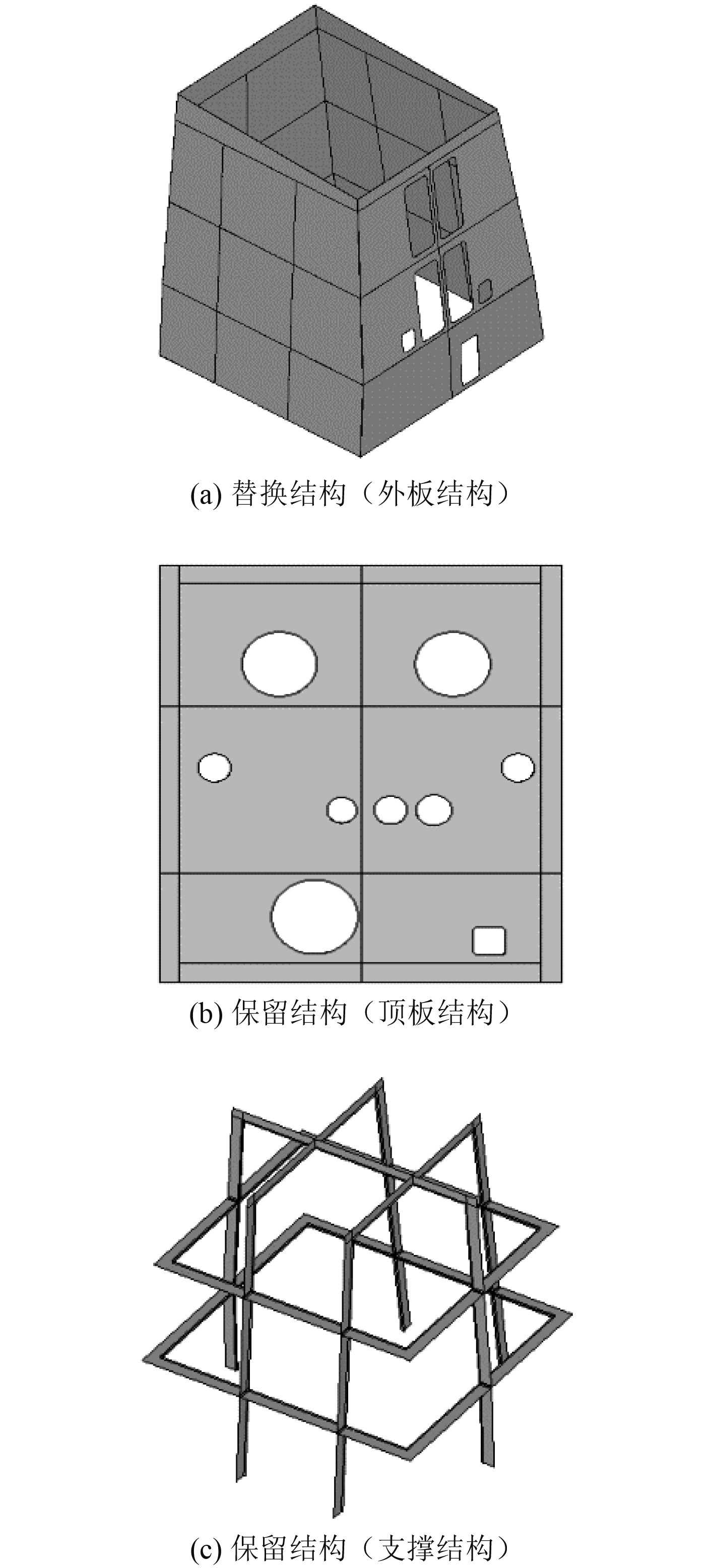
1 有限元分析 1.1 SPS烟囱设计方案与有限元模型

采用钢/聚氨酯夹层板替换钢加筋板结构，示意图如图1所示。以158 000 DWT散货船原钢制烟囱为替代目标，钢制烟囱为加筋板架构成，结构由顶板、内部加强支撑、外板组成，具体结构图和主要尺寸如图2和表1所示。SPS烟囱结构替代设计方案为保留钢质烟囱结构的顶板结构和内部支撑结构，去掉外板结构上的角钢，将外板结构初步采用符合SPS结构建造要求的钢/聚氨酯夹层板进行替换，夹层板尺寸为上下面板厚度均为3 mm，芯层厚度为15 mm，钢制烟囱外板厚度为7 mm，顶板厚度为8 mm，顶板加强角钢尺寸125 mm×80 mm×7 mm，支撑结构T型材尺寸400 mm×120 mm×7 mm，具体的替换和保留结构如图3所示。

图 1 夹层板替换钢加筋板结构示意图 Fig. 1 Schematic diagram of the structure of the steel plate replaced by the sandwich plate

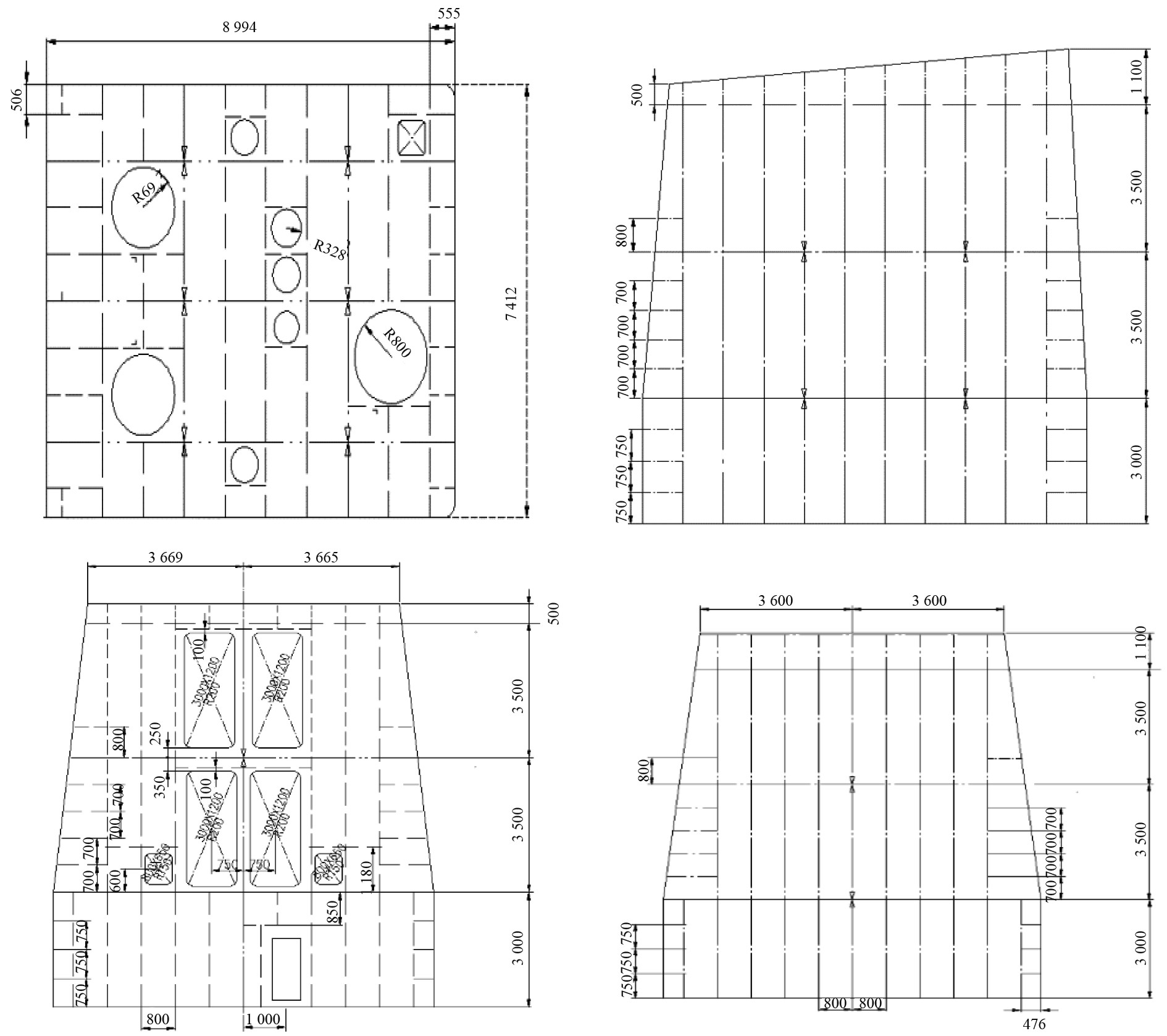
图 2 钢质烟囱结构详细尺寸图 Fig. 2 Detailed dimensions of steel chimney structure

表 1 钢质烟囱结构主要尺寸图 Tab.1 Main dimensions of steel chimney structure

图 3 SPS烟囱替换和保留结构图 Fig. 3 SPS chimney replacement and retention structure diagram

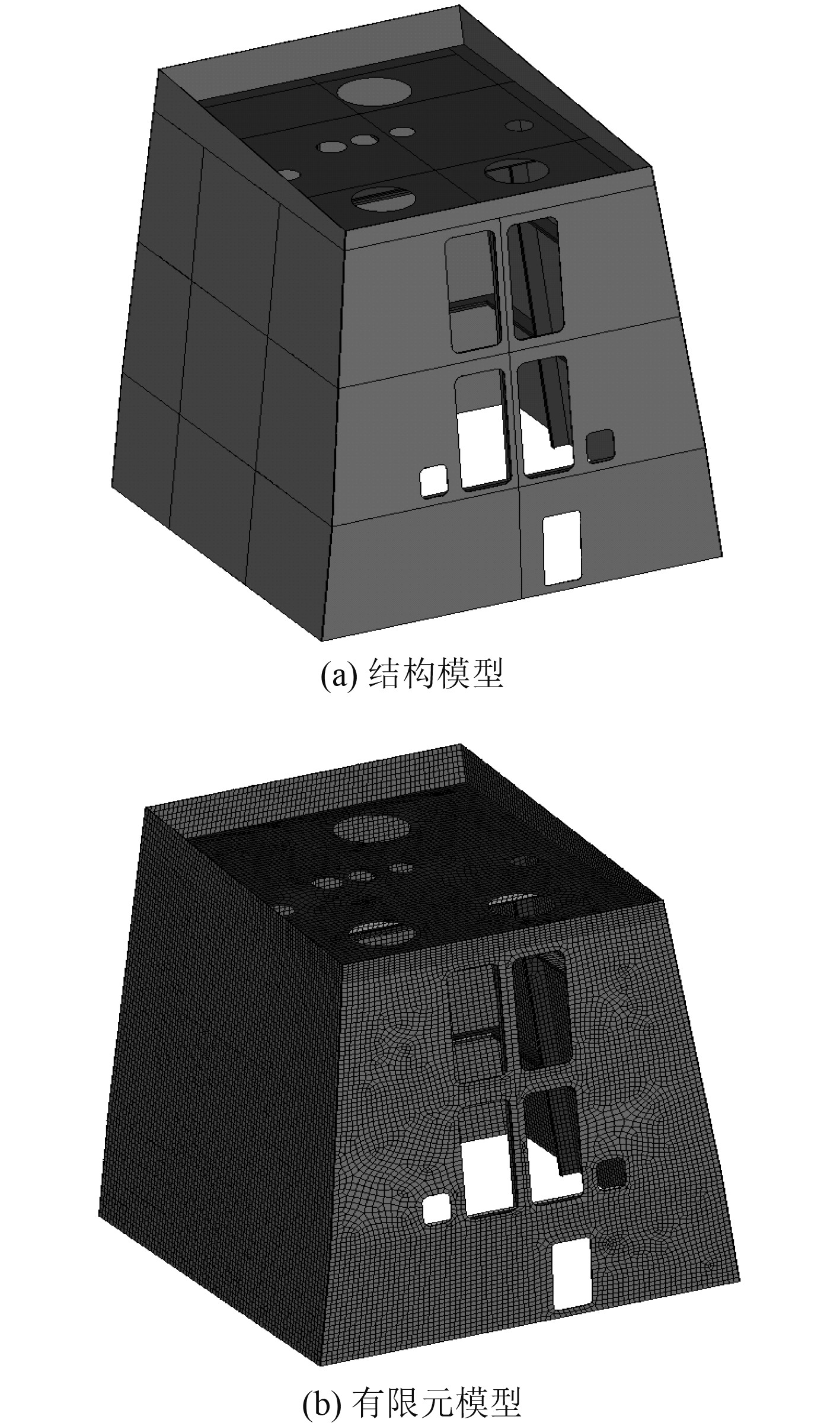
根据《钢夹层板材料船舶结构建造指南》的要求进行建模，对烟囱的底部四边施加固支约束，设计载荷为自重和风载荷共同作用的组合载荷，风载荷值由文献[5]提供的公式求得，大小为238.2 kN，夹层板面板、顶板和强构件都采用AH36钢，芯层材料为聚氨酯，材料属性和有限元模型如表2和图4所示。

表 2 夹层板材料属性表 Tab.2 Material Properties Table of Sandwich Panel

图 4 SPS烟囱模型图 Fig. 4 SPS chimney model diagram
2 基于响应面法的SPS烟囱优化过程 2.1 响应面模型的构建

依据文献[6]提供的构建响应面模型的方法，利用响应面2阶多项式进行模型的表述：

$y(x) = {a_0} + \sum\nolimits_{i = 1}^n {{a_i}{x_i} + \sum\nolimits_{i = 1}^n {{b_i}} } x_i^2 + \sum\nolimits_{j = 2}^n {\sum\nolimits_{i = 1}^{j - 1} {{c_i}{x_i}{x_j}} } \;\;{\text{。}}$

式中： $ {y}\left({x}\right) $ 为目标值； $ {{x}}_{{i}} $ ， $ {{x}}_{{j}} $ 为设计变量，i=1，2，……，k； $ {a}_{0} $ ， $ {a}_{i} $ ， $ {b}_{i} $ ， $ {c}_{i} $ 为待定系数。

2.1.1 设计变量的确定

考虑SPS烟囱结构的结构形式和钢/聚氨酯夹层板的结构特点，在其他因素不变时，选取夹层板的上面板厚度h1、芯层厚度h2、下面板厚度h3、支撑腹板高度h4、支撑腹板厚度h5、支撑面板厚度h6为设计变量。

2.1.2 约束条件和目标函数

为了同时实现钢制烟囱结构轻量化和提升结构力学性能的目标，SPS烟囱结构的重量要小于原钢制烟囱结构的重量，结构位移和等效应力要小于原钢制烟囱结构最大位移和等效应力值，设结构位移为D（x），结构等效应力为S（x），单位分别为mm和MPa，结构重量为G，单位为kg，根据优化目标和约束条件，建立SPS烟囱结构的优化数学模型如下：

$ \begin{array}{l} \min (D(x)\;\;\;{\rm{ }}S(x))\;\;,\\ C\;T\left\{ \begin{array}{l} D(x) \leqslant {D^{'}}(x)\;\;, \\ S(x) \leqslant {S^{'}}(x)\;\;, \\ {h_b} \leqslant {h_a} \leqslant {h_t}\;\;, \\ G \leqslant \bar G \;\;{\text{。}}\end{array} \right. \end{array}$

式中： $ {{D}}^{{'}}\left({x}\right) $ 为替代目标原钢制烟囱结构最大位移； $ {S}^{{'}}\left(x\right) $ 为替代目标原钢制烟囱结构最大等效应力； $ {{h}}_{{t}} $ ， $ {{h}}_{{b}} $ 分别为设计变量的上下限； $ {{h}}_{{a}} $ 为设计变量，a=1，2，3，4，5，6； $ \bar G $ 为结构重量的最大值。

2.1.3 构建模型试验设计

有多种试验设计的方法，考虑试验设计的经济性，结构优化分析的高效率和适用性，采用Design-Export优化分析软件中拟合精度较高的Box-Behnken Design（BBD）[6]试验设计方法进行试验设计与分析，BBD试验设计中每个选取的设计变量有3个水平，分别用−1，0，+1表示，结合结构轻量化和SPS结构建造指南的要求，SPS烟囱设计变量的取值范围如表3所示。

表 3 设计变量取值范围 Tab.3 Design variable value range

依据不同设计变量的范围选取合适的试验样本点，得出54组试验方案。使用Ansys对各组方案进行有限元计算，得到SPS烟囱结构位移和应力结果，采用数学公式计算结构重量，部分计算结果如表4所示。

表 4 夹层板烟囱的BBD设计表 Tab.4 BBD design table of sandwich panel chimney
2.2 构建模型的检验与分析

为简化计算和提高模型的稳定性[7]，可去除影响较小的1，2阶设计变量项，利用响应面法，构建D（x）和S（x）的2阶响应面优化模型形式如下：

$\begin{aligned} D(x) = & {\rm{4}}{\rm{.34}} - 0.{\rm{20}}{h_1} - 0.{\rm{12}}{h_2} - 0.{\rm{15}}{h_3} - 0.{\rm{68}}{h_4} - {\rm{0}}{\rm{.75}}{h_{\rm{5}}} -\\ & {\rm{0}}{\rm{.42}}{h_{\rm{6}}} + {\rm{0}}{\rm{.032}}{h_1}{h_{\rm{3}}}{\rm{ + 0}}{\rm{.033}}{h_1}{h_{\rm{4}}}{\rm{ + 0}}{\rm{.029}}{h_1}{h_{\rm{5}}} \;+\\ &{\rm{ 0}}{\rm{.02}}{h_1}{h_{\rm{6}}} + {\rm{ 0}}{\rm{.025}}{h_{\rm{2}}}{h_{\rm{4}}}{\rm{ + 0}}{\rm{.028}}{h_{\rm{2}}}{h_{\rm{5}}}{\rm{ + 0}}{\rm{.019}}{h_{\rm{2}}}{h_{\rm{6}}}+\\ &{\rm{ 0}}{\rm{.023}}{h_{\rm{3}}}{h_{\rm{4}}} + {\rm{ 0}}{\rm{.012}}{h_{\rm{3}}}{h_{\rm{5}}} + {\rm{ 0}}{\rm{.013}}{h_{\rm{3}}}{h_{\rm{6}}}{\rm{ + }}0.0{\rm{91}}{h_{\rm{4}}}{h_{\rm{5}}}{\rm{ + }} \\ & {\rm{ 0}}{\rm{.078}}{h_{\rm{4}}}{h_{\rm{6}}}+ {\rm{ 0}}{\rm{.15}}{h_{\rm{5}}}{h_{\rm{6}}} + 0.0{\rm{23}}{h_1}^2 +0.0{\rm{14}}{h_3}^2 +\\ & 0.0{\rm{65}}{h_4}^2 + \;0.{\rm{16}}{h_{\rm{5}}}^2 + 0.0{\rm{48}}{h_{\rm{6}}}^2\;\;, \\ S(x) = & {\rm{90}}.75 - 1.6{\rm{7}}{h_1} - 2.32{h_2} - 1.69{h_3} - 8.47{h_4} -\\ & 18.48{h_5} - 0.51{h_6} + 0.028{h_1}{h_2} - {\rm{0}}{\rm{.33}}{h_1}{h_3}+{\rm{ 0}}{\rm{.2}}{h_1}{h_4}+\\ &{\rm{ 0}}{\rm{.4}}{h_1}{h_{\rm{5}}} \; {\rm{ }} - {\rm{0}}{\rm{.47}}{h_1}{h_{\rm{6}}} + \;{\rm{2}}{\rm{.48}}{h_{\rm{2}}}{h_3} - 0.{\rm{84}}{h_{\rm{2}}}{h_{\rm{5}}} +\\ & 0.{\rm{24}}{h_2}{h_{\rm{6}}} + 0.{\rm{17}}{h_{\rm{3}}}{h_4} - {\rm{2}}{\rm{.3}}{h_3}{h_{\rm{5}}} - {\rm{0}}{\rm{.21}}{h_3}{h_{\rm{6}}} +\\ & {\rm{1}}{\rm{.53}}{h_{\rm{4}}}{h_{\rm{5}}}{\rm{ + 0}}{\rm{.19}}{h_{\rm{4}}}{h_{\rm{6}}} + {\rm{ 3}}{\rm{.65}}{h_{\rm{5}}}{h_{\rm{6}}} -0.{\rm{40}}{h_1}^2 +\\ & 0.{\rm{77}}{h_2}^2 + 0.{\rm{87}}{h_3}^2 + 0.4{\rm{0}}{h_4}^2 + {\rm{4}}.{\rm{99}}{h_{\rm{5}}}^2+{\rm{ 2}}{\rm{.92}}{h_{\rm{6}}}^2\;\;{\text{。}} \end{aligned} $

为了检验优化模型的显著性和适应度，是否能有效反映目标与设计变量之间的关系，采用方差分析和模型决定系数对D（x）和S（x）进行检验，模型的方差分析如表5和表6所示。F值为优化模型的均方与优化模型误差均方的比值，P值为与F值相关的重要检验指标，是检验优化模型可信度的指标，通常小于0.05时，就表明优化模型显著[6]。当采用Design-Export软件进行优化分析时，构建优化模型的P值和F值由软件分析得出。由分析结果可知，D（x）和S（x）的F值分别为2565.68和49.98，且对应的 $ P<0.000\;1 $ ，远小于0.05，初步表明优化模型具有良好的显著性，之后要通过R2（决定系数）进行进一步检验模型的拟合优度。R2值越趋近于1表明模型与真实情况越相符。当变量增加后，R2值也会增加，不能准确反映变量对模型的真实影响，因此需要使用 $ {{R}}_{{adj}}^{{2}} $ （校正决定系数）进行误差分析。F值，R2与 $ {{R}}_{{adj}}^{{2}} $ 的公式如下：

表 5 优化模型方差检验 Tab.5 Optimization model variance test

表 6 模型方差数值分析 Tab.6 Numerical analysis of model variance
$ \begin{array}{l} F = \dfrac{{{{S{S_R}} / k}}}{{{{S{S_E}} / {(n - k - 1)}}}} = \dfrac{{M{S_R}}}{{M{S_E}}}\;\;,\\ \!{R^2} = 1 - \dfrac{{\displaystyle\sum\nolimits_{i = 1}^n {{{\left( {{y_i} - {{\hat y}_i}} \right)}^2}} }}{{\displaystyle\sum\nolimits_{i = 1}^n {{{({y_i} - {{\bar y}_{}})}^2}} }}\;\;,\\ \!R_{adj}^{\rm{2}} = 1 - \dfrac{{n - 1\displaystyle\sum\nolimits_{i = 1}^n {{{\left( {{y_i} - {{\hat y}_i}} \right)}^2}} }}{{n - k - 1\displaystyle\sum\nolimits_{i = 1}^n {{{({y_i} - \bar y)}^2}} }}\;\;{\text{。}} \end{array}$

式中：n为样本量；k为模型各阶变量总数目也可表示为自由度； $ {y}_{i} $ 为试验值； $ \bar y $ 为试验值的平均值； $ {\widehat{y}}_{i} $ 为优化模型得到的响应值。

校正决定系数 $ {R}_{adj}^{2} $ 与预测决定系数 $ {R}_{pred}^{2} $ 值之间越接近，同时两者越接近1，说明优化模型拟合的越合理[8]。模型决定系数分析见表7。可知，2个模型的 $ {R}^{2} $ 值分别为0.9996和0.9811，且 $ {R}_{adj}^{2} $ 与 $ {R}_{pred}^{2} $ 的值很接近，说明2个模型具有较高的拟合度。

表 7 模型决定系数分析 Tab.7 Model determination coefficient analysis

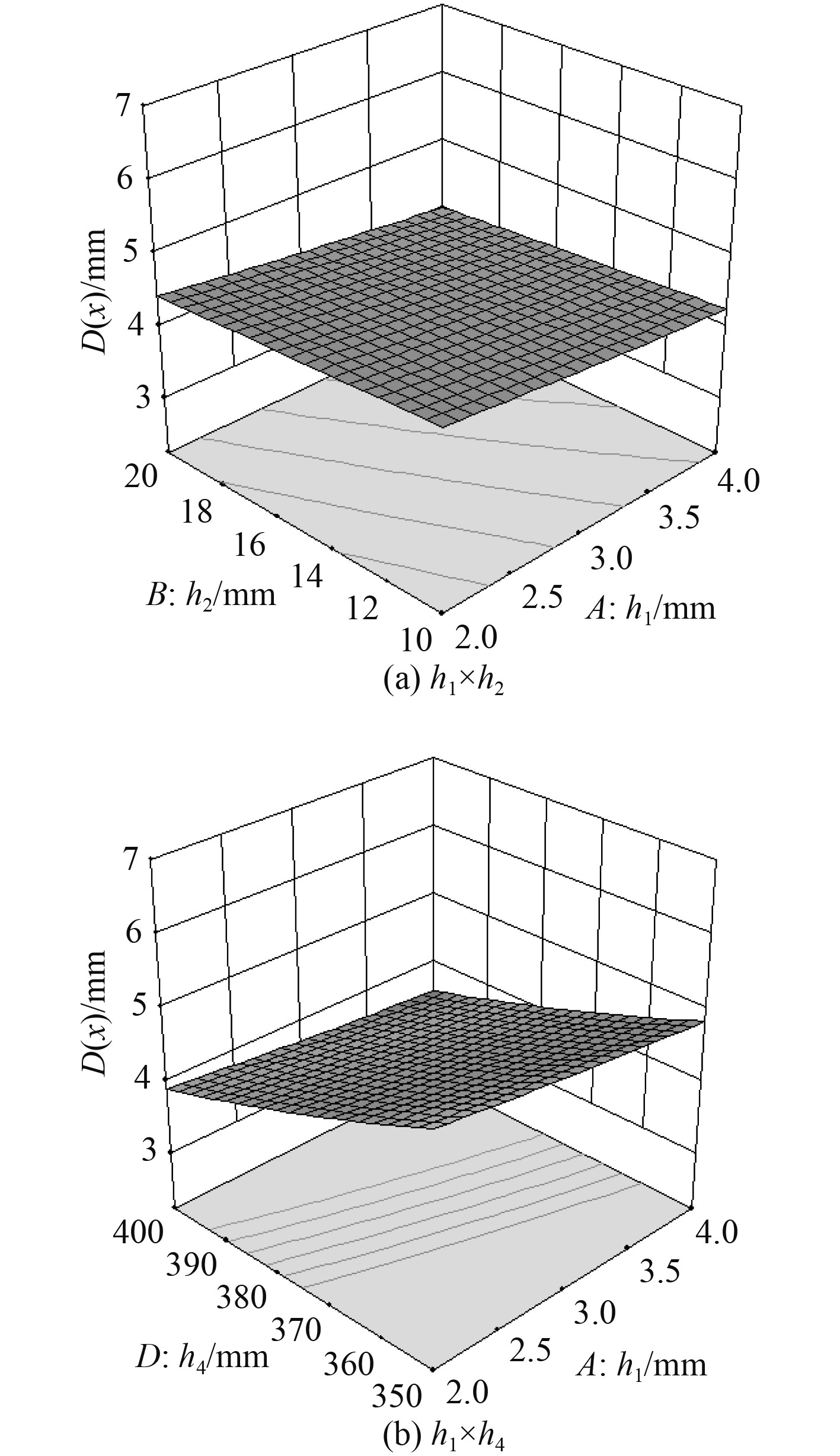
图5为选取的有代表性的设计变量对烟囱结构位移相互作用的响应曲面图，在其他因素不变的情况下，分析其中2个变量相互作用对结构位移的影响。由图5（a）可知，随着h1增加，结构位移缓慢减小，增大h2结构位移的变化趋势相同，表明当其他因素不变时，增大夹层板上面板厚度h1和芯层厚度h2，结构的抗变形能力增强。由图5（b）可知，随着h4的增加，结构位移显著减小，表明支撑的高度对结构的位移有显著影响。

图 5 设计变量对结构位移相互影响的响应曲面 Fig. 5 Response surface of design variables interacting with structural displacement

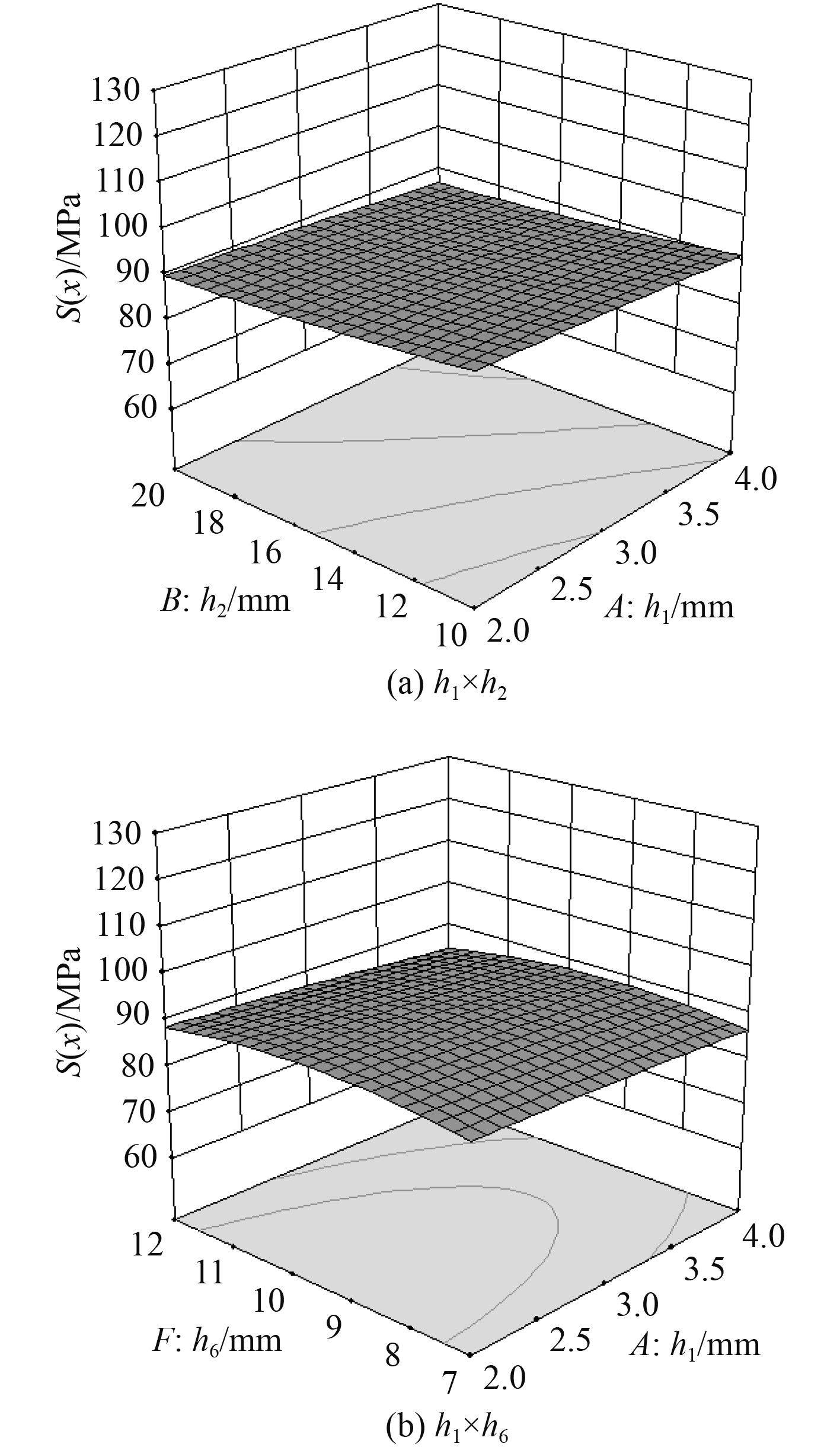
图6为设计变量对烟囱结构应力相互作用的响应曲面图，在其他因素不变的情况下，分析其中2个变量相互作用对结构应力的影响。由图6（a）可知，随着h1增大，结构应力缓慢减小，同样结构应力随h2的增大也缓慢减小，表明当其他因素不变时，增大夹层板面板厚度h1，芯层厚度h2，烟囱结构承受外力的能力增强，结构等效应力减小。由图6（b）可知，随支撑构件高度h4增加，结构等效应力显著减小。这是因为随着h4的增加，提高了整体结构抵抗外力的能力。由等高线图可知，曲线呈椭圆形，表明两者相互影响较为明显[6]。由不同设计变量对结构位移和应力影响的对比分析可知，相对于夹层板面板和芯层厚度，支撑结构的腹板高度和面板厚度对烟囱结构位移和应力的影响较大。

图 6 设计变量对结构应力相互影响的响应曲面 Fig. 6 Response surface of design variables interacting with structural stress
3 SPS烟囱优化结果分析 3.1 SPS烟囱优化结果

由上述优化模型和分析方法对SPS烟囱结构进行优化后，依据结构轻量化和力学性能改变的需求，得到SPS烟囱结构在较好满足优化目标时各设计变量的值如表8所示，将由优化模型分析得到的最优设计变量进行仿真计算的值与优化模型预测值进行对比，结构位移的仿真值与预测值误差为0.91%，等效应力的仿真值与预测值的误差为2.77%，因此建立的优化模型能够对SPS烟囱结构进行优化。

表 8 仿真计算值与优化模型预测值对比 Tab.8 Comparison of simulation calculated value and predicted value of optimized model
3.2 优化结果分析

将原钢制烟囱，SPS替代烟囱、进行结构优化后的SPS烟囱、进行尺寸调整的适用SPS烟囱的仿真结果进行对比。由表9可知，与原钢制烟囱相比，SPS替代烟囱位移增加2.75%，应力降低5.79%，重量减轻2.61%，SPS优化烟囱位移减少18.25%，应力降低30.98%，重量减轻12.39%，考虑板厚的加工工艺，对SPS优化烟囱得到的各变量的尺寸进行合理调整，调整后的SPS适用烟囱位移减少19.50%，应力降低31.96%，烟囱减重13.16%。优化后的2种烟囱与SPS替代烟囱相比，位移分别减少20.44%和21.65%，应力分别降低26.74%和27.77%，重量分别减轻10.04%和10.83%。

表 9 4种烟囱结构结果对比 Tab.9 Comparison of four chimney structure results

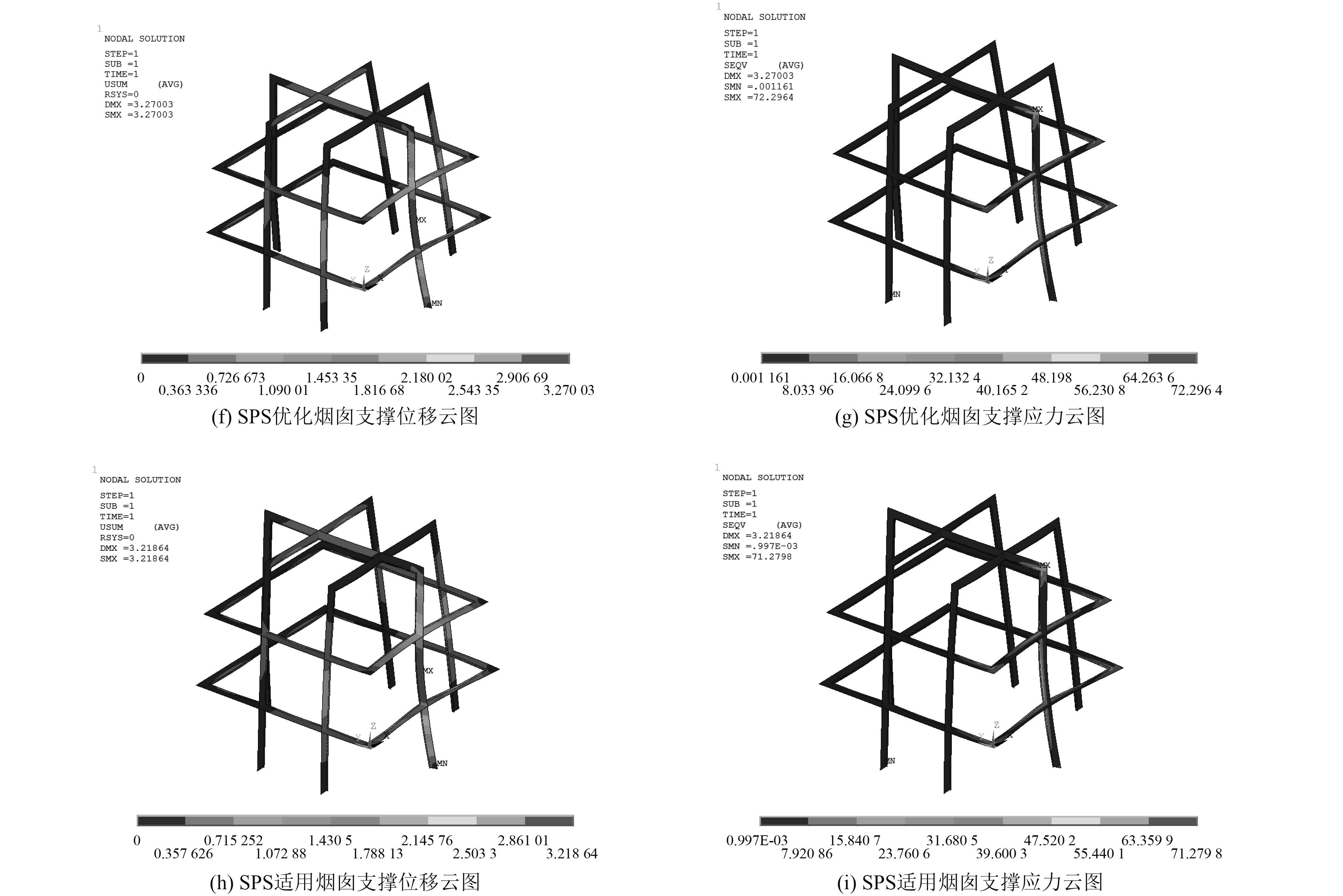
图7为4种烟囱结构的有限元分析结果云图，取支撑结构进行对比，顶板和外板结构的分析方法相同。由图7可知，4种烟囱结构的最大等效应力出现的位置基本相同，均出现在支撑结构顶部与侧部连接T型材处，支撑结构最大位移出现的位置也基本相同，出现在侧部中心线的中部附近，进行优化后应力和位移都有显著减小，表明结构优化能够在实现烟囱结构轻量化时，有效地提高烟囱结构的力学性能。

图 7


图 7 4种烟囱支撑结构计算云图 Fig. 7 Compute cloud of four chimney support structures
4 结　语

采用Design-expert中的BBD进行试验设计，运用Ansys有限元分析软件对原钢制烟囱，SPS替代烟囱及试验设计方案进行仿真分析，得到原钢制烟囱和全部SPS烟囱结构的位移和应力。采用响应面法将试验设计分析结果进行拟合，得到不同设计变量：夹层板上面板厚度，芯层厚度，下面板厚度，支撑高度和厚度下的结构位移和应力的2阶响应面方程，对比分析结果得到如下结论：

1）在选取的6个设计变量中，支撑结构高度和厚度对SPS烟囱结构位移和应力的影响较大，对支撑结构进行优化能够显著减小SPS烟囱结构位移和应力。

2）对原钢制烟囱进行SPS结构替代设计，将SPS替代设计烟囱进行结构参数优化，得到优化后的结构参数。结果表明：与SPS替代烟囱相比，优化和进行结构尺寸适用性调整后的SPS烟囱位移分别减少20.44%和21.65%，应力分别降低26.74%和27.77%，重量分别减轻10.04%和10.83%，表明优化结果有效，优化方法在烟囱结构力学性能分析中具有适用性。

参考文献
[1]
尚高峰. 轻量化船舶结构极限强度研究[D]. 北京: 中国舰船研究院, 2011.
SHANG Gaofeng. Research on ultimate strength of lightweight ship structure[D]. Beijing: China Ship Research Institute, 2011.
[2]
鲍诺, 王春洁. 基于响应面法的结构动力学模型修正[J]. 振动与冲击, 2013, 32(16): 54-58.
BAO Nuo, WANG Chun jie. Model updating of structure dynamics based on response surface methodology[J]. Vibration and Shock, 2013, 32(16): 54-58. DOI:10.3969/j.issn.1000-3835.2013.16.010
[3]
郑彬, 张敬东. 基于响应面法的龙门加工中心回转工作台结构优化设计[J]. 机械强度, 2018, 40(5): 1131-1137.
ZHENG Bin, ZHANG Jingdong. Structure optimization design for the rotary worktable of gantry machining center based on response surface methodology[J]. Mechanical Strength, 2018, 40(5): 1131-1137.
[4]
王萌, 张合, 王晓锋. 响应面法复合车身结构优化[J]. 南京理工大学学报, 2017, 41(2): 145-151.
WANG Meng, ZHANG He, WANG Xiao feng. Composite body structure optimization based on response surface approximation method[J]. Journal of Nanjing University of Science and Technology, 2017, 41(2): 145-151.
[5]
汤晶, 王博, 罗瑞锋. 自升式平台风载荷规范计算方法分析研究[J]. 船舶工程, 2016, 38(S1): 35-38.
TANG Jing, WANG Bo, LUO Rui feng. Analysis and research on the calculation method of wind load specification for jack-up platform[J]. Ship Engineering, 2016, 38(S1): 35-38.
[6]
李莉, 张赛, 何强, 等. 响应面法在试验设计与优化中的应用[J]. 实验室研究与探索, 2015, 34(8): 41-45.
LI Li, ZHANG Sai, HE Qiang, et al. Application of response surface methodology in experiment design and optimization[J]. Research and Exploration in Laboratory, 2015, 34(8): 41-45. DOI:10.3969/j.issn.1006-7167.2015.08.011
[7]
余跃. 大变形结构耐撞性分析优化及应用技术研究[D]. 杭州: 浙江大学, 2017.
YU Yue. Research on optimization and application technology of crashworthiness of large deformation structures[D]. Hangzhou: Zhejiang University, 2017.
[8]
黄重阳. 基于响应面法的散货船结构优化设计[D]. 大连: 大连理工大学, 2011.
HUANG Chongyang. Optimization design of bulk carrier structure based on response surface method[D]. Dalian: Dalian University of Technology, 2011.
[9]
王果, 何沁园. 折叠式夹层板面内连接结构优化设计方法研究[J]. 舰船科学技术, 2019, 41(21): 27-36.
WANG Guo, HE Qin yuan. Research on the optimal design method of the internal connection structure of the folded sandwich panel[J]. Ship Science and Technology, 2019, 41(21): 27-36.